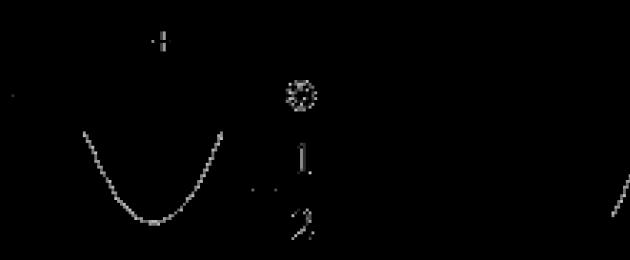
Problem från samlingen av L. A. Kuznetsova

Om problemet kräver en fullständig studie av funktionen f (x) = x 2 4 x 2 - 1 med konstruktionen av dess graf, kommer vi att överväga denna princip i detalj.

För att lösa ett problem av denna typ bör du använda egenskaperna och graferna för grundläggande elementära funktioner. Forskningsalgoritmen inkluderar följande steg:

Att hitta definitionsdomänen

Eftersom forskning bedrivs på definitionsdomänen för funktionen är det nödvändigt att börja med detta steg.

Exempel 1

Det givna exemplet involverar att hitta nollorna i nämnaren för att utesluta dem från ODZ.

4 x 2 - 1 = 0 x = ± 1 2 ⇒ x ∈ - ∞ ; - 1 2 ∪ - 1 2 ; 1 2 ∪ 1 2 ; +∞

Som ett resultat kan du få rötter, logaritmer och så vidare. Sedan kan ODZ sökas efter en rot av en jämn grad av typen g (x) 4 med olikheten g (x) ≥ 0, för logaritmen log a g (x) med olikheten g (x) > 0.

Studera gränserna för ODZ och hitta vertikala asymptoter

Det finns vertikala asymptoter vid gränserna för funktionen, när de ensidiga gränserna vid sådana punkter är oändliga.

Exempel 2

Tänk till exempel att gränspunkterna är lika med x = ± 1 2.

Sedan är det nödvändigt att studera funktionen för att hitta den ensidiga gränsen. Då får vi det: lim x → - 1 2 - 0 f (x) = lim x → - 1 2 - 0 x 2 4 x 2 - 1 = = lim x → - 1 2 - 0 x 2 (2 x - 1 ) (2 x + 1) = 1 4 (- 2) · - 0 = + ∞ lim x → - 1 2 + 0 f (x) = lim x → - 1 2 + 0 x 2 4 x - 1 = = lim x → - 1 2 + 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 2) (+ 0) = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 0) 2 = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 ( + 0 ) 2 = + ∞

Detta visar att de ensidiga gränserna är oändliga, vilket betyder att de räta linjerna x = ± 1 2 är de vertikala asymptoterna i grafen.

Studie av en funktion och om den är jämn eller udda

När villkoret y (- x) = y (x) är uppfyllt anses funktionen vara jämn. Detta tyder på att grafen är placerad symmetriskt med avseende på Oy. När villkoret y (- x) = - y (x) är uppfyllt anses funktionen vara udda. Detta betyder att symmetrin är relativ till koordinaternas ursprung. Om åtminstone en olikhet inte är uppfylld får vi en funktion av allmän form.

Likheten y (- x) = y (x) indikerar att funktionen är jämn. Vid konstruktion är det nödvändigt att ta hänsyn till att det kommer att finnas symmetri med avseende på Oy.

För att lösa olikheten används intervall av ökande och minskande med villkoren f " (x) ≥ 0 respektive f " (x) ≤ 0.

Definition 1

Stationära punkter- det här är punkterna som vänder derivatan till noll.

Kritiska punkter- dessa är interna punkter från definitionsdomänen där derivatan av funktionen är lika med noll eller inte existerar.

När du fattar ett beslut måste följande anmärkningar beaktas:

för befintliga intervall med ökande och minskande olikheter av formen f " (x) > 0, är kritiska punkter inte inkluderade i lösningen;
punkter där funktionen definieras utan en finit derivata måste inkluderas i intervallen för ökande och minskande (till exempel y = x 3, där punkten x = 0 gör funktionen definierad, derivatan har värdet oändligt vid detta punkt, y " = 1 3 x 2 3, y "(0) = 1 0 = ∞, x = 0 ingår i det ökande intervallet);
För att undvika meningsskiljaktigheter rekommenderas att man använder matematisk litteratur som rekommenderas av utbildningsministeriet.

Inkludering av kritiska punkter i intervall av ökande och minskande om de uppfyller funktionens definitionsdomän.

Definition 2

För bestämma intervallen för ökning och minskning av en funktion, är det nödvändigt att hitta:

derivat;
kritiska punkter;
dela upp definitionsdomänen i intervall med hjälp av kritiska punkter;
bestäm tecknet för derivatan på vart och ett av intervallen, där + är en ökning och - är en minskning.

Exempel 3

Hitta derivatan på definitionsdomänen f " (x) = x 2 " (4 x 2 - 1) - x 2 4 x 2 - 1 " (4 x 2 - 1) 2 = - 2 x (4 x 2 - 1) 2 .

Lösning

För att lösa behöver du:

hitta stationära punkter, detta exempel har x = 0;
hitta nollorna i nämnaren, exemplet tar värdet noll vid x = ± 1 2.

Vi placerar punkter på tallinjen för att bestämma derivatan på varje intervall. För att göra detta räcker det att ta vilken punkt som helst från intervallet och utföra en beräkning. Om resultatet är positivt visar vi + på grafen, vilket betyder att funktionen ökar och - betyder att den minskar.

Till exempel f " (- 1) = - 2 · (- 1) 4 - 1 2 - 1 2 = 2 9 > 0, vilket betyder att det första intervallet till vänster har ett +-tecken. Tänk på tallinjen.

Svar:

funktionen ökar med intervallet - ∞; -12 och (-12; 0];
det finns en minskning av intervallet [0; 12) och 12; + ∞ .

I diagrammet, med hjälp av + och -, visas funktionens positivitet och negativitet, och pilarna indikerar minskning och ökning.

Extremumpunkter för en funktion är punkter där funktionen är definierad och genom vilka derivatan byter tecken.

Exempel 4

Om vi betraktar ett exempel där x = 0, så är värdet på funktionen i det lika med f (0) = 0 2 4 · 0 2 - 1 = 0. När tecknet för derivatan ändras från + till - och passerar genom punkten x = 0, anses punkten med koordinater (0; 0) vara den maximala punkten. När tecknet ändras från - till + får vi en minimipoäng.

Konvexitet och konkavitet bestäms genom att lösa olikheter av formen f "" (x) ≥ 0 och f "" (x) ≤ 0. Mindre vanligt används namnet konvexitet ner istället för konvexitet och konvexitet uppåt istället för konvexitet.

Definition 3

För bestämma intervallen för konkavitet och konvexitet nödvändig:

hitta den andra derivatan;
hitta nollorna för den andra derivatan;
dela upp definitionsområdet i intervall med de uppträdande punkterna;
bestämma intervallets tecken.

Exempel 5

Hitta andraderivatan från definitionsdomänen.

Lösning

f "" (x) = - 2 x (4 x 2 - 1) 2 " = = (- 2 x) " (4 x 2 - 1) 2 - - 2 x 4 x 2 - 1 2 " (4 x 2 - 1) 4 = 24 x 2 + 2 (4 x 2 - 1) 3

Vi hittar nollorna för täljaren och nämnaren, där vi i vårt exempel har att nollorna för nämnaren x = ± 1 2

Nu måste du rita punkterna på tallinjen och bestämma tecknet för den andra derivatan från varje intervall. Det förstår vi

Svar:

funktionen är konvex från intervallet - 1 2 ; 12;
funktionen är konkav från intervallen - ∞; - 12 och 12; + ∞ .

Definition 4

Böjningspunkt– detta är en punkt av formen x 0 ; f (x 0). När den har en tangent till grafen för funktionen, när den passerar genom x 0 ändrar funktionen tecken till det motsatta.

Detta är med andra ord en punkt genom vilken andraderivatan passerar och byter tecken, och vid själva punkterna är den lika med noll eller existerar inte. Alla punkter anses vara funktionens domän.

I exemplet var det tydligt att det inte finns några böjningspunkter, eftersom andraderivatan ändrar tecken när den passerar genom punkterna x = ± 1 2. De ingår i sin tur inte i definitionsområdet.

Hitta horisontella och sneda asymptoter

När du definierar en funktion i oändligheten måste du leta efter horisontella och sneda asymptoter.

Definition 5

Sned asymptoter avbildas med räta linjer som ges av ekvationen y = k x + b, där k = lim x → ∞ f (x) x och b = lim x → ∞ f (x) - k x.

För k = 0 och b inte lika med oändlighet, finner vi att den sneda asymptoten blir horisontell.

Med andra ord anses asymptoter vara linjer som grafen för en funktion närmar sig i oändligheten. Detta underlättar snabb konstruktion av en funktionsgraf.

Om det inte finns några asymptoter, men funktionen är definierad vid båda oändligheterna, är det nödvändigt att beräkna gränsen för funktionen vid dessa oändligheter för att förstå hur grafen för funktionen kommer att bete sig.

Exempel 6

Låt oss betrakta det som ett exempel

k = lim x → ∞ f (x) x = lim x → ∞ x 2 4 x 2 - 1 x = 0 b = lim x → ∞ (f (x) - k x) = lim x → ∞ x 2 4 x 2 - 1 = 1 4 ⇒ y = 1 4

är en horisontell asymptot. Efter att ha undersökt funktionen kan du börja konstruera den.

Beräkna värdet av en funktion vid mellanliggande punkter

För att göra grafen mer exakt rekommenderas det att hitta flera funktionsvärden vid mellanliggande punkter.

Exempel 7

Från exemplet vi betraktade är det nödvändigt att hitta funktionens värden vid punkterna x = - 2, x = - 1, x = - 3 4, x = - 1 4. Eftersom funktionen är jämn får vi att värdena sammanfaller med värdena vid dessa punkter, det vill säga vi får x = 2, x = 1, x = 3 4, x = 1 4.

Låt oss skriva och lösa:

F (- 2) = f (2) = 2 2 4 2 2 - 1 = 4 15 ≈ 0, 27 f (- 1) - f (1) = 1 2 4 1 2 - 1 = 1 3 ≈ 0 , 33 f - 3 4 = f 3 4 = 3 4 2 4 3 4 2 - 1 = 9 20 = 0 , 45 f - 1 4 = f 1 4 = 1 4 2 4 1 4 2 - 1 = - 1 12 ≈ - 0,08

För att bestämma maxima och minima för funktionen, böjningspunkter och mellanpunkter är det nödvändigt att konstruera asymptoter. För bekväm beteckning registreras intervall av ökande, minskande, konvexitet och konkavitet. Låt oss titta på bilden nedan.

Det är nödvändigt att rita graflinjer genom de markerade punkterna, vilket gör att du kan närma dig asymptoterna genom att följa pilarna.

Detta avslutar den fullständiga utforskningen av funktionen. Det finns fall av att konstruera några elementära funktioner för vilka geometriska transformationer används.

Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter

När du ritar funktionsdiagram är det användbart att följa följande plan:

1. Hitta definitionsdomänen för funktionen och bestäm eventuella diskontinuitetspunkter.

2. Bestäm om funktionen är jämn eller udda eller ingetdera. Om funktionen är jämn eller udda räcker det att överväga dess värden vid x>0, och sedan symmetriskt med avseende på OY-axeln eller ursprunget för koordinater, återställ det för värdena x<0 .

3. Undersök funktionen för periodicitet. Om funktionen är periodisk räcker det att överväga den på en period.

4. Hitta skärningspunkterna för funktionsgrafen med koordinataxlarna (om möjligt)

5. Gör en studie av funktionen i extremumet och hitta intervallen för ökning och minskning av funktionen.

6. Hitta kurvans böjpunkter och intervallen för konvexitet och konkavitet för funktionen.

7. Hitta asymptoterna i grafen för funktionen.

8. Konstruera en graf över funktionen med hjälp av resultaten från steg 1-7. Ibland hittas flera ytterligare punkter för större noggrannhet; deras koordinater beräknas med hjälp av ekvationen för kurvan.

Exempel. Utforska funktion y=x 3-3x och bygga en graf.

1) Funktionen definieras på intervallet (-∞; +∞). Det finns inga brytpunkter.

2) Funktionen är udda, eftersom f(-x) = -x3 -3(-x) = -x3 +3x = -f(x), därför är det symmetriskt om ursprunget.

3) Funktionen är inte periodisk.

4) Skärningspunkter för grafen med koordinataxlarna: x 3 -3x=0, x = , x = -, x = 0, de där. grafen för funktionen skär koordinataxlarna i punkterna: ( ; 0 ), (0; 0 ), (-; 0 ).

5) Hitta möjliga extrema punkter: y′ = 3x2 -3; 3x2-3=0; x =-1; x = 1. Funktionens definitionsdomän kommer att delas in i intervall: (-∞; -1), (-1; 1), (1; +∞). Låt oss hitta tecknen på derivatan i varje resulterande intervall:

På intervallet (-∞; -1) y′>0 – funktionen ökar

På intervallet (-1; 1) y′<0 – funktionen minskar

På intervallet (1; +∞) y′>0 – funktionen ökar. Punkt x =-1 – maxpunkt; x = 1 – lägsta poäng.

6) Hitta böjningspunkterna: y′′ = 6x; 6x = 0; x = 0. Punkt x = 0 delar upp definitionsdomänen i intervall (-∞; 0), (0; +∞). Låt oss hitta tecknen för den andra derivatan i varje resulterande intervall:

På intervallet (-∞;0) y′′<0 – funktionen är konvex

På intervallet (0; +∞) y′′>0 – funktionen är konkav. x = 0– böjningspunkt.

7) Grafen har inga asymptoter

8) Låt oss plotta funktionen:

Exempel. Utforska funktionen och konstruera dess graf.

1) Funktionens definitionsdomän är intervallen (-¥; -1) È (-1; 1) È (1; ¥). Värdeintervall för denna funktion är intervallet (-¥; ¥).

Funktionens brytpunkter är punkterna x = 1, x = -1.

2) Funktionen är udda, eftersom .

3) Funktionen är inte periodisk.

4) Grafen skär koordinataxlarna i punkten (0; 0).

5) Hitta kritiska punkter.

Kritiska punkter: x = 0; x = -; x = ; x = -1; x = 1.

Vi hittar intervallen för ökande och minskande funktion. För att göra detta bestämmer vi tecknen för derivatan av funktionen på intervall.

-¥ < x< -, y¢> 0, funktionen ökar

-< x < -1, y¢ < 0, функция убывает

1 < x < 0, y¢ < 0, функция убывает

0 < x < 1, y¢ < 0, функция убывает

1 < x < , y¢ < 0, функция убывает

< x < ¥, y¢ > 0, funktionen ökar

Det är klart att poängen X= -är maxpunkten och punkten X= är minimipunkten. Funktionsvärdena vid dessa punkter är lika med 3/2 respektive -3/2.

6) Hitta andraderivatan av funktionen

Sned asymptotekvation: y = x.

8) Låt oss bygga en graf över funktionen.

Solver Kuznetsov.
III Diagram

Uppgift 7. Gör en fullständig studie av funktionen och konstruera dess graf.

Innan du börjar ladda ner dina alternativ, försök att lösa problemet enligt exemplet nedan för alternativ 3. Vissa av alternativen är arkiverade i .rar-format

7.3 Gör en fullständig studie av funktionen och rita upp den

Lösning.

1) Definitionsomfång: eller , det vill säga .
.
Alltså: .

2) Det finns inga skärningspunkter med Ox-axeln. Faktum är att ekvationen har inga lösningar.
Det finns inga skärningspunkter med Oy-axeln, eftersom .

3) Funktionen är varken jämn eller udda. Det finns ingen symmetri kring ordinataaxeln. Det finns inte heller någon symmetri kring ursprunget. Därför att
.
Vi ser att och .

4) Funktionen är kontinuerlig i definitionsdomänen
.

; .

; .
Följaktligen är punkten en diskontinuitetspunkt av det andra slaget (oändlig diskontinuitet).

5) Vertikala asymptoter:

Låt oss hitta den sneda asymptoten . Här

;
.
Därför har vi horisontell asymptot: y=0. Det finns inga sneda asymptoter.

6) Låt oss hitta den första derivatan. Första derivatan:
.
Och det är varför
.
Låt oss hitta stationära punkter där derivatan är lika med noll, det vill säga
.

7) Låt oss hitta den andra derivatan. Andra derivatan:
.
Och detta är lätt att verifiera, eftersom

Den här lektionen täcker ämnet "Undersökning av en funktion och relaterade problem." Den här lektionen behandlar grafiska funktioner med hjälp av derivator. Funktionen studeras, dess graf konstrueras och ett antal relaterade problem löses.

Ämne: Derivat

Lektion: Utforska en funktionoch relaterade uppgifter

Det är nödvändigt att studera denna funktion, konstruera en graf, hitta intervall för monotoni, maximum, minimum och vilka problem som följer med kunskap om denna funktion.

Låt oss först dra full nytta av informationen som tillhandahålls av funktionen utan derivator.

1. Hitta intervallen för konstanttecken för funktionen och konstruera en skiss av grafen för funktionen:

1) Låt oss hitta.

2) Funktionsrötter: , härifrån

3) Intervaller för konstanttecken för funktionen (se fig. 1):

Ris. 1. Intervaller av konstant tecken för en funktion.

Nu vet vi att i intervallet och grafen är ovanför X-axeln, i intervallet - under X-axeln.

2. Låt oss bygga en graf i närheten av varje rot (se fig. 2).

Ris. 2. Graf över en funktion i närheten av roten.

3. Konstruera en graf över funktionen i närheten av varje diskontinuitetspunkt i definitionsdomänen. Definitionsdomänen bryter vid punkten. Om värdet är nära punkten, så tenderar värdet för funktionen att (se fig. 3).

Ris. 3. Graf över funktionen i närheten av diskontinuitetspunkten.

4. Låt oss bestämma hur grafen beter sig i närheten av punkter i oändligheten:

Låt oss skriva det med gränser

. Det är viktigt att funktionen för mycket stora värden nästan inte skiljer sig från enhet.

Låt oss hitta derivatan, intervallen för dess konstanta tecken och de kommer att vara monotoniska intervaller för funktionen, hitta de punkter där derivatan är lika med noll och ta reda på var maximipunkten är och var minimipunkten är.

Härifrån, . Dessa punkter är interna punkter i definitionsdomänen. Låt oss ta reda på vilket tecken på derivatan som finns på intervallen, och vilken av dessa punkter som är maxpunkten och vilken som är minimumpunkten (se fig. 4).

Ris. 4. Intervaller för konstant tecken för derivatan.

Från fig. 4 kan man se att punkten är en minimipunkt, punkten är en maxpunkt. Funktionens värde vid punkten är . Funktionens värde vid punkten är 4. Låt oss nu bygga en graf över funktionen (se fig. 5).

Ris. 5. Funktionsdiagram.

Så byggde vi graf för en funktion. Låt oss beskriva det. Låt oss skriva ner de intervall över vilka funktionen minskar monotont: , är de intervall där derivatan är negativ. Funktionen ökar monotont på intervallen och . - minimipunkt, - högsta punkt.

Hitta antalet rötter i ekvationen beroende på parametervärdena.

1. Konstruera en graf över funktionen. Grafen för denna funktion är ritad ovan (se fig. 5).

2. Dissekera grafen med en familj av räta linjer och skriv ner svaret (se fig. 6).

Ris. 6. Skärningspunkten för en funktions graf med räta linjer.

1) När - en lösning.

2) För - två lösningar.

3) När - tre lösningar.

4) När - två lösningar.

5) När - tre lösningar.

6) När - två lösningar.

7) När - en lösning.

Således löste vi ett av de viktiga problemen, nämligen att hitta antalet lösningar på ekvationen beroende på parametern . Det kan finnas olika specialfall, till exempel där det kommer att finnas en lösning, eller två lösningar, eller tre lösningar. Observera att dessa specialfall, alla svar på dessa specialfall finns i det allmänna svaret.

1. Algebra och början av analys, årskurs 10 (i två delar). Handledning för läroanstalter(profilnivå) utg. A.G. Mordkovich. -M.: Mnemosyne, 2009.

2. Algebra och början av analys, årskurs 10 (i två delar). Problembok för läroanstalter (profilnivå), red. A.G. Mordkovich. -M.: Mnemosyne, 2007.

3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algebra och matematisk analys för 10:e klass ( handledning för elever i skolor och klasser med fördjupade studier i matematik).-M.: Prosveshchenie, 1996.

4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Fördjupning i algebra och matematisk analys.-M.: Education, 1997.

5. Samling av problem i matematik för sökande till högre läroanstalter (redigerad av M.I. Skanavi).- M.: Higher School, 1992.

6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebraisk simulator.-K.: A.S.K., 1997.

7. Zvavich L.I., Shlyapochnik L.Ya., Chinkina Algebra och början av analys. 8-11 årskurser: En manual för skolor och klasser med fördjupning i matematik (didaktiskt material).- M.: Bustard, 2002.

8. Sahakyan S.M., Goldman A.M., Denisov D.V. Problem med algebra och analysprinciper (en manual för elever i årskurs 10-11 vid allmänna läroanstalter). - M.: Prosveshchenie, 2003.

9. Karp A.P. Samling av problem om algebra och principer för analys: lärobok. traktamente för 10-11 årskurser. med djup studerat Matematik.-M.: Utbildning, 2006.

10. Glazer G.I. Matematikens historia i skolan. Årskurs 9-10 (handbok för lärare).-M.: Utbildning, 1983

Ytterligare webbresurser

2. Portal Naturvetenskap ().

Gör det hemma

Nr 45.7, 45.10 (Algebra och analysens början, årskurs 10 (i två delar). Problembok för allmänna utbildningsinstitutioner (profilnivå) redigerad av A. G. Mordkovich. - M.: Mnemosyne, 2007.)

Uppgiften är att genomföra en fullständig studie av funktionen och bygga dess graf.

Varje elev gick igenom liknande uppgifter.

Vidare presentation förutsätter goda kunskaper. Vi rekommenderar att du hänvisar till detta avsnitt om du har några frågor.

Funktionsforskningsalgoritmen består av följande steg.

Hitta definitionsdomänen för en funktion.

Detta är ett mycket viktigt steg för att studera funktionen, eftersom alla ytterligare åtgärder kommer att utföras på definitionsdomänen.

I vårt exempel måste vi hitta nollorna i nämnaren och exkludera dem från området med reella tal.

(I andra exempel kan det finnas rötter, logaritmer etc. Låt oss komma ihåg att i dessa fall söks definitionsdomänen på följande sätt:
för en rot av jämn grad, till exempel, finns definitionsdomänen från ojämlikheten;
för logaritmen - definitionsdomänen hittas från olikheten ).

Studie av beteendet hos en funktion på gränsen för definitionsdomänen, hitta vertikala asymptoter.

Vid definitionsdomänens gränser har funktionen vertikala asymptoter, om vid dessa gränspunkter är oändliga.

I vårt exempel är gränspunkterna för definitionsdomänen .

Låt oss undersöka funktionens beteende när vi närmar oss dessa punkter från vänster och höger, för vilka vi hittar ensidiga gränser:

Eftersom ensidiga gränser är oändliga, är de raka linjerna grafens vertikala asymptoter.

Undersökning av en funktion för jämnhet eller udda.

Funktionen är även, Om . Funktionens paritet indikerar grafens symmetri kring ordinatan.

Funktionen är udda, Om . Funktionens uddahet anger grafens symmetri i förhållande till ursprunget.

Om ingen av jämlikheterna är uppfyllda, har vi en funktion av en generell form.

I vårt exempel gäller jämlikheten, därför är vår funktion jämn. Vi kommer att ta hänsyn till detta när vi konstruerar grafen - den kommer att vara symmetrisk kring oy-axeln.

Att hitta intervall av ökande och minskande funktioner, extrema punkter.

Intervallerna för att öka och minska är lösningar på ojämlikheterna och resp.

Punkterna där derivatan försvinner kallas stationär.

Kritiska punkter för funktionen anropa de interna punkterna i definitionsdomänen där derivatan av funktionen är lika med noll eller inte existerar.

KOMMENTAR(om kritiska punkter ska inkluderas i intervallen för ökning och minskning).

Vi kommer att inkludera kritiska punkter i de ökande och minskande intervallen om de tillhör funktionens domän.

Således, för att bestämma intervallen för ökande och minskande funktioner

först hittar vi derivatan;
för det andra finner vi kritiska punkter;
för det tredje delar vi upp definitionsdomänen efter kritiska punkter i intervall;
för det fjärde bestämmer vi tecknet för derivatan på vart och ett av intervallen. Plustecknet kommer att motsvara ökningsintervallet, minustecknet kommer att motsvara intervallet för minskning.

Gå!

Vi hittar derivatan på definitionsdomänen (om svårigheter uppstår, se avsnitt).

Vi hittar kritiska punkter för detta:

Vi plottar dessa punkter på talaxeln och bestämmer tecknet för derivatan inom varje resulterande intervall. Alternativt kan du ta vilken punkt som helst i intervallet och beräkna värdet på derivatan vid den punkten. Om värdet är positivt sätter vi ett plustecken över detta gap och går vidare till nästa, om det är negativt sätter vi ett minustecken osv. T.ex, , därför sätter vi ett plus ovanför det första intervallet till vänster.

Vi sammanfattar:

Schematiskt markerar plus/minus intervallen där derivatan är positiv/negativ. Ökande/fallande pilar visar riktningen för ökning/minskning.

Funktionens extrema punkterär de punkter där funktionen definieras och passerar genom vilka derivatan byter tecken.

I vårt exempel är extrempunkten x=0. Funktionens värde vid denna punkt är . Eftersom derivatan ändrar tecken från plus till minus när den passerar genom punkten x=0, så är (0; 0) en punkt med lokalt maximum. (Om derivatan ändrade tecken från minus till plus, så skulle vi ha en lokal minimipunkt).

Att hitta konvexitets- och konkavitetsintervallen för en funktion och böjningspunkter.

Intervallerna för konkavitet och konvexitet för en funktion hittas genom att lösa ojämlikheterna och resp.

Ibland kallas konkavitet konvex ner och konvex kallas konvex upp.

Här gäller också anmärkningar liknande de från stycket om intervaller för ökning och minskning.

Således, för att bestämma konkavitets- och konvexitetsintervallen för en funktion:

först finner vi andraderivatan;
för det andra hittar vi nollorna för täljaren och nämnaren för andraderivatan;
för det tredje delar vi upp definitionsdomänen med de erhållna poängen i intervall;
för det fjärde bestämmer vi tecknet för andraderivatan på vart och ett av intervallen. Plustecknet kommer att motsvara konkavitetsintervallet, minustecknet mot det konvexa intervallet.

Gå!

Vi hittar den andra derivatan på definitionsdomänen.

I vårt exempel finns det inga nollor i täljaren, utan nollor i nämnaren.

Vi plottar dessa punkter på talaxeln och bestämmer tecknet för den andra derivatan inom varje resulterande intervall.

Vi sammanfattar:

Punkten kallas böjningspunkt, om det vid en given punkt finns en tangent till grafen för funktionen och andraderivatan av funktionen ändrar tecken när den passerar genom .

Med andra ord kan böjningspunkter vara punkter genom vilka andraderivatan ändrar tecken, vid själva punkterna är den antingen noll eller existerar inte, men dessa punkter ingår i definitionsdomänen för funktionen.

I vårt exempel finns det inga böjningspunkter, eftersom andraderivatan ändrar tecken när den passerar genom punkterna, och de ingår inte i funktionens definitionsdomän.

Hitta horisontella och sneda asymptoter.

Horisontella eller sneda asymptoter bör endast sökas när funktionen är definierad vid oändlighet.

Sned asymptoter söks i form av raka linjer, var och .

Om k=0 och b är inte lika med oändlighet, då blir den sneda asymptoten horisontell.

Vilka är dessa asymptoter egentligen?

Dessa är linjerna som grafen för en funktion närmar sig i oändligheten. Därför är de till stor hjälp för att rita en funktion.

Om det inte finns några horisontella eller sneda asymptoter, men funktionen är definierad vid plus oändlighet och (eller) minus oändlighet, bör du beräkna gränsen för funktionen vid plus oändlighet och (eller) minus oändlighet för att få en uppfattning om funktionsgrafens beteende.

För vårt exempel

- horisontell asymptot.

Detta avslutar studiet av funktionen, vi fortsätter med att rita grafen.

Vi beräknar funktionsvärdena vid mellanliggande punkter.

För mer exakt plottning rekommenderar vi att du hittar flera funktionsvärden vid mellanliggande punkter (det vill säga vid alla punkter från funktionens definitionsdomän).

För vårt exempel låt oss hitta värdena fungerar vid punkterna x=-2, x=-1, x=-3/4, x=-1/4. På grund av funktionens paritet kommer dessa värden att sammanfalla med värdena i punkterna x=2, x=1, x=3/4, x=1/4.

Bygga en graf.

Först konstruerar vi asymptoter, plottar punkterna för lokala maxima och minima för funktionen, böjningspunkter och mellanliggande punkter. För bekvämligheten med att konstruera en graf kan du också schematiskt ange intervallen för ökning, minskning, konvexitet och konkavitet, det är inte för inte vi studerade funktionen =).