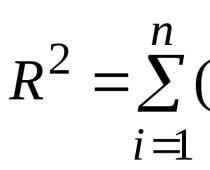Längden på en vektor, vinkeln mellan vektorer - dessa begrepp är naturligt tillämpbara och intuitiva när man definierar en vektor som ett segment i en viss riktning. Nedan kommer vi att lära oss hur man bestämmer vinkeln mellan vektorer i det tredimensionella rummet, dess cosinus och överväger teorin med exempel.
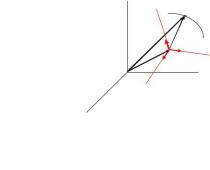
För att överväga konceptet med en vinkel mellan vektorer, låt oss vända oss till en grafisk illustration: låt oss definiera två vektorer a → och b → , som inte är noll, på ett plan eller i tredimensionellt rum. Låt oss också sätta en godtycklig punkt O och avsätta vektorerna OA → = b → och O B → = b → från den
Definition 1
hörn mellan vektorerna a → och b → kallas vinkeln mellan strålarna OA och O B.
Den resulterande vinkeln kommer att betecknas enligt följande: a → , b → ^
Uppenbarligen har vinkeln förmågan att ta värden från 0 till π eller från 0 till 180 grader.
a → , b → ^ = 0 när vektorerna är samriktade och a → , b → ^ = π när vektorerna är motsatta.
Definition 2
Vektorerna kallas vinkelrät om vinkeln mellan dem är 90 grader eller π 2 radianer.
Om åtminstone en av vektorerna är noll, är vinkeln a → , b → ^ inte definierad.
Cosinus för en vinkel mellan två vektorer, och därmed själva vinkeln, kan vanligtvis bestämmas antingen med hjälp av skalärprodukten av vektorerna, eller med hjälp av cosinussatsen för en triangel byggd på basis av två givna vektorer.
Per definition är den inre produkten a → , b → = a → b → cos a → , b → ^ .
Om de givna vektorerna a → och b → är icke-noll, så kan vi dividera höger och vänster sida av likheten med produkten av längderna av dessa vektorer, och på så sätt erhålla en formel för att hitta cosinus för vinkeln mellan icke- noll vektorer:
cos a → , b → ^ = a → , b → a → b →
Denna formel används när indata inkluderar längder på vektorer och deras punktprodukt.
Exempel 1
Initialdata: vektorerna a → och b → . Deras längder är 3 respektive 6, och deras prickprodukt är -9 . Det är nödvändigt att beräkna cosinus för vinkeln mellan vektorerna och hitta själva vinkeln.
Lösning
De initiala uppgifterna är tillräckliga för att tillämpa formeln ovan, sedan cos a → , b → ^ = - 9 3 6 = - 1 2 ,
Låt oss nu definiera vinkeln mellan vektorerna: a → , b → ^ = a r c cos (- 1 2) = 3 π 4
Svar: cos a → , b → ^ = - 1 2 , a → , b → ^ = 3 π 4
Oftare finns det problem där vektorer ges av koordinater i ett rektangulärt koordinatsystem. För sådana fall är det nödvändigt att härleda samma formel, men i koordinatform.
Längden av en vektor definieras som kvadratroten av summan av kvadraterna av dess koordinater, och skalärprodukten av vektorer är lika med summan av produkterna av motsvarande koordinater. Då ser formeln för att hitta cosinus för vinkeln mellan vektorer på planet a → = (a x, a y), b → = (b x, b y) ut så här:
cos a → , b → ^ = a x b x + a y b y a x 2 + a y 2 b x 2 + b y 2
Och formeln för att hitta cosinus för vinkeln mellan vektorer i det tredimensionella rummet a → = (a x, a y, a z), b → = (b x , b y , b z) kommer att se ut så här: cos a → , b → ^ = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Exempel 2
Initialdata: vektorerna a → = (2 , 0 , - 1), b → = (1 , 2 , 3) i ett rektangulärt koordinatsystem. Det är nödvändigt att bestämma vinkeln mellan dem.
Lösning
- För att lösa problemet kan vi omedelbart tillämpa formeln:
cos a → , b → ^ = 2 1 + 0 2 + (- 1) 3 2 2 + 0 2 + (- 1) 2 1 2 + 2 2 + 3 2 = - 1 70 ⇒ a → , b → ^ = a r c cos (- 1 70) = - a r c cos 1 70
- Du kan också bestämma vinkeln med formeln:
cos a → , b → ^ = (a → , b →) a → b → ,
men beräkna först längderna på vektorerna och skalärprodukten med koordinater: a → = 2 2 + 0 2 + (- 1) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 1 + 0 2 + (- 1) 3 = - 1 cos a → , b → ^ = a → , b → ^ a → b → = - 1 5 14 = - 1 70 ⇒ a → , b → ^ = - a r c cos 1 70
Svar: a → , b → ^ = - a r c cos 1 70
Problem är också vanliga när koordinaterna för tre punkter i ett rektangulärt koordinatsystem anges och det är nödvändigt att bestämma någon vinkel. Och sedan, för att bestämma vinkeln mellan vektorerna med punkternas givna koordinater, är det nödvändigt att beräkna vektorernas koordinater som skillnaden mellan motsvarande punkter i början och slutet av vektorn.
Exempel 3
Initialdata: punkterna A (2 , - 1) , B (3 , 2) , C (7 , - 2) ges på planet i ett rektangulärt koordinatsystem. Det är nödvändigt att bestämma cosinus för vinkeln mellan vektorerna A C → och B C → .
Lösning
Hitta koordinaterna för vektorerna genom koordinaterna för de givna punkterna A C → = (7 - 2 , - 2 - (- 1)) = (5 , - 1) B C → = (7 - 3 , - 2 - 2) = (4 , - 4)
Nu använder vi formeln för att bestämma cosinus för vinkeln mellan vektorer på planet i koordinater: cos A C → , B C → ^ = (AC → , B C →) A C → B C → = 5 4 + (- 1) (- 4 ) 5 2 + (- 1) 2 4 2 + (- 4) 2 = 24 26 32 = 3 13
Svar: cos A C → , B C → ^ = 3 13
Vinkeln mellan vektorer kan bestämmas med hjälp av cosinussatsen. Låt oss skjuta upp vektorerna OA → = a → och O B → = b → från punkten O, då, enligt cosinussatsen i triangeln O A B, blir likheten sann:
A B 2 \u003d O A 2 + O B 2 - 2 O A O B cos (∠ A O B) ,
vilket motsvarar:
b → - a → 2 = a → + b → - 2 a → b → cos (a → , b →) ^
och härifrån härleder vi formeln för cosinus för en vinkel:
cos (a → , b →) ^ = 1 2 a → 2 + b → 2 - b → - a → 2 a → b →
För att tillämpa den resulterande formeln behöver vi längden på vektorer, som lätt bestäms av deras koordinater.
Även om denna metod har en plats att vara, används formeln fortfarande oftare:
cos (a → , b →) ^ = a → , b → a → b →
Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter
Låt oss hitta sambandet mellan vektorerna j (strömdensitetsvektor) och E (fältstyrka) vid samma punkt på ledaren. Eftersom i en isotrop ledare strömbärarna vid varje punkt rör sig i vektorns E riktning, sammanfaller riktningarna j och E. Spänningen som appliceras på ledarens ändar är Edl, och dess motstånd. Strömmen I är den totala strömmen genom S - ledarens tvärsnittsarea. Då är strömmen dI strömmen genom det elementära området dS. Genom att ersätta dessa uttryck i formeln. Låt oss skriva ner. .
Bild 12 från presentationen "Conductor Resistance" till fysiklektioner på ämnet "motstånd"Mått: 720 x 540 pixlar, format: jpg. För att ladda ner en bild gratis för användning i en fysiklektion, högerklicka på bilden och klicka på "Spara bild som...". Du kan ladda ner hela presentationen "Resistance.ppt" i ett 66 KB zip-arkiv.
Ladda ner presentationenMotstånd
"Science of physics" - Fysik som vetenskap. Fysiken uppstod redan på de gamla grekernas tid på 500-talet f.Kr. ljudfenomen. Ämne. Materia. elektriska fenomen. fysiska fenomen. Filosofi. Elektriska fenomen är växelverkan mellan elektriska laddningar, blixtar. Vattenmolekyl. Fysikens kopplingar är så olika att människor ibland inte ser dem.
"Abram Fedorovich Ioffe" - Ioffe på ett seminarium om halvledarfysik. Fysikaliskt-tekniska institutet. Fysikaliskt-tekniska institutet. Yrkeshögskolan. Shockley och Joffe. Byggnaden av universitetet i München. Ioffe vid konstruktionen av FTI-cyklotronen. En av de sista bilderna av Ioffe. Kapitsa i Cambridge. Foto av Kapitza. A. Ioffe och hans landsman S. Timosjenko är studenter vid S:t Petersburgs institut.
"Elektricitets historia" - XXI-talet - elektrisk energi har äntligen blivit en integrerad del av livet. XIX-talet - Faraday upptäcker elektromagnetisk induktion och elektrolysens lagar. Det är känt att om vissa ämnen gnuggas mot ull, drar de till sig lätta föremål. 1800-talet - Maxwell formulerar sina ekvationer. Joule, Lenz, Ohms arbete om studier av elektrisk ström.
"Magnetisk induktion" - Ampere Force. Grundläggande egenskaper hos magnetfältet. Interaktioner mellan ledare med ström kallas magnetiska. Riktningen på Ampères kraft kan bestämmas med hjälp av vänsterhandsregeln. Magnetfältet genereras av elektrisk ström (rörelseladdningar). Magnetfältet existerar egentligen oberoende av oss, av vår kunskap om det.
"Partikelspridning" - Kontrast i röntgenspridning. Shturmans katt. Tröghetsradie och translationell friktionskonstant. Gyreringsradien för en homogen sfärisk partikel är relaterad till dess radie r0. Girationsradie och gränsviskositet. Kontrastvariation med H2O/D2O-blandningar. Lösningsmedelsspridningsdensitet.
Utöver de tidigare övervägda operationerna att addera och subtrahera vektorer, samt multiplicera en vektor med en skalär (se § 2), finns det också operationer för vektormultiplikation. Två vektorer kan multipliceras med varandra på två sätt: det första sättet resulterar i någon ny vektor, det andra sättet leder till ett skalärt värde. Observera att operationen att dividera en vektor med en vektor inte existerar.
Nu ska vi överväga sektorprodukten av vektorer. Vi kommer att introducera den skalära produkten av vektorer senare, när vi behöver den.
Vektorprodukten av två vektorer A och B är en vektor C som har följande egenskaper:
1) modulen för vektorn C är lika med produkten av modulerna för de multiplicerade vektorerna med sinus för vinkeln α mellan dem (fig. 35):
2) vektorn C är vinkelrät mot planet i vilket vektorerna A och B ligger, och dess riktning är kopplad till riktningarna A och B enligt den rätta skruvregeln: om du ser efter vektorn C, rotationen från den första faktor till den andra som görs längs den kortaste vägen utförs medurs pil.
Symboliskt kan vektorprodukten skrivas på två sätt:
|AB | eller .
Vi kommer att använda den första av dessa metoder, och ibland, för att göra det lättare att läsa formlerna, sätter vi ett kommatecken mellan faktorerna. Du bör inte använda ett snett kors och hakparenteser samtidigt: [A B], En inmatning av denna form är inte tillåten: [AB] = ABsi nα. Till vänster finns en vektor, till höger är modulen för denna vektor, det vill säga en skalär. Följande jämställdhet är sant:
|
|
Eftersom tvärproduktens riktning bestäms av rotationsriktningen från den första faktorn till den andra, beror resultatet av vektormultiplikation av två vektorer på ordningen på faktorerna. Att ändra ordningen på faktorerna orsakar en förändring i riktningen för den resulterande vektorn till motsatt (Fig. 35)
Vektorprodukten har alltså inte kommutativitetsegenskapen.
Det kan bevisas att vektorprodukten är distributiv, det vill säga
Vektorprodukten av två polära eller två axiella vektorer är en axiell vektor. Vektorprodukten av en axiell vektor och en polär vektor (eller vice versa) kommer dock att vara en polär vektor. Att ändra tillståndet som bestämmer riktningen för de axiella vektorerna till motsatt kommer i detta fall att leda till en teckenändring framför vektorprodukten och samtidigt till en teckenändring framför en av faktorerna. värdet uttryckt av vektorprodukten förblir oförändrat.
Modulen för korsprodukten kan ges en enkel geometrisk tolkning: uttrycket ABsi nα är numeriskt lika med arean av parallellogrammet byggt på vektorerna A och B (fig. 36; vektorn C \u003d [AB] är riktad i detta fall vinkelrätt mot ritningens plan, bortom ritningen).
Låt vektorerna A och B vara inbördes vinkelräta (fig. 37).
Vi bildar en dubbel vektorprodukt av dessa vektorer:
det vill säga vi multiplicerar vektorn B med A, och sedan multiplicerar vi vektorn A med vektorn som resulterar från den första multiplikationen. Vektorn [VA] har en modul lika med 
, och bildar vinklar lika med π/2 med vektorerna A och B. Därför är modulen för vektorn D lika med |A |*||=A *BA =A2B. Riktningen för vektorn D, som är lätt att se från fig. 37, sammanfaller med vektorns B riktning. Detta ger oss anledning att skriva följande likhet:
|
|
Formel (11.3) kommer att användas mer än en gång i det följande. Vi betonar att det endast är giltigt om vektorerna A och B är inbördes vinkelräta.
Ekvation (10.9) upprättar en koppling mellan modulerna för vektorerna v och ω. Med hjälp av korsprodukten kan ett uttryck skrivas som ger förhållandet mellan själva vektorerna. Låt kroppen rotera runt z-axeln med en vinkelhastighet ω (Fig. 38). Det är lätt att se att vektorprodukten av ω och radievektorn för punkten vars hastighet v vi vill hitta är en vektor som sammanfaller i riktning med vektorn v och har en modul lika med ωr sinα =ωR , dvs. v [se formel (10.9)]. Således är vektorprodukten [ωR] lika i båda riktningarna och modulo till vektorn v:
|
v=[ωr] |
Formel (11.4) kan ges en annan form. För att göra detta representerar vi radievektorn r som summan av två komponenter - en vektor r z , parallell med z-axeln och en vektor vinkelrät mot z-axeln: r = r z + R (se fig. 38). Ersätter detta uttryck med formeln (11.4) och använder fördelningsförmågan för vektorprodukten [se. (11.2)], får vi:
Vektorerna ω och rz är kolinjära. Därför är deras vektorprodukt lika med noll (sinα=0). Därför kan man skriva det
I det följande, när vi betraktar rotationsrörelse, kommer vi alltid att beteckna med R komponenten av radievektorn r, vinkelrät mot rotationsaxeln, ritad från en punkt tagen på axeln. Modulen för denna vektor ger punktens avstånd R från axeln.
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0
