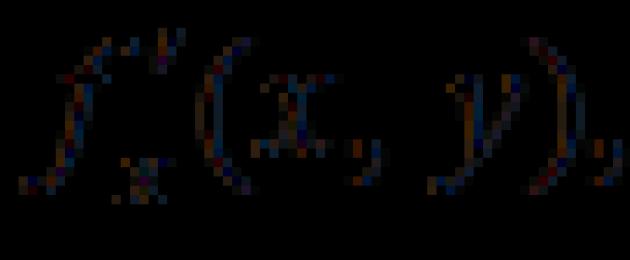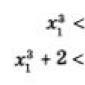Låt en funktion av två variabler ges. Låt oss öka argumentet och lämna argumentet oförändrat. Då kommer funktionen att få ett inkrement, vilket kallas ett partiellt inkrement med avseende på variabeln och betecknas:

På liknande sätt, genom att fixa argumentet och ge argumentet ett inkrement, får vi en partiell ökning av funktionen med avseende på variabeln:

Värdet kallas hela ökningen av funktionen vid punkten.

Definition 4. Den partiella derivatan av en funktion av två variabler med avseende på en av dessa variabler är gränsen för förhållandet mellan motsvarande partiella ökning av funktionen och ökningen av den givna variabeln när den senare tenderar till noll (om denna gräns existerar). Den partiella derivatan betecknas som: eller, eller.

Därför har vi per definition:

Partiella derivator av en funktion beräknas enligt samma regler och formler som en funktion av en variabel, med hänsyn till att när man differentierar med avseende på en variabel, anses den vara konstant, och när man differentierar med avseende på en variabel, anses den vara konstant. konstant.

Exempel 3. Hitta partiella derivator av funktioner:

Lösning. a) För att hitta antar vi ett konstant värde och differentierar som en funktion av en variabel:

På liknande sätt, om vi antar ett konstant värde, finner vi:

Definition 5. Den totala differentialen för en funktion är summan av produkterna av de partiella derivatorna av denna funktion och inkrementen av motsvarande oberoende variabler, d.v.s.

Med tanke på att differentialerna för de oberoende variablerna sammanfaller med deras inkrement, dvs. , formeln för den totala differentialen kan skrivas som

Exempel 4. Hitta den totala differentialen för en funktion.

Lösning. Sedan finner vi genom formeln för den totala differentialen

Partiella derivator av högre ordning

Partiella derivator kallas också partiella derivator av första ordningen eller första partiella derivator.

Definition 6. Andra ordningens partiella derivator av en funktion är partiella derivator av första ordningens partiella derivator.

Det finns fyra andra ordningens partiella derivator. De är betecknade enligt följande:

De partiella derivatorna av 3:e, 4:e och högre ordningen definieras på liknande sätt. Till exempel, för en funktion har vi:

Partiella derivator av andra eller högre ordningen taget med avseende på olika variabler kallas blandade partiella derivator. För en funktion är dessa derivator. Observera att i fallet när blandade derivat är kontinuerliga, så sker likhet.

Exempel 5. Hitta andra ordningens partiella derivator av en funktion

Lösning. Första ordningens partiella derivator för denna funktion finns i exempel 3:

Differentiering och med avseende på variablerna x och y får vi

Exempel. Hitta partiella derivator av funktionen y x yxz

Lösning. Inställningen y = const finner vi xy x z

Inställningen x =const finner vi 2 2) 1 (1 y x x y xx y z

Exempel. Hitta värdena för funktionens partiella derivator vid punkten M (1, - 1, 0). xyzyxu)ln(

Lösning. Inställningen y = const , z = const , finner vi 10 11 22 1)02(1 22 22 , Ì czy yz yx x yzx yxx u

På liknande sätt hittar vi 10 11 22 1)20(1 22 22 , M czx xz yx y xzy yxy u 110 , M cyx xyxy z

Den geometriska betydelsen av den partiella derivatan (till exempel) är tangenten för lutningen av tangenten ritad vid punkten M 0 (x 0, y 0, z 0) till ytsektionen av planet y \u003d y 0. xz

Antag att funktionen z = f (x , y) har kontinuerliga partiella derivator), (yxf x z x), (yxf y z y

Dessa derivator är i sin tur funktioner av de oberoende variablerna x och y. Vi kallar också partiella derivator av första ordningen.), (yxf x), (yxf y

Partiella derivator av 2:a ordningen kallas partiella derivator av partiella derivator av 1:a ordningen. För en funktion z \u003d f (x, y) av två variabler kan fyra partiella derivator av 2:a ordningen hittas, som betecknas med följande mod:

I det allmänna fallet kanske blandade partiella derivator inte sammanfaller, men följande sats är giltig för dem: Sats. Om de blandade partiella derivaten och är kontinuerliga vid någon punkt M (x, y), så är de lika, dvs. xyfyxf), (yxfyxf yxxy

Partiella derivator av n:e ordningen är partiella derivator av partiella derivator av (n – 1):e ordningen. De betecknas etc. 221 , yx z x z n n n

Exempel. Hitta partiella derivator av 2:a ordningen av funktionen)1 sin(23 xyyxz

Lösning. successivt hitta); 1 cos(3 22 xyyyx x z cy); 1 cos(2 3 xyxyx y z cx

); 1 sin(6)1 cos(3 22 22 2 2 xyyxy xyyyx xx z cy cy); 1 sin()1 cos(6)1 cos(3 2 22 2 xyyx xyyyx z cx cx

)1 sin()1 cos(6 1 cos(2 2 3 2 xyyx xyxyx xxy z cy cy)1 sin(2)1 cos(2 23 3 2 2 xyxx xyxyx yy z cx cx

Betrakta funktionen z = f(x, y). Låt oss ge argumentet x ett inkrement Δ x , och argumentet y ett inkrement Δ y. Då kommer z att få ett inkrement som kallas det totala inkrementet för funktionen z.), (yxfyyxxfz

Antag att f(x, y) i punkt M(x, y) har kontinuerliga partiella derivator.

Definition. 1:a ordningens differential för funktionen z \u003d f (x, y) är huvuddelen av den totala ökningen Δ z för denna funktion, linjär med avseende på Δ x och Δ y , betecknad med symbolen dz eller df och beräknas med formeln y y z x x z zd

Eftersom differentialerna för oberoende variabler sammanfaller med deras inkrement, dvs dx = Δ x , dy = Δ y , kan denna formel skrivas som: dy y z dx x z zd

Den geometriska betydelsen av den totala differentialen för en funktion av två variabler f (x, y) i punkten (x 0, y 0) är ökningen av applikatet (z-koordinaten) för tangentplanet till ytan under övergången från punkten (x 0, y 0) till punkten (x 0 + x, y 0 + y).

Den geometriska betydelsen av den totala differentialen för en funktion av två variabler är en rumslig analog till den geometriska betydelsen av differentialen för en funktion av en variabel.

2:a ordningens differential för en funktion z \u003d f (x, y) är differentialen för dess 1:a ordningens differential och betecknas) (zzddd

Om alla partiella derivator av 2:a ordningen av funktionen z \u003d f (x, y) är kontinuerliga, sker formeln: 2 2 2 y y z yx yx z x x z zdddddd

Exempel. Hitta differentialer av 1:a och 2:a ordningen för funktionen y x yz 2 x

Lösning. Hitta partiella derivator av 1:a och 2:a ordningen: y yx x z 1 2 2 2 y x x y z

; 202 1 2 2 2 åå å xy xx z cy ; 1 2 2 2 y xy yyx z cx 33 22 22 2)2(0 y x yx y x x y y z cy

Därför kommer differentialer av 1:a och 2:a ordningen att skrivas som: dy y x xdx y xyz)() 1 2(d 2 2 2 32 222) 1 2(22 y y x yx y xxyzdddddd

Låt funktionen f(x, y) vara differentierbar i punkten (x, y). Låt oss hitta den totala ökningen av denna funktion :), (yxfyyxxfz zyxfyyxxf), (

Om vi ​​ersätter ett uttryck i denna formel får vi en ungefärlig formel: y yf x xf dzz y y yxf x x yxf yyxxf), (

Exempel. Beräkna ett ungefärligt värde baserat på värdet på funktionen vid x = 1, y = 2, z = 102, 1 ln 04, 1 99, 1 zxu y ln

Lösning. Från det givna uttrycket bestämmer vi x \u003d 1, 04 - 1 \u003d 0,04, y \u003d 1,99 - 2 \u003d -0,01, z \u003d 1,02 - 1 \u003d 0,02. Hitta värdet på funktionen u (x, funktionen u) y, z) = 11 ln

Hitta partiella derivator: 1 12 12 ln 2 1 zx xy x u y y 0 ln 2 ln zx xx y u y y

Den totala differentialen för funktionen u är: 2 1 ln 2 1 zx z z u y

05, 001, 004, 0 02, 0 21 01, 0004, 01 02, 001, 004, 0 zu yu xudu

Det exakta värdet för detta uttryck är: 1, 049275225687319176. 05, 105, 01)1, 2, 1(02, 1 ln 04, 1 99, 1 duu

Tangentplanet till ytan vid dess punkt M 0 är det plan som innehåller alla tangenter till kurvorna som ritas på ytan genom denna punkt.

Normalen till ytan i punkten M 0 är den räta linjen som går genom denna punkt och vinkelrät mot tangentplanet ritat vid den givna punkten.

Om ytan ges av ekvationen F (x, y, z) \u003d 0, har ekvationen för tangentplanet vid punkten M 0 (x 0, y 0, z 0) formen: 0)) ( (00 0000 zz. MF åå. MFxx. MF z yx

Ekvationerna för normalen som dras till ytan i punkten M 0 (x 0 , y 0 , z 0) skrivs enligt följande:)()()(0 0 0 MF zz MF yy MF xx zyx

Om ytan ges av ekvationen z \u003d f (x, y), så har ekvationen för tangentplanet vid punkten M 0 (x 0, y 0, z 0) formen :)) (, (000) 0000 yyyxf xxxxfzz y x

och normalekvationerna kommer att skrivas enligt följande: 1), (0 00 0 zz yxf yy yxf xx yx

Exempel. Komponera ekvationerna för tangentplanet och normalen till ytan i punkten M 0 (x 0, y 0, z 0) om 01332 22 yzxzxyyx. 1, 200yx

Lösning. Genom att ersätta x 0 och y 0 i ytans ekvation finner vi värdet av z 0: därifrån finner vi z 0 = 1. Därför är M 0 (2, - 1, 1) kontaktpunkten. 01)1(32)1(23)1(2400 2zz

Av problemets tillstånd ges ytan implicit. Beteckna och hitta de partiella derivatorna i punkten M 0 (2, – 1, 1): 1332), (22 yzxzxyyxzyx.

, 32 zyx. F x 21)1(322)(0 MF x, 334 zxy. F y 51323)1(4)(0 MF y, 3 yx. F z 1)1(32)(0 MF z

Vi ersätter de hittade värdena för partiella derivator i ekvationen för tangentplanet 0))((00 0000 zz. MF yy. MFxx. MF z yx

Normalekvationerna har formen 1 1 5 1 2 2 zyx

Definition. Funktionen z = f (x , y) har ett maximum vid punkten M 0 (x 0 , y 0) om det finns en sådan grannskap till denna punkt att för alla punkter M (x , y) från denna grannskap gäller olikheten ), (00 yxfyxf

Definition. Andra ordningens partiella derivator av en funktion är partiella derivator av dess första ordningens partiella derivator.

Partiell derivativ notation av andra ordningen:

För praktiska exempel gäller följande likhet:

Således är det mycket bekvämt att kontrollera riktigheten av att hitta partiella derivator av första ordningen i termer av andra ordningens blandade derivator.

Exempel.

A) Hitta andra ordningens partiella derivator av en funktion

Lösning.

1. Vi betraktar en variabel y

2. Den resulterande funktionen är återigen differentierad med "x", dvs. hitta andraderivatan med avseende på "x":

3. Vi betraktar en variabel X konstant, vi tillämpar regeln för att differentiera summan, regeln för att ta den konstanta faktorn ur tecknet för derivatan och tabellderivatan för potensfunktionen:

4. Återigen differentierar vi den resulterande funktionen med avseende på "y", dvs. hitta den andra derivatan med avseende på "y":

5. Låt oss hitta den blandade derivatan "x med y". För att göra detta, differentierar vi den första derivatan med avseende på "x" med avseende på "y".

5. Låt oss hitta den blandade derivatan "y på x". För att göra detta, differentierar vi den första derivatan med avseende på "Y" med avseende på "X".

b) Hitta partiella derivator av första ordningen av funktionen Kontrollera att Skriv ner den totala differentialen av första ordningen dz.

Lösning.

1. Låt oss hitta de partiella derivatorna av första ordningen, genom att tillämpa reglerna för beräkning av produktens derivata, summan, ta den konstanta faktorn ur tecknet för derivatan och tabellintegralen för trigonometriska funktioner:

2. Hitta blandade derivator av andra ordningen:

3. Komponera den totala skillnaden av den första ordningen:

V) Visa att den givna funktionen uppfyller ekvationen

Lösning.

1. Hitta den partiella derivatan av den givna funktionen med avseende på "x":

2. Multiplicera det resulterande uttrycket x 2 :

3. Från den resulterande funktionen hittar vi den partiella derivatan med avseende på "x":

4. Hitta den partiella derivatan av den givna funktionen med avseende på "y":

5. Beräkna andraderivatan med avseende på "y":

6. Multiplicera den resulterande funktionen med vid 2 :

7. Subtrahera från resultatet som erhållits i punkt 5, resultatet av punkt 6:

Vilket var det som behövde visas.

Relaterad information:

1. V3: ((101)) 07/04/14. Linjära inhomogena differentialekvationer av andra ordningen med konstanta koefficienter (allmän lösning)

Funktioner av två variabler, partiella derivator, differentialer och gradient

Ämne 5.Funktioner av två variabler.

partiella derivat

Definition av en funktion av två variabler, sätt att ställa.

Privata derivat.

Gradientfunktion för en variabel

Att hitta de största och minsta värdena av en funktion av två variabler i ett slutet avgränsat område

1. Definition av en funktion av flera variabler, sätt att ställa

För funktioner av två variabler
definitionsdomän är en del uppsättning punkter på ett plan
, och intervallet är gapet på axeln
.

För en visuell presentation funktioner av två variabler nyh tillämpa nivålinjer.

Exempel . För funktion
bygga en graf och plana linjer. Skriv ekvationen för en nivålinje som går genom en punkt
.

Linjär funktionsgrafär plan i rymden.

För en funktion är grafen ett plan som går genom punkterna
,
,
.

Funktionsnivålinjerär parallella linjer vars ekvation
.

För linjär funktion av två variabler
nivålinjer ges av ekvationen
och representera en familj av parallella linjer i planet.

4

Funktionsdiagram 0 1 2 X

Funktionsnivålinjer

Privat proiderivata funktioner av två variabler

Tänk på funktionen
. Låt oss ge en variabel vid punkten
godtycklig ökning
, lämnar variabelt värde oförändrad. Motsvarande funktionsökning

kallad partiell ökning av en funktion med variabel vid punkten
.

Liknande definierad partiell ökning av en funktionefter variabel: .

Beteckningpartiell derivata med avseende på: , ,
,
.

Partiell derivata av en funktion med avseende på en variabel kallas gränsen :

Beteckningar: , ,
,
.

För att hitta den partiella derivatan
med avseende på en variabel används reglerna för att differentiera en funktion av en variabel, antar att variabeln är konstant.

På samma sätt, för att hitta den partiella derivatan med avseende på en variabel variabel anses konstant .

Exempel . För funktion
hitta partiella derivator
,
och beräkna deras värden vid en punkt
.

Partiell derivata av en funktion
per variabel är under antagandet att den är konstant:

Hitta den partiella derivatan av funktionen med avseende på , förutsatt att den är konstant:

Låt oss beräkna värdena för partiella derivator för
,
:

;
.

Partiella derivator av andra ordningen funktioner av flera variabler kallas partiella derivator av partiella derivator av första ordningen.

Låt oss skriva partiella derivator av 2:a ordningen för funktionen:

;
;

;
.

;
etc.

Om de blandade partiella derivatorna av en funktion av flera variabler är kontinuerliga någon gång
, då de lika med varandra vid denna tidpunkt. Därför, för en funktion av två variabler, beror inte värdena på blandade partiella derivator av differentieringsordningen:

.

Exempel. För en funktion, hitta andra ordningens partiella derivator
Och
.

Lösning

Den blandade partiella derivatan hittas genom successiv differentiering först av funktionen med avseende på (antar konstant), sedan differentiera derivatan
genom att (antar konstant).

Derivatan hittas genom att först differentiera funktionen med avseende på , sedan derivatan med avseende på .

Blandade partiella derivator är lika med varandra:
.

3. Gradient av en funktion av två variabler

gradientegenskaper

Exempel . Givet en funktion
. Hitta Gradient
vid punkten
och bygga den.

Lösning

Hitta koordinaterna för gradienten - partiella derivator.

Vid punkten
lutning är lika med . Vektor start
vid punkt och slut vid punkt .

5

4. Hitta de största och minsta värdena av en funktion av två variabler i ett slutet avgränsat område

Formulering av problemet. Låt på planet en sluten avgränsad domän
ges av ett system av formens ojämlikheter
. Det krävs att man hittar punkter i regionen där funktionen tar de största och minsta värdena.

Viktigt är extrema problem, vars matematiska modell innehåller linjär begränsningar (ekvationer, ojämlikheter) och linjär fungera
.

Formulering av problemet. Hitta de största och minsta värdena för en funktion
(2.1)

under restriktioner

(2.2)

. (2.3)

Eftersom det inte finns några kritiska punkter för en linjär funktion av många variabler inuti områden
, då uppnås endast den optimala lösningen som ger den objektiva funktionen ett extremum i utkanten av regionen. För det område som definieras av linjära begränsningar är de möjliga extrempunkterna hörnpunkter. Detta gör att vi kan överväga lösningen på problemet grafisk metod.

Grafisk lösning av ett system av linjära ojämlikheter

För att lösa detta problem grafiskt är det nödvändigt att grafiskt kunna lösa system av linjära olikheter med två variabler.

Procedur:

Observera att ojämlikheten
definierar höger koordinat halvplan(från axel
), och ojämlikheten
- övre koordinathalvplanet(från axel
).

Exempel. Lös grafisk ojämlikhet
.

Vi skriver gränslinjens ekvation
och konstruera den från två punkter, t.ex.
Och
. En rät linje delar ett plan i två halvplan.

Punktkoordinater
tillfredsställa ojämlikheten (
är sant), vilket betyder att koordinaterna för alla punkter i halvplanet som innehåller punkten uppfyller olikheten. Lösningen av ojämlikheten kommer att vara koordinaterna för punkterna i halvplanet som ligger till höger om gränslinjen, inklusive punkterna på gränsen. Det önskade halvplanet är markerat i figuren.

Lösning
system av ojämlikheter kallas tillåtlig, om dess koordinater är icke-negativa , . Uppsättningen av tillåtna lösningar till systemet med ojämlikheter bildar ett område som ligger i den första fjärdedelen av koordinatplanet.

Exempel. Konstruera lösningsområdet för systemet av ojämlikheter

Lösningarna på ojämlikheter är:

1)
- halvplan placerat till vänster och under i förhållande till den räta linjen ( )
;

2)
är ett halvplan beläget i det högra-undre halvplanet relativt den räta linjen ( )
;

3)
- halvplanet till höger om den räta linjen ( )
;

4) - ett halvplan ovanför abskissaxeln, det vill säga en rät linje ( )
.

0

Domän av tillåtna lösningar givet system av linjära ojämlikheter är uppsättningen av punkter belägna inuti och på gränsen för fyrhörningen
, vilket är genomskärning fyra halvplan.

Geometrisk representation av en linjär funktion

(nivålinjer och gradient)

Låt oss fixa värdet
, får vi ekvationen
, som geometriskt definierar en rät linje. Vid varje punkt tar den direkta funktionen på värdet och är nivålinje. Ger olika värden, t.ex.

, ... , vi får en uppsättning nivålinjer - uppsättning av parallella direkt.

Låt oss bygga lutning- vektor
, vars koordinater är lika med värdena för koefficienterna för variablerna i funktionen
. Denna vektor är: 1) vinkelrät mot varje rät linje (nivålinje)
; 2) visar ökningsriktningen för målfunktionen.

Exempel . Rita nivålinjer och funktionsgradient
.

Nivålinjer vid , , är raka

,
,

, parallella med varandra. Gradienten är en vektor vinkelrät mot varje nivålinje.

Grafisk upptäckt av de största och minsta värdena av en linjär funktion i en region

Geometrisk beskrivning av problemet. Hitta i lösningsområdet för systemet med linjära ojämlikheter punkten genom vilken nivålinjen passerar, motsvarande det största (minsta) värdet av en linjär funktion med två variabler.

Sekvensering:

4. Hitta koordinaterna för punkt A genom att lösa ekvationssystemet för linjer som skär varandra i punkt A, och beräkna funktionens minsta värde
. På samma sätt - för punkt B och funktionens största värde
. byggd på punkter.variabler Privatderivatfunktioner flera variabler och differentieringsteknik. Extremum funktionertvåvariabler och hans nödvändiga...

Begreppet en funktion av många variabler

Låt det finnas n-variabler och varje x 1, x 2 ... x n från en viss mängd x tilldelas en definition. numret Z, sedan på uppsättningen x ges funktionen Z \u003d f (x 1, x 2 ... x n) för många variabler.

X - område med definierade funktioner

x 1, x 2 ... x n - oberoende variabel (argument)

Z - funktion Exempel: Z \u003d P x 2 1 * x 2 (cylindervolym)

Tänk på Z \u003d f (x; y) - f-tion av 2 variabler x (x 1, x 2 ersatt av x, y). Resultaten överförs analogt till andra funktioner av många variabler. Området för att definiera funktionen för 2 variabler är hela sladden av kvadraten (ooh) eller en del av den. Mn-i värdet av den th funktionen av 2 variabler - ytan i ett 3-dimensionellt utrymme.

Tekniker för att konstruera grafer: - Rassm-t-snitt över kvadratens yta || koordinatrutor.

Exempel: x \u003d x 0, zn. kvadrat X || 0yz y \u003d y 0 0xz Typ av funktion: Z \u003d f (x 0, y); Z=f(x, y 0)

Till exempel: Z=x2 +y2 -2y

Z= x 2 +(y-1) 2 -1 x=0 Z=(y-1) 2 -1 y=1 Z= x 2 -1 Z=0 x 2 +(y-1) 2 -1

Parabolcirkel(centrum(0;1)

Gränser och kontinuitet för funktioner för två variabler

Låt Z = f (x; y) ges, då är A gränsen för f-tionen i m. (x 0, y 0), om för någon godtyckligt liten put. nummer E>0 substantiv-t positivt tal b>0, det för alla x,y som uppfyller |x-x 0 |<б; |y-y 0 |<б выполняется нерав-во |f(x,y)-A|

Z \u003d f (x; y) är kontinuerlig i t. (x 0, y 0), om: - den är definierad i denna t .; - har en ändlig gräns vid x, tenderar till x 0 och y till y 0; - denna gräns = värde

fungerar i t. (x 0, y 0), dvs. limf (x; y) \u003d f (x 0, y 0)

Om funktionen är kontinuerlig i varje. t. mn-va X, då är den kontinuerlig i detta område

Differentiell funktion, dess geometri. Användningen av dif-la i ungefärliga värden.

dy=f’(x)∆x – differentialfunktion

dy=dx, dvs. dy=f '(x)dx om y=x

Ur en geologs synvinkel är en funktionsdifferential ett steg i ordinatan för tangenten som ritas till grafen för funktionen i en punkt med abskissan x 0

Dif-l används vid beräkning av ca. funktionsvärden enligt formeln: f(x 0 +∆x)~f(x 0)+f’(x 0)∆x

Ju närmare ∆x är x, desto mer exakt blir resultatet.

Partiella derivator av första och andra ordningen

Första ordningens derivata (som kallas privat)

A. Låt x, y vara inkrementen av oberoende variabler x och y vid någon punkt från regionen X. Då kallas värdet lika med z = f(x + x, y + y) = f(x, y) för total ökning vid punkten x 0, y 0. Om variabeln x är fixerad, och variabeln y ökas med y, får vi zу = f(x, y, + y) – f(x, y)

Den partiella derivatan av variabeln y definieras på liknande sätt, dvs.

Den partiella derivatan av en funktion av 2 variabler hittas enligt samma regler som för funktioner av en variabel.

Skillnaden är att när man differentierar en funktion med avseende på variabeln x, betraktas y som const, och när man differentierar med avseende på y, betraktas x som const.

Isolerade konster är kopplade till funktionen med additions-/subtraktionsoperationer.

De associerade konsterna är kopplade till funktionen med multiplikation/divisionsoperationer.

Derivata av isolerad const = 0

1.4.Total differential av en funktion av 2 variabler och dess tillämpningar

Låt z = f(x,y), då

tz = - kallas ett helt steg

Partiell derivata av 2:a ordningen

För kontinuerliga funktioner av 2 variabler sammanfaller de blandade partiella derivatorna av 2:a ordningen.

Användningen av partiella derivator för att bestämma partiella derivator av max- och min-funktioner kallas extrema.

A. Punkter kallas max eller min z = f(x,y) om det finns några segment så att för alla x och y från detta område f(x,y)

T. Om en extremumpunkt för en funktion av 2 variabler ges, så är värdet av partiella derivator vid denna punkt lika med 0, d.v.s. ,

Punkterna där första ordningens partiella derivator kallas stationära eller kritiska.

Därför, för att hitta extremumpunkterna för en funktion av 2 variabler, används tillräckliga extremumvillkor.

Låt funktionen z = f(x,y) vara två gånger differentierbar, och låt den stationära punkten,

1) och maxA<0, minA>0.

1.4.(*)full differential. Den geometriska betydelsen av differentialen. Tillämpning av differentialen i ungefärliga beräkningar

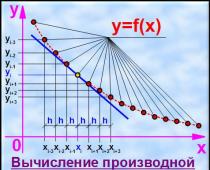
O. Låt funktionen y = f(x) definieras i något område vid punkterna . En funktion f(x) kallas differentierbar vid en punkt om den ökar vid denna punkt , där representeras i formen (1)

Där A är ett konstant värde oberoende av , vid en fast punkt x, - oändligt liten vid . En relativt linjär funktion A kallas differentialen för funktionen f(x) i en punkt och betecknas med df() eller dy.

Således kan uttryck (1) skrivas som ().

Funktionsdifferentialen i uttryck (1) har formen dy = A . Liksom alla linjära funktioner är den definierad för vilket värde som helst medan ökningen av funktionen endast måste beaktas för de för vilka + hör till domänen för funktionen f(x).

För att underlätta notationen av differentialen betecknas inkrementet med dx och kallas differentialen för den oberoende variabeln x. Därför skrivs differentialen som dy = Adx.

Om funktionen f(x) är differentierbar vid varje punkt i något intervall, så är dess differential en funktion av två variabler - punkten x och variabeln dx:

T. För att funktionen y = g(x) ska vara differentierbar någon gång , är det nödvändigt och tillräckligt att den har en derivata vid denna punkt, medan

(*)Bevis. Nödvändighet.

Låt funktionen f(x) vara differentierbar vid punkten , dvs. . Sedan

Därför finns derivatan f'() och är lika med A. Därför dy = f'()dx

Lämplighet.

Låt det finnas en derivata f'(), dvs. = f'(). Då är kurvan y = f(x) ett tangentsegment. För att beräkna värdet av en funktion vid en punkt x, ta en punkt i en del av dess grannskap, så att det inte är svårt att hitta f() och f’()/