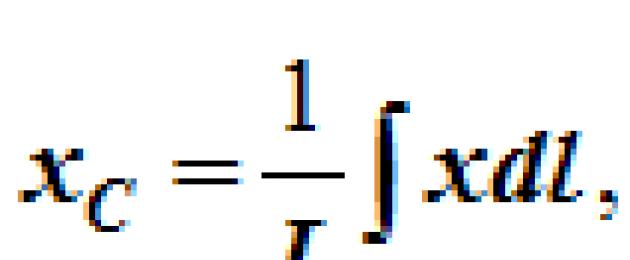How to find the center of gravity of a trapezoid formula. Methods for determining the coordinates of the center of gravity

Center of gravity of a circular arc

The arc has an axis of symmetry. The center of gravity lies on this axis, i.e. y C = 0 .

dl– arc element, dl = Rdφ, R– radius of the circle, x = Rcosφ, L= 2αR,

Hence:

x C = R(sinα/α).

Center of gravity of a circular sector

Radius sector R with central angle 2 α has an axis of symmetry Ox, where the center of gravity is located.

We divide the sector into elementary sectors, which can be considered triangles. The centers of gravity of elementary sectors are located on a circular arc of radius (2/3) R.

The center of gravity of the sector coincides with the center of gravity of the arc AB:

Semicircle:

37. Kinematics. Kinematics of a point. Methods for specifying the movement of a point.

Kinematics– a branch of mechanics in which the movement of material bodies is studied from a geometric point of view, without taking into account mass and the forces acting on them. Ways to specify the movement of a point: 1) natural, 2) coordinate, 3) vector.

Kinematics of a point- a branch of kinematics that studies the mathematical description of the movement of material points. The main task of kinematics is to describe movement using a mathematical apparatus without identifying the reasons causing this movement.

Natural sp. the trajectory of the point, the law of its movement along this trajectory, the beginning and direction of the arc coordinate are indicated: s=f(t) – the law of the point’s movement. For linear motion: x=f(t).

Coordinate sp. the position of a point in space is determined by three coordinates, changes in which determine the law of motion of the point: x=f 1 (t), y=f 2 (t), z=f 3 (t).

If the motion is in a plane, then there are two equations of motion. The equations of motion describe the trajectory equation in parametric form. By excluding the parameter t from the equations, we obtain the trajectory equation in the usual form: f(x,y)=0 (for a plane).

Vector sp. the position of a point is determined by its radius vector drawn from some center. A curve that is drawn by the end of a vector is called. hodograph this vector. Those. trajectory – radius vector hodograph.

38. Relationship between coordinate and vector, coordinate and natural methods of specifying the movement of a point.

RELATIONSHIP OF THE VECTOR METHOD WITH THE COORDINATE AND NATURAL METHOD expressed by the ratios:

where is the unit unit of the tangent to the trajectory at a given point, directed towards the distance reference, and is the unit unit of the normal to the trajectory at a given point, directed towards the center of curvature (see Fig. 3).

CONNECTION OF THE COORDINATE METHOD WITH THE NATURAL. Trajectory equation f(x, y)=z; f 1 (x, z)=y is obtained from the equations of motion in coordinate form by eliminating the time t. Additional analysis of the values that the coordinates of a point can take determines that section of the curve that is a trajectory. For example, if the motion of a point is given by the equations: x=sin t; y=sin 2 t=x 2 , then the trajectory of the point is that section of the parabola y=x 2 for which -1≤x≤+1, 0≤x≤1. The beginning and direction of distance counting are chosen arbitrarily, this further determines the sign of the speed and the magnitude and sign of the initial distance s 0 .

The law of motion is determined by the dependence:

the sign + or - is determined depending on the accepted direction of distance measurement.

Point speed is a kinematic measure of its motion, equal to the time derivative of the radius vector of this point in the reference system under consideration. The velocity vector is directed tangent to the trajectory of the point in the direction of movement

Velocity vector (v) is the distance that a body travels in a certain direction per unit of time. Please note that the definition velocity vector is very similar to the definition of speed, except for one important difference: the speed of a body does not indicate the direction of movement, but the velocity vector of a body indicates both the speed and direction of movement. Therefore, two variables are needed that describe the velocity vector of the body: speed and direction. Physical quantities that have a value and a direction are called vector quantities.

Speed vector body may change from time to time. If either its speed or direction changes, the speed of the body also changes. A constant velocity vector implies a constant speed and a constant direction, whereas the term constant speed only implies a constant value without taking direction into account. The term "velocity vector" is often used interchangeably with the term "velocity". They both express the distance a body travels per unit time

Point acceleration is a measure of the change in its speed, equal to the derivative with respect to time of the speed of this point or the second derivative of the radius vector of the point with respect to time. Acceleration characterizes the change in the velocity vector in magnitude and direction and is directed towards the concavity of the trajectory.

Acceleration vector

This is the ratio of the change in speed to the period of time during which this change occurred. The average acceleration can be determined by the formula:

Where - acceleration vector.

The direction of the acceleration vector coincides with the direction of change in speed Δ = - 0 (here 0 is the initial speed, that is, the speed at which the body began to accelerate).

At time t1 (see Fig. 1.8) the body has a speed of 0. At time t2 the body has speed . According to the rule of vector subtraction, we find the vector of speed change Δ = - 0. Then you can determine the acceleration like this:

6.1. General information

Center of Parallel Forces
Let us consider two parallel forces directed in one direction, and , applied to the body at points A 1 and A 2 (Fig.6.1). This system of forces has a resultant, the line of action of which passes through a certain point WITH. Point position WITH can be found using Varignon's theorem:

If you turn the forces and near the points A 1 and A 2 in one direction and at the same angle, we get new system parallel salas having the same modules. In this case, their resultant will also pass through the point WITH. This point is called the center of parallel forces.
Let's consider a system of parallel and identically directed forces applied to a solid body at points. This system has a resultant.
If each force of the system is rotated near the points of their application in the same direction and at the same angle, then new systems of identically directed parallel forces with the same modules and points of application will be obtained. The resultant of such systems will have the same modulus R, but every time a different direction. Having folded my strength F 1 and F 2 we find that their resultant R 1, which will always pass through the point WITH 1, the position of which is determined by the equality . Folding further R 1 and F 3, we find their resultant, which will always pass through the point WITH 2 lying on a straight line A 3 WITH 2. Having completed the process of adding forces to the end, we will come to the conclusion that the resultant of all forces will indeed always pass through the same point WITH, whose position relative to the points will be unchanged.
Dot WITH, through which the line of action of the resultant system of parallel forces passes for any rotation of these forces near the points of their application in the same direction at the same angle is called the center of parallel forces (Fig. 6.2).

Fig.6.2

Let us determine the coordinates of the center of parallel forces. Since the position of the point WITH relative to the body is unchanged, then its coordinates do not depend on the choice of coordinate system. Let's turn all the forces around their application so that they become parallel to the axis OU and apply Varignon’s theorem to rotated forces. Because R" is the resultant of these forces, then, according to Varignon’s theorem, we have , because , , we get

From here we find the coordinate of the center of parallel forces zc:

To determine the coordinates xc Let's create an expression for the moment of forces about the axis Oz.

To determine the coordinates yc let's turn all the forces so that they become parallel to the axis Oz.

The position of the center of parallel forces relative to the origin (Fig. 6.2) can be determined by its radius vector:

6.2. Center of gravity of a rigid body

Center of gravity of a rigid body is a point invariably associated with this body WITH, through which the line of action of the resultant forces of gravity passes given body, for any position of the body in space.
The center of gravity is used to study the stability of equilibrium positions of bodies and continuum, under the influence of gravity and in some other cases, namely: in the strength of materials and in structural mechanics - when using Vereshchagin’s rule.
There are two ways to determine the center of gravity of a body: analytical and experimental. The analytical method for determining the center of gravity directly follows from the concept of the center of parallel forces.
The coordinates of the center of gravity, as the center of parallel forces, are determined by the formulas:

Where R- whole body weight; pk- weight of body particles; xk, yk, zk- coordinates of body particles.
For a homogeneous body, the weight of the entire body and any part of it is proportional to the volume P=Vγ, pk =vk γ, Where γ - weight per unit volume, V- body volume. Substituting expressions P, pk into the formula for determining the coordinates of the center of gravity and, reducing by common multiplier γ , we get:

Dot WITH, whose coordinates are determined by the resulting formulas, is called center of gravity of the volume.
If the body is a thin homogeneous plate, then the center of gravity is determined by the formulas:

Where S- area of the entire plate; sk- area of its part; xk, yk- coordinates of the center of gravity of the plate parts.
Dot WITH in this case it is called center of gravity area.
Numerators of expressions defining the coordinates of the center of gravity flat figures, are called with static moments of area relative to the axes at And X:

Then the center of gravity of the area can be determined by the formulas:

For bodies whose length is many times greater than the cross-sectional dimensions, determine the center of gravity of the line. The coordinates of the line's center of gravity are determined by the formulas:

Where L- line length; lk- the length of its parts; xk, yk, zk- coordinate of the center of gravity of parts of the line.

6.3. Methods for determining the coordinates of the centers of gravity of bodies

Based on the obtained formulas, we can propose practical ways determining the centers of gravity of bodies.
1. Symmetry. If a body has a center of symmetry, then the center of gravity is at the center of symmetry.
If the body has a plane of symmetry. For example, the XOU plane, then the center of gravity lies in this plane.
2. Splitting. For bodies consisting of bodies with simple shapes, the splitting method is used. The body is divided into parts, the center of gravity of which is determined by the method of symmetry. The center of gravity of the entire body is determined by the formulas for the center of gravity of volume (area).

Example. Determine the center of gravity of the plate shown in the figure below (Fig. 6.3). The plate can be divided into rectangles in different ways and determine the coordinates of the center of gravity of each rectangle and their area.

Fig.6.3

Answer: xc=17.0cm; yc=18.0cm.

3. Addition. This method is a special case of the partitioning method. It is used when the body has cutouts, slices, etc., if the coordinates of the center of gravity of the body without the cutout are known.

Example. Determine the center of gravity of a circular plate having a cutout radius r = 0,6 R(Fig. 6.4).

Fig.6.4

A round plate has a center of symmetry. Let's place the origin of coordinates at the center of the plate. Plate area without cutout, cutout area. Square plate with cutout; .
The plate with a cutout has an axis of symmetry О1 x, hence, yc=0.

4. Integration. If the body cannot be divided into a finite number of parts, the positions of the centers of gravity of which are known, the body is divided into arbitrary small volumes, for which the formula using the partitioning method takes the form: .
Then they go to the limit, directing the elementary volumes to zero, i.e. contracting volumes into points. The sums are replaced by integrals extended to the entire volume of the body, then the formulas for determining the coordinates of the center of gravity of the volume take the form:

Formulas for determining the coordinates of the center of gravity of an area:

The coordinates of the center of gravity of the area must be determined when studying the equilibrium of plates, when calculating the Mohr integral in structural mechanics.

Example. Determine the center of gravity of a circular arc of radius R with central angle AOB= 2α (Fig. 6.5).

Rice. 6.5

The arc of a circle is symmetrical to the axis Oh, therefore, the center of gravity of the arc lies on the axis Oh, yс = 0.
According to the formula for the center of gravity of a line:

6.Experimental method. Centers of gravity inhomogeneous bodies complex configuration can be determined experimentally: by hanging and weighing. The first method is to suspend the body on a cable at various points. The direction of the cable on which the body is suspended will give the direction of gravity. The point of intersection of these directions determines the center of gravity of the body.
The weighing method involves first determining the weight of a body, such as a car. Then the pressure of the vehicle's rear axle on the support is determined on the scales. By drawing up an equilibrium equation relative to a point, for example, the axis of the front wheels, you can calculate the distance from this axis to the center of gravity of the car (Fig. 6.6).

Fig.6.6

Sometimes, when solving problems, it is necessary to simultaneously use different methods for determining the coordinates of the center of gravity.

6.4. Centers of gravity of some protozoa geometric shapes

To determine the centers of gravity of bodies of frequently occurring shapes (triangle, circular arc, sector, segment), it is convenient to use reference data (Table 6.1).

Table 6.1

Coordinates of the center of gravity of some homogeneous bodies

№	Name of the figure	Drawing
	Arc of a circle: the center of gravity of an arc of a uniform circle is on the axis of symmetry (coordinate uc=0). R- radius of the circle.
	Homogeneous circular sector uc=0). where α is half the central angle; R- radius of the circle.
	Segment: the center of gravity is located on the axis of symmetry (coordinate uc=0). where α is half the central angle; R- radius of the circle.
	Semicircle:
	Triangle: the center of gravity of a homogeneous triangle is at the point of intersection of its medians. Where x1, y1, x2, y2, x3, y3- coordinates of the triangle vertices
	Cone: the center of gravity of a uniform circular cone lies at its height and is located at a distance of 1/4 of the height from the base of the cone.

Center of gravity - the point through which the line of action of the resultant passes elementary forces gravity. It has the property of a center of parallel forces (E.M. Nikitin, § 42). That's why formulas for determining the position of the center of gravity of various bodies have the form:
x c = (∑ G i x i) / ∑ G i ;
(1) y c = (∑ G i y i) / ∑ G i ;
z c = (∑ G i z i) / ∑ G i .

If the body whose center of gravity needs to be determined can be identified with a figure made up of lines (for example, a closed or open contour made of wire, as in Fig. 173), then the weight G i of each segment l i can be represented as the product
G i = l i d,
where d is the constant weight of a unit length of material for the entire figure.

After substituting their l i d values into formulas (1) instead of G i, the constant factor d in each term of the numerator and denominator can be taken out of brackets (beyond the sign of the sum) and reduced. Thus, formulas for determining the coordinates of the center of gravity of a figure composed of line segments, will take the form:
x c = (∑ l i x i) / ∑ l i ;
(2) y c = (∑ l i y i) / ∑ l i ;
z c = (∑ l i z i) / ∑ l i .

If the body has the form of a figure composed of planes or curved surfaces arranged in various ways (Fig. 174), then the weight of each plane (surface) can be represented as follows:
G i = F i p,
where F i is the area of each surface, and p is the weight per unit area of the figure.

After substituting this value of G i into formulas (1), we obtain formulas for the coordinates of the center of gravity of a figure composed of areas:
x c = (∑ F i x i) / ∑ F i ;
(3) y c = (∑ F i y i) / ∑ F i ;
z c = (∑ F i z i) / ∑ F i .

If a homogeneous body can be divided into simple parts of a certain geometric shape (Fig. 175), then the weight of each part
G i = V i γ,
where V i is the volume of each part, and γ is the weight per unit volume of the body.

After substituting the values of G i into formulas (1), we obtain formulas for determining the coordinates of the center of gravity of a body composed of homogeneous volumes:
x c = (∑ V i x i) / ∑ V i ;
(4) y c = (∑ V i y i) / ∑ V i ;
z c = (∑ V i z i) / ∑ V i .

When solving some problems of determining the position of the center of gravity of bodies, it is sometimes necessary to know where the center of gravity of an arc of a circle, a circular sector or a triangle is located.

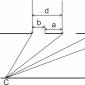
If the radius of the arc r and the central angle 2α subtended by the arc and expressed in radians are known, then the position of the center of gravity C (Fig. 176, a) relative to the center of the arc O is determined by the formula:
(5) x c = (r sin α)/α.

If the chord AB=b of the arc is given, then in formula (5) you can make the replacement
sin α = b/(2r)
and then
(5a) x c = b/(2α).

In the particular case for a semicircle, both formulas will take the form (Fig. 176, b):
(5b) x c = OC = 2r/π = d/π.

The position of the center of gravity of a circular sector, if its radius r is given (Fig. 176, c), is determined using the formula:
(6) x c = (2r sin α)/(3α).

If the sector chord is given, then:
(6a) x c = b/(3α).

In the special case for a semicircle, both last formulas will take the form (Fig. 176, d)
(6b) x c = OC = 4r/(3π) = 2d/(3π).

The center of gravity of the area of any triangle is located from any side at a distance equal to one third of the corresponding height.

U right triangle the center of gravity is at the intersection of perpendiculars raised to the legs from points located at a distance of one third of the length of the legs, counting from the vertex right angle(Fig. 177).

When solving problems of determining the position of the center of gravity of any homogeneous body, composed either of thin rods (lines), or of plates (areas), or of volumes, it is advisable to adhere to the following order:

1) draw a body, the position of the center of gravity of which needs to be determined. Since all body dimensions are usually known, scale must be observed;

2) break the body into component parts (line segments or areas, or volumes), the position of the centers of gravity is determined based on the size of the body;

3) determine either lengths, or areas, or volumes components;

4) select the location of the coordinate axes;

5) determine the coordinates of the centers of gravity of the components;

6) found values of lengths or areas or volumes individual parts, as well as the coordinates of their centers of gravity, substitute into the appropriate formulas and calculate the coordinates of the center of gravity of the entire body;

7) using the found coordinates, indicate in the figure the position of the body’s center of gravity.

§ 23. Determination of the position of the center of gravity of a body composed of thin homogeneous rods

§ 24. Determination of the position of the center of gravity of figures composed of plates

In the last problem, as well as in the problems given in the previous paragraph, dividing the figures into their component parts does not cause any particular difficulties. But sometimes the figure has a form that allows it to be divided into its component parts in several ways, for example, a thin rectangular plate with a triangular cutout (Fig. 183). When determining the position of the center of gravity of such a plate, its area can be divided into four rectangles (1, 2, 3 and 4) and one right triangle 5 - in several ways. Two options are shown in Fig. 183, a and b.

The most rational way of dividing a figure into its component parts is that which produces the smallest number of parts. If there are cutouts in the figure, then they can also be included among the component parts of the figure, but the area of the cut-out part is considered negative. Therefore, this division is called the method of negative areas.

The plate in Fig. 183, in is divided using this method into only two parts: rectangle 1 with the area of the entire plate, as if it were whole, and triangle 2 with the area, which we consider negative.

§ 26. Determination of the position of the center of gravity of a body composed of parts having a simple geometric shape

To solve problems of determining the position of the center of gravity of a body made up of parts having a simple geometric shape, you must have the skills to determine the coordinates of the center of gravity of figures made up of lines or areas.

Based on the above general formulas, you can specify specific methods for determining the coordinates of the centers of gravity of bodies.

1. Symmetry. If a homogeneous body has a plane, axis or center of symmetry (Fig. 7), then its center of gravity lies, respectively, in the plane of symmetry, axis of symmetry or in the center of symmetry.

Fig.7

2. Splitting. The body is divided into a finite number of parts (Fig. 8), for each of which the position of the center of gravity and area are known.

Fig.8

3.Negative area method. A special case of the partitioning method (Fig. 9). It applies to bodies that have cutouts if the centers of gravity of the body without the cutout and the cutout part are known. A body in the form of a plate with a cutout is represented by a combination of a solid plate (without a cutout) with an area S 1 and an area of the cut out part S 2 .

Fig.9

4.Grouping method. It is a good complement to the last two methods. After dividing a figure into its component elements, it is convenient to combine some of them again in order to then simplify the solution by taking into account the symmetry of this group.

Centers of gravity of some homogeneous bodies.

1) Center of gravity of a circular arc. Consider the arc AB radius R with a central angle. Due to symmetry, the center of gravity of this arc lies on the axis Ox(Fig. 10).

Fig.10

Let's find the coordinate using the formula. To do this, select on the arc AB element MM' length, the position of which is determined by the angle. Coordinate X element MM' will . Substituting these values X and d l and keeping in mind that the integral must be extended over the entire length of the arc, we obtain:

Where L- arc length AB, equal to .

From here we finally find that the center of gravity of a circular arc lies on its axis of symmetry at a distance from the center ABOUT, equal

where the angle is measured in radians.

2) Center of gravity of the triangle's area. Consider a triangle lying in the plane Oxy, the coordinates of the vertices of which are known: A i(x i,y i), (i= 1,2,3). Breaking the triangle into narrow strips parallel to the side A 1 A 2, we come to the conclusion that the center of gravity of the triangle must belong to the median A 3 M 3 (Fig. 11).

Fig.11

Breaking a triangle into strips parallel to the side A 2 A 3, we can verify that it must lie on the median A 1 M 1 . Thus, the center of gravity of a triangle lies at the point of intersection of its medians, which, as is known, separates a third part from each median, counting from the corresponding side.

In particular, for the median A 1 M 1 we obtain, taking into account that the coordinates of the point M 1 is the arithmetic mean of the coordinates of the vertices A 2 and A 3:

x c = x 1 + (2/3)∙(x M 1 - x 1) = x 1 + (2/3)∙[(x 2 + x 3)/2-x 1 ] = (x 1 +x 2 +x 3)/3.

Thus, the coordinates of the triangle’s center of gravity are the arithmetic mean of the coordinates of its vertices:

x c =(1/3)Σ x i ; y c =(1/3)Σ y i.

3) Center of gravity of the area of a circular sector. Consider a sector of a circle with radius R with a central angle of 2α, located symmetrically relative to the axis Ox(Fig. 12) .

It's obvious that y c = 0, and the distance from the center of the circle from which this sector is cut to its center of gravity can be determined by the formula:

Fig.12

The easiest way to calculate this integral is by dividing the integration domain into elementary sectors with an angle dφ. Accurate to infinitesimals of the first order, such a sector can be replaced by a triangle with a base equal to R× dφ and height R. The area of such a triangle dF=(1/2)R 2 ∙dφ, and its center of gravity is at a distance of 2/3 R from the vertex, therefore in (5) we put x = (2/3)R∙cosφ. Substituting in (5) F= α R 2, we get:

Using the last formula, we calculate, in particular, the distance to the center of gravity semicircle.

Substituting α = π/2 into (2), we obtain: x c = (4R)/(3π) ≅ 0.4 R .

Example 1. Let us determine the center of gravity of the homogeneous body shown in Fig. 13.

Fig.13

The body is homogeneous, consisting of two parts with a symmetrical shape. Coordinates of their centers of gravity:

Their volumes:

Therefore, the coordinates of the center of gravity of the body

Example 2. Let us find the center of gravity of a plate bent at a right angle. Dimensions are in the drawing (Fig. 14).

Fig.14

Coordinates of the centers of gravity:

Areas:

Rice. 6.5.

Example 3. A square sheet cm has a square hole cut out cm (Fig. 15). Let's find the center of gravity of the sheet.

Fig.15

In this problem, it is more convenient to divide the body into two parts: a large square and a square hole. Only the area of the hole should be considered negative. Then the coordinates of the center of gravity of the sheet with the hole:

coordinate since the body has an axis of symmetry (diagonal).

Example 4. The wire bracket (Fig. 16) consists of three sections of equal length l.

Fig.16

Coordinates of the centers of gravity of the sections:

Therefore, the coordinates of the center of gravity of the entire bracket are:

Example 5. Determine the position of the center of gravity of the truss, all the rods of which have the same linear density (Fig. 17).

Let us recall that in physics the density of a body ρ and its specific gravity g are related by the relation: γ= ρ g, Where g- acceleration free fall. To find the mass of such a homogeneous body, you need to multiply the density by its volume.

Fig.17

The term “linear” or “linear” density means that to determine the mass of a truss rod, the linear density must be multiplied by the length of this rod.

To solve the problem, you can use the partitioning method. Representing a given truss as a sum of 6 individual rods, we obtain:

Where L i length i th truss rod, and x i, y i- coordinates of its center of gravity.

The solution to this problem can be simplified by grouping the last 5 bars of the truss. It is easy to see that they form a figure with a center of symmetry located in the middle of the fourth rod, where the center of gravity of this group of rods is located.

Thus, a given truss can be represented by a combination of only two groups of rods.

The first group consists of the first rod, for it L 1 = 4 m, x 1 = 0 m, y 1 = 2 m. The second group of rods consists of five rods, for it L 2 = 20 m, x 2 = 3 m, y 2 = 2 m.

The coordinates of the center of gravity of the truss are found using the formula:

x c = (L 1 ∙x 1 +L 2 ∙x 2)/(L 1 + L 2) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙y 1 +L 2 ∙y 2)/(L 1 + L 2) = (4∙2 + 20∙2)/24 = 2 m.

Note that the center WITH lies on the straight line connecting WITH 1 and WITH 2 and divides the segment WITH 1 WITH 2 regarding: WITH 1 WITH/SS 2 = (x c - x 1)/(x 2 - x c ) = L 2 /L 1 = 2,5/0,5.

Self-test questions

What is the center of parallel forces called?

How are the coordinates of the center of parallel forces determined?

How to determine the center of parallel forces whose resultant is zero?

What properties does the center of parallel forces have?

What formulas are used to calculate the coordinates of the center of parallel forces?

What is the center of gravity of a body?

Why can the gravitational forces of the Earth acting on a point on a body be taken as a system of parallel forces?

Write down the formula for determining the position of the center of gravity of inhomogeneous and homogeneous bodies, the formula for determining the position of the center of gravity of flat sections?

Write down the formula for determining the position of the center of gravity of simple geometric shapes: rectangle, triangle, trapezoid and half circle?

What is the static moment of area?

Give an example of a body whose center of gravity is located outside the body.

How are the properties of symmetry used in determining the centers of gravity of bodies?

What is the essence of the negative weights method?

Where is the center of gravity of a circular arc?

What graphical construction can you find the center of gravity of a triangle?

Write down the formula that determines the center of gravity of a circular sector.

Using formulas that determine the centers of gravity of a triangle and a circular sector, derive a similar formula for a circular segment.

What formulas are used to calculate the coordinates of the centers of gravity of homogeneous bodies, flat figures and lines?

What is called the static moment of the area of a plane figure relative to the axis, how is it calculated and what dimension does it have?

How to determine the position of the center of gravity of an area if the position of the centers of gravity of its individual parts is known?

What auxiliary theorems are used to determine the position of the center of gravity?

Lecture 4. Center of gravity.

This lecture covers the following issues

1. Center of gravity of a solid body.

2. Coordinates of the centers of gravity of inhomogeneous bodies.

3. Coordinates of the centers of gravity of homogeneous bodies.

4. Methods for determining the coordinates of centers of gravity.

5. Centers of gravity of some homogeneous bodies.

The study of these issues is necessary in the future to study the dynamics of the movement of bodies taking into account sliding and rolling friction, the dynamics of the movement of the center of mass of a mechanical system, kinetic moments, to solve problems in the discipline “Strength of Materials”.

Bringing parallel forces.

After we have considered bringing a flat system and an arbitrary spatial system of forces to the center, we again return to considering the special case of a system of parallel forces.

Bringing two parallel forces.

In the course of considering such a system of forces, the following three cases of reduction are possible.

1. System of two collinear forces. Let us consider a system of two parallel forces directed in one direction P And Q, applied at points A And IN. We will assume that the forces are perpendicular to this segment (Fig. 1, A).

WITH, belonging to the segment AB and satisfying the condition:

AC/NE = Q/P.(1)

Main vector of the system R C = P + Q is equal in modulus to the sum of these forces: R C = P + Q.

WITH taking into account (1) is equal to zero:MC = P ∙ AC- Q∙ CB = 0.

Thus, as a result of the casting we got: R C ≠ 0, MC= 0. This means that main vector is equivalent to the resultant passing through the center of reduction, that is:

The resultant of collinear forces is equal in modulus to their sum, and its line of action divides the segment connecting the points of their application, in inverse proportion to the moduli of these forces in an internal manner.

Note that the position of the point WITH will not change if the forces R And Q turn an angleα. Dot WITH, which has this property is called center of parallel forces.

2. System of two anticollinear and forces not equal in magnitude. May the strength P And Q, applied at points A And IN, parallel, directed in opposite directions and unequal in magnitude (Fig. 1, b).

Let us choose a point as the reduction center WITH, which still satisfies relation (1) and lies on the same line, but outside the segment AB.

The main vector of this system R C = P + Q the modulus will now be equal to the difference between the moduli of the vectors: R C = Q - P.

The main point regarding the center WITH is still zero:MC = P ∙ AC- Q∙ NE= 0, so

Resultant anticollinear and forces that are not equal in magnitude are equal to their difference, directed towards the greater force, and its line of action divides the segment connecting the points of their application, in inverse proportion to the external moduli of these forces.

Fig.1

3. System of two anticollinear and forces equal in magnitude. Let's take the previous case of reduction as the initial one. Let's fix the force R, and strength Q let us direct the modulus to the force R.

Then at Q → R in formula (1) the relation AC/NE → 1. This means that AC → NE, that is, the distance AC →∞ .

In this case, the module of the main vector R C → 0, and the modulus of the main moment does not depend on the position of the center of reduction and remains equal to the original value:

MC = P ∙ AC- Q∙ NE = P ∙ ( AC- NE) =P ∙ AB.

So, in the limit we have obtained a system of forces for which R C = 0, MC≠ 0, and the center of reduction is removed to infinity, which cannot be replaced by the resultant. It is not difficult to recognize a couple of forces in this system, so a pair of forces has no resultant.

Center of the system of parallel forces.

Consider the system n strength P i, applied at pointsA i (x i , y i , z i) and parallel to the axisOv with orth l(Fig. 2).

If we exclude in advance the case of a system equivalent to a pair of forces, it is not difficult, based on the previous paragraph, to prove the existence of its resultantR.

Let's determine the coordinates of the centerC(x c, y c, z c) parallel forces, that is, the coordinates of the point of application of the resultant of this system.

For this purpose, we use Varignon’s theorem, based on which:

M0 (R) = Σ M0(P i).

Fig.2

The vector-moment of a force can be represented as a vector product, therefore:

M 0 (R) = r c× R = Σ M0i(P i) = Σ ( r i× P i ).

Considering that R = Rv ∙ l, A P i = Pvi ∙ l and using the properties of the vector product, we get:

r c × Rv ∙ l = Σ ( r i × Pvi ∙ l),

r c ∙ R v× l = Σ ( r i ∙ Pvi × l) = Σ ( r i ∙ Pvi ) × l,

or:

[ r c R v - Σ ( r i Pvi )] × l= 0.

The last expression is valid only if the expression in square brackets is equal to zero. Therefore, omitting the indexvand taking into account that the resultantR = Σ P i , from here we get:

r c = (Σ P i r i )/(Σ P i ).

Projecting the last vector equality on the coordinate axis, we obtain the required expression for the coordinates of the center of parallel forces:

x c = (Σ P i x i)/(Σ P i );

y c = (Σ P i y i )/(Σ P i );(2)

z c = (Σ P i z i )/(Σ P i ).

Center of gravity of bodies.

Coordinates of the centers of gravity of a homogeneous body.

Let's consider solid weight P and volume V in the coordinate system Oxyz, where are the axes x And y connected to the surface of the earth, and the axis z aimed at the zenith.

If we break the body into elementary parts with a volume∆ V i , then the force of attraction will act on each part of it∆ P i, directed towards the center of the Earth. Let us assume that the dimensions of the body are significantly smaller than the dimensions of the Earth, then the system of forces applied to the elementary parts of the body can be considered not converging, but parallel (Fig. 3), and all the conclusions of the previous chapter are applicable to it.

Fig.3

Definition . The center of gravity of a solid body is the center of parallel forces of gravity of the elementary parts of this body.

Let us remind you that specific gravity of an elementary part of the body is called the ratio of its weight∆ P i to volume ∆ V i : γ i = ∆ P i/ ∆ V i . For a homogeneous body this value is constant:γ i = γ = P/ V.

Substituting ∆ into (2) P i = γ i ∙∆ V i instead of P i, taking into account the last remark and reducing the numerator and denominator byg, we get expressions for the coordinates of the center of gravity of a homogeneous body:

x c = (Σ ∆ V i∙ x i)/(Σ ∆ V i);

y c = (Σ ∆ V i∙ y i )/(Σ ∆ V i);(3)

z c = (Σ ∆ V i∙ z i )/(Σ ∆ V i).

Several theorems are useful in determining the center of gravity.

1) If a homogeneous body has a plane of symmetry, then its center of gravity is in this plane.

If the axes X And at located in this plane of symmetry, then for each point with coordinates. And the coordinate according to (3), will be equal to zero, because in total All members with opposite signs are destroyed in pairs. This means that the center of gravity is located in the plane of symmetry.

2) If a homogeneous body has an axis of symmetry, then the center of gravity of the body is on this axis.

Indeed, in this case, if the axiszdraw along the axis of symmetry, for each point with coordinatesyou can find a point with coordinates and coordinates and , calculated using formulas (3), will be equal to zero.

The third theorem is proved in a similar way.

3) If a homogeneous body has a center of symmetry, then the center of gravity of the body is at this point.

And a few more comments.

First. If the body can be divided into parts for which the weight and position of the center of gravity are known, then there is no need to consider each point, and in formulas (3) P i – determined as the weight of the corresponding part and– as the coordinates of its center of gravity.

Second. If the body is homogeneous, then the weight of an individual part of it, Where - specific gravity of the material from which the body is made, and V i - the volume of this part of the body. And formulas (3) will take a more convenient form. For example,

And similarly, where - volume of the whole body.

Third note. Let the body have the form of a thin plate with an area F and thickness t, lying in the plane Oxy. Substituting in (3)∆ V i =t ∙ ∆F i , we obtain the coordinates of the center of gravity of a homogeneous plate:

x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

y c = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).

z c = (Σ ∆ F i∙ z i ) / (Σ ∆ F i).

Where – coordinates of the center of gravity of individual plates;– total body area.

Fourth note. For a body in the form of a thin curved rod of length L with cross-sectional area a elementary volume∆ V i = a ∙∆ L i , That's why coordinates of the center of gravity of a thin curved rod will be equal:

x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);

y c = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)

z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).

Where – coordinates of the center of gravityi-th section; .

Note that, according to the definition, the center of gravity is a geometric point; it can also lie outside the boundaries of a given body (for example, for a ring).

Note.

In this section of the course we do not differentiate between gravity, gravity and body weight. In reality, gravity is the difference between the gravitational force of the Earth and the centrifugal force caused by its rotation.

Coordinates of the centers of gravity of inhomogeneous bodies.

Center of gravity coordinates inhomogeneous solid(Fig.4) in the selected reference system are determined as follows:

Fig.4

Where - weight per unit volume of a body (specific gravity)

- whole body weight.

non-uniform surface(Fig. 5), then the coordinates of the center of gravity in the selected reference system are determined as follows:

Fig.5

Where - weight per unit body area,

- whole body weight.

If the solid is non-uniform line(Fig. 6), then the coordinates of the center of gravity in the selected reference system are determined as follows:

Fig.6

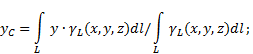
Where - weight per body length,

Whole body weight.

Methods for determining the coordinates of the center of gravity.

Based on the general formulas obtained above, it is possible to indicate specific methods determining the coordinates of the centers of gravity of bodies.

Fig.7

2. Splitting. The body is divided into a finite number of parts (Fig. 8), for each of which the position of the center of gravity and area are known.

Fig.8

S =S 1 +S 2.

Fig.9

S = S 1 - S 2.

Centers of gravity of some homogeneous bodies.

1) Center of gravity of a circular arc. Consider the arc AB radiusR with central angle. Due to symmetry, the center of gravity of this arc lies on the axisOx(Fig. 10).

Fig.10

Let's find the coordinate according to the formula . To do this, select on the arc AB element MM ’ length, whose position is determined by the angle. Coordinate X element MM' will. Substituting these values X And d l and keeping in mind that the integral must be extended over the entire length of the arc, we obtain:

where L is the length of arc AB, equal to .

From here we finally find that the center of gravity of a circular arc lies on its axis of symmetry at a distance from the center O equal

where is the angle measured in radians.

2) Center of gravity of the triangle's area. Consider a triangle lying in the plane Oxy, the coordinates of the vertices of which are known: A i (x i,y i ), (i= 1,2,3). Breaking the triangle into narrow strips parallel to the side A 1 A 2, we come to the conclusion that the center of gravity of the triangle must belong to the median A 3 M 3 (Fig. 11).

Fig.11

In particular, for the median A 1 M 1 we obtain, taking into account that the coordinates of the point M 1 - this is the arithmetic mean of the coordinates of the vertices A 2 and A 3 :

x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.

Thus, the coordinates of the triangle’s center of gravity are the arithmetic mean of the coordinates of its vertices:

x c =(1/3) Σ x i ; y c =(1/3) Σ y i .

3) Center of gravity of the area of a circular sector. Consider a sector of a circle with radius R with central angle 2α , located symmetrically about the axis Ox (Fig. 12) .

It's obvious that y c = 0, and the distance from the center of the circle from which this sector is cut to its center of gravity can be determined by the formula:

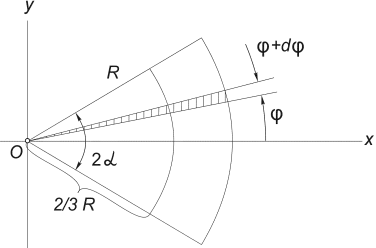
Fig.12

The easiest way to calculate this integral is by dividing the integration domain into elementary sectors with an angle dφ . Accurate to infinitesimals of the first order, such a sector can be replaced by a triangle with a base equal to R × dφ and height R. The area of such a triangle dF =(1/2)R 2 ∙ dφ , and its center of gravity is at a distance of 2/3 R from the vertex, therefore in (5) we put x = (2/3)R∙ cosφ. Substituting in (5) F= α R 2, we get:

Using the last formula, we calculate, in particular, the distance to the center of gravity semicircle.

Substituting α = π /2 into (2), we obtain: x c = (4 R)/(3π) ≅ 0.4 R .

Example 1.Let us determine the center of gravity of the homogeneous body shown in Fig. 13.

Fig.13

Solution.The body is homogeneous, consisting of two parts with a symmetrical shape. Coordinates of their centers of gravity:

Their volumes:

Therefore, the coordinates of the center of gravity of the body

Example 2. Let us find the center of gravity of a plate bent at a right angle. Dimensions are in the drawing (Fig. 14).

Fig.14

Solution. Coordinates of the centers of gravity:

Areas:

That's why:

Example 3. On a square sheet cm square hole cut cm (Fig. 15). Let's find the center of gravity of the sheet. Example 4. Find the position of the center of gravity of the plate shown in Fig. 16. Dimensions are given in centimeters.

Fig.16

Solution. Let's divide the plate into figures (Fig. 17), centers the severity of which is known.

The areas of these figures and the coordinates of their centers of gravity:

1) a rectangle with sides 30 and 40 cm,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; at 1 =20 cm.

2) a right triangle with a base of 50 cm and a height of 40 cm;S 2 =0,5 ∙ 50 ∙ 40= 1000 cm 2 ; X 2 =30+50/3=46.7 cm; y 2 =40/3 =13.3 cm;

3) half circle radius circle r = 20 cm;S 3 =0,5 ∙π∙ 20 2 =628 cm 2 ; X 3 =4 R /3 π =8.5 cm; at

Solution. Recall that in physics the density of a bodyρ and its specific gravitygrelated by the relation:γ = ρ g , Whereg - acceleration of gravity. To find the mass of such a homogeneous body, you need to multiply the density by its volume.

Fig.19

The term “linear” or “linear” density means that to determine the mass of a truss rod, the linear density must be multiplied by the length of this rod.

To solve the problem, you can use the partitioning method. Representing a given truss as a sum of 6 individual rods, we obtain:

WhereL i lengthi th truss rod, andx i , y i - coordinates of its center of gravity.

Thus, a given truss can be represented by a combination of only two groups of rods.

The first group consists of the first rod, for itL 1 = 4 m,x 1 = 0 m,y 1 = 2 m. The second group of rods consists of five rods, for itL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.

The coordinates of the center of gravity of the truss are found using the formula:

x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Self-test questions

- What is called the center of parallel forces?

- How are the coordinates of the center of parallel forces determined?

- How to determine the center of parallel forces whose resultant is zero?

- What properties does the center of parallel forces have?

- What formulas are used to calculate the coordinates of the center of parallel forces?

- What is the center of gravity of a body called?

- Why can the gravitational forces of the Earth acting on a point on a body be taken as a system of parallel forces?

- Write down the formula for determining the position of the center of gravity of inhomogeneous and homogeneous bodies, the formula for determining the position of the center of gravity of flat sections?

- Write down the formula for determining the position of the center of gravity of simple geometric shapes: rectangle, triangle, trapezoid and half a circle?

- What is called the static moment of area?

- Give an example of a body whose center of gravity is located outside the body.

- How are the properties of symmetry used in determining the centers of gravity of bodies?

- What is the essence of the method of negative weights?

- Where is the center of gravity of a circular arc located?

- What graphical construction can be used to find the center of gravity of a triangle?

- Write down the formula that determines the center of gravity of a circular sector.

- Using formulas that determine the centers of gravity of a triangle and a circular sector, derive a similar formula for a circular segment.

- What formulas are used to calculate the coordinates of the centers of gravity of homogeneous bodies, flat figures and lines?

- What is called the static moment of the area of a plane figure relative to the axis, how is it calculated and what dimension does it have?

- How to determine the position of the center of gravity of an area if the position of the centers of gravity of its individual parts is known?

- What auxiliary theorems are used to determine the position of the center of gravity?

Total:0
In contact with 0
Google+ 0
OK 0
Facebook 0