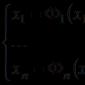Differential equations.

Basic concepts about ordinary differential equations.

Definition 1. Ordinary differential equation n-th order for the function y argument x is called a relation of the form

where F is a given function of its arguments. In the name of this class of mathematical equations, the term "differential" emphasizes that they include derivatives (functions formed as a result of differentiation); the term - "ordinary" says that the desired function depends on only one real argument.

An ordinary differential equation may not explicitly contain an argument x, the desired function and any of its derivatives, but the highest derivative must be included in the equation n- order. For example

a) is a first order equation;

b) is a third order equation.

When writing ordinary differential equations, the notation of derivatives through differentials is often used:

in) is a second order equation;

d) is a first order equation,

forming after division by dx equivalent form of the equation: .

A function is called a solution to an ordinary differential equation if, when substituted into it, it becomes an identity.

For example, the 3rd order equation

Has a solution .

To find by one method or another, for example, selection, one function that satisfies an equation does not mean solving it. To solve an ordinary differential equation means to find all functions that form an identity when substituted into the equation. For equation (1.1), the family of such functions is formed with the help of arbitrary constants and is called the general solution of the ordinary differential equation n th order, and the number of constants coincides with the order of the equation: y(x): In this case, the solution is called the general integral of equation (1.1).

For example, the following expression is a general solution to a differential equation: , and the second term can also be written as , since an arbitrary constant divided by 2 can be replaced by a new arbitrary constant .

By setting some admissible values ​​for all arbitrary constants in the general solution or in the general integral, we obtain a certain function that no longer contains arbitrary constants. This function is called a particular solution or a particular integral of equation (1.1). To find the values ​​of arbitrary constants, and hence the particular solution, various additional conditions to equation (1.1) are used. For example, the so-called initial conditions for (1.2) can be given

In the right parts of the initial conditions (1.2), the numerical values ​​of the function and derivatives are given, and the total number of initial conditions is equal to the number of arbitrary constants being determined.

The problem of finding a particular solution to equation (1.1) from initial conditions is called the Cauchy problem.

§ 2. Ordinary differential equations of the 1st order - basic concepts.

Ordinary differential equation of the 1st order ( n=1) has the form: or, if it can be resolved with respect to the derivative: . Common decision y=y(x, C) or the general integral of the 1st order equations contain one arbitrary constant. The only initial condition for the 1st order equation allows you to determine the value of the constant from the general solution or from the general integral. Thus, a particular solution will be found or, which is also the Cauchy problem will be solved. The question of the existence and uniqueness of a solution to the Cauchy problem is one of the central ones in the general theory of ordinary differential equations. For a first-order equation, in particular, the theorem is valid, which is accepted here without proof.

Theorem 2.1. If in an equation a function and its partial derivative are continuous in some region D plane XOY , and a point is given in this region, then there exists and, moreover, a unique solution that satisfies both the equation and the initial condition.

The geometrically general solution of the 1st order equation is a family of curves in the plane XOY, which do not have common points and differ from each other in one parameter - the value of the constant C. These curves are called integral curves for the given equation. The integral curves of the equation have an obvious geometric property: at each point, the tangent of the slope of the tangent to the curve is equal to the value of the right side of the equation at that point: . In other words, the equation is given in the plane XOY field of directions of tangents to integral curves. Comment: It should be noted that for the equation the equation and the so-called equation in symmetric form are given .

First order differential equations with separable variables.

Definition. A differential equation with separable variables is an equation of the form (3.1)

or an equation of the form (3.2)

In order to separate the variables in equation (3.1), i.e. reduce this equation to the so-called equation with separated variables, perform the following actions:

;

Now we need to solve the equation g(y)=0. If it has a real solution y=a, then y=a will also be a solution of equation (3.1).

Equation (3.2) is reduced to an equation with separated variables by dividing by the product:

, which allows us to obtain the general integral of equation (3.2): . (3.3)

The integral curves (3.3) will be supplemented with solutions if such solutions exist.

Solve the equation: .

Separating variables:

.

Integrating, we get

Ordinary differential equations.

The solution of various geometric, physical and engineering problems often leads to equations that relate independent variables that characterize a particular problem with some function of these variables and derivatives of this function of various orders.

As an example, we can consider the simplest case of uniformly accelerated motion of a material point.

It is known that the displacement of a material point during uniformly accelerated motion is a function of time and is expressed by the formula:

In turn, the acceleration a is the time derivative t from speed V, which is also a derivative with respect to time t from moving S. Those.

Then we get:
- the equation relates the function f(t) to the independent variable t and the second-order derivative of the function f(t).

Definition. differential equation called an equation relating independent variables, their functions and derivatives (or differentials) of this function.

Definition. If a differential equation has one independent variable, then it is called ordinary differential equation, if there are two or more independent variables, then such a differential equation is called partial differential equation.

Definition. The highest order of derivatives in an equation is called the order of the differential equation.

Example.

- ordinary differential equation of the 1st order. In general, it is written
.

- ordinary differential equation of the 2nd order. In general, it is written

- differential equation in partial derivatives of the first order.

Definition. General solution differential equation is such a differentiable function y = (x, C), which, when substituted into the original equation instead of an unknown function, turns the equation into an identity.

Properties of the general solution.

1) Because Since the constant C is an arbitrary value, then in general the differential equation has an infinite number of solutions.

2) Under any initial conditions x \u003d x 0, y (x 0) \u003d y 0, there is such a value C \u003d C 0 for which the solution of the differential equation is the function y \u003d  (x, C 0).

Definition. A solution of the form y \u003d  (x, C 0) is called private decision differential equation.

Definition. Cauchy problem(Augustin Louis Cauchy (1789-1857) - French mathematician) is called finding any particular solution to a differential equation of the form y \u003d  (x, C 0) that satisfies the initial conditions y (x 0) \u003d y 0.

Cauchy's theorem. (theorem on the existence and uniqueness of the solution of the differential equation of the 1st order)

If the functionf(x, y) is continuous in some domainDin planeXOYand has a continuous partial derivative in this region
, then whatever the point (x 0 , y 0 ) in the area ofD, there is only one solution
equations
, defined in some interval containing the point x 0 , accepting at x = x 0 meaning (X 0 ) = y 0 , i.e. there is a unique solution to the differential equation.

Definition. integral differential equation is any equation that does not contain derivatives, for which this differential equation is a consequence.

Example. Find the general solution of the differential equation
.

The general solution of the differential equation is sought by integrating the left and right sides of the equation, which is preliminarily transformed as follows:

Now let's integrate:

is the general solution of the original differential equation.

Suppose some initial conditions are given: x 0 = 1; y 0 = 2, then we have

By substituting the obtained value of the constant into the general solution, we obtain a particular solution for given initial conditions (the solution of the Cauchy problem).

Definition. integral curve the graph y = (x) of the solution of a differential equation on the XOY plane is called.

Definition. special decision of a differential equation is such a solution, at all points of which the Cauchy uniqueness condition is called (cf. Cauchy's theorem.) is not satisfied, i.e. in a neighborhood of some point (x, y) there are at least two integral curves.

The singular solutions do not depend on the constant C.

Special solutions cannot be obtained from the general solution for any values ​​of the constant C. If we construct a family of integral curves of a differential equation, then the special solution will be represented by a line that touches at least one integral curve at each of its points.

Note that not every differential equation has singular solutions.

Example.
Find a special solution if it exists.

This differential equation also has a special solution at= 0. This solution cannot be obtained from the general one, however, when substituting into the original equation, we obtain an identity. opinion that the solution y = 0 can be obtained from the general solution for FROM 1 = 0 wrong, because C 1 = e C  0.

First order differential equations.

Definition. First order differential equation is the relation connecting the function, its first derivative and the independent variable, i.e. aspect ratio:

If this ratio is converted to the form
then this first-order differential equation will be called the equation, allowed with respect to the derivative.

We represent the function f(x,y) as:
then, substituting into the above equation, we have:

this so-called differential form first order equations.

Equations of the formy ’ = f ( x ).

Let the function f(x) be defined and continuous on some interval

a< x < b. В таком случае все решения данного дифференциального уравнения находятся как
. If the initial conditions x 0 and y 0 are given, then the constant C can be determined.

Separable Variable Equations

Definition. Differential equation
called separable equation if it can be written in the form

.

This equation can also be represented as:

Let's move on to new notation

We get:

After finding the corresponding integrals, a general solution of a differential equation with separable variables is obtained.

If the initial conditions are given, then when they are substituted into the general solution, a constant value C is found, and, accordingly, a particular solution.

Example. Find the general solution of the differential equation:

The integral on the left side is taken by parts (see Fig. Integration by parts.):

this is the general integral of the original differential equation, since the desired function and is not expressed in terms of the independent variable. This is what difference general (private) integral from the general (private) solutions.

To check the correctness of the obtained answer, we differentiate it with respect to the variable x.

- right

Example. Find a solution to a differential equation
provided y(2) = 1.

for y(2) = 1 we get

Total:
or
- private decision;

Examination:
, total

- right.

Example. solve the equation

- general integral

- common decision

Example. solve the equation

Example. solve the equation
provided y(1) = 0.

The integral on the left side will be taken by parts (see Fig. Integration by parts.).

If y(1) = 0, then

So the private integral is:
.

Example. Solve the equation.

To find the integral on the left side of the equation, see Table of basic integrals. item 16. We get the general integral:

Example. solve the equation

Let's transform the given equation:

We have obtained the general integral of this differential equation. If we express the desired function y from this relation, then we obtain the general solution.

Example. solve the equation
.

;
;

Suppose some initial conditions x 0 and y 0 are given. Then:

We get a private solution

Homogeneous equations.

Definition. The function f(x, y) is called homogeneousn– th dimension with respect to their arguments x and y, if for any value of the parameter t (except zero) the identity holds:

Example. Is the function homogeneous?

Thus, the function f(x, y) is homogeneous of the 3rd order.

Definition. Differential equation of the form
called homogeneous, if its right side f(x, y) is a homogeneous function of dimension zero with respect to its arguments.

Any equation of the form is homogeneous if the functions P(x, y) and Q(x, y) are homogeneous functions of the same dimension.

The solution of any homogeneous equation is based on reducing this equation to an equation with separable variables.

Consider the homogeneous equation

Because function f(x, y) is homogeneous of zero dimension, then we can write:

Because the parameter t is generally arbitrary, suppose that . We get:

The right side of the resulting equality actually depends on only one argument
, i.e.

The original differential equation can thus be written as:

thus, we have obtained an equation with separable variables for the unknown function u.

Example. solve the equation
.

We introduce an auxiliary function u.

.

Note that the function introduced by us u is always positive, because otherwise, the original differential equation containing
.

We substitute into the original equation:

Separating variables:

Integrating, we get:

Passing from the auxiliary function back to the y function, we obtain the general solution:

Equations Reducing to Homogeneous.

In addition to the equations described above, there is a class of equations that, with the help of certain substitutions, can be reduced to homogeneous ones.

These are equations of the form
.

If the determinant
then the variables can be separated by substitution

where  and  are solutions of the system of equations

Example. solve the equation

We get

Finding the value of the determinant
.

We solve the system of equations

We apply the substitution in the original equation:

Replacing the variable
when substituting into the expression written above, we have:

A method for solving differential equations with separable variables is considered. An example of a detailed solution of a differential equation with separable variables is given.

Content

Definition

Let s (x), q (x)- functions of the variable x ;
p (y), r (y)- functions of the variable y .

A differential equation with separable variables is an equation of the form

Method for solving a differential equation with separable variables

Consider the equation:
(i) .
We express the derivative y in terms of differentials.
;
.
Multiply by dx .
(ii)
Divide the equation by s (x)r(y). This can be done if s (x) r(y) ≠ 0. For s (x) r(y) ≠ 0 we have
.
Integrating, we obtain the general integral in quadratures
(iii) .

Since we divided by s (x)r(y), then we get the integral of the equation for s (x) ≠ 0 and r (y) ≠ 0. Next, you need to solve the equation
r (y) = 0.
If this equation has roots, then they are also solutions of equation (i). Let the equation r (y) = 0. has n roots a i , r (a i ) = 0, i = 1, 2, ... , n. Then the constants y = a i are solutions of equation (i). Some of these solutions may already be contained in the general integral (iii).

Note that if the original equation is given in the form (ii), then the equation should also be solved
s (x) = 0.
Its roots b j , s (b j ) = 0, j = 1, 2, ... , m. give solutions x = b j .

An example of solving a differential equation with separable variables

solve the equation

We express the derivative in terms of differentials:


Multiply by dx and divide by . For y ≠ 0 we have:

Let's integrate.

We calculate the integrals using the formula.



Substituting, we obtain the general integral of the equation
.

Now consider the case, y = 0 .
It is obvious that y = 0 is a solution to the original equation. It is not included in the general integral.
So let's add it to the final result.

; y= 0 .

References:
N.M. Gunther, R.O. Kuzmin, Collection of problems in higher mathematics, Lan, 2003.

Often, the mere mention of differential equations makes students feel uncomfortable. Why is this happening? Most often, because when studying the basics of the material, a gap in knowledge arises, due to which the further study of diffurs becomes simply torture. Nothing is clear what to do, how to decide where to start?

However, we will try to show you that diffuses are not as difficult as they seem.

Basic concepts of the theory of differential equations

From school, we know the simplest equations in which we need to find the unknown x. In fact differential equations only slightly different from them - instead of a variable X they need to find a function y(x) , which will turn the equation into an identity.

Differential equations are of great practical importance. This is not abstract mathematics that has nothing to do with the world around us. With the help of differential equations, many real natural processes are described. For example, string vibrations, the movement of a harmonic oscillator, by means of differential equations in the problems of mechanics, find the speed and acceleration of a body. Also DU are widely used in biology, chemistry, economics and many other sciences.

Differential equation (DU) is an equation containing the derivatives of the function y(x), the function itself, independent variables and other parameters in various combinations.

There are many types of differential equations: ordinary differential equations, linear and non-linear, homogeneous and non-homogeneous, differential equations of the first and higher orders, partial differential equations, and so on.

The solution to a differential equation is a function that turns it into an identity. There are general and particular solutions of remote control.

The general solution of the differential equation is the general set of solutions that turn the equation into an identity. A particular solution of a differential equation is a solution that satisfies additional conditions specified initially.

The order of a differential equation is determined by the highest order of the derivatives included in it.

Ordinary differential equations

Ordinary differential equations are equations containing one independent variable.

Consider the simplest ordinary differential equation of the first order. It looks like:

This equation can be solved by simply integrating its right side.

Examples of such equations:

Separable Variable Equations

In general, this type of equation looks like this:

Here's an example:

Solving such an equation, you need to separate the variables, bringing it to the form:

After that, it remains to integrate both parts and get a solution.

Linear differential equations of the first order

Such equations take the form:

Here p(x) and q(x) are some functions of the independent variable, and y=y(x) is the required function. Here is an example of such an equation:

Solving such an equation, most often they use the method of variation of an arbitrary constant or represent the desired function as a product of two other functions y(x)=u(x)v(x).

To solve such equations, a certain preparation is required, and it will be quite difficult to take them “on a whim”.

An example of solving a DE with separable variables

So we have considered the simplest types of remote control. Now let's take a look at one of them. Let it be an equation with separable variables.

First, we rewrite the derivative in a more familiar form:

Then we will separate the variables, that is, in one part of the equation we will collect all the “games”, and in the other - the “xes”:

Now it remains to integrate both parts:

We integrate and obtain the general solution of this equation:

Of course, solving differential equations is a kind of art. You need to be able to understand what type an equation belongs to, and also learn to see what transformations you need to make with it in order to bring it to one form or another, not to mention just the ability to differentiate and integrate. And it takes practice (as with everything) to succeed in solving DE. And if at the moment you don’t have time to figure out how differential equations are solved or the Cauchy problem has risen like a bone in your throat or you don’t know how to properly format a presentation, contact our authors. In a short time, we will provide you with a ready-made and detailed solution, the details of which you can understand at any time convenient for you. In the meantime, we suggest watching a video on the topic "How to solve differential equations":

A method for solving differential equations reducing to equations with separable variables is considered. An example of a detailed solution of a differential equation that reduces to an equation with separable variables is given.

Content

Formulation of the problem

Consider the differential equation
(i) ,
where f is a function, a, b, c are constants, b ≠ 0 .
This equation is reduced to an equation with separable variables.

Solution method

We make a substitution:
u = ax + by + c
Here y is a function of x . Therefore, u is also a function of x .
Differentiate with respect to x
u′ = (ax + by + c)′ = a + by′
Substitute (i)
u′ = a + by′ = a + b f(ax + by + c) = a + b f (u)
Or:
(ii)
Separate variables. Multiply by dx and divide by a + b f (u). If a + b f (u) ≠ 0, then

By integrating, we obtain the general integral of the original equation (i) in squares:
(iii) .

Finally, consider the case
(iv) a + b f (u) = 0.
Suppose this equation has n roots u = r i , a + b f (r i ) = 0, i = 1, 2, ...n. Since the function u = r i is constant, its derivative with respect to x is equal to zero. Therefore, u = r i is a solution to the equation (ii).
However, the equation (ii) does not match the original equation (i) and, perhaps, not all solutions u = r i , expressed in terms of the variables x and y , satisfy the original equation (i).

Thus, the solution to the original equation is the general integral (iii) and some roots of the equation (iv).

An example of solving a differential equation that reduces to an equation with separable variables

solve the equation
(1)

We make a substitution:
u = x - y
Differentiate with respect to x and perform transformations:
;

Multiply by dx and divide by u 2 .

If u ≠ 0, then we get:

We integrate:

We apply the formula from the table of integrals:

We calculate the integral

Then
;
, or

Common decision:
.

Now consider the case u = 0 , or u = x - y = 0 , or
y=x.
Since y′ = (x)′ = 1, then y = x is a solution to the original equation (1) .

;
.

References:
N.M. Gunther, R.O. Kuzmin, Collection of problems in higher mathematics, Lan, 2003.