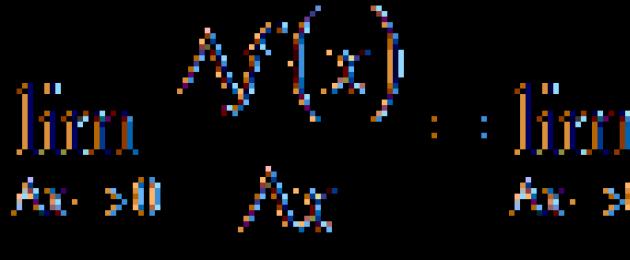Al derivar la primera fórmula de la tabla, partiremos de la definición de la función derivada en un punto. vamos a donde X– cualquier número real, es decir, X– cualquier número del dominio de definición de la función. Anotemos el límite de la relación entre el incremento de la función y el incremento del argumento en:

Cabe señalar que bajo el signo límite se obtiene la expresión, que no es la incertidumbre del cero dividida por cero, ya que el numerador no es infinito. pequeño valor, es decir, cero. En otras palabras, el incremento de una función constante es siempre cero.

De este modo, derivada de una función constantees igual a cero en todo el dominio de definición.

Derivada de una función de potencia.

Fórmula derivada función de potencia parece , donde el exponente pag– cualquier número real.

Primero demostremos la fórmula del exponente natural, es decir, de pag = 1, 2, 3,…

Usaremos la definición de derivada. Anotemos el límite de la relación entre el incremento de una función de potencia y el incremento del argumento:

Para simplificar la expresión en el numerador, recurrimos a la fórmula binomial de Newton:

Por eso,

Esto prueba la fórmula para la derivada de una función potencia para un exponente natural.

Derivada de una función exponencial.

Presentamos la derivación de la fórmula derivada basada en la definición:

Hemos llegado a la incertidumbre. Para expandirlo, introducimos una nueva variable y en . Entonces . En la última transición, utilizamos la fórmula para pasar a una nueva base logarítmica.

Sustituyamos en el límite original:

Si recordamos el segundo límite notable, llegamos a la fórmula para la derivada de la función exponencial:

Derivada de una función logarítmica.

Demostremos la fórmula para la derivada de una función logarítmica para todos X del dominio de definición y todos los valores válidos de la base a logaritmo Por definición de derivada tenemos:

Como habrás notado, durante la demostración las transformaciones se realizaron utilizando las propiedades del logaritmo. Igualdad es cierto debido al segundo límite notable.

Derivadas de funciones trigonométricas.

Para derivar fórmulas para derivadas de funciones trigonométricas, tendremos que recordar algunas fórmulas trigonométricas, así como el primer límite destacable.

Por definición de la derivada de la función seno tenemos .

Usemos la fórmula de diferencia de senos:

Queda por abordar el primer límite destacable:

Por tanto, la derivada de la función pecado x Hay porque x.

La fórmula de la derivada del coseno se demuestra exactamente de la misma manera.

Por tanto, la derivada de la función porque x Hay –pecado x.

Deduciremos fórmulas para la tabla de derivadas de tangente y cotangente utilizando reglas de diferenciación probadas (derivada de una fracción).

Derivadas de funciones hiperbólicas.

Las reglas de diferenciación y la fórmula para la derivada de la función exponencial de la tabla de derivadas nos permiten derivar fórmulas para las derivadas del seno, coseno, tangente y cotangente hiperbólicos.

Derivada de la función inversa.

Para evitar confusiones durante la presentación, denotamos en subíndice el argumento de la función mediante el cual se realiza la diferenciación, es decir, es la derivada de la función. f(x) Por X.

Ahora formulemos Regla para encontrar la derivada de una función inversa.

Deja que las funciones y = f(x) Y x = g(y) mutuamente inversos, definidos en los intervalos y respectivamente. Si en un punto existe una derivada finita distinta de cero de la función f(x), entonces en el punto hay una derivada finita de la función inversa g(y), y . en otra publicación .

Esta regla puede reformularse para cualquier X del intervalo, entonces obtenemos .

Comprobemos la validez de estas fórmulas.

Encontremos la función inversa del logaritmo natural. (Aquí y es una función y X- argumento). Habiendo resuelto esta ecuación para X, obtenemos (aquí X es una función y y– su argumento). Eso es, y funciones mutuamente inversas.

De la tabla de derivadas vemos que Y .

Asegurémonos de que las fórmulas para encontrar las derivadas de la función inversa nos lleven a los mismos resultados:

Como puede ver, obtuvimos los mismos resultados que en la tabla de derivadas.

Ahora tenemos el conocimiento para probar las fórmulas de derivadas inversas. funciones trigonométricas.

Empecemos por la derivada del arcoseno.

. Luego, usando la fórmula para la derivada de la función inversa, obtenemos

Ya sólo queda realizar las transformaciones.

Dado que el rango del arcoseno es el intervalo , Eso (ver la sección sobre funciones elementales básicas, sus propiedades y gráficas). Por tanto, no lo estamos considerando.

Por eso, . El dominio de definición de la derivada arcoseno es el intervalo (-1; 1) .

Para el arco coseno todo se hace exactamente de la misma forma:

Encontremos la derivada del arcotangente.

Para la función inversa es .

Expresemos el arcotangente en términos de arcocoseno para simplificar la expresión resultante.

Dejar arctgx = z, Entonces

Por eso,

La derivada del arco cotangente se encuentra de forma similar:

Cálculo diferencial de una función de una variable.

1. Introducción

Análisis matemático- una rama de las matemáticas que tomó forma en el siglo XVIII e incluye dos partes principales: cálculo diferencial e integral. La derivada de una función es uno de los conceptos matemáticos básicos del cálculo diferencial. El análisis surgió gracias a los esfuerzos de muchos matemáticos (principalmente I. Newton y G. Leibniz) y jugó un papel muy importante en el desarrollo de las ciencias naturales: apareció un método poderoso y bastante universal para estudiar funciones que surgen al resolver diversos problemas aplicados.

2. Función numérica. Esquema de estudio de funciones.

(Ver notas sobre el tema “Función de potencia”)

1) El dominio de la función.

2) Conjunto de valores de funciones.

3) Uniformidad, imparidad de la función.

4) Monotonicidad de la función.

5) Reversibilidad de la función.

6) Función ceros.

7) Intervalos de signo constante de una función.

8) Función limitada.

Ejercicios:

1. Encuentra el dominio de una función:

A) ; b) ; V) .

A) ; b) ; G).

3. El concepto de límite de una función en un punto.

Veamos las gráficas de algunas funciones. Estudiemos el comportamiento de funciones cercanas al punto. x0 , es decir, en alguna vecindad del punto x0 .

Arroz. 1. figura. 2. figura. 3.

Una función tiene una propiedad que la distingue de las otras dos funciones.

1. A medida que se acerca el argumento X A x0 a la izquierda y a la derecha los valores correspondientes de la función están arbitrariamente cerca del mismo número A.

Las otras dos funciones no tienen esta propiedad.

2. A medida que se acerca el argumento X A x0 a la izquierda los valores correspondientes de la función están arbitrariamente cerca del número A, y a medida que se acerca el argumento X A x0 a la derecha los valores correspondientes de la función están arbitrariamente cerca del número EN.

3. Función al aproximar un argumento. X A x0 La izquierda y la derecha adquieren valores diferentes.

Conclusión: Si al abordar el argumento X A x0 a la izquierda y a la derecha los puntos con coordenadas están arbitrariamente cerca del punto con coordenadas, entonces.

Ejemplo: ¿La función límite en los puntos x 1, x 2, x 3, x 4, x 5?

Respuesta: Función tiene un límite en los puntos x 1, x 3;

función no tiene límite en los puntos x2, x4, x5.

Comentario:

4. Definición de una función continua en un punto y en un intervalo

Es conveniente asociar el concepto de continuidad de una función con la idea de la gráfica de esta función como una recta “continua” (sólida). Consideraremos línea continua aquella trazada sin levantar el lápiz del papel.

Pregunta: ¿Cuáles de estas funciones son continuas?

Arroz. 1. figura. 2. figura. 3.

Arroz. 4. figura. 5.

Respuesta: De estas funciones, la función que se muestra en la Fig. 1 es continua. No. 3, ya que su gráfica es una línea “continua” (sólida).

Pregunta: ¿Qué propiedades tiene la función que se muestra en la figura? No. 3, y no tiene otras funciones?

Respuesta:

1. La función se define en el punto x 0. Esta propiedad no se cumple para la función que se muestra en la Fig. N° 1.

2. Existe un límite finito de la función en el punto x 0. Esta propiedad no se cumple para las funciones mostradas en la Fig. N° 2, 5.

3. El límite de la función en el punto x 0 es igual al valor de la función en este punto, es decir . Esta propiedad no se cumple para la función que se muestra en la Fig. No. 4.

Propiedades que se cumplen para la función que se muestra en la Fig. No. 3, y permiten definir una función continua en un punto x0 .

Definición: Se dice que una función es continua en un punto x0, Si .

Comentario: Si la función es continua en el punto x0, luego señale x0 Se llama punto de continuidad de una función si la función no es continua en el punto. x0, luego señale x0 se llama punto de ruptura de la función.

Definición: Una función se llama continua en un intervalo si es continua en todos los puntos de ese intervalo.

5. Incremento de argumento, incremento de función.

Sea dada la función , .

x0- valor inicial del argumento, ;

X- valor final del argumento, ;

f(x0) – valor inicial de la función;

f(x 0 +Dx) – el valor final de la función.

Definición: La diferencia entre los valores final e inicial del argumento se llama incremento del argumento. D x = x – x 0

Definición: La diferencia entre los valores final e inicial de una función se llama incremento de la función. D y = f(x 0 +D x) – f (x 0)

Comentario:

1. Incremento geométrico del argumento. Dx– es la diferencia entre las abscisas de los puntos del gráfico de funciones correspondientes a los valores final e inicial del argumento.
2. Geométricamente, el incremento de una función. D y– es la diferencia de ordenadas de los puntos de la gráfica de la función correspondientes a los valores final e inicial del argumento.
3. El incremento de argumento y el incremento de función pueden ser positivos o negativos.

6. El concepto de función derivada. Significado físico derivada de una función

Considere el problema de la tasa de cambio de la función, donde X Y en puede ser cualquier cantidad física.

x0- valor del argumento inicial; f(x0) – valor inicial de la función;

x 0 +D x – el valor final del argumento; f(x 0 +Dx) – el valor final de la función;

D y = f(x 0 +D x) – f (x 0) – incremento de función;

– tasa de cambio promedio de una función durante un intervalo Dx .

– tasa de cambio instantánea de una función, tasa de cambio de una función en un punto x0.

Definición: Derivada de una función en un punto x0 llamado límite de la relación de incremento D funciona en un punto x0 incrementar Dx argumento a medida que el incremento del argumento tiende a cero.

Conclusión: Derivada de una función en un punto x0 es la tasa de cambio de la función en un punto x0.

Teorema: Derivada de una función constante y = c en cualquier punto igual a cero.

Teorema: Derivada de una función y = x en cualquier punto igual a uno .

.

Comentario: Encontrar la derivada de una función dada se llama derivación.

7. Reglas para derivar suma, producto, cociente de funciones.

Considere la función , que consta de otras dos funciones y tiene derivadas en el segmento:

3) .

Teorema número 1: La derivada de la suma (diferencia) de dos funciones es igual a la suma (diferencia) de las derivadas de estas funciones.

Ejemplo: Calcular la derivada de una función.

Teorema número 2: La derivada del producto de dos funciones está determinada por la fórmula:

Consecuencia: El factor constante se puede sacar del signo de la derivada: .

Prueba: .

Ejemplo

Ejercicios:

2) ;

La derivada de la función de potencia en se calcula mediante la fórmula:

Comentario: La fórmula es válida para una función potencia con cualquier exponente. ,

Ejemplo: Calcular derivadas de funciones:

Conclusión: .

Ejercicios: Calcular derivadas de funciones:

1) ; 2) ; 3) ;

4) ; 5) ;

6) ; 7) .

Teorema número 3: La derivada del cociente de dos funciones está determinada por la fórmula:

Consecuencias: ;

Ejemplo: Calcular derivadas de funciones:

2) . .

3) . .

Ejercicios: Calcular derivadas de funciones:

1. ; 2. ; 3. ;

4. ; 5. ; 6. ;

7. ; 8. ; 9. .

8. El concepto de función compleja.

Regla para derivar una función compleja

Dejemos que se defina una función en el conjunto y una función en el conjunto, y para , el valor correspondiente es . Luego se define una función en el conjunto, que se llama función compleja de X (función de función).

Una variable se denomina argumento intermedio de una función compleja.

Ejemplo:

Ejercicios:

1. En qué funciones elementales constan estas funciones complejas:

1) ; 2) ;

3) ; 4) .

1. A partir de estas funciones elementales, cree funciones complejas:

1) , ; 2) , ;

3) , . 4) , , .

Conclusión: La derivada de una función compleja es igual al producto de las derivadas de las funciones elementales que la componen .

Ejemplo: Calcular derivadas de funciones:

- potencia, lineal; , .

- potencia, cuadrática; , .

.

Ejercicios: Calcular derivadas de funciones:

1. ; 2. ;

3. ; 4. ;

5. ; 6. .

9. Derivada de exponencial, funciones logarítmicas

Ejemplo: Calcular derivadas de funciones:

1. . .

2. . .

3. . .

Ejemplo: Calcular derivadas de funciones:

1. . .

2. . .

Ejercicios: Calcula la derivada de la función:

1. ; 2. ; 3. ;

4. ; 5. ; 6. ;

7. ; 8. .

10. Derivadas de funciones trigonométricas

Derivadas de funciones trigonométricas inversas

.

Ejemplo: Calcular derivadas de funciones:

1. . .

2. . .

Tarea

. .

Tarea: Calcula la derivada de una función.

.

Ejercicio: Calcula la derivada de una función.

Derivadas de funciones trigonométricas inversas

; ;

; .

Ejercicios: Calcular derivadas de funciones:

1. 2. 3. 4.

5. 6. 7. 8. 9.

10. 11. 12. 13.

11. Significado geométrico derivada de una función

Consideremos la función.

Tomemos un punto fijo en la gráfica de la función. y un punto arbitrario . Dibujemos una secante . si el punto METRO moverse a un punto indefinidamente m 0 según la gráfica de la función, entonces la secante M 0 M Ocuparán diferentes posiciones incluso si el punto coincide. METRO con un punto m 0 la secante tomará su posición límite M 0 T , luego recto M 0 T será tangente a la gráfica de la función en el punto m 0 .

Definición: Tangente a la gráfica de una función en el punto m 0 llamada posición límite M 0 T secante como tiende el punto METRO a tiempo al punto M 0.

b- ángulo de inclinación de la secante M 0 M

a- ángulo tangente M 0 T a la dirección positiva del eje x.

Coeficiente angular de la secante M 0 M .

pendiente tangente M 0 T .

Considere un triángulo rectángulo M 0 MA (). Tangente de un ángulo agudo triángulo rectángulo igual a la relación del lado opuesto al adyacente:

Eso es . Y eso significa .

Determinemos la derivada de la función en el punto x0 : .

, , por eso, .

Conclusión: El significado geométrico de la derivada de una función es que la derivada de la función en es igual a la pendiente de la tangente trazada a la gráfica de la función en el punto de la abscisa.

Ejemplo:

1. Encuentra el coeficiente angular de la tangente trazada a la gráfica de la función en los puntos. .

; ; ; ; ; .

Respuesta: ; ; .

2. Encuentra el ángulo de inclinación de la tangente trazada a la gráfica de la función en el punto de la abscisa.

; ; ; ; . paralelo a la línea;

vamos a instalar condición necesaria existencia de un extremo.

teorema de fermat: Si el punto interno x0 del dominio de definición de una función continua hay un punto extremo y en este punto hay una derivada, entonces es igual a cero.

Comentario: Sin embargo, la igualdad de la derivada de la función a cero en el punto x0 todavía no da derecho a afirmar que x0 – punto extremo de la función.

Navegación de páginas.

La derivada es constante.

Al deducir la primera fórmula de la tabla, partiremos de la definición de la derivada de una función en un punto. Tomemos , donde x es cualquier número real, es decir, x es cualquier número del dominio de definición de la función. Anotemos el límite de la relación entre el incremento de la función y el incremento del argumento en:

Cabe señalar que bajo el signo de límite se obtiene la expresión, que no es , ya que el numerador no contiene un valor infinitesimal, sino precisamente cero. En otras palabras, el incremento de una función constante es siempre cero.

De este modo, la derivada de una función constante es igual a cero en todo el dominio de definición.

Ejemplo.

Encuentra derivadas de las siguientes funciones constantes.

Solución.

En el primer caso tenemos la derivada número natural 3, en el segundo caso tenemos que tomar la derivada del parámetro a, que puede ser cualquier número real, en el tercero, la derivada de un número irracional, en el cuarto caso tenemos la derivada de cero (cero es un número entero ), en el quinto - la derivada de una fracción racional.

Respuesta:

Las derivadas de todas estas funciones son iguales a cero para cualquier x real (en todo el dominio de definición)

Derivada de una función de potencia.

La fórmula para la derivada de una función de potencia tiene la forma , donde el exponente p es cualquier número real.

Primero demostremos la fórmula del exponente natural, es decir, para p = 1, 2, 3, ...

Usaremos la definición de derivada. Anotemos el límite de la relación entre el incremento de una función de potencia y el incremento del argumento:

Para simplificar la expresión en el numerador, recurrimos a la fórmula:

Por eso,

Esto prueba la fórmula para la derivada de una función potencia para un exponente natural.

Se deben considerar dos casos: para x positivo y x negativo.

Supongamos primero. En este caso . Tomemos el logaritmo de la igualdad en base e y apliquemos la propiedad del logaritmo:

Llegó implícitamente función dada. Encontramos su derivada:

Queda por realizar la prueba para x negativo.

Cuando el exponente p es un número par, entonces la función de potencia también está definida para y es par (ver sección). Eso es, . En este caso, también puedes utilizar la demostración mediante la derivada logarítmica.

Cuando p es número impar, entonces la función de potencia también está definida para , y es impar. Eso es, . En este caso, no se puede utilizar la derivada logarítmica. Para probar la fórmula en este caso, puedes usar las reglas de derivación y la regla para encontrar la derivada de una función compleja:

La última transición es posible debido al hecho de que si p es un número impar, entonces p-1 es un número par o cero (para p=1), por lo tanto, para x negativo la igualdad es verdadera .

Por tanto, la fórmula para la derivada de una función potencia está probada para cualquier p real.

Ejemplo.

Encuentra derivadas de funciones.

Solución.

Llevamos la primera y tercera funciones a forma tabular, usando las propiedades de una potencia, y aplicamos la fórmula para la derivada de una función de potencia:

Derivada de una función exponencial.

Presentamos la derivación de la fórmula derivada basada en la definición:

Hemos llegado a la incertidumbre. Para expandirlo, introducimos una nueva variable y en . Entonces . En la última transición, utilizamos la fórmula para pasar a una nueva base logarítmica.

Sustituyamos en el límite original:

Por definición de la derivada de la función seno tenemos .

Usemos la fórmula de diferencia de senos:

Queda por abordar el primer límite destacable:

Por tanto, la derivada de la función sen x es cos x.

La fórmula para la derivada del coseno se demuestra exactamente de la misma manera.

Al resolver problemas de diferenciación, nos referiremos constantemente a la tabla de derivadas de funciones básicas; de lo contrario, ¿por qué la compilamos y probamos cada fórmula? Te recomendamos que recuerdes todas estas fórmulas en el futuro te ahorrará mucho tiempo.

Copyright por estudiantes inteligentes

Reservados todos los derechos.
Protegido por la ley de derechos de autor. Ninguna parte del sitio, incluidos los materiales internos y la apariencia, puede reproducirse de ninguna forma ni utilizarse sin el permiso previo por escrito del titular de los derechos de autor.

Se presentan las derivadas de funciones trigonométricas inversas y la derivación de sus fórmulas. También se dan expresiones para derivadas de orden superior. Enlaces a páginas con una descripción más detallada de la derivación de fórmulas.

Contenido

Ver también: Funciones trigonométricas inversas, sus gráficas y fórmulas.

Primero, derivamos la fórmula para la derivada del arcoseno. Dejar
y= arcosen x.
Dado que el arcoseno es la función inversa del seno, entonces
.
Aquí y es una función de x. Derivar con respecto a la variable x:
.
Aplicamos:
.
Entonces encontramos:
.

Porque entonces .
.
Entonces
Y la fórmula anterior toma la forma:
.

. De aquí
.
Exactamente de esta manera puedes obtener la fórmula para la derivada del arco coseno. Sin embargo, es más fácil utilizar una fórmula que relacione funciones trigonométricas inversas:
.

Entonces Se presenta una descripción más detallada en la página “Derivación de derivadas de arcoseno y arcocoseno”. ahí se da derivación de derivadas de dos maneras

- discutido anteriormente y según la fórmula para la derivada de la función inversa.

Derivación de derivadas de arcotangente y arcocotangente.

De la misma forma encontraremos las derivadas de arcotangente y arcocotangente.
y= Dejar.
arctán x
.
Arctangente es la función inversa de la tangente:
.
Derivar con respecto a la variable x:
.
Entonces encontramos:
.

Aplicamos la fórmula para la derivada de una función compleja:
.

Derivada del arco cotangente:

De la misma forma encontraremos las derivadas de arcotangente y arcocotangente.
.
Derivados arcoseno
.
Ya hemos encontrado la derivada de primer orden del arcoseno:
;
.
Al derivar, encontramos la derivada de segundo orden:
.
También se puede escribir de la siguiente forma: De aquí obtenemos ecuación diferencial
.

, que se satisface con las derivadas arcoseno de primer y segundo orden:

Al diferenciar esta ecuación, podemos encontrar derivadas de orden superior.

Derivada de arcoseno de enésimo orden
,
La derivada del arcoseno de enésimo orden tiene la siguiente forma:
;
.
donde es un polinomio de grado. Está determinado por las fórmulas:

Aquí .
.

El polinomio satisface la ecuación diferencial:

Derivada del arcocoseno de enésimo orden
.
Las derivadas del arco coseno se obtienen a partir de las derivadas del arco seno utilizando la fórmula trigonométrica:
.

Por tanto, las derivadas de estas funciones difieren sólo en el signo:

Derivadas de arcotangente
.

Dejar . Encontramos la derivada del arco cotangente de primer orden:

.
Dividamos la fracción en su forma más simple:

Aquí está la unidad imaginaria, .

.

Diferenciamos una vez y llevamos la fracción a un denominador común:
.

Sustituyendo obtenemos:

Derivada de arcotangente de enésimo orden
;
.

Así, la derivada del arcotangente de enésimo orden se puede representar de varias formas:

Derivadas del arco cotangente
.
Entonces, la derivada de enésimo orden del arco tangente difiere solo en signo de la derivada del arco tangente:
.

Sustituyendo , encontramos:
.

Referencias:
NUEVO MÉJICO. Gunter, R.O. Kuzmin, Colección de problemas de matemáticas superiores, “Lan”, 2003.

Ver también:

sujeto :

Objetivo : Formarse una idea de las derivadas de funciones trigonométricas inversas.

Tareas:

1. enseñar a encontrar derivadas de funciones dadas,trabajar con los estudiantes en la capacidad de diferenciar estas funciones usando
trabajo independiente y examen mutuo;

2. Desarrollar el interés por las matemáticas, la informática y educativo habilidades,
la capacidad de analizar los errores de otros estudiantes;

3. desarrollar la atención y la independencia

1. Momento organizacional
Saludo a los estudiantes, les presento las reglas de la lección y les explico cómo completar correctamente la hoja de calificación.
2.Etapa motivacional
Los estudiantes deben leer lo que deben saber y poder hacer sobre este tema.
Antes de empezar, lee la regla RECUERDA.
3.Etapa operativa
Los estudiantes comienzan a completar las tareas en la hoja de trabajo (adjunta)
4. Resumen de la lección
Reflexión.

Hoy en clase:

Descubrí…

Fue interesante…

Fue dificil…

Logré…

Intentaré…

HOJA DE ESTUDIO

sobre este tema: Derivadas de funciones trigonométricas y trigonométricas inversas.

2 lecciones.

COMO RESULTADO DE ESTUDIAR EL TEMA, NECESITAS

SABER: fórmulas de diferenciación para Funciones trigonométricas y trigonométricas inversas.

SER CAPAZ DE: encontrar derivadas de funciones trigonométricas y trigonométricas inversas.

Recordar , que necesitas trabajar según un algoritmo.

No olvide revisar la verificación, tomar notas en los márgenes y completar la hoja de calificación del tema.

Por favor, no deje ninguna pregunta que tenga sin respuesta.

Sea objetivo durante la revisión por pares, le ayudará tanto a usted como a la persona que está revisando.

¡TE DESEO ÉXITO!

z ADANIE №1

Lee y aprende las fórmulas para diferenciar funciones trigonométricas inversas: (2 puntos)

Si la función es compleja, entonces

Dónde z – función elemental

Considere ejemplos:

y = arcosen(x) entonces y / =

y = arcctg(3x 2 -4) entonces

y/=

Encuentra derivadas:(3 puntos)

y= arcosen(-x) y = arctan(-x) y = arcos(2x)

PAG VE Y REVISA №1

z ADANIE №2

Resuelve cualquiera de los ejemplos: (3b)

A ) y = arcos(5x - 3)

b ) y = arcctg(7x+1)

PAG VE Y REVISA №2

z ADANIE №3

a) Considere nuevamente la solución del ejemplo:

b) Encontrar derivadas de funciones (4 puntos)

arcosen(2x 2 - 5x)

arccos(4x 2 - 6x)

PAG VE Y REVISA №3

z ADANIE №4

¡Bien hecho! Tu puedes empezartrabajo de prueba No. 1.

TAREA N° 5

a) Considere la solución al ejemplo:

b) Encontrar derivadas de funciones (6 puntos)

y=

PAG VE Y REVISA №5

¡Bien hecho! Tu puedes empezartrabajo de prueba No. 2.

COMPROBACIÓN DEL TRABAJO No. 1

Completa una de las opciones (11b)

1v 2v

1. Encuentra las derivadas de las siguientes funciones:

a) 2 puntos

y = arctan(-2x) y = arcos(3x)

segundo) 4 puntos

y = arcos(3x 2 - 2) y = arcctg(2x 3 +1)

c) 5 puntos

y = arcosen(x 2 - 5x) + tan (2x+1) y = arccos(3x 2 - 2x) + ctg(x+4) máx.

puntos

recibió

punto

OMS

comprobado

calificación

1

2 segundo

3 segundo

2

3b

3

4b

4

1 1 b

5

6 segundo

6

1 4 b

total

43 segundo

TOTAL 43 puntos

“5” - 33 – 43 puntos;

“4” - 24 – 32 puntos;

“3” - 18 – 23 puntos.