La derivada de una función es uno de los temas difíciles en currículum escolar. No todos los graduados responderán a la pregunta de qué es un derivado.
Este artículo explica de manera simple y clara qué es un derivado y por qué es necesario.. No lucharemos ahora por el rigor matemático de la presentación. Lo más importante es entender el significado.
Recordemos la definición:
La derivada es la tasa de cambio de la función.
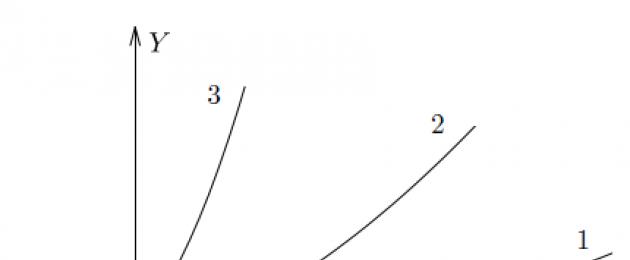
La figura muestra gráficas de tres funciones. ¿Cuál crees que crece más rápido?

La respuesta es obvia: la tercera. Tiene la tasa de cambio más alta, es decir, la derivada más grande.
Aquí hay otro ejemplo.
Kostya, Grisha y Matvey consiguieron trabajo al mismo tiempo. Veamos cómo cambiaron sus ingresos durante el año:

Puedes ver todo en el gráfico de inmediato, ¿verdad? Los ingresos de Kostya se han más que duplicado en seis meses. Y los ingresos de Grisha también aumentaron, pero solo un poco. Y los ingresos de Matthew se redujeron a cero. Las condiciones iniciales son las mismas, pero la tasa de cambio de la función, es decir, derivado, - diferente. En cuanto a Matvey, la derivada de su ingreso es generalmente negativa.
Intuitivamente, podemos estimar fácilmente la tasa de cambio de una función. Pero, ¿cómo lo hacemos?
Lo que realmente estamos viendo es qué tan abruptamente sube (o baja) la gráfica de la función. En otras palabras, qué tan rápido cambia y con x. Obviamente, la misma función en diferentes puntos puede tener un valor diferente de la derivada, es decir, puede cambiar más rápido o más lento.
La derivada de una función se denota por .
Vamos a mostrar cómo encontrar usando la gráfica.

Se dibuja una gráfica de alguna función. Tome un punto en él con una abscisa. Dibuja una tangente a la gráfica de la función en este punto. Queremos evaluar qué tan abruptamente sube la gráfica de la función. Un valor útil para esto es tangente de la pendiente de la tangente.
La derivada de una función en un punto es igual a la tangente de la pendiente de la tangente trazada a la gráfica de la función en ese punto.
Tenga en cuenta: como ángulo de inclinación de la tangente, tomamos el ángulo entre la tangente y la dirección positiva del eje.
A veces los estudiantes preguntan cuál es la tangente a la gráfica de una función. Esta es una línea recta que tiene el único punto común con el gráfico de esta sección, además, como se muestra en nuestra figura. Parece una tangente a un círculo.
Encontremos . Recordemos que la tangente de un ángulo agudo en triángulo rectángulo igual a la razón del cateto opuesto al adyacente. Del triangulo:
Encontramos la derivada usando la gráfica sin siquiera saber la fórmula de la función. Tales tareas se encuentran a menudo en el examen de matemáticas bajo el número.
Hay otra correlación importante. Recuerda que la recta viene dada por la ecuación
La cantidad en esta ecuación se llama pendiente de una recta. Es igual a la tangente del ángulo de inclinación de la recta al eje.
.
eso lo conseguimos
Recordemos esta fórmula. Expresa el significado geométrico de la derivada.
La derivada de una función en un punto es igual a la pendiente de la tangente trazada a la gráfica de la función en ese punto.
En otras palabras, la derivada es igual a la tangente de la pendiente de la tangente.
Ya hemos dicho que una misma función puede tener diferentes derivadas en diferentes puntos. Veamos cómo se relaciona la derivada con el comportamiento de la función.
Dibujemos una gráfica de alguna función. Permita que esta función aumente en algunas áreas y disminuya en otras, y en diferentes proporciones. Y que esta función tenga puntos máximos y mínimos.

En un punto, la función es creciente. La tangente a la gráfica, dibujada en el punto, forma un ángulo agudo con la dirección positiva del eje. Entonces la derivada es positiva en el punto.
En el punto, nuestra función es decreciente. La tangente en este punto forma un ángulo obtuso con la dirección positiva del eje. Como la tangente de un ángulo obtuso es negativa, la derivada en el punto es negativa.
Esto es lo que sucede:
Si una función es creciente, su derivada es positiva.
Si decrece, su derivada es negativa.
¿Y qué pasará en los puntos máximo y mínimo? Vemos que en (punto máximo) y (punto mínimo) la tangente es horizontal. Por lo tanto, la tangente de la pendiente de la tangente en estos puntos es cero y la derivada también es cero.
El punto es el punto máximo. En este punto, el aumento de la función se reemplaza por una disminución. En consecuencia, el signo de la derivada cambia en el punto de "más" a "menos".
En el punto, el punto mínimo, la derivada también es igual a cero, pero su signo cambia de "menos" a "más".
Conclusión: con la ayuda de la derivada se puede averiguar todo lo que nos interesa sobre el comportamiento de la función.
Si la derivada es positiva, entonces la función es creciente.
Si la derivada es negativa, entonces la función es decreciente.
En el punto máximo, la derivada es cero y cambia de signo de más a menos.
En el punto mínimo, la derivada también es cero y cambia de signo de menos a más.
Escribimos estos hallazgos en forma de tabla:
| aumenta | punto máximo | decreciente | punto mínimo | aumenta | |
| + | 0 | - | 0 | + |
Hagamos dos pequeñas aclaraciones. Necesitará uno de ellos cuando resuelva problemas de examen. Otro - en el primer año, con un estudio más serio de funciones y derivadas.
Un caso es posible cuando la derivada de una función en algún punto es igual a cero, pero la función no tiene un máximo ni un mínimo en este punto. Este llamado :

En un punto, la tangente a la gráfica es horizontal y la derivada es cero. Sin embargo, antes del punto, la función aumentó, y después del punto continúa aumentando. El signo de la derivada no cambia, se ha mantenido positivo como era.
También sucede que en el punto de máximo o mínimo, la derivada no existe. En el gráfico, esto corresponde a una ruptura brusca, cuando es imposible trazar una tangente en un punto dado.

Pero, ¿cómo encontrar la derivada si la función no está dada por un gráfico, sino por una fórmula? En este caso, se aplica
Primero, trate de encontrar el alcance de la función:
¿Lograste? Comparemos las respuestas:
¿Está bien? ¡Bien hecho!
Ahora tratemos de encontrar el rango de la función:

¿Fundar? Comparar:
¿Estuvo de acuerdo? ¡Bien hecho!
Trabajemos con los gráficos nuevamente, solo que ahora es un poco más difícil: encontrar tanto el dominio de la función como el rango de la función.
Cómo encontrar tanto el dominio como el rango de una función (avanzado)

Esto es lo que sucedió:
Con gráficos, creo que lo averiguaste. Ahora intentemos encontrar el dominio de la función de acuerdo con las fórmulas (si no sabe cómo hacerlo, lea la sección sobre):
¿Lograste? Comprobación respuestas:
- , ya que la expresión raíz debe ser mayor o igual a cero.
- , ya que es imposible dividir por cero y la expresión radical no puede ser negativa.
- , ya que, respectivamente, para todos.
- porque no se puede dividir por cero.
Sin embargo, aún nos queda un momento más que no ha sido resuelto...
Permítanme reiterar la definición y centrarme en ella:
¿Observó? La palabra "solo" es un elemento muy, muy importante de nuestra definición. Voy a tratar de explicar a usted en los dedos.
Digamos que tenemos una función dada por una línea recta. . Cuando sustituimos este valor en nuestra "regla" y lo obtenemos. Un valor corresponde a un valor. Incluso podemos hacer una tabla de varios valores y trazar una función dada para verificar esto.
"¡Mirar! - dices, - "" se encuentra dos veces!" Entonces, ¿tal vez la parábola no es una función? ¡No lo es!
¡El hecho de que "" aparezca dos veces está lejos de ser una razón para acusar a la parábola de ambigüedad!
El caso es que, al calcular, nos salió un juego. Y al calcular con, tenemos un juego. Así es, la parábola es una función. Mira el cuadro:

¿Entiendo? Si no, aquí hay un ejemplo de la vida real para ti, ¡lejos de las matemáticas!
Digamos que tenemos un grupo de solicitantes que se conocieron al presentar documentos, cada uno de los cuales dijo en una conversación dónde vive:

De acuerdo, es bastante realista que varios chicos vivan en la misma ciudad, pero es imposible que una persona viva en varias ciudades al mismo tiempo. Esta es, por así decirlo, una representación lógica de nuestra "parábola": Varias x diferentes corresponden a la misma y.
Ahora vamos a pensar en un ejemplo donde la dependencia no es una función. Digamos que estos mismos muchachos dijeron qué especialidades solicitaron:

Aquí tenemos una situación completamente diferente: una persona puede solicitar fácilmente una o varias direcciones. Eso es un elemento los conjuntos se ponen en correspondencia varios elementos conjuntos Respectivamente, no es una función.
Pongamos a prueba tus conocimientos en la práctica.
Determina a partir de las imágenes qué es una función y qué no lo es:

¿Entiendo? y aquí está respuestas:
- La función es - B,E.
- No es una función - A, B, D, D.
¿Usted pregunta por qué? Sí, he aquí por qué:

En todas las figuras excepto A) y MI) hay varios para uno!
Estoy seguro de que ahora puede distinguir fácilmente una función de una no función, decir qué es un argumento y qué es una variable dependiente, y también determinar el alcance del argumento y el alcance de la función. Pasemos a la siguiente sección: ¿cómo definir una función?
Formas de configurar una función
¿Qué crees que significan las palabras? "establecer función"? Así es, significa explicarles a todos de qué función estamos hablando en este caso. Además, explica de tal manera que todos te entiendan correctamente y las gráficas de funciones dibujadas por las personas según tu explicación fueran las mismas.
¿Cómo puedo hacer eso? ¿Cómo configurar una función? La forma más fácil, que ya se ha utilizado más de una vez en este artículo: utilizando una fórmula. Escribimos una fórmula y, al sustituirla por un valor, calculamos el valor. Y como recordarán, una fórmula es una ley, una regla según la cual queda claro para nosotros y para otra persona cómo una X se convierte en una Y.
Por lo general, esto es exactamente lo que hacen: en las tareas, vemos funciones listas para usar definidas por fórmulas; sin embargo, hay otras formas de configurar una función que todos olvidan y, por lo tanto, la pregunta "¿de qué otra manera puede configurar una función?" confunde Echemos un vistazo a todo en orden y comencemos con el método analítico.
Manera analítica de definir una función.
El método analítico es la tarea de una función que utiliza una fórmula. Esta es la forma más universal, completa e inequívoca. Si tiene una fórmula, entonces sabe absolutamente todo sobre la función: puede hacer una tabla de valores en ella, puede construir un gráfico, determinar dónde aumenta y dónde disminuye la función, en general, explórela. en su totalidad.
Consideremos una función. ¿Que importa?
"¿Qué significa?" - usted pregunta. Voy a explicar ahora.
Déjame recordarte que en la notación, la expresión entre paréntesis se llama argumento. Y este argumento puede ser cualquier expresión, no necesariamente simple. En consecuencia, sea cual sea el argumento (expresión entre paréntesis), lo escribiremos en su lugar en la expresión.
En nuestro ejemplo, se verá así:
Considere otra tarea relacionada con el método analítico de especificar una función que tendrá en el examen.
Encuentre el valor de la expresión, at.
Estoy seguro de que al principio te asustaste al ver esa expresión, ¡pero no hay absolutamente nada de miedo en ella!
Todo es igual que en el ejemplo anterior: sea cual sea el argumento (expresión entre paréntesis), lo escribiremos en cambio en la expresión. Por ejemplo, para una función.
¿Qué se debe hacer en nuestro ejemplo? En su lugar, debe escribir, y en lugar de -:
acortar la expresión resultante:
¡Eso es todo!
Trabajo independiente
Ahora trata de encontrar el significado de las siguientes expresiones tú mismo:
- , si
- , si
¿Lograste? Comparemos nuestras respuestas: Estamos acostumbrados al hecho de que la función tiene la forma
Incluso en nuestros ejemplos, definimos la función de esta manera, pero analíticamente es posible definir la función implícitamente, por ejemplo.
Intente construir esta función usted mismo.
¿Lograste?
Así es como lo construí.
¿Con qué ecuación terminamos?
¡Correctamente! Lineal, lo que significa que la gráfica será una línea recta. Hagamos una tabla para determinar qué puntos pertenecen a nuestra línea:
Justo de eso hablábamos... Uno corresponde a varios.
Tratemos de dibujar lo que sucedió:

¿Lo que tenemos es una función?
¡Así es, no! ¿Por qué? Intenta responder a esta pregunta con una imagen. ¿Qué obtuviste?

“¡Porque un valor corresponde a varios valores!”
¿Qué conclusión podemos sacar de esto?
Así es, una función no siempre se puede expresar explícitamente, ¡y lo que está "disfrazado" como una función no siempre es una función!
Manera tabular de definir una función
Como su nombre indica, este método es un plato simple. Sí Sí. Como el que ya hicimos. Por ejemplo:
Aquí notó inmediatamente un patrón: Y es tres veces más grande que X. Y ahora la tarea de “piensa muy bien”: ¿crees que una función dada en forma de tabla es equivalente a una función?
¡No hablemos por mucho tiempo, pero dibujemos!
Asi que. Dibujamos una función dada de ambas maneras:

¿Ves la diferencia? ¡No se trata de los puntos marcados! Mira más de cerca:

¿Lo has visto ahora? Cuando establecemos la función de forma tabular, reflejamos en la gráfica solo aquellos puntos que tenemos en la tabla y la recta (como en nuestro caso) pasa solo por ellos. Cuando definimos una función de forma analítica, podemos tomar cualquier punto y nuestra función no se limita a ellos. Aquí hay una característica de este tipo. ¡Recuerda!
Manera gráfica de construir una función.
La forma gráfica de construir una función no es menos conveniente. Dibujamos nuestra función, y otra persona interesada puede encontrar a qué es igual y en cierto x, y así sucesivamente. Los métodos gráficos y analíticos se encuentran entre los más comunes.
Sin embargo, aquí debe recordar lo que hablamos al principio: ¡no todos los "garabatos" dibujados en el sistema de coordenadas son una función! ¿Recordado? Por si acaso, copio aquí la definición de lo que es una función:
Como regla general, las personas suelen nombrar exactamente esas tres formas de especificar una función que hemos analizado: analítica (usando una fórmula), tabular y gráfica, olvidando por completo que una función puede describirse verbalmente. ¿Como esto? ¡Sí, muy fácil!
Descripción verbal de la función.
¿Cómo describir la función verbalmente? Tomemos nuestro ejemplo reciente: . Esta función se puede describir como "todo valor real de x corresponde a su triple valor". Eso es todo. Nada complicado. Por supuesto, objetará: "¡hay funciones tan complejas que es simplemente imposible establecerlas verbalmente!" Sí, hay algunas, pero hay funciones que son más fáciles de describir verbalmente que establecer con una fórmula. Por ejemplo: "cada valor natural de x corresponde a la diferencia entre las cifras que la componen, tomándose como minuendo la cifra mayor contenida en la entrada del número". Ahora considere cómo nuestro descripción verbal funciones se implementan en la práctica:
La figura más grande de número dado- , respectivamente, - reducido, entonces:
Principales tipos de funciones.
Ahora pasemos a lo más interesante: considere los principales tipos de funciones con las que trabajó / trabajó y trabajará en el curso de la escuela y el instituto de matemáticas, es decir, los conoceremos, por así decirlo, y les daremos breve descripción. Lea más sobre cada función en la sección correspondiente.
Función lineal
Una función de la forma, donde, son números reales.
La gráfica de esta función es una línea recta, por lo que la construcción función lineal se reduce a encontrar las coordenadas de dos puntos.
Posición directa en Plano coordinado depende del factor de pendiente.

Alcance de la función (también conocido como rango de argumentos) - .
El rango de valores es .
función cuadrática
Función de la forma, donde
El gráfico de la función es una parábola, cuando las ramas de la parábola se dirigen hacia abajo, cuando - hacia arriba.
Muchas propiedades de una función cuadrática dependen del valor del discriminante. El discriminante se calcula mediante la fórmula
La posición de la parábola en el plano de coordenadas en relación con el valor y el coeficiente se muestra en la figura:

Dominio
El rango de valores depende del extremo de la función dada (el vértice de la parábola) y el coeficiente (la dirección de las ramas de la parábola)
proporcionalidad inversa
La función dada por la fórmula, donde
El número se llama el factor de proporcionalidad inversa. Dependiendo de qué valor, las ramas de la hipérbola están en diferentes cuadrados:

Dominio - .
El rango de valores es .
RESUMEN Y FÓRMULA BÁSICA
1. Una función es una regla según la cual a cada elemento de un conjunto se le asigna un único elemento del conjunto.
- - esta es una fórmula que denota una función, es decir, la dependencia de una variable con otra;
- - variable, o, argumento;
- - valor dependiente: cambia cuando cambia el argumento, es decir, de acuerdo con alguna fórmula específica que refleja la dependencia de un valor con respecto a otro.
2. Valores de argumento válidos, o el alcance de una función, es lo que se relaciona con el posible bajo el cual la función cobra sentido.
3. Rango de valores de función- estos son los valores que toma, con valores válidos.
4. Hay 4 formas de configurar la función:
- analítico (usando fórmulas);
- tabular;
- gráfico
- descripción verbal.
5. Principales tipos de funciones:
- : , donde, son números reales;
- : , dónde;
- : , dónde.
La derivada de una función $y = f(x)$ en un punto dado $х_0$ es el límite de la razón del incremento de la función al correspondiente incremento de su argumento, siempre que este último tienda a cero:
$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$
La diferenciación es la operación de encontrar una derivada.
Tabla de derivadas de algunas funciones elementales
| Función | Derivado |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^(n-1)$ |
| $(1)/(x)$ | $-(1)/(x^2)$ |
| $√x$ | $(1)/(2√x)$ |
| $e^x$ | $e^x$ |
| $lnx$ | $(1)/(x)$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-senx$ |
| $tgx$ | $(1)/(cos^2x)$ |
| $ctgx$ | $-(1)/(sen^2x)$ |
Reglas básicas de diferenciación
1. La derivada de la suma (diferencia) es igual a la suma (diferencia) de derivadas
$(f(x) ± g(x))"= f"(x)±g"(x)$
Encuentra la derivada de la función $f(x)=3x^5-cosx+(1)/(x)$
La derivada de la suma (diferencia) es igual a la suma (diferencia) de las derivadas.
$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + senx - (1)/(x^2)$
2. Derivado de un producto
$(f(x) g(x))"= f"(x) g(x)+ f(x) g(x)"$
Encuentra la derivada $f(x)=4x cosx$
$f"(x)=(4x)" cosx+4x (cosx)"=4 cosx-4x senx$
3. Derivada del cociente
$((f(x))/(g(x)))"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $
Encuentra la derivada $f(x)=(5x^5)/(e^x)$
$f"(x)=((5x^5)" e^x-5x^5 (e^x)")/((e^x)^2)=(25x^4 e^x- 5x^5 e^x)/((e^x)^2)$
4. La derivada de una función compleja es igual al producto de la derivada de la función externa y la derivada de la función interna
$f(g(x))"=f"(g(x)) g"(x)$
$f"(x)=cos"(5x) (5x)"=-sen(5x) 5= -5sen(5x)$
El significado físico de la derivada.
si un punto material se mueve en forma rectilínea y su coordenada cambia dependiendo del tiempo según la ley $x(t)$, entonces la velocidad instantánea de este punto es igual a la derivada de la función.
El punto se mueve a lo largo de la línea de coordenadas según la ley $x(t)= 1.5t^2-3t + 7$, donde $x(t)$ es la coordenada en el momento $t$. ¿En qué momento la velocidad del punto será igual a $12$?
1. La velocidad es una derivada de $x(t)$, así que encontremos la derivada de la función dada
$v(t) = x"(t) = 1.5 2t -3 = 3t -3$
2. Para encontrar en qué momento $t$ la velocidad fue igual a $12$, componemos y resolvemos la ecuación:
El significado geométrico de la derivada.
Recuerda que la ecuación de una línea recta no paralela a los ejes de coordenadas se puede escribir como $y = kx + b$, donde $k$ es la pendiente de la línea recta. El coeficiente $k$ es igual a la tangente de la pendiente entre la recta y el sentido positivo del eje $Ox$.
La derivada de la función $f(x)$ en el punto $x_0$ es igual a la pendiente $k$ de la tangente a la gráfica en el punto dado:
Por lo tanto, podemos hacer una igualdad general:
$f"(x_0) = k = tgα$
En la figura, la tangente a la función $f(x)$ es creciente, por lo que el coeficiente $k > 0$. Como $k > 0$, entonces $f"(x_0) = tgα > 0$. El ángulo $α$ entre la tangente y la dirección positiva $Ox$ es agudo.
En la figura, la tangente a la función $f(x)$ es decreciente, por lo tanto el coeficiente $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
En la figura, la tangente a la función $f(x)$ es paralela al eje $Ох$, por lo tanto el coeficiente $k = 0$, por lo tanto $f"(x_0) = tg α = 0$. El punto $ x_0$ en el que $f "(x_0) = 0$, llamado extremo.
La figura muestra la gráfica de la función $y=f(x)$ y la tangente a esta gráfica trazada en el punto de abscisa $x_0$. Encuentra el valor de la derivada de la función $f(x)$ en el punto $x_0$.
La tangente a la gráfica crece, por tanto, $f"(x_0) = tg α > 0$
Para encontrar $f"(x_0)$, encontramos la tangente de la pendiente entre la tangente y la dirección positiva del eje $Ox$. Para ello, completamos la tangente al triángulo $ABC$.
Encuentra la tangente del ángulo $BAC$. (La tangente de un ángulo agudo en un triángulo rectángulo es la razón del cateto opuesto al cateto adyacente).
$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0.25$
$f"(x_0) = tg USTED = $0.25
Respuesta: $0.25
La derivada también se usa para encontrar los intervalos de funciones crecientes y decrecientes:
Si $f"(x) > 0$ en un intervalo, entonces la función $f(x)$ es creciente en ese intervalo.
Si $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
La figura muestra la gráfica de la función $y = f(x)$. Encuentra entre los puntos $х_1,х_2,х_3…х_7$ aquellos puntos donde la derivada de la función es negativa.
En respuesta, anote el número de puntos de datos.
institución educativa municipal
"Escuela secundaria Saltykovskaya
Distrito Rtishchevsky de la región de Saratov
Clase magistral de matemáticas.
en 11º grado
sobre este tema
"FUNCIÓN DERIVADA
EN LAS TAREAS DEL USO”
profesora de matematicas
Beloglázova L. S.
2012-2013 año académico
El propósito de la clase magistral. : desarrollar las habilidades de los estudiantes en la aplicación de conocimientos teóricos sobre el tema "Derivada de una función" para resolver problemas de un solo examen de Estado.
Tareas
Educativo: generalizar y sistematizar el conocimiento de los estudiantes sobre el tema
"La derivada de la función", para considerar los prototipos de los problemas USE sobre este tema, para brindar a los estudiantes la oportunidad de probar sus conocimientos mientras resuelven problemas por su cuenta.
Desarrollando: promover el desarrollo de la memoria, la atención, la autoestima y las habilidades de autocontrol; básico competencias básicas(comparación, comparación, clasificación de objetos, determinación de métodos adecuados para resolver tarea de aprendizaje sobre la base de algoritmos dados, la capacidad de actuar de forma independiente en una situación de incertidumbre, controlar y evaluar sus actividades, encontrar y eliminar las causas de las dificultades).
Educativo: promover:
la formación de la actitud responsable de los estudiantes hacia el aprendizaje;
desarrollo de un interés sostenible por las matemáticas;
creando una motivación intrínseca positiva para estudiar matemáticas.
Tecnología: aprendizaje individual diferenciado, TIC.
Métodos de enseñanza: verbal, visual, práctico, problemático.
Formas de trabajo: individual, frontal, en parejas.
Equipo y materiales para la lección: proyector, pantalla, PC para cada alumno, simulador (Anexo No. 1), presentación para la lección (Anexo No. 2), individualmente - tarjetas diferenciadas para Trabajo independiente en parejas (Anexo No. 3), lista de sitios de Internet, diferenciados individualmente tareas para el hogar (Anexo No. 4).
Explicación para la clase magistral. Esta clase magistral se lleva a cabo en el grado 11 para preparar el examen. Dirigido a la aplicación de material teórico sobre el tema "Derivada de una función" en la resolución de problemas de examen.
Duración de la clase magistral- 30 minutos.
La estructura de la clase magistral.
I. Momento organizativo -1 min.
II Comunicación del tema, objetivos de la clase magistral, motivación para actividades educativas-1 min.
tercero Trabajo de frente. Formación "Asignaciones B8 USO". Análisis de trabajo con el simulador - 6 min.
IV.Individualmente - trabajo diferenciado en parejas. Resolución autónoma de problemas B14. Comprobación mutua - 7 min.
v Revisión de tareas individuales. Tarea con parámetro C5 USE
3 minutos
VI. Pruebas en línea. Análisis de los resultados de las pruebas - 9 min.
VIII. Tarea diferenciada individualmente -1 min.
VIII Calificaciones de la lección - 1 min.
IX Resumen de la lección. Reflexión -1 min.
Progreso de la clase magistral
yo .Organizar el tiempo.
Yo .Comunicación del tema, objetivos de la clase magistral, motivación de las actividades educativas.
(Diapositivas 1-2, Apéndice No. 2)
El tema de nuestra lección es "La derivada de una función en las tareas del examen". Todo el mundo conoce el dicho "La bobina es pequeña y cara". Uno de estos "carretes" en matemáticas es la derivada. La derivada se usa para resolver muchos tareas practicas matemáticas, física, química, economía y otras disciplinas. Le permite resolver problemas de manera simple, hermosa e interesante.
El tema "Derivado" se presenta en las tareas de la parte B (B8, B14) del examen estatal unificado. Algunas tareas de C5 también se pueden resolver usando un derivado. Pero para resolver estos problemas se requiere una buena preparación matemática y un pensamiento no estándar.
Ha trabajado con los documentos que regulan la estructura y el contenido de los materiales de medición de control para el examen estatal unificado de matemáticas de 2013. Concluya quequé conocimientos y habilidades necesita para resolver con éxito los problemas del examen sobre el tema "Derivado".
(Diapositivas 3-4, Apéndice No. 2)
Nosotros estudió"Codificador elementos de contenido en MATEMÁTICAS para compilar materiales de medición de control para realizar un examen estatal unificado”,
“Codificador de requisitos para el nivel de formación de los egresados”,"Especificación materiales de medición de control","Versión de demostración"controlar los materiales de medición del examen estatal unificado 2013 "ydescubierto qué conocimientos y habilidades sobre una función y su derivada se necesitan para resolver con éxito problemas sobre el tema "Derivada".
Necesario
SABER
PAGS reglas para el cálculo de derivados;
derivadas de funciones elementales básicas;
significado geométrico y físico de la derivada;
la ecuación de la tangente a la gráfica de la función;
estudio de una función con la ayuda de una derivada.
SER CAPAZ DE
realizar acciones con funciones (describir el comportamiento y las propiedades de una función según la gráfica, hallar sus valores máximos y mínimos).
USAR
conocimientos y habilidades adquiridos en actividades prácticas y en la vida cotidiana.
Tienes conocimientos teóricos sobre el tema "Derivada". Hoy vamos aAPRENDER A APLICAR LOS CONOCIMIENTOS SOBRE LA FUNCIÓN DERIVADA PARA LA SOLUCIÓN DE PROBLEMAS DE USO. ( Diapositiva 4, solicitud número 2)
Después de todo, no sin razón. Aristóteles dijo que “LA INTELIGENCIA CONSISTE NO SÓLO EN EL CONOCIMIENTO, SINO TAMBIÉN EN LA CAPACIDAD DE APLICAR EL CONOCIMIENTO EN LA PRÁCTICA”( Diapositiva 5, solicitud número 2)
Al final de la lección, volveremos al objetivo de nuestra lección y descubriremos si lo hemos logrado.
tercero . Trabajo de frente. Capacitación "Asignaciones B8 USO" (Anexo N° 1) . Análisis de trabajo con el simulador.
Elija la respuesta correcta de las cuatro dadas.
¿Cuál es, en su opinión, la dificultad de completar la tarea B8?
¿Cuáles crees que son los errores típicos que cometen los graduados en el examen al resolver este problema?
Al responder las preguntas de la tarea B8, debería poder describir el comportamiento y las propiedades de una función en el gráfico de la derivada, y en el gráfico de la función, el comportamiento y las propiedades de la derivada de la función. Y esto requiere buenos conocimientos teóricos sobre los siguientes temas: “Significado geométrico y mecánico de la derivada. Tangente a la gráfica de una función. Aplicación de la derivada al estudio de funciones.
Analice qué tareas le causaron dificultades.
¿Qué preguntas teóricas necesitas saber?
IV. Individualmente - trabajo diferenciado en parejas. Resolución autónoma de problemas B14. Verificación mutua. (Anexo No. 3)
Recuerde el algoritmo para resolver problemas (B14 USE) para encontrar puntos extremos, extremos de una función, los valores más grandes y más pequeños de una función en un intervalo usando una derivada.
Resolver problemas usando la derivada.
A los estudiantes se les planteó el siguiente problema:
“Piénsalo, ¿se pueden resolver algunos problemas de B14 de otra manera, sin usar una derivada?”
1 par(Lukyanova D., Gavryushina D.)
1)B14. Encuentre el punto mínimo de la función y \u003d 10x-ln (x + 9) + 6
2) B14.Encuentra el mayor valor de una funcióny =
- Intenta resolver el segundo problema de dos maneras.
2 pares(Saninskaya T., Sazanov A.)
1)B14.Encuentra el valor más pequeño de la función y=(x-10) en el segmento
2) B14. Encuentre el punto máximo de la función y \u003d - ![]()
(Los estudiantes defienden su solución escribiendo los pasos principales para resolver problemas en la pizarra. Estudiantes de 1 pareja (Lukyanova D., Gavryushina D.) proporcionar dos formas de resolver el problema #2).
Solución de un problema. Conclusión a extraer por los estudiantes:
"Algunos problemas de USE B14 para encontrar los valores más pequeños y más grandes de una función se pueden resolver sin usar una derivada, según las propiedades de las funciones".
¿Analiza qué error cometiste en la tarea?
¿Qué preguntas teóricas necesitas repetir?
v Revisión de tareas individuales. Tarea con parámetro C5(USE) ( Diapositivas 7-8, Apéndice #2)
A Lukyanova K. se le asignó una tarea individual: elegir un problema con el parámetro (C5) de los manuales de preparación USE y resolverlo usando la derivada.
(El alumno da una solución al problema, basándose en el método funcional-gráfico, como uno de los métodos de resolución de problemas C5 USE y da breve explicacion este método).
¿Qué conocimientos sobre la función y su derivada son necesarios para resolver problemas C5 USO?
V I. Pruebas en línea para las tareas B8, B14. Análisis de los resultados de las pruebas.
Sitio para probar en la lección:
¿Quién no cometió errores?
¿Quién experimentó dificultad en la prueba? ¿Por qué?
¿Qué tareas están mal?
Concluye ¿Qué preguntas teóricas necesitas saber?
VI YO. Tarea diferenciada individualmente
(Diapositiva 9, solicitud número 2), (Anexo No. 4).
He preparado una lista de sitios de Internet para preparar el examen. También puede navegar por estos sitiosnorte – líneapruebas. Para la próxima lección, necesita: 1) repetir material teorico sobre el tema "Derivada de una función";
2) en el sitio "Banco abierto de tareas en matemáticas" ( ) encontrar prototipos de las tareas B8 y B14 y resolver al menos 10 tareas;
3) Lukyanova K., Gavryushina D. resuelven problemas con parámetros. El resto de los alumnos resuelven los problemas 1-8 (opción 1).
VIII. Calificaciones de la lección.
¿Qué calificación te pondrías por la lección?
¿Crees que podrías hacerlo mejor en clase?
IX. Resumen de la lección. Reflexión
Resumamos nuestro trabajo. ¿Cuál era el propósito de la lección? ¿Crees que se ha logrado?
Mira la pizarra y en una frase, eligiendo el principio de la frase, continúa con la frase que más te convenga.
Me sentí…
He aprendido…
me las arreglé…
Fui capaz...
Voy a tratar de …
me sorprendió que …
Quise…
¿Puedes decir que durante la lección hubo un enriquecimiento de tu acervo de conocimientos?
Así que repitió las preguntas teóricas sobre la derivada de una función, aplicaron sus conocimientos en la resolución de prototipos de tareas USE (B8, B14), y Lukyanova K. completó la tarea C5 con un parámetro, que es una tarea de mayor grado de complejidad.
Disfruté trabajar contigo y Espero que pueda aplicar con éxito los conocimientos adquiridos en las lecciones de matemáticas no solo en pasando el examen sino también en estudios posteriores.
Me gustaría terminar la lección con las palabras de un filósofo italiano. Tomás de Aquino“El conocimiento es algo tan preciado que no es vergonzoso obtenerlo de cualquier fuente” (Diapositiva 10, Anexo No. 2).
¡Le deseo éxito en la preparación para el examen!
TRABAJO PRÁCTICO EXTRA-CURRICULAR 2
Transformación de gráficas de funciones.
Objetivo
Trace gráficos de funciones usando varias transformaciones, responda la pregunta del problema.
Finalización de la obra
El trabajo está diseñado para 10 opciones, el número de opción coincide con el último dígito del número de serie en la lista. Por ejemplo, 1, 11, 21, 31... realiza 1 opción, 2,12, 22... - 2 opción, etc.
El trabajo consta de dos partes: la primera parte de las tareas 1 - 5, estas son tareas que deben completarse para obtener un crédito, si estas tareas se completan con un error, debe corregirlas y enviar el trabajo nuevamente para verificación. La segunda parte contiene tareas, al completarlas puede obtener una calificación adicional: la parte principal +2 tareas - "4", la parte principal +3 tareas - "5".
Tarea 1. La gráfica de una función lineal es una línea recta, dos puntos son suficientes para construirla. (Tomamos los valores del argumento x arbitrariamente y consideramos sustituir el valor de la función y en la fórmula).
Para verificar si el gráfico de la función pasa por el punto especificado, debe sustituir las coordenadas del punto en lugar de x e y, si obtiene la igualdad correcta, entonces la línea pasa por el punto especificado; de lo contrario, no pasa .
Tarea 2, 3, 4. Las gráficas de las funciones indicadas se obtienen a partir de las gráficas de las funciones , usando un desplazamiento a lo largo del eje x o y.
![]() , primero traza la función o , luego lo desplazamos en "a" unidades a la derecha o a la izquierda (+ a - a la izquierda, - a a la derecha), luego lo desplazamos en "b" unidades hacia arriba o hacia abajo (+ adentro - arriba, - adentro - abajo)
, primero traza la función o , luego lo desplazamos en "a" unidades a la derecha o a la izquierda (+ a - a la izquierda, - a a la derecha), luego lo desplazamos en "b" unidades hacia arriba o hacia abajo (+ adentro - arriba, - adentro - abajo)
Del mismo modo con otras funciones:
Tarea 5 Para trazar un gráfico de función: , necesitas: 1) construir un gráfico de la función , 2) la parte del gráfico que está por encima del eje x no se modifica, 3) la parte del gráfico que está por debajo del eje x se refleja.
Tareas para solución independiente.
Tarea 1. Trace un gráfico de una función lineal, determine si el gráfico de la función pasa por el punto especificado:

Tarea 2. Trace un gráfico de una función cuadrática, indique el conjunto de valores para esta función.

Tarea 3. Construya un gráfico de una función, determine si la función especificada es creciente o decreciente.

Tarea 4. Construye un gráfico de la función, responde la pregunta de la tarea.

Tarea 5. Construya un gráfico de una función que contenga el signo del módulo.

Tareas para evaluación adicional.
Tarea 6. Trace un gráfico de una función dada por partes, determine si esta función tiene un punto de ruptura:


Tarea 7. Determinar cuántas soluciones tiene el sistema de ecuaciones, justificar la respuesta. Sacar conclusiones respondiendo a las preguntas.
¿Qué gráficas de funciones construiste en este trabajo?
¿Cómo se llama la gráfica de una función lineal?
¿Cómo se llama la gráfica de una función cuadrática?
¿Qué transformaciones de gráficos conoces?
Cómo se ubica la gráfica en el sistema de coordenadas incluso función? ¿Gráfica de una función impar?
- En contacto con 0
- Google+ 0
- OK 0
- Facebook 0