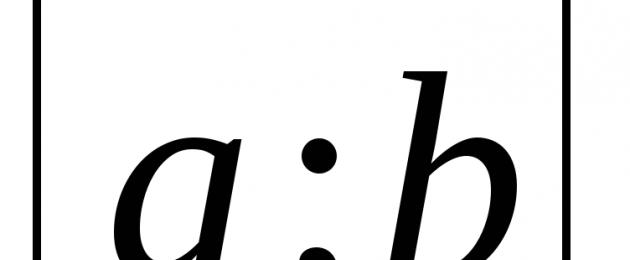En el capítulo anterior, se consideró en detalle uno de los métodos más comunes para aproximar funciones, la interpolación. Pero este camino no es el único. Al resolver varios problemas aplicados y construir circuitos computacionales, a menudo se usan otros métodos. En este capítulo, veremos formas de obtener aproximaciones de la raíz cuadrada media. El nombre de aproximaciones está asociado a espacios métricos en los que se plantea el problema de aproximación de una función. En el Capítulo 1, presentamos los conceptos de "espacio métrico lineal normado" y "espacio euclidiano métrico" y vimos que el error de aproximación está determinado por la métrica del espacio en el que se considera el problema de aproximación. En diferentes espacios, el concepto de error tiene un significado diferente. Teniendo en cuenta el error de interpolación, no nos centramos en esto. Y en este capítulo tendremos que tratar este tema con más detalle.

5.1. Aproximaciones por polinomios trigonométricos y polinomios de Legendre Espacio l2

Considere el conjunto de funciones que son integrables al cuadrado de Lebesgue en el intervalo
, es decir, tal que la integral debe existir
.

Dado que se cumple la desigualdad obvia, a partir de la integrabilidad al cuadrado de las funciones
Y
también debe seguir la integrabilidad al cuadrado de cualquiera de sus combinaciones lineales
, (donde
Y
 cualquier número real), así como la integrabilidad del producto
.

Introduciéndonos en el conjunto de funciones que son integrables al cuadrado de Lebesgue en el intervalo
, la operación del producto escalar

. (5.1.1)

De las propiedades de la integral se deduce que la operación de producto escalar introducida tiene casi todas las propiedades del producto escalar en el espacio euclidiano (ver párrafo 1.10, p. 57):

Solo la primera propiedad no se ejecuta en su totalidad, es decir, no se cumplirá la condición.

De hecho, si
, entonces no se sigue que
en el segmento
. Para que la operación presentada tenga esta propiedad, en lo que sigue conviene no distinguir (considerar equivalentes) las funciones
Y
, para cual

.

En vista de la última observación, hemos visto que el conjunto de funciones integrables del cuadrado de Lebesgue (más precisamente, el conjunto de clases de funciones equivalentes) forma un espacio euclidiano en el que la operación de producto escalar está definida por la fórmula (5.1.1). Este espacio se llama espacio de Lebesgue y se denota
o más corto .

Dado que todo espacio euclidiano es automáticamente tanto normado como métrico, el espacio
es también un espacio normado y métrico. La norma (tamaño del elemento) y la métrica (distancia entre elementos) generalmente se ingresan en él de manera estándar:

(5.1.2)

(5.1.3)

Las propiedades (axiomas) de la norma y la métrica se dan en la Sección 1.10. Elementos espaciales
no son funciones, sino clases de funciones equivalentes. Las funciones que pertenecen a la misma clase pueden tener diferentes valores en cualquier subconjunto finito o incluso contable
. Por lo tanto, las aproximaciones en el espacio
se definen de forma ambigua. Esta característica desagradable del espacio
pagado por la conveniencia de usar el producto escalar.

Tomemos un sistema de coordenadas semicuadrático. Este es un sistema de coordenadas de este tipo, en el que la escala es cuadrática a lo largo de la abscisa, es decir, los valores de división se trazan de acuerdo con la expresión, aquí metro- escala en alguna unidad de longitud, por ejemplo, en cm.

Se traza una escala lineal a lo largo del eje y de acuerdo con la expresión

Ponemos puntos experimentales en este sistema de coordenadas. Si los puntos de este gráfico están ubicados aproximadamente en línea recta, esto confirma nuestra suposición de que la dependencia y desde X está bien expresada por una función de la forma (4.4). Para encontrar los coeficientes a Y B ahora puede aplicar uno de los métodos discutidos anteriormente: el método de hilo estirado, el método de puntos seleccionados o el método promedio.

Método de hilo apretado se aplica de la misma manera que para una función lineal.

Método de puntos seleccionados podemos aplicar así. En un gráfico rectilíneo, tome dos puntos (lejos uno del otro). Denotamos las coordenadas de estos puntos y ( x, y). Entonces podemos escribir

Del sistema reducido de dos ecuaciones, encontramos a Y B y sustituirlos en la fórmula (4.4) y obtener la forma final de la fórmula empírica.

No puede construir un gráfico de línea recta, pero tome los números, ( x,y) directamente desde la tabla. Sin embargo, la fórmula obtenida con esta elección de puntos será menos precisa.

El proceso de convertir un gráfico curvo en una línea recta se llama aplanamiento.

método medio. Se aplica de la misma forma que en el caso de la dependencia lineal. Dividimos los puntos experimentales en dos grupos con el mismo (o casi el mismo) número de puntos en cada grupo. La igualdad (4.4) se puede reescribir como

Encontramos la suma de residuos para los puntos del primer grupo y la igualamos a cero. Hacemos lo mismo para los puntos del segundo grupo. Obtenemos dos ecuaciones con incógnitas. a Y B. Resolviendo el sistema de ecuaciones, encontramos a Y B.

Tenga en cuenta que al aplicar este método, no se requiere construir una línea recta de aproximación. Solo se necesita un diagrama de dispersión en un sistema de coordenadas semicuadrático para comprobar que una función de la forma (4.4) es adecuada para una fórmula empírica.

Ejemplo. Al estudiar el efecto de la temperatura en el transcurso del cronómetro, se obtuvieron los siguientes resultados:

z	-20	-15,4	-9,0	-5,4	-0,6	+4,8	+9,4
	2,6	2,01	1,34	1,08	0,94	1,06	1,25

En este caso, no nos interesa la temperatura en sí, sino su desviación de . Por lo tanto, tomamos como argumento , donde t- temperatura en grados Celsius de la escala habitual.

Habiendo graficado los puntos correspondientes en el sistema de coordenadas cartesianas, notamos que una parábola con un eje paralelo al eje y puede tomarse como una curva de aproximación (Fig. 4). Tomemos un sistema de coordenadas semicuadrático y tracemos puntos experimentales en él. Vemos que estos puntos encajan bastante bien en una línea recta. Entonces la fórmula empírica

se puede buscar en la forma (4.4).

Definamos los coeficientes a Y B por el método del promedio. Para hacer esto, dividimos los puntos experimentales en dos grupos: en el primer grupo, los primeros tres puntos, en el segundo, los cuatro puntos restantes. Usando la igualdad (4.5) encontramos la suma de residuos para cada grupo e igualamos cada suma a cero.

Deje que la tabla contenga los valores de la función obtenida, por ejemplo, del experimento, es decir, medida con un error. Entonces la aproximación usando aparato de interpolación , que se basa en igualar los valores del polinomio en los nodos de interpolación a los valores de la tabla, poco práctico.

Con esta formulación del problema, se debe realizar una aproximación en promedio, es decir, describir en forma tabular función dada alguna dependencia analítica bastante simple con un pequeño número de parámetros. La elección óptima de estos parámetros nos permitirá realizar la aproximación cuadrática media de la función dada por la tabla.

Selección del tipo de dependencia analítica debe comenzar poniendo datos tabulares en Plano coordinado- así se formará el campo de puntos experimentales. Se dibuja una curva suave a través del campo de estos puntos de modo que algunos de los puntos se encuentran en esta curva, algunos de los puntos son más altos y algunos de los puntos son más bajos que la curva dibujada. Por la forma de esta curva, se debe determinar el tipo de dependencia analítica, ya sea lineal, exponencial, hiperbólica o cualquier otra.

Sin embargo, según el gráfico, es muy difícil elegir el tipo de dependencia analítica a simple vista. Por lo que se propuso un método de estimación aproximada y elección del tipo de dependencia analítica. Este método es realmente aproximado e inexacto, ya que la curva se puede dibujar de diferentes maneras a través del campo de puntos experimentales, y se pueden tomar diferentes puntos de referencia en la tabla para el cálculo, y se desconoce la precisión de la técnica propuesta. Al mismo tiempo, puede considerarse como una forma aproximada de elegir el tipo de dependencia.

Se propone el siguiente algoritmo de acciones.

1. En la tabla de origen, seleccione dos puntos con coordenadas (x 1, y 1) y (x n, y n) - puntos de referencia, separados entre sí, y para cada par de coordenadas calcule la media aritmética, la media geométrica y la media armónica.

2. En la curva trazada a través del campo de puntos experimentales, encuentre tres ordenadas correspondientes a las abscisas encontradas x ar, x geom, x harmm:

3. Realizar una comparación encontrada en la curva con la calculada calculando los siguientes módulos de diferencias:

4. De los valores encontrados, se selecciona el mínimo:

5. Conclusiones: si resultó ser mínimo

Dependencia lineal

La dependencia es indicativa

Dependencia fraccionaria-lineal

La dependencia es logarítmica.

Dependencia del poder

Dependencia hiperbólica

Dependencia fraccional-racional

Cualquiera de estas dependencias se puede reducir a una lineal realizando una transformación de coordenadas o la llamada alineación de datos.
Así, la primera etapa finaliza con la elección del tipo de dependencia analítica, cuyos parámetros no están definidos.

Segunda fase consiste en determinar los mejores valores de los coeficientes de la dependencia analítica seleccionada. Para esto, matemática método de mínimos cuadrados.

El método se basa en minimizar la suma de las desviaciones al cuadrado de los valores tabulares dados () de los calculados según la dependencia teórica (): .

Sea la dependencia elegida línea recta: . Sustituir en el funcional: . Entonces el funcional se minimiza:

Para encontrar los mejores valores de los coeficientes y es necesario encontrar las derivadas parciales de con respecto a y e igualarlas a cero:

Después de las transformaciones, el sistema de ecuaciones toma la forma:

Solución de este sistema. ecuaciones lineales le permite encontrar los mejores valores de los coeficientes y dependencia lineal.

Si la dependencia seleccionada es parábola cuadrática:

entonces el funcional se minimiza: .

La parábola tiene tres coeficientes variables, cuyos mejores valores se deben encontrar igualando a cero las derivadas parciales del funcional minimizado con respecto a los coeficientes deseados. Esto nos permite obtener el siguiente sistema de tres ecuaciones lineales para encontrar los coeficientes:

Ejemplo 1 Determine el tipo de dependencia dada por la siguiente tabla.

X
Y	0,55	0,64	0,78	0,85	0,95	0,98	1,06	1,11

Solución.

Los puntos especificados en la tabla deben aplicarse al plano de coordenadas: un campo de datos experimentales. A través de este campo curva suave.

De acuerdo a la tabla se seleccionan dos puntos de anclaje con coordenadas (3; 0,55) y (10; 1,11) y para cada par de abscisas y ordenadas se calcula la media aritmética, geométrica y armónica:

Para las tres abscisas calculadas a lo largo de la curva trazada a través del campo de puntos experimentales, se determinan tres ordenadas correspondientes:

Nota sobre la orientación de los cálculos. A continuación, se definen siete módulos de diferencias:

Se obtienen tres valores mínimos, próximos entre sí

En la segunda etapa, es necesario determinar los mejores valores de los coeficientes para cada una de estas dependencias utilizando el método de mínimos cuadrados y luego calcular la desviación estándar de los valores tabulares dados.

La elección final de la dependencia analítica se realiza por el valor mínimo de la desviación estándar.

Ejemplo 2 La tabla muestra los resultados Estudios experimentales, que se puede aproximar por una línea recta. Encuentra los mejores valores de los coeficientes de la recta aplicando el método de mínimos cuadrados.

Solución.

k	X k	y k	X k Y k	X k 2	Y k teoría	Teoría Y k -Y k	(Teoría Y k -Y k) 2
		66,7			67,50	0,20	0,0400
		71,0	284,0		70,98	0,02	0,0004
		76,3	763,0		76,20	0,10	0,0100
		80,6	1209,0		80,55	0,05	0,0025
		85,7	1799,7		85,77	- 0,07	0,0049
		92,9	2694,1		92,73	0,17	0,0289
		99,4	3578,4		98,82	0,58	0,3364
		113,6	5793,6		111,87	1,73	2,9929
		125,1	8506,8		126,66	- 1,56	2,4336
montos		811,3	24628,6				5,8496

Ecuación general de una recta: .

El sistema de ecuaciones lineales, a partir del cual se deben determinar los mejores valores de los coeficientes y, guiados por el método de los mínimos cuadrados, tiene la forma:

Sustituyamos las sumas calculadas de las columnas 2, 3, 4 y 5 de la última fila de la tabla en el sistema de ecuaciones:

¿De dónde se determinan los coeficientes de dependencia lineal? Entonces la ecuación de la recta teórica tiene la forma:

. (*)

La sexta columna de la tabla muestra los valores de función calculados por la ecuación teórica para los valores dados del argumento. La séptima columna de la tabla muestra los valores de las diferencias entre los valores dados de la función (3ª columna) y los valores teóricos (6ª columna) calculados por la ecuación (*).

La octava columna muestra las desviaciones al cuadrado de los valores teóricos de los valores experimentales y se determina la suma de las desviaciones al cuadrado. Ahora puedes encontrar

Ejemplo 3 Deje que los datos experimentales dados en la tabla se aproximen mediante una parábola cuadrática: Encuentra los mejores valores para los coeficientes de la parábola aplicando el método de los mínimos cuadrados.

Solución.

k	X k	y k	X k 2	X k 3	X k 4	X k Y k	X k 2 Y k	Y k teoría	Teoría Y k -Y k
		29,8						29,28	0,52	0,2704
		22,9				45,8	91,6	22,22	0,68	0,4624
		17,1				68,4	273,6	17,60	-0,50	0,2500
		15,1				75,5	377,5	15,56	-0,46	0,2116
		10,7				85,6	684,8	11,53	-0,83	0,6889
		10,1				101,0	1010,0	10,60	-0,50	0,2500
		10,6				127,2	1526,4	11,06	-0,46	0,2116
		15,2				228,0	3420,0	14,38	0,82	0,6724
Sumi		122,5				731,5	7383,9			3,0173

El sistema de ecuaciones lineales para determinar los coeficientes de una parábola tiene la forma:

Desde la última fila de la tabla, las sumas correspondientes se sustituyen en el sistema de ecuaciones:

La solución del sistema de ecuaciones le permite determinar los valores de los coeficientes:

Entonces, la dependencia dada por la tabla sobre el segmento se aproxima mediante una parábola cuadrática:

El cálculo de acuerdo con la fórmula dada para los valores dados del argumento permite formar la novena columna de la tabla que contiene los valores teóricos de la función.

La suma de las desviaciones al cuadrado de los valores teóricos de los experimentales se da en la última línea de la columna 11 de la tabla. Esto le permite determinar Desviación Estándar:

PRÁCTICA #3

Tema: Métodos para resolver sistemas de ecuaciones

método de Gauss - método de exclusión sucesiva de incógnitas - pertenece al grupo métodos precisos y si no hubiera error de cálculo, se podría obtener una solución exacta.

Para los cálculos manuales, es recomendable realizar los cálculos en una tabla que contenga una columna de control. A continuación se muestra una versión general de dicha tabla para resolver un sistema de ecuaciones lineales de cuarto orden.

				miembros gratis	columna de control

				miembros gratis	columna de control

Ejemplo 1 Usando el método de Gauss, resuelva el sistema de ecuaciones de cuarto orden:

Estos valores aproximados de las raíces pueden sustituirse en el sistema original de ecuaciones y calcularse derechos residuales de autor - , que son las diferencias entre la parte derecha e izquierda de cada ecuación del sistema al sustituir las raíces encontradas en la parte izquierda. Luego se sustituyen como miembros libres del sistema residual y se obtienen enmiendas

raíces - :

Aproximación de la raíz cuadrada media de una función.

Considere el problema de la mejor aproximación cuadrática media de una función por un polinomio
según el sistema
.

Definición 1.

Un polinomio generalizado de orden m en el sistema ( k ) es una combinación lineal

donde C k son coeficientes reales arbitrarios.

Una tarea. Encuentra polinomio
, que se desvía menos de la función f en la métrica L 2, es decir, satisfaciendo la condición:

Teorema 1.

Si el sistema
es linealmente independiente, entonces el problema de la mejor aproximación a la raíz cuadrada media con respecto a este sistema tiene una solución única.

Escribamos el cuadrado de la distancia entre la función y el polinomio:

(1)

Es obvio que el valor
es una función cuadrática definida no negativa de variables
, y tal función alcanza su valor mínimo. Por lo tanto, existe la solución del problema de aproximación de la raíz cuadrada media.

Probemos la unicidad de la solución.

Anotamos las condiciones necesarias para el mínimo:

, i=0,…,m.

Calculando las derivadas parciales con respecto a c i de la expresión (1), obtenemos un sistema lineal de ecuaciones:

(2)

El sistema (2) se llama sistema normal.

Escribimos el determinante de este sistema

(3)

El determinante del sistema (3) es el llamado determinante de Gram sistemas
. Se sabe que si el sistema
es linealmente independiente, entonces el determinante
0 (fácil de demostrar por contradicción). Según la condición del teorema
0 y el sistema (2) tiene solución única.

1.6. Polinomios ortogonales clásicos y su aplicación en problemas de aproximación de funciones.

Sea H un espacio de Hilbert con producto interior y, en consecuencia, la norma
. Un ejemplo importante de tal espacio es el llamado espacio
es el espacio de funciones f(x) para el cual la integral es finita:

(1)

Aquí h(x) es el llamado función de peso, satisfaciendo las condiciones:

Si =(0,+ ), entonces se debe cumplir la siguiente condición:

esos. debe existir cualquier momento de la función de peso.

Definición 1.

Para
producto escalar se define:

(2)

y, en consecuencia, la norma:

según la condición (1).

Usando la desigualdad de Cauchy-Bunyakovsky-Schwarz, obtenemos

Por lo tanto, el producto escalar existe para

Definición 2.

La distancia entre los elementos f y g está determinada por la igualdad:

.

Surge la pregunta de cómo entender el elemento cero. Si la norma
, ¿se sigue que f=g? Se introduce la terminología: f=g casi en todas partes, es decir, pueden diferir en un número finito de puntos.

Definición 3.

f y g ortogonal en un segmento con peso h(x), si =0 (escrito brevemente
).

Si en un espacio de Hilbert tomamos cualquier sistema linealmente independiente
, i=0,1,2,…, entonces se puede ortogonalizar.

Tomemos un sistema como ejemplo:
En
conjunto finito funciones de poder es linealmente independiente, por lo que se pueden construir polinomios ortogonales sobre la base de este sistema. Se conoce el siguiente procedimiento de ortogonalización recurrente (procedimiento de Gram-Schmidt):

(3)

Los coeficientes b k+1,j se determinan a partir de las condiciones de ortogonalidad:

Multiplicando sucesivamente (3) por
obtenemos

(4)

Ejemplo 1

Sea h(x)1, =[-1,1].

Construya los tres primeros polinomios ortogonales según el procedimiento (3) - (4).

A continuación tenemos:

Como consecuencia,

Para un sistema de polinomios ortogonales en el segmento [-1,1] con peso h(x)=1, la fórmula de Rodrigues es cierta:

(5)

De (5) obtenemos sucesivamente:

Los polinomios así obtenidos se denominan polinomios de Legendre.

Comentario.

Los polinomios ortogonales encontrados usando el procedimiento (3) - (4) solo pueden diferir en factores de los que se construyen usando la fórmula explícita de Rodrigues (5).

El cuadrado de la norma para estos polinomios es:

Es decir, estos polinomios no están normalizados, ya que

Para todos los polinomios clásicos existe una fórmula recurrente. Para polinomios de Legendre, tiene la siguiente forma:

Permitir
Consideremos la aproximación de la raíz cuadrada media:

donde
- raíz del error cuadrático medio de aproximación,

- un segmento de la serie de Fourier para la función f(x) en el sistema de polinomios ortogonales (P k (x)).

Debido a la ortogonalidad de los polinomios de Legendre, el sistema de ecuaciones normales (2) del §1.5 se vuelve diagonal y su solución conduce a las siguientes expresiones para los coeficientes c k:

(7)

es decir, se asegura el mínimo de la norma en L 2.

Describamos en detalle el error de aproximación

Por otro lado

debido a la ortogonalidad.

Sustituyendo en (8), obtenemos

. (9)

Ejemplo 2

Sea f(x)=|x|.

Aproximar f(x) sobre [-1,1] en el polinomio rms de segundo grado. Calcule el error cuadrático medio de la raíz.

Usamos el sistema ortogonal de Legendre:

Los coeficientes c k se encuentran por la fórmula (7), teniendo en cuenta la forma de los polinomios de Legendre:

1.7. Algunas propiedades generales de los polinomios ortogonales.

El polinomio P n (x) es ortogonal a cualquier polinomio algebraico de m-ésimo grado M m (x) para m

M m (x) se puede representar de forma única como una combinación lineal de polinomios de Legendre:

La igualdad (10) es idéntica, por lo que los coeficientes ak se calculan únicamente igualando los coeficientes a potencias más altas. Multiplicando ambas partes de (10) por P n (x), tenemos

debido a la ortogonalidad del sistema

El polinomio P n (x) tiene exactamente n raíces reales y distintas en el segmento [-1,1].

Nótese que, en virtud del teorema de Gauss, el polinomio P n (x) no puede tener más de n raíces (generalmente complejas). Sean P n (x) menos de n raíces reales simples. Vamos a denotarlos
A partir de estos puntos construimos el polinomio fundamental

Considere un polinomio:
es un polinomio de grado (k+n) que tiene ceros
incluso la multiplicidad. Entonces el nuevo polinomio
conserva su signo al pasar por estos ceros, es decir conserva el signo en [-1,1]. De ahí se sigue que

Pero esto contradice la propiedad 1, ya que P n (x) debe ser necesariamente ortogonal a M k (x).

Entre dos ceros adyacentes del polinomio P n (x) se encuentra exactamente un cero del polinomio P n-1 (x).

Se prueba por inducción con la ayuda de la relación recurrente (6).

Para n-par, el polinomio P n (x) es una función par de x, para n-impar, P n (x) es una función impar de x.

Junto con los polinomios de Legendre, los siguientes sistemas de polinomios se denominan polinomios ortogonales clásicos (en adelante, (a,b) es el intervalo de ortogonalidad, r(x) es la función de peso).

1) Polinomios de Jacobi {R PAGS (yo,m) ( X)) - en pero = -1, B= 1 r( X) = (1-X) yo (1 + X) m , yo> -1, m > -1. Los casos especiales especiales de los polinomios de Jacobi corresponden a los siguientes valores de l y m: yo= m- polinomios ultraesféricos (estos a veces se llaman polinomios de Gegenbauer); yo\u003d m \u003d - 1 / 2, es decir -polinomios Chebyshev 1er tipo T norte (X); yo= m = 1 / 2, es decir - polinomios Chebyshev 2do tipo tu norte (X);

2) polinomios Laguerre L norte (X) - en pero = 0, B= + ∞ y r( X) = mi -X(también se les llama polinomios de Chebyshev-Laguerre) y polinomios de Laguerre generalizados - en . 3) METROpiernas hermita H norte (X) - en pero = -∞, B= + ∞ y (también se les llama polinomios de Chebyshev-Hermite).

A menudo los valores de la función interpolada tu, tu2 , ..., yn se determinan a partir del experimento con algunos errores, por lo que no es razonable utilizar la aproximación exacta en los nodos de interpolación. En este caso, es más natural aproximar la función no por puntos, sino por promedio, es decir, en una de las normas Lp.

Espacio 1 p - conjunto de funciones d(x), definido en el segmento [a,b] y módulo integrable con p-ésimo grado, si la norma se define

La convergencia en tal norma se llama convergencia en promedio. El espacio 1,2 se llama espacio de Hilbert y la convergencia en él es rms.

Sean dadas la función Ax) y el conjunto de funciones φ(x) de algún espacio lineal normado. En el contexto del problema de interpolación, aproximación y aproximación, se pueden formular los siguientes dos problemas.

Primera tarea es una aproximación con una precisión dada, es decir, de acuerdo con un mi encontrar un φ(x) tal que la desigualdad |[Ax) - φ(x)|| GRAMO..

Segunda tarea es una busqueda la mejor aproximación es decir, la búsqueda de una función φ*(x) que satisfaga la relación:

Definamos sin demostración una condición suficiente para la existencia de la mejor aproximación. Para ello, en el espacio lineal de funciones, elegimos un conjunto parametrizado por la expresión

donde se supondrá que el conjunto de funciones φ[(x), ..., φn(x) es linealmente independiente.

Se puede demostrar que en cualquier espacio normado con aproximación lineal (2.16) existe la mejor aproximación, aunque es única en cualquier espacio lineal.

Consideremos el espacio de Hilbert LzCp) de funciones reales integrables al cuadrado con peso p(x) > 0 en [ , donde el producto escalar ( g, h) determinado por

fórmula:

Sustituyendo la combinación lineal (2.16) en la condición de mejor aproximación, encontramos

Igualando a cero las derivadas con respecto a los coeficientes (D, k= 1, ..., П, obtenemos un sistema de ecuaciones lineales

El determinante del sistema de ecuaciones (2.17) se llama determinante de Gram. El determinante de Gram es distinto de cero, ya que se supone que el sistema de funciones φ[(x), ..., φn(x) es linealmente independiente.

Por lo tanto, la mejor aproximación existe y es única. Para obtenerlo, es necesario resolver el sistema de ecuaciones (2.17). Si el sistema de funciones φ1(x), ..., φn(x) es ortogonalizado, es decir, (φ/, φ,) = sy, donde SCH,yo = 1, ..., PAGS, entonces el sistema de ecuaciones se puede resolver de la forma:

Los coeficientes encontrados según (2.18) Q, ..., p se denominan coeficientes de la serie de Fourier generalizada.

Si un conjunto de funciones φ t (X), ..., φ "(x), ... forma un sistema completo, entonces, en virtud de la igualdad de Parseval para Π -» con la norma de error decrece indefinidamente. Esto significa que la mejor aproximación converge rms a Dx) con cualquier precisión dada.

Observamos que la búsqueda de los coeficientes de mejor aproximación resolviendo el sistema de ecuaciones (2.17) es prácticamente irrealizable, ya que a medida que aumenta el orden de la matriz de Gram, su determinante tiende rápidamente a cero y la matriz se vuelve mal condicionada. Resolver un sistema de ecuaciones lineales con una matriz de este tipo conducirá a una pérdida significativa de precisión. Vamos a ver.

Sea como un sistema de funciones φ„ i =1, ..., П, se eligen los grados, es decir, φ* = X 1 ", 1 = 1, ..., PAGS, luego, asumiendo el segmento como un segmento de aproximación, encontramos la matriz de Gram

La matriz de Gram de la forma (2.19) también se denomina matriz de Hilbert. Este es un ejemplo clásico de la llamada matriz mal condicionada.

Usando MATLAB, calculamos el determinante de la matriz de Hilbert en la forma (2.19) para algunos primeros valores pags. El listado 2.5 muestra el código del programa correspondiente.

Listado 23

% Calcular el determinante de las matrices de Hilbert % Limpiar el espacio de trabajo limpiar todo;

%escoger valor máximo orden de la matriz de Hilbert pt = 6;

%construir un bucle para generar matrices %Hilbert y calcular sus determinantes

para n = 1: nmax d(n)=det(hi I b(n)); final

%mostrar los valores de los determinantes %de las matrices de Hilbert

f o g ta t extremo corto

Después de resolver el código del Listado 2.5, los valores determinantes de la matriz de Hilbert para las primeras seis matrices deberían aparecer en la ventana de comandos de MATLAB. La siguiente tabla muestra los valores numéricos correspondientes de los órdenes de la matriz (n) y sus determinantes (d). La tabla muestra claramente qué tan rápido el determinante de la matriz de Hilbert tiende a cero a medida que aumenta el orden y, a partir de los órdenes 5 y 6, se vuelve inaceptablemente pequeño.

Tabla de valores del determinante de matrices de Hilbert

La ortogonalización numérica del sistema de funciones φ, i = 1, ..., Π también conduce a una notable pérdida de precisión, por lo tanto, para tener en cuenta una gran cantidad de términos en la expansión (2.16), es necesario ya sea para llevar a cabo la ortogonalización analíticamente, es decir, exactamente, o para usar un sistema ya hecho de funciones ortogonales.

Si durante la interpolación, los grados se usan generalmente como un sistema de funciones base, entonces durante la aproximación, en promedio, los polinomios que son ortogonales con un peso dado se eligen como funciones base. Los más comunes son los polinomios de Jacobi, un caso especial de los cuales son los polinomios de Legendre y Chebyshev. También se utilizan polinomios de Lagsrr y Hermite. Se pueden encontrar más detalles sobre estos polinomios, por ejemplo, en el apéndice polinomios ortogonales libros.