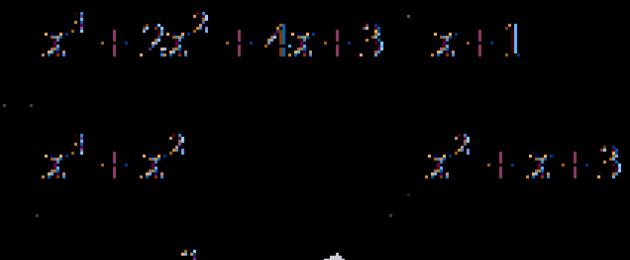Solución de la ecuación de 5º grado en radicales. Solución de ecuaciones de grados superiores

Al canal de youtube de nuestro sitio web para estar al tanto de todas las nuevas lecciones en video.

Primero, recordemos las fórmulas básicas de los grados y sus propiedades.

producto de un numero a ocurre sobre sí mismo n veces, podemos escribir esta expresión como a a … a=a n

1. un 0 = 1 (un ≠ 0)

3. un norte un metro = un norte + metro

4. (un n) m = un nm

5. un norte segundo norte = (ab) norte

7. a n / a m \u003d a n - m

Poder o ecuaciones exponenciales - estas son ecuaciones en las que las variables están en potencias (o exponentes), y la base es un número.

Ejemplos de ecuaciones exponenciales:

En este ejemplo, el número 6 es la base, siempre está en la parte inferior, y la variable X grado o medida.

Demos más ejemplos de ecuaciones exponenciales.
2 x * 5 = 10
16x-4x-6=0

Ahora veamos cómo se resuelven las ecuaciones exponenciales.

Tomemos una ecuación simple:

2 x = 2 3

Tal ejemplo se puede resolver incluso en la mente. Se puede ver que x=3. Después de todo, para que la izquierda y parte derecha fueran iguales, debes poner el número 3 en lugar de x.
Ahora veamos cómo se debe tomar esta decisión:

2 x = 2 3
x = 3

Para resolver esta ecuación, eliminamos mismos motivos(es decir, doses) y anotó lo que sobraba, estos son grados. Tenemos la respuesta que estábamos buscando.

Ahora resumamos nuestra solución.

Algoritmo para resolver la ecuación exponencial:
1. Necesito verificar lo mismo si las bases de la ecuación a la derecha ya la izquierda. Si los motivos no son los mismos, estamos buscando opciones para resolver este ejemplo.
2. Después de que las bases sean iguales, equiparar grado y resolver la nueva ecuación resultante.

Ahora resolvamos algunos ejemplos:

Comencemos de forma sencilla.

Las bases de los lados izquierdo y derecho son iguales al número 2, lo que significa que podemos descartar la base e igualar sus grados.

x+2=4 Ha resultado la ecuación más simple.
x=4 - 2
x=2
Respuesta: x=2

En el siguiente ejemplo, puedes ver que las bases son diferentes, estas son 3 y 9.

3 3x - 9x + 8 = 0

Para empezar, trasladamos el nueve al lado derecho, obtenemos:

Ahora necesitas hacer las mismas bases. Sabemos que 9=3 2 . Usemos la fórmula de la potencia (a n) m = a nm .

3 3x \u003d (3 2)x + 8

Obtenemos 9 x + 8 \u003d (3 2) x + 8 \u003d 3 2 x + 16

3 3x \u003d 3 2x + 16 ahora está claro que las bases en los lados izquierdo y derecho son iguales e iguales a tres, lo que significa que podemos descartarlas e igualar los grados.

3x=2x+16 obtuvo la ecuación más simple
3x-2x=16
x=16
Respuesta: x=16.

Veamos el siguiente ejemplo:

2 2x + 4 - 10 4x \u003d 2 4

En primer lugar, nos fijamos en las bases, las bases son diferentes dos y cuatro. Y tenemos que ser iguales. Transformamos el cuádruple según la fórmula (a n) m = a nm .

4 x = (2 2) x = 2 2x

Y también usamos una fórmula a n a m = a n + m:

2 2x+4 = 2 2x 2 4

Añadir a la ecuación:

2 2x 2 4 - 10 2 2x = 24

Dimos un ejemplo por las mismas razones. Pero nos interfieren otros números 10 y 24. ¿Qué hacer con ellos? Si observa de cerca, puede ver que en el lado izquierdo repetimos 2 2x, aquí está la respuesta: podemos poner 2 2x fuera de paréntesis:

2 2x (2 4 - 10) = 24

Calculemos la expresión entre paréntesis:

2 4 — 10 = 16 — 10 = 6

Dividimos toda la ecuación por 6:

Imagina 4=2 2:

2 2x \u003d 2 2 bases son iguales, descartarlas e igualar los grados.
2x \u003d 2 resultó ser la ecuación más simple. Lo dividimos por 2, obtenemos
X = 1
Respuesta: x = 1.

Resolvamos la ecuación:

9x - 12*3x +27= 0

Transformemos:
9 x = (3 2) x = 3 2x

Obtenemos la ecuación:
3 2x - 12 3x +27 = 0

Las bases son las mismas para nosotros, igual a 3. En este ejemplo, se puede ver que el primer triple tiene un grado dos veces (2x) que el segundo (solo x). En este caso, puede decidir método de sustitución. El número de menor grado se reemplaza por:

Entonces 3 2x \u003d (3 x) 2 \u003d t 2

Reemplazamos todos los grados con x en la ecuación con t:

t 2 - 12t + 27 \u003d 0
Obtenemos una ecuación cuadrática. Resolvemos a través del discriminante, obtenemos:
D=144-108=36
t1 = 9
t2 = 3

Volver a variables X.

Tomamos t 1:
t 1 \u003d 9 \u003d 3 x

Es decir,

3x = 9
3 x = 3 2
x1 = 2

Se encontró una raíz. Buscamos el segundo, de t 2:
t 2 \u003d 3 \u003d 3 x
3 x = 3 1
x2 = 1
Respuesta: x 1 \u003d 2; x2 = 1.

En el sitio puede en la sección AYUDAR A DECIDIR para hacer preguntas de interés, definitivamente le responderemos.

Únete a un grupo

En general, una ecuación que tiene un grado superior a 4 no se puede resolver en radicales. Pero a veces todavía podemos encontrar las raíces del polinomio de la izquierda en la ecuación de mayor grado, si lo representamos como un producto de polinomios en un grado de no más de 4. La solución de este tipo de ecuaciones se basa en la descomposición del polinomio en factores, por lo que te recomendamos revisar este tema antes de estudiar este artículo.

La mayoría de las veces, uno tiene que lidiar con ecuaciones de grados más altos con coeficientes enteros. En estos casos, podemos tratar de encontrar raíces racionales, y luego factorizar el polinomio para luego convertirlo a una ecuación de menor grado, la cual será fácil de resolver. En el marco de este material, consideraremos tales ejemplos.

Ecuaciones de grado superior con coeficientes enteros

Todas las ecuaciones de la forma a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 , podemos reducir a una ecuación del mismo grado multiplicando ambos lados por a n n - 1 y cambiando la variable de la forma y = a n x:

un norte X norte + un norte - 1 X norte - 1 + . . . + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 + … + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 + … + segundo 1 y + segundo 0 = 0

Los coeficientes resultantes también serán números enteros. Así, necesitaremos resolver la ecuación reducida de grado n con coeficientes enteros, que tiene la forma x n + a n x n - 1 + ... + a 1 x + a 0 = 0.

Calculamos las raíces enteras de la ecuación. Si la ecuación tiene raíces enteras, debes buscarlas entre los divisores del término libre a 0. Escribámoslos y sustituyémoslos en la igualdad original uno por uno, comprobando el resultado. Una vez que hemos obtenido una identidad y hallado una de las raíces de la ecuación, podemos escribirla de la forma x - x 1 · P n - 1 (x) = 0 . Aquí x 1 es la raíz de la ecuación, y P n - 1 (x) es el cociente de x n + a n x n - 1 + ... + a 1 x + a 0 dividido por x - x 1 .

Sustituye los restantes divisores en P n - 1 (x) = 0 , comenzando por x 1 , ya que las raíces se pueden repetir. Después de obtener la identidad, se considera encontrada la raíz x 2, y la ecuación se puede escribir como (x - x 1) (x - x 2) P n - 2 (x) \u003d 0. Aquí P n - 2 (x ) será el cociente de dividir P n - 1 (x) por x - x 2 .

Seguimos ordenando los divisores. Encuentra todas las raíces enteras y denota su número como m. Después de eso, la ecuación original se puede representar como x - x 1 x - x 2 · … · x - x m · P n - m (x) = 0 . Aquí P n - m (x) es un polinomio de n - m -ésimo grado. Para el cálculo es conveniente usar el esquema de Horner.

Si nuestra ecuación original tiene coeficientes enteros, no podemos terminar con raíces fraccionarias.

Como resultado, obtuvimos la ecuación P n - m (x) = 0, cuyas raíces se pueden encontrar de cualquier manera conveniente. Pueden ser irracionales o complejos.

vamos a mostrar en ejemplo específico cómo se aplica dicho esquema de solución.

Ejemplo 1

Condición: encuentra la solución de la ecuación x 4 + x 3 + 2 x 2 - x - 3 = 0 .

Solución

Comencemos por encontrar raíces enteras.

Tenemos una intersección igual a menos tres. Tiene divisores iguales a 1, -1, 3 y -3. Sustituyámoslos en la ecuación original y veamos cuál de ellos dará como resultado identidades.

Para x igual a uno, obtenemos 1 4 + 1 3 + 2 1 2 - 1 - 3 \u003d 0, lo que significa que uno será la raíz de esta ecuación.

Ahora dividamos el polinomio x 4 + x 3 + 2 x 2 - x - 3 por (x - 1) en una columna:

Entonces x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Obtuvimos una identidad, lo que significa que encontramos otra raíz de la ecuación, igual a - 1.

Dividimos el polinomio x 3 + 2 x 2 + 4 x + 3 por (x + 1) en una columna:

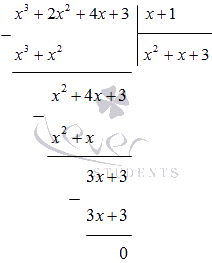
eso lo conseguimos

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Sustituimos el siguiente divisor en la ecuación x 2 + x + 3 = 0, comenzando desde - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Las igualdades resultantes serán incorrectas, lo que significa que la ecuación ya no tiene raíces enteras.

Las raíces restantes serán las raíces de la expresión x 2 + x + 3 .

D \u003d 1 2 - 4 1 3 \u003d - 11< 0

De aquí se sigue que este trinomio cuadrado no tiene raíces reales, sino que las hay complejas conjugadas: x = - 1 2 ± i 11 2 .

Aclaremos que en lugar de dividir en una columna, se puede utilizar el esquema de Horner. Esto se hace así: después de haber determinado la primera raíz de la ecuación, completamos la tabla.

En la tabla de coeficientes, podemos ver inmediatamente los coeficientes del cociente de la división de polinomios, lo que significa x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

Después de encontrar la siguiente raíz, igual a -1, obtenemos lo siguiente:

Responder: x \u003d - 1, x \u003d 1, x \u003d - 1 2 ± i 11 2.

Ejemplo 2

Condición: resuelve la ecuación x 4 - x 3 - 5 x 2 + 12 = 0.

Solución

El miembro libre tiene divisores 1 , - 1 , 2 , - 2 , 3 , - 3 , 4 , - 4 , 6 , - 6 , 12 , - 12 .

Veámoslos en orden:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Entonces x = 2 será la raíz de la ecuación. Divide x 4 - x 3 - 5 x 2 + 12 por x - 2 usando el esquema de Horner:

Como resultado, obtenemos x - 2 (x 3 + x 2 - 3 x - 6) = 0 .

2 3 + 2 2 - 3 2 - 6 = 0

Entonces 2 volverá a ser una raíz. Divide x 3 + x 2 - 3 x - 6 = 0 por x - 2:

Como resultado, obtenemos (x - 2) 2 (x 2 + 3 x + 3) = 0 .

Verificar los divisores restantes no tiene sentido, ya que la igualdad x 2 + 3 x + 3 = 0 es más rápida y conveniente de resolver usando el discriminante.

Resolvamos la ecuación cuadrática:

X 2 + 3 X + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Obtenemos un par complejo conjugado de raíces: x = - 3 2 ± i 3 2 .

Responder: X = - 3 2 ± yo 3 2 .

Ejemplo 3

Condición: encuentra las raíces reales de la ecuación x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Solución

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Realizamos la multiplicación 2 3 de ambas partes de la ecuación:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Reemplazamos las variables y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Como resultado, obtuvimos una ecuación estándar de cuarto grado, que se puede resolver de acuerdo con el esquema estándar. Verifiquemos los divisores, dividamos y al final obtenemos que tiene 2 raíces reales y \u003d - 2, y \u003d 3 y dos complejas. No presentaremos la solución completa aquí. En virtud del reemplazo, las raíces reales de esta ecuación serán x = y 2 = - 2 2 = - 1 yx = y 2 = 3 2 .

Responder: x 1 \u003d - 1, x 2 \u003d 3 2

Si nota un error en el texto, resáltelo y presione Ctrl+Enter

En el siglo XVI, los matemáticos se toparon con los números complejos casi por accidente (ver Capítulo 11). PARA siglo XVIII los números complejos se consideraban una extensión del dominio de los números reales, pero trabajar con ellos aún conducía a un error de paridad, ya que Leonard E, en su gran trabajo sobre investigaciones aritméticas de teoría de números (1801), evitó el uso de los llamados "imaginarios". números". Me parece que la parte más importante de este trabajo es la primera demostración del teorema fundamental del álgebra. Gauss se dio cuenta de la importancia de este teorema y creó varias demostraciones adicionales durante los años siguientes. En 1849 revisó la primera versión, esta vez usando números complejos. Usando términos modernos, podemos decir que para cualquier ecuación polinomial finita con coeficientes reales o complejos, todas sus raíces serán números reales o complejos. Por lo tanto, obtenemos una respuesta negativa a la antigua pregunta de si la solución de ecuaciones polinómicas requiere alto orden crear números de orden superior a los complejos.

Uno de los problemas más espinosos del álgebra de esa época era la cuestión de si es posible resolver por métodos algebraicos, es decir, utilizando un número finito de pasos algebraicos, un polinomio de quinto orden, una quíntica. Ahora la escuela enseña la fórmula para resolver ecuaciones cuadráticas, y desde el siglo XVI se conocen métodos similares para resolver ecuaciones de tercer y cuarto grado (Capítulo 11). Pero no se ha encontrado ningún método para las quínticas. Puede parecer que el teorema fundamental del álgebra contiene la promesa de una respuesta positiva, pero en realidad simplemente garantiza que existen soluciones, no dice nada sobre la existencia de fórmulas que den soluciones exactas (los métodos numéricos y gráficos aproximados ya existían por ese momento). Y luego hubo dos genios matemáticos con un destino trágico.

Niels Henrik Abel (1802–1829) nació en una familia grande y pobre que vivía en un pequeño pueblo de Noruega, un país devastado por largos años de guerra con Inglaterra y Suecia. La maestra, que era amiga del chico, le daba clases particulares, pero tras la muerte de su padre, a los dieciocho años, a pesar de edad temprana y frágil salud, Abel se vio obligado a mantener a su familia. En 1824, publicó un artículo científico en el que afirmaba que la quíntica no se puede resolver algebraicamente, como, de hecho, cualquier polinomio de orden superior. Abel creyó que este artículo le serviría de pase al mundo científico y se lo envió a Gauss en la Universidad de Göttingen. Desafortunadamente, Gauss nunca llegó a cortar las páginas con un cuchillo (cualquier lector tenía que hacer eso en esos días) y no leyó el artículo. En 1826, el gobierno noruego finalmente proporcionó fondos para que Abel viajara por Europa. Temiendo que el contacto personal con Gauss no le traería grandes alegrías, el matemático decidió no visitar Göttingen y en su lugar se fue a Berlín. Allí se hizo amigo de August Leopold Crelle (1780–1855), un matemático, arquitecto e ingeniero que asesoraba al Ministerio de Educación de Prusia en cuestiones de matemáticas. Krell estaba a punto de fundar el Journal of Clean and matemáticas Aplicadas". Entonces Abel tuvo la oportunidad de distribuir su trabajo y publicó mucho, especialmente en los primeros números de la Revista, que inmediatamente comenzó a ser considerada una publicación científica muy prestigiosa y autorizada. El noruego publicó allí una versión extendida de su prueba de que la quíntica no se puede resolver por métodos algebraicos. Y luego se fue a París. Este viaje molestó mucho a Abel, pues prácticamente no recibió el apoyo de los matemáticos franceses que tanto necesitaba. Se acercó a Augustin Louis Cauchy (1789-1857), quien en ese momento era la principal luminaria Análisis matemático pero era muy complejo. Como dijo el propio Abel, "Cauchy está loco y no se puede hacer nada al respecto, aunque en la actualidad es el único capaz de algo en matemáticas". Si se trata de justificar la falta de respeto y el desprecio que emana de Gauss y Cauchy, se puede decir que la Quintic alcanzó cierta fama y atrajo la atención tanto de respetados matemáticos como de originales. Abel regresó a Noruega, donde sufría cada vez más de tuberculosis. Continuó enviando su obra a Crelle, pero murió en 1829, sin saber hasta qué punto su reputación en mundo cientifico. Dos días después de su muerte, Abel recibió una oferta para ocupar un puesto científico en Berlín.

Abel demostró que cualquier polinomio por encima del cuarto orden no se puede resolver usando radicales, como raíces cuadradas, raíces cúbicas o de orden superior. Sin embargo, Galois formuló las condiciones explícitas bajo las cuales, en casos especiales, estos polinomios podrían resolverse y el método para resolverlos. Évariste Galois (1811–1832) vivió una vida corta y agitada. Era un matemático increíblemente dotado. Galois era implacable con aquellos a quienes consideraba menos talentosos que él y, al mismo tiempo, no podía soportar la injusticia social. No mostró aptitudes para las matemáticas hasta que leyó Elementos de geometría de Legendre (publicado en 1794, este libro fue el principal libro de texto durante los siguientes cien años). Luego se tragó literalmente el resto de obras de Legendre y, más tarde, de Abel. Su entusiasmo, confianza en sí mismo e intolerancia lo llevaron a consecuencias verdaderamente nefastas en su trato con profesores y examinadores. Galois participó en el concurso de admisión a la Escuela Politécnica, la cuna de las matemáticas francesas, pero por falta de preparación reprobó el examen. Algún tiempo después de conocer a un nuevo maestro que reconoció su talento, logró mantener su temperamento bajo control. En marzo de 1829, Galois publicó su primer artículo sobre fracciones continuas, que consideró su obra más significativa. Envió un mensaje sobre sus descubrimientos a la Academia de Ciencias y Cauchy prometió presentarlos, pero se olvidó. Además, simplemente perdió el manuscrito.

El segundo fracaso de Galois para ingresar a la Escuela Politécnica entró en el folclore matemático. Estaba tan acostumbrado a tener constantemente ideas matemáticas complejas en la cabeza que se enfurecía por las mezquindades de los examinadores. Como los examinadores tenían dificultad para entender sus explicaciones, arrojó un paño de borrado en la cara de uno de ellos. Poco después, su padre murió, habiéndose suicidado como resultado de intrigas de la iglesia. Un motín casi estalló en su funeral. En febrero de 1830, Galois escribió los siguientes tres artículos y los envió a la Academia de Ciencias para el Gran Premio de matemáticas. Joseph Fourier, entonces secretario de la academia, murió sin haberlos leído, y tras su muerte los artículos no se encontraron entre sus papeles. Tal flujo de decepciones derribaría a cualquiera. Galois se rebeló contra los que estaban en el poder porque sintió que no reconocían sus méritos y mataron a su padre. Se sumergió de lleno en la política, convirtiéndose en un republicano ardiente, lo que no fue la decisión más sabia en Francia en 1830. En un último intento desesperado, envió un artículo científico al famoso físico y matemático francés Siméon Denis Poisson (1781-1840), quien en respuesta exigió pruebas adicionales.

Esta fue la gota que colmó el vaso. En 1831, Galois fue arrestado dos veces, primero por supuestamente pedir el asesinato del rey Luis Felipe y luego para protegerlo, ¡las autoridades temían una revuelta republicana! Esta vez, fue condenado a seis meses de prisión por cargos falsos de llevar ilegalmente el uniforme del disuelto batallón de artillería al que se unió. En libertad condicional, se dedicó a un negocio que le disgustaba tanto como todo lo demás en la vida. En las cartas a su devoto amigo Chevalier, se siente su desilusión. El 29 de mayo de 1832 aceptó un desafío a duelo, cuyas razones no se comprenden del todo. “Fui víctima de una coqueta deshonrosa. Mi vida se está desvaneciendo en una pelea miserable”, escribe en una Carta a todos los republicanos. lo mas trabajo notable Galois fue esbozado la noche anterior al duelo fatal. Las quejas están esparcidas en los márgenes: "No tengo más tiempo, no tengo más tiempo". Tuvo que dejar a otros los detalles de los pasos intermedios que no eran esenciales para comprender la idea principal. Necesitaba poner por escrito la base de sus descubrimientos: los orígenes de lo que ahora se llama el teorema de Galois. Terminó su testamento pidiéndole a Chevalier que "solicitara a Jacobi y Gauss que dieran su opinión públicamente, no sobre la corrección, sino sobre la importancia de estos teoremas". A primera hora de la mañana, Galois fue al encuentro de su rival. Tuvieron que disparar desde una distancia de 25 pasos. Galois resultó herido y murió en el hospital a la mañana siguiente. Tenía sólo veinte años.

Galois se basó en el trabajo de Lagrange y Cauchy, pero desarrolló un método más general. fue extremadamente importante logro en el campo de la resolución de quínticas. El científico prestó menos atención a las ecuaciones originales oa la interpretación gráfica y pensó más en la naturaleza de las propias raíces. Para simplificar, Galois consideró únicamente las llamadas quínticas irreducibles, es decir, aquellas que no se podían factorizar en forma de polinomios de orden inferior (como decíamos, para cualquier ecuación polinomial hasta el cuarto orden existen fórmulas para encontrar sus raíces). En general, un polinomio irreducible con coeficientes racionales es un polinomio que no se puede descomponer en polinomios más simples que tienen coeficientes racionales. Por ejemplo, (x 5 - 1) se puede factorizar (x-1)(x 4 + x 3 + x 2 + x + 1), mientras que (x 5 - 2) irreducible. El objetivo de Galois era determinar las condiciones bajo las cuales todas las soluciones de una ecuación polinomial general irreducible se pueden encontrar en términos de radicales.

La clave de la solución es que las raíces de cualquier ecuación algebraica irreducible no son independientes, se pueden expresar una en función de la otra. Estas relaciones se formalizaron en el grupo de todas las permutaciones posibles, el llamado grupo de simetría de raíces: ¡para una quíntica, este grupo contiene 5! = 5 x 4 x 3 x 2 x 1 = 120 elementos. Los algoritmos matemáticos de la teoría de Galois son muy complejos y, muy probablemente, en parte debido a esto, inicialmente se entendieron con gran dificultad. Pero después de que el nivel de abstracción hizo posible pasar de las soluciones algebraicas de las ecuaciones a la estructura algebraica de los grupos asociados a ellas, Galois pudo predecir la resolución de la ecuación basándose en las propiedades de dichos grupos. Además, su teoría también proporcionaba un método mediante el cual se podían encontrar estas raíces. Con respecto a las quínticas, el matemático Joseph Liouville (1809-1882), quien en 1846 publicó más trabajos de Galois en su Journal of Pure and Applied Mathematics, señaló que el joven científico demostró un “hermoso teorema”, y para que “para que una ecuación irreducible del grado original sea resoluble en términos de radicales, es necesario y suficiente que todas sus raíces sean funciones racionales cualesquiera dos de ellas". Como esto es imposible para una quíntica, no se puede resolver con radicales.

En tres años, el mundo matemático ha perdido dos de sus nuevas estrellas más brillantes. Siguieron acusaciones mutuas y examen de conciencia, y Abel y Galois lograron un merecido reconocimiento, pero solo a título póstumo. En 1829, Carl Jacobi, a través de Legendre, se enteró del manuscrito "perdido" de Abel, y en 1830 estalló un escándalo diplomático cuando el cónsul noruego en París exigió que se encontrara el artículo de su compatriota. Al final, Cauchy encontró el artículo, ¡solo para perderlo nuevamente en los editores de la academia! En el mismo año, Abel recibió el Gran Premio de Matemáticas (junto con Jacobi), pero ya estaba muerto. En 1841 se publicó su biografía. En 1846, Liouville editó algunos de los manuscritos de Galois para su publicación, y en su introducción lamentó que la academia hubiera rechazado inicialmente el trabajo de Galois debido a su complejidad: "de hecho, la claridad de la presentación es necesaria cuando el autor lleva al lector fuera del camino trillado hacia territorios salvajes inexplorados". Continúa: “¡Galois ya no existe! No caigamos en críticas inútiles. ¡Desechemos los defectos y miremos las virtudes! Fruta breve vida Galois cabe en sólo sesenta páginas. El editor de la revista matemática para candidatos a la École Normale y la Ecole Polytechnique comentó sobre el caso de Galois de la siguiente manera: “Un candidato con una gran inteligencia fue eliminado por un examinador con un nivel de pensamiento más bajo. Barbarus hic ego sum, quia non intelligor illis".

En primer lugar, la segunda página de este trabajo no está cargada de nombres, apellidos, descripciones de la posición en la sociedad, títulos y elegías en honor de algún príncipe avaro, cuyo bolso se abrirá con estos incienso - con la amenaza de cerrarlo cuando terminan las alabanzas. No verán aquí elogios respetuosos, escritos en letras tres veces mayores que el propio texto, dirigidos a quienes tienen un alto cargo en la ciencia, a algún sabio mecenas -algo obligatorio (diría inevitable) para alguien a la edad de veinte que quiere escribir algo. No le digo a nadie aquí que estoy en deuda con sus consejos y apoyo por todas las cosas buenas de mi trabajo. No digo esto porque sería mentira. Si tuviera que mencionar a alguno de los grandes de la sociedad o de la ciencia (en la actualidad la diferencia entre estas dos clases de personas es casi imperceptible), juro que no sería en señal de agradecimiento. A ellos les debo que publiqué el primero de estos dos artículos tan tarde, y que escribí todo esto en la cárcel, en un lugar que difícilmente puede considerarse adecuado para la reflexión científica, y a menudo me sorprende mi moderación y mi capacidad para mantengo mi boca en el castillo en relación con Zoils estúpido y vicioso. Me parece que puedo usar la palabra "Zoils" sin temor a que me acusen de indecencia, ya que así me refiero a mis oponentes. No voy a escribir aquí sobre cómo y por qué fui enviado a prisión, pero debo decir que mis manuscritos la mayoría de las veces simplemente se perdían en las carpetas de los caballeros de la academia, aunque, a decir verdad, no puedo imaginar tal indiscreción. por parte de las personas en cuya conciencia la muerte de Abel. En mi opinión, a cualquiera le gustaría ser comparado con este brillante matemático. Baste decir que mi artículo sobre la teoría de ecuaciones fue enviado a la Academia de Ciencias en febrero de 1830, que los extractos del mismo fueron enviados en febrero de 1829 y, sin embargo, no se imprimió nada, e incluso el manuscrito resultó ser imposible volver.

Galois, prefacio inédito, 1832

Clase: 9

Objetivos básicos:

Consolidar el concepto de ecuación racional entera de grado.
Formular los principales métodos para resolver ecuaciones de grados superiores (n > 3).
Enseñar los métodos básicos para la resolución de ecuaciones de grado superior.
Enseñar por la forma de la ecuación para determinar la mayor metodo efectivo sus decisiones

Formas, métodos y técnicas pedagógicas que son utilizados por el profesor en la lección:

Sistema de formación de conferencias-seminario (conferencias - explicación de nuevo material, seminarios - resolución de problemas).
Tecnologías de la información y la comunicación (encuesta frontal, trabajo oral con la clase).
Formaciones diferenciadas, grupales e individuales.
El uso del método de investigación en la formación orientada al desarrollo. aparato matematico y habilidades mentales de cada estudiante individual.
Material impreso: un resumen individual de la lección (conceptos básicos, fórmulas, declaraciones, material de lectura comprimido en forma de diagramas o tablas).

Plan de estudios:

Organizando el tiempo.
El propósito de la etapa: incluir a los estudiantes en Actividades de aprendizaje definir el contenido de la lección.
Actualización de conocimientos de los alumnos.
El propósito de la etapa: actualizar los conocimientos de los estudiantes sobre temas relacionados previamente estudiados
Aprender un nuevo tema (conferencia). El propósito de la etapa: formular los principales métodos para resolver ecuaciones de grados superiores (n > 3)
Resumiendo.
El propósito de la etapa: resaltar una vez más los puntos clave del material estudiado en la lección.
Tarea.
Propósito de la etapa: formular tarea para estudiantes.

Resumen de la lección

1. Momento organizativo.

La redacción del tema de la lección: “Ecuaciones de grados superiores. Métodos para su solución”.

2. Actualización de los conocimientos de los alumnos.

Estudio teórico - conversación. Repetición de alguna información previamente estudiada de la teoría. Los estudiantes formulan definiciones básicas y dan enunciados de los teoremas necesarios. Se dan ejemplos, demostrando el nivel de conocimientos adquiridos previamente.

El concepto de una ecuación con una variable.
El concepto de la raíz de la ecuación, la solución de la ecuación.
concepto ecuación lineal con una variable, el concepto de una ecuación cuadrática con una variable.
El concepto de equivalencia de ecuaciones, ecuación-consecuencias (el concepto de raíces extrañas), transición no por consecuencia (el caso de pérdida de raíces).
El concepto de totalidad expresión racional con una variable.
El concepto de una ecuación racional completa norte grado. La forma estándar de una ecuación racional completa. entero reducido ecuación racional.
Transición a un conjunto de ecuaciones de menor grado al factorizar la ecuación original.
El concepto de polinomio norte grado de X. El teorema de Bezout. Consecuencias del teorema de Bezout. Teoremas de raíces ( Z-raíces y q-raíces) de una ecuación racional completa con coeficientes enteros (reducidos y no reducidos, respectivamente).
esquema de Horner.

3. Aprender un tema nuevo.

Consideraremos toda la ecuación racional norteª potencia de la forma estándar con una variable desconocida x:Pn(x)= 0 , donde PAGS norte (x) = un norte x norte + un norte-1 x norte-1 + un 1 x + un 0– polinomio norte grado de X, a norte ≠ 0 . Si a n = 1 entonces tal ecuación se llama ecuación racional entera reducida norte grado. Consideremos tales ecuaciones para diferentes valores norte y enumere los métodos principales de su solución.

norte= 1 es una ecuación lineal.

norte= 2 es una ecuación cuadrática. Fórmula discriminante. Fórmula para calcular raíces. El teorema de Vieta. Selección de un cuadrado completo.

norte= 3 es una ecuación cúbica.

método de agrupación.

Ejemplo: x 3 – 4x 2 – x+ 4 = 0 (x - 4) (x 2– 1) = 0 X 1 = 4 , x2 = 1,X 3 = -1.

Ecuación cúbica recíproca de la forma hacha 3 + bx 2 + bx + a= 0. Resolvemos combinando términos con los mismos coeficientes.

Ejemplo: X 3 – 5X 2 – 5X + 1 = 0 (X + 1)(X 2 – 6X + 1) = 0 X 1 = -1, X 2 = 3 + 2, X 3 = 3 – 2.

Selección de raíces Z en base al teorema. esquema de Horner. Al aplicar este método, es necesario enfatizar que la enumeración en este caso es finita, y seleccionamos las raíces de acuerdo con un cierto algoritmo de acuerdo con el teorema sobre Z-raíces de la ecuación racional entera reducida con coeficientes enteros.

Ejemplo: X 3 – 9X 2 + 23X– 15 = 0. La ecuación se reduce. Escribimos los divisores del término libre ( + 1; + 3; + 5; + 15). Apliquemos el esquema de Horner:

	X 3	X 2	X 1	X 0	producción
	1	-9	23	-15
1	1	1 x 1 - 9 = -8	1 x (-8) + 23 = 15	1 x 15 - 15 = 0	1 - raíz
	X 2	X 1	X 0

Obtenemos ( X – 1)(X 2 – 8X + 15) = 0 X 1 = 1, X 2 = 3, X 3 = 5.

Ecuación con coeficientes enteros. Selección de raíces Q en base al teorema. esquema de Horner. Al aplicar este método, es necesario enfatizar que la enumeración en este caso es finita y seleccionamos las raíces de acuerdo con un cierto algoritmo de acuerdo con el teorema de q-raíces de una ecuación racional entera no reducida con coeficientes enteros.

Ejemplo: 9 X 3 + 27X 2 – X– 3 = 0. La ecuación no se reduce. Escribimos los divisores del término libre ( + 1; + 3). Escribamos los divisores del coeficiente a la mayor potencia de la incógnita. ( + 1; + 3; + 9) Por lo tanto, buscaremos raíces entre los valores ( + 1; + ; + ; + 3). Apliquemos el esquema de Horner:

	X 3	X 2	X 1	X 0	producción
	9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 - 1 = 35	1 x 35 - 3 = 32 ≠ 0	1 no es una raíz
-1	9	-1 x 9 + 27 = 18	-1 x 18 - 1 = -19	-1 x (-19) - 3 = 16 ≠ 0	-1 no es una raíz
	9	x9 + 27 = 30	x 30 - 1 = 9	x 9 - 3 = 0	raíz
	X 2	X 1	X 0

Obtenemos ( X – )(9X 2 + 30X + 9) = 0 X 1 = , X 2 = - , X 3 = -3.

Para la conveniencia del cálculo al elegir Q -raíces puede ser conveniente hacer un cambio de variable, pasar a la ecuación anterior y ajustar Z -raíces.

Si el intercepto es 1

.

Si es posible utilizar la sustitución de la forma y=kx

.

Fórmula Cardano. Existe un método universal para resolver ecuaciones cúbicas: esta es la fórmula de Cardano. Esta fórmula está asociada con los nombres de los matemáticos italianos Gerolamo Cardano (1501–1576), Nicolo Tartaglia (1500–1557), Scipio del Ferro (1465–1526). Esta fórmula se encuentra fuera del alcance de nuestro curso.

norte= 4 es una ecuación de cuarto grado.

método de agrupación.

Ejemplo: X 4 + 2X 3 + 5X 2 + 4X – 12 = 0 (X 4 + 2X 3) + (5X 2 + 10X) – (6X + 12) = 0 (X + 2)(X 3 + 5X- 6) = 0 (X + 2)(X– 1)(X 2 + X + 6) = 0 X 1 = -2, X 2 = 1.

Método de sustitución de variables.

Ecuación bicuadrática de la forma hacha 4 + bx 2+s = 0 .

Ejemplo: X 4 + 5X 2 - 36 = 0. Sustitución y = X 2. De aquí y 1 = 4, y 2 = -9. Es por eso X 1,2 = + 2 .

Ecuación recíproca de cuarto grado de la forma hacha 4 + bx 3+c X 2 + bx + a = 0.

Resolvemos combinando términos con los mismos coeficientes reemplazando la forma

hacha 4 + bx 3 + cx 2 – bx + a = 0.

Ecuación hacia atrás generalizada del cuarto grado de la forma hacha 4 + bx 3 + cx 2 + kbx + k2 un = 0.

Reemplazo general. Algunas sustituciones estándar.

Ejemplo 3 . Reemplazo de vista general(sigue de la forma de una ecuación particular).

norte = 3.

Ecuación con coeficientes enteros. Selección de raíces Q norte = 3.

Formula general. Existe un método universal para resolver ecuaciones de cuarto grado. Esta fórmula está asociada al nombre de Ludovico Ferrari (1522-1565). Esta fórmula se encuentra fuera del alcance de nuestro curso.

norte > 5 - ecuaciones de quinto y grados superiores.

Ecuación con coeficientes enteros. Selección de raíces Z en base al teorema. esquema de Horner. El algoritmo es similar al discutido anteriormente para norte = 3.

Ecuación con coeficientes enteros. Selección de raíces Q basado en el teorema. esquema de Horner. El algoritmo es similar al discutido anteriormente para norte = 3.

Ecuaciones simétricas. Cualquier ecuación recíproca de grado impar tiene una raíz X= -1 y después de descomponerlo en factores, obtenemos que un factor tiene la forma ( X+ 1), y el segundo factor es una ecuación recíproca de grado par (su grado es uno menos que el grado de la ecuación original). Cualquier ecuación recíproca de grado par junto con una raíz de la forma x = φ también contiene la raíz del formulario. Usando estas declaraciones, resolvemos el problema al reducir el grado de la ecuación en estudio.

Método de sustitución de variables. Uso de la homogeneidad.

No existe una fórmula general para resolver ecuaciones enteras de quinto grado (esto fue demostrado por el matemático italiano Paolo Ruffini (1765-1822) y el matemático noruego Nils Henrik Abel (1802-1829)) y potencias superiores (esto fue demostrado por el francés matemático Evariste Galois (1811-1832)).

Recuerde nuevamente que en la práctica es posible utilizar combinaciones los métodos enumerados anteriormente. Es conveniente pasar a un conjunto de ecuaciones de menor grado por factorización de la ecuación original.
Fuera del alcance de nuestra discusión de hoy, se utilizan ampliamente en la práctica métodos gráficos resolver ecuaciones y métodos de solución aproximada ecuaciones de grados superiores.

Hay situaciones en las que la ecuación no tiene raíces R.

Usando la propiedad de monotonicidad de las funciones

4. Resumiendo.

Resumen: ahora dominamos los métodos básicos para resolver varias ecuaciones de grados superiores (para n > 3). Nuestra tarea es aprender a usar de manera efectiva los algoritmos anteriores. Dependiendo del tipo de ecuación, tendremos que aprender a determinar qué método de solución es el más efectivo en este caso, así como aplicar correctamente el método elegido.

5. Tarea.

: ítem 7, páginas 164–174, números 33–36, 39–44, 46,47.

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Posibles temas de informes o resúmenes sobre este tema:

fórmula cardano
Método gráfico para la resolución de ecuaciones. Ejemplos de solución.
Métodos de solución aproximada de ecuaciones.

Análisis de la asimilación del material e interés de los estudiantes en el tema:

La experiencia demuestra que el interés de los estudiantes es en primer lugar la posibilidad de seleccionar Z-raíces y q-raíces de ecuaciones usando un algoritmo bastante simple usando el esquema de Horner. Los estudiantes también están interesados en varios tipos estándar de sustitución de variables, que pueden simplificar significativamente el tipo de problema. Los métodos gráficos de solución suelen ser de particular interés. En este caso, también puede analizar las tareas en un método gráfico para resolver ecuaciones; discutir la vista general de la gráfica para un polinomio de 3, 4, 5 grados; analizar cómo se relaciona el número de raíces de ecuaciones de 3, 4, 5 grados con el tipo de la gráfica correspondiente. A continuación se muestra una lista de libros donde puede encontrar información adicional sobre este tema.

Bibliografía:

Vilenkin N. Ya. etc. “Álgebra. Un libro de texto para estudiantes en los grados 9 con un estudio profundo de las matemáticas ”- M., Educación, 2007 - 367 p.
Vilenkin N.Ya., Shibasov L.P., Shibasova Z.F.“Detrás de las páginas de un libro de texto de matemáticas. Aritmética. Álgebra. Grados 10-11” – M., Enlightenment, 2008 – 192 p.
Vygodsky M.Ya."Manual de matemáticas" - M., AST, 2010 - 1055 p.
Galitsky M. L.“Colección de problemas de álgebra. Tutorial para los grados 8-9 con un estudio profundo de las matemáticas ”- M., Educación, 2008 - 301 p.
Zvavich L. I. et al.. “Álgebra y los comienzos del análisis. 8–11 celdas Un manual para escuelas y clases con un estudio profundo de las matemáticas ”- M., Drofa, 1999 - 352 p.
Zvavich L.I., Averyanov D.I., Pigarev B.P., Trushanina T.N."Tareas de matemáticas para prepararse para un examen escrito en el grado 9" - M., Educación, 2007 - 112 p.
Ivanov A.A., Ivanov A.P."Pruebas temáticas para la sistematización del conocimiento en matemáticas" parte 1 - M., Fizmatkniga, 2006 - 176 p.
Ivanov A.A., Ivanov A.P."Pruebas temáticas para la sistematización del conocimiento en matemáticas" parte 2 - M., Fizmatkniga, 2006 - 176 p.
Ivanov AP“Pruebas y papeles de prueba matemáticas. Tutorial". - M., Fizmatkniga, 2008 - 304 p.
Leibson K. L.“Colección de tareas prácticas en matemáticas. Parte 2–9 clase” – M., MTsNMO, 2009 – 184 p.
Makarychev Yu.N., Mindyuk N.G."Álgebra. Capítulos adicionales para libro de texto escolar Grado 9 Libro de texto para estudiantes de escuelas y clases con un estudio profundo de las matemáticas.” - M., Educación, 2006 - 224 p.
Mordkovich A.G."Álgebra. Estudio en profundidad. Octavo grado. Libro de texto” – M., Mnemosyne, 2006 – 296 p.
Savin AP “diccionario enciclopédico joven matemático” – M., Pedagogía, 1985 – 352 p.
Survillo G. S., Simonov A. S. “Materiales didácticos en álgebra para el grado 9 con un estudio profundo de las matemáticas” – M., Enlightenment, 2006 – 95 p.
Chulkov P. V.“Ecuaciones y desigualdades en el curso escolar de matemáticas. Lectures 1–4” – M., Primero de septiembre de 2006 – 88 p.
Chulkov P. V.“Ecuaciones y desigualdades en el curso escolar de matemáticas. Lectures 5–8” – M., Primero de septiembre de 2009 – 84 p.

Considerar resolución de ecuaciones con una variable de grado superior a la segunda.

El grado de la ecuación P(x) = 0 es el grado del polinomio P(x), es decir la mayor de las potencias de sus términos con coeficiente distinto de cero.

Entonces, por ejemplo, la ecuación (x 3 - 1) 2 + x 5 \u003d x 6 - 2 tiene un quinto grado, porque después de las operaciones de abrir corchetes y traer otros similares, obtenemos una ecuación equivalente x 5 - 2x 3 + 3 \u003d 0 de quinto grado.

Recuerda las reglas que se necesitarán para resolver ecuaciones de grado mayor que el segundo.

Proposiciones sobre las raíces de un polinomio y sus divisores:

1. Polinomio enésimo grado tiene un número de raíces que no excede el número n, y las raíces de multiplicidad m ocurren exactamente m veces.

2. Un polinomio de grado impar tiene al menos una raíz real.

3. Si α es la raíz de Р(х), entonces Р n (х) = (х – α) · Q n – 1 (x), donde Q n – 1 (x) es un polinomio de grado (n – 1) .

5. Un polinomio reducido con coeficientes enteros no puede tener raíces racionales fraccionarias.

6. Para un polinomio de tercer grado

P 3 (x) \u003d ax 3 + bx 2 + cx + d una de dos cosas es posible: se descompone en un producto de tres binomios

P 3 (x) \u003d a (x - α) (x - β) (x - γ), o se descompone en el producto de un binomio y un trinomio cuadrado P 3 (x) \u003d a (x - α) ( x 2 + βx + γ ).

7. Cualquier polinomio de cuarto grado se expande en el producto de dos trinomios cuadrados.

8. Un polinomio f(x) es divisible por un polinomio g(x) sin resto si existe un polinomio q(x) tal que f(x) = g(x) q(x). Para dividir polinomios, se aplica la regla de "división por una esquina".

9. Para que el polinomio P(x) sea divisible por el binomio (x – c), es necesario y suficiente que el número c sea la raíz de P(x) (Corolario del teorema de Bezout).

10. Teorema de Vieta: Si x 1, x 2, ..., x n son las raíces reales del polinomio

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, entonces se cumplen las siguientes igualdades:

x 1 + x 2 + ... + x n \u003d -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x norte - 1 x norte \u003d un 2 / un 0,

x 1 x 2 x 3 + ... + x norte - 2 x norte - 1 x norte \u003d -a 3 / a 0,

x 1 x 2 x 3 x n \u003d (-1) n a n / a 0.

Solución de ejemplos

Ejemplo 1

Encuentre el resto después de dividir P (x) \u003d x 3 + 2/3 x 2 - 1/9 por (x - 1/3).

Solución.

Según el corolario del teorema de Bezout: "El resto de dividir un polinomio por un binomio (x - c) es igual al valor del polinomio en c". Encontremos P(1/3) = 0. Por lo tanto, el resto es 0 y el número 1/3 es la raíz del polinomio.

Respuesta: R = 0.

Ejemplo 2

Divide la "esquina" 2x 3 + 3x 2 - 2x + 3 por (x + 2). Encuentra el resto y el cociente incompleto.

Solución:

2x 3 + 3x 2 – 2x + 3| x + 2

2x 3 + 4x 2 2x 2 – x

X 2 – 2 X

Respuesta: R = 3; cociente: 2x 2 - x.

Métodos básicos para resolver ecuaciones de grados superiores

1. Introducción de una nueva variable

El método de introducir una nueva variable ya es familiar del ejemplo ecuaciones bicuadráticas. Consiste en que para resolver la ecuación f (x) \u003d 0, se introduce una nueva variable (sustitución) t \u003d xn o t \u003d g (x) y f (x) se expresa a través de t, obteniendo un nueva ecuación r (t). Luego, resolviendo la ecuación r(t), encuentra las raíces:

(t 1 , t 2 , …, t n). Después de eso, se obtiene un conjunto de n ecuaciones q(x) = t 1 , q(x) = t 2 , ... , q(x) = t n, a partir de las cuales se encuentran las raíces de la ecuación original.

Ejemplo 1

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Solución:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Reemplazo (x 2 + x + 1) = t.

t2 - 3t + 2 = 0.

t 1 \u003d 2, t 2 \u003d 1. Reemplazo inverso:

x2 + x + 1 = 2 o x2 + x + 1 = 1;

x2 + x - 1 = 0 o x2 + x = 0;

Respuesta: De la primera ecuación: x 1, 2 = (-1 ± √5) / 2, de la segunda: 0 y -1.

2. Factorización por el método de agrupación y fórmulas de multiplicación abreviada

La base de este método tampoco es nueva y consiste en agrupar términos de tal manera que cada grupo contenga un factor común. Para hacer esto, a veces tienes que usar algunos trucos artificiales.

Ejemplo 1

x 4 - 3x 2 + 4x - 3 = 0.

Solución.

Imagina - 3x 2 = -2x 2 - x 2 y agrupa:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 \u003d 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 \u003d 0 o x 2 + x - 3 \u003d 0.

Respuesta: No hay raíces en la primera ecuación, de la segunda: x 1, 2 \u003d (-1 ± √13) / 2.

3. Factorización por el método de coeficientes indefinidos

La esencia del método es que el polinomio original se descompone en factores con coeficientes desconocidos. Usando la propiedad de que los polinomios son iguales si sus coeficientes son iguales a las mismas potencias, se encuentran los coeficientes de expansión desconocidos.

Ejemplo 1

x 3 + 4x 2 + 5x + 2 = 0.

Solución.

Un polinomio de tercer grado se puede descomponer en un producto de factores lineales y cuadrados.

x 3 + 4x 2 + 5x + 2 \u003d (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 \u003d x 3 + (b - a) x 2 + (cx - ab) x - ac.

Resolviendo el sistema:

(b – a = 4,
(c - ab = 5,
(-ac=2,

(un = -1,
(b=3,
(c = 2, es decir

x 3 + 4x 2 + 5x + 2 \u003d (x + 1) (x 2 + 3x + 2).

Las raíces de la ecuación (x + 1) (x 2 + 3x + 2) = 0 son fáciles de encontrar.

Respuesta 1; -2.

4. El método de selección de la raíz por el coeficiente más alto y libre.

El método se basa en la aplicación de teoremas:

1) Cualquier raíz entera de un polinomio con coeficientes enteros es un divisor del término libre.

2) Para que la fracción irreducible p / q (p es un número entero, q es un natural) sea la raíz de una ecuación con coeficientes enteros, es necesario que el número p sea un divisor entero del término libre a 0, y q es un divisor natural del coeficiente más alto.

Ejemplo 1

6x 3 + 7x 2 - 9x + 2 = 0.

Solución:

6: q = 1, 2, 3, 6.

Por lo tanto p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.

Habiendo encontrado una raíz, por ejemplo, 2, encontraremos otras raíces usando la división por una esquina, el método de coeficientes indefinidos o el esquema de Horner.

Respuesta: -2; 1/2; 1/3.

¿Tiene usted alguna pregunta? ¿No sabes cómo resolver ecuaciones?
Para obtener la ayuda de un tutor, regístrese.
¡La primera lección es gratis!

sitio, con copia total o parcial del material, se requiere un enlace a la fuente.

total:0
En contacto con 0
Google+ 0
OK 0
Facebook 0