La resolución de problemas de matemáticas para los estudiantes suele ir acompañada de muchas dificultades. Ayudar al estudiante a hacer frente a estas dificultades, así como enseñarle cómo aplicar su conocimiento teórico en la resolución de problemas específicos en todas las secciones del curso de la asignatura "Matemáticas" es el objetivo principal de nuestro sitio.
Comenzando a resolver problemas sobre el tema, los estudiantes deben ser capaces de construir un punto en un plano de acuerdo con sus coordenadas, así como encontrar las coordenadas de un punto dado.
El cálculo de la distancia entre dos puntos tomados en el plano A (x A; y A) y B (x B; y B) se realiza mediante la fórmula d \u003d √ ((x A - x B) 2 + (y A - y B) 2), donde d es la longitud del segmento que une estos puntos en el plano.
Si uno de los extremos del segmento coincide con el origen, y el otro tiene coordenadas M (x M; y M), entonces la fórmula para calcular d tomará la forma OM = √ (x M 2 + y M 2).
1. Calcular la distancia entre dos puntos dadas las coordenadas de estos puntos
Ejemplo 1.
Encuentre la longitud del segmento que conecta Plano coordinado puntos A(2; -5) y B(-4; 3) (Fig. 1).
Solución.
La condición del problema está dada: x A = 2; x B \u003d -4; y A = -5 y y B = 3. Calcula d.
Aplicando la fórmula d \u003d √ ((x A - x B) 2 + (y A - y B) 2), obtenemos:
d \u003d AB \u003d √ ((2 - (-4)) 2 + (-5 - 3) 2) \u003d 10.
2. Cálculo de las coordenadas de un punto que equidista de tres puntos dados
Ejemplo 2
Encuentre las coordenadas del punto O 1, que es equidistante de los tres puntos A(7; -1) y B(-2; 2) y C(-1; -5).
Solución.
De la formulación de la condición del problema se deduce que O 1 A \u003d O 1 B \u003d O 1 C. Deje que el punto deseado O 1 tenga coordenadas (a; b). De acuerdo con la fórmula d \u003d √ ((x A - x B) 2 + (y A - y B) 2) encontramos:
O 1 A \u003d √ ((a - 7) 2 + (b + 1) 2);
O 1 V \u003d √ ((a + 2) 2 + (b - 2) 2);
O 1 C \u003d √ ((a + 1) 2 + (b + 5) 2).
Componemos un sistema de dos ecuaciones:
(√((a - 7) 2 + (b + 1) 2) = √((a + 2) 2 + (b - 2) 2),
(√((a - 7) 2 + (b + 1) 2) = √((a + 1) 2 + (b + 5) 2).
Después de cuadrar la izquierda y partes correctas ecuaciones escribimos:
((a - 7) 2 + (b + 1) 2 \u003d (a + 2) 2 + (b - 2) 2,
((a - 7) 2 + (b + 1) 2 = (a + 1) 2 + (b + 5) 2 .
Simplificando, escribimos
(-3a + b + 7 = 0,
(-2a - b + 3 = 0.
Habiendo resuelto el sistema, obtenemos: a = 2; b = -1.
El punto O 1 (2; -1) es equidistante de los tres puntos dados en la condición de que no se encuentran en una línea recta. Este punto es el centro de un círculo que pasa por tres puntos dados (Figura 2).
3. Cálculo de la abscisa (ordenada) de un punto que se encuentra en el eje de abscisa (ordenada) y está a una distancia dada de este punto
Ejemplo 3
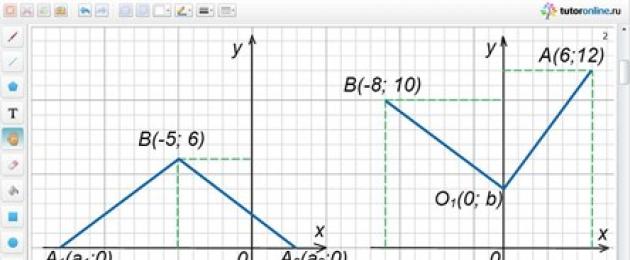
La distancia del punto B(-5; 6) al punto A que se encuentra en el eje x es 10. Encuentra el punto A.
Solución.
De la formulación de la condición del problema se sigue que la ordenada del punto A es cero y AB = 10.
Denotando la abscisa del punto A a través de a, escribimos A(a; 0).
AB \u003d √ ((a + 5) 2 + (0 - 6) 2) \u003d √ ((a + 5) 2 + 36).
Obtenemos la ecuación √((a + 5) 2 + 36) = 10. Simplificándola, tenemos
un 2 + 10a - 39 = 0.
Las raíces de esta ecuación a 1 = -13; y 2 = 3.
Obtenemos dos puntos A 1 (-13; 0) y A 2 (3; 0).
Examen:
A 1 B \u003d √ ((-13 + 5) 2 + (0 - 6) 2) \u003d 10.
A 2 B \u003d √ ((3 + 5) 2 + (0 - 6) 2) \u003d 10.
Ambos puntos obtenidos se ajustan a la condición del problema (Fig. 3).
4. Cálculo de la abscisa (ordenada) de un punto que se encuentra en el eje de abscisa (ordenada) y está a la misma distancia de dos puntos dados
Ejemplo 4
Encuentre un punto en el eje Oy que esté a la misma distancia de los puntos A (6; 12) y B (-8; 10).
Solución.
Sean las coordenadas del punto requerido por la condición del problema, que se encuentra sobre el eje Oy, O 1 (0; b) (en el punto que se encuentra sobre el eje Oy, la abscisa es igual a cero). De la condición se deduce que O 1 A \u003d O 1 B.
De acuerdo con la fórmula d \u003d √ ((x A - x B) 2 + (y A - y B) 2) encontramos:
O 1 A \u003d √ ((0 - 6) 2 + (b - 12) 2) \u003d √ (36 + (b - 12) 2);
O 1 V \u003d √ ((a + 8) 2 + (b - 10) 2) \u003d √ (64 + (b - 10) 2).
Tenemos la ecuación √(36 + (b - 12) 2) = √(64 + (b - 10) 2) o 36 + (b - 12) 2 = 64 + (b - 10) 2 .
Después de la simplificación, obtenemos: b - 4 = 0, b = 4.
Requerido por la condición del punto problemático O 1 (0; 4) (Figura 4).
5. Cálculo de las coordenadas de un punto que está a la misma distancia de los ejes de coordenadas y de algún punto dado
Ejemplo 5
Encuentre el punto M ubicado en el plano de coordenadas a la misma distancia de los ejes de coordenadas y del punto A (-2; 1).
Solución.
El punto M requerido, al igual que el punto A (-2; 1), está ubicado en la segunda esquina de coordenadas, ya que es equidistante de los puntos A, P 1 y P 2 (Figura 5). Las distancias del punto M a los ejes de coordenadas son las mismas, por tanto, sus coordenadas serán (-a; a), donde a > 0.
De las condiciones del problema se sigue que MA = MP 1 = MP 2, MP 1 = a; PM2 = |-a|,
esos. |-a| = un.
De acuerdo con la fórmula d \u003d √ ((x A - x B) 2 + (y A - y B) 2) encontramos:
MA \u003d √ ((-a + 2) 2 + (a - 1) 2).
Hagamos una ecuación:
√ ((-a + 2) 2 + (a - 1) 2) = a.
Después de elevar al cuadrado y simplificar, tenemos: a 2 - 6a + 5 = 0. Resolvemos la ecuación, encontramos a 1 = 1; y 2 = 5.
Obtenemos dos puntos M 1 (-1; 1) y M 2 (-5; 5), satisfaciendo la condición del problema. 
6. Cálculo de las coordenadas de un punto que está a la misma distancia especificada del eje de abscisas (ordenadas) y de este punto
Ejemplo 6
Encuentre un punto M tal que su distancia desde el eje y y desde el punto A (8; 6) sea igual a 5.
Solución.
De la condición del problema se sigue que MA = 5 y la abscisa del punto M es igual a 5. Sea la ordenada del punto M igual a b, entonces M(5; b) (Figura 6).
De acuerdo con la fórmula d \u003d √ ((x A - x B) 2 + (y A - y B) 2) tenemos:
MA \u003d √ ((5 - 8) 2 + (b - 6) 2).
Hagamos una ecuación:
√((5 - 8) 2 + (b - 6) 2) = 5. Simplificándolo, obtenemos: b 2 - 12b + 20 = 0. Las raíces de esta ecuación son b 1 = 2; b 2 \u003d 10. Por lo tanto, hay dos puntos que satisfacen la condición del problema: M 1 (5; 2) y M 2 (5; 10).
Se sabe que muchos estudiantes, al momento de resolver problemas por su cuenta, necesitan consultas constantes sobre técnicas y métodos para resolverlos. A menudo, un estudiante no puede encontrar la manera de resolver un problema sin la ayuda de un maestro. El alumno puede obtener los consejos necesarios para la resolución de problemas en nuestra web.
¿Tiene usted alguna pregunta? ¿No estás seguro de cómo encontrar la distancia entre dos puntos en un plano?
Para obtener la ayuda de un tutor, regístrese.
¡La primera lección es gratis!
sitio, con copia total o parcial del material, se requiere un enlace a la fuente.
Sea , (Figura 2.3). Requerido para encontrar.
Figura 2.3. La distancia entre dos puntos.
De rectangular por el teorema de Pitágoras tenemos
Es decir ,
Esta fórmula es válida para cualquier arreglo de puntos y .
II. La división del segmento a este respecto:
Permitir , . Se requiere encontrar acostado en el segmento y dividirlo en esta proporción (Figura 2.4.).
Figura 2.4. La división del segmento en este sentido.
De semejanza ~ , es decir , , de donde . Igualmente.
De este modo,
- la fórmula para dividir un segmento en relación con .
si, entonces
son las coordenadas del centro del segmento.
Comentario. Las fórmulas derivadas también se pueden generalizar al caso de un sistema de coordenadas cartesianas rectangulares espaciales. Deje puntos , . Luego
- fórmula para hallar la distancia entre los puntos y .
La fórmula para dividir un segmento en relación con .
Además del cartesiano en el plano y en el espacio, puede construir una gran cantidad de otros sistemas de coordenadas, es decir, formas de caracterizar la posición de un punto en un plano o en el espacio usando dos o tres parámetros numéricos (coordenadas). Veamos algunos de sistemas existentes coordenadas
En un avión, uno puede definir sistema de coordenadas polares , que se utiliza, en particular, en el estudio de los movimientos de rotación.
Figura 2.5. Sistema de coordenadas polares.
Fijamos un punto en el plano y una media línea que emerge de él, y también elegimos una unidad de escala (Figura 2.5). El punto se llama polo , media línea - eje polar . Asignemos dos números a un punto arbitrario:
– radio polar , igual a la distancia del punto M al polo O;
– ángulo polar , igual al ángulo entre el eje polar y la línea media.
Medido en radianes, el conteo de la dirección positiva de los valores es en sentido contrario a las manecillas del reloj, generalmente se asume que es .
El polo corresponde al radio polar, el ángulo polar para él no está definido.
Encontremos la relación entre coordenadas rectangulares y polares (Figura 2.6).
Figura 2.6. Relación entre los sistemas de coordenadas rectangulares y polares.
Consideraremos el origen del sistema de coordenadas rectangulares como un polo, y tomaremos la viga como eje polar. Sea - en un sistema de coordenadas cartesianas rectangulares y - en un sistema de coordenadas polares. Encuentra la relación entre coordenadas rectangulares y polares.
De rectangular, y de rectangular. Entonces las fórmulas
Expresar las coordenadas rectangulares de un punto en términos de sus coordenadas polares.
La relación inversa se expresa mediante las fórmulas
Comentario. El ángulo polar también se puede determinar a partir de la fórmula, habiendo determinado previamente por coordenadas rectangulares en qué cuarto se encuentra el punto.
Ejemplo 1 Encuentre las coordenadas polares del punto.
Solución. Calcular; El ángulo polar se encuentra a partir de las condiciones:
Por lo tanto, por lo tanto.
Ejemplo 2 Encuentre las coordenadas rectangulares del punto.
Solución. Calcular
Obtenemos .
En el espacio tridimensional, además del sistema de coordenadas cartesianas rectangulares, a menudo se utilizan sistemas de coordenadas cilíndricas y esféricas.
Sistema de coordenadas cilíndricas es un sistema de coordenadas polares en el plano , al que se suma el eje espacial, perpendicular a este plano (Figura 2.7). La posición de cualquier punto se caracteriza por tres números - sus coordenadas cilíndricas: , donde y son las coordenadas polares (radio polar y ángulo polar) de la proyección del punto sobre el plano en el que se elige el sistema de coordenadas polares, - las coordenadas aplicadas , que es igual a la distancia desde el punto hasta el plano especificado.
Figura 2.7. Sistema de coordenadas cilíndricas
Para establecer la relación entre el sistema de coordenadas cartesianas rectangulares y el sistema de coordenadas cilíndricas, los ordenaremos uno respecto del otro como en la figura 2.8 (colocaremos el plano en el plano, y el eje polar coincide con la dirección positiva del eje , el eje es común en ambos sistemas de coordenadas).
Sean las coordenadas rectangulares del punto , las coordenadas cilíndricas de este punto y la proyección del punto sobre el plano . Luego
fórmulas que relacionan coordenadas rectangulares y cilíndricas de un punto.
Figura 2.8. Relación entre cartesiano rectangular
y sistemas de coordenadas cilíndricas
Comentario. Las coordenadas cilíndricas se utilizan a menudo cuando se consideran cuerpos de revolución y el eje se ubica a lo largo del eje de rotación.
Sistema de coordenadas esféricas se puede construir de la siguiente manera. Elegimos el eje polar en el plano. A través del punto dibujamos una línea perpendicular al plano (normal). Entonces cualquier punto en el espacio se puede asociar con tres números reales, donde es la distancia desde el punto hasta, es el ángulo entre el eje y la proyección del segmento sobre el plano, es el ángulo entre la normal y el segmento. Darse cuenta de , , .
Si colocamos el plano en el plano , y elegimos el eje polar que coincide con la dirección positiva del eje , elegimos el eje como normal (Figura 2.9), entonces obtenemos fórmulas que unen estos dos sistemas de coordenadas
Figura 2.9. Relación entre cartesiano esférico y rectangular
sistemas coordinados
escalares, o escalares se caracterizan completamente por su valor numérico en el sistema de unidades elegido. Cantidades vectoriales o los vectores, además de un valor numérico, también tienen una dirección. Por ejemplo, si decimos que el viento sopla a una velocidad de 10 m/s, entonces introduciremos el valor escalar de la velocidad del viento, pero si decimos que el viento del suroeste sopla a una velocidad de 10 m/s , entonces en este caso la velocidad del viento ya será un vector.
Vector se llama un segmento dirigido, que tiene una cierta longitud, es decir, un segmento de cierta longitud, en el que uno de los puntos límite se toma como el comienzo y el segundo, como el final. El vector se denotará como , o (Figura 2.10).
La longitud de un vector se denota con el símbolo o y se llama módulo del vector. Un vector cuya longitud es 1 se llama único . El vector se llama cero , si su principio y fin coinciden, y se denota por θ o . El vector cero no tiene dirección definida y tiene una longitud igual a cero. Los vectores que se encuentran en la misma recta o en rectas paralelas se llaman colineal . Dos vectores y se llaman igual si son colineales, tienen la misma longitud y la misma dirección. Todos los vectores cero se consideran iguales.
Dos vectores colineales distintos de cero que tienen módulos iguales, pero en sentido contrario, se denominan opuesto . El vector opuesto a se denota por , para el vector opuesto .
al número operaciones de línea sobre vectores incluyen las operaciones de suma, resta de vectores y multiplicación de un vector por un número, es decir operaciones que dan como resultado un vector.
Definamos estas operaciones sobre vectores. Sean dos vectores y dados. Tomemos un punto O arbitrario y construyamos un vector, del punto A apartamos el vector. Entonces el vector que conecta el comienzo del primer término del vector con el final del segundo se llama suma de estos vectores y se denota por . La regla considerada para encontrar la suma de vectores se llama reglas triangulares (Figura 2.11).
La misma suma de vectores se puede obtener de otra forma (Figura 2.12). Aparta el vector y el vector del punto. Construyamos sobre estos vectores como sobre los lados de un paralelogramo. El vector, que es la diagonal del paralelogramo trazado desde el vértice, será la suma. Esta regla para encontrar la suma se llama reglas del paralelogramo .
La suma de cualquier número finito de vectores se puede obtener usando la regla de la línea quebrada (Figura 2.13). Desde un punto arbitrario, posponemos el vector, luego posponemos el vector, etc. El vector que une el principio del primero con el final del segundo es la suma
| |
diferencia dos vectores y se llama tal vector , cuya suma con el vector restado da el vector . De aquí regla de construcción de vector de diferencia(Figura 2.14). De un punto apartamos un vector y un vector . El vector que conecta los extremos del vector reducido y el vector a restar y dirigido desde el vector que se resta al vector reducido es la diferencia.
Producto vectorial a un número real λ se llama vector que es colineal al vector , tiene una longitud y la misma dirección que el vector si , y una dirección opuesta al vector si .
Introducido operaciones lineales sobre los vectores tienen propiedades :
10 Conmutatividad de la suma: .
veinte . Asociatividad de adición: .
treinta . La existencia de un elemento neutro por adición: .
40 . La existencia del elemento opuesto por adición:
cincuenta . Distributividad de la multiplicación por un número con respecto a la suma de vectores: .
60 . Distributividad de multiplicar un vector por la suma de dos números:
70. Propiedad de asociatividad con respecto a la multiplicación de un vector por un producto de números: .
Sea el sistema de vectores dado:
La expresión , donde λ i (i = 1,2,…, n) son algunos números, se llama combinación lineal sistemas de vectores (2.1). El sistema de vectores (2.1) se llama linealmente dependiente , si su combinación lineal es igual a cero, siempre que no todos los números λ 1 , λ 2 , …, λ n sean iguales a cero. El sistema de vectores (2.1) se llama independiente linealmente , si su combinación lineal es igual a cero solo bajo la condición de que todos los números λ i = 0 (). ¿Puedes dar otra definición? dependencia lineal vectores El sistema de vectores (2.1) se llama linealmente dependiente , si cualquier vector de este sistema se expresa linealmente en función del resto, en caso contrario el sistema de vectores (2.1) independiente linealmente .
Para vectores que se encuentran en un plano, las siguientes afirmaciones son verdaderas.
10 Cualquier tres vectores en el plano son linealmente dependientes.
veinte . Si el número de estos vectores en el plano es mayor que tres, entonces también son linealmente dependientes.
treinta . Para que dos vectores en el plano sean linealmente independientes, es necesario y suficiente que no sean colineales.
Entonces el número máximo es lineal. vectores independientes plana es de dos.
Los vectores se llaman coplanario si están en el mismo plano o son paralelos al mismo plano. Las siguientes afirmaciones son verdaderas para vectores espaciales.
10 Cualesquiera cuatro vectores espaciales son linealmente dependientes.
veinte . Si el número de vectores dados en el espacio es mayor que cuatro, entonces también son linealmente dependientes.
treinta . Para que tres vectores sean linealmente independientes, es necesario y suficiente que no sean coplanares.
Por tanto, el número máximo de vectores linealmente independientes en el espacio es tres.
Cualquier subsistema maximal de vectores linealmente independientes a través del cual se expresa cualquier vector de este sistema se llama base considerado sistemas vectoriales . Es fácil concluir que la base en el plano consta de dos vectores no colineales y la base en el espacio consta de tres vectores no coplanares. El número de vectores base se llama rango sistemas vectoriales. Los coeficientes de la expansión de un vector en términos de vectores base se denominan coordenadas vectoriales en esta base.
Deje que los vectores formen una base y sea , entonces los números λ 1 , λ 2 , λ 3 son las coordenadas del vector en la base. En este caso, escriben. Se puede demostrar que la expansión del vector en términos de la base es única. El significado principal de la base es que las operaciones lineales en vectores se convierten en operaciones lineales ordinarias en números: las coordenadas de estos vectores. Usando las propiedades de las operaciones lineales en vectores, podemos demostrar el siguiente teorema.
Teorema. Cuando se suman dos vectores, se suman sus correspondientes coordenadas. Cuando un vector se multiplica por un número, todas sus coordenadas se multiplican por ese número.
Así, si y , entonces , donde y donde , λ es un número.
Usualmente, el conjunto de todos los vectores en el plano, reducidos a un origen común, con las operaciones lineales introducidas, se denota por V 2 , y el conjunto de todos los vectores espaciales, reducidos a un origen común, se denota por V 3 . Los conjuntos V 2 y V 3 se llaman espacios de vectores geométricos.
Ángulo entre vectores y se llama al ángulo menor (), por el cual uno de los vectores debe girarse hasta coincidir con el segundo después de llevar estos vectores a un origen común.
producto punto dos vectores se llama un número igual al producto de los módulos de estos vectores por el coseno del ángulo entre ellos. Producto escalar de vectores y denotar , o
Si el ángulo entre los vectores y es igual, entonces
Desde un punto de vista geométrico, el producto escalar de vectores es igual al producto del módulo de un vector y la proyección de otro vector sobre él. De la igualdad (2.2) se sigue que
De aquí condición de ortogonalidad de dos vectores: dos vectores Y son ortogonales si y solo si su producto escalar es igual a cero, es decir .
El producto escalar de vectores no es una operación lineal porque da como resultado un número, no un vector.
Propiedades del producto escalar.
1º. - conmutatividad.
2º. - distributividad.
3º. – asociatividad con respecto a un factor numérico.
4º. - propiedad de un cuadrado escalar.
La propiedad 4º implica la definición longitud vectorial :
Sea una base dada en el espacio V 3 , donde los vectores son vectores unitarios (se les llama orts), la dirección de cada uno de los cuales coincide con la dirección positiva de los ejes de coordenadas Ox, Oy, Oz de un sistema de coordenadas cartesianas rectangulares .
Expandamos el vector espacial V 3 de acuerdo con esta base (Figura 2.15):
Los vectores se denominan componentes de un vector a lo largo de los ejes de coordenadas, o componentes, de un número a x , a y , a z son las coordenadas cartesianas rectangulares del vector pero. La dirección del vector está determinada por los ángulos α, β, γ que forma con las líneas de coordenadas. El coseno de estos ángulos se llama vector guía. Entonces los cosenos directores están determinados por las fórmulas:
Es fácil demostrar que
Expresamos el producto escalar en forma de coordenadas.
Sea y . Multiplicando estos vectores como polinomios y considerando que obtenemos una expresión para encontrar producto escalar en forma de coordenadas:
esos. el producto escalar de dos vectores es igual a la suma de los productos apareados de las coordenadas del mismo nombre.
De (2.6) y (2.4) se sigue la fórmula para encontrar longitud vectorial :
De (2.6) y (2.7) obtenemos una fórmula para determinar ángulo entre vectores:
Una terna de vectores se dice ordenada si se indica cuál de ellos se considera el primero, cuál el segundo y cuál el tercero.
Ordenado trio de vectores llamado Correcto , si después de llevarlos a un comienzo común desde el final del tercer vector, el giro más corto desde el primer al segundo vector es en sentido antihorario. En caso contrario, el triple de vectores se llama izquierda . Por ejemplo, en la figura 2.15, los vectores , , forman el triple derecho de vectores, y los vectores , , forman el triple izquierdo de vectores.
El concepto de sistemas de coordenadas derecha e izquierda en el espacio tridimensional se introduce de manera similar.
arte vectorial vector a vector se llama vector (otra notación) que:
1) tiene longitud , donde es el ángulo entre los vectores y ;
2) es perpendicular a los vectores y (), es decir perpendicular al plano que contiene los vectores y ;
Por definición, encontramos el producto vectorial de coordenadas orts , , :
Si , , entonces las coordenadas del producto vectorial de un vector y un vector están determinadas por la fórmula:
Se sigue de la definición significado geométrico producto vectorial : el módulo del vector es igual al área del paralelogramo construido sobre los vectores y .
Propiedades del producto vectorial:
40 . , si los vectores y son colineales, o uno de estos vectores es cero.
Ejemplo 3 El paralelogramo se construye sobre los vectores y , donde , , . Calcula la longitud de las diagonales de este paralelogramo, el ángulo entre las diagonales y el área del paralelogramo.
Solución. La construcción de vectores y se muestra en la Figura 2.16, la construcción de un paralelogramo sobre estos vectores se muestra en la Figura 2.17.
Llevemos a cabo una solución analítica de este problema. Expresamos los vectores que definen las diagonales del paralelogramo construido a través de los vectores y , y luego a través de y . Encontramos , . Luego, encontramos las longitudes de las diagonales del paralelogramo, como las longitudes de los vectores construidos
El ángulo entre las diagonales del paralelogramo se denota por . Entonces de la fórmula del producto escalar de vectores tenemos:
Como consecuencia, .
Usando las propiedades del producto vectorial, calculamos el área del paralelogramo:
Sean tres vectores , y . Imagine que un vector se multiplica vectorialmente por y un vector y el vector resultante se multiplica escalarmente por un vector, determinando así el número. Se llama vector-escalar o producto mixto tres vectores , y . Denotado o .
Vamos a averiguar significado geométrico del producto mixto (Figura 2.18). Que , , no sea coplanar. Construyamos un paralelepípedo sobre estos vectores como sobre aristas. El producto vectorial es un vector cuyo módulo es igual al área del paralelogramo (la base del paralelepípedo) construido sobre los vectores y dirigido perpendicularmente al plano del paralelogramo.
Producto escalar (igual al producto del módulo del vector y la proyección sobre ). La altura del paralelepípedo construido es el valor absoluto de esta proyección. Por tanto, el valor absoluto del producto mixto de tres vectores es igual al volumen del paralelepípedo construido sobre los vectores , y , es decir .
Por tanto, el volumen de la pirámide triangular construida sobre los vectores , y , se calcula mediante la fórmula .
Anotamos algo más propiedades de productos mixtos vectores
1 o. El signo del producto es positivo si los vectores , , forman un sistema con el mismo nombre que el principal, y negativo en caso contrario.
En realidad, el producto escalar es positivo si el ángulo entre y es agudo y negativo si el ángulo es obtuso. Con un ángulo agudo entre y, los vectores y están situados en el mismo lado con respecto a la base del paralelepípedo, y por lo tanto, desde el extremo del vector, la rotación de a se verá de la misma manera que desde el extremo de el vector, es decir en la dirección positiva (en sentido contrario a las agujas del reloj).
En un ángulo obtuso, y los vectores y están ubicados en lados diferentes en relación con el plano del paralelogramo que se encuentra en la base del paralelepípedo y, por lo tanto, desde el final del vector, la rotación de a es visible en la dirección negativa ( agujas del reloj).
2 o El producto mixto no cambia con una permutación circular de sus factores: .
3 o Cuando se intercambian dos vectores cualesquiera, el producto mixto cambia sólo de signo. Por ejemplo, , . , . - sistemas desconocidos.
Sistema(3.1) se llama homogéneo si todos los miembros libres son . Sistema (3.1) se llama heterogéneo , si al menos uno de los miembros libres de .
solución del sistema se llama un conjunto de números, al sustituir los cuales en las ecuaciones del sistema en lugar de las correspondientes incógnitas, cada ecuación del sistema se convierte en una identidad. Un sistema que no tiene solución se llama incompatible, o polémico . Un sistema que tiene al menos una solución se llama articulación .
El sistema de unión se llama cierto si tiene solución única. Si un sistema conjunto tiene más de una solución, entonces se llama incierto . Un sistema homogéneo es siempre compatible, ya que tiene, según por lo menos, solución cero . La expresión de las incógnitas, a partir de la cual se puede obtener cualquier solución particular del sistema, se llama solución común , y cualquier solución particular del sistema es su decisión privada . Dos sistemas con las mismas incógnitas son equivalentes (son equivalentes a ) si cada solución de uno de ellos es solución del otro o ambos sistemas son inconsistentes.
Considerar métodos para resolver sistemas. ecuaciones lineales.
Uno de los principales métodos para resolver sistemas de ecuaciones lineales es método de Gauss, o método secuencial exclusión de incógnitas. La esencia de este método es reducir el sistema de ecuaciones lineales a una forma escalonada. En este caso, las ecuaciones tienen que realizar lo siguiente transformaciones elementales :
1. Permutación de las ecuaciones del sistema.
2. Agregar otra ecuación a una ecuación.
3. Multiplicar ambos lados de la ecuación por un número distinto de cero.
Como resultado, el sistema tomará la forma:
Continuando con este proceso, eliminamos la incógnita de todas las ecuaciones, comenzando con la tercera. Para ello, multiplicamos la segunda ecuación por números y sumamos a la 3ª, ..., a la -ésima ecuación del sistema. Los siguientes pasos del método de Gauss se llevan a cabo de manera similar. Si como resultado de las transformaciones se obtiene una ecuación idéntica, la eliminamos del sistema. Si en algún paso del método de Gauss se obtiene una ecuación de la forma:
entonces el sistema bajo consideración es inconsistente y su solución posterior se detiene. Si la ecuación de la forma (3.2) no ocurre al realizar transformaciones elementales, entonces en no más de - pasos el sistema (3.1) se transformará a una forma escalonada:
Para obtener una solución particular del sistema, será necesario en (3.4) asignar valores específicos a las variables libres.
Tenga en cuenta que dado que en el método de Gauss todas las transformaciones se realizan en los coeficientes en ecuaciones desconocidas y términos libres, entonces en la práctica este método se suele aplicar a una matriz compuesta por coeficientes de incógnitas y una columna de términos libres. Esta matriz se llama extendida. Con la ayuda de transformaciones elementales, esta matriz se reduce a una forma escalonada. Posteriormente, se restaura el sistema utilizando la matriz obtenida y se le aplican todas las consideraciones anteriores.
Ejemplo 1 Sistema de resolución:
Solución. Componemos la matriz aumentada y la reducimos a una forma escalonada:
~ *) ~ **) ~ ***)
*) - la segunda línea se multiplica por y la tercera línea se tacha.
En los §§ 5, 6 y 10 de este capítulo consideramos algunos de los problemas más simples de la geometría analítica, a los que a menudo se reducen muchos problemas más complejos. Uno de esos problemas es el problema de la distancia entre dos puntos.
Deja entrar el plano elegido sistema rectangular coordenadas dadas dos puntos Expresemos la distancia d entre estos dos puntos a través de sus coordenadas.
Encontremos las proyecciones de los puntos A y B en los ejes de coordenadas (Fig. 8). Tendrá:

Por uno de estos puntos, por ejemplo A, trazamos una recta paralela al eje x hasta que se corta en el punto C con una recta
Del triángulo rectángulo ACB obtenemos:
![]()
(aquí AC y CB son las longitudes de los lados del triángulo ASV). Pero desde
(Cap. 1, § 3), luego
Es claro que aquí hay que tomar valor aritmético raíz.
Así, la distancia entre dos puntos dados es igual a la raíz cuadrada de la suma de las diferencias al cuadrado de las coordenadas del mismo nombre de estos puntos.
Comentario. Si estos puntos A a B están ubicados en una línea recta paralela al eje de coordenadas, entonces no obtendremos un triángulo ABC, pero la fórmula (3) será válida en este caso también. En efecto, si, por ejemplo, los puntos A a B se encuentran en una línea recta paralela al eje Ox, entonces, obviamente, (Capítulo I, § 3). Lo mismo se obtendrá de la fórmula (3), ya que en este caso
El cálculo de distancias entre puntos según sus coordenadas en un plano es elemental, en la superficie de la Tierra es un poco más complicado: consideraremos medir la distancia y el acimut inicial entre puntos sin transformaciones de proyección. Primero, comprendamos la terminología.
Introducción
Longitud de arco de círculo máximo- la distancia más corta entre dos puntos cualquiera ubicados en la superficie de la esfera, medida a lo largo de la línea que conecta estos dos puntos (dicha línea se llama ortodrómica) y pasa a lo largo de la superficie de la esfera u otra superficie de revolución. La geometría esférica es diferente de la euclidiana habitual y las ecuaciones de distancia también toman una forma diferente. En geometría euclidiana, la distancia más corta entre dos puntos es una línea recta. En una esfera, no hay líneas rectas. Estas líneas en la esfera son parte de grandes círculos, círculos cuyos centros coinciden con el centro de la esfera. Acimut inicial- acimut, tomando el cual, al partir del punto A, siguiendo el círculo máximo la distancia más corta hasta el punto B, el punto final será el punto B. Al pasar del punto A al punto B a lo largo de la línea del círculo máximo, el acimut desde el la posición actual hasta el punto final B es constante y está cambiando. El acimut inicial es diferente de uno constante, por lo que el acimut desde el punto actual hasta el final no cambia, pero la ruta no es la distancia más corta entre dos puntos.A través de dos puntos cualesquiera en la superficie de la esfera, si no están directamente opuestos entre sí (es decir, no son antípodas), se puede dibujar un gran círculo único. Dos puntos dividen el gran círculo en dos arcos. La longitud de un arco corto es la distancia más corta entre dos puntos. Se pueden dibujar un número infinito de círculos grandes entre dos puntos antípodas, pero la distancia entre ellos será la misma en cualquier círculo e igual a la mitad de la circunferencia del círculo, o π*R, donde R es el radio de la esfera.

En un plano (en un sistema de coordenadas rectangulares), los círculos máximos y sus fragmentos, como se mencionó anteriormente, son arcos en todas las proyecciones, excepto en la gnomónica, donde los círculos máximos son líneas rectas. En la práctica, esto significa que los aviones y otros transportes aéreos siempre utilizan la ruta de la distancia mínima entre puntos para ahorrar combustible, es decir, el vuelo se realiza a lo largo de la distancia de un gran círculo, en el avión parece un arco.

La forma de la Tierra se puede describir como una esfera, por lo que las ecuaciones de distancia del gran círculo son importantes para calcular la distancia más corta entre puntos en la superficie de la Tierra y se usan a menudo en la navegación. Calcular la distancia por este método es más eficiente y en muchos casos más preciso que calcularla para coordenadas proyectadas (en sistemas de coordenadas rectangulares), porque, en primer lugar, no necesita trasladar coordenadas geográficas en un sistema de coordenadas rectangulares (realizar transformaciones de proyección) y, en segundo lugar, muchas proyecciones, si se eligen incorrectamente, pueden generar distorsiones de longitud significativas debido a las características de las distorsiones de proyección. Se sabe que no una esfera, sino un elipsoide describe la forma de la Tierra con mayor precisión, sin embargo, este artículo considera el cálculo de distancias en una esfera, para los cálculos se usa una esfera con un radio de 6372795 metros, lo que puede conducir a un error en el cálculo de distancias del orden del 0,5%.
Fórmulas
Hay tres formas de calcular la distancia esférica de un gran círculo. 1. Teorema del coseno esférico En el caso de distancias pequeñas y profundidad de bits de cálculo pequeña (número de decimales), el uso de la fórmula puede dar lugar a errores de redondeo significativos. φ1, λ1; φ2, λ2 - latitud y longitud de dos puntos en radianes Δλ - diferencia de coordenadas en longitud Δδ - diferencia angular Δδ = arccos (sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ) Para convertir la distancia angular a métrica, debe multiplicar la diferencia angular por el radio Tierra (6372795 metros), las unidades de la distancia final serán iguales a las unidades en que se expresa el radio (en este caso, metros). 2. Fórmula Haversine Se utiliza para evitar problemas con distancias cortas. 3. Modificación por antípodas La fórmula anterior también está sujeta al problema de las antípodas, para solucionarlo se utiliza la siguiente modificación.Mi implementación en PHP
// Radio de la tierra define("EARTH_RADIUS", 6372795); /* * Distancia entre dos puntos * $φA, $λA - latitud, longitud del primer punto, * $φB, $λB - latitud, longitud del segundo punto * Basado en http://gis-lab.info/ qa /great-circles.html * Mikhail Kobzarev< >* */ función calcularLaDistancia ($φA, $λA, $φB, $λB) ( // convertir coordenadas a radianes $lat1 = $φA * M_PI / 180; $lat2 = $φB * M_PI / 180; $long1 = $λA * M_PI / 180; $long2 = $λB * M_PI / 180; // cosenos y senos de diferencias de latitud y longitud $cl1 = cos($lat1); $cl2 = cos($lat2); $sl1 = sin($lat1) ) ; $sl2 = sin($lat2); $delta = $long2 - $long1; $cdelta = cos($delta); $sdelta = sin($delta); // calcular la longitud del círculo máximo $y = sqrt( pow( $cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2)); $x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta; // $ad = atan2($y, $x); $dist = $ad * EARTH_RADIUS; return $dist; ) Ejemplo de llamada de función: $lat1 = 77.1539; $largo1 = -139.398; $lat2 = -77.1804; $largo2 = -139,55; echo calcularLaDistancia($lat1, $long1, $lat2, $long2) . "metros"; // Devuelve "17166029 metros"Artículo tomado del sitio.
Teorema 1. Para dos puntos cualesquiera y un plano, la distancia entre ellos se expresa mediante la fórmula:
Por ejemplo, si se dan puntos y, entonces la distancia entre ellos:
2. Área de un triángulo.
Teorema 2.
Para cualquier punto
, que no se encuentra en una línea recta, el área del triángulo se expresa mediante la fórmula:
Por ejemplo, encontremos el área del triángulo formado por los puntos , y.
Comentario. Si el área de un triángulo es cero, esto significa que los puntos se encuentran en la misma línea.
3. División de un segmento en una razón dada.
Sea dado un segmento arbitrario en el plano y sea
- cualquier punto de este segmento que no sean los puntos finales. El número definido por la igualdad se llama actitud, donde el punto divide al segmento.
El problema de dividir un segmento en una razón dada es que, según una razón dada y unas coordenadas de puntos dadas
y encuentre las coordenadas del punto.
Teorema 3.
Si un punto divide un segmento
en una relación
,
entonces las coordenadas de este punto están determinadas por las fórmulas: ![]() (1.3), donde son las coordenadas del punto y son las coordenadas del punto.
(1.3), donde son las coordenadas del punto y son las coordenadas del punto.
Consecuencia: si es el punto medio
, donde y, entonces (1.4) (porque).
Por ejemplo. Dados los puntos y. Encuentre las coordenadas de un punto que está el doble de cerca que de
Solución: El punto deseado divide el segmento
en cuanto a porque ![]() , luego
, luego ![]() ,
,![]() , recibió
, recibió
Coordenadas polares
El más importante después del sistema de coordenadas rectangulares es el sistema de coordenadas polares. Consiste en un cierto punto llamado polo, y el rayo que emana de él - eje polar. Además, se establece la unidad de escala para medir las longitudes de los segmentos. 
Sea dado un sistema de coordenadas polares y sea un punto arbitrario del plano. Sea la distancia al punto
al punto ; - el ángulo por el cual el eje polar debe girarse para coincidir con el haz.
Punto coordenadas polares se llaman números. En este caso, el número se considera la primera coordenada y se llama radio polar, el número es la segunda coordenada y se llama ángulo polar.
Designado . El radio polar puede tener cualquier valor no negativo:. Generalmente se cree que el ángulo polar varía dentro de los siguientes límites: Sin embargo, en algunos casos es necesario determinar los ángulos contados desde el eje polar en el sentido de las agujas del reloj.
Relación entre las coordenadas polares de un punto y sus coordenadas rectangulares.
Supondremos que el origen del sistema de coordenadas rectangulares está en el polo, y el semieje positivo de la abscisa coincide con el eje polar. 
Sea en un sistema de coordenadas rectangulares y sea en un sistema de coordenadas polares. Definido– triángulo rectángulo desde. Entonces (1.5). Estas fórmulas expresan coordenadas rectangulares en términos de coordenadas polares.
Por otra parte, según el teorema de Pitágoras y
![]() (1.6) - estas fórmulas expresan coordenadas polares en términos de rectangulares.
(1.6) - estas fórmulas expresan coordenadas polares en términos de rectangulares.
Tenga en cuenta que la fórmula define dos valores del ángulo polar, ya que. De estos dos valores del ángulo, elija aquel en el que se satisfagan las igualdades.
Por ejemplo, encontremos las coordenadas polares del punto ..o, desde cuartos.
Ejemplo 1: Encuentra un punto simétrico a un punto 
Relativo a la bisectriz del primer ángulo coordenado.
Solución:
Pasemos por el punto PERO directo yo 1 perpendicular a la bisectriz yo primer ángulo coordenado. Permitir . en línea recta yo 1 posponer el segmento SA 1 , igual al segmento COMO. triángulos rectángulos A.O.S.O. Y PERO 1 ENTONCES son iguales entre sí (en dos patas). De esto se deduce que | OA| = |OA 1 |. triangulos ALHARACA Y OEA 1 también son iguales entre sí (a lo largo de la hipotenusa y el ángulo agudo). Concluimos que |AD| = |OE| = 4,|OD| = |EA 1 | = 2, es decir punto tiene coordenadas x = 4, y = -2, esos. PERO 1 (4;-2).
Tenga en cuenta que la afirmación general se cumple: el punto A 1 , simétrico a un punto con respecto a la bisectriz del primer y tercer ángulo coordenado, tiene coordenadas , es decir .
Ejemplo 2: Encuentre el punto en el que la recta que pasa por los puntos y , cruzará el eje Oh.
Solución:
Coordenadas del punto de búsqueda DESDE come ( X; 0). Y dado que los puntos PERO,EN Y DESDE se encuentran en la misma línea recta, entonces la condición (X 2 -X 1 )(y 3 -y 1 )-(X 3 -X 1 )(y 2 -y 1 ) = 0 (fórmula (1.2), área del triángulo A B C es igual a cero!), ¿dónde están las coordenadas del punto PERO, - puntos EN, - puntos DESDE. Obtenemos, es decir, , . De ahí el punto DESDE tiene coordenadas ,, es decir..
Ejemplo 3: Los puntos , se dan en el sistema de coordenadas polares. Encontrar: pero) distancia entre puntos y ; b) area de un triangulo OM 1 METRO 2 (SOBRE- poste).
Solución:
a) Usamos las fórmulas (1.1) y (1.5):
es decir, .
b) usando la fórmula para el área de un triángulo con lados pero Y B y el ángulo entre ellos (), encontramos el área del triángulo OM 1 METRO 2 . .
- En contacto con 0
- Google+ 0
- OK 0
- Facebook 0