En este apartado volveremos a abandonar el bello y acogedor reino de los números enteros, en el que caminamos (casi digo deambulamos) mientras estudiamos la teoría de las comparaciones. Si rastreamos la historia del surgimiento y desarrollo del conocimiento humano sobre los números, surgirá un hecho bastante paradójico: a lo largo de casi toda su historia centenaria, la humanidad ha utilizado en la práctica y ha estudiado de cerca una fracción excepcionalmente pequeña de todo el conjunto de números. viviendo en la naturaleza. Durante mucho tiempo, la gente desconocía por completo la existencia, como se vio más tarde, de la inmensa mayoría de los números reales, dotados de propiedades asombrosas y misteriosas y ahora llamados trascendentales. Juzgue usted mismo (enumero las etapas aproximadas de desarrollo del concepto de número real):
1) Una ingeniosa abstracción matemática de un número natural, procedente de las profundidades de miles de años.
La genialidad de esta abstracción es asombrosa y su importancia para el desarrollo de la humanidad supera, quizás, incluso la invención de la rueda. Nos hemos acostumbrado tanto a ello que hemos dejado de admirar este logro tan destacado de la mente humana. Sin embargo, intente, para mayor autenticidad, imaginarse no como un estudiante de matemáticas, sino como un hombre primitivo o, digamos, un estudiante de filología, para formular exactamente qué tienen en común tres chozas, tres toros, tres plátanos y tres tomógrafos ultrasónicos ( ¿Qué tienen en común tres compañeros de bebida que no consideramos aquí)? Explicar a alguien que no sea matemático qué es el número natural “tres” es una tarea casi desesperada, pero un niño humano de cinco años ya siente internamente esta abstracción y es capaz de operar inteligentemente con ella, pidiéndole a su madre tres dulces. de dos.
2) Fracciones, es decir números racionales positivos
Las fracciones surgieron naturalmente al resolver problemas sobre la división de propiedades, medición terrenos, cálculo de tiempos, etc. EN antigua Grecia Los números racionales en general eran un símbolo de la armonía del mundo circundante y una manifestación del principio divino, y todos los segmentos, hasta algún tiempo, se consideraban conmensurables, es decir. la proporción de sus longitudes tenía que expresarse como un número racional, de lo contrario sería una tubería (y los dioses no pueden permitirlo).
3) Números negativos y cero (según algunas fuentes científicas
Las cifras negativas se interpretaron inicialmente como deuda en los cálculos financieros y de trueque, pero luego resultó que sin números negativos y en otros ámbitos de la actividad humana no hay escapatoria (quien no lo crea, que mire el termómetro por la ventana en invierno). El número cero, en mi opinión, inicialmente no sirvió como símbolo de espacio vacío y ausencia de cantidad, sino como símbolo de igualdad e integridad del proceso de liquidación (todo lo que le debía a su vecino, se lo devolvía a él, y ahora es cero, es decir, es una lástima).
4) Números algebraicos irracionales
Los números irracionales fueron descubiertos en la escuela pitagórica al intentar medir la diagonal de un cuadrado con su lado, pero mantuvieron este descubrimiento en terrible secreto- ¡No importa cuántos problemas haya! Sólo los estudiantes más estables y probados mentalmente fueron iniciados en este descubrimiento, y fue interpretado como un fenómeno repugnante que violaba la armonía del mundo. Pero la necesidad y la guerra obligaron a la humanidad a aprender a decidir. ecuaciones algebraicas no sólo de primer grado con coeficientes enteros. Después de Galileo, los proyectiles comenzaron a volar en parábolas, después de Kepler, los planetas volaron en elipses, la mecánica y la balística se convirtieron en ciencias exactas y en todas partes era necesario resolver y resolver ecuaciones cuyas raíces eran números irracionales. Por lo tanto, tuvimos que aceptar la existencia de raíces irracionales de ecuaciones algebraicas, por repugnantes que parezcan. Además, los métodos para resolver ecuaciones cúbicas y de cuarto grado, descubiertos en el siglo XVI por los matemáticos italianos Scipione del Ferro, Niccolo Tartaglia (Tartaglia es un apodo que significa tartamudo, no sé su nombre real), Ludovic Ferrari y Raphael. Bombelli condujo a la invención de números complejos completamente "sobrenaturales", que no estaban destinados a recibir pleno reconocimiento hasta el siglo XIX. Las irracionalidades algebraicas se han establecido firmemente en la práctica humana desde el siglo XVI.
En esta historia del desarrollo del concepto de número, no hubo lugar para los números trascendentales, es decir, números que no son raíces de ninguna ecuación algebraica con coeficientes racionales o, lo que es equivalente (después de la reducción a un denominador común), enteros. Es cierto que incluso los antiguos griegos conocían el notable número p, que, como se vio más tarde, es trascendental, pero sólo lo conocían como la relación entre la circunferencia de un círculo y su diámetro. La cuestión de la verdadera naturaleza de este número era de poco interés para nadie hasta que la gente se hartó y resolvió sin éxito el antiguo problema griego de la cuadratura de un círculo, y el propio número p apareció de alguna manera misteriosamente en varias secciones de las matemáticas y las ciencias naturales.
Sólo en 1844 Liouville construyó el primer ejemplo histórico de un número trascendental, y el mundo matemático se sorprendió ante el hecho mismo de la existencia de tales números. Sólo en el siglo XIX el brillante Georg Cantor comprendió, utilizando el concepto de potencia de un conjunto, que existe una abrumadora mayoría de números trascendentales en la recta numérica. Sólo en el quinto párrafo de este pequeño libro centraremos finalmente nuestra atención en los números trascendentales.
Punto 24. Medida y categoría en una recta.
En este párrafo proporcionaré información preliminar del análisis matemático necesaria para comprender la presentación adicional. En matemáticas, se han inventado bastantes formalizaciones diferentes del concepto de "pequeñez" de un conjunto. Necesitaremos dos de ellos: conjuntos de medida cero y conjuntos de la primera categoría de Baire. Ambos conceptos se basan en el concepto de contabilidad de un conjunto. Se sabe que el conjunto de los números racionales es contable (| q|= A 0), y que cualquier conjunto infinito contiene un subconjunto contable, es decir Los conjuntos contables son los “más pequeños” de los infinitos. Entre cualquier conjunto contable y el conjunto números naturales norte hay un mapeo biyectivo, es decir los elementos de cualquier conjunto contable se pueden renumerar o, en otras palabras, cualquier conjunto contable se puede organizar en una secuencia. Ningún intervalo en la línea es un conjunto contable. Esto se desprende obviamente del siguiente teorema.
Teorema 1 (Cantor). Para cualquier secuencia ( un) números reales y para cualquier intervalo I hay un punto R ACERCA DE I tal que pag № un para cualquiera norte ACERCA DE norte .
Prueba. Proceso. Cogemos un segmento (precisamente un segmento, junto con los extremos) I 1M I tal que a 1P I 1 . De un segmento I 1 tomar un segmento I 2M I 1 tal que a 2p I 2, etc Continuando el proceso, desde el segmento En 1 tomar un segmento I norte m I norte-1 tal que a norte P I norte. Como resultado de este proceso, obtenemos una secuencia de segmentos anidados I 1er I 2J...J I n... intersección
que, como sabemos por el primer curso, no están vacíos, es decir contiene algún punto
. Es obvio que cacerola en frente de todos No norte .
No creo que los lectores no se hayan encontrado antes con esta elegante demostración (aunque en mi práctica me he encontrado con estudiantes muy oscuros), es solo que la idea de esta demostración se usará más adelante en la demostración del teorema de Baire y por tanto, es útil recordarlo con antelación.
Definición. Un montón de A firmemente en el intervalo I, si tiene una intersección no vacía con cada subintervalo de I. Un montón de A apretado si está apretado R. Un montón de A no es denso en ninguna parte si no es denso en ningún intervalo de la recta real, es decir Cada intervalo en la línea contiene un subintervalo que se encuentra completamente en el complemento de A .
Es fácil entender que muchos A ningún lugar es denso si y sólo si su complemento A ў contiene un conjunto abierto denso. Es fácil entender que muchos A ningún lugar es estrecho si y sólo si su cierre
No tiene puntos internos.
En ningún lugar los conjuntos densos en una línea se sienten intuitivamente pequeños en el sentido de que están llenos de agujeros y los puntos de tal conjunto están ubicados en una línea muy raramente. Formulemos algunas propiedades de conjuntos en masa en ninguna parte densos en forma de teorema.
Teorema 2. 1) Cualquier subconjunto de un conjunto no denso en ninguna parte no es denso en ninguna parte.
2) La unión de dos (o cualquier número finito) conjuntos en ninguna parte densos no es densa en ninguna parte.
3) El cierre de un conjunto en ninguna parte denso no es en ninguna parte denso.
Prueba. 1) Obviamente.
2) si A 1 y A 2 no son densos en ninguna parte, entonces para cada intervalo I habrá intervalos I 1 millón ( I \ A 1) y I 2M ( I 1 \ A 2). Medio, I 2M I \(A 1 yo A 2), lo que significa que A 1 yo A 2 no está apretado en ninguna parte.
3) Obviamente, cualquier intervalo abierto contenido en A ў, también está contenido en
.
Por tanto, la clase de conjuntos densos en ninguna parte está cerrada bajo la operación de toma de subconjuntos, la operación de cierre y uniones finitas. Una unión contable de conjuntos densos en ninguna parte, en términos generales, no tiene por qué ser un conjunto denso en ninguna parte. Un ejemplo de esto es el conjunto de los números racionales, que es denso en todas partes, pero es una unión contable de puntos individuales, cada uno de los cuales forma un conjunto único de elementos que no es denso en ninguna parte. R .
Definición. Un conjunto que puede representarse como una unión finita o contable de conjuntos no densos en ninguna parte se denomina conjunto de primera categoría (según Baer). Un conjunto que no se puede representar de esta forma se denomina conjunto de segunda categoría.
Teorema 3. 1) El complemento de cualquier conjunto de la primera categoría sobre la recta es denso.
2) Sin intervalo en R no es un conjunto de la primera categoría.
3) La intersección de cualquier secuencia de conjuntos abiertos densos es un conjunto denso.
Prueba. Las tres propiedades formuladas en el teorema son esencialmente equivalentes. Probemos el primero. Dejar
– representación de un conjunto A primera categoría en forma de una unión contable de conjuntos densos en ninguna parte, I– intervalo arbitrario. El siguiente es el proceso como en la demostración del teorema de Cantor. Seleccionemos un segmento (es decir, un segmento, junto con los extremos) I 1 millón ( I \ A 1). Esto se puede hacer porque, además del conjunto denso en ninguna parte A 1 dentro del intervalo I siempre hay un subintervalo completo y éste, a su vez, contiene un segmento completo dentro de sí mismo. Seleccionemos un segmento I 2M ( yo 1 \ A 2). Seleccionemos un segmento I 3M ( I 2 \ A 3) etc. Intersección de segmentos anidados
no está vacío, de ahí el complemento I \ A no está vacío, lo que significa que el complemento A ў ajustado.
El segundo enunciado del teorema se deriva directamente del primero, el tercer enunciado también se deriva del primero, si tan solo haces un esfuerzo y pasas a los complementos de una secuencia de conjuntos abiertos densos.
Definición. Una clase de conjuntos que contiene todas las uniones finitas o contables posibles de sus miembros y cualquier subconjunto de sus miembros se llama s - ideal.
Obviamente, la clase de todos los conjuntos contables en la mayoría de los casos es un s-ideal. Después de pensarlo un poco, es fácil comprender que la clase de todos los conjuntos de la primera categoría en la línea también es un s-ideal. Otro ejemplo interesante de un ideal s lo proporciona la clase de los llamados conjuntos nulos (o conjuntos de medida cero).
Definición. Un montón de A METRO R se llama conjunto de medida cero (conjunto nulo) si A puede cubrirse con no más que un conjunto contable de intervalos, cuya longitud total sea menor que cualquier número predeterminado e >0, es decir para cualquier e > 0 existe tal secuencia de intervalos En, Qué
y e Ѕ en Ѕ<
e
.
El concepto de conjunto nulo es otra formalización del concepto intuitivo de “pequeñez” de un conjunto: los conjuntos nulos son conjuntos de longitud pequeña. Es obvio que un punto individual es un conjunto nulo y que cualquier subconjunto de un conjunto nulo es en sí mismo un conjunto nulo. Por lo tanto, el hecho de que los conjuntos nulos formen un s-ideal se deriva del siguiente teorema.
Teorema 4 (Lebesgue). Cualquier unión contable de conjuntos nulos es un conjunto nulo.
Prueba. Dejar yo– conjuntos nulos, i= 1, 2,... . Entonces para todos i hay una secuencia de intervalos I yo( j=1, 2, ...) tal que
Y
. Conjunto de todos los intervalos I ij cubre A y la suma de sus longitudes es menor que e, ya que ![]() . Medio, A- conjunto nulo.
. Medio, A- conjunto nulo.
Ningún intervalo o segmento es un conjunto nulo, porque justo
Teorema 5 (Heine-Borel). Si una secuencia finita o infinita de intervalos En cubre el intervalo I, Eso
S S En Ѕ і Ѕ I Ѕ .
No daré aquí una demostración de este teorema intuitivamente obvio, porque puede encontrarse en cualquier curso más o menos serio de análisis matemático.
Del teorema de Heine-Borel se deduce que el s -ideal de conjuntos nulos, como los s -ideales de no más que conjuntos contables y conjuntos de la primera categoría, no contiene intervalos ni segmentos. Lo que estos tres ideales s también tienen en común es que incluyen todos los conjuntos finitos y contables. Además, existen innumerables conjuntos de la primera categoría de medida cero. El ejemplo más familiar de tal conjunto es el conjunto perfecto (*) de Cantor. C M, formado por números cuya notación ternaria no contiene uno. Recuerde el proceso de construcción del conjunto perfecto de Cantor: el segmento se divide en tres partes iguales y se descarta el intervalo abierto medio. Cada uno de los dos tercios restantes del segmento se divide nuevamente en tres partes iguales y se eliminan los intervalos abiertos intermedios, etc. Es obvio que el conjunto que queda después de este proceso no es denso en ninguna parte, es decir primera categoría. Es fácil calcular que la longitud total de las partes medias descartadas es igual a uno, es decir Con tiene medida cero. Se sabe que Con incontable, porque incontables secuencias infinitas que consisten en ceros y dos (cada elemento Con se representa por una fracción ternaria en la que después del punto decimal hay precisamente una secuencia de ceros y dos).
Sugiero que los lectores comprueben por sí mismos que hay conjuntos de la primera categoría que no son conjuntos nulos, y que hay conjuntos nulos que no son conjuntos de la primera categoría (sin embargo, si le resulta difícil encontrar ejemplos relevantes, no desesperes, basta con leer este punto hasta el Teorema 6).
Por tanto, la imagen de las relaciones entre los tres ideales s considerados es la siguiente:
Entonces, hemos introducido dos conceptos de conjuntos pequeños. No tiene nada de paradójico que un conjunto que es pequeño en un sentido pueda ser grande en otro sentido. El siguiente teorema ilustra bien esta idea y muestra que, en algunos casos, los conceptos de pequeñez que introdujimos pueden resultar diametralmente opuestos.
Teorema 6. La recta numérica se puede dividir en dos conjuntos complementarios. A Y EN Entonces A hay un conjunto de la primera categoría, y EN tiene medida cero.
Prueba. Dejar a 1 , a 2 ,…, a n ,… – conjunto numerado de números racionales (o cualquier otro subconjunto contable en todas partes denso R). Dejar yo ij– intervalo abierto de longitud 1/2 i+j con centro en el punto un yo. Consideremos los conjuntos:
, j =1,2,...;
; A = R \ B = B ў .
Obviamente, para cualquier e >0, podemos elegir j de modo que 1/2 j< e . Тогда
![]() ,
,
por eso, EN- conjunto nulo.
Más,
– subconjunto abierto denso R porque es la unión de una secuencia de intervalos abiertos y contiene todos los puntos racionales. Esto significa que su complemento gjў no es denso en ninguna parte, por lo tanto
– un conjunto de la primera categoría.
¿No es un resultado sorprendente? Del teorema demostrado se deduce que cada subconjunto de la línea puede representarse como una unión del conjunto nulo y un conjunto de la primera categoría. EN siguiente punto veremos una partición específica R en dos subconjuntos, uno de los cuales es el trascendental número de Liouville - mide cero, pero de la segunda categoría según Baire. ¡Date prisa al siguiente punto!
| Problemas |
1. Dé un ejemplo de dos conjuntos densos en todas partes cuya intersección no sea densa en todas partes. Dé un ejemplo de un conjunto denso en todas partes cuyo complemento también lo sea en todas partes. 2. ¿Existe un conjunto incontable de medida cero que sea denso en el intervalo? 5. deja que el conjunto mi tiene medida cero en el segmento. ¿Su cierre es un conjunto de medida cero? 6. deja que el conjunto mi no es denso en ninguna parte del segmento y tiene medida cero. ¿Su cierre es un conjunto de medida cero? 7. ¿Hay dos conjuntos incontables y densos en todas partes en una línea cuya intersección está vacía? 8. Construya en el segmento un conjunto perfecto, en ninguna parte denso, de medidas distintas de cero. 9.
Dejar s>0, UN R. Dicen que hay muchos A tiene cero s Medida de Hausdorff -dimensional si para cualquier e >0 existe una secuencia de intervalos En tal que: 10. deja la secuencia fn (X) de funciones continuas converge puntualmente a la función F (X) en el segmento . Demuestre que el conjunto de puntos de discontinuidad de la función F (X) en este segmento es un conjunto de la primera categoría. **) |
| NS | NOTICIAS DE CULTURA |
|
NUEVA LLEGADA AL HERMTAGE Artista Valentin Serov. "Chica con melocotones" El autor captó con sensibilidad y transmitió hábilmente el estado de ánimo de la modelo, que por un momento estuvo pensando en cosas tristes: sigue siendo el mismo mostrador, la misma báscula, siempre estás vendiendo estos malditos melocotones, y pasan los años y no uno se casa y sigue siendo niña... Iván Kramskoi. "Desconocido." El fondo del lienzo y la propia composición del tema están representados en tonos sombríos e intensos. Y con una aguda disonancia, un grito escarlata desconocido que perturba el alma. X en la ecuación 0,48 C X + 456,67 = 8974. Artista de la corte olvidado "Retrato de una dama de alto rango" Montañas del Cáucaso. A la derecha está el castillo de Tamara, a la izquierda hay una dama viva de pie, pero se desconoce qué come y quién la colocó tan alto. Escultor Mukhina. "El trabajador y el granjero colectivo". Material - queso feta. Artista Salieri. "Mozart al piano". El llamado arte “ready-made” (“el arte de los objetos listos para usar”), cuando el artista saca de contexto un objeto ordinario y lo convierte en un hecho artístico. Esta composición consta de 2 botellas: "Mozart", delante de ella, "Royal". Artista Vermeer. "Chica de azul" Una imagen extraña y grotesca. Sus personajes se presentan en forma de rayos X. Realmente una chica. Realmente en azul. Wassily Kandinsky. «Composición N 456642695244962». Como sabes, la idea de crear cuadros abstractos se le ocurrió al artista cuando miraba el trapo con el que limpiaba sus pinceles. El trapo con el que se secó los pies le convenció de que estaba en el camino correcto. Esta obra es otra imagen de los famosos trapos. Artista Min Zdrav. Póster "Joven mirando el bacilo del tifus, ampliado 10000000000 veces" El cuadro de Medvedev "Tres conos". Fedotov "El desayuno de un aristócrata". Lienzo. Aceite. Pan. |
|
La palabra "trascendental" generalmente se asocia con la meditación trascendental y diversos esoterismos. Pero para utilizarlo correctamente, es necesario al menos distinguirlo del término "trascendental" y, como máximo, recordar su papel en las obras de Kant y otros filósofos.
Este concepto proviene del latín trasciende: "trascender", "superar", "ir más allá". En general, denota algo que es fundamentalmente inaccesible al conocimiento empírico o que no se basa en la experiencia. Los requisitos previos para el término surgieron en la filosofía del neoplatonismo: el fundador del movimiento, Plotino, creó la doctrina del Uno, el primer principio todo bien, que no puede ser conocido ni mediante el esfuerzo del pensamiento ni con la ayuda de los sentidos. experiencia. “El Uno no es un ser, sino su padre”, explica el filósofo.
El término "trascendente" se reveló más plenamente en la filosofía de Immanuel Kant, donde se utilizó para caracterizar cosas que existen independientemente de la conciencia y actúan sobre nuestros sentidos, sin dejar de ser fundamentalmente incognoscibles, tanto en la práctica como en la teoría. Lo opuesto a la trascendencia es: significa la inalienabilidad, la conexión interna de alguna cualidad de un objeto con el objeto mismo, o la cognoscibilidad del objeto a través de la experiencia personal. Por ejemplo, si asumimos que el Universo fue creado según algún plan superior, el plan en sí es trascendental para nosotros; sólo podemos construir hipótesis al respecto. Pero si este plan existe en realidad, sus consecuencias son inmanentes para nosotros, manifestándose en las leyes físicas y circunstancias en las que nos encontramos. Por tanto, en algunos conceptos teológicos, Dios es trascendental y está fuera de la existencia que creó.
Algunas cosas en sí todavía son accesibles al conocimiento a priori: por ejemplo, el espacio y el tiempo, las ideas de Dios, la bondad y la belleza, las categorías lógicas. Es decir, los objetos trascendentales están, en sentido figurado, “preestablecidos por defecto” en nuestra mente.
El concepto de trascendencia también existe en matemáticas: un número trascendental es un número que no se puede calcular mediante álgebra ni expresar algebraicamente (es decir, no puede ser la raíz de un polinomio con coeficientes enteros que no sea idéntico a cero). Estos incluyen, por ejemplo, los números π y e.
Un concepto cercano a "trascendental", pero de diferente significado, es "trascendental". Inicialmente, simplemente denotaba el área de categorías mentales abstractas, y luego fue desarrollado por Kant, cayendo en su propia trampa: resultó imposible construir un sistema filosófico solo sobre datos empíricos, y no reconoció ningún otras fuentes de experiencia además de la empírica. Para salir, el filósofo tuvo que admitir que algunas cosas en sí todavía son accesibles al conocimiento a priori: por ejemplo, el espacio y el tiempo, las ideas de Dios, la bondad y la belleza, las categorías lógicas. Es decir, los objetos trascendentales están, en sentido figurado, "preinstalados por defecto" en nuestra mente, mientras que la información sobre ellos existe por sí sola y no se deriva de nuestra experiencia.
Hay otro concepto relacionado: la trascendencia. En el sentido más amplio de la palabra, significa la transición de la frontera entre dos áreas dispares, especialmente la transición de la esfera de este mundo a la esfera del otro mundo, trascendental. Para simplificar, tomemos un ejemplo de ciencia ficción: un mundo paralelo para una persona común y corriente es un fenómeno trascendental. Pero cuando el héroe se encuentra en este mundo paralelo o de alguna manera es capaz de percibirlo, esto es trascendencia. O un ejemplo más complejo de la filosofía existencial: Jean-Paul Sartre creía que el hombre es trascendental porque va más allá de cualquier experiencia personal posible: podemos estudiarnos a nosotros mismos y al mundo que nos rodea desde diferentes ángulos, pero nunca estaremos siquiera cerca de conocerlo plenamente. nosotros mismos. Pero al mismo tiempo, una persona tiene la capacidad de trascender: trasciende cualquier cosa, dándole algún significado. La trascendencia es un elemento importante en la religión: ayuda a la persona a liberarse de su naturaleza material y tocar algo más allá.
De la filosofía, el concepto de trascendentalidad migró a la psicología: el psicólogo suizo Carl Jung introdujo el concepto de "función trascendental", una función que une el consciente y el inconsciente. En particular, un psicoanalista puede realizar una función trascendental: ayuda al paciente a analizar imágenes del inconsciente (por ejemplo, sueños) y a vincularlas con los procesos conscientes de su psique.
Cómo decir
Incorrecto "Me inscribí en una clase de meditación trascendental". Así es, "trascendental".
Correcto “Cuando entro en un templo, experimento una sensación de fusionarme con algo trascendental”.
Correctamente “El arte trasciende los objetos familiares del mundo material, llenándolos de un significado superior”.
Ejemplos
Historia
El concepto de número trascendental fue introducido por primera vez por J. Liouville en 1844, cuando demostró el teorema de que un número algebraico no puede aproximarse demasiado bien mediante una fracción racional.
|heading3= Herramientas de extensión
sistemas numéricos |encabezado4= Jerarquía de números |lista4=
|
|||||||||||||
| Números complejos | |||||||||||||
Extracto que caracteriza el número trascendental.
– ¿Cómo puedes estar sano... cuando sufres moralmente? ¿Es posible mantener la calma en nuestra época cuando una persona tiene sentimientos? - dijo Anna Pávlovna. – ¿Estarás conmigo toda la noche, espero?– ¿Qué pasa con las vacaciones del enviado inglés? Es Miercoles. "Necesito mostrarme allí", dijo el príncipe. "Mi hija me recogerá y me llevará".
– Pensé que las vacaciones actuales fueron canceladas. Je vous avoue que toutes ces fetes et tous ces feux d "artifice start a devenir insipides. [Lo confieso, todas estas fiestas y fuegos artificiales se están volviendo insoportables.]
“Si supieran que querías esto, cancelarían las vacaciones”, dijo el príncipe, por costumbre, como un reloj al que se le da cuerda, diciendo cosas que no quería que le creyeran.
- Ne me tourmentez pas. Eh bien, qu"a t on decide par rapport a la depeche de Novosiizoff? Vous savez tout. [No me atormentes. Bueno, ¿qué decidiste con motivo del envío de Novosiltsov? Lo sabes todo.]
- ¿Cómo puedo decírtelo? - dijo el príncipe en tono frío y aburrido. - ¿Q "a t on decide? On a decide que Buonaparte a brule ses vaisseaux, et je crois que nous sommes en train de bruler les notres. [¿Qué decidieron? Decidieron que Bonaparte quemó sus barcos; y nosotros también, al parecer , están dispuestos a quemar el nuestro.] - El príncipe Vasily siempre hablaba con pereza, como un actor que interpreta el papel de una obra antigua. Anna Pavlovna Sherer, por el contrario, a pesar de sus cuarenta años, estaba llena de animación e impulso.
Ser entusiasta se convirtió en su posición social y, a veces, cuando ni siquiera quería, para no engañar las expectativas de las personas que la conocían, se convertía en entusiasta. La sonrisa comedida que aparecía constantemente en el rostro de Anna Pavlovna, aunque no correspondía con sus rasgos anticuados, expresaba, como niños mimados, una conciencia constante de su querido defecto, que no quiere, no puede y no considera necesario corregir. sí misma.
En medio de una conversación sobre acciones políticas, Anna Pavlovna se acaloró.
– ¡Oh, no me hables de Austria! Quizás no entiendo nada, pero Austria nunca ha querido ni quiere la guerra. Ella nos está traicionando. Sólo Rusia debe ser la salvadora de Europa. Nuestro benefactor conoce su elevada vocación y será fiel a ella. Eso es algo en lo que creo. Nuestro buen y maravilloso soberano tiene el papel más grande del mundo, y es tan virtuoso y bueno que Dios no lo dejará, y cumplirá su llamado de aplastar la hidra de la revolución, que ahora es aún más terrible en la persona. de este asesino y villano. Sólo nosotros debemos expiar la sangre de los justos... ¿En quién podemos confiar, os pregunto?... Inglaterra, con su espíritu comercial, no quiere ni puede comprender toda la altura del alma del emperador Alejandro. Ella se negó a limpiar Malta. Quiere ver, buscar el pensamiento subyacente de nuestras acciones. ¿Qué le dijeron a Novosiltsov?... Nada. No entendieron, no pueden comprender el desinterés de nuestro emperador, que no quiere nada para sí y lo quiere todo para el bien del mundo. ¿Y qué prometieron? Nada. ¡Y lo que prometieron no sucederá! Prusia ya ha declarado que Bonaparte es invencible y que toda Europa no puede hacer nada contra él... Y no creo ni una palabra ni de Hardenberg ni de Gaugwitz. Cette famause neutralite prussienne, ce n"est qu"un piege. [Esta notoria neutralidad de Prusia es sólo una trampa.] Creo en un solo Dios y en el elevado destino de nuestro querido emperador. ¡Él salvará a Europa!... - Se detuvo de repente con una sonrisa burlona ante su ardor.
Considere la secuencia numérica (xn) dada por la fórmula
Demostremos que esta sucesión tiene límite, para ello consideramos la sucesión auxiliar (yn) dada por la fórmula
Demostremos que (yn) es una secuencia numérica decreciente acotada desde abajo (una secuencia numérica (an) se llama secuencia acotada desde abajo si existe un número c tal que la desigualdad se cumple para cualquier entero positivo n). En realidad,
Consideremos el cociente y comparémoslo con la unidad, tenemos:

De aquí, usando la desigualdad de Bernoulli, obtenemos

De este modo,

Ahora demostremos que (yn) está acotado desde abajo, para ello usamos la desigualdad de Bernoulli:
Dado que (yn) es una secuencia numérica decreciente acotada desde abajo, tiene un límite. Y finalmente demostramos la convergencia de la sucesión.

Límite de secuencia
y se llama número e, es decir, número de Euler.
Cálculo aproximado del valor del número e.
En la práctica, cuando se encuentra el número e, por regla general, es necesario conocer su valor aproximado. Si es una variante (una variante generalmente se indica como una variable que toma una determinada secuencia de valores)
aplicando la fórmula binomial obtenemos:

Si fijamos k y, suponiendo n>k, descartamos todos los términos de la última parte después de la (k+1)ésima desigualdad, obtenemos la siguiente desigualdad:
Aumentando n aquí hasta el infinito, vamos al límite, ya que todos los paréntesis tienen un límite de 1, encontramos:
Esta desigualdad es válida para cualquier número natural k. Por lo tanto, tenemos
desde aquí queda claro que
En este caso, dicen que yn es la (n+1)ésima suma parcial de una serie infinita
y la relación límite que acabamos de escribir muestra que e es su suma, y también dicen que el número e se puede expandir en esta serie, es decir
Estimemos el grado de cercanía de yn a e. Para hacer esto, considere la diferencia entre cualquier valor yn+m (donde m=1,2,3,..) después de yn, y yn mismo. Tenemos

Si entre paréntesis reemplazamos todos los factores en los denominadores de las fracciones por n+2, obtenemos la desigualdad:
que sólo se verá reforzado si reemplazamos los corchetes por la suma de una progresión geométrica infinita con denominador
Si mantenemos n sin cambios aquí y m aumentamos hasta el infinito, entonces la variante yn+m tomará una secuencia de valores yn+1, yn+2, yn+2, yn+3,..., yn+m. ,..., obviamente convergiendo a e . Es por eso
y desde
Si usamos y para denotar la relación de diferencias
(obviamente está contenido entre 0 y 1), entonces también podemos escribir
Reemplazando yn aquí con su expresión expandida, llegamos a una fórmula que servirá como fórmula exacta inicial para calcular e:
Descartando el último término "adicional" y reemplazando cada uno de los términos restantes con su aproximación decimal, obtenemos un valor aproximado de e. Si nos proponemos calcular e usando la última fórmula, con una precisión de, por ejemplo , 1/107, entonces, primero, debemos establecer cómo tomar el número n a nuestra disposición para lograr esta precisión. Al calcular secuencialmente los números inversos de factoriales (Apéndice 2), vemos que para n = 10 el término "adicional" de la última fórmula será más estrecho
por lo tanto, descartándolo, obtenemos un error significativamente menor que el límite establecido. Convertimos cada uno de los términos restantes en una fracción decimal, redondeando (para un margen de precisión) al octavo dígito de manera que el error en valor absoluto sea menor que media unidad en el octavo lugar, es decir, menor que 1/2.108 (Apéndice 2). Por tanto, es obvio que la corrección por eliminar el término adicional es inferior a 3/108. Si ahora también tenemos en cuenta las correcciones por redondeo, queda claro que la corrección total al valor aproximado obtenido del número e se encuentra entre los números
De ahí que el propio número e esté contenido entre las fracciones 2.718 28 78 y 2.718 281 86, es decir, podemos decir que e = 2.718 281 80, 000 000 1
Así, usando la fórmula
es posible calcular un valor aproximado de e hasta cualquier signo deseado.
Trascendencia del número e
Al igual que el número p, el número e es trascendental, es decir, no puede ser raíz de ninguna ecuación algebraica con coeficientes racionales, y no hay forma de construir un segmento cuya longitud esté expresada por el número e. Demostremos la trascendencia (irracionalidad) de este número, para ello volvemos a la fórmula ya utilizada anteriormente:
Supongamos que e es igual a una fracción racional.
Entonces para este n se cumple la siguiente igualdad:
(donde 0<и<1).
Multiplicando ambos lados de la última igualdad por n!, reduciendo los denominadores de todas las fracciones excepto la última, obtenemos un número entero a la izquierda y un número entero con una fracción a la derecha.
lo cual es imposible. La contradicción resultante demuestra que el número e es trascendental, es decir, irracional.
4.2. Números algebraicos y trascendentales
Los números reales a veces también se dividen en algebraicos y trascendentales.
Los números algebraicos son números que son raíces de polinomios algebraicos con coeficientes enteros, por ejemplo, 4,. Todos los demás números (no algebraicos) se consideran trascendentales. Dado que cada número racional p/q es la raíz del correspondiente polinomio de primer grado con coeficientes enteros qx -p, entonces todos los números trascendentales son irracionales.
Resaltemos los rasgos característicos de los números considerados (naturales, racionales, reales): modelan sólo una propiedad: la cantidad; son unidimensionales y todos están representados por puntos en una línea recta, llamada eje de coordenadas.
5. Números complejos
5.1. numeros imaginarios
Aún más extraños que los irracionales fueron los números de nueva naturaleza, descubiertos por el científico italiano Cardano en 1545. Demostró que un sistema de ecuaciones que no tiene soluciones en el conjunto de números reales tiene soluciones de la forma,. Sólo necesita aceptar actuar sobre tales expresiones de acuerdo con las reglas del álgebra ordinaria y asumir que · = -.
Cardano calificó tales cantidades de “puramente negativas” e incluso “sofísticamente negativas”, las consideró inútiles y trató de no utilizarlas.
Durante mucho tiempo, estos números se consideraron imposibles, inexistentes, imaginarios. Descartes los llamó imaginarios, Leibniz: "un fenómeno del mundo de las ideas, una entidad ubicada entre el ser y el no ser".
De hecho, con la ayuda de tales números es imposible expresar ni el resultado de medir cualquier cantidad ni el cambio en cualquier cantidad.
En el eje de coordenadas no había lugar para números imaginarios. Sin embargo, los científicos notaron que si tomamos el número real b en la parte positiva del eje de coordenadas y lo multiplicamos por, obtenemos un número imaginario b, ubicado en una ubicación desconocida. Pero si volvemos a multiplicar este número por, obtenemos -b, es decir, el número original, pero en la parte negativa del eje de coordenadas. Entonces, mediante dos multiplicaciones por lanzamos el número b de positivo a negativo, y exactamente en el medio de este lanzamiento el número era imaginario. Así es como encontramos un lugar para números imaginarios en puntos sobre un eje de coordenadas imaginario perpendicular al centro del eje de coordenadas real. Los puntos del plano entre los ejes imaginario y real representan los números encontrados por Cardano, que en la forma general a + b·i contienen los números reales a y el imaginario b·i en un complejo (composición), por eso se llaman números complejos.
Este fue el cuarto nivel de generalización de números.
La técnica de las operaciones con números imaginarios se desarrolló gradualmente. A principios de los siglos XVII y XVII, se construyó una teoría general de las raíces de enésimas potencias, primero a partir de números negativos y luego de cualquier número complejo, basada en la siguiente fórmula del matemático inglés A. Moivre:
Usando esta fórmula, también fue posible derivar fórmulas para los cosenos y senos de múltiples arcos.
Leonhard Euler derivó una fórmula notable en 1748:
que unía la función exponencial con la trigonométrica. Utilizando la fórmula de Euler, fue posible elevar el número e a cualquier potencia compleja. Es interesante, por ejemplo, que... Puede encontrar el sen y el cos de números complejos, calcular los logaritmos de dichos números, etc.
Durante mucho tiempo, incluso los matemáticos consideraron misteriosos los números complejos y los utilizaron sólo para manipulaciones matemáticas. Así, el matemático suizo Bernoulli utilizó números complejos para resolver integrales. Un poco más tarde, aprendieron a expresar soluciones de ecuaciones diferenciales lineales con coeficientes constantes utilizando números imaginarios. Estas ecuaciones se encuentran, por ejemplo, en la teoría de las oscilaciones de un punto material en un medio resistente.
Grupos de matrices algebraicas
Sistemas de cierre algebraico
Comencemos con el concepto de operación algebraica. Sea A un álgebra universal con un conjunto de operaciones algebraicas U. Cada operación U de U tiene una cierta aridad n, nN(0). Para cualquier número natural n, la operación n-aria u es una aplicación de An a A...
El poder de los números primos
Los números mutuamente primos son números naturales o enteros que no parecen ser iguales al mayor número mayor que 1, o que de otra manera parecen ser iguales a su mayor igual a 1. Por lo tanto, 2 y 3 son intercambiables. Es muy simple, pero 2 y 4 no son (divididos por 2)...
Grafos y sus funciones.
Consideremos operaciones algebraicas básicas sobre funciones y sus gráficas, como suma y resta (y = f(x) ±g(x)), multiplicación (y = f(x) g(x)), división (y = f( x)/g(x)). Al construir este tipo de gráfico, debes considerar...
Números complejos: su pasado y presente
Matemáticas en la Edad Media
Una condición necesaria para aplicar el método fan cheng a sistemas de ecuaciones fue la introducción de números negativos. Por ejemplo, al resolver un sistema, obtenemos una tabla. Siguiente paso: restar los elementos de la tercera columna de la derecha de los elementos de la primera...
Numerología
Pitágoras consideraba que los números no eran simplemente sustitutos abstractos de las cosas reales, sino entidades vivientes que reflejaban las propiedades del espacio, la energía o la vibración del sonido. La principal ciencia de los números, la aritmética...
Numerología
Cuenta la leyenda que los números armónicos, cuya proporción da origen a la música de las esferas, fueron descubiertos por Pitágoras. Flammarion relata esta leyenda de la siguiente manera: “Dicen que al pasar por una fragua, escuchó el sonido de martillos...
Aplicación práctica de fórmulas de cuadratura con pesas de Chebyshev-Hermite
Dejemos que se especifique una función de peso uniforme en todo el eje. (1.1) Derivando esta función sucesivamente, encontramos (1.2) Es fácil demostrar por inducción que la derivada de orden n de la función (1.1) es el producto de esta función por algún polinomio de grado n...
Introduzcamos un nuevo número no válido cuyo cuadrado sea -1. Denotamos este número con el símbolo I y lo llamamos unidad imaginaria. Entonces, (2.1) Entonces. (2.2) 1. Forma algebraica de un número complejo Si, entonces el número (2.3) se llama número complejo...
Secuencias numéricas definidas de forma recurrente.
Al resolver muchos problemas, a menudo hay que lidiar con secuencias dadas de forma recurrente, pero, a diferencia de la secuencia de Fibonacci, no siempre es posible obtener su tarea analítica...
Ecuaciones trascendentales con parámetros y métodos para sus soluciones.
Una ecuación trascendental es una ecuación que contiene funciones trascendentales (irracionales, logarítmicas, exponenciales, trigonométricas y trigonométricas inversas) de una incógnita (variable), por ejemplo la ecuación...
Números asombrosos
Hace mucho tiempo, cuando se ayudaban a contar con guijarros, la gente prestaba atención a las figuras correctas que se podían hacer con los guijarros. Simplemente puedes poner los guijarros en una fila: uno, dos, tres. Si los pones en dos filas para hacer rectángulos...
Números asombrosos
A veces, los números perfectos se consideran un caso especial de números amigables: cada número perfecto es amigable consigo mismo. Nicómaco de Geras, un famoso filósofo y matemático, escribió: "Los números perfectos son hermosos. Pero se sabe...
Propiedades fractales de los procesos sociales.
Los fractales geométricos son figuras estáticas. Este enfoque es bastante aceptable, siempre y cuando no sea necesario considerar fenómenos naturales como corrientes de agua que caen, remolinos turbulentos de humo...
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0

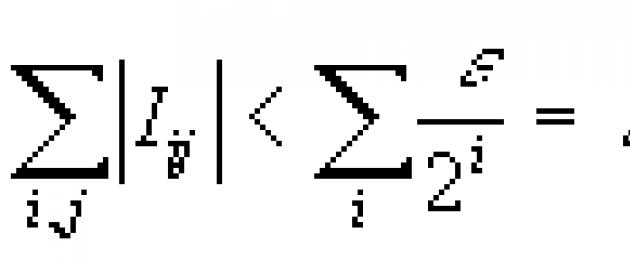
 y ½ En Ѕ
< e
при всех norte. Demostrar que la familia de todos los conjuntos es cero. s-la medida dimensional de Hausdorff forma un s -ideal; en s=1 coincide con la clase de conjuntos nulos, y para 0< s <1 является его
собственным подклассом.
y ½ En Ѕ
< e
при всех norte. Demostrar que la familia de todos los conjuntos es cero. s-la medida dimensional de Hausdorff forma un s -ideal; en s=1 coincide con la clase de conjuntos nulos, y para 0< s <1 является его
собственным подклассом.





