Պարզ ասած՝ դրանք ջրի մեջ եփած բանջարեղեն են՝ հատուկ բաղադրատոմսով։ Կդիտարկեմ երկու նախնական բաղադրիչ (բուսական աղցան և ջուր) և պատրաստի արդյունքը՝ բորշը։ Երկրաչափորեն այն կարելի է պատկերացնել որպես ուղղանկյուն, որի մի կողմը ներկայացնում է գազար, իսկ մյուս կողմը ներկայացնում է ջուր։ Այս երկու կողմերի գումարը ցույց կտա բորշը։ Նման «բորշի» ուղղանկյունի անկյունագիծը և մակերեսը զուտ մաթեմատիկական հասկացություններ են և երբեք չեն օգտագործվում բորշի բաղադրատոմսերում:
Ինչպե՞ս են հազարն ու ջուրը մաթեմատիկական տեսանկյունից բորշի վերածվում։ Ինչպե՞ս կարող է երկու ուղիղ հատվածների գումարը դառնալ եռանկյունաչափություն: Սա հասկանալու համար մեզ անհրաժեշտ են գծային անկյունային ֆունկցիաներ։
Մաթեմատիկայի դասագրքերում գծային անկյունային ֆունկցիաների մասին ոչինչ չես գտնի։ Բայց առանց դրանց մաթեմատիկա չի կարող լինել։ Մաթեմատիկայի օրենքները, ինչպես բնության օրենքները, գործում են՝ անկախ նրանից մենք գիտենք դրանց գոյության մասին, թե ոչ։
Գծային անկյունային ֆունկցիաները գումարման օրենքներ են։Տեսեք, թե ինչպես է հանրահաշիվը վերածվում երկրաչափության, իսկ երկրաչափությունը՝ եռանկյունաչափության:
Հնարավո՞ր է անել առանց գծային անկյունային ֆունկցիաների: Դա հնարավոր է, քանի որ մաթեմատիկոսները դեռ կարողանում են առանց նրանց: Մաթեմատիկոսների հնարքն այն է, որ նրանք մեզ միշտ ասում են միայն այն խնդիրների մասին, որոնք իրենք գիտեն լուծել, և երբեք չեն խոսում այն խնդիրների մասին, որոնք իրենք չեն կարող լուծել։ Նայել։ Եթե գիտենք գումարման և մեկ անդամի արդյունքը, ապա մյուս անդամը գտնելու համար օգտագործում ենք հանում: Բոլորը. Մենք այլ խնդիրներ չգիտենք և չգիտենք ինչպես լուծել դրանք։ Ի՞նչ պետք է անենք, եթե գիտենք միայն գումարման արդյունքը և չգիտենք երկու տերմինները: Այս դեպքում ավելացման արդյունքը պետք է տարրալուծվի երկու տերմինի` օգտագործելով գծային անկյունային ֆունկցիաներ: Հաջորդը, մենք ինքներս ենք ընտրում, թե ինչ կարող է լինել մեկ տերմինը, և գծային անկյունային ֆունկցիաները ցույց են տալիս, թե ինչ պետք է լինի երկրորդ անդամը, որպեսզի գումարման արդյունքը լինի հենց այն, ինչ մեզ անհրաժեշտ է: Նման զույգ տերմինների թիվը կարող է լինել անսահման թվով։ IN Առօրյա կյանքՄենք կարող ենք լավ անել, առանց գումարը քայքայելու, մեզ համար բավարար է: Բայց երբ գիտական հետազոտությունբնության օրենքները, գումարի կազմալուծումը նրա բաղադրիչների կարող է շատ օգտակար լինել:
Գումարի մեկ այլ օրենք, որի մասին մաթեմատիկոսները չեն սիրում խոսել (նրանց մեկ այլ հնարք) պահանջում է, որ տերմիններն ունենան նույն չափման միավորները։ Աղցանի, ջրի և բորշի համար դրանք կարող են լինել քաշի, ծավալի, արժեքի կամ չափման միավոր:
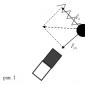
Նկարը ցույց է տալիս մաթեմատիկական տարբերության երկու մակարդակ: Առաջին մակարդակը թվերի դաշտի տարբերություններն են, որոնք նշված են ա, բ, գ. Ահա թե ինչ են անում մաթեմատիկոսները։ Երկրորդ մակարդակը չափման միավորների դաշտի տարբերություններն են, որոնք ցույց են տրված քառակուսի փակագծերում և նշված են տառով. U. Ահա թե ինչ են անում ֆիզիկոսները։ Մենք կարող ենք հասկանալ երրորդ մակարդակը՝ նկարագրվող օբյեկտների տարածքի տարբերությունները: Տարբեր առարկաներ կարող են ունենալ նույն թվով չափման միավորներ: Որքան կարևոր է սա, մենք կարող ենք տեսնել բորշի եռանկյունաչափության օրինակով: Եթե տարբեր օբյեկտների համար միևնույն միավորի նշանակմանը բաժանորդագրություններ ավելացնենք, կարող ենք հստակ ասել, թե ինչ մաթեմատիկական մեծություն է նկարագրում որոշակի առարկա և ինչպես է այն փոխվում ժամանակի ընթացքում կամ մեր գործողությունների պատճառով: Նամակ ՎՋուր կնշանակեմ նամակով ՍԵս կնշանակեմ աղցանը նամակով Բ- բորշ. Ահա թե ինչպիսի տեսք կունենան բորշի գծային անկյունային ֆունկցիաները:
Եթե վերցնենք ջրի մի մասը և աղցանի մի մասը, դրանք միասին կվերածվեն բորշի մեկ բաժին։ Այստեղ ես առաջարկում եմ ձեզ մի փոքր ընդմիջել բորշչից և հիշել ձեր հեռավոր մանկությունը։ Հիշո՞ւմ եք, թե ինչպես մեզ սովորեցրին նապաստակներն ու բադերը միասին հավաքել: Պետք էր գտնել, թե քանի կենդանի կլինի։ Ի՞նչ էին մեզ սովորեցնում անել այն ժամանակ: Մեզ սովորեցրել են առանձնացնել չափման միավորները թվերից և գումարել թվերը: Այո, ցանկացած թիվ կարելի է ավելացնել ցանկացած այլ թվի: Սա ուղիղ ճանապարհ է դեպի ժամանակակից մաթեմատիկայի աուտիզմ. մենք դա անում ենք անհասկանալի, ինչ, անհասկանալի ինչու, և շատ վատ ենք հասկանում, թե ինչպես է դա առնչվում իրականությանը, քանի որ երեք մակարդակների տարբերության պատճառով մաթեմատիկոսները գործում են միայն մեկով: Ավելի ճիշտ կլինի սովորել, թե ինչպես անցնել չափման մեկ միավորից մյուսը:
Նապաստակները, բադերը և փոքրիկ կենդանիները կարելի է կտոր-կտոր հաշվել։ Տարբեր առարկաների չափման մեկ ընդհանուր միավորը թույլ է տալիս դրանք միասին ավելացնել: Սա խնդրի մանկական տարբերակն է։ Դիտարկենք նմանատիպ խնդիր մեծահասակների համար: Ի՞նչ եք ստանում, երբ ավելացնում եք նապաստակներ և գումար: Այստեղ երկու հնարավոր լուծում կա.
Առաջին տարբերակ. Մենք որոշում ենք նապաստակների շուկայական արժեքը և ավելացնում այն առկա գումարին: Մենք ստացել ենք մեր հարստության ընդհանուր արժեքը դրամական արտահայտությամբ։
Երկրորդ տարբերակ. Դուք կարող եք ավելացնել նապաստակների թիվը մեր ունեցած թղթադրամների թվին: Քանակը կստանանք շարժական գույքկտորներով։
Ինչպես տեսնում եք, ավելացման նույն օրենքը թույլ է տալիս ստանալ տարբեր արդյունքներ: Ամեն ինչ կախված է նրանից, թե կոնկրետ ինչ ենք ուզում իմանալ։
Բայց վերադառնանք մեր բորշչին։ Այժմ մենք կարող ենք տեսնել, թե ինչ կլինի գծային անկյունային ֆունկցիաների տարբեր անկյունային արժեքների համար:
Անկյունը զրո է։ Մենք աղցան ունենք, բայց ջուր չունենք: Մենք չենք կարող բորշ պատրաստել: Բորշի քանակը նույնպես զրո է։ Սա ամենևին չի նշանակում, որ զրո բորշը հավասար է զրոյական ջրի։ Զրոյական աղցանով բորշը կարող է լինել զրո (աջ անկյուն):
Անձամբ ինձ համար սա հիմնական մաթեմատիկական ապացույցն է այն բանի, որ . Զրոն չի փոխում թիվը, երբ ավելացվում է: Դա տեղի է ունենում, քանի որ ինքնին ավելացումն անհնար է, եթե կա միայն մեկ տերմին, իսկ երկրորդը բացակայում է: Դուք կարող եք զգալ այս մասին, ինչպես ցանկանում եք, բայց հիշեք, որ զրոյով բոլոր մաթեմատիկական գործողությունները հորինվել են հենց մաթեմատիկոսների կողմից, այնպես որ մի կողմ նետեք ձեր տրամաբանությունը և հիմարաբար խցկեք մաթեմատիկոսների հորինած սահմանումները. զրոն հավասար է զրոյի», «զրո կետից այն կողմ» և այլ անհեթեթություններ: Բավական է մեկ անգամ հիշել, որ զրոն թիվ չէ, և դուք այլևս երբեք հարց չեք ունենա՝ զրոն բնական թիվ է, թե ոչ, քանի որ նման հարցը կորցնում է իմաստը՝ ինչպե՞ս կարելի է թիվ համարել այն, ինչը թիվ չէ։ ? Դա նման է այն հարցին, թե ինչ գույնի պետք է դասակարգվի անտեսանելի գույնը: Թվի վրա զրո ավելացնելը նույնն է, ինչ չկա ներկով ներկելը: Մենք թափահարեցինք չոր վրձինը և բոլորին ասացինք, որ «մենք նկարել ենք»: Բայց ես մի փոքր շեղվում եմ.
Անկյունը զրոյից մեծ է, բայց քառասունհինգ աստիճանից պակաս: Հազար ունենք շատ, բայց ջուրը քիչ է։ Արդյունքում կստանանք հաստ բորշ։
Անկյունը քառասունհինգ աստիճան է։ Մենք ունենք հավասար քանակությամբ ջուր և աղցան։ Սա կատարյալ բորշ է (ներեցեք ինձ, խոհարարներ, դա պարզապես մաթեմատիկա է):
Անկյունը քառասունհինգ աստիճանից մեծ է, բայց իննսուն աստիճանից պակաս։ Մենք շատ ջուր ունենք և քիչ աղցան: Դուք կստանաք հեղուկ բորշ:
Աջ անկյունը։ Մենք ջուր ունենք։ Աղցանից մնում են միայն հիշողություններ, քանի որ մենք շարունակում ենք անկյունը չափել այն գծից, որը ժամանակին նշում էր աղցանը: Մենք չենք կարող բորշ պատրաստել: Բորշի քանակը զրո է։ Այս դեպքում պահեք և ջուր խմեք, քանի դեռ ունեք)))
Այստեղ. Այսպիսի մի բան. Այստեղ ես կարող եմ պատմել այլ պատմություններ, որոնք այստեղ ավելի քան տեղին կլինեն:
Երկու ընկերներ իրենց բաժիններն ունեին ընդհանուր բիզնեսում: Նրանցից մեկին սպանելուց հետո ամեն ինչ գնաց մյուսի վրա։
Մաթեմատիկայի առաջացումը մեր մոլորակի վրա.
Այս բոլոր պատմությունները պատմվում են մաթեմատիկայի լեզվով՝ օգտագործելով գծային անկյունային ֆունկցիաներ։ Ուրիշ ժամանակ ես ձեզ ցույց կտամ այս ֆունկցիաների իրական տեղը մաթեմատիկայի կառուցվածքում։ Միևնույն ժամանակ վերադառնանք բորշի եռանկյունաչափությանը և դիտարկենք կանխատեսումները։
Շաբաթ, 26 հոկտեմբերի, 2019 թ
Չորեքշաբթի, 7 օգոստոսի, 2019 թ
Ավարտելով զրույցը, մենք պետք է հաշվի առնենք անսահման հավաքածու: Բանն այն է, որ «անսահմանություն» հասկացությունն ազդում է մաթեմատիկոսների վրա, ինչպես բոա կոնստրուկտորը` նապաստակի վրա: Անսահմանության դողդոջուն սարսափը զրկում է մաթեմատիկոսներին ողջախոհություն. Ահա մի օրինակ.
Բնօրինակ աղբյուրը գտնվում է. Ալֆան նշանակում է իրական թիվ: Վերոնշյալ արտահայտություններում հավասարության նշանը ցույց է տալիս, որ եթե անսահմանությանը ավելացնեք թիվ կամ անվերջություն, ոչինչ չի փոխվի, արդյունքը կլինի նույն անսահմանությունը: Եթե որպես օրինակ վերցնենք անսահման բազմությունը բնական թվեր, ապա դիտարկված օրինակները կարելի է ներկայացնել հետևյալ կերպ.
Հստակ ապացուցելու համար, որ նրանք իրավացի էին, մաթեմատիկոսները հայտնվեցին բազմաթիվ տարբեր մեթոդներով: Անձամբ ես այս բոլոր մեթոդներին նայում եմ որպես դափերի հետ պարող շամանների։ Ըստ էության, դրանք բոլորն էլ հանգում են նրան, որ կա՛մ սենյակներից մի քանիսը չբնակեցված են, և՛ նոր հյուրեր են ներխուժում, կա՛մ այցելուներից մի քանիսին դուրս են նետում միջանցք՝ հյուրերի համար տեղ բացելու համար (շատ մարդկայնորեն): Նման որոշումների վերաբերյալ իմ տեսակետները հայտնել եմ ձևով ֆանտաստիկ պատմությունՇիկահերի մասին. Ինչի՞ վրա է հիմնված իմ պատճառաբանությունը: Անսահման թվով այցելուների տեղափոխումը անսահման ժամանակ է պահանջում: Այն բանից հետո, երբ մենք ազատեցինք հյուրի համար առաջին սենյակը, այցելուներից մեկը միշտ կքայլի միջանցքով իր սենյակից մյուսը մինչև ժամանակի վերջը: Իհարկե, ժամանակի գործոնը հիմարորեն կարելի է անտեսել, բայց դա կլինի «հիմարների համար օրենք չի գրված» կատեգորիայի մեջ։ Ամեն ինչ կախված է նրանից, թե ինչ ենք մենք անում՝ հարմարեցնել իրականությունը մաթեմատիկական տեսություններին կամ հակառակը:
Ի՞նչ է «անվերջ հյուրանոցը»: Անսահման հյուրանոցը այն հյուրանոցն է, որը միշտ ունի ցանկացած թվով դատարկ մահճակալներ՝ անկախ նրանից, թե քանի սենյակ է զբաղված: Եթե անվերջանալի «այցելու» միջանցքի բոլոր սենյակները զբաղված են, ապա կա եւս մեկ անվերջ միջանցք՝ «հյուրերի» սենյակներով։ Այդպիսի միջանցքներ կլինեն անսահման թվով։ Ավելին, «անսահման հյուրանոցը» ունի անսահման թվով հարկեր անսահման թվով շենքերում անսահման թվով մոլորակների վրա անսահման թվով տիեզերքներում, որոնք ստեղծված են անսահման թվով Աստվածների կողմից: Մաթեմատիկոսները չեն կարողանում հեռու մնալ սովորականից առօրյա խնդիրներԱստված-Ալլահ-Բուդդան միշտ միայն մեկն է, կա միայն մեկ հյուրանոց, կա միայն մեկ միջանցք: Այսպիսով, մաթեմատիկոսները փորձում են նենգափոխել հյուրանոցի համարների սերիական համարները՝ համոզելով մեզ, որ հնարավոր է «խցկել անհնարինը»։
Ես ձեզ ցույց կտամ իմ տրամաբանության տրամաբանությունը՝ օգտագործելով բնական թվերի անսահման բազմության օրինակը: Նախ պետք է պատասխանել մի շատ պարզ հարցի՝ բնական թվերի քանի՞ բազմություն կա՝ մեկ կամ շատ: Այս հարցին ճիշտ պատասխան չկա, քանի որ թվերը մենք ինքներս ենք հորինել բնության մեջ: Այո, բնությունը հիանալի է հաշվում, բայց դրա համար նա օգտագործում է այլ մաթեմատիկական գործիքներ, որոնք մեզ ծանոթ չեն: Ես ձեզ կասեմ, թե ինչ է մտածում բնությունը մեկ այլ անգամ: Քանի որ մենք թվեր ենք հորինել, մենք ինքներս ենք որոշելու, թե բնական թվերի քանի բազմություն կա: Դիտարկենք երկու տարբերակն էլ, ինչպես վայել է իրական գիտնականներին։
Տարբերակ առաջին. «Թող մեզ տրվի» բնական թվերի մի շարք, որը հանգիստ պառկած է դարակի վրա: Այս հավաքածուն վերցնում ենք դարակից։ Վերջ, այլ բնական թվեր չեն մնացել դարակում ու տանելու տեղ։ Մենք չենք կարող ավելացնել մեկը այս հավաքածուին, քանի որ այն արդեն ունենք: Իսկ եթե իսկապես ուզում ես: Ոչ մի խնդիր։ Մենք արդեն վերցրած հավաքածուից կարող ենք վերցնել և վերադարձնել դարակ։ Դրանից հետո մենք կարող ենք դարակից վերցնել և ավելացնել այն, ինչ մնացել է։ Արդյունքում մենք կրկին կստանանք բնական թվերի անսահման բազմություն։ Մեր բոլոր մանիպուլյացիաները կարող եք գրել այսպես.
Ես գրեցի գործողությունները հանրահաշվական և բազմությունների տեսական նշումներով՝ բազմության տարրերի մանրամասն ցուցակով: Ստորագրությունը ցույց է տալիս, որ մենք ունենք բնական թվերի մեկ և միակ հավաքածու: Ստացվում է, որ բնական թվերի բազմությունը կմնա անփոփոխ միայն այն դեպքում, եթե նրանից հանվի մեկը և գումարվի նույն միավորը։
Տարբերակ երկու. Մենք մեր դարակում ունենք բնական թվերի շատ տարբեր անսահման հավաքածուներ: Շեշտում եմ՝ ՏԱՐԲԵՐ, չնայած նրան, որ դրանք գործնականում չեն տարբերվում։ Վերցնենք այս հավաքածուներից մեկը: Այնուհետև բնական թվերի մեկ այլ բազմությունից վերցնում ենք մեկը և ավելացնում արդեն վերցրած բազմությանը։ Մենք նույնիսկ կարող ենք ավելացնել բնական թվերի երկու հավաքածու։ Սա այն է, ինչ մենք ստանում ենք.
«Մեկ» և «երկու» ենթագրերը ցույց են տալիս, որ այդ տարրերը պատկանել են տարբեր խմբերի։ Այո, եթե մեկը ավելացնեք անսահման բազմությանը, արդյունքը նույնպես կլինի անսահման բազմություն, բայց այն նույնը չի լինի, ինչ սկզբնական հավաքածուն: Եթե մեկ անսահման բազմությանն ավելացնեք ևս մեկ անսահման բազմություն, ապա ստացվում է նոր անսահման բազմություն, որը բաղկացած է առաջին երկու բազմությունների տարրերից:
Բնական թվերի բազմությունը հաշվելու համար օգտագործվում է այնպես, ինչպես քանոնը՝ չափելու համար։ Հիմա պատկերացրեք, որ դուք մեկ սանտիմետր ավելացրել եք քանոնին։ Սա կլինի այլ տող, որը հավասար չէ բնօրինակին:
Կարող եք ընդունել կամ չընդունել իմ պատճառաբանությունը՝ դա ձեր գործն է։ Բայց եթե երբևէ մաթեմատիկական խնդիրների հանդիպեք, մտածեք, թե արդյոք դուք գնում եք մաթեմատիկոսների սերունդների կողմից տրորված կեղծ դատողությունների ճանապարհով: Չէ՞ որ մաթեմատիկա սովորելը նախ և առաջ մեր մեջ ձևավորում է մտածողության կայուն կարծրատիպ և միայն դրանից հետո ավելացնում մեր մտավոր կարողությունները (կամ հակառակը՝ զրկում ազատ մտածելուց)։
pozg.ru
Կիրակի, 4 օգոստոսի, 2019 թ
Ես ավարտում էի մի հոդվածի հետգրությունը և տեսա այս հրաշալի տեքստը Վիքիպեդիայում.
Կարդում ենք՝ «... հարուստ տեսական հիմքԲաբելոնի մաթեմատիկան չուներ ամբողջական բնույթ և վերածվեց մի շարք տարբեր տեխնիկաների, որոնք զուրկ էին ընդհանուր համակարգից և ապացույցների բազայից»:
Վա՜յ։ Որքան խելացի ենք մենք և որքան լավ ենք տեսնում ուրիշների թերությունները: Արդյո՞ք մեզ համար դժվար է ժամանակակից մաթեմատիկային նայել նույն համատեքստում: Թեթևակի վերափոխելով վերը նշված տեքստը, ես անձամբ ստացա հետևյալը.
Ժամանակակից մաթեմատիկայի հարուստ տեսական հիմքը չունի ամբողջական բնույթ և վերածվում է անհամաչափ հատվածների մի շարքի՝ զուրկ ընդհանուր համակարգից և ապացույցների բազայից:
Ես հեռու չեմ գնա իմ խոսքերը հաստատելու համար. այն ունի լեզու և պայմանականություններ, որոնք տարբերվում են մաթեմատիկայի շատ այլ ճյուղերի լեզվից և պայմանականություններից: Մաթեմատիկայի տարբեր ճյուղերում նույն անունները կարող են տարբեր նշանակություն ունենալ։ Ուզում եմ հրապարակումների մի ամբողջ շարք նվիրել ժամանակակից մաթեմատիկայի ամենաակնառու սխալներին։ Կհանդիպենք շուտով:
Շաբաթ, 3 օգոստոսի, 2019 թ
Ինչպե՞ս բազմությունը բաժանել ենթաբազմությունների: Դա անելու համար հարկավոր է մուտքագրել նոր չափման միավոր, որն առկա է ընտրված հավաքածուի որոշ տարրերում: Դիտարկենք մի օրինակ։
Թող որ մենք շատ լինենք Աբաղկացած չորս հոգուց. Այս հավաքածուն ձևավորվում է «մարդկանց» հիման վրա: Եկեք նշենք այս հավաքածուի տարրերը տառով Ա, համարով բաժանորդը ցույց կտա այս հավաքածուի յուրաքանչյուր անձի սերիական համարը: Ներկայացնենք չափման նոր միավոր «գենդեր» և այն նշանակենք տառով բ. Քանի որ սեռական հատկանիշները բնորոշ են բոլոր մարդկանց, մենք բազմապատկում ենք հավաքածուի յուրաքանչյուր տարր Աելնելով սեռից բ. Ուշադրություն դարձրեք, որ մեր «մարդկանց» խումբն այժմ դարձել է «գենդերային հատկանիշներ ունեցող մարդկանց» խումբ։ Սրանից հետո սեռական հատկանիշները կարող ենք բաժանել արականի bmև կանացի bwսեռական հատկանիշներ. Այժմ մենք կարող ենք կիրառել մաթեմատիկական ֆիլտր. մենք ընտրում ենք այս սեռական հատկանիշներից մեկը, անկախ նրանից, թե որ մեկը՝ արական, թե իգական: Եթե մարդն ունի, ուրեմն բազմապատկում ենք մեկով, եթե նման նշան չկա՝ բազմապատկում ենք զրոյով։ Եվ հետո մենք օգտագործում ենք սովորական դպրոցական մաթեմատիկա: Տեսեք, թե ինչ է տեղի ունեցել.
Բազմապատկելուց, կրճատելուց և վերադասավորվելուց հետո մենք հայտնվեցինք երկու ենթաբազմության մեջ՝ տղամարդկանց ենթաբազմություն Բմև կանանց ենթաբազմություն Bw. Մաթեմատիկոսները մոտավորապես նույն կերպ են մտածում, երբ կիրառում են բազմությունների տեսությունը գործնականում: Բայց նրանք մեզ մանրամասներ չեն ասում, այլ տալիս են մեզ վերջնական արդյունքը. «շատ մարդիկ բաղկացած են տղամարդկանց և կանանց ենթաբազմությունից»: Բնականաբար, ձեզ մոտ կարող է հարց առաջանալ՝ որքանո՞վ է ճիշտ կիրառվել մաթեմատիկան վերը նշված վերափոխումների մեջ: Համարձակվում եմ ձեզ վստահեցնել, որ ըստ էության ամեն ինչ ճիշտ է արվել, բավական է իմանալ թվաբանության, բուլյան հանրահաշվի և մաթեմատիկայի այլ ճյուղերի մաթեմատիկական հիմքերը։ Ինչ է դա? Մեկ այլ անգամ ես ձեզ կասեմ այս մասին:
Ինչ վերաբերում է սուպերբազմություններին, ապա դուք կարող եք միավորել երկու բազմություն մեկ սուպերբազմության մեջ՝ ընտրելով այս երկու հավաքածուների տարրերում առկա չափման միավորը:
Ինչպես տեսնում եք, չափման միավորները և սովորական մաթեմատիկան բազմությունների տեսությունը դարձնում են անցյալի մասունք: Նշան է, որ բազմությունների տեսության հետ ամեն ինչ լավ չէ, այն է, որ մաթեմատիկոսները հորինել են իրենց լեզուն և բազմությունների տեսության նշումը: Մաթեմատիկոսները վարվեցին այնպես, ինչպես ժամանակին արեցին շամանները: Միայն շամանները գիտեն, թե ինչպես «ճիշտ» կիրառել իրենց «գիտելիքները»: Նրանք մեզ սովորեցնում են այս «գիտելիքը»:
Եզրափակելով, ես ուզում եմ ձեզ ցույց տալ, թե ինչպես են մաթեմատիկոսները շահարկում:
Երկուշաբթի, 7 հունվարի, 2019 թ
Ք.ա. հինգերորդ դարում հին հույն փիլիսոփա Զենոն Էլեյացին ձևակերպեց իր հայտնի ապորիաները, որոնցից ամենահայտնին «Աքիլես և կրիա» ապորիան է։ Ահա թե ինչ է այն հնչում.
Ենթադրենք, Աքիլլեսը վազում է տաս անգամ ավելի արագ, քան կրիան և հազար քայլ հետ է մնում նրանից։ Այն ժամանակահատվածում, ինչ Աքիլլեսին կպահանջվի այս տարածությունը վազելու համար, կրիան հարյուր քայլ կսողա նույն ուղղությամբ։ Երբ Աքիլեսը վազում է հարյուր քայլ, կրիան սողում է ևս տասը քայլ և այլն։ Գործընթացը կշարունակվի անվերջ, Աքիլլեսը երբեք չի հասնի կրիային:
Այս պատճառաբանությունը տրամաբանական ցնցում դարձավ հետագա բոլոր սերունդների համար։ Արիստոտելը, Դիոգենեսը, Կանտը, Հեգելը, Հիլբերտը... Նրանք բոլորն այս կամ այն կերպ դիտարկում էին Զենոնի ապորիան։ Ցնցումն այնքան ուժեղ էր, որ « ...քննարկումները շարունակվում են մինչ օրս գիտական հանրությունը չի կարողացել ընդհանուր կարծիքի գալ պարադոքսների էության շուրջ...ներգրավվել են հարցի ուսումնասիրության մեջ. մաթեմատիկական վերլուծություն, բազմությունների տեսություն, նոր ֆիզիկական և փիլիսոփայական մոտեցումներ; դրանցից ոչ մեկը չդարձավ խնդրի ընդհանուր ընդունված լուծում...«[Wikipedia, «Zeno's Aporia». Բոլորը հասկանում են, որ իրենց խաբում են, բայց ոչ ոք չի հասկանում, թե ինչից է բաղկացած խաբեությունը։
Մաթեմատիկական տեսանկյունից Զենոնն իր ապորիայում հստակ ցույց տվեց անցումը քանակից դեպի ։ Այս անցումը ենթադրում է կիրառություն մշտականի փոխարեն։ Որքան հասկանում եմ, չափման փոփոխական միավորների օգտագործման մաթեմատիկական ապարատը կամ դեռ չի մշակվել, կամ չի կիրառվել Զենոնի ապորիայի վրա։ Մեր սովորական տրամաբանության կիրառումը մեզ տանում է ծուղակի մեջ: Մենք, մտածողության իներցիայի շնորհիվ, փոխադարձ արժեքին կիրառում ենք ժամանակի հաստատուն միավորներ։ Ֆիզիկական տեսանկյունից սա կարծես թե ժամանակն է դանդաղում, մինչև այն ամբողջովին դադարի այն պահին, երբ Աքիլլեսը կհասնի կրիային: Եթե ժամանակը կանգ առնի, Աքիլլեսն այլևս չի կարող շրջանցել կրիային:
Եթե շրջենք մեր սովորական տրամաբանությունը, ամեն ինչ իր տեղը կընկնի։ Աքիլլեսը վազում է հաստատուն արագությամբ։ Նրա ճանապարհի յուրաքանչյուր հաջորդ հատվածը տասն անգամ ավելի կարճ է, քան նախորդը: Ըստ այդմ, դրա հաղթահարման վրա ծախսված ժամանակը նախորդից տասն անգամ պակաս է։ Եթե այս իրավիճակում կիրառենք «անսահմանություն» հասկացությունը, ապա ճիշտ կլինի ասել՝ «Աքիլլեսը անսահման արագ կհասնի կրիային»։
Ինչպե՞ս խուսափել այս տրամաբանական թակարդից։ Մնացեք ժամանակի մշտական միավորների մեջ և մի անցեք փոխադարձ միավորների: Զենոնի լեզվով դա հետևյալն է.
Այն ժամանակ, ինչ Աքիլլեսին կպահանջվի հազար քայլ վազելու համար, կրիան հարյուր քայլ կսողա նույն ուղղությամբ։ Առաջինին հավասար հաջորդ ժամանակամիջոցում Աքիլլեսը կվազի ևս հազար քայլ, իսկ կրիան կսողա հարյուր քայլ: Այժմ Աքիլլեսը ութ հարյուր քայլ առաջ է կրիայից։
Այս մոտեցումը ադեկվատ կերպով նկարագրում է իրականությունը՝ առանց որևէ տրամաբանական պարադոքսների։ Բայց սա խնդրի ամբողջական լուծում չէ։ Էյնշտեյնի հայտարարությունը լույսի արագության անդիմադրելիության մասին շատ նման է Զենոնի «Աքիլլեսը և կրիան» ապորիային։ Մենք դեռ պետք է ուսումնասիրենք, վերանայենք ու լուծենք այս խնդիրը։ Եվ լուծումը չպետք է անվերջ փնտրել մեծ թվեր, բայց չափման միավորներով։
Զենոնի մեկ այլ հետաքրքիր ապորիա պատմում է թռչող նետի մասին.
Թռչող նետը անշարժ է, քանի որ ժամանակի յուրաքանչյուր պահին այն հանգստի վիճակում է, և քանի որ այն հանգստանում է ժամանակի յուրաքանչյուր պահի, այն միշտ հանգստանում է:
Այս ապորիայում տրամաբանական պարադոքսը հաղթահարվում է շատ պարզ. բավական է պարզաբանել, որ ժամանակի յուրաքանչյուր պահին թռչող սլաքը հանգստանում է տարածության տարբեր կետերում, ինչը, ըստ էության, շարժում է: Այստեղ հարկ է նշել ևս մեկ կետ. Ճանապարհին մեքենայի մեկ լուսանկարից անհնար է որոշել ոչ նրա շարժման փաստը, ոչ էլ հեռավորությունը: Որոշելու համար, թե արդյոք մեքենան շարժվում է, ձեզ անհրաժեշտ է երկու լուսանկար՝ արված նույն կետից ժամանակի տարբեր կետերում, բայց դուք չեք կարող որոշել դրանցից հեռավորությունը: Ավտոմեքենայի հեռավորությունը որոշելու համար անհրաժեշտ է ժամանակի մեկ կետում տարածության տարբեր կետերից արված երկու լուսանկար, բայց դրանցից դուք չեք կարող որոշել շարժման փաստը (իհարկե, հաշվարկների համար դեռ լրացուցիչ տվյալներ են պետք, եռանկյունաչափությունը կօգնի ձեզ ) Այն, ինչի վրա ուզում եմ հատուկ ուշադրություն հրավիրել, այն է, որ ժամանակի երկու կետը և տարածության երկու կետը տարբեր բաներ են, որոնք չպետք է շփոթել, քանի որ դրանք տարբեր հնարավորություններ են տալիս հետազոտության համար:
Ես ձեզ ցույց կտամ գործընթացը օրինակով: Մենք ընտրում ենք «կարմիր պինդ պզուկը»՝ սա մեր «ամբողջությունն է»: Միևնույն ժամանակ մենք տեսնում ենք, որ այս բաները աղեղով են, և կան առանց աղեղի։ Դրանից հետո մենք ընտրում ենք «ամբողջության» մի մասը և կազմում «աղեղով»: Ահա թե ինչպես են շամանները ստանում իրենց սնունդը՝ կապելով իրենց հավաքածուների տեսությունը իրականության հետ:
Հիմա եկեք մի փոքր հնարք անենք: Վերցնենք «պինդ պզուկով աղեղով» և միավորենք այս «ամբողջությունները» ըստ գույնի՝ ընտրելով կարմիր տարրերը։ Մենք շատ «կարմիր» ստացանք։ Հիմա վերջնական հարցը. ստացված սեթերը «աղեղով» և «կարմիր» նույն հավաքածուն են, թե՞ երկու տարբեր սեթ: Պատասխանը գիտեն միայն շամանները։ Ավելի ճիշտ՝ իրենք իրենք ոչինչ չգիտեն, բայց ինչպես ասում են՝ այդպես էլ կլինի։
Այս պարզ օրինակը ցույց է տալիս, որ բազմությունների տեսությունը լիովին անօգուտ է, երբ խոսքը վերաբերում է իրականությանը: Ո՞րն է գաղտնիքը: Մենք ձևավորեցինք մի շարք «կարմիր պինդ բշտիկով և աղեղով»: Ձևավորումը տեղի է ունեցել չորս տարբեր չափման միավորներով՝ գույն (կարմիր), ամրություն (պինդ), կոպտություն (կռուտիտ), զարդարանք (աղեղով): Միայն չափման միավորների հավաքածուն թույլ է տալիս ադեկվատ կերպով նկարագրել իրական առարկաները մաթեմատիկայի լեզվով. Ահա թե ինչ տեսք ունի.
Տարբեր ինդեքսներով «ա» տառը նշանակում է տարբեր չափման միավորներ։ Չափման միավորները, որոնցով նախնական փուլում տարբերվում է «ամբողջը», ընդգծված են փակագծերում։ Չափման միավորը, որով կազմվում է հավաքածուն, հանվում է փակագծերից։ Վերջին տողը ցույց է տալիս վերջնական արդյունքը` հավաքածուի տարրը: Ինչպես տեսնում եք, եթե մենք օգտագործում ենք չափման միավորներ հավաքածու կազմելու համար, ապա արդյունքը կախված չէ մեր գործողությունների հերթականությունից: Եվ սա մաթեմատիկա է, և ոչ թե շամանների պարը դափերով։ Շամանները կարող են «ինտուիտիվորեն» հանգել նույն արդյունքին՝ պնդելով, որ դա «ակնհայտ է», քանի որ չափման միավորները նրանց «գիտական» զինանոցի մաս չեն կազմում։
Օգտագործելով չափման միավորները, շատ հեշտ է բաժանել մեկ հավաքածու կամ միավորել մի քանի հավաքածուներ մեկ սուպերսեթի մեջ: Եկեք մանրամասն նայենք այս գործընթացի հանրահաշիվին:
ԵՌԱՆԻՉԱԿԱՆ ՖՈՒՆԿՑԻԱՆԵՐԻ ԱՐԺԵՔՆԵՐԻ ՍԵՂԱՆԱԿ
Արժեքների աղյուսակ եռանկյունաչափական ֆունկցիաներկազմված է 0, 30, 45, 60, 90, 180, 270 և 360 աստիճանի անկյունների և դրանց համապատասխան անկյան արժեքների համար՝ վրադյաններով։ Եռանկյունաչափական ֆունկցիաներից աղյուսակում ներկայացված են սինուսը, կոսինուսը, տանգենսը, կոտանգենսը, սեկանտը և կոսեկանտը: Լուծման հարմարության համար դպրոցի օրինակներԱղյուսակում եռանկյունաչափական ֆունկցիաների արժեքները գրված են կոտորակի տեսքով՝ պահպանելով թվերի քառակուսի արմատը հանելու նշանները, ինչը շատ հաճախ օգնում է նվազեցնել բարդ մաթեմատիկական արտահայտությունները: Շոշափողի և կոտանգենսի համար որոշ անկյունների արժեքներ չեն կարող որոշվել: Նման անկյունների շոշափողի և կոտանգենսի արժեքների համար եռանկյունաչափական ֆունկցիաների արժեքների աղյուսակում կա գծիկ: Ընդհանրապես ընդունված է, որ նման անկյունների շոշափողն ու կոտանգենսը հավասար է անսահմանության։ Առանձին էջում կան եռանկյունաչափական ֆունկցիաների կրճատման բանաձեւեր։
Եռանկյունաչափական սինուսի ֆունկցիայի արժեքների աղյուսակը ցույց է տալիս հետևյալ անկյունների արժեքները՝ sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 աստիճաններով, որը համապատասխանում է sin 0 pi, sin pi/6, sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi անկյունների ռադիանի չափով: Սինուսների դպրոցական աղյուսակ.
Եռանկյունաչափական կոսինուս ֆունկցիայի համար աղյուսակը ցույց է տալիս արժեքները հետևյալ անկյունների համար՝ cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 աստիճաններով, որը համապատասխանում է cos 0 pi-ին։ , cos pi 6-ով, cos pi-ով 4-ով, cos pi-ով 3-ով, cos pi-ով 2-ով, cos pi-ով, cos 3 pi-ով 2-ով, cos 2-ով անկյունների ռադիանի չափով: Կոսինուսների դպրոցական աղյուսակ.
Եռանկյունաչափական շոշափող ֆունկցիայի եռանկյունաչափական աղյուսակը տալիս է արժեքներ հետևյալ անկյունների համար՝ tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 աստիճանով, որը համապատասխանում է tg 0 pi, tg pi/6, tg pi/4, tg pi/3, tg pi, tg 2 pi անկյունների ռադիանի չափով: Եռանկյունաչափական շոշափող ֆունկցիաների հետևյալ արժեքները սահմանված չեն tan 90, tan 270, tan pi/2, tan 3 pi/2 և համարվում են անսահմանության հավասար:
Եռանկյունաչափական ֆունկցիայի կոտանգենսի համար եռանկյունաչափական աղյուսակում տրված են հետևյալ անկյունների արժեքները. , ctg pi/3, tg pi/ 2, tan 3 pi/2 անկյունների ռադիանի չափով։ Եռանկյունաչափական կոտանգենս ֆունկցիաների հետևյալ արժեքները սահմանված չեն ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi և համարվում են անսահմանության հավասար:
Եռանկյունաչափական ֆունկցիաների secant և cosecant արժեքները տրված են նույն անկյունների համար աստիճաններով և ռադիաններով, ինչպես սինուսը, կոսինուսը, շոշափողը, կոտանգենսը:

Ոչ ստանդարտ անկյունների եռանկյունաչափական ֆունկցիաների արժեքների աղյուսակը ցույց է տալիս սինուսի, կոսինուսի, շոշափողի և կոտանգենսի արժեքները 15, 18, 22,5, 36, 54, 67,5 72 աստիճաններով և ռադիաններով pi/12: , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 ռադիան։ Եռանկյունաչափական ֆունկցիաների արժեքներն արտահայտվում են կոտորակներով և քառակուսի արմատներով՝ դպրոցական օրինակներում կոտորակների կրճատումը հեշտացնելու համար:

Եվս երեք եռանկյունաչափական հրեշներ: Առաջինը 1,5 մեկուկես աստիճանի շոշափողն է կամ pi-ի բաժանված 120-ի: Երկրորդը pi-ի կոսինուսն է՝ բաժանված 240-ի, pi/240: Ամենաերկարը pi-ի կոսինուսն է՝ բաժանված 17-ի, pi/17:

Սինուսի և կոսինուսի ֆունկցիաների արժեքների եռանկյունաչափական շրջանակը տեսողականորեն ներկայացնում է սինուսի և կոսինուսի նշանները՝ կախված անկյան մեծությունից: Հատկապես շիկահերների համար կոսինուսի արժեքներն ընդգծված են կանաչ գծիկով՝ շփոթությունը նվազեցնելու համար: Աստիճանների փոխարկումը ռադիանների նույնպես շատ պարզ է ներկայացված, երբ ռադիաններն արտահայտվում են pi-ով:

Սա եռանկյունաչափական աղյուսակներկայացնում է սինուսի, կոսինուսի, շոշափողի և կոտանգենսի արժեքները 0 զրոյից մինչև 90 իննսուն աստիճան անկյունների համար մեկ աստիճանի ընդմիջումներով: Առաջին քառասունհինգ աստիճանի համար եռանկյունաչափական ֆունկցիաների անվանումները պետք է դիտարկվեն աղյուսակի վերևում: Առաջին սյունակը պարունակում է աստիճաններ, հաջորդ չորս սյունակներում գրված են սինուսների, կոսինուսների, տանգենսների և կոտանգենսների արժեքները:
Քառասունհինգ աստիճանից մինչև իննսուն աստիճան անկյունների համար եռանկյունաչափական ֆունկցիաների անունները գրված են աղյուսակի ներքևում։ Վերջին սյունակը պարունակում է աստիճաններ, կոսինուսների, սինուսների, կոտանգենսների և տանգենսների արժեքները գրված են նախորդ չորս սյունակներում: Դուք պետք է զգույշ լինեք, քանի որ եռանկյունաչափական աղյուսակի ներքևի եռանկյունաչափական ֆունկցիաների անունները տարբերվում են աղյուսակի վերևի անուններից: Սինուսներն ու կոսինուսները փոխվում են, ինչպես շոշափողն ու կոտանգենսը: Դա պայմանավորված է եռանկյունաչափական ֆունկցիաների արժեքների համաչափությամբ:

Եռանկյունաչափական ֆունկցիաների նշանները ներկայացված են վերևի նկարում: Սինուսը դրական արժեքներ ունի 0-ից մինչև 180 աստիճան կամ 0-ից մինչև pi: Սինուսը բացասական արժեքներ ունի 180-ից մինչև 360 աստիճան կամ pi-ից մինչև 2 pi: Կոսինուսի արժեքները դրական են 0-ից 90 և 270-ից 360 աստիճան կամ 0-ից 1/2 pi և 3/2-ից մինչև 2 pi: Տանգենսը և կոտանգենսը ունեն դրական արժեքներ 0-ից 90 աստիճան և 180-ից 270 աստիճան, որոնք համապատասխանում են 0-ից մինչև 1/2 pi և pi-ից մինչև 3/2 pi արժեքներին: Տանգենսի և կոտանգենսի բացասական արժեքներն են 90-ից մինչև 180 աստիճան և 270-ից մինչև 360 աստիճան կամ 1/2 pi-ից մինչև pi և 3/2 pi-ից մինչև 2 pi: 360 աստիճանից կամ 2 pi-ից ավելի անկյունների համար եռանկյունաչափական ֆունկցիաների նշանները որոշելիս պետք է օգտագործել այդ ֆունկցիաների պարբերականության հատկությունները:
Եռանկյունաչափական ֆունկցիաները սինուսը, տանգենսը և կոտանգենսը կենտ ֆունկցիաներ են: Բացասական անկյունների համար այս ֆունկցիաների արժեքները բացասական կլինեն: Կոսինուսը հավասարաչափ եռանկյունաչափական ֆունկցիա է՝ կոսինուսի արժեքը բացասական անկյունդրական կլինի: Եռանկյունաչափական ֆունկցիաները բազմապատկելիս և բաժանելիս պետք է պահպանվեն նշանների կանոնները:
Եռանկյունաչափական սինուսի ֆունկցիայի արժեքների աղյուսակը ցույց է տալիս հետևյալ անկյունների արժեքները
ՓաստաթուղթԱռանձին էջում կան կրճատման բանաձեւեր եռանկյունաչափականգործառույթները. IN սեղանարժեքներՀամարեռանկյունաչափականգործառույթներըսինուստրվածարժեքներՀամարհետեւյալըանկյուններըմեղք 0, մեղք 30, մեղք 45 ...
Առաջարկվող մաթեմատիկական ապարատը n-չափային հիպերկոմպլեքս թվերի բարդ հաշվարկի ամբողջական անալոգն է՝ n ազատության ցանկացած աստիճանով և նախատեսված է ոչ գծային մաթեմատիկական մոդելավորման համար։
Փաստաթուղթ... գործառույթներըհավասար է գործառույթներըՊատկերներ. Այս թեորեմից պետք է, Ինչ Համարգտնելով U, V կոորդինատները, բավական է հաշվարկել ֆունկցիան... երկրաչափություն; բազմանիստ գործառույթները(երկչափի բազմաչափ անալոգներ եռանկյունաչափականգործառույթները), դրանց հատկությունները, սեղաններև դիմում; ...
-
Եռանկյունաչափական ֆունկցիաների արժեքների աղյուսակ
Նշում. Եռանկյունաչափական ֆունկցիայի արժեքների այս աղյուսակը նշում է √ նշանը քառակուսի արմատ. Կոտորակը նշելու համար օգտագործեք «/» նշանը:
տես նաեւօգտակար նյութեր.
Համար եռանկյունաչափական ֆունկցիայի արժեքը որոշելը, գտե՛ք այն եռանկյունաչափական ֆունկցիան ցույց տվող գծի հատման կետում։ Օրինակ, սինուս 30 աստիճան - մենք փնտրում ենք մեղք (սինուս) վերնագրով սյունակը և գտնում ենք այս աղյուսակի սյունակի հատումը «30 աստիճան» տողի հետ, նրանց խաչմերուկում մենք կարդում ենք արդյունքը՝ մեկ կես: Նմանապես մենք գտնում ենք կոսինուս 60աստիճաններ, սինուս 60աստիճաններ (ևս մեկ անգամ, մեղքի սյունակի և 60 աստիճանի գծի խաչմերուկում մենք գտնում ենք sin 60 = √3/2 արժեքը) և այլն: Նույն կերպ են հայտնաբերվում նաև այլ «հանրաճանաչ» անկյունների սինուսների, կոսինուսների և տանգենսների արժեքները:
Սինուս pi, կոսինուս pi, շոշափող pi և այլ անկյուններ ռադիաններով
Կոսինուսների, սինուսների և տանգենսների ստորև բերված աղյուսակը նույնպես հարմար է եռանկյունաչափական ֆունկցիաների արժեքը գտնելու համար, որոնց արգումենտն է. տրված է ռադիաններով. Դա անելու համար օգտագործեք անկյունային արժեքների երկրորդ սյունակը: Դրա շնորհիվ դուք կարող եք հանրաճանաչ անկյունների արժեքը աստիճաններից վերածել ռադիանի: Օրինակ՝ եկեք առաջին տողում գտնենք 60 աստիճանի անկյունը և դրա տակ կարդանք դրա արժեքը ռադիաններով։ 60 աստիճանը հավասար է π/3 ռադիանի:
Pi թիվը միանշանակ արտահայտում է շրջագծի կախվածությունը անկյան աստիճանի չափից։ Այսպիսով, պի ռադիանները հավասար են 180 աստիճանի։
Պի (ռադիաններով) արտահայտված ցանկացած թիվ կարելի է հեշտությամբ վերածել աստիճանների՝ փոխարինելով pi (π) 180-ով:.
Օրինակներ:
1. Sine pi.
sin π = մեղք 180 = 0
Այսպիսով, pi-ի սինուսը նույնն է, ինչ 180 աստիճանի սինուսը և հավասար է զրոյի:2. Կոսինուս pi.
cos π = cos 180 = -1
Այսպիսով, pi-ի կոսինուսը նույնն է, ինչ 180 աստիճանի կոսինուսը և հավասար է մինուս մեկին:3. Շոշափող pi
tg π = tg 180 = 0
Այսպիսով, շոշափող pi-ը նույնն է, ինչ 180 աստիճանի շոշափողը և հավասար է զրոյի:Սինուսի, կոսինուսի, շոշափող արժեքների աղյուսակ 0 - 360 աստիճան անկյունների համար (ընդհանուր արժեքներ)
անկյան α արժեքը
(աստիճաններ)անկյան α արժեքը
ռադիաններով(pi-ի միջոցով)
մեղք
(սինուս)cos
(կոսինուս)tg
(շոշափող)ctg
(կոտանգենս)վրկ
(հատված)cosec
(կիսական)0 0 0 1 0 - 1 - 15 π/12 2 - √3 2 + √3 30 π/6 1/2 √3/2 1/√3 √3 2/√3 2 45 π/4 √2/2 √2/2 1 1 √2 √2 60 π/3 √3/2 1/2 √3 1/√3 2 2/√3 75 5π/12 2 + √3 2 - √3 90 π/2 1 0 - 0 - 1 105 7π/12 - - 2 - √3 √3 - 2 120 2π/3 √3/2 -1/2 -√3 -√3/3 135 3π/4 √2/2 -√2/2 -1 -1 -√2 √2 150 5π/6 1/2 -√3/2 -√3/3 -√3 180 π 0 -1 0 - -1 - 210 7π/6 -1/2 -√3/2 √3/3 √3 240 4π/3 -√3/2 -1/2 √3 √3/3 270 3π/2 -1 0 - 0 - -1 360 2պ 0 1 0 - 1 - Եթե եռանկյունաչափական ֆունկցիաների արժեքների աղյուսակում ֆունկցիայի արժեքի փոխարեն նշվում է գծիկ (տանգենս (tg) 90 աստիճան, կոտանգենս (ctg) 180 աստիճան), ապա անկյան աստիճանի չափման տվյալ արժեքի համար ֆունկցիան. կոնկրետ արժեք չունի. Եթե գծիկ չկա, բջիջը դատարկ է, ինչը նշանակում է, որ մենք դեռ չենք մուտքագրել անհրաժեշտ արժեքը: Մեզ հետաքրքրում է, թե ինչ հարցումներով են օգտվողները գալիս մեզ և լրացնում աղյուսակը նոր արժեքներով, չնայած այն հանգամանքին, որ ամենասովորական անկյունային արժեքների կոսինուսների, սինուսների և տանգենտների արժեքների վերաբերյալ ընթացիկ տվյալները բավականին բավարար են մեծ մասը լուծելու համար: խնդիրներ։
Սին, cos, tg եռանկյունաչափական ֆունկցիաների արժեքների աղյուսակ ամենահայտնի անկյունների համար
0, 15, 30, 45, 60, 90 ... 360 աստիճան
(թվային արժեքներ «ըստ Bradis աղյուսակների»)անկյան α արժեքը (աստիճաններ) անկյան α արժեքը ռադիաններով մեղք (սինուս) cos (կոսինուս) tg (շոշափող) ctg (կոտանգենս) 0 0 15 0,2588
0,9659
0,2679
30 0,5000
0,5774
45 0,7071
0,7660
60 0,8660
0,5000
1,7321
7π/18
Հիմնական եռանկյունաչափական ֆունկցիաների աղյուսակ 0, 30, 45, 60, 90, ... աստիճանի անկյունների համար
$\sin$, $\cos$, $\tan$ և $\cot$ ֆունկցիաների եռանկյունաչափական սահմանումներից կարող եք պարզել դրանց արժեքները $0$ և $90$ աստիճանի անկյունների համար.
$\sin0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ սահմանված չէ;
$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ որոշված չէ:
Դպրոցական երկրաչափության դասընթացում սովորելիս ուղղանկյուն եռանկյուններգտնել $0°$, $30°$, $45°$, $60°$ և $90°$ անկյունների եռանկյունաչափական ֆունկցիաները։
Գտնված եռանկյունաչափական ֆունկցիաների արժեքները նշված անկյունների համար աստիճաններով և ռադիաններով, համապատասխանաբար ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ pi)(3) $, $\frac(\pi)(2)$) հիշելու և օգտագործելու հեշտության համար մուտքագրվում են աղյուսակ, որը կոչվում է. եռանկյունաչափական աղյուսակ, Եռանկյունաչափական ֆունկցիաների հիմնական արժեքների աղյուսակեւ այլն։
Կրճատման բանաձևեր օգտագործելիս եռանկյունաչափական աղյուսակը կարող է ընդլայնվել մինչև $360°$ անկյան տակ և, համապատասխանաբար, $2\pi$ ռադիաններ.
Օգտագործելով եռանկյունաչափական ֆունկցիաների պարբերականության հատկությունները, յուրաքանչյուր անկյուն, որն արդեն հայտնիից կտարբերվի $360°$-ով, կարելի է հաշվարկել և գրանցել աղյուսակում։ Օրինակ, $0°$ անկյան եռանկյունաչափական ֆունկցիան կունենա նույն արժեքը $0°+360°$ անկյան համար, իսկ $0°+2 \cdot 360°$ անկյան համար և $0°+3 \cdot 360°$ անկյան համար: և այլն։
Օգտագործելով եռանկյունաչափական աղյուսակը, կարող եք որոշել միավոր շրջանագծի բոլոր անկյունների արժեքները:
Դպրոցական երկրաչափության դասընթացում դուք պետք է մտապահեք եռանկյունաչափական աղյուսակում հավաքված եռանկյունաչափական ֆունկցիաների հիմնական արժեքները՝ եռանկյունաչափական խնդիրներ լուծելու հարմարության համար:
Օգտագործելով սեղան
Աղյուսակում բավական է գտնել անհրաժեշտ եռանկյունաչափական ֆունկցիան և այն անկյան կամ ռադիանների արժեքը, որոնց համար անհրաժեշտ է հաշվարկել այս ֆունկցիան։ Ֆունկցիայի հետ տողի և արժեքի հետ սյունակի հատման կետում ստանում ենք տվյալ արգումենտի եռանկյունաչափական ֆունկցիայի ցանկալի արժեքը։
Նկարում կարող եք տեսնել, թե ինչպես կարելի է գտնել $\cos60°$-ի արժեքը, որը հավասար է $\frac(1)(2)$-ի:
Ընդլայնված եռանկյունաչափական աղյուսակը օգտագործվում է նույն կերպ: Դրա օգտագործման առավելությունը, ինչպես արդեն նշվեց, գրեթե ցանկացած անկյան եռանկյունաչափական ֆունկցիայի հաշվարկն է։ Օրինակ՝ հեշտությամբ կարող եք գտնել $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 արժեքը °$:
Հիմնական եռանկյունաչափական ֆունկցիաների Բրադիսի աղյուսակները
Բացարձակապես ցանկացած անկյան արժեքի եռանկյունաչափական ֆունկցիան աստիճանների և րոպեների ամբողջ արժեքի համար հաշվարկելու ունակությունը տրամադրվում է Բրադիսի աղյուսակների օգտագործմամբ: Օրինակ՝ գտե՛ք $\cos34°7"$ արժեքը: Աղյուսակները բաժանված են 2 մասի` $\sin$ և $\cos$ արժեքների աղյուսակ և $ արժեքների աղյուսակ: \tan$ և $\cot$.
Բրադիսի աղյուսակները հնարավորություն են տալիս ստանալ եռանկյունաչափական ֆունկցիաների մոտավոր արժեքներ մինչև 4 տասնորդական տեղերի ճշգրտությամբ:
Օգտագործելով Bradis աղյուսակները
Օգտագործելով Bradis աղյուսակները սինուսների համար՝ մենք գտնում ենք $\sin17°42"$: Դա անելու համար սինուսների և կոսինուսների աղյուսակի ձախ սյունակում մենք գտնում ենք աստիճանների արժեքը՝ $17°$, իսկ վերին տողում. մենք գտնում ենք րոպեների արժեքը՝ $42"$: Նրանց խաչմերուկում մենք ստանում ենք ցանկալի արժեքը.
$\sin17°42"=0,304$:
$\sin17°44"$ արժեքը գտնելու համար անհրաժեշտ է օգտագործել աղյուսակի աջ կողմի ուղղումը: Այս դեպքում $42"$ արժեքին, որը գտնվում է աղյուսակում, պետք է ուղղում ավելացնել $2-ի համար: $, որը հավասար է $0,0006$-ի: Ստանում ենք.
$\sin17°44"=0.304+0.0006=0.3046$:
$\sin17°47"$ արժեքը գտնելու համար մենք օգտագործում ենք նաև աղյուսակի աջ կողմի ուղղումը, միայն այս դեպքում հիմք ենք ընդունում $\sin17°48"$ արժեքը և հանում ենք ուղղումը $1"$-ով: :
$\sin17°47"=0.3057-0.0003=0.3054$:
Կոսինուսները հաշվարկելիս մենք կատարում ենք նմանատիպ գործողություններ, սակայն աջ սյունակում դիտում ենք աստիճանները, իսկ աղյուսակի ներքևի սյունակում՝ րոպեները։ Օրինակ՝ $\cos20°=0,9397$։
Մինչև $90°$ շոշափող արժեքների և փոքր անկյան կոտանգենսի համար ուղղումներ չկան: Օրինակ՝ գտնենք $\tan 78°37"$, որն ըստ աղյուսակի հավասար է $4,967$-ի։
- հետ շփման մեջ 0
- Google+ 0
- լավ 0
- Ֆեյսբուք 0