Se si costruiscono prima gli asintoti della curva, in molti casi la costruzione di un grafico della funzione diventa più semplice.

Il destino dell'asintoto è pieno di tragedia. Immagina com'è: tutta la tua vita si muove in linea retta verso il tuo caro obiettivo, avvicinandoti il ​​più possibile, ma senza mai raggiungerlo. Ad esempio, sforzati di connettere il tuo percorso di vita con il percorso della persona desiderata, ad un certo punto avvicinatela quasi da vicino, ma senza nemmeno toccarla. Oppure aspirare a guadagnare un miliardo, ma prima di raggiungere questo obiettivo ed entrare nel Guinness dei primati per il tuo caso mancano centesimi. E cose simili. Così è con un asintoto: si sforza costantemente di raggiungere la curva del grafico della funzione, si avvicina alla minima distanza possibile, ma non la tocca mai.

Definizione 1. Gli asintoti sono quelle rette alle quali il grafico di una funzione si avvicina arbitrariamente quando la variabile tende a più infinito o meno infinito.

Definizione 2. Una linea retta è chiamata asintoto del grafico di una funzione se la distanza dal punto variabile M il grafico della funzione fino a questa linea tende a zero man mano che il punto si allontana indefinitamente M dall'origine lungo qualsiasi ramo del grafico della funzione.

Esistono tre tipi di asintoti: verticale, orizzontale e obliquo.

Asintoti verticali

La prima cosa che devi sapere sugli asintoti verticali è che sono paralleli all'asse Ehi .

Definizione. Dritto X = UNÈ asintoto verticale del grafico della funzione , se punto X = UNÈ punto di discontinuità del secondo tipo per questa funzione.

Dalla definizione segue che la retta X = UNè l'asintoto verticale del grafico della funzione F(X) se è soddisfatta almeno una delle condizioni:

In questo caso, la funzione F(X) potrebbero non essere affatto definiti, rispettivamente, quando X ≥ UN E X ≤ UN .

Commento:

Esempio 1. Grafico di una funzione sì= ln X ha un asintoto verticale X= 0 (cioè coincidente con l'asse Ehi) al confine del dominio di definizione, poiché il limite della funzione quando x tende a zero da destra è uguale a meno infinito:

(immagine sopra).

te stesso e poi vedere le soluzioni

Esempio 2. Trova gli asintoti del grafico della funzione.

Esempio 3. Trovare gli asintoti del grafico di una funzione

Asintoti orizzontali

La prima cosa che devi sapere sugli asintoti orizzontali è che sono paralleli all'asse Bue .

Se (il limite di una funzione poiché l'argomento tende a più o meno infinito è uguale a un determinato valore B), Quello sì = B – asintoto orizzontale storto sì = F(X ) (a destra quando X tende a più infinito, a sinistra quando X tende a meno infinito e a due lati se i limiti in cui X tende a più o meno infinito sono uguali).

Esempio 5. Grafico di una funzione

A UN> 1 ha lasciato l'asimpototo orizzontale sì= 0 (cioè coincidente con l'asse Bue), poiché il limite della funzione poiché “x” tende a meno infinito è zero:

La curva non ha un asintoto orizzontale destro, poiché il limite della funzione poiché “x” tende a più infinito è uguale a infinito:

Asintoti obliqui

Gli asintoti verticale e orizzontale che abbiamo esaminato sopra sono paralleli agli assi delle coordinate, quindi per costruirli avevamo solo bisogno di un certo numero: il punto sull'ascissa o sull'asse delle ordinate attraverso il quale passa l'asintoto. Per un asintoto obliquo è necessaria una pendenza maggiore k, che mostra l'angolo di inclinazione della linea, e il termine libero B, che mostra quanto la linea è sopra o sotto l'origine. Coloro che non hanno dimenticato la geometria analitica, e da essa le equazioni della retta, noteranno che per l'asintoto obliquo trovano equazione di una retta con pendenza. L'esistenza di un asintoto obliquo è determinata dal seguente teorema, in base al quale si trovano i coefficienti appena citati.

Teorema. Per fare la curva sì = F(X) aveva un asintoto sì = kx + B , è necessario e sufficiente che vi siano limiti finiti k E B della funzione considerata man mano che la variabile tende X a più infinito e meno infinito:

(1)

(2)

I numeri trovati in questo modo k E B e sono i coefficienti degli asintoti obliqui.

Nel primo caso (poiché x tende a più infinito) si ottiene un asintoto inclinato destro, nel secondo (poiché x tende a meno infinito) si ottiene un asintoto obliquo sinistro. L'asintoto obliquo destro è mostrato in Fig. sotto.

Quando si trova l'equazione per un asintoto obliquo, è necessario tenere conto della tendenza di X sia a più infinito che a meno infinito. Per alcune funzioni, ad esempio quelle razionali frazionarie, questi limiti coincidono, ma per molte funzioni questi limiti sono diversi e solo uno di essi può esistere.

Se i limiti coincidono e x tende a più infinito e meno infinito, la retta sì = kx + B è l'asintoto bilaterale della curva.

Se almeno uno dei limiti che definiscono l'asintoto sì = kx + B , non esiste, allora il grafico della funzione non ha un asintoto obliquo (ma può averne uno verticale).

È facile vedere che l'asintoto orizzontale sì = Bè un caso speciale di obliquo sì = kx + B A k = 0 .

Pertanto, se in qualsiasi direzione una curva ha un asintoto orizzontale, allora in questa direzione non ce n'è uno inclinato e viceversa.

Esempio 6. Trovare gli asintoti del grafico di una funzione

Soluzione. La funzione è definita sull'intera linea numerica tranne X= 0, cioè

Dunque, al punto di rottura X= 0 la curva può avere un asintoto verticale. Infatti, il limite della funzione quando x tende a zero da sinistra è uguale a più infinito:

Quindi, X= 0 – asintoto verticale del grafico di questa funzione.

Il grafico di questa funzione non ha un asintoto orizzontale, poiché il limite della funzione quando x tende a più infinito è uguale a più infinito:

Scopriamo la presenza di un asintoto obliquo:

Ho limiti finiti k= 2 e B= 0. Dritto sì = 2Xè l'asintoto bidirezionale del grafico di questa funzione (figura all'interno dell'esempio).

Esempio 7. Trovare gli asintoti del grafico di una funzione

Soluzione. La funzione ha un punto di interruzione X= −1 . Calcoliamo i limiti unilaterali e determiniamo il tipo di discontinuità:

Conclusione: X= −1 è un punto di discontinuità del secondo tipo, quindi la retta X= −1 è l'asintoto verticale del grafico di questa funzione.

Cerchiamo asintoti obliqui. Perché questa funzione- frazionario-razionale, i limiti a e a volontà coincidono. Quindi, troviamo i coefficienti per sostituire la linea retta - asintoto obliquo nell'equazione:

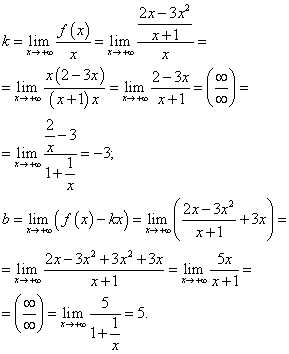
Sostituendo i coefficienti trovati nell'equazione della retta con il coefficiente di pendenza, otteniamo l'equazione dell'asintoto obliquo:

sì = −3X + 5 .

Nella figura, il grafico della funzione è indicato in bordeaux e gli asintoti sono indicati in nero.

Esempio 8. Trovare gli asintoti del grafico di una funzione

Soluzione. Poiché questa funzione è continua, il suo grafico non ha asintoti verticali. Cerchiamo asintoti obliqui:

.

Pertanto, il grafico di questa funzione ha un asintoto sì= 0 in e non ha asintoto in .

Esempio 9. Trovare gli asintoti del grafico di una funzione

Soluzione. Per prima cosa cerchiamo gli asintoti verticali. Per fare ciò, troviamo il dominio di definizione della funzione. Una funzione è definita quando la disuguaglianza e . Segno della variabile X corrisponde al segno. Consideriamo quindi la disuguaglianza equivalente. Da ciò si ottiene il dominio di definizione della funzione: . Un asintoto verticale può trovarsi solo sul confine del dominio di definizione della funzione. Ma X= 0 non può essere un asintoto verticale, poiché la funzione è definita in X = 0 .

Considera il limite di destra in (non esiste un limite di sinistra):

.

Punto X= 2 è un punto di discontinuità del secondo tipo, quindi la retta X= 2 - asintoto verticale del grafico di questa funzione.

Cerchiamo asintoti obliqui:

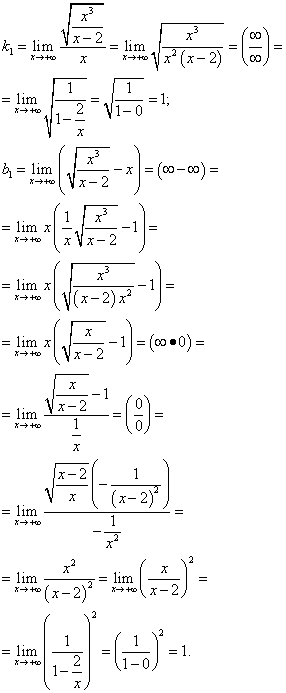
COSÌ, sì = X+ 1 - asintoto obliquo del grafico di questa funzione in . Cerchiamo un asintoto obliquo in:

COSÌ, sì = −X − 1 - asintoto obliquo a .

Esempio 10. Trovare gli asintoti del grafico di una funzione

Soluzione. Una funzione ha un dominio di definizione . Poiché l'asintoto verticale del grafico di questa funzione può trovarsi solo sul confine del dominio di definizione, troviamo i limiti unilaterali della funzione in .

Questo è esattamente il modo in cui è formulato compito tipico, e si tratta di trovare TUTTI gli asintoti del grafico (verticale, inclinato/orizzontale). Anche se, per essere più precisi nel porre la questione, stiamo parlando di ricerche sulla presenza di asintoti (dopotutto, potrebbero non essercene affatto).

Cominciamo con qualcosa di semplice:

Esempio 1

Soluzione È conveniente scomporlo in due punti:

1) Innanzitutto controlliamo se esistono asintoti verticali. Il denominatore va a zero in , ed è subito chiaro che a questo punto la funzione soffre divario infinito, e la retta data dall'equazione è l'asintoto verticale del grafico della funzione. Ma, prima di giungere a tale conclusione, è necessario trovare dei limiti unilaterali:

Ti ricordo la tecnica di calcolo su cui mi sono soffermato allo stesso modo nell'articolo continuità della funzione. Punti di interruzione. Nell'espressione sotto il segno limite sostituiamo . Non c'è niente di interessante nel numeratore:
.

Ma nel denominatore risulta infinitesimale numero negativo :
, determina il destino del limite.

Il limite di sinistra è infinito e, in linea di principio, è già possibile emettere un verdetto sulla presenza di un asintoto verticale. Ma i limiti unilaterali non sono necessari solo per questo: AIUTANO A COMPRENDERE COME individuare il grafico della funzione e costruirlo CORRETTAMENTE. Dobbiamo quindi calcolare anche il limite destrorso:

Conclusione: i limiti unilaterali sono infiniti, il che significa che la retta è l'asintoto verticale del grafico della funzione in .

Primo limite finito, il che significa che è necessario “continuare la conversazione” e trovare il secondo limite:

Anche il secondo limite finito.

Quindi il nostro asintoto è:

Conclusione: la retta data dall'equazione è l'asintoto orizzontale del grafico della funzione in .

Trovare l'asintoto orizzontale puoi usare una formula semplificata:

Se esiste un limite finito, allora la retta è l'asintoto orizzontale del grafico della funzione in .

È facile vedere che il numeratore e il denominatore della funzione stesso ordine di crescita, il che significa che il limite cercato sarà finito:

Risposta:

A seconda delle condizioni, non è necessario completare il disegno, ma se è in pieno svolgimento studio delle funzioni, quindi sulla bozza facciamo subito uno schizzo:

In base ai tre limiti trovati, prova a capire da solo come potrebbe essere posizionato il grafico della funzione. È davvero difficile? Trova 5-6-7-8 punti e segnali sul disegno. Tuttavia, il grafico di questa funzione è costruito utilizzando trasformazioni del grafico di una funzione elementare, e i lettori che hanno esaminato attentamente l'Esempio 21 dell'articolo sopra possono facilmente indovinare di che tipo di curva si tratta.

Esempio 2

Trovare gli asintoti del grafico di una funzione

Questo è un esempio che puoi risolvere da solo. Lascia che ti ricordi che il processo è convenientemente diviso in due punti: asintoti verticali e asintoti obliqui. Nella soluzione campione l'asintoto orizzontale viene trovato utilizzando uno schema semplificato.

In pratica, le funzioni frazionarie-razionali si incontrano più spesso e, dopo l'allenamento sulle iperboli, complicheremo il compito:

Esempio 3

Trovare gli asintoti del grafico di una funzione

Soluzione: Uno, due e fatto:

1) Si trovano gli asintoti verticali in punti di discontinuità infinita, quindi è necessario verificare se il denominatore va a zero. Decidiamo equazione quadratica :

Il discriminante è positivo, quindi l'equazione ha due radici reali, e il lavoro aumenta notevolmente =)

Per trovare ulteriormente limiti unilaterali trinomio quadratico conveniente fattorizzare:
(per la notazione compatta, il “meno” era incluso nella prima parentesi). Per andare sul sicuro controlliamo aprendo le parentesi mentalmente o su una bozza.

Riscriviamo la funzione nella forma

Troviamo i limiti unilaterali nel punto:

E al punto:

Pertanto le rette sono asintoti verticali del grafico della funzione in questione.

2) Se guardi la funzione, è abbastanza ovvio che il limite sarà finito e abbiamo un asintoto orizzontale. Mostriamo in breve la sua presenza:

Pertanto, la linea retta (asse delle ascisse) è l'asintoto orizzontale del grafico di questa funzione.

Risposta:

I limiti e gli asintoti trovati forniscono molte informazioni sul grafico della funzione. Prova a immaginare mentalmente il disegno tenendo conto dei seguenti fatti:

Disegna la tua versione del grafico sulla bozza.

Naturalmente, i limiti rilevati non determinano chiaramente l'aspetto del grafico e potresti commettere un errore, ma l'esercizio stesso ti fornirà un aiuto inestimabile durante studio completo delle funzioni. L'immagine corretta è alla fine della lezione.

Esempio 4

Trovare gli asintoti del grafico di una funzione

Esempio 5

Trovare gli asintoti del grafico di una funzione

Questi sono compiti per una soluzione indipendente. Entrambi i grafici hanno ancora una volta asintoti orizzontali, che vengono immediatamente rilevati dalle seguenti caratteristiche: nell'Esempio 4 ordine di crescita denominatore è maggiore dell'ordine di crescita del numeratore e nell'esempio 5 il numeratore e il denominatore stesso ordine di crescita. Nella soluzione campione, la prima funzione viene esaminata per la presenza di asintoti obliqui per intero e la seconda per il limite.

Gli asintoti orizzontali, secondo la mia impressione soggettiva, sono notevolmente più comuni di quelli “veramente inclinati”. Il caso generale tanto atteso:

Esempio 6

Trovare gli asintoti del grafico di una funzione

Soluzione: classico del genere:

1) Poiché il denominatore è positivo, allora la funzione continuo lungo tutta la linea numerica e non ci sono asintoti verticali. ...Va bene? Non è la parola giusta: eccellente! Il punto n.1 è chiuso.

2) Verifichiamo la presenza di asintoti obliqui:

Primo limite finito, quindi andiamo avanti. Durante il calcolo del secondo limite da eliminare incertezza "infinito meno infinito" Portiamo l'espressione ad un denominatore comune:

Anche il secondo limite finito, quindi, il grafico della funzione in questione ha un asintoto obliquo:

Conclusione:

Pertanto, quando il grafico della funzione infinitamente vicino si avvicina ad una linea retta:

Nota che interseca il suo asintoto obliquo all'origine, e tali punti di intersezione sono abbastanza accettabili: è importante che “tutto sia normale” all'infinito (in effetti, è qui che parliamo di asintoti).

Esempio 7

Trovare gli asintoti del grafico di una funzione

Soluzione: Non c'è niente di particolare da commentare, quindi faccio un esempio approssimativo di soluzione pulita:

1) Asintoti verticali. Esploriamo il punto.

La linea retta è l'asintoto verticale del grafico in .

2) Asintoti obliqui:

La linea retta è l'asintoto obliquo del grafico in .

Risposta:

I limiti unilaterali e gli asintoti rilevati ci consentono di prevedere con elevata sicurezza l'aspetto del grafico di questa funzione. Disegno corretto alla fine della lezione.

Esempio 8

Trovare gli asintoti del grafico di una funzione

Questo è un esempio di soluzione indipendente; per comodità di calcolo di alcuni limiti, puoi dividere il numeratore per il denominatore termine per termine. Ancora una volta, quando analizzi i risultati, prova a disegnare un grafico di questa funzione.

Ovviamente, i proprietari degli asintoti obliqui “reali” sono i grafici di quelle funzioni razionali frazionarie il cui più alto grado di numeratore uno in più il grado più alto del denominatore. Se è maggiore, non ci sarà più un asintoto obliquo (ad esempio, ).

Ma nella vita accadono altri miracoli:

Esempio 9

Soluzione: funzione continuo sull'intera linea numerica, il che significa che non ci sono asintoti verticali. Ma potrebbero esserci persone inclini. Controlliamo:

Ricordo come, all'università, mi imbattei in una funzione simile e semplicemente non potevo credere che avesse un asintoto obliquo. Finché non ho calcolato il secondo limite:

A rigor di termini, ci sono due incertezze qui: e , ma in un modo o nell'altro, è necessario utilizzare il metodo di soluzione, che è discusso negli Esempi 5-6 dell'articolo sui limiti della maggiore complessità. Moltiplichiamo e dividiamo per l'espressione coniugata per utilizzare la formula:

Risposta:

Forse l'asintoto obliquo più popolare.

Finora l'infinito è stato “tagliato con lo stesso pennello”, ma succede che il grafico della funzione due diversi asintoti obliqui a e a:

Esempio 10

Esaminare il grafico di una funzione per verificare la presenza di asintoti

Soluzione: l'espressione radicale è positiva, il che significa dominio di definizione- Qualsiasi numero è valido e non possono esserci bastoncini verticali.

Controlliamo se esistono asintoti obliqui.

Se “x” tende a “meno infinito”, allora:
(quando si inserisce una "X" sotto radice quadrataè necessario aggiungere il segno meno per non perdere la negatività del denominatore)

Sembra insolito, ma qui l’incertezza è “infinito meno infinito”. Moltiplicare numeratore e denominatore per l'espressione coniugata:

Pertanto, la linea retta è l'asintoto obliquo del grafico in .

Con “più infinito” tutto è più banale:

E la linea retta è a .

Risposta:

Se ;
, Se .

Non posso resistere all'immagine grafica:

Questo è uno dei rami iperboli .

Non è raro che la potenziale disponibilità di asintoti sia inizialmente limitata dominio della funzione:

Esempio 11

Esaminare il grafico di una funzione per verificare la presenza di asintoti

Soluzione: è ovvio che , quindi consideriamo solo il semipiano destro, dove è presente il grafico della funzione.

1) Funzione continuo sull'intervallo , il che significa che se esiste un asintoto verticale, allora può essere solo l'asse delle ordinate. Studiamo il comportamento della funzione in prossimità del punto Giusto:

notare che non c'è incertezza qui(tali casi sono stati enfatizzati all'inizio dell'articolo Metodi per risolvere i limiti).

Pertanto, la linea retta (asse delle ordinate) è l'asintoto verticale per il grafico della funzione in .

2) Lo studio sull'asintoto obliquo può essere effettuato secondo lo schema completo, ma nell'articolo Le regole dell'Ospedale lo abbiamo scoperto funzione lineare Di più ordine elevato crescita rispetto a quella logaritmica, quindi: (vedi Esempio 1 della stessa lezione).

Conclusione: l'asse x è l'asintoto orizzontale del grafico della funzione in .

Risposta:

Se ;
, Se .

Disegno per chiarezza:

È interessante notare che una funzione apparentemente simile non ha alcun asintoto (chi lo desidera può verificarlo).

Due esempi finali per lo studio autonomo:

Esempio 12

Esaminare il grafico di una funzione per verificare la presenza di asintoti

Per verificare la presenza di asintoti verticali, devi prima trovare dominio di una funzione, e poi calcolare un paio di limiti unilaterali nei punti “sospetti”. Anche gli asintoti obliqui non sono esclusi, poiché la funzione è definita all'infinito “più” e “meno”.

Esempio 13

Esaminare il grafico di una funzione per verificare la presenza di asintoti

Ma qui possono esserci solo asintoti obliqui e le direzioni dovrebbero essere considerate separatamente.

Spero che tu abbia trovato l'asintoto giusto =)

Ti auguro successo!

Soluzioni e risposte:

Esempio 2:Soluzione :
. Troviamo i limiti unilaterali:

Dritto è l'asintoto verticale del grafico della funzione a .
2) Asintoti obliqui.

Dritto .
Risposta:

Disegno all'esempio 3:

Esempio 4:Soluzione :
1) Asintoti verticali. La funzione subisce un'interruzione infinita in un punto . Calcoliamo i limiti unilaterali:

Nota: un numero infinitesimo negativo elevato a una potenza pari è uguale a un numero infinitesimo positivo: .

Dritto è l'asintoto verticale del grafico della funzione.
2) Asintoti obliqui.

Dritto (asse delle ascisse) è l'asintoto orizzontale del grafico della funzione a .
Risposta: . .
Allora, quando Il grafico non ha un asintoto inclinato.

Quindi, dritto è l'asintoto orizzontale del grafico di questa funzione in .
Risposta: asse x a .

Matematica superiore per studenti per corrispondenza e altro >>>

(Vai alla pagina principale)

Zeri di funzione. Intervalli di segno costante di una funzione.

Metodo dell'intervallo

Una parte significativa del materiale riguardante i derivati ​​e lo studio delle funzioni a cui tradizionalmente fa riferimento curriculum scolastico, e questo articolo non fa eccezione alla regola. Oggi ci eserciteremo a trovare zeri e intervalli di segno costante di una funzione, e analizzeremo anche in dettaglio il metodo degli intervalli, che può essere paragonato a un rinforzo affidabile all'interno delle mura dell'argomento in esame.

Se il tuo progetto di costruzione è nella fase iniziale, inizia con una lezione introduttiva sui grafici delle funzioni. Inoltre, è consigliabile leggere gli articoli Dominio della funzione, Asintoti del grafico e, in sostanza, le informazioni contenute in questa pagina sono una continuazione logica. Il materiale, naturalmente, sarà utile per gli studenti delle scuole superiori.

Definizione . Un asintoto del grafico di una funzione è una linea retta che ha la proprietà che la distanza da un punto sul grafico di una funzione a questa linea retta tende a zero quando il punto del grafico si sposta indefinitamente dall'origine..

Secondo i metodi per trovarli, si distinguono tre tipi di asintoti: verticale, orizzontale, obliquo.

Ovviamente quelli orizzontali sono casi particolari di quelli inclinati (a ).

Trovare gli asintoti del grafico di una funzione si basa sulle seguenti affermazioni.

Teorema 1 . Sia definita la funzione almeno in un semiintorno di un punto e almeno uno dei suoi limiti unilaterali in questo punto sia infinito, cioè equalizzato. Allora la retta è l'asintoto verticale del grafico della funzione.

Pertanto, gli asintoti verticali del grafico di una funzione vanno ricercati nei punti di discontinuità della funzione o agli estremi del suo dominio di definizione (se si tratta di numeri finiti).

Teorema 2 . Lascia che la funzione sia definita per valori di argomento sufficientemente grandi in valore assoluto e che vi sia un limite finito della funzione . Allora la retta è l'asintoto orizzontale del grafico della funzione.

Può succedere , UN , e sono numeri finiti, allora il grafico ha due diversi asintoti orizzontali: mancino e destrorso. Se esiste solo uno dei limiti finiti o , il grafico ha un asintoto orizzontale sinistrorso o destrorso.

Teorema 3 . Lascia che la funzione sia definita per valori dell'argomento sufficientemente grandi in valore assoluto e che ci siano limiti finiti E . Allora la retta è l'asintoto obliquo del grafico della funzione.

Si noti che se almeno uno di questi limiti è infinito, allora non esiste un asintoto obliquo.

Un asintoto obliquo, come uno orizzontale, può essere unilaterale.

Esempio. Trova tutti gli asintoti del grafico della funzione.

Soluzione.

La funzione è definita in . Troviamo i suoi limiti unilaterali nei punti.

Perché E (gli altri due limiti unilaterali potrebbero non essere più trovati), allora le rette sono asintoti verticali del grafico della funzione.

Calcoliamo

(applicare la regola di L'Hopital) = .

Ciò significa che la retta è un asintoto orizzontale.

Dato che esiste l’asintoto orizzontale, non cerchiamo più quelli inclinati (non esistono).

Risposta: Il grafico ha due asintoti verticali e uno orizzontale.

Ricerca generale sulle funzionisì = F (X ).

L'ambito della funzione. Trova il suo dominio di definizione D(F). Se non è troppo difficile, è utile trovare anche la portata E(F). (Tuttavia, in molti casi, la questione di trovare E(F) viene posticipato finché non vengono trovati gli estremi della funzione.)

Proprietà speciali della funzione. Scopri le proprietà generali di una funzione: uniformità, disparità, periodicità, ecc. Non tutte le funzioni hanno proprietà come pari o dispari. Una funzione ovviamente non è né pari né dispari se il suo dominio di definizione è asimmetrico rispetto al punto 0 sull'asse Bue.

Allo stesso modo, per qualsiasi funzione periodica, il dominio di definizione consiste o nell'intero asse reale o nell'unione di sistemi di intervalli che si ripetono periodicamente. Asintoti verticali. D(F Scopri come si comporta la funzione quando l'argomento si avvicina ai punti di confine del dominio di definizione

), se tali punti di confine esistono. In questo caso possono comparire asintoti verticali. Se una funzione ha punti di discontinuità in cui non è definita, allora questi punti dovrebbero essere controllati anche per la presenza di asintoti verticali della funzione. D(F) include raggi della forma (a;+) o (−;b), quindi puoi provare a trovare asintoti obliqui (o asintoti orizzontali) per x+ o x−, rispettivamente, cioè trova limxf(x). Asintoti obliqui : sì = kx + B, dove k=limx+xf(x) e b=limx+(f(x)−x). Gli asintoti sono orizzontali : sì = B, dove limxf(x)=b.

Trovare i punti di intersezione del grafico con gli assi. Ehi Trovare il punto di intersezione del grafico con l'asse F. Bue Per fare ciò è necessario calcolare il valore F(X(0).

Trova anche i punti di intersezione del grafico con l'asse, perché trovare le radici dell'equazione

) = 0 (o assicurati che non ci siano radici). Spesso l'equazione può essere risolta solo approssimativamente, ma separare le radici aiuta a comprendere meglio la struttura del grafico.

Successivamente, è necessario determinare il segno della funzione sugli intervalli tra le radici e i punti di interruzione.

Trovare i punti di intersezione del grafico con l'asintoto.

In alcuni casi potrebbe essere necessario trovare punti caratteristici del grafico che non sono stati menzionati nei paragrafi precedenti.

2. La curva y = f (x) ha un asintoto verticale x = a, se in . Per determinare gli asintoti verticali è necessario trovare quei valori dell'argomento vicino ai quali f (x) aumenta indefinitamente in valore assoluto. Se tali valori dell'argomento sono a1, a2, ..., allora le equazioni degli asintoti verticali saranno

x = a1, x = a2...

3. Per determinare l'asintoto obliquo y = kx + b della curva y = f (x), è necessario trovare i numeri k e b dalle formule

(i casi dovrebbero essere considerati separatamente). Esistono asintoti inclinati della curva y = f (x) se e solo se questi limiti hanno valore finito. Per determinare questi limiti è conveniente utilizzare la regola di L'Hopital.

Esempio. Trova gli asintoti della curva

Soluzione. Non esistono asintoti orizzontali. Troviamo l'asintoto verticale dalla condizione

2x + 3 = 0 => x = - 3/2, mentre y
, Quando
, sì
, Quando
. Determiniamo gli asintoti obliqui, la cui equazione ha la forma: y = kx + b

Poiché k e b hanno valori finiti e sono uguali tra loro in x
e a x
, allora esiste un unico asintoto obliquo la cui equazione è

Studio generale delle funzioni

Uno studio completo di una funzione solitamente significa risolvere le seguenti domande:

Determinazione del dominio di esistenza di una funzione.

Identificare il problema di uniformità e disparità di una funzione.

Determinazione dei punti di interruzione della funzione.

Determinazione degli asintoti del grafico di una funzione.

Determinazione degli intervalli di aumento e diminuzione di una funzione.

Determinazione dell'estremo di una funzione.

Determinazione degli intervalli di convessità e concavità di un grafico di funzione.

Determinazione dei punti di flesso.

Trovare l'intersezione con gli assi delle coordinate.

Rappresentazione grafica di una funzione.

Esempio. Esploriamo la funzione

D(y) = (
). La funzione è continua su tutto il dominio di definizione. Non ci sono punti di rottura.

La funzione non è né pari, né dispari, né periodica.

Non ci sono punti di rottura.

Non ci sono asintoti verticali;
, non ci sono asintoti obliqui.

5, 6.
. Punti critici x = -2, x = 0.

	( )				( )
Cartello		= 0
Comportamento della funzione	In aumento	3			In aumento

7, 8.
,
in x = 1,
non esiste in x = 0.

	( )				( )
Cartello		=		= 0
Comportamento della funzione	Parte superiore convessa	Non un punto di flesso	Parte superiore convessa	Punto di flesso	Convesso verso il basso

9.
x = 0 e x = -5.

Compito 1

Calcolare il determinante del secondo ordine della matrice A

Calcolare il determinante della matrice B del terzo ordine

Calcola il determinante della matrice B espandendolo su qualsiasi riga e colonna

Calcola il determinante della matrice B utilizzando le proprietà dei determinanti. Ridurre il calcolo del determinante del terzo ordine al calcolo di un determinante del secondo ordine

Opzione 1

Opzione 2

Opzione 3

Opzione 4

Opzione 5

Opzione 6

Opzione 7

Opzione 8
Opzione 9
Opzione 10

Compito 2

1. Risolvi il sistema di equazioni utilizzando il metodo Cramer Ah = a

Risolvere il sistema di equazioni utilizzando il metodo Cramer INX = B

Risolvere il sistema di equazioni utilizzando il metodo di Gauss INX = B

Compito 3.

Ah = a

Risolvere un sistema di equazioni utilizzando il metodo delle matrici INX = B

Compito 4.

Calcolare il rango della matrice.

1., 2.
;

3.
4.

5.
6.

7.
8

9.
10.

Compito 5

Dati due vertici di un triangolo Δ ABC: A (X 1 ,y 1 ), IN(X 2 ,y 2 ) e punto D (X 3 , sì 3 )intersezioni di altezza:

a) creare un'equazione di altezze, mediane, bisettrici di un triangolo Δ ABC.

b) trovare le equazioni delle rette passanti per i vertici del triangolo e parallele ai lati.

c) determinare la lunghezza delle altezze del triangolo e la distanza dal punto M (X 4 , sì 4 ) ai lati del triangolo.

	X 1	sì 1	X 2	sì 2	X 3	sì 3	X 4	sì 4

Compito 6.

Vengono fornite le coordinate dei vertici della piramide ABCD: UN (X 1 ,y 1 , z 1 ), IN(X 2 ,y 2 , z 3 ) ,C (X 2 , sì 2 , z 2 ) ,D (X 4 , sì 4 , z 3 )

1) lunghezza del bordo AB;.

2) angolo tra le nervature AB E UND;

3) angolo tra i bordi A.D e il bordo ABC;

4) zona del viso ABC;

5) volume della piramide;

6) Equazione di una retta AB;

7) equazione del piano ABC;

8) Equazione dell'altezza caduta dal vertice D fino all'orlo ABC.

N

X 1

sì 1

z 1

X 2

sì 2

z 2

X 3

sì 3

z 3

X 4

sì 4

z 4

Compito 7.

Attività 8. Trova il dominio della funzione

5.

7.

8.

9.

10.

Attività 9. Rappresentare graficamente la funzione

1.

2.

3.

4

5.

6.

7.

8.

9.

10.

Compito 10. Trova i limiti della funzione

1.a)
, B)
, V)
,

G)
, D)

2.a)
, B)
, V)
,

G)
, D)

3.a)
, B)
, V)
,

G)
, D)

4.a)
, B)
, V)
,

G)
, D)

5.a)
, B)
, V)
,

G)
, D)

6.a)
, B)
, V)
,

G)
, D)

7.a)
, B)
, V)
,

G)
, D)

8.a)
, B)
, V)
,

G)
, D)

9.a)
, B)
, V)
,

G)
, D)

10.a)
, B)
, V)
,

G)
, D)

Compito 11. Trova la derivata

1.
, B),

V)
, G)
, D)
, e)

2.a)
, B)
, V)
,

G)
, D)
,e)

3.a), b)
, V)
, G)
, D)
, e)

4.a)
, B)
, V)
,

G)
, D)
, e)

5.a)
, B)
, V)
, G)
, D)
,

e)

6.a)
, B)
, V)
, G)
, D)
,

e)

7.a)
, B),

V)
, G)
, D)
,

e)

8.a)
, B)
, V)
, G)
, D)
,

e)

9.a)
, B)
, V)
,

G)
, D)
, e)

10.a)
, B)
, V)
,

G)
, D)
, e)

Attività 12. Mostra che la funzione soddisfa l'uguaglianza

Attività 13. Trova la derivata seconda di una funzione definita parametricamente.

1 .
6.

2.
7

3.
8

4.
9.

5.
10.

Compito 14. Trova i limiti utilizzando la regola di L'Hopital

Compito 15. Trova gli estremi delle funzioni date.

1.
6.

2.
7.

3.
8.

4.
9.

5.
10.

Attività 16. Trova il valore più grande e più piccolo sui segmenti indicati e agli intervalli indicati.

Compito 17. Condotta ricerca completa determinate funzioni e disegnarne i grafici.

1.
6.

2.
7.

3.
8.

4.
9.

5.
10.

Letteratura:

Bavrin I.I. Corso di matematica superiore.-M.: Illuminismo, 1992.-400 p.

Bronshtein I.N., Semendyaev K.A. Manuale di matematica.

M, 1967, 608 s

Corso generale di matematica superiore per economisti, a cura di V.I. Ermakov-M. "Infra-M". Teush V.L. Corso di matematica superiore. - M.: scienza sovietica

, 1958, 270 pag. Shipachev V.S. Matematica superiore: Esercitazione

M. Scuola superiore, 1990.-479 p.

Matematica superiore per economisti: libro di testo per le università / N.Sh Kremer, B.A Putko e altri; M: UNITÀ, 2002. – 461 pag.

Valiev K.G., Dzhalladova I.A. Vishcha Matematica: Preside. Pos_bnik.

Quanti asintoti può avere il grafico di una funzione? Non uno, uno, due, tre... o infiniti. Non andremo lontano con gli esempi; ricordiamo le funzioni elementari. Una parabola, una parabola cubica e un'onda sinusoidale non hanno affatto asintoti. grafico esponenziale, ha un asintoto unico. L'arcotangente e l'arcotangente ne hanno due, e la tangente e la cotangente ne hanno infiniti. Non è raro che un grafico abbia sia asintoti orizzontali che verticali. Iperbole, ti amerò sempre.

Cosa significa trovare gli asintoti del grafico di una funzione?

Ciò significa capire le loro equazioni e tracciare linee rette se il problema lo richiede. Il processo prevede la ricerca dei limiti di una funzione.

Asintoti verticali del grafico di una funzione

L'asintoto verticale del grafico, di regola, si trova nel punto di discontinuità infinita della funzione. È semplice: se in un punto la funzione subisce una discontinuità infinita, allora la retta specificata dall'equazione è l'asintoto verticale del grafico.

Nota: tieni presente che la voce viene utilizzata per fare riferimento a due concetti completamente diversi. Che si tratti di un punto o di un'equazione di una retta dipende dal contesto.

Quindi, per stabilire la presenza di un asintoto verticale in un punto, è sufficiente dimostrare che almeno uno dei limiti unilaterali è infinito. Molto spesso questo è il punto in cui il denominatore della funzione è zero. In sostanza abbiamo già trovato gli asintoti verticali negli ultimi esempi della lezione sulla continuità di una funzione. Ma in alcuni casi c'è solo un limite unilaterale, e se è infinito, allora di nuovo: ama e favorisci l'asintoto verticale. L'illustrazione più semplice: e l'asse delle ordinate.

Da quanto sopra segue anche un fatto ovvio: se la funzione è continua, allora non ci sono asintoti verticali. Per qualche motivo mi è venuta in mente una parabola. Davvero, dove puoi “attaccare” una linea retta qui? ...sì... capisco... I seguaci di zio Freud sono diventati isterici =)

L'affermazione opposta è generalmente falsa: ad esempio, la funzione non è definita sull'intera retta numerica, ma è completamente priva di asintoti.

Asintoti inclinati del grafico di una funzione

Obliquo (es caso speciale- orizzontale) si possono tracciare asintoti se l'argomento della funzione tende a “più infinito” o a “meno infinito”. Pertanto il grafico di una funzione non può avere più di 2 asintoti inclinati. Ad esempio, il grafico di una funzione esponenziale ha un singolo asintoto orizzontale in, e il grafico dell'arcotangente in ha due di questi asintoti, e anche diversi.

Quando il grafico in entrambi i punti si avvicina a un singolo asintoto obliquo, è consuetudine combinare gli “infiniti” sotto un'unica voce. Ad esempio, ...hai indovinato correttamente: .