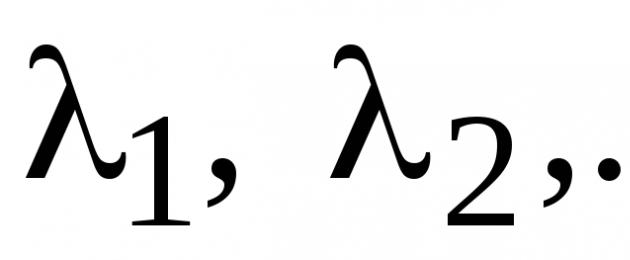I vettori sono linearmente dipendenti? Vettori linearmente dipendenti e linearmente indipendenti

Dipendenza lineare vettori

Al momento di decidere vari compiti, di regola, non si ha a che fare con un vettore, ma con un certo insieme di vettori della stessa dimensione. Tali aggregati sono chiamati sistema di vettori e denotare

Definizione.Combinazione lineare di vettori chiamato vettore del modulo

dove sono i numeri reali. Si dice anche che un vettore sia espresso linearmente in termini di vettori o scomposto in questi vettori.

Ad esempio, siano dati tre vettori: , , . La loro combinazione lineare con i coefficienti rispettivamente 2, 3 e 4 costituisce il vettore

Definizione. L'insieme di tutte le possibili combinazioni lineari di un sistema di vettori è chiamato span lineare di questo sistema.

Definizione. Viene chiamato un sistema di vettori diversi da zero linearmente dipendente, se ci sono numeri che non sono contemporaneamente uguali a zero, tali che la combinazione lineare di un dato sistema con i numeri indicati sia uguale al vettore zero:

Se l'ultima uguaglianza per un dato sistema di vettori è possibile solo per , allora viene chiamato questo sistema di vettori linearmente indipendenti.

Ad esempio, un sistema di due vettori è linearmente indipendente; sistema di due vettori ed è linearmente dipendente, poiché .

Sia il sistema di vettori (19) linearmente dipendente. Selezioniamo il termine della somma (20) in cui il coefficiente è , ed esprimiamolo attraverso i restanti termini:

Come si può vedere da questa uguaglianza, uno dei vettori del sistema linearmente dipendente (19) si è rivelato espresso in termini di altri vettori di questo sistema (o è espanso in termini dei suoi restanti vettori).

Proprietà di un sistema vettoriale linearmente dipendente

1. Un sistema costituito da un vettore diverso da zero è linearmente indipendente.

2. Un sistema contenente un vettore zero è sempre linearmente dipendente.

3. Un sistema contenente più di un vettore è linearmente dipendente se e solo se tra i suoi vettori c'è, secondo almeno, un vettore che è espresso linearmente in termini degli altri.

Significato geometrico dipendenza lineare nel caso di vettori bidimensionali su un piano: quando un vettore si esprime attraverso un altro, si ha, cioè questi vettori sono collineari o, che è lo stesso, situati su linee parallele.

Nel caso spaziale della dipendenza lineare di tre vettori, questi sono paralleli a un piano, cioè complanare. Basta “correggere” le lunghezze di questi vettori con i fattori corrispondenti affinché uno di essi diventi la somma degli altri due o si esprima attraverso di essi.

Teorema. Nello spazio, qualsiasi sistema contenente vettori è linearmente dipendente da .

Esempio. Scopri se i vettori sono linearmente dipendenti.

Soluzione. Facciamo un'uguaglianza vettoriale. Scrivendo in forma vettoriale di colonna, otteniamo

Pertanto, il problema si è ridotto alla risoluzione del sistema

Risolviamo il sistema utilizzando il metodo gaussiano:

Di conseguenza, otteniamo un sistema di equazioni:

che ha infinite soluzioni, tra le quali ce n'è sicuramente una diversa da zero, quindi i vettori sono linearmente dipendenti.

In questo articolo tratteremo:

• cosa sono i vettori collineari;
• quali sono le condizioni per la collinearità dei vettori;
• quali proprietà esistono dei vettori collineari;
• qual è la dipendenza lineare dei vettori collineari.

Definizione 1

I vettori collineari sono vettori paralleli a una linea o che giacciono su una linea.

Esempio 1

Condizioni di collinearità dei vettori

Due vettori sono collineari se è vera una delle seguenti condizioni:

• condizione 1 . I vettori aeb sono collineari se esiste un numero λ tale che a = λ b;
• condizione 2 . I vettori a e b sono collineari con rapporti di coordinate uguali:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• condizione 3 . I vettori a e b sono collineari a condizione che il prodotto vettoriale e il vettore zero siano uguali:

un ∥ b ⇔ un, b = 0

Nota 1

Condizione 2 non applicabile se una delle coordinate del vettore è zero.

Nota 2

Condizione 3 si applica solo a quei vettori specificati nello spazio.

Esempi di problemi per studiare la collinearità dei vettori

Esempio 1

Esaminiamo i vettori a = (1; 3) e b = (2; 1) per la collinearità.

Come risolvere?

In questo caso è necessario utilizzare la 2a condizione di collinearità. Per dati vettori assomiglia a questo:

L'uguaglianza è falsa. Da ciò possiamo concludere che i vettori a e b non sono collineari.

Risposta : un | | B

Esempio 2

Quale valore m del vettore a = (1; 2) eb = (- 1; m) è necessario affinché i vettori siano collineari?

Come risolvere?

Utilizzando la seconda condizione di collinearità, i vettori saranno collineari se le loro coordinate sono proporzionali:

Ciò dimostra che m = - 2.

Risposta: m = - 2 .

Criteri di dipendenza lineare e indipendenza lineare di sistemi vettoriali

Teorema

Sistema vettoriale spazio vettorialeè linearmente dipendente solo se uno dei vettori del sistema può essere espresso in termini dei rimanenti vettori del sistema dato.

Prova

Sia il sistema e 1 , e 2 , . . . , e n è linearmente dipendente. Scriviamo una combinazione lineare di questo sistema uguale al vettore zero:

un 1 e 1 + un 2 e 2 + . . . + a n e n = 0

in cui almeno uno dei coefficienti di combinazione non è uguale a zero.

Sia a k ≠ 0 k ∈ 1 , 2 , . . . , N.

Dividiamo entrambi i membri dell'uguaglianza per un coefficiente diverso da zero:

a k - 1 (ak - 1 a 1) e 1 + (ak - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

Indichiamo:

A k - 1 am , dove m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

In questo caso:

β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n e n = 0

oppure e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

Ne consegue che uno dei vettori del sistema si esprime attraverso tutti gli altri vettori del sistema. Che è ciò che doveva essere dimostrato (ecc.).

Adeguatezza

Sia uno dei vettori espresso linearmente attraverso tutti gli altri vettori del sistema:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n

Trasferiamo il vettore e k in lato destro questa uguaglianza:

0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n

Poiché il coefficiente del vettore e k è uguale a - 1 ≠ 0, otteniamo una rappresentazione non banale dello zero mediante un sistema di vettori e 1, e 2, . . . , e n , e questo, a sua volta, significa questo questo sistema i vettori sono linearmente dipendenti. Che è ciò che doveva essere dimostrato (ecc.).

Conseguenza:

• Un sistema di vettori è linearmente indipendente quando nessuno dei suoi vettori può essere espresso in termini di tutti gli altri vettori del sistema.
• Un sistema di vettori che contiene un vettore zero o due vettori uguali è linearmente dipendente.

Proprietà dei vettori linearmente dipendenti

1. Per i vettori bidimensionali e tridimensionali è soddisfatta la seguente condizione: due vettori linearmente dipendenti sono collineari. Due vettore collineare- linearmente dipendente.
2. Per i vettori tridimensionali è soddisfatta la seguente condizione: tre vettori linearmente dipendenti sono complanari. (3 vettori complanari sono linearmente dipendenti).
3. Per i vettori n-dimensionali è soddisfatta la seguente condizione: n+1 vettori sono sempre linearmente dipendenti.

Esempi di risoluzione di problemi che coinvolgono la dipendenza lineare o l'indipendenza lineare dei vettori

Esempio 3

Controlliamo i vettori a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 per indipendenza lineare.

Soluzione. I vettori sono linearmente dipendenti perché la dimensione dei vettori è inferiore al numero di vettori.

Esempio 4

Controlliamo l'indipendenza lineare dei vettori a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1.

Soluzione. Troviamo i valori dei coefficienti ai quali la combinazione lineare sarà uguale al vettore zero:

x1a + x2b + x3c1 = 0

Scriviamo l'equazione vettoriale in forma lineare:

x1 + x2 = 0 x1 + 2 x2 - x3 = 0 x1 + x3 = 0

Risolviamo questo sistema utilizzando il metodo di Gauss:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

Dalla 2a riga sottraiamo la 1a, dalla 3a alla 1a:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

Dalla 1a riga sottraiamo la 2a, alla 3a aggiungiamo la 2a:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Dalla soluzione segue che il sistema ha molte soluzioni. Ciò significa che esiste una combinazione diversa da zero di valori di tali numeri x 1, x 2, x 3 per la quale la combinazione lineare di a, b, c è uguale al vettore zero. Pertanto, i vettori a, b, c lo sono linearmente dipendente. ​​​​​​​

Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio

Definizione 1. Una combinazione lineare di vettori è la somma dei prodotti di questi vettori e scalari
:

Definizione 2. Sistema vettoriale
si dice sistema linearmente dipendente se la loro combinazione lineare (2.8) è nulla:

e tra i numeri
ce n'è almeno uno diverso da zero.

Definizione 3. Vettori
sono detti linearmente indipendenti se la loro combinazione lineare (2.8) svanisce solo nel caso in cui tutti i numeri.

Da queste definizioni si possono ricavare i seguenti corollari.

Corollario 1. In un sistema di vettori linearmente dipendenti, almeno un vettore può essere espresso come combinazione lineare degli altri.

Prova. Sia soddisfatta la (2.9) e, per chiarezza, sia il coefficiente
. Abbiamo allora:
. Si noti che è vero anche il contrario.

Corollario 2. Se il sistema di vettori
contiene un vettore zero, allora questo sistema è (necessariamente) linearmente dipendente: la dimostrazione è ovvia.

Corollario 3. Se tra N vettori
Qualunque k(
) i vettori sono linearmente dipendenti, questo è tutto N i vettori sono linearmente dipendenti (ometteremo la dimostrazione).

2 0 . Combinazioni lineari di due, tre e quattro vettori. Consideriamo i problemi della dipendenza lineare e dell'indipendenza dei vettori su una linea retta, sul piano e nello spazio. Presentiamo i teoremi corrispondenti.

Teorema 1. Affinché due vettori siano linearmente dipendenti è necessario e sufficiente che siano collineari.

Necessità. Passiamo ai vettori E linearmente dipendente. Ciò significa che la loro combinazione lineare
=0 e (per motivi di certezza)
. Ciò implica l'uguaglianza
e (per definizione di moltiplicazione di un vettore per un numero) vettori E collineare.

Adeguatezza. Passiamo ai vettori E collineare ( ║) (assumiamo che siano diversi dal vettore zero; altrimenti la loro dipendenza lineare è ovvia).

Per il Teorema (2.7) (vedi §2.1, punto 2 0) quindi
tale che
, O
– la combinazione lineare è pari a zero, e il coefficiente at uguale a 1 – vettori E linearmente dipendente.

Da questo teorema segue il seguente corollario.

Conseguenza. Se i vettori E non sono collineari, allora sono linearmente indipendenti.

Teorema 2. Affinché tre vettori siano linearmente dipendenti è necessario e sufficiente che siano complanari.

Necessità. Passiamo ai vettori ,E linearmente dipendente. Mostriamo che sono complanari.

Dalla definizione di dipendenza lineare dei vettori consegue l'esistenza dei numeri
E tale che la combinazione lineare
, e allo stesso tempo (per essere precisi)
. Quindi da questa uguaglianza possiamo esprimere il vettore :=
, cioè il vettore uguale alla diagonale di un parallelogramma costruito sui vettori sul lato destro di questa uguaglianza (Fig. 2.6). Ciò significa che i vettori ,E giacciono sullo stesso piano.

Adeguatezza. Passiamo ai vettori ,E complanare. Mostriamo che sono linearmente dipendenti.

Escludiamo il caso di collinearità di una qualsiasi coppia di vettori (perché allora questa coppia è linearmente dipendente e per il Corollario 3 (vedi paragrafo 1 0) tutti e tre i vettori sono linearmente dipendenti). Si noti che questa ipotesi esclude anche l'esistenza di un vettore zero tra questi tre.

Spostiamo tre vettori complanari su un piano e portiamoli ad un'origine comune. Fino alla fine del vettore tracciare linee parallele ai vettori E ; otteniamo i vettori E (Fig. 2.7) - la loro esistenza è assicurata dal fatto che i vettori E vettori che per ipotesi non sono collineari. Ne consegue che il vettore =+. Riscrivendo questa uguaglianza nella forma (–1) ++=0, concludiamo che i vettori ,E linearmente dipendente.

Dal teorema dimostrato seguono due corollari.

Corollario 1. Permettere E vettori non collineari, vettore – arbitrario, giacente nel piano definito dai vettori E , vettore. Poi ci sono i numeri E tale che

=+. (2.10)

Corollario 2. Se i vettori ,E non sono complanari, quindi sono linearmente indipendenti.

Teorema 3. Quattro vettori qualsiasi sono linearmente dipendenti.

Ometteremo la dimostrazione; con alcune modifiche copia la dimostrazione del Teorema 2. Diamo un corollario di questo teorema.

Conseguenza. Per tutti i vettori non complanari ,,e qualsiasi vettore
E tale che

. (2.11)

Commento. Per i vettori nello spazio (tridimensionale), i concetti di dipendenza e indipendenza lineare hanno, come segue dai Teoremi 1-3 sopra, un significato geometrico semplice.

Siano due vettori linearmente dipendenti E . In questo caso, uno di essi è una combinazione lineare del secondo, cioè differisce semplicemente da esso per un fattore numerico (ad esempio,
). Dal punto di vista geometrico, ciò significa che entrambi i vettori si trovano su una linea comune; possono avere direzioni uguali o opposte (Fig. 2.8 xx).

Se due vettori si trovano ad angolo tra loro (Fig. 2.9 xx), in questo caso è impossibile ottenerne uno moltiplicando l'altro per un numero: tali vettori sono linearmente indipendenti. Pertanto, l'indipendenza lineare di due vettori E significa che questi vettori non possono essere disposti su una linea retta.

Scopriamo il significato geometrico della dipendenza lineare e dell'indipendenza di tre vettori.

Passiamo ai vettori ,E sono linearmente dipendenti e lasciano (per essere precisi) il vettore è una combinazione lineare di vettori E , cioè situato nel piano contenente i vettori E . Ciò significa che i vettori ,E giacciono sullo stesso piano. È vero anche il contrario: se i vettori ,E giacciono sullo stesso piano e sono linearmente dipendenti.

Quindi, i vettori ,E sono linearmente indipendenti se e solo se non giacciono sullo stesso piano.

3 0 . Il concetto di base. Uno dei concetti più importanti nell'algebra lineare e vettoriale è il concetto di base. Introduciamo alcune definizioni.

Definizione 1. Una coppia di vettori si dice ordinata se viene specificato quale vettore di questa coppia è considerato il primo e quale il secondo.

Definizione 2. Coppia ordinata ,i vettori non collineari è detta base sul piano definito dai vettori dati.

Teorema 1. Qualsiasi vettore sul piano può essere rappresentato come una combinazione lineare del sistema base di vettori ,:

(2.12)

e questa rappresentazione è l'unica.

Prova. Passiamo ai vettori E formare una base. Quindi qualsiasi vettore può essere rappresentato nella forma
.

Per dimostrare l'unicità, supponiamo che esista un'altra scomposizione
. Abbiamo allora = 0, e almeno una delle differenze è diversa da zero. Quest'ultimo significa che i vettori E linearmente dipendente, cioè collineare; ciò contraddice l'affermazione secondo cui costituiscono una base.

Ma poi c'è solo decomposizione.

Definizione 3. Una terna di vettori si dice ordinata se viene indicato quale vettore è considerato il primo, quale il secondo e quale il terzo.

Definizione 4. Nello spazio una terna ordinata di vettori non complanari è chiamata base.

Anche qui vale il teorema di scomposizione e unicità.

Teorema 2. Qualsiasi vettore può essere rappresentato come una combinazione lineare del sistema vettoriale di base ,,:

(2.13)

e questa rappresentazione è unica (ometteremo la dimostrazione del teorema).

Negli sviluppi (2.12) e (2.13) le quantità sono chiamate coordinate vettoriali in una determinata base (più precisamente, mediante coordinate affini).

Con base fissa
E
puoi scrivere
.

Ad esempio, se viene fornita la base
e questo è dato
, allora questo significa che esiste una rappresentazione (scomposizione)
.

4 0 . Operazioni lineari su vettori in forma di coordinate. L'introduzione di una base consente di sostituire le operazioni lineari sui vettori con operazioni lineari ordinarie sui numeri: le coordinate di questi vettori.

Diamo qualche base
. Ovviamente, specificando le coordinate del vettore in questa base si determina completamente il vettore stesso. Valgono le seguenti proposte:

a) due vettori
E
sono uguali se e solo se le loro coordinate corrispondenti sono uguali:

b) quando si moltiplica un vettore
per numero le sue coordinate vengono moltiplicate per questo numero:

; (2.15)

c) quando si aggiungono vettori, vengono aggiunte le loro coordinate corrispondenti:

Ometteremo le dimostrazioni di queste proprietà; Dimostriamo la proprietà b) solo a titolo di esempio. Abbiamo

==

Commento. Nello spazio (sull'aereo) puoi scegliere infinite basi.

Diamo un esempio di transizione da una base all'altra, stabiliamo relazioni tra coordinate vettoriali in basi diverse.

Esempio 1. Nel sistema di base
sono dati tre vettori:
,
E
. In base ,,vettore ha decomposizione. Trova le coordinate vettoriali nella base
.

Soluzione. Abbiamo espansioni:
,
,
; quindi,
=
+2
+
= =
, questo è
nella base
.

Esempio 2. Inserisci qualche base
quattro vettori sono dati dalle loro coordinate:
,
,
E
.

Scopri se i vettori si formano
base; se la risposta è positiva, trova la scomposizione del vettore su questa base.

Soluzione. 1) i vettori formano una base se sono linearmente indipendenti. Facciamo una combinazione lineare di vettori
(
) e scoprire cosa
E va a zero:
=0. Abbiamo:

=
+
+
=

Definendo l'uguaglianza dei vettori in forma di coordinate, otteniamo il seguente sistema di equazioni (algebriche lineari omogenee):
;
;
, il cui determinante
=1
, cioè il sistema ha (solo) una soluzione banale
. Ciò significa indipendenza lineare dei vettori
e quindi costituiscono una base.

2) espandere il vettore su questa base. Abbiamo: =
o in forma coordinata.

Passando all'uguaglianza dei vettori in forma di coordinate, otteniamo un sistema di equazioni algebriche lineari disomogenee:
;
;
. Risolvendolo (ad esempio, utilizzando la regola di Cramer), otteniamo:
,
,
E (
)
. Abbiamo la scomposizione vettoriale nella base
:=.

5 0 . Proiezione di un vettore su un asse. Proprietà delle proiezioni. Lascia che ci sia un asse l, cioè una linea retta con una direzione scelta su di essa e sia dato un vettore Definiamo il concetto di proiezione vettoriale per asse l.

Definizione. Proiezione vettoriale per asse l viene chiamato il prodotto del modulo di questo vettore e il coseno dell'angolo formato dall'asse l e vettore (Fig. 2.10):

. (2.17)

Un corollario di questa definizione è l'affermazione che vettori uguali hanno proiezioni uguali (sullo stesso asse).

Notiamo le proprietà delle proiezioni.

1) proiezione della somma dei vettori su un asse l uguale alla somma delle proiezioni dei termini dei vettori sullo stesso asse:

2) la proiezione del prodotto di uno scalare per un vettore è uguale al prodotto di questo scalare per la proiezione di un vettore sullo stesso asse:

=
. (2.19)

Conseguenza. La proiezione di una combinazione lineare di vettori sull'asse è uguale alla combinazione lineare delle loro proiezioni:

Tralasceremo le dimostrazioni delle proprietà.

6 0 . Sistema di coordinate cartesiane rettangolari nello spazio.Scomposizione di un vettore in vettori unitari degli assi. Si scelgano come base tre vettori unitari reciprocamente perpendicolari; introduciamo notazioni speciali per loro
. Collocando i loro inizi in un punto O, noi indirizzeremo lungo di essi (ai sensi dell'orts
) assi coordinati Bue,Ehi eO z(un asse con direzione, origine e unità di lunghezza selezionate su di esso è chiamato asse delle coordinate).

Definizione. Un sistema ordinato di tre assi di coordinate reciprocamente perpendicolari con un'origine comune e un'unità di lunghezza comune è chiamato sistema di coordinate cartesiane rettangolari nello spazio.

Asse Bue chiamato asse delle ascisse, Ehi– asse delle ordinate uO z – applicatore ad asse.

Affrontiamo l'espansione di un vettore arbitrario in termini di base
. Dal teorema (vedi §2.2, paragrafo 3 0, (2.13)) segue che
può essere ampliato in modo univoco sulla base
(qui invece di designare le coordinate
utilizzo
):

. (2.21)

B (2.21)
Coordinate vettoriali dell'essenza (rettangolare cartesiano). . Il significato delle coordinate cartesiane è stabilito dal seguente teorema.

Teorema. Coordinate cartesiane rettangolari
vettore sono proiezioni di questo vettore rispettivamente sull'asse Bue,Ehi eO z.

Prova. Posizioniamo il vettore all'origine del sistema di coordinate - punto O. Quindi la sua fine coinciderà con un certo punto
.

Esaminiamo il punto
tre piani paralleli ai piani coordinati Oyz,Oxz E Ossi(Fig. 2.11xx). Otteniamo quindi:

. (2.22)

Nella (2.22) i vettori
E
sono chiamate componenti vettoriali
lungo gli assi Bue,Ehi eO z.

Lascia passare
E sono indicati rispettivamente gli angoli formati dal vettore con orti
. Quindi per i componenti otteniamo le seguenti formule:

=
=
,
=
=
,
=
=
(2.23)

Dalla (2.21), (2.22) (2.23) troviamo:

=
=
;=
=
;=
=
(2.23)

– coordinate
vettore ci sono proiezioni di questo vettore sugli assi delle coordinate Bue,Ehi eO z rispettivamente.

Commento. Numeri
sono chiamati coseni direzionali del vettore .

Modulo vettoriale (diagonale di un parallelepipedo rettangolare) si calcola con la formula:

. (2.24)

Dalle formule (2.23) e (2.24) ne consegue che i coseni direzionali possono essere calcolati utilizzando le formule:

=
;
=
;
=
. (2.25)

Elevando entrambi i lati di ciascuna delle uguaglianze nella (2.25) e sommando termine per termine i lati sinistro e destro delle uguaglianze risultanti, arriviamo alla formula:

– non tre angoli qualsiasi formano una certa direzione nello spazio, ma solo quelli i cui coseni sono legati dalla relazione (2.26).

7 0 . Vettore raggio e coordinate puntuali.Determinazione di un vettore in base al suo inizio e alla sua fine. Introduciamo una definizione.

Definizione. Il raggio vettore (indicato ) è il vettore che collega l'origine O con questo punto (Fig. 2.12 xx):

. (2.27)

Qualsiasi punto nello spazio corrisponde ad un certo raggio vettore (e viceversa). Pertanto, i punti nello spazio sono rappresentati nell'algebra vettoriale dai loro vettori del raggio.

Ovviamente le coordinate
punti M sono proiezioni del suo raggio vettore
sugli assi coordinati:

(2.28’)

e così

(2.28)

– il raggio vettore di un punto è un vettore le cui proiezioni sugli assi coordinati sono uguali alle coordinate di questo punto. Ciò porta a due voci:
E
.

Otteniamo formule per il calcolo delle proiezioni vettoriali
secondo le coordinate del suo punto di origine
e il punto finale
.

Disegniamo i vettori del raggio
e vettore
(Fig. 2.13). Lo capiamo

=
=(2.29)

– le proiezioni del vettore sui vettori unitari delle coordinate sono pari alle differenze tra le corrispondenti coordinate di fine e inizio del vettore.

8 0 . Alcuni problemi che coinvolgono le coordinate cartesiane.

1) condizioni di collinearità dei vettori . Dal teorema (vedi §2.1, paragrafo 2 0, formula (2.7)) segue che per collinearità di vettori E è necessario e sufficiente che valga la seguente relazione: =. Da questa uguaglianza vettoriale otteniamo tre uguaglianze in forma di coordinate:, che implica la condizione per la collinearità dei vettori in forma di coordinate:

(2.30)

– per collinearità di vettori E è necessario e sufficiente che le loro coordinate corrispondenti siano proporzionali.

2) distanza tra i punti . Dalla rappresentazione (2.29) segue che la distanza
tra i punti
E
è determinato dalla formula

=
=. (2.31)

3) divisione di un segmento in un dato rapporto . Diamo i punti
E
e atteggiamento
. Ho bisogno di trovare
– coordinate del punto M (Fig. 2.14).

Dalla condizione di collinearità dei vettori si ha:
, Dove
E

. (2.32)

Dalla (2.32) otteniamo in forma coordinata:

Dalle formule (2.32’) si ottengono le formule per calcolare le coordinate del punto medio del segmento
, supponendo
:

Commento. Conteremo i segmenti
E
positivo o negativo a seconda che la loro direzione coincida con quella iniziale
segmento fino alla fine
, o non corrisponde. Quindi, utilizzando le formule (2.32) – (2.32”), puoi trovare le coordinate del punto che divide il segmento
esternamente, cioè in modo tale che il punto di divisione Mè sulla continuazione del segmento
, e non al suo interno. Allo stesso tempo, ovviamente,
.

4) Equazione della superficie sferica . Creiamo un'equazione per una superficie sferica: il luogo geometrico dei punti
, equidistanti a distanza da un centro fisso: un punto
. È ovvio che in questo caso
e tenendo conto della formula (2.31)

L'equazione (2.33) è l'equazione della superficie sferica desiderata.

Presentato da noi operazioni lineari sui vettori consentono di creare varie espressioni per quantità vettoriali e trasformarli utilizzando le proprietà impostate per queste operazioni.

Sulla base di un dato insieme di vettori a 1, ..., a n, puoi creare un'espressione della forma

dove a 1, ... e n sono numeri reali arbitrari. Questa espressione si chiama combinazione lineare di vettori un 1, ..., un n. I numeri α i, i = 1, n, rappresentano coefficienti di combinazione lineare. Viene anche chiamato un insieme di vettori sistema di vettori.

In relazione al concetto introdotto di combinazione lineare di vettori, si pone il problema di descrivere un insieme di vettori che può essere scritto come combinazione lineare di un dato sistema di vettori a 1, ..., a n. Inoltre, sorgono domande naturali sulle condizioni in cui esiste una rappresentazione di un vettore sotto forma di combinazione lineare e sull'unicità di tale rappresentazione.

Definizione 2.1. I vettori a 1, ... e n sono chiamati linearmente dipendente, se esiste un insieme di coefficienti α 1 , ... , α n tale che

α 1 a 1 + ... + α n а n = 0 (2.2)

e almeno uno di questi coefficienti è diverso da zero. Se l'insieme di coefficienti specificato non esiste, vengono chiamati i vettori linearmente indipendenti.

Se α 1 = ... = α n = 0, allora, ovviamente, α 1 a 1 + ... + α n a n = 0. Tenendo presente questo, possiamo dire questo: vettori a 1, ..., e n sono linearmente indipendenti se dall'uguaglianza (2.2) segue che tutti i coefficienti α 1 , ... , α n sono uguali a zero.

Il seguente teorema spiega perché il nuovo concetto è chiamato il termine "dipendenza" (o "indipendenza") e fornisce un semplice criterio per la dipendenza lineare.

Teorema 2.1. Affinché i vettori a 1, ..., en, n > 1, siano linearmente dipendenti, è necessario e sufficiente che uno di essi sia una combinazione lineare degli altri.

◄ Necessità. Supponiamo che i vettori a 1, ... e n siano linearmente dipendenti. Secondo la Definizione 2.1 di dipendenza lineare, nell'uguaglianza (2.2) a sinistra c'è almeno un coefficiente diverso da zero, ad esempio α 1. Lasciando il primo termine a sinistra dell'uguaglianza, spostiamo gli altri a destra, cambiando segno, come al solito. Dividendo l'uguaglianza risultante per α 1, otteniamo

a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n /α 1 ⋅ a n

quelli. rappresentazione del vettore a 1 come combinazione lineare dei restanti vettori a 2, ..., a n.

Adeguatezza. Supponiamo, ad esempio, che il primo vettore a 1 possa essere rappresentato come una combinazione lineare dei restanti vettori: a 1 = β 2 a 2 + ... + β n a n. Trasferendo tutti i termini da destra a sinistra otteniamo a 1 - β 2 a 2 - ... - β n a n = 0, cioè una combinazione lineare di vettori a 1, ..., an con coefficienti α 1 = 1, α 2 = - β 2, ..., α n = - β n, pari a vettore nullo. In questa combinazione lineare, non tutti i coefficienti sono zero. Secondo la Definizione 2.1, i vettori a 1, ..., e n sono linearmente dipendenti.

La definizione e il criterio per la dipendenza lineare sono formulati per implicare la presenza di due o più vettori. Tuttavia, possiamo anche parlare di una dipendenza lineare di un vettore. Per realizzare questa possibilità, invece di “i vettori sono linearmente dipendenti”, è necessario dire “il sistema di vettori è linearmente dipendente”. È facile vedere che l'espressione “un sistema di un vettore è linearmente dipendente” significa che questo singolo vettore è zero (in una combinazione lineare c'è solo un coefficiente e non dovrebbe essere uguale a zero).

Il concetto di dipendenza lineare ha una semplice interpretazione geometrica. Le tre affermazioni seguenti chiariscono questa interpretazione.

Teorema 2.2. Due vettori sono linearmente dipendenti se e solo se collineare.

◄ Se i vettori a e b sono linearmente dipendenti, allora uno di essi, ad esempio a, è espresso attraverso l'altro, cioè a = λb per un numero reale λ. Secondo la definizione 1.7 funziona vettori per numero, i vettori a e b sono collineari.

Siano ora i vettori a e b collineari. Se sono entrambi nulli, allora è ovvio che sono linearmente dipendenti, poiché qualsiasi loro combinazione lineare è uguale al vettore zero. Sia uno di questi vettori diverso da 0, ad esempio il vettore b. Indichiamo con λ il rapporto tra le lunghezze dei vettori: λ = |a|/|b|. I vettori collineari possono essere unidirezionale O diretto in modo opposto. In quest'ultimo caso cambiamo il segno di λ. Allora, verificando la Definizione 1.7, siamo convinti che a = λb. Secondo il Teorema 2.1, i vettori aeb sono linearmente dipendenti.

Osservazione 2.1. Nel caso di due vettori, tenendo conto del criterio della dipendenza lineare, il teorema dimostrato può essere riformulato così: due vettori sono collineari se e solo se uno di essi è rappresentato come il prodotto dell'altro da un numero. Questo è un criterio conveniente per la collinearità di due vettori.

Teorema 2.3. Tre vettori sono linearmente dipendenti se e solo se complanare.

◄ Se tre vettori a, b, c sono linearmente dipendenti, allora, secondo il Teorema 2.1, uno di essi, ad esempio a, è una combinazione lineare degli altri: a = βb + γc. Combiniamo le origini dei vettori b e c nel punto A. Allora i vettori βb, γс avranno un'origine comune nel punto A e lungo secondo la regola del parallelogramma, la loro somma è quelli. il vettore a sarà un vettore con origine A e la fine, che è il vertice di un parallelogramma costruito sui vettori componenti. Pertanto tutti i vettori giacciono sullo stesso piano, cioè complanari.

Siano complanari i vettori a, b, c. Se uno di questi vettori è zero, allora è ovvio che sarà una combinazione lineare degli altri. È sufficiente prendere tutti i coefficienti di una combinazione lineare uguali a zero. Pertanto, possiamo supporre che tutti e tre i vettori non siano zero. Compatibile iniziato di questi vettori in un punto comune O. Lascia che le loro estremità siano rispettivamente i punti A, B, C (Fig. 2.1). Per il punto C tracciamo rette parallele alle rette passanti per coppie di punti O, A e O, B. Designando i punti di intersezione come A" e B", otteniamo un parallelogramma OA"CB", quindi OC" = OA" + OB". Il vettore OA" e il vettore diverso da zero a = OA sono collineari, e quindi il primo di essi può essere ottenuto moltiplicando il secondo per un numero reale α:OA" = αOA. Allo stesso modo, OB" = βOB, β ∈ R. Di conseguenza, otteniamo che OC" = α OA. + βOB, cioè il vettore c è una combinazione lineare dei vettori a e b. Secondo il Teorema 2.1, i vettori a, b, c sono linearmente dipendenti.

Teorema 2.4. Quattro vettori qualsiasi sono linearmente dipendenti.

◄ Eseguiamo la dimostrazione secondo lo stesso schema del Teorema 2.3. Considera quattro vettori arbitrari a, b, c e d. Se uno dei quattro vettori è zero, o tra di essi ci sono due vettori collineari, oppure tre dei quattro vettori sono complanari, allora questi quattro vettori sono linearmente dipendenti. Ad esempio, se i vettori a e b sono collineari, allora possiamo creare la loro combinazione lineare αa + βb = 0 con coefficienti diversi da zero, quindi aggiungere i restanti due vettori a questa combinazione, prendendo zero come coefficienti. Otteniamo una combinazione lineare di quattro vettori uguali a 0, in cui sono presenti coefficienti diversi da zero.

Pertanto, possiamo assumere che tra i quattro vettori selezionati, nessun vettore è zero, nessuno due è collineare e nessuno tre è complanare. Scegliamo il punto O come inizio comune. Quindi le estremità dei vettori a, b, c, d saranno alcuni punti A, B, C, D (Fig. 2.2). Per il punto D tracciamo tre piani paralleli ai piani OBC, OCA, OAB, e siano A", B", C" i punti di intersezione di questi piani rispettivamente con le rette OA, OB, OS. Otteniamo un parallelepipedo OA" C "B" C" B"DA", e i vettori a, b, c giacciono sui suoi bordi emergenti dal vertice O. Poiché il quadrilatero OC"DC" è un parallelogramma, allora OD = OC" + OC " A sua volta, il segmento OC" è un parallelogramma OA"C"B", quindi OC" = OA" + OB" e OD = OA" + OB" + OC" .

Resta da notare che le coppie di vettori OA ≠ 0 e OA" , OB ≠ 0 e OB" , OC ≠ 0 e OC" sono collineari, e quindi è possibile selezionare i coefficienti α, β, γ in modo che OA" = αOA, OB" = βOB e OC" = γOC. Alla fine otteniamo OD = αOA + βOB + γOC. Di conseguenza, il vettore OD è espresso attraverso gli altri tre vettori, e tutti e quattro i vettori, secondo il Teorema 2.1, sono linearmente dipendenti.

UN 1 = { 3, 5, 1 , 4 }, UN 2 = { –2, 1, -5 , -7 }, UN 3 = { -1, –2, 0, –1 }.

Soluzione. Cerchiamo una soluzione generale del sistema di equazioni

UN 1 X 1 + UN 2 X 2 + UN 3 X 3 = Θ

Metodo di Gauss. Per fare ciò, scriviamo questo sistema omogeneo in coordinate:

Matrice del sistema

Il sistema consentito ha la forma: (rA = 2, N= 3). Il sistema è cooperativo e incerto. La sua soluzione generale ( X 2 – variabile libera): X 3 = 13X 2 ; 3X 1 – 2X 2 – 13X 2 = 0 => X 1 = 5X 2 => X o = . La presenza di una soluzione particolare diversa da zero, ad esempio, indica che i vettori UN 1 , UN 2 , UN 3 linearmente dipendente.

Esempio 2.

Scopri se un dato sistema di vettori è linearmente dipendente o linearmente indipendente:

1. UN 1 = { -20, -15, - 4 }, UN 2 = { –7, -2, -4 }, UN 3 = { 3, –1, –2 }.

Soluzione. Consideriamo un sistema omogeneo di equazioni UN 1 X 1 + UN 2 X 2 + UN 3 X 3 = Θ

o in forma estesa (per coordinate)

Il sistema è omogeneo. Se non è degenerato, allora ha una soluzione unica. Nel caso sistema omogeneo– soluzione zero (banale). Ciò significa che in questo caso il sistema di vettori è indipendente. Se il sistema è degenere allora ha soluzioni diverse da zero e quindi è dipendente.

Controlliamo la degenerazione del sistema:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Il sistema non è degenere e, quindi, i vettori UN 1 , UN 2 , UN 3 linearmente indipendenti.

Incarichi. Scopri se un dato sistema di vettori è linearmente dipendente o linearmente indipendente:

1. UN 1 = { -4, 2, 8 }, UN 2 = { 14, -7, -28 }.

2. UN 1 = { 2, -1, 3, 5 }, UN 2 = { 6, -3, 3, 15 }.

3. UN 1 = { -7, 5, 19 }, UN 2 = { -5, 7 , -7 }, UN 3 = { -8, 7, 14 }.

4. UN 1 = { 1, 2, -2 }, UN 2 = { 0, -1, 4 }, UN 3 = { 2, -3, 3 }.

5. UN 1 = { 1, 8 , -1 }, UN 2 = { -2, 3, 3 }, UN 3 = { 4, -11, 9 }.

6. UN 1 = { 1, 2 , 3 }, UN 2 = { 2, -1 , 1 }, UN 3 = { 1, 3, 4 }.

7. UN 1 = {0, 1, 1 , 0}, UN 2 = {1, 1 , 3, 1}, UN 3 = {1, 3, 5, 1}, UN 4 = {0, 1, 1, -2}.

8. UN 1 = {-1, 7, 1 , -2}, UN 2 = {2, 3 , 2, 1}, UN 3 = {4, 4, 4, -3}, UN 4 = {1, 6, -11, 1}.

9. Dimostrare che un sistema di vettori sarà linearmente dipendente se contiene:

a) due vettori uguali;

b) due vettori proporzionali.