La derivata di una funzione è uno degli argomenti complicati in curriculum scolastico. Non tutti i laureati risponderanno alla domanda su cosa sia un derivato.
Questo articolo spiega in modo semplice e chiaro cos'è un derivato e perché è necessario.. Non ci impegneremo ora per il rigore matematico della presentazione. La cosa più importante è capire il significato.
Ricordiamo la definizione:
La derivata è il tasso di variazione della funzione.
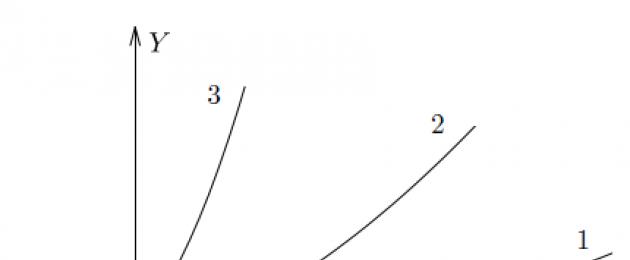
La figura mostra i grafici di tre funzioni. Quale pensi cresca più velocemente?

La risposta è ovvia: la terza. Ha il più alto tasso di variazione, cioè il più grande derivato.
Ecco un altro esempio.
Kostya, Grisha e Matvey hanno trovato lavoro contemporaneamente. Vediamo come è cambiato il loro reddito durante l'anno:

Puoi vedere tutto sul grafico subito, giusto? Il reddito di Kostya è più che raddoppiato in sei mesi. E anche il reddito di Grisha è aumentato, ma solo di poco. E il reddito di Matthew è sceso a zero. Le condizioni di partenza sono le stesse, ma la velocità di variazione della funzione, ad es. derivato, - diverso. Per quanto riguarda Matvey, il derivato del suo reddito è generalmente negativo.
Intuitivamente, possiamo facilmente stimare la velocità di variazione di una funzione. Ma come lo facciamo?
Quello che stiamo veramente osservando è quanto ripidamente il grafico della funzione sale (o scende). In altre parole, quanto velocemente y cambia con x. Ovviamente, la stessa funzione in punti diversi può avere un valore diverso della derivata, cioè può cambiare più velocemente o più lentamente.
La derivata di una funzione è indicata da .
Mostriamo come trovare usando il grafico.

Viene disegnato un grafico di alcune funzioni. Prendi un punto con un'ascissa. Disegna una tangente al grafico della funzione a questo punto. Vogliamo valutare quanto ripidamente sale il grafico della funzione. Un valore utile per questo è tangente della pendenza della tangente.
La derivata di una funzione in un punto è uguale alla tangente della pendenza della tangente tracciata sul grafico della funzione in quel punto.
Nota: come angolo di inclinazione della tangente, prendiamo l'angolo tra la tangente e la direzione positiva dell'asse.
A volte gli studenti chiedono qual è la tangente al grafico di una funzione. Questa è una retta che ha l'unico punto in comune con il grafico in questa sezione, inoltre, come mostrato nella nostra figura. Sembra una tangente a un cerchio.
Cerchiamo . Ricordiamo che la tangente di un angolo acuto in triangolo rettangolo uguale al rapporto tra la gamba opposta e quella adiacente. Dal triangolo:
Abbiamo trovato la derivata usando il grafico senza nemmeno conoscere la formula della funzione. Tali compiti si trovano spesso nell'esame di matematica sotto il numero.
C'è un'altra importante correlazione. Ricordiamo che la retta è data dall'equazione
Viene chiamata la quantità in questa equazione pendenza di una retta. È uguale alla tangente dell'angolo di inclinazione della retta all'asse.
.
Lo capiamo
Ricordiamo questa formula. Esprime il significato geometrico della derivata.
La derivata di una funzione in un punto è uguale alla pendenza della tangente tracciata sul grafico della funzione in quel punto.
In altre parole, la derivata è uguale alla tangente della pendenza della tangente.
Abbiamo già detto che una stessa funzione può avere derivate diverse in punti diversi. Vediamo come la derivata è correlata al comportamento della funzione.
Tracciamo un grafico di alcune funzioni. Lascia che questa funzione aumenti in alcune aree e diminuisca in altre e a velocità diverse. E lascia che questa funzione abbia punti massimo e minimo.

Ad un certo punto, la funzione è in aumento. La tangente al grafico, tracciata nel punto, forma un angolo acuto con la direzione positiva dell'asse. Quindi la derivata è positiva al punto.
A questo punto, la nostra funzione sta diminuendo. La tangente in questo punto forma un angolo ottuso con la direzione positiva dell'asse. Poiché la tangente di un angolo ottuso è negativa, la derivata nel punto è negativa.
Ecco cosa succede:
Se una funzione è crescente, la sua derivata è positiva.
Se diminuisce, la sua derivata è negativa.
E cosa accadrà al massimo e al minimo? Vediamo che in (punto massimo) e (punto minimo) la tangente è orizzontale. Pertanto, la tangente della pendenza della tangente in questi punti è zero e anche la derivata è zero.
Il punto è il punto massimo. A questo punto l'aumento della funzione è sostituito da una diminuzione. Di conseguenza, il segno della derivata cambia nel punto da "più" a "meno".
Nel punto - il punto di minimo - anche la derivata è uguale a zero, ma il suo segno cambia da "meno" a "più".
Conclusione: con l'aiuto della derivata, puoi scoprire tutto ciò che ci interessa sul comportamento della funzione.
Se la derivata è positiva, allora la funzione è crescente.
Se la derivata è negativa, la funzione è decrescente.
Nel punto massimo, la derivata è zero e cambia segno da più a meno.
Nel punto minimo, anche la derivata è zero e cambia segno da meno a più.
Scriviamo questi risultati sotto forma di tabella:
| aumenta | punto massimo | decrescente | punto minimo | aumenta | |
| + | 0 | - | 0 | + |
Facciamo due piccole precisazioni. Ne avrai bisogno per risolvere i problemi dell'esame. Un altro - nel primo anno, con uno studio più serio di funzioni e derivati.
Un caso è possibile quando la derivata di una funzione in un punto è uguale a zero, ma la funzione non ha né un massimo né un minimo a questo punto. Questo cosiddetto :

In un punto, la tangente al grafico è orizzontale e la derivata è zero. Tuttavia, prima del punto la funzione è aumentata - e dopo il punto continua ad aumentare. Il segno della derivata non cambia: è rimasto positivo com'era.
Succede anche che nel punto di massimo o minimo la derivata non esista. Sul grafico, ciò corrisponde a un'interruzione netta, quando è impossibile tracciare una tangente in un dato punto.

Ma come trovare la derivata se la funzione è data non da un grafico, ma da una formula? In questo caso, si applica
Per prima cosa, prova a trovare l'ambito della funzione:
Sei riuscito? Confrontiamo le risposte:
Va bene? Molto bene!
Ora proviamo a trovare l'intervallo della funzione:

Fondare? Confrontare:
Era d'accordo? Molto bene!
Lavoriamo di nuovo con i grafici, solo che ora è un po' più difficile: trovare sia il dominio della funzione che l'intervallo della funzione.
Come trovare sia il dominio che l'intervallo di una funzione (avanzato)

Ecco cosa è successo:
Con la grafica, penso che tu l'abbia capito. Ora proviamo a trovare il dominio della funzione secondo le formule (se non sai come fare, leggi la sezione su):
Sei riuscito? Controllo risposte:
- , poiché l'espressione radice deve essere maggiore o uguale a zero.
- , poiché è impossibile dividere per zero e l'espressione radicale non può essere negativa.
- , poiché, rispettivamente, per tutti.
- perché non puoi dividere per zero.
Tuttavia, abbiamo ancora un momento che non è stato risolto ...
Vorrei ribadire la definizione e concentrarmi su di essa:
Si accorse? La parola "solo" è un elemento molto, molto importante della nostra definizione. Proverò a spiegarti sulle dita.
Diciamo di avere una funzione data da una retta. . Quando, sostituiamo questo valore nella nostra "regola" e lo otteniamo. Un valore corrisponde a un valore. Possiamo anche creare una tabella di vari valori e tracciare una determinata funzione per verificarlo.
"Aspetto! - dici, - "" si incontra due volte!" Quindi forse la parabola non è una funzione? No, lo è!
Il fatto che "" ricorra due volte è tutt'altro che un motivo per accusare la parabola di ambiguità!
Il fatto è che, calcolando, abbiamo ottenuto un gioco. E quando calcoliamo, abbiamo un gioco. Quindi è vero, la parabola è una funzione. Guarda il grafico:

Fatto? In caso contrario, ecco un esempio di vita reale per te, lontano dalla matematica!
Diciamo che abbiamo un gruppo di candidati che si sono incontrati durante la presentazione dei documenti, ognuno dei quali ha raccontato in una conversazione dove vive:

D'accordo, è abbastanza realistico che più ragazzi vivano nella stessa città, ma è impossibile che una persona viva in più città contemporaneamente. Questa è, per così dire, una rappresentazione logica della nostra "parabola" - Diverse x differenti corrispondono alla stessa y.
Ora facciamo un esempio in cui la dipendenza non è una funzione. Diciamo che questi stessi ragazzi hanno detto per quali specialità hanno fatto domanda:

Qui abbiamo una situazione completamente diversa: una persona può facilmente fare domanda per una o più direzioni. Cioè un elemento gli insiemi sono messi in corrispondenza più elementi imposta. Rispettivamente, non è una funzione.
Mettiamo alla prova le tue conoscenze nella pratica.
Determina dalle immagini cos'è una funzione e cosa non lo è:

Fatto? Ed ecco risposte:
- La funzione è - B,E.
- Non una funzione - A, B, D, D.
Ti chiedi perché? Sì, ecco perché:

In tutte le figure tranne IN) e E) ce ne sono diversi per uno!
Sono sicuro che ora puoi facilmente distinguere una funzione da una non funzione, dire cos'è un argomento e cos'è una variabile dipendente e anche determinare l'ambito dell'argomento e l'ambito della funzione. Passiamo alla sezione successiva: come definire una funzione?
Modi per impostare una funzione
Cosa pensi significhino le parole "imposta funzione"? Esatto, significa spiegare a tutti di quale funzione stiamo parlando in questo caso. Inoltre, spiega in modo tale che tutti ti capiscano correttamente e che i grafici delle funzioni disegnati dalle persone secondo la tua spiegazione fossero gli stessi.
Come posso fare ciò? Come impostare una funzione? Il modo più semplice, che è già stato utilizzato più di una volta in questo articolo: usando una formula. Scriviamo una formula e, sostituendovi un valore, calcoliamo il valore. E come ricorderete, una formula è una legge, una regola secondo la quale diventa chiaro a noi e ad un'altra persona come una X si trasformi in una Y.
Di solito, questo è esattamente quello che fanno: nelle attività vediamo funzioni già pronte definite da formule, tuttavia, ci sono altri modi per impostare una funzione che tutti dimenticano, e quindi la domanda "in quale altro modo puoi impostare una funzione?" confonde. Diamo un'occhiata a tutto in ordine e iniziamo con il metodo analitico.
Modo analitico per definire una funzione
Il metodo analitico è compito di una funzione che utilizza una formula. Questo è il modo più universale, completo e inequivocabile. Se hai una formula, allora sai assolutamente tutto sulla funzione: puoi creare una tabella di valori su di essa, puoi costruire un grafico, determinare dove la funzione aumenta e dove diminuisce, in generale, esplorala in toto.
Consideriamo una funzione. Cosa importa?
"Cosa significa?" - tu chiedi. Ti spiego ora.
Lascia che ti ricordi che nella notazione, l'espressione tra parentesi è chiamata argomento. E questo argomento può essere qualsiasi espressione, non necessariamente semplice. Di conseguenza, qualunque sia l'argomento (espressione tra parentesi), lo scriveremo invece nell'espressione.
Nel nostro esempio, sarà simile a questo:
Considera un'altra attività relativa al metodo analitico per specificare una funzione che avrai nell'esame.
Trova il valore dell'espressione, in.
Sono sicuro che all'inizio eri spaventato quando hai visto un'espressione del genere, ma non c'è assolutamente nulla di spaventoso in essa!
Tutto è come nell'esempio precedente: qualunque sia l'argomento (espressione tra parentesi), lo scriveremo invece nell'espressione. Ad esempio, per una funzione.
Cosa si dovrebbe fare nel nostro esempio? Invece, devi scrivere, e invece di -:
abbreviare l'espressione risultante:
È tutto!
Lavoro indipendente
Ora prova a trovare tu stesso il significato delle seguenti espressioni:
- , Se
- , Se
Sei riuscito? Confrontiamo le nostre risposte: Siamo abituati al fatto che la funzione ha la forma
Anche nei nostri esempi, definiamo la funzione in questo modo, ma analiticamente è possibile definire la funzione in modo implicito, ad esempio.
Prova a costruire tu stesso questa funzione.
Sei riuscito?
Ecco come l'ho costruito.
Con quale equazione siamo finiti?
Destra! Lineare, il che significa che il grafico sarà una linea retta. Facciamo una tabella per determinare quali punti appartengono alla nostra linea:
È proprio di questo che stavamo parlando... Uno corrisponde a molti.
Proviamo a disegnare cosa è successo:

Quello che abbiamo è una funzione?
Esatto, no! Come mai? Prova a rispondere a questa domanda con una foto. Cosa hai preso?

"Perché un valore corrisponde a più valori!"
Quale conclusione possiamo trarre da ciò?
Esatto, una funzione non può sempre essere espressa in modo esplicito e ciò che è "mascherato" da funzione non è sempre una funzione!
Modo tabulare di definire una funzione
Come suggerisce il nome, questo metodo è un piatto semplice. Si si. Come quello che abbiamo già fatto. Per esempio:
Qui hai immediatamente notato uno schema: Y è tre volte più grande di X. E ora il compito “pensa molto bene”: pensi che una funzione data sotto forma di tabella sia equivalente a una funzione?
Non parliamo a lungo, ma disegniamo!
Così. Disegniamo una funzione data in entrambi i modi:

Vedi la differenza? Non si tratta di punti segnati! Dare un'occhiata più da vicino:

L'hai visto ora? Quando impostiamo la funzione in modo tabulare, riflettiamo sul grafico solo quei punti che abbiamo nella tabella e la linea (come nel nostro caso) passa solo attraverso di essi. Quando definiamo una funzione in modo analitico, possiamo prendere qualsiasi punto e la nostra funzione non si limita ad essi. Ecco una tale caratteristica. Ricordare!
Modo grafico per costruire una funzione
Il modo grafico di costruire una funzione non è meno conveniente. Disegniamo la nostra funzione e un'altra persona interessata può trovare ciò a cui y è uguale a una certa x, e così via. I metodi grafici e analitici sono tra i più comuni.
Tuttavia, qui devi ricordare di cosa abbiamo parlato all'inizio: non tutti gli "scarabocchi" disegnati nel sistema di coordinate sono una funzione! Ricordato? Per ogni evenienza, copierò qui la definizione di cosa sia una funzione:
Di norma, le persone di solito nominano esattamente questi tre modi per specificare una funzione che abbiamo analizzato: analitica (usando una formula), tabulare e grafica, dimenticando completamente che una funzione può essere descritta verbalmente. Come questo? Sì, molto facile!
Descrizione verbale della funzione
Come descrivere verbalmente la funzione? Prendiamo il nostro esempio recente - . Questa funzione può essere descritto come "ogni valore reale di x corrisponde al suo valore triplo". È tutto. Niente di complicato. Naturalmente, obietterai: "ci sono funzioni così complesse che è semplicemente impossibile impostarle verbalmente!" Sì, ce ne sono alcune, ma ci sono funzioni che sono più facili da descrivere verbalmente che da impostare con una formula. Ad esempio: "ogni valore naturale di x corrisponde alla differenza tra le cifre di cui è composto, mentre la cifra più grande contenuta nella voce del numero viene presa come minuendo". Ora considera come il nostro descrizione verbale le funzioni sono implementate in pratica:
La cifra più grande dato numero- , rispettivamente, - ridotto, quindi:
Principali tipi di funzioni
Passiamo ora al più interessante: considereremo i principali tipi di funzioni con cui hai lavorato / lavorerai e lavorerai nel corso della scuola e dell'istituto di matematica, ovvero li conosceremo, per così dire, e dare loro breve descrizione. Maggiori informazioni su ciascuna funzione nella sezione corrispondente.
Funzione lineare
Una funzione della forma, dove, sono numeri reali.
Il grafico di questa funzione è una retta, quindi la costruzione di una funzione lineare si riduce alla ricerca delle coordinate di due punti.
Posizione diretta su piano delle coordinate dipende dal fattore di pendenza.

Ambito della funzione (aka intervallo di argomenti) - .
L'intervallo di valori è .
funzione quadratica
Funzione del modulo, dove
Il grafico della funzione è una parabola, quando i rami della parabola sono diretti verso il basso, quando - verso l'alto.
Molte proprietà di una funzione quadratica dipendono dal valore del discriminante. Il discriminante è calcolato dalla formula
La posizione della parabola sul piano delle coordinate rispetto al valore e al coefficiente è mostrata in figura:

Dominio
L'intervallo di valori dipende dall'estremo della funzione data (il vertice della parabola) e dal coefficiente (la direzione dei rami della parabola)
Proporzionalità inversa
La funzione data dalla formula, dove
Il numero è chiamato fattore di proporzionalità inversa. A seconda del valore, i rami dell'iperbole sono in quadrati diversi:

Dominio - .
L'intervallo di valori è .
RIASSUNTO E FORMULA BASE
1. Una funzione è una regola secondo la quale ad ogni elemento di un insieme viene assegnato un elemento unico dell'insieme.
- - questa è una formula che denota una funzione, cioè la dipendenza di una variabile da un'altra;
- - variabile, o argomento;
- - valore dipendente - cambia quando l'argomento cambia, ovvero secondo una formula specifica che riflette la dipendenza di un valore da un altro.
2. Valori di argomento validi, o l'ambito di una funzione, è ciò che è correlato al possibile in base al quale la funzione ha senso.
3. Intervallo di valori della funzione- ecco quali valori ci vogliono, con valori validi.
4. Esistono 4 modi per impostare la funzione:
- analitico (usando formule);
- tabulare;
- grafico
- descrizione verbale.
5. Principali tipi di funzioni:
- : , dove, sono numeri reali;
- : , dove;
- : , dove.
La derivata di una funzione $y = f(x)$ in un dato punto $x_0$ è il limite del rapporto tra l'incremento della funzione e il corrispondente incremento del suo argomento, purché quest'ultimo tenda a zero:
$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$
La differenziazione è l'operazione di trovare una derivata.
Tabella delle derivate di alcune funzioni elementari
| Funzione | Derivato |
| $c$ | $0$ |
| $ x $ | $1$ |
| $x^n$ | $nx^(n-1)$ |
| $(1)/(x)$ | $-(1)/(x^2)$ |
| $√x$ | $(1)/(2√x)$ |
| $e^x$ | $e^x$ |
| $lnx$ | $(1)/(x)$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $(1)/(cos^2x)$ |
| $ctgx$ | $-(1)/(peccato^2x)$ |
Regole di base della differenziazione
1. La derivata della somma (differenza) è uguale alla somma (differenza) delle derivate
$(f(x) ± g(x))"= f"(x)±g"(x)$
Trova la derivata della funzione $f(x)=3x^5-cosx+(1)/(x)$
La derivata della somma (differenza) è uguale alla somma (differenza) delle derivate.
$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$
2. Derivato di un prodotto
$(f(x) g(x))"= f"(x) g(x)+ f(x) g(x)"$
Trova la derivata $f(x)=4x cosx$
$f"(x)=(4x)" cosx+4x (cosx)"=4 cosx-4x sinx$
3. Derivata del quoziente
$((f(x))/(g(x)))"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $
Trova la derivata $f(x)=(5x^5)/(e^x)$
$f"(x)=((5x^5)" e^x-5x^5 (e^x)")/((e^x)^2)=(25x^4 e^x- 5x^5 e^x)/((e^x)^2)$
4. La derivata di una funzione complessa è uguale al prodotto della derivata della funzione esterna e della derivata della funzione interna
$f(g(x))"=f"(g(x)) g"(x)$
$f"(x)=cos"(5x) (5x)"=-peccato(5x) 5= -5peccato(5x)$
Il significato fisico della derivata
Se punto materiale si muove rettilineo e la sua coordinata cambia a seconda del tempo secondo la legge $x(t)$, quindi la velocità istantanea di questo punto è uguale alla derivata della funzione.
Il punto si muove lungo la linea delle coordinate secondo la legge $x(t)= 1.5t^2-3t + 7$, dove $x(t)$ è la coordinata al tempo $t$. In quale momento la velocità del punto sarà pari a $ 12 $?
1. La velocità è una derivata di $x(t)$, quindi troviamo la derivata della funzione data
$v(t) = x"(t) = 1,5 2t -3 = 3t -3$
2. Per trovare in quale momento $t$ la velocità era pari a $12$, componiamo e risolviamo l'equazione:
Il significato geometrico della derivata
Ricordiamo che l'equazione di una retta non parallela agli assi delle coordinate può essere scritta come $y = kx + b$, dove $k$ è la pendenza della retta. Il coefficiente $k$ è uguale alla tangente della pendenza tra la retta e la direzione positiva dell'asse $Ox$.
La derivata della funzione $f(x)$ nel punto $x_0$ è uguale alla pendenza $k$ della tangente al grafico nel punto dato:
Possiamo quindi fare un'uguaglianza generale:
$f"(x_0) = k = tgα$
Nella figura la tangente alla funzione $f(x)$ è crescente, quindi il coefficiente $k > 0$. Poiché $k > 0$, allora $f"(x_0) = tgα > 0$. L'angolo $α$ tra la tangente e la direzione positiva $Ox$ è acuto.
Nella figura la tangente alla funzione $f(x)$ è decrescente, da cui il coefficiente $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
Nella figura, la tangente alla funzione $f(x)$ è parallela all'asse $Ох$, quindi il coefficiente $k = 0$, quindi $f"(x_0) = tg α = 0$. Il punto $ x_0$ in cui $f "(x_0) = 0$, chiamato estremo.
La figura mostra il grafico della funzione $y=f(x)$ e la tangente a questo grafico tracciata nel punto con l'ascissa $x_0$. Trova il valore della derivata della funzione $f(x)$ nel punto $x_0$.
La tangente al grafico aumenta, quindi $f"(x_0) = tg α > 0$
Per trovare $f"(x_0)$, troviamo la tangente della pendenza tra la tangente e la direzione positiva dell'asse $Ox$. Per fare questo, completiamo la tangente al triangolo $ABC$.
Trova la tangente dell'angolo $BAC$. (La tangente di un angolo acuto in un triangolo rettangolo è il rapporto tra la gamba opposta e la gamba adiacente.)
$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0,25$
$f"(x_0) = tg TU = $0,25
Risposta: $ 0,25
La derivata viene utilizzata anche per trovare gli intervalli di funzioni crescenti e decrescenti:
Se $f"(x) > 0$ su un intervallo, allora la funzione $f(x)$ aumenta su questo intervallo.
Se $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
La figura mostra il grafico della funzione $y = f(x)$. Trova tra i punti $х_1,х_2,х_3…х_7$ quei punti in cui la derivata della funzione è negativa.
In risposta, annotare il numero di punti dati.
Comunale Istituto d'Istruzione
"Scuola secondaria di Saltykovskaja
Distretto di Rtishchevsky della regione di Saratov
Master in matematica
in 11a elementare
su questo argomento
"FUNZIONE DERIVATA
NEI COMPITI DELL'UTILIZZO"
Insegnante di matematica condotto
Beloglazova L.S.
2012-2013 anno accademico
Lo scopo della master class : sviluppare le capacità degli studenti nell'applicare le conoscenze teoriche sul tema "Derivata di una funzione" per risolvere problemi di un singolo esame di stato.
Compiti
Educativo: generalizzare e sistematizzare le conoscenze degli studenti sull'argomento
"La derivata della funzione", per considerare i prototipi dei problemi USE su questo argomento, per fornire agli studenti l'opportunità di testare le proprie conoscenze risolvendo i problemi da soli.
Sviluppando: promuovere lo sviluppo delle capacità di memoria, attenzione, autostima e autocontrollo; di base competenze fondamentali(confronto, confronto, classificazione di oggetti, determinazione di metodi adeguati per la risoluzione compito di apprendimento sulla base di determinati algoritmi, la capacità di agire autonomamente in una situazione di incertezza, di controllare e valutare le proprie attività, di trovare ed eliminare le cause delle difficoltà).
Educativo: promuovere:
la formazione di un atteggiamento responsabile degli studenti nei confronti dell'apprendimento;
sviluppo di un interesse sostenibile per la matematica;
creando una motivazione intrinseca positiva allo studio della matematica.
Tecnologia: apprendimento differenziato individualmente, ICT.
Metodi di insegnamento: verbale, visivo, pratico, problematico.
Forme di lavoro: individuale, frontale, in coppia.
Attrezzatura e materiali per la lezione: proiettore, schermo, PC per ogni studente, simulatore (Appendice n. 1), presentazione per la lezione (Appendice n. 2), individualmente - carte differenziate per lavoro indipendente A coppie (Appendice n. 3), elenco di siti Internet, individualmente differenziati compiti a casa (Appendice n. 4).
Spiegazione per la master class. Questa master class si tiene nel grado 11 per preparare l'esame. Rivolto all'applicazione di materiale teorico sul tema "Derivata di una funzione" nella risoluzione di problemi d'esame.
Durata della master class- 30 minuti.
La struttura della master class
I. Momento organizzativo -1 min.
II.Comunicazione del tema, obiettivi della master class, motivazione per le attività didattiche-1 min.
III. Lavoro frontale. Formazione "Incarichi B8 USO". Analisi del lavoro con il simulatore - 6 min.
IV.Individualmente - lavoro differenziato in coppia. Risoluzione dei problemi indipendente B14. Controllo reciproco - 7 min.
v. Controllo dei compiti individuali. Operazione con parametro C5 USE
3 min.
VI .Test in linea. Analisi dei risultati del test - 9 min.
VII. Compiti a casa differenziati individualmente -1 min.
VIII Voti per la lezione - 1 min.
IX. Riepilogo della lezione. Riflessione -1 min.
Avanzamento del corso di perfezionamento
io .Organizzare il tempo.
II .Comunicazione del tema, obiettivi della master class, motivazione delle attività didattiche.
(Diapositive 1-2, Appendice n. 2)
L'argomento della nostra lezione è "La derivata di una funzione nei compiti dell'esame". Tutti conoscono il detto "La bobina è piccola e costosa". Uno di questi "bocchetti" in matematica è il derivato. La derivata è usata per risolverne molti compiti pratici matematica, fisica, chimica, economia e altre discipline. Ti permette di risolvere i problemi in modo semplice, bello, interessante.
L'argomento "Derivato" è presentato nei compiti della parte B (B8, B14) dell'esame di stato unificato. Alcuni compiti C5 possono anche essere risolti usando una derivata. Ma per risolvere questi problemi sono necessarie una buona preparazione matematica e un pensiero non standard.
Hai lavorato con i documenti che regolano la struttura e il contenuto dei materiali di misurazione del controllo per l'esame di stato unificato in matematica 2013. Concludi chequali conoscenze e abilità sono necessarie per risolvere con successo i problemi dell'esame sull'argomento "Derivato".
(Diapositive 3-4, Appendice n. 2)
Noi studiato"Codificatore elementi di contenuto in MATEMATICA per la compilazione di materiali di misurazione di controllo per lo svolgimento di un esame di stato unificato”,
"Codificatore dei requisiti per il livello di formazione dei laureati","Specifica controllare i materiali di misura","Versione demo"controllo materiali di misura dell'esame di stato unificato 2013" ecapito quali conoscenze e abilità su una funzione e la sua derivata sono necessarie per risolvere con successo i problemi sull'argomento "Derivata".
Necessario
SAPERE
P regole per il calcolo dei derivati;
derivate di funzioni elementari di base;
significato geometrico e fisico della derivata;
l'equazione della tangente al grafico della funzione;
studio di una funzione con l'aiuto di una derivata.
ESSERE IN GRADO DI
eseguire azioni con funzioni (descrivere il comportamento e le proprietà di una funzione in base al grafico, trovarne i valori massimo e minimo).
UTILIZZO
conoscenze e abilità acquisite nelle attività pratiche e nella vita di tutti i giorni.
Hai conoscenze teoriche sull'argomento "Derivato". Oggi lo faremoIMPARA AD APPLICARE LE CONOSCENZE SULLA FUNZIONE DERIVATA PER LA RISOLVERE I PROBLEMI DI UTILIZZO. ( Diapositiva 4, domanda numero 2)
Dopotutto, non senza ragione Lo disse Aristotele “L'INTELLIGENZA CONSISTE NON SOLO NELLA CONOSCENZA, MA ANCHE NELLA CAPACITÀ DI APPLICARE LA CONOSCENZA NELLA PRATICA”( Diapositiva 5, domanda numero 2)
Alla fine della lezione, torneremo all'obiettivo della nostra lezione e scopriremo se l'abbiamo raggiunto?
III . Lavoro frontale. Formazione "Incarichi B8 UTILIZZO" (Allegato n. 1) . Analisi del lavoro con il simulatore.
Scegli la risposta corretta tra le quattro date.
Qual è, secondo te, la difficoltà nel portare a termine l'attività B8?
Quali pensi siano gli errori tipici che i laureati commettono durante l'esame quando risolvono questo problema?
Quando rispondi alle domande del compito B8, dovresti essere in grado di descrivere il comportamento e le proprietà di una funzione sul grafico della derivata e sul grafico della funzione, il comportamento e le proprietà della derivata della funzione. E ciò richiede buone conoscenze teoriche sui seguenti argomenti: “Significato geometrico e meccanico della derivata. Tangente al grafico di una funzione. Applicazione della derivata allo studio delle funzioni.
Analizza quali compiti ti hanno causato difficoltà?
Quali domande teoriche devi sapere?
IV. Individualmente - lavoro differenziato in coppia. Risoluzione dei problemi indipendente B14. Verifica reciproca. (Appendice n. 3)
Richiama l'algoritmo per la risoluzione dei problemi (B14 USE) per trovare punti estremi, funzione extrema, i valori più grandi e più piccoli della funzione sull'intervallo usando la derivata.
Risolvi i problemi usando la derivata.
Agli studenti è stato chiesto il seguente problema:
"Pensaci, alcuni problemi di B14 possono essere risolti in un modo diverso, senza usare una derivata?"
1 paio(Lukyanova D., Gavryusina D.)
1)B14. Trova il punto minimo della funzione y \u003d 10x-ln (x + 9) + 6
2) B14.Trova il valore più grande di una funzioney =
- Prova a risolvere il secondo problema in due modi.
2 paia(Saninskaya T., Sazanov A.)
1)B14.Trova il valore più piccolo della funzione y=(x-10) sul segmento
2) B14. Trova il punto massimo della funzione y \u003d - ![]()
(Gli studenti difendono la loro soluzione scrivendo alla lavagna i passaggi principali per la risoluzione dei problemi. Studenti di 1 coppia (Lukyanova D., Gavryusina D.) fornire due modi per risolvere il problema n. 2).
Soluzione di un problema. Conclusione a cura degli studenti:
"Alcuni problemi B14 USE sulla ricerca dei valori più piccoli e più grandi di una funzione possono essere risolti senza utilizzare una derivata, in base alle proprietà delle funzioni."
Analizza quale errore hai commesso nell'attività?
Quali domande teoriche devi ripetere?
v. Controllo dei compiti individuali. Task con parametro C5(USE) ( Diapositive 7-8, Appendice n. 2)
A Lukyanova K. è stato assegnato un compito a casa individuale: scegliere un problema con il parametro (C5) dai manuali per la preparazione dell'esame e risolverlo utilizzando la derivata.
(Lo studente fornisce una soluzione al problema, basata sul metodo grafico-funzionale, come uno dei metodi per risolvere i problemi C5 USE e fornisce breve spiegazione questo metodo).
Quale conoscenza della funzione e della sua derivata è necessaria per risolvere i problemi C5 USE?
V I. Test in linea per le attività B8, B14. Analisi dei risultati dei test.
Sito per il test nella lezione:
Chi non ha commesso errori?
Chi ha riscontrato difficoltà nel test? Come mai?
Quali compiti sono sbagliati?
Concludi quali domande teoriche devi sapere?
VI IO. Compiti a casa differenziati individualmente
(Diapositiva 9, domanda numero 2), (Appendice n. 4).
Ho preparato un elenco di siti Internet per prepararmi all'esame. Puoi anche navigare in questi sitin – lineatest. Per la prossima lezione, devi: 1) ripetere materiale teorico sul tema "Derivata di una funzione";
2) sul sito "Banca aperta degli incarichi in matematica" ( ) trovare prototipi delle attività B8 e B14 e risolvere almeno 10 attività;
3) Lukyanova K., Gavryushina D. risolvono problemi con i parametri. Il resto degli studenti risolve i problemi 1-8 (opzione 1).
VIII. Gradi delle lezioni.
Che voto ti daresti per la lezione?
Pensi di poter fare di meglio in classe?
IX. Riassunto della lezione. Riflessione
Riassumiamo il nostro lavoro. Qual era lo scopo della lezione? Pensi che sia stato raggiunto?
Guarda la lavagna e in una frase, scegliendo l'inizio della frase, continua la frase che ti si addice di più.
Mi sono sentito…
Ho studiato…
Sono riuscito …
Potevo...
Cercherò …
ne sono rimasto sorpreso …
Volevo…
Puoi dire che durante la lezione c'è stato un arricchimento del tuo bagaglio di conoscenze?
Quindi hai ripetuto le domande teoriche sulla derivata di una funzione, hanno applicato le loro conoscenze nella risoluzione di prototipi di attività USE (B8, B14) e Lukyanova K. ha completato l'attività C5 con un parametro, che è un'attività con un grado di complessità maggiore.
Mi è piaciuto lavorare con te e Spero che sarai in grado di applicare con successo le conoscenze acquisite nelle lezioni di matematica non solo in superare l'esame ma anche in ulteriori studi.
Vorrei concludere la lezione con le parole di un filosofo italiano Tommaso d'Aquino“La conoscenza è una cosa così preziosa che non è vergognoso ottenerla da nessuna fonte” (Diapositiva 10, Appendice n. 2).
Ti auguro successo nella preparazione per l'esame!
LAVORI PRATICI EXTRA-CURRICULUM 2
Trasformazione di grafici di funzioni.
Obbiettivo
Tracciare grafici di funzioni utilizzando varie trasformazioni, rispondere alla domanda del problema.
Completamento dell'opera
Il lavoro è progettato per 10 opzioni, il numero dell'opzione corrisponde all'ultima cifra del numero di serie nell'elenco. Ad esempio, 1, 11, 21, 31 ... eseguire 1 opzione, 2,12, 22 ... - 2 opzioni, ecc.
Il lavoro è composto da due parti: la prima parte delle attività 1 - 5, queste sono attività che devono essere completate per ottenere credito, se queste attività vengono completate con un errore, è necessario correggerle e inviare nuovamente il lavoro per la verifica . La seconda parte contiene compiti, completando i quali puoi guadagnare un voto aggiuntivo: la parte principale +2 compiti - "4", la parte principale +3 compiti - "5".
Compito 1. Il grafico di una funzione lineare è una retta, per costruirla bastano due punti. (Prendiamo arbitrariamente i valori dell'argomento x e consideriamo di sostituire il valore della funzione y nella formula).
Per verificare se il grafico della funzione passa per il punto specificato, devi sostituire le coordinate del punto invece di x e y, se ottieni l'uguaglianza corretta, la linea passa per il punto specificato, altrimenti non passa .
Compito 2, 3, 4. I grafici delle funzioni indicate sono ottenuti dai grafici delle funzioni , utilizzando uno spostamento lungo l'asse x o y.
![]() , prima traccia la funzione o , quindi lo spostiamo di unità "a" a destra o a sinistra (+ a - a sinistra, - a a destra), quindi lo spostiamo di unità "b" su o giù (+ in - su, - in - fuori uso)
, prima traccia la funzione o , quindi lo spostiamo di unità "a" a destra o a sinistra (+ a - a sinistra, - a a destra), quindi lo spostiamo di unità "b" su o giù (+ in - su, - in - fuori uso)
Allo stesso modo con altre funzioni:
Attività 5 Per tracciare un grafico di funzione: , è necessario: 1) costruire un grafico della funzione , 2) la parte del grafico che si trova sopra l'asse x viene lasciata invariata, 3) la parte del grafico che si trova al di sotto dell'asse x viene specchiata.
Compiti per soluzione indipendente.
Attività 1. Tracciare un grafico di una funzione lineare, determinare se il grafico della funzione passa per il punto specificato:

Attività 2. Traccia un grafico di una funzione quadratica, indica l'insieme di valori per questa funzione.

Attività 3. Costruisci un grafico di una funzione, determina se la funzione specificata è in aumento o in diminuzione.

Compito 4. Costruisci un grafico della funzione, rispondi alla domanda del compito.

Attività 5. Costruisci un grafico di una funzione contenente il segno del modulo.

Compiti per una valutazione aggiuntiva.
Attività 6. Traccia un grafico di una funzione data a tratti, determina se questa funzione ha un punto di interruzione:


Compito 7. Determina quante soluzioni ha il sistema di equazioni, giustifica la risposta. Trai le conclusioni rispondendo alle domande.
Quali grafici delle funzioni hai costruito in questo lavoro?
Qual è il nome del grafico di una funzione lineare?
Qual è il nome del grafico di una funzione quadratica?
Quali trasformazioni del grafico conosci?
Come si trova il grafico di una funzione pari nel sistema di coordinate? Grafico di una funzione dispari?
- In contatto con 0
- Google+ 0
- ok 0
- Facebook 0