Trasformazioni di coordinate affini per manichini. Trasformazioni affini mediante coordinate omogenee

In coordinate omogenee si scrive un punto come per qualsiasi fattore di scala. Inoltre, se a un punto viene data la sua rappresentazione in coordinate omogenee, allora le sue coordinate cartesiane bidimensionali possono essere trovate come e .

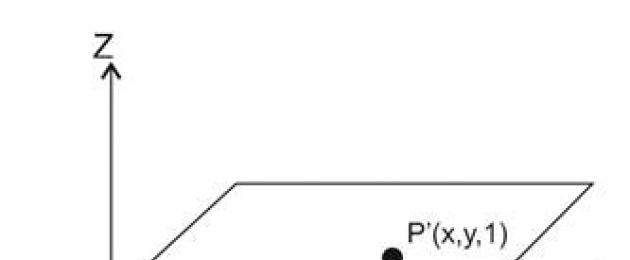
Il significato geometrico delle coordinate omogenee è il seguente (Fig. 6). punto arbitrario su una retta

Riso. 6. Interpretazione geometrica di coordinate omogenee

Si stabilisce quindi una corrispondenza biunivoca tra il punto di produzione con coordinate (x, y) e l'insieme delle triple di numeri della forma (W×x, W×y, W), W≠0, che consente consideriamo i numeri W×x, W×y, W come nuove le coordinate di questo punto. Pertanto, le coordinate omogenee possono essere rappresentate come un'inclusione di un piano bidimensionale scalato con un coefficiente W nel piano z = W (qui z = 1) nello spazio tridimensionale.

L'uso di coordinate omogenee risulta conveniente per risolvere anche i problemi più semplici.

Se il dispositivo di visualizzazione funziona solo con numeri interi (o se è necessario lavorare solo con numeri interi), allora per un valore arbitrario di W (ad esempio W=1), un punto con coordinate omogenee (0,5; 0,1; 2,5) non può essere rappresentato. Tuttavia, con una scelta ragionevole di W, è possibile garantire che le coordinate di questo punto siano intere. In particolare, a W=10 per l'esempio considerato abbiamo (5; 1; 25).

Un altro caso. Affinché i risultati della trasformazione non comportino un overflow aritmetico, per un punto con coordinate (80000; 40000; 1000) si può prendere, ad esempio, W=0,001. Di conseguenza, otteniamo (80; 40; 1).

Tuttavia, l'applicazione principale delle coordinate omogenee sono le trasformazioni geometriche, poiché utilizzando triple di coordinate omogenee e matrici del terzo ordine, è possibile descrivere qualsiasi trasformazione affine nel piano. Allo stesso modo, con l'aiuto di quadruple di coordinate omogenee e matrici del quarto ordine, si può descrivere qualsiasi trasformazione nello spazio tridimensionale.

Come è noto, le trasformazioni di traslazione, ridimensionamento e rotazione in forma matriciale sono scritte come

P' = P × S;

La traduzione viene implementata separatamente (usando l'addizione) dal ridimensionamento e dalla rotazione (usando la moltiplicazione). Se i punti sono espressi in coordinate omogenee, allora tutte e tre le trasformazioni possono essere implementate usando le moltiplicazioni. Qui considereremo le trasformazioni bidimensionali.

Le equazioni di trasporto sono scritte sotto forma di una matrice di trasformazione di coordinate omogenee come segue:

P' = P × T(dx, dy),

.

A volte tali espressioni sono scritte come segue:

Si consideri, ad esempio, uno spostamento di due punti. Sia necessario spostare il punto P al punto P' a distanza (dx1, dy1), e poi a P'' a distanza (dx2, dy2). Il trasferimento totale deve essere uguale alla distanza (dх1+d2, dу1+dу2). Scriviamo i dati nel modulo

P' = P × T (dx1, dy1);

P'' = P' × T (dx2, dy2).

Sostituendo la prima formula con la seconda, otteniamo

P'' = P × (T (dx1, dy1) × T (dx2, dy2)).

Il prodotto matriciale T (dx1, dy1) ∙ T (dx2, dy2) è

Pertanto, il trasferimento risultante è (dx1+dx2, dy1+dy2), cioè riporti successivi sono additivi.

Le equazioni di ridimensionamento in forma matriciale che utilizzano coordinate omogenee sono scritte come

,

.

P' = P' × S(Sx, Sy).

Il prodotto matrice S(Sx1, Sy1) × S(Sx2, Sy2) è

Quindi i ridimensionamenti successivi sono moltiplicativi.

Infine, l'equazione di rotazione (nel sistema destrorso) può essere rappresentata come

.

Le rotazioni successive sono additivi.

Composizione di trasformazioni 2D utilizzando coordinate omogenee. Viene chiamato il prodotto matrice in diversi casi concatenazione, unione, concatenazione e composizione. Useremo l'ultimo di questi termini.

Si consideri, ad esempio, la rotazione di un oggetto rispetto a un punto arbitrario P1. Poiché sappiamo solo come ruotare attorno all'origine, suddivideremo il problema originale in tre sottoattività:

Traslazione, in cui il punto P1 viene spostato all'origine;

Giro;

Traslazione, in cui il punto dall'origine ritorna alla sua posizione originale P1.

La sequenza di queste trasformazioni è mostrata in fig. 7.1.

Riso. 7.1. Ruota un oggetto attorno a un punto arbitrario

La trasformazione risultante ha la forma

Usando un approccio simile, puoi scalare l'oggetto rispetto a un punto arbitrario P1: sposta P1 all'origine, scala, torna al punto P1. La trasformazione risultante in questo caso sarà simile

Consideriamo una trasformazione più complessa. Assumiamo di aver bisogno di ridimensionare, ruotare e posizionare un oggetto nel posto giusto (la casa in Fig. 7.2), dove il centro di rotazione e ridimensionamento è il punto P1.

Riso. 7.2. esempio di sequenza di conversione

La sequenza di trasformazioni consiste nello spostare il punto P1 all'origine, ridimensionarlo e ruotarlo, quindi spostarsi dall'origine in una nuova posizione P2. La struttura dei dati del programma applicativo che contiene questa trasformazione può contenere i fattori di scala, l'angolo di rotazione e gli importi di traslazione, oppure la matrice di trasformazione risultante può essere scritta:

T (-x1, -y1) × S (Sx, Sy) × R (A) × T (x2, y2).

In generale, la moltiplicazione di matrici non è commutativa. Se M1 e M2 sono traslazioni, ridimensionamenti o rotazioni elementari, la commutatività si verifica nei seguenti casi speciali:

M1	M2
Scala di traslazione Ruota scala (quando Sx=Sy)	Sposta scala Ruota Ruota

La composizione della forma più generale, composta dalle operazioni R, S e T, ha la matrice

La sua parte superiore 2×2 è la matrice combinata di rotazione e ridimensionamento, mentre tx e ty descrivono la traslazione complessiva. Il calcolo di P∙M come prodotto di un vettore e di una matrice 3 × 3 richiede 9 moltiplicazioni e 6 addizioni. La struttura dell'ultima colonna della matrice generalizzata consente di semplificare le azioni effettivamente eseguite.

Per prima cosa, definiamo cosa sono le trasformazioni. Diciamo di avere un modello (per semplicità, sia un triangolo). E tre spazi di coordinate: oggetto (in cui è descritto questo triangolo), mondo e spazio della telecamera. Quindi, una trasformazione è un'espressione delle coordinate di un oggetto che si trova in un sistema di coordinate (obiettivo) utilizzando le coordinate di un altro sistema di coordinate (prima quello mondiale e poi quello della telecamera).

Come ho scritto prima, l'utilizzo di spazi di coordinate differenti rende più facile creare un mondo virtuale. Gli oggetti vengono creati nello spazio degli oggetti e ogni oggetto ha il proprio spazio delle coordinate. Lo spazio mondiale collega tutti gli oggetti del mondo virtuale e ti consente di fare cose molto difficili, molto semplici (ad esempio, spostare oggetti). Dopo che la scena è stata creata e tutti gli oggetti sono stati spostati, le coordinate mondiali vengono convertite nello spazio delle coordinate della telecamera. Useremo solo una fotocamera, ma in situazioni reali puoi crearne diverse. Diverse fotocamere, ad esempio, sono state utilizzate nel brillante gioco Earth 2150: Escape from the blue planet.

Quindi di cosa sto parlando: le trasformazioni sono necessarie per utilizzare più spazi di coordinate.

Innanzitutto, ricordiamo qualcosa sui vettori. La figura seguente ci aiuterà in questo:

Cosa vediamo qui: lo spazio mondiale delle coordinate formato dagli assi x, y, z. vettori unitari io, j, K sono chiamati ort o vettori di base dello spazio delle coordinate mondiali. Usando la somma di questi vettori, puoi ottenere qualsiasi vettore nello spazio delle coordinate mondiali.

vè un vettore che collega l'origine delle coordinate mondiali e l'origine delle coordinate dell'oggetto. La lunghezza del vettore v è uguale alla distanza tra l'origine delle coordinate mondiali e l'origine delle coordinate dell'oggetto. Considera la forma vettoriale v=(5,2,5):

v=x* io+y* j+z* K = 5*io + 2*j + 5*K

Come ho scritto sopra, con l'aiuto dei vettori di base, puoi rappresentare qualsiasi punto (vettore) di un dato spazio, come dimostra questa equazione.

vettori p,q,r sono i vettori di base dello spazio degli oggetti. Notare che io,j,K non necessariamente uguale p,q,r.

In questa figura ho omesso una serie di dettagli: ci sono tre punti nello spazio delle coordinate dell'oggetto che formano un triangolo. Inoltre, non ho etichettato la fotocamera che punta verso il triangolo.

Trasformazioni di coordinate lineari mediante matrici

Per prima cosa, diamo un'occhiata ai vettori unitari io,j,K, che coincidono in direzione con gli assi coordinati dello spazio mondiale e sono chiamati ort o vettori di base dello spazio mondiale.

Scriviamo questi vettori in forma di coordinate come matrici:

io= [ io x io y io z ] = [ 1 0 0 ] j= [ j x j y j z ] = [ 0 1 0 ] K= [ k x k y k z ] = [ 0 0 0 ]

Qui i vettori sono rappresentati da matrici 1x3 (matrici di righe).

Possiamo scrivere questi vettori di base usando una singola matrice:

E anche, cosa più importante, possiamo scrivere questi vettori in questo modo:

Come puoi vedere, il risultato è una matrice di identità 3x3 o 4x4.

Sembrerebbe che esista una cosa del genere? Pensa, è possibile scrivere alcuni stupidi vettori di base dello spazio in una matrice. Ma no, non "pensare"!!! È qui che si nasconde uno dei segreti più terribili della programmazione tridimensionale.

Come ho scritto sopra, qualsiasi punto presente nel mondo virtuale può essere scritto in forma vettoriale:

v=x* io+y* j+z* K

Dove v- punto nello spazio, x,y,z - coordinate del punto v, un io,j,K- vettori di base dello spazio. Nota che qui stiamo parlando di un punto, ma stiamo considerando un vettore. Spero che tu ricordi che un vettore e un punto sono essenzialmente la stessa cosa.

La formula sopra è chiamata forma vettoriale di un vettore. C'è un altro nome: una combinazione lineare di vettori. È così, tra l'altro.

Ora esaminiamo di nuovo il vettore. v. Scriviamolo in una matrice di righe: v = [ 5 2 5 ]

Nota che la lunghezza del vettore vè la distanza dall'inizio dello spazio delle coordinate del mondo all'inizio dello spazio delle coordinate dell'oggetto.

Proviamo a moltiplicare questo vettore per una matrice in cui sono scritti i vettori di base dello spazio mondiale (spero che ricordi la formula di moltiplicazione delle matrici):

Di conseguenza, otteniamo la seguente equazione:

v M = [ (xi x + yj x + zk x) (xi y + yj y + zk y) (xi z + yj z + zk z) ]

Abbiamo un vettore. Quelli. il risultato della moltiplicazione di un vettore per una matrice è un vettore. In questo caso, il vettore non è cambiato. Ma se gli elementi della matrice non sono uno (sulla diagonale principale) e zero (tutti gli altri elementi), ma alcuni altri numeri, il vettore cambierà. Pertanto, possiamo dire che la matrice M esegue una trasformazione di spazi di coordinate. Considera la formula generale:

a, b - vettori, M - matrice di trasformazione degli spazi delle coordinate. La formula può essere letta così: "la matrice M trasforma il punto a nel punto b".

Per chiarezza, diamo un'occhiata a un esempio. Dobbiamo convertire le coordinate dallo spazio degli oggetti (p,q) allo spazio mondiale (i,j):

io,j- vettori di base dello spazio mondiale, p,q sono i vettori di base dello spazio degli oggetti. Nell'immagine puoi vedere che lo spazio delle coordinate dell'oggetto è ruotato di -45 gradi attorno all'asse z (non è visibile nell'immagine). Inoltre, i vettori q,p 1,5 volte più vettori io,j, il che significa che gli oggetti definiti nello spazio degli oggetti appariranno una volta e mezza più piccoli nello spazio mondiale.

Per visualizzare come apparirà il modello dello spazio degli oggetti dopo la trasformazione, puoi disegnare una cornice per i vettori io,j:

Puoi disegnare la stessa cornice per p,q, ma non ho ingombrato il disegno.

Ora, supponiamo di avere un triangolo disegnato nello spazio degli oggetti (Figura a). Nello spazio mondiale, questo triangolo sarà ruotato di 45 gradi e ridotto di un terzo (fig. b):

Ora raccogliamo tutti gli elementi del mosaico: come sappiamo, la trasformazione può essere fatta utilizzando una matrice. Le righe di matrici sono vettori di base. Le coordinate dei vettori di base dello spazio delle coordinate mondiali nello spazio degli oggetti sono le seguenti:

io = [ 0.473 0.473 ] j = [ -0.473 0.473 ]

Come facciamo a sapere le coordinate? Innanzitutto, sappiamo che gli spazi delle coordinate sono ruotati di 45 gradi l'uno rispetto all'altro. In secondo luogo, i vettori della base spaziale dell'oggetto sono 1,5 volte più lunghi dei vettori della base spaziale mondiale. Sapendo questo, possiamo facilmente calcolare le coordinate dei vettori io,j.

Di conseguenza, otteniamo la seguente matrice di trasformazione (in questo caso, rotazione o rotazione):

Oppure nello spazio 3D:

Tutti i valori sono approssimativi.

Questa è la matrice di trasformazione delle coordinate dallo spazio degli oggetti allo spazio inerziale (vi ricordo che i vettori di base dello spazio inerziale coincidono con i vettori di base dello spazio mondiale). Per trasformare un triangolo dallo spazio degli oggetti allo spazio inerziale, è necessario moltiplicare tutti i punti (vettori) del triangolo per la matrice di trasformazione.

Nell'ultimo esempio, abbiamo riscontrato due trasformazioni: rotazione e ridimensionamento. Entrambe queste trasformazioni sono lineari.

Ora che abbiamo esaminato esempi di trasformazioni lineari, possiamo familiarizzare con la definizione:

Le trasformazioni lineari sono trasformazioni di coordinate che non distorcono gli spazi. Quelli. tutte le linee parallele rimangono parallele (c'è però un'eccezione). O semplicemente: con le trasformazioni lineari, un triangolo non si trasformerà mai in un cerchio o in un quadrato, ma rimarrà sempre un triangolo.

Ora che capiamo approssimativamente cosa sono le trasformazioni lineari, diamo un'occhiata a formule specifiche:

Scala

k 1 ,k 2 ,k 3 - fattori di scala. Se k 1, c'è un aumento degli oggetti.

Rotazione o rotazione (Rotazione)

Ruota attorno all'asse x:

Rotazione attorno all'asse y:

Rotazione attorno all'asse z:

A proposito, è questa matrice (di rotazione attorno all'asse z) che abbiamo usato sopra.

La rotazione può essere non solo attorno agli assi che formano lo spazio delle coordinate, ma anche attorno a linee arbitrarie. La formula per girare intorno a una retta arbitraria è piuttosto complicata, non siamo ancora pronti per prenderla in considerazione.

La cosa più importante da ricordare da quanto sopra è che le righe della matrice di trasformazione contengono i vettori di base del nuovo spazio di coordinate, espressi in termini di coordinate del vecchio spazio di coordinate. .

Se capisci questa semplice cosa (che i vettori di base del nuovo spazio sono scritti nella matrice), allora guardando la matrice di trasformazione, puoi facilmente vedere il nuovo spazio delle coordinate.

E l'ultimo:
Le trasformazioni lineari non possono spostare gli oggetti. Quelli. gli oggetti possono essere ingranditi/ridotti, ruotati, ma rimarranno fermi.

Trasformazioni affini

Le trasformazioni affini sono trasformazioni lineari con traslazione. Con l'aiuto di trasformazioni affini, puoi spostare gli oggetti.

La formula è molto semplice:

A = bM + v;

Dove b è il punto originale, M è la matrice di trasformazione lineare, a è il punto di trasformazione e v è il vettore che collega i due spazi. O in altre parole, è un vettore la cui lunghezza è uguale alla distanza tra due spazi di coordinate.

Nell'immagine all'inizio della lezione, è proprio la trasformazione affine che serve: prima una trasformazione lineare dallo spazio degli oggetti a quello inerziale, e poi il trasferimento di tutti i punti dello spazio degli oggetti nello spazio del mondo usando il vettore v.

Per semplificare i calcoli nella programmazione grafica 3D, vengono utilizzati vettori quadridimensionali, matrici 4x4 e cosiddette coordinate omogenee. La quarta dimensione non gioca alcun ruolo, viene introdotta solo per semplificare i calcoli.

Un vettore 4D ha, hai indovinato, quattro componenti: x, y, z e w. La quarta componente del vettore è chiamata coordinata omogenea.

È molto difficile rappresentare geometricamente una coordinata omogenea. Considereremo quindi uno spazio omogeneo tridimensionale con coordinate (x, y, w). Immagina che un piano bidimensionale sia definito nel punto w=1. Di conseguenza, un punto bidimensionale è rappresentato in uno spazio omogeneo dalle seguenti coordinate (x,y,1). Tutti i punti nello spazio che non sono in un piano (sono nei piani in cui w != 1) possono essere calcolati proiettando su un piano bidimensionale. Per fare ciò, è necessario dividere tutti i componenti di questo punto in uno omogeneo. Quelli. se w!=1, nel piano "fisico" (dove lavoriamo e dove w=1) le coordinate del punto saranno le seguenti: (x/w,y/w,w/w) o (x/w) ,y/w ,uno). Guarda l'immagine:

Le coordinate vettoriali sono le seguenti:

V 1 = [ 3 3 3 ] v 2 = [ 3 1 0 ] v 3 = [ 3 -2 -2 ]

Questi vettori sono proiettati nel piano "fisico" (w=1) come segue:

V 1 = [ 1 1 1 ] v 3 = [ -1,5 1 1 ]

La figura mostra tre vettori. Si noti che quando un punto giace nel piano w=0, allora questo punto non può essere proiettato nel piano fisico (vettore v 2).

Per ogni punto del piano fisico esiste un numero infinito di punti in uno spazio omogeneo.

Nello spazio quadridimensionale, tutto è esattamente lo stesso. Lavoriamo nello spazio fisico dove w = 1: (x, y, z, 1). Se come risultato dei calcoli w != 1, allora devi dividere tutte le coordinate del punto in una omogenea: (x/w,y/w,z/w,w/w) o (x/w, y/w,z/w,1). C'è un altro caso speciale in cui w = 0. Lo considereremo più avanti.

Ora passiamo alla pratica: perché diavolo ti serve una coordinata omogenea?

Come abbiamo già scoperto, una matrice 3x3 rappresenta una trasformazione lineare, cioè non contiene un trasferimento (trasferimento). Per il trasferimento viene utilizzato un vettore separato (e questa è già una trasformazione affine):

V = aM + b

Quelli. moltiplichiamo tutti i punti (vettori) dell'oggetto per la matrice di trasformazione M per andare al sistema di coordinate inerziale (i cui vettori di base sono gli stessi dei vettori di base del sistema di coordinate mondiale), quindi arriviamo allo spazio mondiale usando il vettore b. Come promemoria, il vettore b collega l'inizio dello spazio degli oggetti e l'inizio dello spazio mondiale.

Quindi, usando quattro dimensioni, puoi stipare sia le trasformazioni lineari (rotazione, ridimensionamento) che la traduzione in una matrice.

Immagina che la quarta componente sia sempre uguale a uno (anche se abbiamo già scoperto che non è così). Ora la trasformazione lineare può essere rappresentata usando una matrice 4x4:

Diamo un'occhiata alla formula per moltiplicare i vettori per una matrice di trasformazione nello spazio quadridimensionale:

V x = (xi x + yj x + zk x + w*0) v y = (xi y + yj y + zk y + w*0) v z = (xi z + yj z + zk z + w*0) v w = (x*0 + y*0 + z*0 + w*1) Come puoi vedere, le componenti del vettore trasformato usando una matrice 4x4 sono uguali alle componenti del vettore trasformato usando una matrice 3x3. Il quarto componente, come concordato, sarà sempre uguale a uno, quindi può essere semplicemente scartato. Pertanto, possiamo dire che le trasformazioni effettuate dalle matrici 3x3 e 3x4 sono equivalenti.

Ora diamo un'occhiata alla matrice di trasferimento:

Moltiplica qualsiasi vettore dallo spazio degli oggetti (vedi la figura all'inizio della lezione) per questa matrice e puoi esprimere questo vettore nello spazio delle coordinate mondiali (questo è se i vettori della base dell'oggetto e dello spazio mondiale sono uguali).

Nota che anche questa è una trasformazione lineare, solo nello spazio 4D.

Utilizzando il prodotto matrice, possiamo combinare la matrice di rotazione e la matrice di traslazione:

Quest'ultima matrice è esattamente ciò di cui avevamo bisogno sin dall'inizio. Dovresti avere una buona comprensione di cosa significano esattamente tutti i suoi elementi (ad eccezione della 4a colonna).

Inglese: Wikipedia sta rendendo il sito più sicuro. Stai utilizzando un vecchio browser web che non sarà in grado di connetterti a Wikipedia in futuro. Aggiorna il tuo dispositivo o contatta il tuo amministratore IT.

中文: 维基 百科 正 在 使 网站 更加 安全 您 正 在 使用 的 ， 这 在 将来 将来 无法 连接 维基 百科。 更新 您 的 设备 或 或 的 的 管理员 提供 更 长 长 ， 具 技术性 技术性 的 仅 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 tivamente CIAO）。

spagnolo: Wikipedia è haciendo el sitio más seguro. Usato está utilizando un navigador web viejo que no será capaz de conectarse a Wikipedia en el futuro. Actualice su dispositivo o contattare un su amministratore informativo. Più abajo hay una attualizzazione più larga e più tecnica in inglese.

ﺎﻠﻋﺮﺒﻳﺓ: ويكيبيديا تسعى لتأمين الموقع أكثر من ذي قبل. أنت تستخدم متصفح وب قديم لن يتمكن من الاتصال بموقع ويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بغداري تقنية المعلومات الخاص بك. يوجد تحديث فني أطول ومغرق في التقنية باللغة الإنجليزية تاليا.

Francais: Wikipedia va bientôt augmenter la securité de son site. Vous utilisez actuellement un browser web ancien, qui ne pourra plus se connecter à Wikipédia lorsque ce sera fait. Merci de mettre à jour votre appareil o contacter votre administrateur informatique à cette fin. Des informations supplementaires plus Techniques et en anglais sont disponibles ci-dessous.

日本語: ウィキペディア で は サイト の セキュリティ を て い ます。 ご 利用 の は バージョン が 古く 、 今後 、 、 接続 でき なく なる 可能 可能 性 が デバイス を する 、 、 管理 管理 者 者 ご ください。 技術 面 の 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 更新 tivamente更新 更新 更新 詳しい 詳しい 詳しい 詳しい HIP情報は以下に英語で提供しています。

Tedesco: Wikipedia erhöht die Sicherheit der Webseite. Du benutzt einen alten Webbrowser, der in Zukunft nicht mehr auf Wikipedia zugreifen können wird. Bitte aktualisiere dein Gerät oder sprich deinen IT-Administrator an. Ausführlichere (und technisch detailliertere) Hinweise findest Du unten in englischer Sprache.

Italiano: Wikipedia sta facendo il sito più sicuro. Stai usando un browser web che non sarà in grado di passare a Wikipedia in futuro. Per favore, aggiorna il tuo dispositivo o contatta il tuo amministratore informatico. Più in basso è disponibile un aggiornamento più dettagliato e tecnico in inglese.

magiaro: Biztonságosabb lesz a Wikipedia. Un böngésző, amit használsz, nem lesz képes kapcsolódni a jövőben. Használj modernebb szoftvert vagy jelezd a problemát a rendszergazdádnak. Alább olvashatod a reszletesebb magyarázatot (angolul).

Svezia: Wikipedia per saperne di più. Du använder en äldre webbläsare som inte kommer att kunna läsa Wikipedia i framtiden. Uppdatera in enhet eller kontakta in IT-administratör. Det finns en längre och mer teknisk förklaring på engelska längre ned.

हिन्दी: विकिपीडिया साइट को और अधिक सुरक्षित बना रहा है। आप एक पुराने वेब ब्राउज़र का उपयोग कर रहे हैं जो भविष्य में विकिपीडिया से कनेक्ट नहीं हो पाएगा। कृपया अपना डिवाइस अपडेट करें या अपने आईटी व्यवस्थापक से संपर्क करें। नीचे अंग्रेजी में एक लंबा और अधिक तकनीकी अद्यतन है।

Stiamo rimuovendo il supporto per le versioni non sicure del protocollo TLS, in particolare TLSv1.0 e TLSv1.1, su cui si basa il software del browser per connettersi ai nostri siti. Questo di solito è causato da browser obsoleti o smartphone Android meno recenti. Oppure potrebbe essere l'interferenza del software "Web Security" aziendale o personale, che in realtà riduce la sicurezza della connessione.

È necessario aggiornare il browser Web o risolvere in altro modo questo problema per accedere ai nostri siti. Questo messaggio rimarrà fino al 1 gennaio 2020. Dopo tale data, il tuo browser non sarà in grado di stabilire una connessione ai nostri server.

M 1 \u003d (x 1, y 1), M \u003d (x, y). Poiché il punto M divide il segmento M 0 M 1 rispetto a λ, allora

; (1)

Con questa trasformazione affine, i punti M 0, M 1, M andranno ai punti M 0 ′, M 1 ′, M′ con le stesse coordinate dei punti M 0, M 1, M, ma solo nel sistema di coordinate O "e " 1 e" 2. Queste coordinate sono ancora connesse da relazioni (1), da cui segue che M′ divide il segmento M 0 ′M 1 ′ rispetto a λ, il che dimostra il teorema.

3. Espressione analitica di trasformazioni affini (formule di transizione).

Un compito: Come, conoscendo i parametri di un sistema rispetto a un altro, è possibile determinare la posizione di un punto in entrambi i sistemi di coordinate (cioè come trovare le formule per il passaggio da un sistema (vecchio) a un altro nuovo sistema.

Consideriamo casi di trasformazione per sistemi di coordinate affini.

1) Sia dato il sistema R \u003d (O, (e 1, e 2)) e sia dato M \u003d (x, y) R, O (0,0) R - le coordinate dell'inizio. e 1 (1.0) R , e 2 (0.1) R sono le coordinate dei vettori base.

2) Sia dato il secondo sistema di coordinate R′=(O, (e 1 ′, e 2 ′)) e siano noti i parametri che definiscono la nuova base e la nuova origine delle coordinate attraverso il vecchio sistema di coordinate, cioè О′(x 0 ,y 0) R , e 1 ′(С 11 ,С 12) R , e 2 ′(С 12 ,С 22) R

Impostiamo l'attività per trovare le coordinate del punto M nel nuovo sistema di coordinate (M(x′,y′) R ′). Indichiamo le coordinate incognite del punto M(x′,y′).

Per tre punti O, O′, M: O′M=O′O +OM. О′М è il vettore raggio del punto M nel nuovo sistema di coordinate, il che significa che le sue coordinate coincideranno con le coordinate del vettore О′М nel sistema R′ (О′М↔М R ′)=>О ′М(x′,y′) R ′ => O′M \u003d x′e 1 ′+y′e 2 ′ (1) ; О′О è il vettore raggio del punto О′ nel sistema R′, cioè le sue coordinate coincideranno con le coordinate (2) ; OM ↔ M R => OM = xe 1 + ye 2 (3). Quella. il vettore O′M=OM − 00′ dopo la sostituzione in questo vettore uguaglianza di scomposizione (1),(2) e (3) apparirà come:

x′e 1 ′+y′e 2 ′= xe 1 +ye 2 −(x 0 e 1 +y 0 e 2) (4); perché la condizione contiene parametri che determinano le coordinate dei nuovi vettori base attraverso la vecchia base, otteniamo le seguenti uguaglianze vettoriali per i nuovi vettori base:

e 1 ′(C 11, C 12) R => e 1 ′= C 11 e 1 + C 21 e 2;

e 2 ′(C 12, C 22) R => e 2 ′= C 12 e 1 + C 22 e 2; (5)

Sostituiamo (5) nel lato sinistro di (4) e raggruppiamo rispetto ai vettori di base e 1 ed e 2 .

x′(C 11 e 1 +C 21 e 2)+y′(C 12 e 1 +C 22 e 2)- xe 1 -xe 2 +x 0 e 1 -ye 2 +x 0 e 1 +y 0 e 2=0.
(x′C 11 + y′C 12 e 1 -x+x 0)e 1 + (x′C 21 +y′ C 22 -y+y 0)e 2 =0.

Perché (e 1, e 2) formano una base, allora questo è un sistema linearmente indipendente per il quale è soddisfatta l'ultima uguaglianza vettoriale a condizione che tutti i coefficienti del lato sinistro siano uguali a zero, cioè a condizione

(6);

(6) - formule per il passaggio dal vecchio sistema R al nuovo sistema R′ con variabili x′ e y′.

Poiché le colonne del determinante sono le coordinate dei vettori base e 1 ′ ed e 2 ′, allora questo determinante non svanisce mai, cioè il sistema (6) è risolvibile in modo univoco rispetto alle variabili x′ e y′, il che permette sempre di trovare una formula per la transizione inversa da R′ a R.

Per le formule (6), ci sono due casi speciali

1. sostituzione della base;

2. trasferimento dell'inizio.

1. Sistema R′ ottenuto dal sistema R cambiando la base mantenendo la stessa origine R=(O, (e 1 , e 2)) → R′=(O, (e 1 ′, e 2 ′)), t .e. O (x 0, y 0) \u003d O (0,0) \u003d x 0 \u003d y 0 \u003d 0, quindi le formule per modificare la base assumeranno la forma:

(7)

2. Si ottenga da R il sistema R′ trasferendo l'origine dal punto O al punto O′ con la stessa base conservata:
R \u003d (O, (e 1, e 2)) → R′ \u003d (O′, (e 1, e 2)) \u003d e 1 ′ (1.0), e 2 ′ (0.1), t .circa . le formule assumeranno la forma.