5. Equazione cicloide parametrica ed equazione in coordinate cartesiane

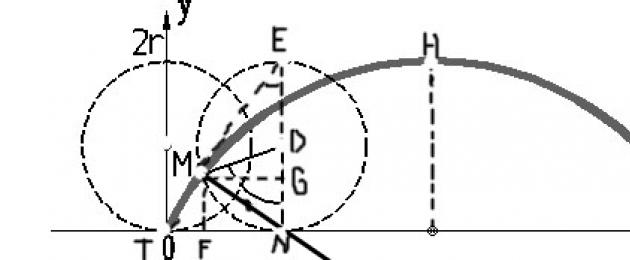
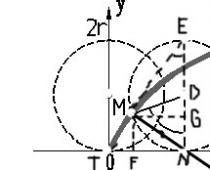
Supponiamo di avere una cicloide formata da una circonferenza di raggio a con centro nel punto A.

Se scegliamo come parametro che determina la posizione del punto l'angolo t=∟NDM di cui è riuscito a ruotare il raggio, che all'inizio del rotolamento aveva una posizione verticale AO, allora le coordinate xey del punto M saranno essere espresso come segue:

x= OF = ON - NF = NM - MG = at-a sin t,

y= FM = NG = ND – GD = a – a costo t

Quindi le equazioni parametriche della cicloide hanno la forma:

Quando t cambia da -∞ a +∞, si otterrà una curva costituita da un numero infinito di rami come quelli mostrati in questa figura.

Inoltre, oltre all'equazione parametrica della cicloide, esiste anche la sua equazione in coordinate cartesiane:

Dove r è il raggio del cerchio che forma la cicloide.

6. Problemi nel reperire parti di una cicloide e figure formate da una cicloide

Compito n. 1. Trova l'area di una figura delimitata da un arco di una cicloide la cui equazione è data parametricamente

e l'asse del bue.

Soluzione. Per risolvere questo problema, utilizzeremo i fatti che conosciamo dalla teoria degli integrali, vale a dire:

Area di un settore curvo.

Consideriamo una funzione r = r(ϕ) definita su [α, β].

ϕ 0 ∈ [α, β] corrisponde a r 0 = r(ϕ 0) e, quindi, al punto M 0 (ϕ 0 , r 0), dove ϕ 0,

r 0 - coordinate polari del punto. Se ϕ cambia, “attraversando” l’intero [α, β], allora il punto variabile M descriverà una qualche curva AB, dato

equazione r = r(ϕ).

Definizione 7.4. Un settore curvilineo è una figura delimitata da due raggi ϕ = α, ϕ = β e da una curva AB definita in polarità

coordinate dall'equazione r = r(ϕ), α ≤ ϕ ≤ β.

Quanto segue è vero

Teorema. Se la funzione r(ϕ) > 0 ed è continua su [α, β], allora l'area

il settore curvilineo si calcola con la formula:

Questo teorema è stato dimostrato in precedenza nell'argomento dell'integrale definito.

Sulla base del teorema precedente, il nostro problema di trovare l'area di una figura limitata da un arco di cicloide, la cui equazione è data dai parametri parametrici x= a (t – sin t), y= a (1 – cost t), e l’asse Ox, si riduce alla seguente soluzione .

Soluzione. Dall'equazione della curva dx = a(1−cos t) dt. Il primo arco della cicloide corrisponde a una variazione del parametro t da 0 a 2π. Quindi,

Compito n. 2. Trova la lunghezza di un arco della cicloide

Il seguente teorema ed il suo corollario sono stati studiati anche nel calcolo integrale.

Teorema. Se la curva AB è data dall’equazione y = f(x), dove f(x) e f ’ (x) sono continue su , allora AB è rettificabile e

Conseguenza. Sia AB dato parametricamente

L AB = (1)

Siano le funzioni x(t), y(t) continuamente differenziabili su [α, β]. Poi

la formula (1) può essere scritta come segue

Facciamo un cambio di variabili in questo integrale x = x(t), quindi y’(x)= ;

dx= x’(t)dt e quindi:

Ora torniamo a risolvere il nostro problema.

Soluzione. Abbiamo, e quindi

Compito n.3. Dobbiamo trovare l'area superficiale S formata dalla rotazione di un arco della cicloide

L=((x,y): x=a(t – sin t), y=a(1 – costo), 0≤ t ≤ 2π)

Nel calcolo integrale, esiste la seguente formula per trovare l'area della superficie di un corpo di rivoluzione attorno all'asse x di una curva definita parametricamente su un segmento: x=φ(t), y=ψ(t) (t 0 ≤ t ≤ t 1)

Applicando questa formula alla nostra equazione cicloide otteniamo:

Compito n. 4. Trova il volume del corpo ottenuto ruotando l'arco cicloide

Lungo l'asse del Bue.

Nel calcolo integrale, quando si studiano i volumi, vale la seguente osservazione:

Se la curva che delimita un trapezio curvilineo è data da equazioni parametriche e le funzioni in queste equazioni soddisfano le condizioni del teorema sul cambiamento di variabile in un certo integrale, allora il volume del corpo di rivoluzione del trapezio attorno all'asse del Bue sarà essere calcolato con la formula

Usiamo questa formula per trovare il volume di cui abbiamo bisogno.

Il problema è risolto.

Conclusione

Quindi, nel corso di questo lavoro, sono state chiarite le proprietà di base della cicloide. Abbiamo anche imparato come costruire una cicloide e scoperto il significato geometrico di una cicloide. Come si è scoperto, la cicloide ha enormi applicazioni pratiche non solo in matematica, ma anche nei calcoli tecnologici e nella fisica. Ma la cicloide ha altri pregi. Fu utilizzato dagli scienziati del XVII secolo quando svilupparono tecniche per lo studio delle linee curve, quelle tecniche che alla fine portarono all'invenzione del calcolo differenziale e integrale. Fu anche una delle “pietre di paragone” su cui Newton, Leibniz e i loro primi ricercatori testarono la potenza di nuovi e potenti metodi matematici. Infine, il problema della brachistocrona portò all'invenzione del calcolo delle variazioni, così necessario per i fisici di oggi. Pertanto, la cicloide si è rivelata indissolubilmente legata a uno dei periodi più interessanti della storia della matematica.

Letteratura

1. Berman G.N. Cicloide. – M., 1980

2. Verov S.G. Brachistocrona, o un altro segreto della cicloide // Quantistica. – 1975. - N. 5

3. Verov S.G. I segreti della cicloide // Quantistici. – 1975. - N. 8.

4. Gavrilova R.M., Govorukhina A.A., Kartasheva L.V., Kostetskaya G.S., Radchenko T.N. Applicazioni di un integrale definito. Istruzioni metodologiche e compiti individuali per gli studenti del 1° anno della Facoltà di Fisica. - Rostov n/a: UPL RSU, 1994.

5. Gindikin S.G. L'età stellare della cicloide // Quantistica. – 1985. - N. 6.

6. Fikhtengolts G.M. Corso di calcolo differenziale e integrale. T.1. – M., 1969

Questa linea è chiamata “busta”. Ogni linea curva è un inviluppo delle sue tangenti.

La materia e il movimento, e il metodo che essi costituiscono, consentono a ciascuno di realizzare il proprio potenziale nella conoscenza della verità. Sviluppare una metodologia per lo sviluppo di una forma di pensiero dialettico-materialista e padroneggiare un metodo cognitivo simile è il secondo passo verso la risoluzione del problema dello sviluppo e della realizzazione delle capacità umane. Frammento XX Opportunità...

In questa situazione, le persone possono sviluppare nevrastenia, una nevrosi, la cui base del quadro clinico è uno stato astenico. Sia nel caso della nevrastenia che nel caso dello scompenso della psicopatia nevrastenica, l'essenza della difesa mentale (psicologica) si riflette nel ritiro dalle difficoltà nella debolezza irritabile con disfunzioni vegetative: o la persona inconsciamente “reagisce” di più all'attacco. ..

Vari tipi di attività; sviluppo dell'immaginazione spaziale e dei concetti spaziali, pensiero figurativo, spaziale, logico, astratto degli scolari; sviluppare la capacità di applicare conoscenze e abilità geometriche e grafiche per risolvere vari problemi applicati; familiarità con il contenuto e la sequenza delle fasi delle attività progettuali nel campo tecnico e...

Archi. Le spirali sono anche evolventi di curve chiuse, ad esempio l'evolvente di un cerchio. I nomi di alcune spirali sono dati dalla somiglianza delle loro equazioni polari con le equazioni delle curve in coordinate cartesiane, ad esempio: · spirale parabolica (a - r)2 = bj, · spirale iperbolica: r = a/j. · Asta: r2 = a/j · si-ci-spirale, le cui equazioni parametriche hanno la forma: , =, modi.

A volte la curva è determinata fino a , cioè fino alla relazione di equivalenza minima tale che le curve parametriche

sono equivalenti se esiste un continuo (a volte non decrescente) H dal segmento [ UN 1 ,B 1] per segmento [ UN 2 ,B 2], tale che

Quelle definite da questa relazione sono chiamate semplicemente curve.

Definizioni analitiche

Nei corsi di geometria analitica si dimostra che tra le righe scritte in coordinate cartesiane rettangolari (o anche affini generali) da un'equazione generale di secondo grado

Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0

(dove almeno uno dei coefficienti A, B, C è diverso da zero) si trovano solo i seguenti otto tipi di linee:

a) ellisse;

b) iperbole;

c) parabola (curve non degeneri del secondo ordine);

d) una coppia di linee che si intersecano;

e) una coppia di linee parallele;

f) una coppia di linee coincidenti (una retta);

g) un punto (linee degeneri del secondo ordine);

h) una “linea” che non contiene alcun punto.

Al contrario, qualsiasi linea di ciascuno degli otto tipi indicati è scritta in coordinate cartesiane rettangolari da qualche equazione del secondo ordine. (Nei corsi di geometria analitica si parla solitamente di nove (non otto) tipi di sezioni coniche, perché si distingue tra una "ellisse immaginaria" e una "coppia di linee parallele immaginarie" - geometricamente queste "linee" sono le stesse, poiché entrambe fanno non contengono un solo punto, ma analiticamente sono scritte da equazioni diverse.) Pertanto, le sezioni coniche (degeneri e non degeneri) possono essere definite anche come rette del secondo ordine.

INuna curva su un piano è definita come un insieme di punti le cui coordinate soddisfano l'equazioneF ( X , sì ) = 0 . Allo stesso tempo, per la funzioneF vengono imposte restrizioni che garantiscono che questa equazione abbia un numero infinito di soluzioni divergenti e

questo insieme di soluzioni non riempie il “pezzo di aereo”.

Curve algebriche

Una classe importante di curve sono quelle per le quali la funzioneF ( X , sì ) C'èda due variabili. In questo caso, la curva definita dall'equazioneF ( X , sì ) = 0 , chiamato.

Le curve algebriche definite da un'equazione di 1° grado sono .

Un'equazione di grado 2, avente un numero infinito di soluzioni, determina , cioè degenere e non degenere.

Esempi di curve definite da equazioni di 3° grado: , .

Esempi di curve di 4° grado: e.

Esempio di curva di 6° grado: .

Esempio di curva definita da un'equazione di grado pari: (multifocale).

Vengono considerate le curve algebriche definite da equazioni di grado superiore. Allo stesso tempo, la loro teoria diventa più armoniosa se la considerazione viene portata avanti. In questo caso la curva algebrica è determinata da un'equazione della forma

F ( z 1 , z 2 , z 3 ) = 0 ,

Dove F- un polinomio di tre variabili che sono punti.

Tipi di curve

Una curva piana è una curva in cui tutti i punti giacciono sullo stesso piano.

(linea semplice o arco di Jordan, anche contorno) - un insieme di punti di un piano o di uno spazio che sono in corrispondenza uno a uno e mutuamente continua con i segmenti di linea.

Il percorso è un segmento in formato .

curve analitiche che non sono algebriche. Più precisamente, curve che possono essere definite attraverso la retta di livello di una funzione analitica (o, nel caso multidimensionale, di un sistema di funzioni).

Onda sinusoidale,

Cicloide,

Spirale di Archimede,

Trattore,

linea di catena,

Spirale iperbolica, ecc.

1. Metodi per definire le curve:

analitico – la curva è data da un’equazione matematica;

grafico – la curva è specificata visivamente su un supporto grafico di informazioni;

tabulare: la curva è specificata dalle coordinate di una serie sequenziale di punti.

parametrico (il modo più comune per specificare l'equazione di una curva):

Dove - funzioni dei parametri fluideT, E

(X") 2 + (sì") 2 + (z") 2 > 0 (condizione di regolarità).

Spesso è conveniente utilizzare una rappresentazione invariante e compatta dell'equazione di una curva utilizzando:

dove sul lato sinistro ci sono i punti della curva e il lato destro determina la sua dipendenza da alcuni parametri T. Espandendo questa voce in coordinate, otteniamo la formula (1).

1. Cicloide.

La storia dello studio della cicloide è associata ai nomi di grandi scienziati, filosofi, matematici e fisici come Aristotele, Tolomeo, Galileo, Huygens, Torricelli e altri.

Cicloide(daκυκλοειδής - rotondo) -, che può essere definita come la traiettoria di un punto giacente sul confine di un cerchio che rotola senza scorrere lungo una linea retta. Questo cerchio si chiama generazione.

Uno dei metodi più antichi per formare curve è il metodo cinematico, in cui la curva è ottenuta come traiettoria di un punto. Una curva che si ottiene come traiettoria di un punto fissato su un cerchio, che rotola senza scorrere lungo una retta, lungo un cerchio o altra curva, si chiama cicloidale, che tradotto dal greco significa circolare, che ricorda un cerchio.

Consideriamo innanzitutto il caso in cui il cerchio rotola lungo una linea retta. La curva descritta da un punto fissato su una circonferenza che rotola senza scorrere su una linea retta si chiama cicloide.

Lasciamo che una circonferenza di raggio R rotoli lungo una retta a. C è un punto fisso su un cerchio, nell'istante iniziale situato nella posizione A (Fig. 1). Tracciamo sulla retta a un segmento AB uguale alla lunghezza del cerchio, cioè AB = 2 π R. Dividi questo segmento in 8 parti uguali per i punti A1, A2, ..., A8 = B.

È chiaro che quando il cerchio, rotolando lungo la retta a, compie un giro, cioè ruota di 360, quindi assumerà la posizione (8) e il punto C si sposterà dalla posizione A alla posizione B.

Se il cerchio fa mezza rivoluzione completa, cioè gira di 180, quindi assumerà la posizione (4) e il punto C si sposterà nella posizione più alta C4.

Se il cerchio ruota di un angolo di 45, il cerchio si sposterà nella posizione (1) e il punto C si sposterà nella posizione C1.

La figura 1 mostra anche altri punti della cicloide corrispondenti ai restanti angoli di rotazione del cerchio, multipli di 45.

Collegando i punti costruiti con una curva morbida, otteniamo una sezione della cicloide corrispondente ad un giro completo del cerchio. Ai giri successivi si otterranno le stesse sezioni, cioè La cicloide sarà costituita da una sezione che si ripete periodicamente chiamata arco della cicloide.

Prestiamo attenzione alla posizione della tangente alla cicloide (Fig. 2). Se un ciclista pedala su una strada bagnata, le gocce che escono dalla ruota voleranno tangenzialmente alla cicloide e, in assenza di scudi, potranno schizzare la schiena del ciclista.

Il primo a studiare la cicloide fu Galileo Galilei (1564 – 1642). Ha anche inventato il suo nome.

Proprietà della cicloide:

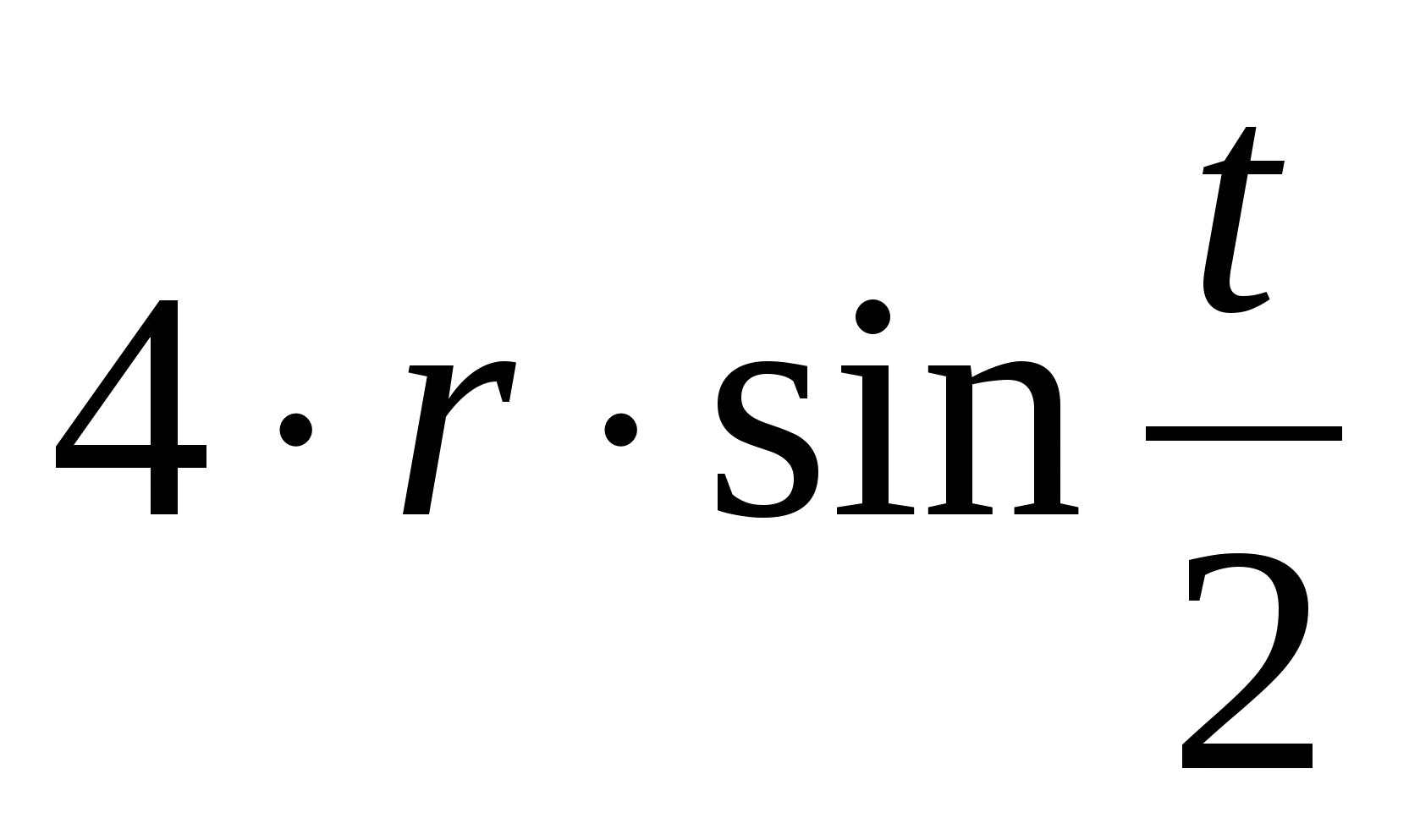
La cicloide ha una serie di proprietà notevoli. Ne menzioniamo alcuni.

Proprietà 1. (Montagna di ghiaccio.) Nel 1696 I. Bernoulli si pose il problema di trovare la curva di discesa più ripida, o, in altre parole, il problema di quale dovesse essere la forma di uno scivolo di ghiaccio per rotolare giù per compiere il viaggio dal punto iniziale A al punto finale B nel più breve tempo possibile (Fig. 3, a). La curva desiderata è stata chiamata “brachistocrona”, cioè curva temporale più breve.

È chiaro che il percorso più breve dal punto A al punto B è il segmento AB. Tuttavia, con un movimento così rettilineo, la velocità viene guadagnata lentamente e il tempo impiegato per la discesa risulta essere ampio (Fig. 3, b).

Più la discesa è ripida, più la velocità aumenta. Con una discesa ripida, però, il percorso lungo la curva si allunga e quindi aumenta il tempo necessario per completarla.

Tra i matematici che risolsero questo problema c'erano: G. Leibniz, I. Newton, G. L'Hopital e J. Bernoulli. Hanno dimostrato che la curva desiderata è una cicloide invertita (Fig. 3, a). I metodi sviluppati da questi scienziati per risolvere il problema della brachistocrona gettarono le basi per una nuova direzione in matematica: il calcolo delle variazioni.

Proprietà 2. (Orologio a pendolo.) Un orologio a pendolo ordinario non può funzionare con precisione, poiché il periodo di oscillazione di un pendolo dipende dalla sua ampiezza: maggiore è l'ampiezza, maggiore è il periodo. Lo scienziato olandese Christiaan Huygens (1629 – 1695) si chiese quale curva dovesse seguire una pallina sul filo di un pendolo affinché il periodo delle sue oscillazioni non dipenda dall'ampiezza. Si noti che in un pendolo ordinario, la curva lungo la quale si muove la palla è un cerchio (Fig. 4).

La curva che stavamo cercando si è rivelata una cicloide invertita. Se, ad esempio, viene realizzata una trincea a forma di cicloide invertita e lungo di essa viene lanciata una palla, il periodo di movimento della palla sotto l'influenza della gravità non dipenderà dalla sua posizione iniziale e dalla sua ampiezza (Fig. 5 ). Per questa proprietà la cicloide è chiamata anche “tautocrona” - una curva di tempi uguali.

Huygens ha realizzato due assi di legno con bordi a forma di cicloide, limitando il movimento del filo a sinistra e a destra (Fig. 6). In questo caso, la palla stessa si muoverà lungo una cicloide invertita e, quindi, il periodo delle sue oscillazioni non dipenderà dall'ampiezza.

Da questa proprietà della cicloide deriva in particolare che, non importa da quale punto dello scivolo di ghiaccio a forma di cicloide rovesciata iniziamo la discesa, impiegheremo lo stesso tempo fino al punto finale.

Equazione cicloide

1. È conveniente scrivere l'equazione della cicloide in termini di α - l'angolo di rotazione del cerchio, espresso in radianti; si noti che α è anche uguale al percorso percorso dal cerchio generatore in linea retta.

x=rα– R peccato α

y=r – r cos α

2. Prendiamo l'asse delle coordinate orizzontali come la linea retta lungo la quale scorre il cerchio generatore di raggio R.

La cicloide è descritta da equazioni parametriche

X = rt – R peccato T,

sì = R – R cos T.

Equazione in:

La cicloide può essere ottenuta risolvendo l'equazione differenziale:

Dalla storia della cicloide

Il primo scienziato a prestare attenzione alla cicloideV, ma una ricerca seria su questa curva iniziò solo nel.

La prima persona a studiare la cicloide fu Galileo Galilei (1564-1642), il famoso astronomo, fisico ed educatore italiano. Ha anche inventato il nome “cicloide”, che significa “che ricorda un cerchio”. Lo stesso Galileo non scrisse nulla sulla cicloide, ma il suo lavoro in questa direzione è menzionato dagli studenti e seguaci di Galileo: Viviani, Toricelli e altri. Toricelli, famoso fisico e inventore del barometro, dedicò molto tempo alla matematica. Durante il Rinascimento non esistevano scienziati specializzati. Un uomo di talento studiò filosofia, fisica e matematica e ovunque ottenne risultati interessanti e fece importanti scoperte. Poco dopo gli italiani, i francesi adottarono la cicloide, chiamandola “roulette” o “trocoide”. Nel 1634 Roberval, l'inventore del famoso sistema di scale, calcolò l'area delimitata dall'arco di una cicloide e dalla sua base. Uno studio approfondito della cicloide fu condotto da un contemporaneo di Galileo. Tra , cioè curve la cui equazione non può essere scritta nella forma di X , sì, la cicloide è la prima di quelle studiate.

Ha scritto sulla cicloide:

La roulette è una linea così comune che dopo la linea retta e il cerchio non esiste linea più frequente; è così spesso delineato davanti agli occhi di tutti che c'è da stupirsi che gli antichi non lo abbiano considerato... perché non è altro che un sentiero descritto nell'aria dal chiodo di una ruota.

La nuova curva ha guadagnato rapidamente popolarità ed è stata sottoposta ad analisi approfondite, che includevano, , Newton,, i fratelli Bernoulli e altri luminari della scienza dei secoli XVII-XVIII. Sulla cicloide, i metodi apparsi in quegli anni furono attivamente affinati. Il fatto che lo studio analitico della cicloide si sia rivelato altrettanto efficace dell'analisi delle curve algebriche fece grande impressione e divenne un argomento importante a favore della “parità di diritti” delle curve algebriche e trascendenti. Epicicloide

Alcuni tipi di cicloidi

Epicicloide - la traiettoria del punto A, giacente su una circonferenza di diametro D, che rotola senza strisciare lungo una circonferenza guida di raggio R (contatto esterno).

La costruzione dell'epicicloide viene eseguita nella seguente sequenza:

Dal centro 0 tracciare un arco ausiliario con raggio pari a 000=R+r;

Dai punti 01, 02, ...012, a partire dai centri, tracciare cerchi di raggio r finché non si intersecano con archi ausiliari nei punti A1, A2, ... A12, che appartengono all'epicicloide.

Ipocicloide

L'ipocicloide è la traiettoria del punto A giacente su una circonferenza di diametro D, che rotola senza scorrere lungo una circonferenza guida di raggio R (tangenza interna).

La costruzione di un ipocicloide viene eseguita nella seguente sequenza:

La circonferenza generatrice di raggio r e la circonferenza direttrice di raggio R si disegnano in modo che si tocchino nel punto A;

Si divide il cerchio generatore in 12 parti uguali, si ottengono i punti 1, 2, ... 12;

Dal centro 0 tracciare un arco ausiliario con raggio pari a 000=R-r;

L'angolo al centro a è determinato dalla formula a =360r/R.

Dividere l'arco di circonferenza guida, limitato dall'angolo a, in 12 parti uguali, ottenendo i punti 11, 21, ...121;

Dal centro 0 si tracciano rette attraverso i punti 11, 21, ...121 fino ad intersecare l'arco ausiliario nei punti 01, 02, ...012;

Dal centro 0 si disegnano archi ausiliari attraverso i punti di divisione 1, 2, ... 12 del cerchio generatore;

Dai punti 01, 02, ...012, a partire dai centri, tracciare cerchi di raggio r finché non si intersecano con archi ausiliari nei punti A1, A2, ... A12, che appartengono all'ipocicloide.

1. Cardioide.

Cardioide ( καρδία - cuore, Il cardioide è un caso particolare: il termine “cardioide” fu introdotto da Castillon nel 1741.

Se prendiamo come polo un cerchio e un punto su di esso, otterremo una cardioide solo se tracciamo segmenti uguali al diametro del cerchio. Per altre dimensioni di segmenti depositati, le concoidi saranno cardioidi allungate o accorciate. Questi cardioidi allungati e accorciati sono altrimenti chiamati coclea di Pascal.

Il cardioide ha varie applicazioni nella tecnologia. Le forme cardioidi vengono utilizzate per realizzare eccentrici e camme per automobili. A volte viene utilizzato quando si disegnano gli ingranaggi. Inoltre, viene utilizzato nella tecnologia ottica.

Proprietà di un cardioide

Cardioide -B M su un cerchio in movimento descriverà una traiettoria chiusa. Questa curva piatta è chiamata cardioide.

2) Il cardioide può essere ottenuto in un altro modo. Segna un punto sul cerchio DI e ne traiamo una trave. Se dal punto UN intersezione di questo raggio con un cerchio, traccia un segmento SONO, lunghezza uguale al diametro del cerchio e il raggio ruota attorno al punto DI, quindi puntare M si muoverà lungo il cardioide.

3) Un cardioide può anche essere rappresentato come una curva tangente a tutti i cerchi aventi centri su un dato cerchio e passante per il suo punto fisso. Quando vengono costruiti più cerchi, il cardioide sembra essere costruito come se fosse da solo.

4) Esiste anche un modo altrettanto elegante e inaspettato di vedere la cardioide. Nella figura puoi vedere una sorgente luminosa puntiforme su un cerchio. Dopo che i raggi luminosi vengono riflessi per la prima volta dal cerchio, viaggiano tangenti alla cardioide. Immagina ora che il cerchio sia il bordo di una tazza; una lampadina brillante viene riflessa in un punto. Il caffè nero viene versato nella tazza, permettendoti di vedere i raggi luminosi riflessi. Di conseguenza, il cardioide viene evidenziato dai raggi di luce.

1. Astroide.

Astroide (dal greco astron - stella ed eidos - vista), curva piatta descritta da un punto su un cerchio che tocca dall'interno un cerchio fisso di quattro volte il raggio e rotola lungo esso senza scivolare. Appartiene agli ipocicloidi. L'astroide è una curva algebrica del 6° ordine.

Astroide.

La lunghezza dell'intero astroide è pari a sei raggi del cerchio fisso e l'area da esso delimitata è pari a tre ottavi del cerchio fisso.

Il segmento tangente all'astroide, racchiuso tra due raggi reciprocamente perpendicolari del cerchio fisso disegnato sulle punte dell'astroide, è uguale al raggio del cerchio fisso, indipendentemente da come è stato scelto il punto.

Proprietà dell'astroide

Ce ne sono quattrokaspa .

Lunghezza dell'arco dal punto 0 all'inviluppo

famiglie di segmenti di lunghezza costante, le cui estremità si trovano su due linee reciprocamente perpendicolari.

Astroid è del sesto ordine.

Equazioni degli asteroidi

Equazione in coordinate cartesiane rettangolari:| x| 2/3 + | sì | 2/3 = R 2/3equazione parametrica:x = Rcos 3 t y = Rsin 3 t

Metodo per costruire un astroide

Disegniamo due linee rette tra loro perpendicolari e disegniamo una serie di segmenti di lunghezzaR , le cui estremità giacciono su queste linee. La figura mostra 12 di questi segmenti (compresi i segmenti delle stesse rette reciprocamente perpendicolari). Più segmenti disegniamo, più precisa sarà la curva che otterremo. Costruiamo ora l'inviluppo di tutti questi segmenti. Questa busta sarà l'astroide.

1. Conclusione

Il lavoro fornisce esempi di problemi con diversi tipi di curve, definite da diverse equazioni o che soddisfano alcune condizioni matematiche. In particolare, curve cicloidali, metodi per definirle, vari metodi di costruzione, proprietà di tali curve.

Le proprietà delle curve cicloidali sono molto spesso utilizzate nella meccanica degli ingranaggi, il che aumenta significativamente la resistenza delle parti nei meccanismi.

Per prima cosa devi scoprire quale curva è chiamata cicloide.

Considera un cerchio di raggio UN con centro nel punto A. Fate rotolare il cerchio in questione senza scivolare lungo l'asse del OX. Si chiama la curva descritta da un punto qualsiasi della circonferenza cicloide.

Questa definizione di cicloide non ha mai soddisfatto gli scienziati: dopo tutto, si basa su concetti meccanici: velocità, somma di movimenti, ecc. Pertanto, i geometri hanno sempre cercato di dare alla cicloide una "definizione puramente geometrica". tale definizione, è necessario innanzitutto studiare le proprietà fondamentali di una cicloide, utilizzando la sua definizione meccanica. Avendo scelto la più semplice e caratteristica di queste proprietà, possiamo usarla come base per una definizione geometrica.

Cominciamo studiando la tangente e la normale alla cicloide. Che è successo tangente a una linea curva, tutti immaginano abbastanza chiaramente; pertanto non lo presenteremo qui. Normale si chiama perpendicolare alla tangente, ripristinata nel punto di contatto. Nella fig. 1.1 mostra la tangente e la normale alla curva AB nel suo punto M.

Consideriamo una cicloide (Fig. 1.2). Una circonferenza rotola lungo una retta AB. Supponiamo che il raggio verticale del cerchio, che nel momento iniziale passava per il punto inferiore della cicloide, sia riuscito a girare di un angolo μ e abbia preso la posizione OM. In altre parole, crediamo che il segmento M o T costituisca una frazione del segmento M o M 1 quanto l'angolo q forma da una rivoluzione completa. In questo caso il punto M 0 è arrivato al punto M.

Il punto M è il punto della cicloide che ci interessa.

Freccia OH rappresenta la velocità di movimento del centro di un cerchio rotante. Tutti i punti del cerchio, compreso il punto M, hanno la stessa velocità orizzontale, ma in più il punto M partecipa alla rotazione del cerchio. La velocità MC, che riceve il punto M sulla circonferenza durante questa rotazione, è diretta lungo la tangente SM 1 al cerchio, cioè perpendicolare al raggio OM. E perché in questo caso, la velocità MS è uguale in grandezza alla velocità MP (cioè la velocità LUI). Pertanto, il parallelogramma delle velocità nel caso del nostro movimento sarà un rombo (il rombo MSKR in Fig. 1.2). La diagonale MK di questo rombo ci darà la tangente alla cicloide.

Tutto quanto sopra permette di risolvere il seguente problema di costruzione: data la linea direttrice AB della cicloide, il raggio r del cerchio generatore e il punto M appartenente alla cicloide (Fig. 1.2). È necessario costruire una tangente al MC alla cicloide.

Avendo un punto M, possiamo facilmente costruire una circonferenza generatrice, nella sua posizione quando un punto della circonferenza cade in M. Per fare ciò, troviamo prima il centro DI utilizzando il raggio MO=r(il punto O dovrebbe giacere su una retta parallela ad AB, a distanza r da essa). Quindi costruiamo un segmento MP di lunghezza arbitraria, parallelo alla retta direttiva. Successivamente costruiamo una linea retta SM 1 , perpendicolare a OM. Su questa linea retta ci allontaniamo dal punto M segmento MC uguale a MP. Su MC e MP, come sui lati, costruiamo un rombo. La diagonale di questo rombo sarà tangente alla cicloide nel punto M.

Questa costruzione è puramente geometrica, anche se l'abbiamo ottenuta utilizzando i concetti della meccanica. Ora possiamo dire addio alla meccanica e ottenere ulteriori conseguenze senza il suo aiuto. Cominciamo con un semplice teorema.

Teorema 1. Angolo tra la tangente alla cicloide (in un punto arbitrario) e la linea direttrice è uguale al complementare di 90° metà dell'angolo di rotazione del raggio del cerchio produttore.

In altre parole, nella Fig. 1.2

? KLT uguale a o

Dimostreremo ora questa uguaglianza. Per abbreviare il discorso concorderemo di chiamare “angolo principale” l’angolo μ di rotazione del raggio del cerchio generatore. Ciò significa che l’angolo MOT in Fig. 1.2 -- angolo principale. Considereremo l'angolo principale acuto. Nel caso in cui il cerchio rotolante compia più di un quarto di giro completo, la dimostrazione sarà simile.

Consideriamo l'angolo SMR. Il lato CM è perpendicolare OM(la tangente al cerchio è perpendicolare al raggio). Il lato MP (orizzontale) è perpendicolare a DA(verso la verticale). Ma l'angolo MOP, per convenzione, è acuto e l'angolo CMR è ottuso. Quindi gli angoli OIL E lavori di costruzione e installazione sommare fino a 180° (angoli con lati tra loro perpendicolari, di cui uno acuto e l'altro ottuso).

Quindi, l'angolo CMP è 180° -ts. Ma, come sai, la diagonale di un rombo divide a metà l'angolo al vertice. Perciò,

KMR = 90°-,

Q.E.D.

Rivolgiamo ora la nostra attenzione alla normale alla cicloide. Rappresentiamo il lato sinistro della Fig. 1.2 è più grande e disegniamo una normale IO (IO? MK; riso. 1.3).

Dalla fig. 1.3 ne consegue che l'angolo EMP è uguale alla differenza tra gli angoli KME E KMR, cioè. pari a 90° - ? KMP.

Ma abbiamo appena dimostrato che l'angolo stesso KMR pari a 90° -

Otteniamo così:

? RME= 90° - ? KMR= 90° - (90° -) =

Abbiamo dimostrato un teorema semplice ma utile. Diamo la sua formulazione:

Teorema 2. Angolo tra la normale alla cicloide (in qualsiasi punto) e la linea direttrice è pari alla metà dell '"angolo base".

Colleghiamo ora il punto (T) della circonferenza generatrice con il punto M (il punto “attuale” della cicloide) con quello inferiore (con il punto di tangenza della circonferenza generatrice e la linea direttrice - Fig. 1.3) . Il triangolo MOT è ovviamente isoscele (OM e DA-- raggi del cerchio generatore). La somma degli angoli alla base di questo triangolo è uguale a 180° - μ, e ciascuno degli angoli alla base è la metà di questa somma. COSÌ, ? OMT= 90° - .

Prestiamo attenzione all'angolo RMT.È uguale alla differenza degli angoli OMT E OMR. Ora lo abbiamo visto ? OMT pari a 90° - ; Per quanto riguarda l'angolo OMR, non è difficile scoprire a cosa è uguale. Dopotutto, l'angolo OMR uguale all'angolo DOM(angoli incrociati interni quando paralleli).

Ciò è subito evidente ? DOM pari a 90° - c. Significa, ? OMP= = 90° - c. Otteniamo così:

RMT = ? OMT - ? OMR = 90° - - (90° - c) = .

Il risultato è notevole: angolo RMT risulta essere uguale all'angolo PME (per il Teorema 2). Pertanto, ME diretto e MT si fonderanno! Il nostro riso. 1.3 non è fatto bene! La posizione corretta delle linee è mostrata in Fig. 1.4.

Formuliamo il risultato ottenuto nella forma del Teorema 3.

Teorema 3 (prima proprietà fondamentale di una cicloide). La normale alla cicloide passa per il punto “fondo” del cerchio generatore.

Questo teorema ha un semplice corollario. L'angolo tra la tangente e la normale è, per definizione, un angolo retto. Questo è l'angolo inscritto nella circonferenza del cerchio generatore. Pertanto, deve poggiare sul diametro del cerchio. COSÌ, TT 1 -- diametro e T 1 -- punto “superiore” del cerchio generatore. Formuliamo il risultato ottenuto.

Corollario (seconda proprietà principale della cicloide). La tangente alla cicloide passa per il punto “superiore” della circonferenza generatrice.

Per spiegare questa proprietà dobbiamo costruire una cicloide.

La cicloide è costruita nella seguente sequenza:

• 1. Sulla linea guida orizzontale è tracciato un segmento AA 12, pari alla lunghezza del cerchio generatore di raggio r, (2рr);
• 2. Costruisci una circonferenza generatrice di raggio r, in modo che la linea direttrice sia tangente ad essa nel punto A;
• 3. Il cerchio e il segmento AA 12 si dividono in più parti uguali, ad esempio 12;
• 4. Dai punti di divisione 1 1, 2 1, ...12 1 si ripristinano le perpendicolari fino ad intersecare con la continuazione dell'asse orizzontale del cerchio nei punti 0 1, 0 2, ...0 12;
• 5. Dai punti di divisione del cerchio 1, 2, ...12 si tracciano linee orizzontali, sulle quali vengono praticate delle tacche con archi di cerchio di raggio r;
• 6. I punti risultanti A 1, A 2, ...A 12 appartengono alla cicloide.

Nella fig. 1.6 la base della cicloide è divisa in 6 parti uguali;

Maggiore è il numero di divisioni, più accurato sarà il disegno. In ogni punto della cicloide che abbiamo costruito disegniamo una tangente, che collega il punto della curva con il punto “superiore” del cerchio generatore. Nel nostro disegno abbiamo sette tangenti (due delle quali sono verticali). Adesso disegnando a mano la cicloide, faremo attenzione che tocchi effettivamente ciascuna di queste tangenti: questo aumenterà notevolmente la precisione del disegno. In questo caso, la cicloide stessa si piegherà attorno a tutte queste tangenti).

Disegniamo la stessa figura. 1,6 normali in tutti i punti trovati della cicloide. Ci saranno un totale di cinque normali, senza contare la guida. Puoi costruire manualmente l'inviluppo di queste normali. Se avessimo preso 12 o 16 punti di divisione invece di sei, nel disegno ci sarebbero state più normali e la busta sarebbe stata delineata più chiaramente. Questo inviluppo di tutte le normali gioca un ruolo importante nello studio delle proprietà di qualsiasi linea curva. Nel caso di una cicloide si rivela un fatto interessante: l'inviluppo delle normali della cicloide è esattamente la stessa cicloide, spostata solo di 2 UN giù e su RA A destra. Questo fatto è caratteristico specificatamente della cicloide.

“Per secondo è stata servita una torta a forma di cicloide...”

I viaggi di J. Swift Gulliver

Tangente e normale ad una cicloide

La definizione più naturale di cerchio sarebbe, forse, la seguente: “un cerchio è il percorso di una particella di un corpo rigido che ruota attorno ad un asse fisso”. Questa definizione è chiara, da essa è facile ricavare tutte le proprietà del cerchio e, soprattutto, ci disegna immediatamente un cerchio come una curva continua, il che non è affatto evidente dalla definizione classica di cerchio come forma geometrica. luogo dei punti del piano equidistanti da un punto.

Perché definiamo un cerchio a scuola? al luogo dei punti? Perché definire un cerchio utilizzando il movimento (rotazione) è sbagliato? Pensiamoci.

Quando studiamo la meccanica non dimostriamo teoremi geometrici: pensiamo di conoscerli già, ci riferiamo semplicemente alla geometria come a qualcosa di già noto.

Se, nel dimostrare teoremi geometrici, ci riferiamo alla meccanica come qualcosa di già noto, commetteremo un errore chiamato “circolo logico (vizioso)”: nel dimostrare una proposizione, ci riferiamo alla proposizione B, e giustifichiamo la proposizione B con l’aiuto della proposizione A In parole povere, Ivan annuisce a Peter, e Peter indica Ivan. Questa situazione è inaccettabile quando si presentano discipline scientifiche. Perciò quando si presenta l'aritmetica si cerca di non riferirsi alla geometria, quando si presenta la geometria si cerca di non riferirsi alla meccanica, ecc. , un circolo logico non funzionerà.

La definizione di cicloide, con cui siamo riusciti a conoscere, non ha mai soddisfatto gli scienziati: dopo tutto, si basa su concetti meccanici: velocità, addizione di movimenti, ecc. Pertanto, i geometri hanno sempre cercato di dare alla cicloide un aspetto puramente geometrico definizione. Ma per dare una tale definizione è necessario prima di tutto studiare le proprietà fondamentali della cicloide, utilizzando la sua definizione meccanica. Avendo scelto la più semplice e caratteristica di queste proprietà, possiamo metterla alla base della definizione geometrica.

Cominciamo studiando la tangente e la normale alla cicloide. Che cosa sia la tangente ad una linea curva, lo capiscono tutti abbastanza chiaramente; La definizione precisa di tangente viene data nei corsi superiori di matematica e non la forniremo qui.

Riso. 16. Tangente e normale ad una curva.

La normale è la perpendicolare alla tangente, ripristinata nel punto di contatto. Nella fig. La Figura 16 mostra la tangente e la normale alla curva AB nel suo punto. Consideriamo la cicloide (Figura 17). Una circonferenza rotola lungo una retta AB.

Supponiamo che il raggio verticale del cerchio, che nel momento iniziale passava per il punto inferiore della cicloide, sia riuscito a girare di un angolo (la lettera greca “phi”) e abbia preso la posizione OM. In altre parole, riteniamo che il segmento MST costituisca una frazione del segmento pari all'angolo di 360° (da una rivoluzione completa). In questo caso il punto è arrivato al punto M.

Riso. 17. Tangente ad una cicloide.

Il punto M è il punto della cicloide che ci interessa.

La freccia OH rappresenta la velocità di movimento del centro del cerchio rotante. Tutti i punti del cerchio, compreso il punto M, hanno la stessa velocità orizzontale, ma in più il punto M partecipa alla rotazione del cerchio. La velocità MC, che riceve il punto M del cerchio durante questa rotazione, è diretta tangenzialmente al cerchio, cioè perpendicolare al raggio OM. Sappiamo già dalla “conversazione tra due veyusipedisti” (vedi pagina 6) che la velocità MS è uguale in grandezza alla velocità MR (cioè la velocità OH). Pertanto, il parallelogramma delle velocità nel caso del nostro movimento sarà un rombo (rombo MSKR in Fig. 17). La diagonale MK di questo rombo ci darà la tangente alla cicloide.

Ora possiamo rispondere alla domanda posta alla fine della conversazione tra Sergei e Vasya (p. 7). Un pezzo di sporco separato da una ruota di bicicletta si muove tangenzialmente alla traiettoria della particella della ruota da cui si è separato. Ma la traiettoria non sarà un cerchio, ma una cicloide, perché la ruota non si limita a ruotare, ma rotola, cioè compie un movimento costituito da traslazione e rotazione.

Tutto quanto sopra permette di risolvere il seguente “problema di costruzione”: data la linea direttiva AB della cicloide, il raggio del cerchio generatore e il punto M appartenente alla cicloide (Fig. 17).

È necessario costruire una tangente al MC alla cicloide.

Avendo un punto M, possiamo facilmente costruire una circonferenza generatrice, nella sua posizione quando un punto della circonferenza cade in M. Per fare ciò, troviamo prima il centro O utilizzando il raggio (il punto O deve giacere su una retta parallela a AB ad una distanza da esso). Quindi costruiamo un segmento MR di lunghezza arbitraria, parallelo alla linea guida. Costruiamo poi una retta perpendicolare a OM, sulla quale dal punto M tracciamo un segmento MC uguale a MR. Su MC e MR, come sui lati, costruiamo un rombo. La diagonale di questo rombo sarà tangente alla cicloide nel punto M.

Questa costruzione è puramente geometrica, anche se l'abbiamo ottenuta utilizzando i concetti della meccanica. Ora possiamo dire addio alla meccanica e ottenere ulteriori conseguenze senza il suo aiuto. Cominciamo con un semplice teorema.

Teorema 1. L'angolo tra la tangente alla cicloide (in un punto arbitrario) e la linea direttrice è uguale alla somma a 90° della metà dell'angolo di rotazione del raggio del cerchio generatore.

In altre parole, nella nostra fig. 17 angolo KLT è uguale a o . Dimostreremo ora questa uguaglianza. Per abbreviare il discorso concorderemo di chiamare “angolo principale” l’angolo di rotazione del raggio del cerchio generatore. Ciò significa che l’angolo MOT in Fig. 17 - angolo principale. Considereremo l'angolo principale acuto. Il lettore stesso modificherà il ragionamento per il caso di un angolo ottuso, cioè per il caso in cui il cerchio rotolante compie più di un quarto di giro completo.

Consideriamo l'angolo SMR. Il lato CM è perpendicolare a OM (la tangente al cerchio è perpendicolare al raggio). Il lato MR (orizzontale) è perpendicolare all'OT (verticale). Ma l'angolo MOT, per convenzione, è acuto (abbiamo concordato di considerare il primo quarto di giro), e l'angolo SMR è ottuso (perché?). Ciò significa che la somma degli angoli MOT e SMR dà come risultato 180° (angoli con i lati tra loro perpendicolari, di cui uno acuto e l'altro ottuso).

Quindi, l'angolo CMP è uguale a Ma, come sai, la diagonale di un rombo divide a metà l'angolo al vertice.

Pertanto, l’angolo è ciò che doveva essere dimostrato.

Rivolgiamo ora la nostra attenzione alla normale alla cicloide. Abbiamo già detto che la normale alla curva è la perpendicolare alla tangente tracciata nel punto di contatto (Fig. 16). Rappresentiamo il lato sinistro della Fig. 17 è più grande e disegneremo una normale (vedi Fig. 18).

Dalla fig. 18 ne consegue che l'angolo EMR è uguale alla differenza tra gli angoli KME e KMR, cioè è pari a 90° - k.KMR.

Riso. 18. Al Teorema 2.

Ma abbiamo appena dimostrato che l'angolo KMR stesso è uguale a . Otteniamo così:

Abbiamo dimostrato un teorema semplice ma utile. Diamo la sua formulazione:

Teorema 2. L'angolo tra la normale alla cicloide (in qualsiasi punto) e la linea direttrice è uguale alla metà dell '"angolo principale".

(Ricordate che l’“angolo primario” è l’angolo di rotazione del raggio del cerchio rotolante)

Colleghiamo ora il punto M (il punto “attuale” della cicloide) con il punto “inferiore” (T) del cerchio generatore (con il punto di tangenza del cerchio generatore e la linea direttrice - vedi Fig. 18).

Il triangolo MOT è ovviamente isoscele (OM e OT sono i raggi del cerchio generatore). La somma degli angoli alla base di questo triangolo è uguale a , e ciascuno degli angoli alla base è la metà di questa somma. COSÌ,

Prestiamo attenzione all'angolo RMT. È uguale alla differenza tra gli angoli OMT e OMR. Abbiamo ora visto che è pari a 90° - per quanto riguarda l'angolo OMR, non è difficile scoprire a cosa è uguale. Dopotutto, l'angolo OMP è uguale all'angolo DOM (angoli trasversali interni quando paralleli).

Riso. 19. Proprietà fondamentali della tangente e della normale ad una cicloide.

È subito evidente che è uguale a . Significa, . Otteniamo così:

Si ottiene un risultato notevole: l'angolo RMT risulta essere uguale all'angolo RME (vedi Teorema 2). Pertanto, ME diretto e MT si fonderanno! Il nostro riso. 18 non è fatto bene! La posizione corretta delle linee è mostrata in Fig. 19.

Come formulare il risultato ottenuto? Lo formuliamo nella forma del Teorema 3.

Teorema 3 (prima proprietà fondamentale di una cicloide). La normale alla cicloide passa per il punto “fondo” del cerchio generatore.

Questo teorema ha un semplice corollario. L'angolo tra la tangente e la normale, per definizione, è una linea retta. Questo è l'angolo inscritto in un cerchio

Pertanto, deve poggiare sul diametro del cerchio. Quindi è il diametro, ed è il punto “superiore” del cerchio generatore. Formuliamo il risultato ottenuto.

Corollario (seconda proprietà principale della cicloide). La tangente alla cicloide passa per il punto “superiore” della circonferenza generatrice.

Riproduciamo ora la costruzione per punti della cicloide, come abbiamo fatto in Fig. 6.

Riso. 20. Cicloide: un involucro delle sue tangenti.

Nella fig. 20 la base della cicloide è divisa in 6 parti uguali; Come sappiamo, maggiore sarà il numero delle divisioni, più accurato sarà il disegno. In ogni punto della cicloide che abbiamo costruito disegniamo una tangente, che collega il punto della curva con il punto “superiore” del cerchio generatore. Nel nostro disegno abbiamo sette tangenti (due delle quali sono verticali). Adesso disegnando a mano la cicloide, faremo attenzione che tocchi effettivamente ciascuna di queste tangenti: questo aumenterà notevolmente la precisione del disegno. In questo caso, la cicloide stessa si piegherà attorno a tutte queste tangenti

Disegniamo la stessa figura. 20 normali in tutti i punti trovati della cicloide. Ci saranno un totale di cinque normali, senza contare la guida. Puoi costruire una piegatura a mano libera di queste normali.

Se avessimo preso 12 o 16 punti di divisione invece di sei, nel disegno ci sarebbero state più normali e la busta sarebbe stata delineata più chiaramente. Questo inviluppo di tutte le normali gioca un ruolo importante nello studio delle proprietà di qualsiasi linea curva. Nel caso della cicloide si rivela un fatto interessante: l'inviluppo delle normali della cicloide è esattamente la stessa cicloide, spostata solo di 2a verso il basso e di 2a a destra. Dovremo occuparci di questo curioso risultato, caratteristico proprio della cicloide.

Le proprietà della tangente e della normale ad una cicloide furono delineate per la prima volta da Toricelli (1608-1647) nel suo libro Lavori geometrici (1644). Toricelli utilizzava l'addizione di movimenti. Un po' più tardi, ma in modo più approfondito, Roberval (lo pseudonimo del matematico francese Gilles Personne, 1602-1672) esaminò queste questioni. Le proprietà di una tangente ad una cicloide furono studiate anche da Cartesio; ha presentato i suoi risultati senza ricorrere alla meccanica.

Cyclomis (dal greco khklpeidYut - rotondo) è una curva trascendentale piatta. Una cicloide è definita cinematicamente come la traiettoria di un punto fisso di un cerchio generatore di raggio r, che rotola senza strisciare lungo una linea retta.

Equazioni

Prendiamo l'asse delle coordinate orizzontali come la retta lungo la quale scorre il cerchio generatore di raggio r.

· La cicloide è descritta da equazioni parametriche

Equazione in coordinate cartesiane:

· La cicloide può essere ottenuta come soluzione dell'equazione differenziale:

Proprietà

• · Cicloide -- funzione periodica lungo l'asse x, con un periodo di 2рr. È conveniente prendere punti singolari (punti di ritorno) della forma t = 2рk, dove k è un numero intero arbitrario, come confini del periodo.
• · Per tracciare la tangente ad una cicloide in un punto arbitrario A, è sufficiente collegare questo punto con il punto superiore del cerchio generatore. Collegando A al punto inferiore del cerchio generatore, otteniamo la normale.
• · La lunghezza dell'arco cicloide è 8r. Questa proprietà fu scoperta da Christopher Wren (1658).
• · L'area sotto ciascun arco della cicloide è tre volte maggiore dell'area del cerchio generatore. Torricelli sostiene che questo fatto fu scoperto da Galileo.
• · Il raggio di curvatura del primo arco della cicloide è uguale.

• · La cicloide “rovesciata” è una curva di discesa più ripida (brachistocrona). Inoltre possiede anche la proprietà della tautocronia: un corpo pesante posto in un punto qualsiasi dell'arco cicloide raggiunge nello stesso tempo l'orizzontale.
• · Il periodo di oscillazione di un punto materiale che scorre lungo una cicloide invertita non dipende dall'ampiezza; questo fatto fu sfruttato da Huygens per creare orologi meccanici precisi.
• · L'evoluta di una cicloide è una cicloide congruente a quella originaria, cioè spostata parallelamente in modo che i vertici si trasformino in “punti”.
• · Le parti della macchina che eseguono contemporaneamente un movimento rotatorio e traslatorio uniforme descrivono curve cicloidali (cicloide, epicicloide, ipocicloide, trocoide, astroide) (cfr. costruzione della lemniscata di Bernoulli).