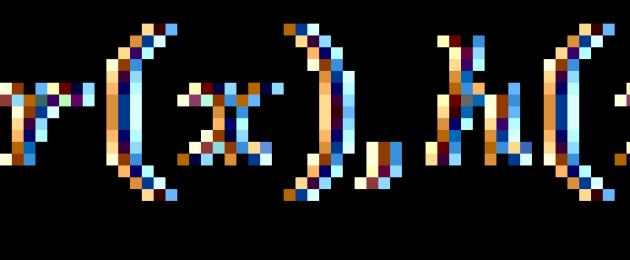Esempi di equazioni razionali per la formazione. Video lezione “Equazioni razionali

Le equazioni razionali sono equazioni contenenti espressioni razionali.

Definizione 1

Le espressioni razionali sono espressioni che possono essere scritte nella forma frazione comune della forma $\frac(m)(n)$, mentre $m$ e $n$ sono numeri interi e $n$ non può essere uguale a zero. Le espressioni razionali includono non solo espressioni contenenti frazioni della forma $\frac(2)(3)$, ma anche espressioni contenenti solo numeri interi, poiché qualsiasi numero intero può essere rappresentato come una frazione impropria.

Ora diamo un'occhiata più in dettaglio a cosa sono le equazioni razionali.

Come accennato in precedenza, le equazioni razionali sono equazioni che contengono espressioni e variabili razionali.

A seconda della posizione esatta della variabile in un'equazione razionale, può essere un'equazione razionale frazionaria o un'intera equazione razionale.

Le equazioni frazionarie possono contenere una frazione con una variabile solo in una parte dell'equazione, mentre le equazioni intere non contengono espressioni frazionarie con una variabile.

Esempi di equazioni razionali intere: $5x+2= 12$; $3y=-7(-4y + 5)$; $7a-14=$256.

Esempi di equazioni razionali frazionarie: $\frac(3x-2)(x+3)+\frac(1)(2)=\frac(5)(x)$; $\frac(7)(2y-3)=5$;

Vale la pena notare che solo le equazioni contenenti una frazione al denominatore sono chiamate equazioni frazionarie-razionali, poiché le equazioni contenenti espressioni frazionarie senza variabili possono essere facilmente ridotte a equazioni lineari intere.

Come risolvere le equazioni razionali?

A seconda che si abbia a che fare con un'equazione razionale intera o frazionaria, vengono utilizzati algoritmi leggermente diversi per la risoluzione.

Algoritmo per la risoluzione di intere equazioni razionali

1. Innanzitutto, è necessario determinare il minimo comune denominatore dell'intera equazione.
2. Quindi è necessario determinare i fattori per i quali deve essere moltiplicato ciascun termine dell'uguaglianza.
3. La fase successiva consiste nel portare tutta l’uguaglianza a un denominatore comune.
4. Infine, cercare le radici dell'uguaglianza razionale intera risultante.

Esempio 1

Risolvi l'equazione: $\frac(5x+9)(2)=\frac(x)(4)$

Per prima cosa troviamo moltiplicatore comune- in questo caso è il numero $4$. Per eliminare il denominatore, moltiplichiamo il lato sinistro per $\frac(2)(2)$, otteniamo:

$10x+18=x$ - l'equazione risultante è lineare, la sua radice è $x=-2$.

Come risolvere le equazioni razionali frazionarie?

Nel caso di equazioni razionali frazionarie, la procedura per la risoluzione è simile all'algoritmo per la risoluzione di equazioni razionali intere, ovvero i punti 1-4 vengono preservati, ma dopo aver trovato le radici attese, nel caso di utilizzo di trasformazioni disuguali, le radici devono essere controllati sostituendoli nell'equazione.

Esempio 2

Risolvi l'equazione razionale frazionaria: $\frac(x-3)(x-5)+\frac(1)(x)=\frac(x+5)(x \cdot (x-5))$

Per ridurre una frazione a un denominatore comune, ecco $x \cdot (x-5)$, moltiplichiamo ogni frazione per uno, presentata sotto forma del fattore necessario da ridurre a un denominatore comune:

$\frac((x-3) \cdot x)((x-5)\cdot x)+\frac(1 \cdot (x-5))(x \cdot (x-5))=\frac( x+5)(x \cdot (x-5))$

Ora che l'intera frazione ha un denominatore comune, possiamo sbarazzarcene:

$(x-3)\cpunto x+(x-5)=x+5$

$x^2 ​​- 3x+x-5 = x+5$

Usiamo il teorema di Vieta per risolvere l'equazione quadratica risultante:

$\begin(cases) x_1 + x_2 = 3 \\ x_1 \cdot x_2 = -10 \\ \end(cases)$

$\begin(cases) x_1=5 \\ x_2=-2 \\ \end(cases)$

Poiché la trasformazione utilizzata per semplificare l'equazione non è equivalente, è necessario verificare le radici risultanti nell'equazione originale, per farlo sostituiamole:

$\frac(-2-3)(-2-5) +\frac(1)(-2)=\frac(-2+5)((-2) \cdot (-2-5))$

$\frac(5)(7)-\frac(1)(2)=\frac(3)(14)$

$\frac(3)(14)=\frac(3)(14)$ - quindi la radice $x_2=-2$ è corretta.

$\frac(5-3)(5-5) +\frac(1)(5)=\frac(5+5)((-2) \cdot (5-5))$

Qui è subito chiaro che al denominatore si forma uno zero, quindi la radice $x_1=5$ è estranea.

Va ricordato che se un'equazione contenente un'espressione della forma $\frac(m)(n)$ a sinistra o a destra è uguale a zero, solo il numeratore della frazione può essere uguale a zero. Ciò è dovuto al fatto che se si trova uno zero da qualche parte nel denominatore, la radice da testare non è la radice dell'equazione, poiché in questo caso l'intera uguaglianza diventa priva di significato. Le radici che portano il denominatore a zero si dicono estranee.

Se un'equazione razionale frazionaria ha una forma piuttosto complessa, per semplificarla ulteriormente e risolverla, è possibile utilizzare la sostituzione di parte dell'equazione con una nuova variabile, probabilmente hai già visto esempi di tali equazioni razionali frazionarie:

Esempio 3

Risolvi l'equazione:

$\frac(1)(x^2+3x-3)+\frac(2)(x^2+3x+1)=\frac(7)(5)$

Per semplificare la soluzione, introduciamo la variabile $t= x^2+3x$:

$\frac(1)(t-3)+\frac(2)(t+1)=\frac(7)(5)$

Il denominatore comune qui è $5 \cdot (t-3)(t+1)$, moltiplica tutte le parti dell'equazione per i fattori necessari per eliminarlo:

$\frac(5(t+1))(5(t-3)(t+1))+\frac(2 \cdot 5(t-3))(5(t+1)(t-3) )=\frac(7(t+1)(t-3))(5(t-3)(t+1))$

$5(t+1)+10(t-3)=7(t+1)(t-3)$

$5t+5+10t-30=7(t^2-3t+t-3)$

$15t-25=7t^2-14t-21$

Usando il discriminante calcoliamo le radici:

$t_1=4;t_2=\frac(1)(7)$

Poiché abbiamo utilizzato trasformazioni non equivalenti, è necessario verificare che le radici risultanti al denominatore debbano soddisfare la condizione $5(t-3)(t+1)≠0$; Entrambe le radici soddisfano questa condizione.

Ora sostituiamo le radici risultanti invece di $t$ e otteniamo due equazioni:

$x^2+3x=4$ e $x^2+3x=\frac(1)(7)$.

Secondo il teorema di Vieta, le radici della prima equazione sono $x_1=-4; x_2=1$, calcoliamo le radici della seconda tramite il discriminante e abbiamo $x_(1,2)=\frac(-3±\sqrt(\frac(67)(7)))(2)$.

Tutte le radici dell'equazione saranno: $x_1=-4; x_2=1, x_(3,4)=\frac(-3±\sqrt(\frac(67)(7)))(2)$.

Trasformazioni per semplificare la forma di un'equazione

Come puoi già vedere sopra, varie trasformazioni vengono utilizzate per risolvere equazioni razionali.

Esistono due tipi di trasformazioni di equazioni: equivalenti (identiche) e disuguali.

Le trasformazioni si dicono equivalenti se portano ad un'equazione di nuovo tipo, le cui radici sono le stesse di quella originale.

Le trasformazioni di identità che possono essere utilizzate per cambiare la forma dell'equazione originale senza ulteriori controlli sono le seguenti:

• Moltiplicare o dividere un'intera equazione per un numero diverso da zero;
• Trasferimento di parti di un'equazione da sinistra a destra e viceversa.

Le trasformazioni non equivalenti sono trasformazioni durante le quali possono apparire radici estranee. Le trasformazioni non equivalenti includono:

• Quadratura di entrambi i lati dell'equazione;
• Eliminare i denominatori contenenti una variabile;

Le radici delle equazioni razionali risolte utilizzando trasformazioni non equivalenti devono essere controllate mediante sostituzione nell'equazione originale, poiché durante le trasformazioni non equivalenti possono apparire radici estranee. Le trasformazioni non equivalenti non sempre portano alla comparsa di radici estranee, ma è comunque necessario tenerne conto.

Risoluzione di equazioni razionali con gradi maggiori di due

I metodi più comunemente usati per risolvere equazioni con gradi maggiori di due sono il metodo del cambiamento variabile, di cui abbiamo discusso sopra usando l'esempio di un'equazione razionale frazionaria, così come il metodo di fattorizzazione.

Diamo uno sguardo più da vicino al metodo di fattorizzazione.

Sia data un'equazione della forma $P(x)= 0$ e $P(x)$ sia un polinomio il cui grado è maggiore di due. Se questa equazione può essere fattorizzata in modo che assuma la forma $P_1(x)P_2(x)P_3(x)..\cdot P_n(x)=0$, allora la soluzione di questa equazione sarà l'insieme delle soluzioni di le equazioni $P_1(x )=0, P_2(x)=0, P_3(x)=0...P_n(x)=0$.

Per chi non se lo ricorda: un termine libero in un'equazione è un termine in equazioni che non contiene una variabile come fattore. Inoltre, avendo trovato una delle radici di tale equazione, è possibile utilizzarla per fattorizzare ulteriormente l'equazione.

Esempio 5

Risolvi l'equazione:

I divisori del termine libero saranno i numeri $±1, ±2, ±3, ±4, ±6, ±8, ±12$ e $±24$. Durante il controllo, la radice appropriata è risultata essere $x=2$. Ciò significa che questo polinomio può essere espanso utilizzando questa radice: $(x-2)(x^2+6+12)=0$.

Il polinomio nella seconda coppia di parentesi radice non ha radici, il che significa che l'unica radice di questa equazione sarà $x=2$.

Un altro tipo di equazione con grado maggiore di due è equazioni biquadratiche della forma $ax^4+bx^2+ c=0$. Tali equazioni vengono risolte sostituendo $x^2$ con $y$, applicandolo, otteniamo un'equazione della forma $ay^2+y+c=0$, dopodiché viene utilizzato il valore risultante della nuova variabile per calcolare la variabile originale.

Esiste anche un altro tipo di equazione chiamata restituibile. Tali equazioni assomigliano a questa: $ax^4+bx^3+cx^2+bx+a=0$. Prendono questo nome per la ripetizione dei coefficienti ai gradi più alti e più bassi.

Un'espressione intera è un'espressione matematica composta da numeri e variabili letterali che utilizza le operazioni di addizione, sottrazione e moltiplicazione. I numeri interi includono anche espressioni che implicano la divisione per qualsiasi numero diverso da zero.

Il concetto di espressione razionale frazionaria

Un'espressione frazionaria è un'espressione matematica che, oltre alle operazioni di addizione, sottrazione e moltiplicazione eseguite con numeri e variabili letterali, nonché la divisione per un numero diverso da zero, contiene anche la divisione in espressioni con variabili letterali.

Le espressioni razionali sono tutte espressioni intere e frazionarie. Le equazioni razionali sono equazioni in cui i lati sinistro e destro sono espressioni razionali. Se in un'equazione razionale i lati sinistro e destro sono espressioni intere, allora tale equazione razionale è chiamata intero.

Se in un'equazione razionale i lati sinistro o destro sono espressioni frazionarie, allora tale equazione razionale è chiamata frazionaria.

Esempi di espressioni razionali frazionarie

1. x-3/x = -6*x+19

2. (x-4)/(2*x+5) = (x+7)/(x-2)

3. (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5))

Schema per la risoluzione di un'equazione razionale frazionaria

1. Trova il denominatore comune di tutte le frazioni incluse nell'equazione.

2. Moltiplica entrambi i lati dell'equazione per un denominatore comune.

3. Risolvi l'intera equazione risultante.

4. Controllare le radici ed escludere quelle che fanno svanire il comune denominatore.

Poiché stiamo risolvendo equazioni razionali frazionarie, ci saranno variabili nei denominatori delle frazioni. Ciò significa che saranno un denominatore comune. E nel secondo punto dell'algoritmo moltiplichiamo per un denominatore comune, quindi potrebbero apparire radici estranee. In cui il denominatore comune sarà uguale a zero, il che significa che moltiplicare per esso non avrà senso. Pertanto, alla fine è necessario controllare le radici ottenute.

Diamo un'occhiata ad un esempio:

Risolvi l'equazione razionale frazionaria: (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5)).

Aderiremo allo schema generale: prima trova il denominatore comune di tutte le frazioni. Otteniamo x*(x-5).

Moltiplica ciascuna frazione per un denominatore comune e scrivi l'intera equazione risultante.

(x-3)/(x-5) * (x*(x-5))= x*(x+3);
1/x * (x*(x-5)) = (x-5);
(x+5)/(x*(x-5)) * (x*(x-5)) = (x+5);
x*(x+3) + (x-5) = (x+5);

Semplifichiamo l'equazione risultante. Otteniamo:

x^2+3*x + x-5 - x - 5 =0;
x^2+3*x-10=0;

Abbiamo ottenuto una semplice riduzione equazione quadratica. Lo risolviamo con uno qualsiasi dei metodi conosciuti, otteniamo le radici x=-2 e x=5.

Ora controlliamo le soluzioni ottenute:

Sostituisci i numeri -2 e 5 nel denominatore comune. A x=-2, il denominatore comune x*(x-5) non svanisce, -2*(-2-5)=14. Ciò significa che il numero -2 sarà la radice dell'equazione razionale frazionaria originale.

Per x=5 il denominatore comune x*(x-5) diventa zero. Pertanto, questo numero non è la radice dell'equazione razionale frazionaria originale, poiché ci sarà una divisione per zero.

Abbiamo già imparato come risolvere le equazioni quadratiche. Estendiamo ora i metodi studiati alle equazioni razionali.

Cos'è un'espressione razionale? Abbiamo già incontrato questo concetto. Espressioni razionali sono espressioni composte da numeri, variabili, loro potenze e simboli di operazioni matematiche.

Di conseguenza, le equazioni razionali sono equazioni della forma: , dove - espressioni razionali.

In precedenza, abbiamo considerato solo quelle equazioni razionali che possono essere ridotte a quelle lineari. Ora diamo un'occhiata a quelle equazioni razionali che possono essere ridotte a equazioni quadratiche.

Esempio 1

Risolvi l'equazione: .

Soluzione:

Una frazione è uguale a 0 se e solo se il suo numeratore è uguale a 0 e il suo denominatore è diverso da 0.

Otteniamo il seguente sistema:

La prima equazione del sistema è un'equazione quadratica. Prima di risolverlo dividiamo tutti i suoi coefficienti per 3. Otteniamo:

Otteniamo due radici: ; .

Poiché 2 non è mai uguale a 0, devono essere soddisfatte due condizioni: . Poiché nessuna delle radici dell'equazione ottenuta sopra coincide con i valori non validi della variabile ottenuti risolvendo la seconda disuguaglianza, sono entrambe soluzioni di questa equazione.

Risposta:.

Quindi, formuliamo un algoritmo per risolvere equazioni razionali:

1. Sposta tutti i termini sul lato sinistro in modo che il lato destro termini con 0.

2. Trasforma e semplifica la parte sinistra, porta tutte le frazioni a un denominatore comune.

3. Uguagliare la frazione risultante a 0 utilizzando il seguente algoritmo: .

4. Annota le radici ottenute nella prima equazione e soddisfa la seconda disuguaglianza nella risposta.

Diamo un'occhiata a un altro esempio.

Esempio 2

Risolvi l'equazione: .

Soluzione

All'inizio spostiamo tutti i termini a sinistra in modo che lo 0 rimanga a destra. Otteniamo:

Ora portiamo il lato sinistro dell'equazione a un denominatore comune:

Questa equazione è equivalente al sistema:

La prima equazione del sistema è un'equazione quadratica.

Coefficienti di questa equazione: . Calcoliamo il discriminante:

Otteniamo due radici: ; .

Risolviamo ora la seconda disuguaglianza: il prodotto dei fattori non è uguale a 0 se e solo se nessuno dei fattori è uguale a 0.

Devono essere soddisfatte due condizioni: . Troviamo che delle due radici della prima equazione, solo una è adatta - 3.

Risposta:.

In questa lezione, abbiamo ricordato cos'è un'espressione razionale e abbiamo anche imparato come risolvere equazioni razionali, che si riducono a equazioni quadratiche.

Nella prossima lezione esamineremo le equazioni razionali come modelli di situazioni reali e esamineremo anche i problemi di movimento.

Riferimenti

1. Bashmakov M.I. Algebra, 8a elementare. - M.: Educazione, 2004.
2. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. e altri. - M.: Educazione, 2010.
3. Nikolsky S.M., Potapov M.A., Reshetnikov N.N., Shevkin A.V. Algebra, 8a elementare. Tutorial per istituzioni educative. - M.: Educazione, 2006.

1. Festival spunti pedagogici "Lezione aperta" ().
2. School.xvatit.com ().
3. Rudocs.exdat.com ().

Compiti a casa

Il minimo comune denominatore viene utilizzato per semplificare questa equazione. Questo metodo è applicabile quando è impossibile scrivere questa equazione con uno espressione razionale su ciascun lato dell'equazione (e utilizzare il metodo di moltiplicazione incrociata). Questo metodo viene utilizzato quando viene data un'equazione razionale con tre o più frazioni (nel caso di due frazioni è meglio utilizzare la moltiplicazione incrociata).

Trova il minimo comune denominatore delle frazioni (o minimo comune multiplo). NOZ è il numero più piccolo uniformemente divisibile per ciascun denominatore.

• A volte NPD è un numero ovvio. Ad esempio, se data l'equazione: x/3 + 1/2 = (3x +1)/6, allora è ovvio che il minimo comune multiplo dei numeri 3, 2 e 6 è 6.
• Se il NCD non è evidente, annota i multipli del denominatore più grande e trova tra loro quello che sarà multiplo degli altri denominatori. Spesso il NOD può essere trovato semplicemente moltiplicando due denominatori. Ad esempio, se l'equazione è x/8 + 2/6 = (x - 3)/9, allora NOS = 8*9 = 72.
• Se uno o più denominatori contengono una variabile, il processo diventa un po’ più complicato (ma non impossibile). In questo caso, il NOC è un'espressione (contenente una variabile) divisa per ciascun denominatore. Ad esempio, nell'equazione 5/(x-1) = 1/x + 2/(3x) NOZ = 3x(x-1), poiché questa espressione è divisa per ciascun denominatore: 3x(x-1)/(x -1) = 3x; 3x(x-1)/3x = (x-1); 3x(x-1)/x = 3(x-1).

Moltiplica sia il numeratore che il denominatore di ciascuna frazione per un numero uguale al risultato della divisione del NOC per il corrispondente denominatore di ciascuna frazione.

• Poiché stai moltiplicando sia il numeratore che il denominatore per lo stesso numero, stai effettivamente moltiplicando la frazione per 1 (ad esempio, 2/2 = 1 o 3/3 = 1).
• Quindi, nel nostro esempio, moltiplica x/3 per 2/2 per ottenere 2x/6, e moltiplica 1/2 per 3/3 per ottenere 3/6 (non è necessario moltiplicare la frazione 3x +1/6 perché è la frazione il denominatore è 6).

Procedi allo stesso modo quando la variabile è al denominatore. Nel nostro secondo esempio, NOZ = 3x(x-1), quindi moltiplica 5/(x-1) per (3x)/(3x) per ottenere 5(3x)/(3x)(x-1); 1/x moltiplicato per 3(x-1)/3(x-1) e ottieni 3(x-1)/3x(x-1); 2/(3x) moltiplicato per (x-1)/(x-1) e ottieni 2(x-1)/3x(x-1). Ora che hai ridotto le frazioni a un denominatore comune, puoi eliminare il denominatore. Per fare ciò, moltiplica ciascun lato dell'equazione per il denominatore comune. Quindi risolvi l'equazione risultante, ovvero trova "x". Per fare ciò, isola la variabile su un lato dell'equazione.

• Nel nostro esempio: 2x/6 + 3/6 = (3x +1)/6. Puoi sommare due frazioni con lo stesso denominatore, quindi scrivi l'equazione come: (2x+3)/6=(3x+1)/6. Moltiplica entrambi i lati dell'equazione per 6 ed elimina i denominatori: 2x+3 = 3x +1. Risolvi e ottieni x = 2.
• Nel nostro secondo esempio (con una variabile al denominatore), l'equazione appare così (dopo la riduzione a un denominatore comune): 5(3x)/(3x)(x-1) = 3(x-1)/3x(x -1) + 2(x-1)/3x(x-1). Moltiplicando entrambi i lati dell'equazione per N3, elimini il denominatore e ottieni: 5(3x) = 3(x-1) + 2(x-1), o 15x = 3x - 3 + 2x -2, o 15x = x - 5 Risolvi e ottieni: x = -5/14.

Mantenere la tua privacy è importante per noi. Per questo motivo, abbiamo sviluppato un'Informativa sulla privacy che descrive come utilizziamo e archiviamo le tue informazioni. Si prega di rivedere le nostre pratiche sulla privacy e di farci sapere se avete domande.

Raccolta e utilizzo delle informazioni personali

Le informazioni personali si riferiscono ai dati che possono essere utilizzati per identificare o contattare una persona specifica.

Ti potrebbe essere chiesto di fornire le tue informazioni personali in qualsiasi momento quando ci contatti.

Di seguito sono riportati alcuni esempi dei tipi di informazioni personali che potremmo raccogliere e di come potremmo utilizzare tali informazioni.

Quali informazioni personali raccogliamo:

• Quando invii una richiesta sul sito, potremmo raccogliere varie informazioni, incluso il tuo nome, numero di telefono, indirizzo email, ecc.

Come utilizziamo le tue informazioni personali:

• Raccolti da noi informazioni personali ci consente di contattarti e informarti su offerte uniche, promozioni e altri eventi e prossimi eventi.
• Di tanto in tanto, potremmo utilizzare le tue informazioni personali per inviare avvisi e comunicazioni importanti.
• Potremmo anche utilizzare le informazioni personali per scopi interni, come condurre audit, analisi dei dati e varie ricerche al fine di migliorare i servizi che forniamo e fornirti consigli sui nostri servizi.
• Se partecipi a un'estrazione a premi, a un concorso o a una promozione simile, potremmo utilizzare le informazioni fornite per amministrare tali programmi.

Divulgazione di informazioni a terzi

Non divulghiamo le informazioni ricevute da te a terzi.

Eccezioni:

• Se necessario - in conformità con la legge, la procedura giudiziaria, in procedimenti legali e/o sulla base di richieste pubbliche o richieste da parte di enti governativi della Federazione Russa - di divulgare i tuoi dati personali. Potremmo anche divulgare informazioni su di te se stabiliamo che tale divulgazione è necessaria o appropriata per scopi di sicurezza, applicazione della legge o altri scopi di importanza pubblica.
• In caso di riorganizzazione, fusione o vendita, potremmo trasferire le informazioni personali che raccogliamo alla terza parte successore applicabile.

Protezione delle informazioni personali

Prendiamo precauzioni, comprese quelle amministrative, tecniche e fisiche, per proteggere le tue informazioni personali da perdita, furto e uso improprio, nonché da accesso non autorizzato, divulgazione, alterazione e distruzione.

Rispettare la tua privacy a livello aziendale

Per garantire che le tue informazioni personali siano sicure, comunichiamo gli standard di privacy e sicurezza ai nostri dipendenti e applichiamo rigorosamente le pratiche sulla privacy.