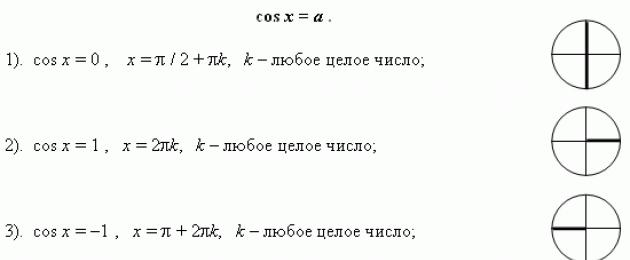La tabella delle equazioni trigonometriche più semplici. Equazioni trigonometriche: formule, soluzioni, esempi

Equazioni trigonometriche .

Le più semplici equazioni trigonometriche .

Metodi per risolvere equazioni trigonometriche.

Equazioni trigonometriche. Un'equazione contenente un'incognita sotto viene chiamato il segno della funzione trigonometrica trigonometrico.

Le più semplici equazioni trigonometriche.

Metodi per risolvere equazioni trigonometriche. La risoluzione di un'equazione trigonometrica consiste di due fasi: trasformazione dell'equazione per renderlo più semplice tipo (vedi sopra) e soluzioneil risultato più semplice equazione trigonometrica. Ce ne sono sette metodi di base per la risoluzione di equazioni trigonometriche.

1. Metodo algebrico. Questo metodo ci è ben noto dall'algebra.

(metodo di sostituzione e sostituzione variabile).

2. Fattorizzazione. Diamo un'occhiata a questo metodo con esempi.

Esempio 1. Risolvi l'equazione: peccato X+cos X = 1 .

Soluzione. Spostiamo tutti i termini dell'equazione a sinistra:

Peccato X+cos X – 1 = 0 ,

Trasformiamo e fattorizziamo l'espressione in

Lato sinistro dell'equazione:

Esempio 2. Risolvi l'equazione: cos 2 X+ peccato X cos X = 1.

Soluzione: cos2 X+ peccato X cos X– peccato 2 X– cos2 X = 0 ,

Peccato X cos X– peccato 2 X = 0 ,

Peccato X· (cos X– peccato X ) = 0 ,

Esempio 3. Risolvi l'equazione: cos2 X–cos 8 X+ cos 6 X = 1.

Soluzione: cos2 X+ cos 6 X= 1 + cos8 X,

2 cos 4 X cos2 X= 2cos²4 X ,

Cos4 X · (cos2 X–cos 4 X) = 0 ,

Cos4 X · 2 peccato 3 X peccato X = 0 ,

1). cos 4 X= 0, 2). peccato 3 X= 0, 3). peccato X = 0 ,

3.

Portando a equazione omogenea. Equazione chiamato omogeneo da per quanto riguarda peccato E cos , Se tutto termini dello stesso grado rispetto a peccato E cos stesso angolo. Per risolvere un'equazione omogenea è necessario: UN) sposta tutti i suoi membri sul lato sinistro; B) mettete tutti i fattori comuni tra parentesi; V) equiparare tutti i fattori e le parentesi a zero; G) parentesi uguali a zero danno equazione omogenea di grado minore, in cui dovrebbe essere divisa cos(O peccato) nel grado senior; D) risolvi il risultato equazione algebrica relativamenteabbronzatura . ESEMPIO Risolvere l'equazione: 3 peccato 2 X+4 peccato X cos X+ 5 cos 2 X = 2. Soluzione: 3peccato 2 X+4 peccato X cos X+5cos2 X= 2peccato 2 X+2cos2 X , Peccato 2 X+4 peccato X cos X+3cos2 X = 0 , Abbronzatura 2 X+ 4 abbronzatura X + 3 = 0 , da qui sì 2 + 4sì +3 = 0 , Le radici di questa equazione sono:sì 1 = - 1, sì 2 = - 3, quindi 1) abbronzatura X= –1, 2) marrone chiaro X = –3,

4. Transizione al semiangolo. Consideriamo questo metodo come esempio:

ESEMPIO Risolvere l'equazione: 3 peccato X– 5 cos X = 7.

Soluzione: 6 peccati ( X/ 2) cos ( X/ 2) – 5 cos² ( X/ 2) + 5 peccato² ( X/ 2) =

7 peccato² ( X/ 2) + 7 cos² ( X/ 2) ,

2 peccato² ( X/ 2) – 6 peccato ( X/ 2) cos ( X/ 2) + 12 cos² ( X/ 2) = 0 ,

tan²( X/ 2) – 3 marrone chiaro ( X/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Introduzione di un angolo ausiliario. Consideriamo un'equazione della forma:

UN peccato X + B cos X = C ,

Dove UN, B, C– coefficienti;X- sconosciuto.

Ora i coefficienti dell'equazione hanno le proprietà di seno e coseno, vale a dire: modulo (valore assoluto) di ciascuno

Classe: 10

“Le equazioni dureranno per sempre.”

A. Einstein

Obiettivi della lezione:

• Educativo:
  • approfondire la comprensione dei metodi per risolvere equazioni trigonometriche;
  • sviluppare le competenze per distinguere e selezionare correttamente i metodi per risolvere equazioni trigonometriche.
• Educativo:
  • coltivare l'interesse cognitivo nel processo educativo;
  • sviluppare la capacità di analizzare un determinato compito;
  • contribuire a migliorare il clima psicologico in classe.
• Sviluppo:
  • promuovere lo sviluppo della capacità di acquisizione indipendente della conoscenza;
  • promuovere la capacità degli studenti di argomentare il proprio punto di vista;

Attrezzatura: poster con formule trigonometriche di base, computer, proiettore, schermo.

1 lezione

I. Aggiornamento delle conoscenze di riferimento

Risolvi oralmente le equazioni:

1) cosx = 1;
2) 2 cosx = 1;
3) cosx = –;
4) sin2x = 0;
5) sinx = –;
6) sinx = ;
7) tgx = ;
8) cos 2 x – sin 2 x = 0

1) x = 2k;
2) x = ± + 2k;
3) x =± + 2k;
4) x = k;
5) x = (–1) + k;
6) x = (–1) + 2k;
7) x = + k;
8) x = + k;

a Z.

II. Imparare nuovo materiale – Oggi esamineremo aspetti più complessi equazioni trigonometriche

. Diamo un'occhiata a 10 modi per risolverli. Successivamente ci saranno due lezioni di consolidamento, e per la lezione successiva ci sarà un test. Nello stand “For Lesson” sono affissi compiti simili a quelli che saranno presenti nel test; è necessario risolverli prima del test; (Il giorno prima del test, affiggi le soluzioni a questi compiti sullo stand).

Passiamo quindi a considerare i modi per risolvere le equazioni trigonometriche. Alcuni di questi metodi probabilmente ti sembreranno difficili, mentre altri ti sembreranno facili, perché... Conosci già alcune tecniche per risolvere le equazioni.

Quattro studenti della classe hanno ricevuto un compito individuale: comprendere e mostrare 4 modi per risolvere equazioni trigonometriche.

(Gli studenti che parlano hanno preparato delle diapositive in anticipo. Il resto della classe scrive i passaggi principali per risolvere le equazioni su un quaderno.) 1 modo. Risolvere equazioni mediante fattorizzazione

peccato 4x = 3 cos 2x

Per risolvere l'equazione usiamo la formula del doppio seno angolare sin 2 = 2 sin cos
2 sin 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0. Il prodotto di questi fattori è uguale a zero se almeno uno dei fattori è uguale a zero.

2x = + k, k Z o sin 2x = 1,5 – non ci sono soluzioni, perché | peccato| 1
x = + k; a Z.
Risposta: x = + k, k Z.

2 studenti. Metodo 2. Risolvere equazioni convertendo la somma o la differenza di funzioni trigonometriche in un prodotto

cos 3x + sin 2x – sin 4x = 0.

Per risolvere l'equazione usiamo la formula sin– sin = 2 sin сos

cos 3x + 2 sin cos = 0,

сos 3x – 2 sin x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. L'equazione risultante è equivalente a un insieme di due equazioni:

L'insieme delle soluzioni della seconda equazione è completamente incluso nell'insieme delle soluzioni della prima equazione. Significa

Risposta:

3 studenti. 3 vie. Risolvere equazioni convertendo il prodotto di funzioni trigonometriche in una somma

peccato 5x cos 3x = peccato 6x cos2x.

Per risolvere l'equazione usiamo la formula

Risposta:

4 studenti. 4 vie. Risoluzione di equazioni che si riducono ad equazioni quadratiche

3 sin x – 2 cos 2 x = 0,
3 peccato x – 2 (1 – peccato 2 x) = 0,
2 peccato 2 x + 3 peccato x – 2 = 0,

Sia sin x = t, dove | t |. Otteniamo equazione quadratica 2t2 + 3t – 2 = 0,

D = 9 + 16 = 25.

Così . non soddisfa la condizione | t |.

Quindi peccato x = . Ecco perché .

Risposta:

III. Consolidamento di quanto appreso dal libro di testo di A. N. Kolmogorov

1. N. 164 (a), 167 (a) (equazione quadratica)
2. N. 168 a) (fattorizzazione)
3. N. 174 a) (conversione di una somma in prodotto)
4. (convertire il prodotto in somma)

(Alla fine della lezione, mostra sullo schermo la soluzione di queste equazioni per verifica)

№ 164 (UN)

2 peccato 2 x + peccato x – 1 = 0.
Sia sin x = t, | t | 1. Allora
2 t 2 + t – 1 = 0, t = – 1, t= . Dove

Risposta: - .

№ 167 (UN)

3 tg 2 x + 2 tg x – 1 = 0.

Sia tg x = 1, quindi otteniamo l'equazione 3 t 2 + 2 t – 1 = 0.

Risposta:

№ 168 (UN)

Risposta:

№ 174 (UN)

Risolvi l'equazione:

Risposta:

Lezione 2 (lezione-lezione)

IV. Imparare nuovo materiale(continua)

– Quindi, continuiamo a studiare i modi per risolvere le equazioni trigonometriche.

5 modi. Risoluzione di equazioni trigonometriche omogenee

Equazioni della forma a sin x + b cos x = 0, dove a e b sono alcuni numeri, sono dette equazioni omogenee di primo grado rispetto a sin x o cos x.

Considera l'equazione

peccato x – cos x = 0. Dividiamo entrambi i membri dell'equazione per cos x. Questo può essere fatto; la perdita della radice non si verificherà, perché , Se cos x = 0, Quello peccato x = 0. Ma questo contraddice l’identità trigonometrica di base peccato 2 x+cos 2 x = 1.

Otteniamo abbronzatura x – 1 = 0.

marrone chiaro x = 1,

Equazioni della forma un peccato 2 x + bcos 2 x + c peccato x cos x = 0 , Dove a, b, c – alcuni numeri sono detti equazioni omogenee di secondo grado rispetto a sin x o cos x.

Considera l'equazione

sin 2 x – 3 sin x cos x + 2 cos 2 = 0. Dividiamo entrambi i membri dell'equazione per cos x e la radice non andrà persa, perché cos x = 0 non è la radice di questa equazione.

tg2x – 3tgx+2 = 0.

Sia tgx = t. D = 9 – 8 = 1.

Allora quindi tg x = 2 oppure tg x = 1.

Di conseguenza, x = arctan 2 + , x =

Risposta: arctg 2 + ,

Consideriamo un'altra equazione: 3 sin 2 x – 3 sin x cos x + 4 cos 2 x = 2.
Trasformiamoci lato destro equazioni nella forma 2 = 2 · 1 = 2 · (sen 2 x + cos 2 x). Quindi otteniamo:
3sen 2 x – 3sen x cos x + 4cos 2 x = 2 (sen 2 x + cos 2 x),
3sen 2 x – 3sen x cos x + 4cos 2 x – 2sen 2 x – 2 cos 2 x = 0,
sin 2 x – 3sin x cos x + 2cos 2 x = 0. (Abbiamo ottenuto la 2a equazione, che abbiamo già analizzato).

Risposta: arctan 2 + k,

6 vie. Risoluzione di equazioni trigonometriche lineari

Un'equazione trigonometrica lineare è un'equazione della forma a peccato x + b cos x = c, dove a, b, c sono alcuni numeri.

Considera l'equazione peccato x + cos x= – 1.
Riscriviamo l'equazione come:

Considerando questo e, otteniamo:

Risposta:

7 vie. Introducendo un ulteriore argomento

Espressione a cos x + b peccato x può essere convertito:

(abbiamo già utilizzato questa trasformazione semplificando le espressioni trigonometriche)

Introduciamo un ulteriore argomento: l'angolo è tale

Poi

Considera l'equazione: 3 sinx + 4 cosx = 1. =

Compiti a casa: N. 164 -170 (c, d).

Metodi per risolvere equazioni trigonometriche.

La risoluzione di un'equazione trigonometrica consiste di due fasi: trasformazione dell'equazione per renderlo più semplice tipo (vedi sopra) e soluzioneil risultato più semplice equazione trigonometrica. Ce ne sono sette metodi di base per la risoluzione di equazioni trigonometriche.

1. Metodo algebrico.

(metodo di sostituzione e sostituzione variabile).

2. Fattorizzazione.

Esempio 1. Risolvi l'equazione: peccato X+cos X = 1 .

Soluzione. Spostiamo tutti i termini dell'equazione a sinistra:

Peccato X+cos X – 1 = 0 ,

Trasformiamo e fattorizziamo l'espressione in

Lato sinistro dell'equazione:

Esempio 2. Risolvi l'equazione: cos 2 X+ peccato X cos X = 1.

Soluzione: cos2 X+ peccato X cos X– peccato 2 X– cos2 X = 0 ,

Peccato X cos X– peccato 2 X = 0 ,

Peccato X· (cos X– peccato X ) = 0 ,

Esempio 3. Risolvi l'equazione: cos2 X–cos 8 X+ cos 6 X = 1.

Soluzione: cos2 X+ cos 6 X= 1 + cos8 X,

2 cos 4 X cos2 X= 2cos²4 X ,

Cos4 X · (cos2 X–cos 4 X) = 0 ,

Cos4 X · 2 peccato 3 X peccato X = 0 ,

1). cos 4 X= 0, 2). peccato 3 X= 0, 3). peccato X = 0 ,

3. Riduzione a equazione omogenea. Equazione chiamato omogeneo da per quanto riguarda peccato E cos , Se tutto termini dello stesso grado rispetto a peccato E cos stesso angolo. Per risolvere un'equazione omogenea è necessario: UN) sposta tutti i suoi membri sul lato sinistro; B) togli tutto fattori comuni oltre le parentesi; V) equiparare tutti i fattori e le parentesi a zero; G) parentesi uguali a zero danno equazione omogenea di grado minore, in cui dovrebbe essere divisa cos(O peccato) nel grado senior; D) risolvere l'equazione algebrica risultante rispetto aabbronzatura . peccato 2 X+4 peccato X cos X+ 5 cos 2 X = 2. Soluzione: 3peccato 2 X+4 peccato X cos X+5cos2 X= 2peccato 2 X+2cos2 X , Peccato 2 X+4 peccato X cos X+3cos2 X = 0 , Abbronzatura 2 X+ 4 abbronzatura X + 3 = 0 , da qui sì 2 + 4sì +3 = 0 , Le radici di questa equazione sono:sì 1 = - 1, sì 2 = - 3, quindi 1) abbronzatura X= –1, 2) marrone chiaro X = –3,

4. Transizione al semiangolo.

Consideriamo questo metodo come esempio:

ESEMPIO Risolvere l'equazione: 3 peccato X– 5 cos X = 7.

Soluzione: 6 peccati ( X/ 2) cos ( X/ 2) – 5 cos² ( X/ 2) + 5 peccato² ( X/ 2) =

7 peccato² ( X/ 2) + 7 cos² ( X/ 2) ,

2 peccato² ( X/ 2) – 6 peccato ( X/ 2) cos ( X/ 2) + 12 cos² ( X/ 2) = 0 ,

tan²( X/ 2) – 3 marrone chiaro ( X/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Introduzione di un angolo ausiliario.

Consideriamo un'equazione della forma:

UN peccato X + B cos X = C ,

Dove UN, B, C– coefficienti;X- sconosciuto.

Ora i coefficienti dell'equazione hanno le proprietà di seno e coseno, vale a dire: modulo (valore assoluto) di ciascuno di cui non più di 1, e la somma dei loro quadrati è 1. Quindi possiamo denotare loro di conseguenza Come cos e peccato (qui - il cosiddetto angolo ausiliario), Eprendi la nostra equazione

Puoi ordinare soluzione dettagliata il tuo compito!!!

Un'uguaglianza contenente un'incognita sotto il segno di una funzione trigonometrica ("sin x, cos x, tan x" o "ctg x") è chiamata equazione trigonometrica e considereremo ulteriormente le loro formule.

Le equazioni più semplici si chiamano `sin x=a, cos x=a, tg x=a, ctg x=a`, dove `x` è l'angolo da trovare, `a` è un numero qualsiasi. Scriviamo le formule di radice per ciascuno di essi.

1. Equazione "peccato x=a".

Per `|a|>1` non ha soluzioni.

Quando `|a| \leq 1` ha un numero infinito di soluzioni.

Formula di radice: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Equazione "cos x=a".

Per `|a|>1` - come nel caso del seno, non ha soluzioni tra numeri reali.

Quando `|a| \leq 1` ha un numero infinito di soluzioni.

Formula di radice: `x=\pm arccos a + 2\pi n, n \in Z`

Casi particolari di seno e coseno nei grafici.

3. Equazione "tg x=a".

Ha un numero infinito di soluzioni per qualsiasi valore di "a".

Formula di radice: `x=arctg a + \pi n, n \in Z`

4. Equazione "ctg x=a".

Ha anche un numero infinito di soluzioni per qualsiasi valore di "a".

Formula di radice: `x=arcctg a + \pi n, n \in Z`

Formule per le radici delle equazioni trigonometriche nella tabella

Per il seno:
Per coseno:
Per tangente e cotangente:
Formule per risolvere equazioni contenenti inverse funzioni trigonometriche:

Metodi per risolvere equazioni trigonometriche

La risoluzione di qualsiasi equazione trigonometrica consiste in due fasi:

• con l'aiuto di trasformarlo nel più semplice;
• risolvere l'equazione più semplice ottenuta utilizzando le formule di radice e le tabelle scritte sopra.

Diamo un'occhiata ai principali metodi di soluzione utilizzando esempi.

Metodo algebrico.

Questo metodo prevede la sostituzione di una variabile e la sua sostituzione in un'uguaglianza.

Esempio. Risolvi l'equazione: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

effettuare una sostituzione: `cos(x+\frac \pi 6)=y`, quindi `2y^2-3y+1=0`,

troviamo le radici: `y_1=1, y_2=1/2`, da cui seguono due casi:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac\pi 6+2\pi n`.

Risposta: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Fattorizzazione.

Esempio. Risolvi l'equazione: `sen x+cos x=1`.

Soluzione. Spostiamo tutti i termini dell'uguaglianza a sinistra: `sin x+cos x-1=0`. Utilizzando , trasformiamo e fattorizziamo il membro sinistro:

`peccato x — 2peccato^2 x/2=0`,

`2sen x/2 cos x/2-2sen^2 x/2=0`,

`2sen x/2 (cos x/2-sen x/2)=0`,

1. `peccato x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

Risposta: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Riduzione ad un'equazione omogenea

Innanzitutto, devi ridurre questa equazione trigonometrica in una delle due forme:

`a sin x+b cos x=0` (equazione omogenea di primo grado) oppure `a sin^2 x + b sin x cos x +c cos^2 x=0` (equazione omogenea di secondo grado).

Quindi dividi entrambe le parti per `cos x \ne 0` - per il primo caso, e per `cos^2 x \ne 0` - per il secondo. Otteniamo le equazioni per `tg x`: `a tg x+b=0` e `a tg^2 x + b tg x +c =0`, che devono essere risolte utilizzando metodi noti.

Esempio. Risolvi l'equazione: `2 sin^2 x+sen x cos x - cos^2 x=1".

Soluzione. Scriviamo il lato destro come `1=sin^2 x+cos^2 x`:

`2 peccato^2 x+peccato x cos x — cos^2 x=` `peccato^2 x+cos^2 x`,

`2 peccato^2 x+sen x cos x — cos^2 x -` ` peccato^2 x — cos^2 x=0`

`peccato^2 x+peccato x cos x — 2 cos^2 x=0`.

Questa è un'equazione trigonometrica omogenea di secondo grado, dividiamo i suoi lati sinistro e destro per `cos^2 x \ne 0`, otteniamo:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2 x+tg x — 2=0`. Introduciamo la sostituzione `tg x=t`, che risulta in `t^2 + t - 2=0`. Le radici di questa equazione sono "t_1=-2" e "t_2=1". Poi:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.

Risposta. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.

Vai a metà angolo

Esempio. Risolvi l'equazione: `11 sin x - 2 cos x = 10`.

Soluzione. Applichiamo le formule del doppio angolo, ottenendo: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0`

Applicando il metodo algebrico sopra descritto, otteniamo:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Risposta. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Introduzione dell'angolo ausiliario

Nell'equazione trigonometrica `a sin x + b cos x =c`, dove a,b,c sono coefficienti e x è una variabile, dividi entrambi i lati per `sqrt (a^2+b^2)`:

`\frac a(sqrt (a^2+b^2)) sin x +` ``\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2 ) +b^2))`.

I coefficienti sul lato sinistro hanno le proprietà di seno e coseno, cioè la somma dei loro quadrati è uguale a 1 e i loro moduli non sono maggiori di 1. Indichiamoli come segue: `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, quindi:

`cos \varphi sin x + sin \varphi cos x =C`.

Diamo uno sguardo più da vicino al seguente esempio:

Esempio. Risolvi l'equazione: `3 sin x+4 cos x=2`.

Soluzione. Dividiamo entrambi i membri dell'uguaglianza per `sqrt (3^2+4^2)`, otteniamo:

`\frac (3 sin x) (quadrato (3^2+4^2))+` `\frac(4 cos x)(quadrato (3^2+4^2))=` `\frac 2(quadrato (3^2+4^2))`

`3/5 peccato x+4/5 cos x=2/5`.

Indichiamo `3/5 = cos \varphi` , `4/5=sin \varphi`. Poiché `sin \varphi>0`, `cos \varphi>0`, prendiamo `\varphi=arcsin 4/5` come angolo ausiliario. Quindi scriviamo la nostra uguaglianza nella forma:

`cos \varphi sin x+sin \varphi cos x=2/5`

Applicando la formula per la somma degli angoli al seno, scriviamo la nostra uguaglianza nella seguente forma:

`peccato (x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Risposta. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Equazioni trigonometriche razionali frazionarie

Queste sono uguaglianze con frazioni i cui numeratori e denominatori contengono funzioni trigonometriche.

Esempio. Risolvi l'equazione. `\frac (sin x)(1+cos x)=1-cos x`.

Soluzione. Moltiplica e dividi il lato destro dell'uguaglianza per "(1+cos x)". Di conseguenza otteniamo:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

`\frac (sin x-sin^2 x)(1+cos x)=0`

Considerando che il denominatore non può essere uguale a zero, otteniamo `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Uguagliamo il numeratore della frazione a zero: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Quindi `sin x=0` o `1-sin x=0`.

1. `peccato x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Dato che ` x \ne \pi+2\pi n, n \in Z`, le soluzioni sono `x=2\pi n, n \in Z` e `x=\pi /2+2\pi n` , `n \in Z`.

Risposta. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

La trigonometria, e in particolare le equazioni trigonometriche, sono utilizzate in quasi tutte le aree della geometria, della fisica e dell'ingegneria. Lo studio inizia al 10 ° grado, ci sono sempre compiti per l'Esame di Stato Unificato, quindi cerca di ricordare tutte le formule delle equazioni trigonometriche: ti saranno sicuramente utili!

Tuttavia, non è nemmeno necessario memorizzarli, l'importante è comprenderne l'essenza ed essere in grado di ricavarla. Non è così difficile come sembra. Verificatelo voi stessi guardando il video.

Concetto di risoluzione di equazioni trigonometriche.

• Per risolvere un'equazione trigonometrica, convertila in una o più equazioni trigonometriche di base. Risolvere un'equazione trigonometrica alla fine si riduce alla risoluzione delle quattro equazioni trigonometriche di base.

Risoluzione di equazioni trigonometriche di base.

• Esistono 4 tipi di equazioni trigonometriche di base:
• peccato x = a; cosx = a
• marrone chiaro x = a; ctg x = a
• Risolvere le equazioni trigonometriche di base implica considerare le diverse posizioni "x" su cerchio unitario e utilizzando una tabella di conversione (o calcolatrice).
• Esempio 1. sin x = 0,866. Utilizzando una tabella di conversione (o una calcolatrice) otterrai la risposta: x = π/3. Il cerchio unitario dà un'altra risposta: 2π/3. Ricorda: tutte le funzioni trigonometriche sono periodiche, ovvero i loro valori si ripetono. Ad esempio, la periodicità di sin x e cos x è 2πn, e la periodicità di tg x e ​​ctg x è πn. Pertanto la risposta è scritta così:
• x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
• Esempio 2. cos x = -1/2. Usando una tabella di conversione (o una calcolatrice) otterrai la risposta: x = 2π/3. Il cerchio unitario dà un'altra risposta: -2π/3.
• x1 = 2π/3 + 2π; x2 = -2π/3 + 2π.
• Esempio 3. tg (x - π/4) = 0.
• Risposta: x = π/4 + πn.
• Esempio 4. ctg 2x = 1.732.
• Risposta: x = π/12 + πn.

Trasformazioni utilizzate nella risoluzione di equazioni trigonometriche.

• Per trasformare le equazioni trigonometriche si utilizzano trasformazioni algebriche (fattorizzazione, riduzione membri omogenei ecc.) e identità trigonometriche.
• Esempio 5: Utilizzando le identità trigonometriche, l'equazione sin x + sin 2x + sin 3x = 0 viene convertita nell'equazione 4cos x*sin (3x/2)*cos (x/2) = 0. Pertanto, le seguenti equazioni trigonometriche di base devono essere risolti: cos x = 0; peccato(3x/2) = 0; cos(x/2) = 0.

• Trovare gli angoli utilizzando valori di funzioni noti.

  • Prima di imparare a risolvere le equazioni trigonometriche, devi imparare a trovare gli angoli utilizzando i valori di funzione noti. Questo può essere fatto utilizzando una tabella di conversione o una calcolatrice.
  • Esempio: cos x = 0,732. La calcolatrice darà la risposta x = 42,95 gradi. La circonferenza unitaria fornirà angoli aggiuntivi, il cui coseno è anch'esso 0,732.

• Metti da parte la soluzione sul cerchio unitario.

  • È possibile tracciare le soluzioni di un'equazione trigonometrica sulla circonferenza unitaria. Le soluzioni di un'equazione trigonometrica sulla circonferenza unitaria sono i vertici di un poligono regolare.
  • Esempio: Le soluzioni x = π/3 + πn/2 sul cerchio unitario rappresentano i vertici del quadrato.
  • Esempio: Le soluzioni x = π/4 + πn/3 sulla circonferenza unitaria rappresentano i vertici di un esagono regolare.

• Metodi per risolvere equazioni trigonometriche.

  • Se una data equazione trigonometrica contiene solo una funzione trigonometrica, risolvila come un'equazione trigonometrica di base. Se una determinata equazione include due o più funzioni trigonometriche, esistono 2 metodi per risolvere tale equazione (a seconda della possibilità della sua trasformazione).
    • Metodo 1.
  • Trasforma questa equazione in un'equazione della forma: f(x)*g(x)*h(x) = 0, dove f(x), g(x), h(x) sono le equazioni trigonometriche di base.
  • Esempio 6. 2cos x + sin 2x = 0. (0< x < 2π)
  • Soluzione. Usando la formula del doppio angolo sin 2x = 2*sen x*cos x, sostituisci sin 2x.
  • 2cos x + 2*sin x*cos x = 2cos x*(sin x + 1) = 0. Ora risolvi le due equazioni trigonometriche di base: cos x = 0 e (sin x + 1) = 0.
  • Esempio 7. cos x + cos 2x + cos 3x = 0. (0< x < 2π)
  • Soluzione: utilizzando le identità trigonometriche, trasforma questa equazione in un'equazione della forma: cos 2x(2cos x + 1) = 0. Ora risolvi le due equazioni trigonometriche di base: cos 2x = 0 e (2cos x + 1) = 0.
  • Esempio 8. sin x - sin 3x = cos 2x. (0< x < 2π)
  • Soluzione: utilizzando le identità trigonometriche, trasforma questa equazione in un'equazione della forma: -cos 2x*(2sin x + 1) = 0. Ora risolvi le due equazioni trigonometriche di base: cos 2x = 0 e (2sin x + 1) = 0 .
    • Metodo 2.
  • Converti l'equazione trigonometrica data in un'equazione contenente una sola funzione trigonometrica. Quindi sostituisci questa funzione trigonometrica con una sconosciuta, ad esempio t (sin x = t; cos x = t; cos 2x = t, tan x = t; tg (x/2) = t, ecc.).
  • Esempio 9. 3sen^2 x - 2cos^2 x = 4sen x + 7 (0< x < 2π).
  • Soluzione. In questa equazione, sostituisci (cos^2 x) con (1 - sin^2 x) (secondo l'identità). L'equazione trasformata è:
  • 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Sostituisci sin x con t. Ora l'equazione è: 5t^2 - 4t - 9 = 0. Questa è un'equazione quadratica che ha due radici: t1 = -1 e t2 = 9/5. La seconda radice t2 non soddisfa l'intervallo della funzione (-1< sin x < 1). Теперь решите: t = sin х = -1; х = 3π/2.
  • Esempio 10. tg x + 2 tg^2 x = ctg x + 2
  • Soluzione. Sostituisci tg x con t. Riscrivi l'equazione originale come segue: (2t + 1)(t^2 - 1) = 0. Ora trova t e poi trova x per t = tan x.

• Equazioni trigonometriche speciali.

  • Esistono diverse equazioni trigonometriche speciali che richiedono trasformazioni specifiche. Esempi:
  • a*peccato x+ b*cos x = c ; a(sen x + cos x) + b*cos x*sen x = c;
  • a*peccato^2 x + b*peccato x*cos x + c*cos^2 x = 0

• Periodicità delle funzioni trigonometriche.

  • Come accennato in precedenza, tutte le funzioni trigonometriche sono periodiche, ovvero i loro valori si ripetono dopo un certo periodo. Esempi:
    • Il periodo della funzione f(x) = sin x è 2π.
    • Il periodo della funzione f(x) = tan x è uguale a π.
    • Il periodo della funzione f(x) = sin 2x è uguale a π.
    • Il periodo della funzione f(x) = cos (x/2) è 4π.
  • Se nel problema è specificato un periodo, calcola il valore di "x" all'interno di quel periodo.
  • Nota: risolvere equazioni trigonometriche non è un compito facile e spesso porta a errori. Pertanto, controlla attentamente le tue risposte. Per fare ciò, puoi utilizzare una calcolatrice grafica per rappresentare graficamente l'equazione data R(x) = 0. In questi casi, le soluzioni verranno presentate come decimali(ovvero, π è sostituito da 3.14).