Costruire il punto medio di un segmento. Costruzione di linee perpendicolari

1. Costruzione di un segmento uguale ad uno dato

Disegniamo le figure indicate nella condizione: raggio sistema operativo e segmento AB.

Costruzione:

Costruiamo una circonferenza di raggio AB centrato in un punto DI.

Il cerchio intersecherà il raggio sistema operativo ad un certo punto D.

Segmento OD- ricercato.

2. Costruire un angolo uguale a quello dato

Costruire:

Prova:

Consideriamo ΔАВС e ΔОDE.

1. AC=OE, come i raggi di un cerchio.

2. AB=OD, come i raggi di un cerchio.

3. BC=DE, come i raggi di un cerchio.

ΔАВС = ΔОDE (su tre lati) А = О

Costruzione:

1. Costruisci un raggio arbitrario.

2. Costruisci due cerchi uguali di raggio arbitrario e un cerchio con centri all'inizio del raggio e al vertice dell'angolo dato.

3. Trova e segna i punti di intersezione dei cerchi con il raggio e con i lati dell'angolo.

4. Costruisci un cerchio con centro nel punto di intersezione del raggio e del cerchio e un raggio uguale alla distanza tra i punti costruiti sui lati dell'angolo.

5. Trova e segna il punto di intersezione dei cerchi.

6. Disegna una nuova semiretta dall'inizio della semiretta attraverso il punto di intersezione costruito dei cerchi.

7. L'angolo formato dai due raggi costruiti è quello richiesto.

3. Costruzione della bisettrice dell'angolo

Dato:

Costruire:

AB - bisettrice

Prova:

Consideriamo ∆АВ e ∆АДВ

1. AC = AD, come i raggi di un cerchio.

2. CB=DB, come i raggi di un cerchio.

3. AB – lato comune.

∆АСВ = ∆ АДВ (su tre lati) il raggio AB è una bisettrice.

Costruzione:

1. Costruisci una circonferenza di raggio arbitrario con il centro nel vertice dell'angolo.

2. Trova e segna i punti di intersezione del cerchio con i lati dell'angolo.

3. Costruisci cerchi con centri nei punti costruiti e lo stesso raggio.

4. Trova e segna il punto di intersezione dei cerchi.

5. Disegna un raggio con la sua origine nel vertice dell'angolo attraverso il punto di intersezione dei cerchi, la bisettrice desiderata dell'angolo.

4. Costruzione di linee perpendicolari

Sta accadendo

Dato:

Costruire:

Prova:

1.AM=MV, come i raggi di un cerchio.

2. AR=РВ, come i raggi di un cerchio ∆АРВ r/b

3. La mediana PM in un triangolo r/b è anche l'ALTEZZA.

Sta accadendo

Dato:

Costruire:

Prova:

AM=AN=MB=BN, come raggi uguali.

Lato comune MN.

∆MVN= ∆MAN (su tre lati)

In r/b ∆AMV il segmento MC è una bisettrice, e quindi anche un'altezza.

Costruzione:

1. Costruisci un cerchio con centro in un dato punto e raggio maggiore della distanza da un dato punto a una linea retta.

2. Trova e segna i punti di intersezione del cerchio e della linea.

3. Costruisci due cerchi uguali con centri in punti costruiti su una linea retta con raggio pari alla lunghezza del segmento.

4. Trova e segna il punto di intersezione dei cerchi.

5. Traccia una linea attraverso un dato punto che non si trova sulla linea e il punto di intersezione dei cerchi: la linea desiderata.

5.Costruzione della metà del segmento

Dato:

Costruire:

O – la metà del segmento AB.

Prova:

∆APQ = ∆BPQ (su tre lati).

∆ ARVr/b.

Il segmento PO è una bisettrice, e quindi una mediana.

Allora il punto O è il centro di AB.

Costruzione:

1. Costruisci due cerchi uguali con centri alle estremità del segmento e raggio uguale a AB.

2. Segna i punti di intersezione dei cerchi.

3. Disegna una linea retta attraverso i punti di intersezione dei cerchi.

4. Designare il punto di intersezione della linea e del segmento: il punto desiderato.

Putivskaya Julia

Il compito di costruire la parte centrale di un segmento definito dalle sue estremità utilizzando vari strumenti

Scaricamento:

Anteprima:

IL PROBLEMA DI COSTRUIRE LA METÀ DI UN SEGMENTO DEFINITO DALLE SUE ESTREMITÀ USANDO VARI STRUMENTI

Putivskaya Yulia Olegovna,

Studente di 9a elementare dell'istituto scolastico municipale "Zinaidinskaya"

scuola media di base"

I primi problemi costruttivi sorsero in tempi antichi. Sono nati dai bisogni economici umani. Già nell'antichità architetti e geometri dovevano risolvere i più semplici problemi costruttivi legati alla loro professione. Le soluzioni ai più semplici problemi di costruzione geometrica che aiutavano le persone nella loro vita economica venivano formulate sotto forma di “regole pratiche” basate su considerazioni visive. Furono questi compiti a costituire la base per l'emergere della geometria visiva, che trovò uno sviluppo abbastanza diffuso tra gli antichi popoli dell'Egitto, Babilonia, India, ecc. Le costruzioni geometriche attirarono l'attenzione matematici dell'antica Grecia già nei secoli VI-V. a.C. Il primo scienziato greco che lavorò alla risoluzione dei problemi di costruzione geometrica fu Talete di Mileto (624-547 a.C.). Quasi tutti i principali geometri greci vi furono impegnati: Pitagora (VI secolo a.C.) e i suoi studenti, Ippocrate (V secolo a.C.), Euclide, Archimede, Apollonio (III secolo a.C.), Pappo (III secolo d.C.) e molti altri.

I matematici della scuola di Pitagora sono già riusciti a far fronte a un problema relativamente complesso come la costruzione di un pentagono regolare. Nel V secolo A.C e. sorsero i famosi problemi classici della quadratura del cerchio, del raddoppio del cubo e della trisezione di un angolo (vedi Capitolo VII). Questi problemi, che, come si è scoperto in seguito, non potevano essere risolti con l'aiuto di una bussola e di un righello, hanno suscitato per molti secoli il vivo interesse di vari ricercatori. Nel IV secolo. A.C e. I pensatori greci svilupparono quello schema generale per risolvere un problema di costruzione geometrica (analisi - costruzione - dimostrazione - ricerca), che usiamo ancora oggi.

L'intera storia della geometria e di alcuni altri rami della matematica è strettamente connessa con lo sviluppo della teoria delle costruzioni geometriche. Gli assiomi più importanti della geometria, formulati dal fondatore del sistema geometrico scientifico, Euclide, intorno al 300. A.C e., mostra chiaramente quale ruolo hanno giocato le costruzioni geometriche nella formazione della geometria. "Da qualsiasi punto a qualsiasi punto si può tracciare una linea retta", "Una linea retta delimitata può essere estesa continuamente", "Un cerchio può essere descritto da qualsiasi centro e con qualsiasi soluzione" - questi postulati di Euclide indicano chiaramente la posizione di base dei metodi costruttivi nella geometria degli antichi.

Mentre studiavo geometria in seconda media, ho imparato a risolvere problemi di costruzione utilizzando compasso e righello. Mi è sorta la domanda: "È possibile risolvere questi semplici problemi utilizzando altri strumenti ed esistono?" Avendo rivolto questa domanda ad un insegnante di matematica, ho ricevuto in cambio il seguente libro: Costruzioni geometriche su un piano, B.I. Argunov e M.B. Balk – Uchpedgiz, 1955.

Dopo aver letto molti dei suoi capitoli, ho appreso che gli strumenti più utilizzati per le costruzioni geometriche sono: righello (a una faccia), compasso, righello a doppia faccia (con bordi paralleli), angolo retto e alcuni altri.

Per la geometria costruttiva è necessario avere una descrizione accurata e, ai fini matematici, completa di un particolare utensile. Questa descrizione è data sotto forma di assiomi. Questi assiomi in forma matematica astratta esprimono quelle proprietà degli strumenti di disegno reali utilizzati per le costruzioni geometriche.

Vorrei formulare gli assiomi corrispondenti.

Assioma del sovrano.

Il righello consente di eseguire le seguenti costruzioni geometriche:

a) costruire un segmento che collega due punti costruiti;

b) costruire una retta passante per due punti costruiti;

c) costruire un raggio che parte da un punto costruito e passa per un altro punto costruito.

Assioma della bussola.

Il compasso permette di eseguire le seguenti costruzioni geometriche:

a) costruire un cerchio se sono stati costruiti il ​​centro del cerchio e gli estremi di un segmento uguale al raggio del cerchio;

b) costruire uno qualsiasi dei due archi aggiuntivi di cerchio se vengono costruiti il ​​centro del cerchio e le estremità dell'arco.

Assioma di un righello a doppia faccia.

Il righello a doppia faccia ti consente di:

a) eseguire una qualsiasi delle costruzioni elencate nell'assioma del righello;

b) costruire in ciascuno dei semipiani definiti dalla linea costruita una linea parallela alla linea data e passante da essa a distanza h, dove h - segmento fisso per un dato righello
(larghezza del righello);

c) se si costruiscono due punti A e B, quindi determinare se ABè maggiore di un segmento fisso (la larghezza del righello) e se AB>h, quindi costruisci due coppie di rette parallele passanti rispettivamente per i punti A e B e separati gli uni dagli altri a distanza H.

Assioma dell'angolo retto.

Un angolo retto consente di eseguire le seguenti costruzioni geometriche:

a) tutte le costruzioni che possono essere fatte con un righello unilaterale;

b) per un dato punto del piano tracciare una linea perpendicolare a una qualche linea costruita;

c) se il segmento AB è costruitoe qualche figura Ф, quindi determina se la figura Ф contiene un punto dal quale il segmento è visibile ad angolo retto, e se tale punto esiste, allora costruisci un tale punto.

Il compito di costruzione consiste nel fatto che è necessario costruire in anticipo una figura utilizzando gli strumenti specificati, se viene fornita un'altra figura e vengono indicate alcune relazioni tra gli elementi della figura desiderata e gli elementi di questa figura.

Ogni figura che soddisfa le condizioni del problema è chiamata soluzione questo compito.

Trovare una soluzione a un problema costruttivo significa ridurlo a un numero finito di costruzioni base, cioè indicare una sequenza finita di costruzioni base, dopodiché la figura desiderata sarà già considerata costruita in virtù degli assiomi accettati della geometria costruttiva. L'elenco delle costruzioni di base accettabili e, di conseguenza, il progresso nella risoluzione del problema dipende in modo significativo da quali strumenti specifici vengono utilizzati per le costruzioni.

Ad esempio, considera il seguente problema:

Costruisci il punto medio di un segmento definito dalle sue estremità A e B.

Troviamo una soluzione a questo problema utilizzando vari strumenti.

1. Bussola e righello

(la costruzione viene studiata in 7a elementare, paragrafo 23 Esempi di problemi di costruzione)

Lasciamo AB - questo segmento. Costruiamo due cerchi con centri A e B di raggio AB ( ). Si intersecano in punti P e Q. Disegniamo una linea retta PQ. Punto O intersezione di questa linea con il segmento AB ed è il punto medio desiderato del segmento AB.

In effetti, triangoli APQ e BPQ uguale su tre lati, quindi 1 = 2 ().

Pertanto, il segmento RO - bisettrice di un triangolo isoscele ARV, e quindi la mediana, cioè il punto DI - la metà del segmento AB.

2. Bussola (immagine sotto la descrizione)

Costruiamo in sequenza:

1. cerchio di centro B e raggio BA;
2. cerchio di centro A e raggio AB;
3. punto comune C - il punto di intersezione dei cerchi con centro B con raggio BA e con centro A con raggio AB;
4. cerchio di centro C e raggio CA;
5. punto comune D - il punto di intersezione delle circonferenze con centro B di raggio BA e centro A di raggio AC, diverso dal punto A;
6. cerchio con centro D e raggio DB;

7) punto comune E - il punto di intersezione delle circonferenze con centro B di raggio BA e centro D di raggio DB, diverso dal punto C;

Tieni presente che i punti A, B ed Eposti sulla stessa retta, con AE = 2AB. Costruiamo ulteriormente:

8) una circonferenza di centro E e raggio EA;

9) una circonferenza di centro A e raggio AB interseca una circonferenza di centro E e raggio EA nei punti M e N

10) una circonferenza di centro M e raggio MA;

11) una circonferenza di centro N e raggio NA;

12) punto comune X - il punto di intersezione di cerchi con centro M di raggio MA e con centro N di raggio NA, diverso da A.

È facile vedere quel punto Xsituato su una linea retta.

Inoltre, il triangolo AMX è simile al triangolo AEM, poiché sono isoscele e hanno un angolo comune MAEalla fondazione. Quindi AX: AM = AM: AE oppure AX: AB = AB: 2AB, COSÌ

AH = AB e quindi il punto X è quello desiderato.

3. Righello a doppia faccia (immagine sotto la descrizione).

Costruiamo in sequenza:

1) dritto AB;

2) linea retta a, parallelo ad AB e passante a distanza h da lei

(h - larghezza del righello);

3) retta b, parallela ad a, situato a distanza h da esso e diverso dalla retta AB;

4) punto C sulla linea b;

5) AC e BC diretti;

6) punti D – il punto di intersezione delle linee a e AC ed E – il punto di intersezione delle linee a e BC;
7) AE e BD diretti;

8) punto P – il punto di intersezione delle linee AE e BD;

9) CP diretto;

10) punto X - punto di intersezione delle rette CP e AB.

Dal momento che DE - linea mediana triangolo ACB, poi AE e BD - la sua mediana, e quindi CP - mediana, quindi il punto X ricercato.

4. Angolo retto (immagine sotto la descrizione)

1) Costruiamo una retta AB;

2) condurre AA diretto"e BB", perpendicolare
dritto AB;

3) seleziona AA"punto arbitrario C, diverso da A;

4) attraverso il punto C tracciamo SS" AC.
Successivamente costruiamo in sequenza:

5) punto D - punto di intersezione delle linee CC" e BB";

6) diretti dC e aC;

7) punto P- il punto di intersezione delle linee AD e BC;

Il punto X è quello desiderato.

Quindi, considerato vari modi risolvere lo stesso problema costruttivo utilizzando strumenti diversi.

Governate. Il metodo più semplice e accurato per determinare la metà di un segmento è misurarne la lunghezza utilizzando un righello e quindi dividere il valore risultante a metà. In questo modo è possibile trovare facilmente e rapidamente il centro desiderato con una precisione fino al millimetro. Tuttavia, oltre a questo metodo ovvio, esiste un altro modo per costruire la parte centrale di un segmento. Tuttavia, non puoi ancora fare a meno di un righello. Il righello aiuterà non solo a calcolare correttamente la distanza, se necessario, ma anche a tracciare una linea retta in modo perfettamente uniforme o a tracciare un segmento, che è una condizione necessaria qualsiasi costruzione.

Matita. Nel caso della costruzione della parte centrale del segmento, la matita è davvero insostituibile. Uno ben affilato dovrebbe essere sempre a portata di mano quando si tratta di disegnare forme geometriche di linee o segmenti. Oggi c'è una vasta selezione di matite di qualsiasi qualità e scopo. Quindi, una matita morbida o dura-morbida è più adatta per disegnare, ma se stiamo parlando per quanto riguarda la costruzione, è meglio dare la preferenza al solido. È conveniente se all'estremità della matita c'è una buona gomma.

Bussola. Per costruire con precisione, e non calcolare o misurare il centro di un segmento, è necessario un compasso. In generale, tale conoscenza può essere necessaria non solo a uno scolaro, ma anche, ad esempio, a uno studente quando studia le basi della geometria descrittiva o della grafica ingegneristica. Tra le altre cose, la capacità di trovare il centro può aiutare anche a rispondere alla domanda: come trovare il centro di un triangolo. Quindi, per costruire, posizioniamo l'ago della bussola a un'estremità del segmento e disegniamo un cerchio la cui lunghezza del diametro è uguale alla lunghezza del segmento. Successivamente, posizioniamo l'ago della bussola sulla seconda estremità del segmento e creiamo lo stesso cerchio.

Come risultato di tali azioni, otteniamo due cerchi identici, sovrapposti l'uno all'altro e intersecati in due punti. Il segmento passa per il centro dei cerchi e ne costituisce il raggio. Usando un righello, traccia una linea retta che passa attraverso i due punti di intersezione dei due cerchi. Di conseguenza, otteniamo la metà del segmento. Se il segmento si trova in un sistema di coordinate e sorge la domanda su come trovare le coordinate della metà del segmento, le azioni sono completamente identiche. Disegniamo anche due cerchi o semicerchi e, tracciando una linea retta che passa attraverso i punti di intersezione dei cerchi o delle loro metà, troviamo il centro del segmento.

Quindi costruiamo una perpendicolare dal centro del segmento rispetto agli assi delle coordinate e otteniamo le coordinate. Di norma, tale perpendicolare viene disegnata con una linea tratteggiata utilizzando un righello e ha contorni poco chiari, quindi sappiamo non solo come trovare il centro di un segmento, ma anche come calcolarne le coordinate eseguendo vari compiti durante gli studi a scuola, all'università o all'istituto, così come in vita quotidiana quando i metodi convenzionali non sono adatti.

L’ordine di costruzione è il seguente (Fig. 2.2):

1. Dalle estremità del segmento AB si tracciano archi di raggio R, maggiori della metà del segmento.

2. I punti di intersezione degli archi sono collegati da una linea retta CD.

La linea CD è perpendicolare al segmento AB, il punto O è il centro del segmento.

Divisione di un segmento

Dividere un segmento in un numero qualsiasi di parti uguali

La divisione del segmento in 6 parti uguali è mostrata in Fig. 2.3.

1. Da qualsiasi estremità del segmento AB, ad esempio dal punto A, traccia un raggio ad angolo acuto rispetto al segmento.

2. Sulla semiretta dal punto A, utilizzando un compasso, tracciamo 6 segmenti uguali di lunghezza arbitraria.

3. La fine dell'ultimo segmento, il punto 6, è collegata al punto B.

4. Da tutti i punti della semiretta tracciamo linee rette parallele a 6B finché non si intersecano con AB.

Queste linee dividono il segmento AB in sei parti uguali.

Fig.2.3 Fig.2.4

Dividere un cerchio in cinque parti uguali

(Costruzione di un pentagono regolare inscritto in un cerchio)

Le costruzioni sono mostrate nella Figura 2.4.

Dal punto C - la metà del raggio del cerchio, come dal centro, facciamo una tacca sul diametro con un arco di raggio CD, otteniamo il punto M. Il segmento DM è uguale alla lunghezza del lato dell'inscritto pentagono regolare. Dopo aver praticato delle tacche sul cerchio di raggio DM, otteniamo i punti di divisione del cerchio in cinque parti uguali (i vertici di un pentagono regolare inscritto).

Dividere un cerchio in sei parti uguali

(Costruzione di un esagono regolare inscritto in una circonferenza)

Le costruzioni sono mostrate nella Figura 2.5.

Il lato di un esagono regolare inscritto in una circonferenza è uguale al raggio della circonferenza.

Per dividere il cerchio in sei parti uguali è necessario realizzare due tacche sul cerchio dai punti 1 e 4 dell'intersezione della linea centrale con il cerchio di raggio R pari al raggio del cerchio. Collegando i punti risultanti con segmenti retti otteniamo un esagono regolare.

Fig.2.5 Fig.2.6

Determinazione del centro di un arco circolare

Le costruzioni sono mostrate nella Figura 2.6.

1. Assegna tre punti arbitrari A, B e C sull'arco.

2. Collega i punti con linee rette.

3. Disegna le perpendicolari attraverso i punti medi delle corde risultanti AB e BC.

Il punto O dell'intersezione delle perpendicolari è il centro dell'arco.

Compagni

La coniugazione è una transizione graduale da una riga all'altra.

Il ruolo delle transizioni fluide nei contorni di vari prodotti tecnici è enorme. Sono determinati dai requisiti di resistenza, idroaerodinamica, estetica industriale e tecnologia. Molto spesso, le connessioni vengono realizzate utilizzando un arco circolare.

Tra la varietà di collegamenti tra linee diverse, consideriamo quelli più comuni:

1. Coniugazione di due rette.

2. Coniugazione di una retta e di un cerchio.

3. Coniugazione di due cerchi.

Gli archi di cerchio con cui viene eseguito l'accoppiamento sono detti archi di accoppiamento.

Algoritmo di costruzione

1. Trova il centro dell'accoppiamento;

2. Trova i punti di coniugazione in cui l'arco di coniugazione si trasforma in linee di accoppiamento.

3. Costruire archi di coniugazione significa collegare i punti di coniugazione con un dato raggio di coniugazione.

Coniugazione di rette che si intersecano utilizzando un arco di raggio dato.

Esempio1. Coniugazione di due rette reciprocamente perpendicolari UN E B arco di un dato raggio R.

Date due rette reciprocamente perpendicolari UN E B. Raggio del raccordo specificato R.(Fig. 2.7a)

Algoritmo di costruzione

1. Trova il centro dell'accoppiamento.

Disegna due linee rette parallele UN E B, ad una distanza pari al raggio R. Queste linee sono il luogo dei centri dei cerchi di raggio R, tangente a queste linee (Fig. 2.7b);

Cerchio

Circonferenza - figura geometrica, costituito da tutti i punti del piano che si trovano ad una data distanza da un dato punto.

Questo punto è chiamato centro del cerchio e la distanza data è chiamata raggio del cerchio.

Il raggio è il segmento che collega il centro della circonferenza ad un punto qualsiasi della circonferenza. Dalla definizione segue che si possono tracciare infiniti raggi ed hanno tutti la stessa lunghezza.

Viene chiamato il segmento che collega due punti su una circonferenza accordo.

Se una corda passa per il centro del cerchio, allora si chiama diametro cerchi.

Il diametro è la corda più lunga.

Puoi anche disegnare un numero infinito di diametri in un cerchio.

Se colleghi due punti su un cerchio non con un segmento, ma con una curva che passa lungo il cerchio stesso, allora viene chiamata la parte del cerchio compresa tra i due punti arco .

Se segni due punti su un cerchio, ottieni due archi. Pertanto, per il nome dell'arco vengono utilizzate tre lettere latine, che possono essere piccole o grandi.

Nella figura sopra possiamo nominare: arco \(BDH\), arco \(ACG\) e altri.

La figura seguente mostra: arco \(AxB\) e arco \(AyB\).

La parte del piano delimitata da un cerchio si chiama cerchio.

Compiti di costruzione

Nei compiti in cui è necessario eseguire strutture, utilizziamo bussola E governate.

È molto importante ricordare che in questi compiti il ​​righello non viene utilizzato come strumento di misura, ma esclusivamente per tracciare una linea retta, una semiretta o un segmento passante per due punti dati, cioè per tracciare una linea retta. Un compasso viene utilizzato per costruire un cerchio o un arco di cerchio.

Consideriamo cinque costruzioni principali in cui utilizziamo le azioni menzionate: costruire una linea retta e un cerchio:

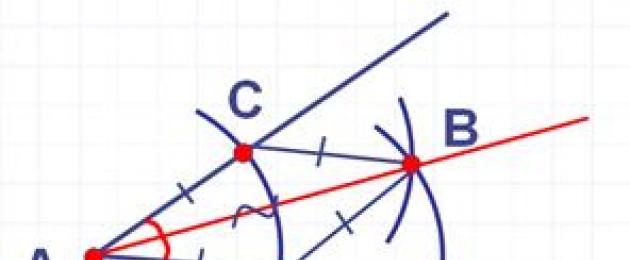
1. Su un dato raggio, dal suo inizio, lasciare un segmento uguale a quello dato.
2. Costruire un angolo uguale a quello dato.
3. Costruzione della bisettrice dell'angolo.

4. Costruzione di linee perpendicolari.
5. Costruzione della metà del segmento.

1. Su un dato raggio, a partire dalla sua origine, traccia un segmento uguale a quello dato.
Guarda il video.

È chiaro che in questo modo abbiamo ottenuto un segmento uguale a quello dato. Secondo la definizione di cerchio, è costituito da punti situati ad una determinata distanza (raggio) da un certo punto (centro del cerchio).

Se il centro è il punto iniziale della semiretta \(C\), il raggio è il segmento dato \(AB\), quindi il punto di intersezione della circonferenza e della semiretta \(D\) è il punto desiderato punto finale segmento \(CD\) uguale al segmento dato \(AB\).

2. Costruire un angolo uguale ad uno dato.

Guarda il video.

Dimostriamo che l'angolo costruito \(ECD\) è l'angolo desiderato, uguale all'angolo dato \(AOB\).

Se abbiamo costruito una circonferenza di centro \(C\) - punto di partenza raggio e raggio uguale a quello di un cerchio di centro \(O\), quindi\(CD\)\(=\)\(OB\).

Abbiamo condotto un raggio \(CE\). Ovviamente \(OA\)\(=\)\(CE\).

Ciò significa che i triangoli \(AOB\) e \(ECD\) sono uguali secondo il terzo segno di uguaglianza dei triangoli, anche i loro angoli sono uguali, compreso l'angolo \(ECD\) uguale all'angolo \(AOB \).

3. Costruzione di una bisettrice di un angolo.

Guarda il video.

Per dimostrare che \(OC\) divide effettivamente in due l'angolo \(AOB\), è sufficiente considerare i triangoli \(AOC\) e \(BOC\).