La pratica dell'esame di stato unificato e dell'esame di stato dell'anno scorso mostra che i problemi di geometria causano difficoltà a molti scolari. Puoi affrontarli facilmente se memorizzi tutte le formule necessarie e ti eserciti a risolvere i problemi.
In questo articolo vedrai le formule per trovare l'area di un trapezio, nonché esempi di problemi con soluzioni. Potresti imbatterti negli stessi nei KIM durante gli esami di certificazione o alle Olimpiadi. Pertanto, trattali con attenzione.
Cosa devi sapere sul trapezio?
Per cominciare, ricordiamocelo trapezio si chiama quadrilatero in cui due lati opposti, detti anche basi, sono paralleli, e gli altri due no.
In un trapezio l'altezza (perpendicolare alla base) può anche essere abbassata. Viene tracciata la linea di mezzo: questa è una linea retta parallela alle basi e uguale alla metà della loro somma. Così come le diagonali che possono intersecarsi formando angoli acuti e ottusi. O, in alcuni casi, ad angolo retto. Inoltre, se il trapezio è isoscele, in esso è inscritto un cerchio. E descrivi un cerchio attorno ad esso.
Formule dell'area del trapezio
Per prima cosa, diamo un'occhiata alle formule standard per trovare l'area di un trapezio. Di seguito considereremo i modi per calcolare l'area degli isoscele e dei trapezi curvilinei.
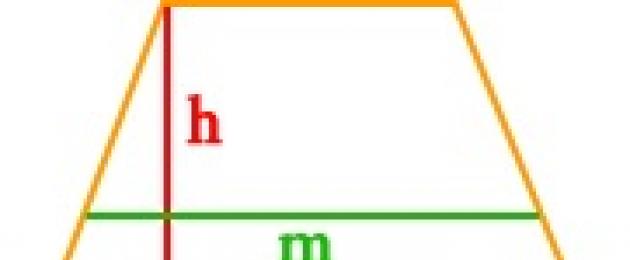
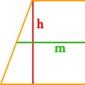
Quindi, immagina di avere un trapezio con basi a e b, in cui l'altezza h è abbassata alla base maggiore. Calcolare l'area di una figura in questo caso è facile come sgusciare le pere. Devi solo dividere la somma delle lunghezze delle basi per due e moltiplicare il risultato per l'altezza: S = 1/2(a+b)*h.
Prendiamo un altro caso: supponiamo che in un trapezio, oltre all'altezza, ci sia una linea mediana m. Conosciamo la formula per trovare la lunghezza della linea mediana: m = 1/2(a + b). Pertanto, possiamo giustamente semplificare la formula per l'area di un trapezio nella seguente forma: S = m* h. In altre parole, per trovare l'area di un trapezio, devi moltiplicare la linea centrale per l'altezza.

Consideriamo un'altra opzione: il trapezio contiene le diagonali d 1 e d 2, che non si intersecano ad angolo retto α. Per calcolare l'area di un tale trapezio, è necessario dividere il prodotto delle diagonali per due e moltiplicare il risultato per il peccato dell'angolo tra di loro: S= 1/2d 1 d 2 *senα.

Consideriamo ora la formula per trovare l'area di un trapezio se non si sa altro che la lunghezza di tutti i suoi lati: a, b, c e d. Questa è una formula macchinosa e complessa, ma ti sarà utile ricordarla per ogni evenienza: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2.
A proposito, gli esempi sopra riportati valgono anche nel caso in cui sia necessaria la formula per l'area di un trapezio rettangolare. Questo è un trapezio, il cui lato confina con le basi ad angolo retto.
Trapezio isoscele
Un trapezio i cui lati sono uguali si dice isoscele. Considereremo diverse opzioni per la formula per l'area di un trapezio isoscele.
Prima opzione: nel caso in cui un cerchio di raggio r sia inscritto in un trapezio isoscele e il lato e la base maggiore formino un angolo acuto α. Un cerchio può essere inscritto in un trapezio purché la somma delle lunghezze delle sue basi sia uguale alla somma delle lunghezze dei lati.

L'area di un trapezio isoscele si calcola come segue: moltiplica il quadrato del raggio del cerchio inscritto per quattro e dividi il tutto per sinα: S = 4r 2 /senα. Un'altra formula dell'area è un caso speciale per l'opzione quando l'angolo tra la base grande e il lato è 30 0: S = 8r2.
Seconda opzione: questa volta prendiamo un trapezio isoscele, nel quale sono disegnate in aggiunta le diagonali d 1 e d 2, nonché l'altezza h. Se le diagonali di un trapezio sono tra loro perpendicolari, l'altezza è la metà della somma delle basi: h = 1/2(a + b). Sapendo questo, è facile trasformare la formula per l'area di un trapezio già familiare in questa forma: S = h2.
Formula per l'area di un trapezio curvo
Cominciamo scoprendo cos'è un trapezio curvo. Immagina un asse delle coordinate e un grafico di una funzione continua e non negativa f che non cambia segno all'interno di un dato segmento sull'asse x. Un trapezio curvilineo è formato dal grafico della funzione y = f(x) - in alto, l'asse x è in basso (segmento), e sui lati - linee rette tracciate tra i punti a e b e il grafico di la funzione.
È impossibile calcolare l'area di una figura così non standard utilizzando i metodi sopra indicati. Qui è necessario applicare l'analisi matematica e utilizzare l'integrale. Vale a dire: la formula di Newton-Leibniz - S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a). In questa formula, F è l'antiderivativa della nostra funzione sul segmento selezionato. E l'area di un trapezio curvilineo corrisponde all'incremento della primitiva su un dato segmento.

Problemi di esempio
Per rendere tutte queste formule più facili da comprendere nella tua testa, ecco alcuni esempi di problemi per trovare l'area di un trapezio. Sarebbe meglio se prima provassi a risolvere i problemi da solo e solo allora confrontassi la risposta che riceverai con la soluzione già pronta.
Compito n. 1: Dato un trapezio. La sua base più grande è di 11 cm, quella più piccola è di 4 cm. Il trapezio ha le diagonali, una lunga 12 cm, la seconda 9 cm.
Soluzione: costruire un trapezio AMRS. Traccia una linea retta РХ passante per il vertice P in modo che sia parallela alla diagonale MC e intersechi la retta AC nel punto X. Otterrai un triangolo APХ.
Considereremo due figure ottenute come risultato di queste manipolazioni: triangolo APX e parallelogramma CMRX.
Grazie al parallelogramma apprendiamo che PX = MC = 12 cm e CX = MR = 4 cm. Da dove possiamo calcolare il lato AX del triangolo ARX: AX = AC + CX = 11 + 4 = 15 cm.
Possiamo anche dimostrare che il triangolo APX è rettangolo (per fare ciò applichiamo il teorema di Pitagora - AX 2 = AP 2 + PX 2). E calcola la sua area: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 cm 2.
Successivamente dovrai dimostrare che i triangoli AMP e PCX hanno la stessa area. La base sarà l'uguaglianza delle parti MR e CX (già dimostrata sopra). E anche le altezze che abbassi su questi lati sono uguali all'altezza del trapezio AMRS.
Tutto ciò ti permetterà di dire che S AMPC = S APX = 54 cm 2.
Compito n. 2:È dato il trapezio KRMS. Sui suoi lati laterali ci sono i punti O ed E, mentre OE e KS sono paralleli. È anche noto che le aree dei trapezi ORME e OKSE sono nel rapporto 1:5. RM = a e KS = b. Devi trovare OE.
Soluzione: traccia una linea parallela a RK passante per il punto M, e designa il punto della sua intersezione con OE come T. A è il punto di intersezione di una linea tracciata attraverso il punto E parallela a RK con la base KS.
Introduciamo un'altra notazione: OE = x. E anche l'altezza h 1 per il triangolo TME e l'altezza h 2 per il triangolo AEC (puoi dimostrare indipendentemente la somiglianza di questi triangoli).
Supponiamo che b > a. Le aree dei trapezi ORME e OKSE sono nel rapporto 1:5, il che ci dà il diritto di creare la seguente equazione: (x + a) * h 1 = 1/5(b + x) * h 2. Trasformiamo e otteniamo: h 1 / h 2 = 1/5 * ((b + x)/(x + a)).
Poiché i triangoli TME e AEC sono simili, abbiamo h 1 / h 2 = (x – a)/(b – x). Combiniamo entrambe le voci e otteniamo: (x – a)/(b – x) = 1/5 * ((b + x)/(x + a)) ↔ 5(x – a)(x + a) = ( b + x)(b – x) ↔ 5(x 2 – a 2) = (b 2 – x 2) ↔ 6x 2 = b 2 + 5a 2 ↔ x = √(5a 2 + b 2)/6.
Pertanto, OE = x = √(5a 2 + b 2)/6.
Conclusione
La geometria non è la scienza più semplice, ma puoi sicuramente affrontare le domande dell'esame. Basta mostrare un po' di perseveranza nella preparazione. E, naturalmente, ricorda tutte le formule necessarie.
Abbiamo provato a raccogliere tutte le formule per calcolare l'area di un trapezio in un unico posto in modo che tu possa usarle quando ti prepari per gli esami e ripassi il materiale.
Assicurati di parlare di questo articolo ai tuoi compagni di classe e ai tuoi amici sui social network. Che ci siano più buoni voti per l'Esame di Stato Unificato e per gli Esami di Stato!
sito web, quando si copia il materiale in tutto o in parte, è richiesto un collegamento alla fonte.
I problemi del trapezio non sembrano difficili in un certo numero di forme studiate in precedenza. Un trapezio rettangolare è considerato un caso speciale. E quando si cerca la sua area, a volte è più conveniente dividerla in due già familiari: un rettangolo e un triangolo. Devi solo pensarci un po’ e troverai sicuramente una soluzione.
Definizione di trapezio rettangolo e sue proprietà
Un trapezio arbitrario ha basi parallele e i lati possono avere angoli arbitrari. Se consideriamo un trapezio rettangolare, uno dei suoi lati è sempre perpendicolare alle basi. Cioè, due angoli saranno pari a 90 gradi. Inoltre appartengono sempre a vertici adiacenti o, in altre parole, allo stesso lato.
Gli altri angoli di un trapezio rettangolare sono sempre acuti e ottusi. Inoltre la loro somma sarà sempre pari a 180 gradi.
Ciascuna diagonale forma un triangolo rettangolo con il lato minore. E l'altezza, che si ricava da un vertice con angolo ottuso, divide la figura in due. Uno di questi è un rettangolo e l'altro è un triangolo rettangolo. A proposito, questo lato è sempre uguale all'altezza del trapezio.
Quali notazioni vengono utilizzate nelle formule presentate?
È conveniente specificare immediatamente tutte le quantità utilizzate nelle diverse espressioni che descrivono un trapezio e presentarle in una tabella:
Formule che descrivono gli elementi di un trapezio rettangolare
Il più semplice riguarda l'altezza e il lato più piccolo:
Alcune altre formule per questo lato di un trapezio rettangolare:
ñ = d*senα;
c = (a - b) * tan α;
c = √ (d 2 - (a - b) 2).
Il primo segue da un triangolo rettangolo. E dice che il cateto collegato all'ipotenusa dà il seno dell'angolo opposto.
Nello stesso triangolo il secondo cateto è uguale alla differenza delle due basi. Pertanto, l'affermazione che equipara la tangente di un angolo al rapporto tra le gambe è vera.
Dallo stesso triangolo si può ricavare una formula basata sulla conoscenza del teorema di Pitagora. Questa è la terza espressione registrata.

Puoi scrivere le formule per l'altro lato. Ce ne sono anche tre:
d = (a - b) /cosα;
d = c/senα;
d = √ (c 2 + (a - b) 2).
I primi due si ottengono ancora dal rapporto tra i lati dello stesso triangolo rettangolo, e il secondo deriva dal teorema di Pitagora.
Quale formula puoi usare per calcolare l'area?
Quello dato per il trapezio libero. Devi solo tenere conto che l'altezza è il lato perpendicolare alle basi.
S = (a+b)*h/2.
Queste quantità non sono sempre fornite esplicitamente. Pertanto, per calcolare l'area di un trapezio rettangolare, dovrai eseguire alcuni calcoli matematici.

Cosa succede se devi calcolare le diagonali?
In questo caso, devi vedere che formano due triangoli rettangoli. Ciò significa che puoi sempre usare il teorema di Pitagora. Allora la prima diagonale sarà espressa come segue:
d1 = √ (c2 + b2)
o in altro modo, sostituendo la “c” con la “h”:
d1 = √ (h2 + b2).
Le formule per la seconda diagonale si ottengono in modo simile:
d2 = √ (c2 + b2) o d 2 = √ (h2 + a2).
Compito n. 1
Condizione. L'area di un trapezio rettangolare è nota ed è pari a 120 dm 2. La sua altezza ha una lunghezza di 8 cm. È necessario calcolare tutti i lati del trapezio. Una condizione aggiuntiva è che una base sia 6 dm più piccola dell'altra.
Soluzione. Dato che abbiamo un trapezio rettangolare di cui è nota l'altezza, possiamo subito dire che uno dei lati misura 8 dm, cioè il lato minore.
Ora puoi contare l'altro: d = √ (c 2 + (a - b) 2). Inoltre qui sono dati contemporaneamente sia il lato c che la differenza delle basi. Quest'ultimo è pari a 6 dm, lo si nota dalla condizione. Allora d sarà uguale alla radice quadrata di (64 + 36), cioè di 100. Così si trova un altro lato, pari a 10 dm.
La somma delle basi può essere trovata dalla formula per l'area. Sarà pari al doppio dell'area divisa per l'altezza. Se conti, risulta 240/8. Ciò significa che la somma delle basi è 30 dm. D'altra parte, la loro differenza è di 6 dm. Combinando queste equazioni, puoi contare entrambe le basi:
a + b = 30 e a - b = 6.
Puoi esprimere a come (b + 6), sostituiscilo nella prima uguaglianza. Quindi risulta che 2b sarà uguale a 24. Pertanto, semplicemente b risulterà essere 12 dm.
Allora l'ultimo lato a è 18 dm.
Risposta. Lati di un trapezio rettangolare: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.

Compito n. 2
Condizione. Dato un trapezio rettangolo. Il suo lato maggiore è uguale alla somma delle basi. La sua altezza è lunga cm 12. Si costruisce un rettangolo i cui lati sono uguali alle basi del trapezio. È necessario calcolare l'area di questo rettangolo.
Soluzione. Devi iniziare con quello che stai cercando. L'area richiesta è determinata come il prodotto di a e b. Entrambe queste quantità sono sconosciute.
Sarà necessario utilizzare uguaglianze aggiuntive. Uno di questi si basa sull'affermazione della condizione: d = a + b. Per questo lato è necessario utilizzare la terza formula, riportata sopra. Risulta: d 2 = c 2 + (a - b) 2 oppure (a + b) 2 = c 2 + (a - b) 2.
È necessario effettuare trasformazioni sostituendo al posto di c il suo valore dalla condizione - 12. Dopo aver aperto le parentesi e aver introdotto termini simili, risulta che 144 = 4 ab.
All'inizio della soluzione è stato detto che a*b fornisce l'area richiesta. Pertanto nell'ultima espressione puoi sostituire questo prodotto con S. Un semplice calcolo darà il valore dell'area. S = 36 cm2.
Risposta. L'area richiesta è 36 cm 2.

Compito n.3
Condizione. L'area di un trapezio rettangolare è 150√3 cm². Un angolo acuto è di 60 gradi. L'angolo formato dalla base piccola e dalla diagonale minore ha lo stesso significato. Dobbiamo calcolare la diagonale più piccola.
Soluzione. Dalle proprietà degli angoli di un trapezio risulta che il suo angolo ottuso è 120º. Quindi la diagonale lo divide in parti uguali, perché una parte di essa è già di 60 gradi. Allora anche l'angolo tra questa diagonale e la seconda base è 60 gradi. Cioè un triangolo formato da una base grande, un lato inclinato e una diagonale minore è equilatero. Pertanto, la diagonale desiderata sarà uguale ad a, così come il lato d = a.
Ora dobbiamo considerare un triangolo rettangolo. Il terzo angolo è di 30 gradi. Ciò significa che il cateto opposto è uguale alla metà dell'ipotenusa. Cioè la base minore del trapezio è uguale alla metà della diagonale desiderata: b = a/2. Da esso bisogna trovare l'altezza pari al lato perpendicolare alle basi. Il lato con la gamba qui. Dal teorema di Pitagora:
c = (a/2) * √3.
Ora non resta che sostituire tutte le quantità nella formula dell'area:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Risolvendo questa equazione si ottiene la radice 20
Risposta. La diagonale più piccola ha una lunghezza di 20 cm.
Sarà utile a tutti i laureati che si apprestano a sostenere l'Esame di Stato Unificato di Matematica rinfrescarsi la memoria sull'argomento “Trapezio libero”. Come hanno dimostrato molti anni di pratica, i problemi planimetrici di questa sezione causano alcune difficoltà a molti studenti delle scuole superiori. Allo stesso tempo, è necessario risolvere i problemi dell'esame di stato unificato sull'argomento "Trapezio libero" quando si superano sia il livello base che quello di profilo del test di certificazione. Pertanto, tutti i laureati dovrebbero essere in grado di affrontare tali esercizi.
Come prepararsi all'esame?
La maggior parte dei problemi planimetrici vengono risolti mediante costruzioni classiche. Se in un problema dell'Esame di Stato unificato è necessario trovare, ad esempio, l'area del trapezio mostrata in figura, vale la pena contrassegnare tutti i parametri noti sul disegno. Successivamente, ricorda i principali teoremi ad essi correlati. Applicandoli sarai in grado di trovare la risposta corretta.
Per rendere davvero efficace la tua preparazione all'esame, fai riferimento al portale educativo Shkolkovo. Qui troverai tutto il materiale di base sugli argomenti “Trapezio libero o che ti aiuterà a superare con successo l'Esame di Stato Unificato. Le principali proprietà della figura, formule e teoremi sono raccolte nella sezione “Informazioni teoriche”.
I laureati potranno inoltre migliorare le proprie capacità di problem solving sul nostro portale matematico. La sezione "Catalogo" presenta un'ampia selezione di esercizi rilevanti di vari livelli di difficoltà. I nostri specialisti aggiornano e integrano regolarmente l'elenco delle attività.
Gli studenti di Mosca e di altre città possono eseguire gli esercizi online in modo coerente. Se necessario, qualsiasi attività può essere salvata nella sezione “Preferiti” e successivamente ripristinata per discuterla con l'insegnante.
In questo articolo è stata fatta per te un'altra selezione di problemi con il trapezio. Le condizioni sono in qualche modo legate alla sua linea mediana. I tipi di attività sono presi da una banca aperta di attività tipiche. Se lo desideri, puoi rinfrescare le tue conoscenze teoriche. Il blog ha già discusso delle attività le cui condizioni sono correlate, nonché. Brevemente sulla linea di mezzo:

La linea mediana del trapezio collega i punti medi dei lati laterali. È parallelo alle basi ed è uguale alla loro semisomma.
Prima di risolvere i problemi, diamo un'occhiata a un esempio teorico.
Dato un trapezio ABCD. La diagonale AC che si interseca con la linea mediana forma il punto K, la diagonale BD il punto L. Dimostrare che il segmento KL è uguale alla metà della differenza delle basi.

Notiamo innanzitutto il fatto che la linea mediana di un trapezio divide in due qualsiasi segmento le cui estremità giacciono sulle sue basi. Questa conclusione suggerisce se stessa. Immagina un segmento che collega due punti delle basi; dividerà questo trapezio in altri due. Si scopre che un segmento parallelo alle basi del trapezio e passante per il centro del lato passerà per il centro dell'altro lato.
Anche questo si basa sul teorema di Talete:
Se più segmenti uguali sono disposti in successione su una delle due linee e attraverso le loro estremità vengono disegnate linee parallele che intersecano la seconda linea, allora verranno tagliati segmenti uguali sulla seconda linea.
Cioè, in questo caso, K è il centro di AC e L è il centro di BD. Pertanto EK è la linea mediana del triangolo ABC, LF è la linea mediana del triangolo DCB. Secondo la proprietà della linea mediana di un triangolo:

Possiamo ora esprimere il segmento KL in termini di basi:
Comprovato!
Questo esempio è fornito per una ragione. Nei compiti per una soluzione indipendente esiste proprio un compito del genere. Solo che non è detto che il segmento che collega i punti medi delle diagonali si trovi sulla linea mediana. Consideriamo i compiti:
27819. Trova la linea mediana del trapezio se le sue basi sono 30 e 16.

Calcoliamo utilizzando la formula:

27820. La linea mediana del trapezio è 28 e la base più piccola è 18. Trova la base più grande del trapezio.

Esprimiamo la base più grande:
Così:
27836. Una perpendicolare calata dal vertice di un angolo ottuso alla base maggiore di un trapezio isoscele lo divide in parti aventi lunghezza 10 e 4. Trova la linea mediana di questo trapezio.

Per trovare la linea di mezzo è necessario conoscere le basi. La base AB è facile da trovare: 10+4=14. Troviamo DC.
Costruiamo la seconda perpendicolare DF:

I segmenti AF, FE ed EB saranno rispettivamente uguali a 4, 6 e 4. Perché?
In un trapezio isoscele le perpendicolari abbassate alla base maggiore lo dividono in tre segmenti. Due di essi, che sono i cateti dei triangoli rettangoli tagliati, sono uguali tra loro. Il terzo segmento è uguale alla base minore, poiché quando si costruiscono le altezze indicate si forma un rettangolo e in un rettangolo i lati opposti sono uguali. In questo compito:

Quindi DC=6. Calcoliamo:

27839. Le basi del trapezio sono nel rapporto 2:3 e la linea mediana è 5. Trova la base più piccola.

Introduciamo il coefficiente di proporzionalità x. Allora AB=3x, DC=2x. Possiamo scrivere:
Pertanto la base più piccola è 2∙2=4.
27840. Il perimetro di un trapezio isoscele è 80, la sua linea mediana è uguale al lato laterale. Trova il lato del trapezio.

In base alla condizione possiamo scrivere:
Se indichiamo la linea di mezzo con il valore x, otteniamo:

La seconda equazione può già essere scritta come:

27841. La linea mediana del trapezio è 7 e una delle sue basi è maggiore dell'altra 4. Trova la base più grande del trapezio.

Indichiamo la base minore (DC) come x, quindi quella maggiore (AB) sarà uguale a x+4. Possiamo scriverlo
Abbiamo scoperto che la base più piccola è all'inizio di cinque, il che significa che quella più grande è uguale a 9.
27842. La linea mediana del trapezio è 12. Una delle diagonali lo divide in due segmenti, la cui differenza è 2. Trova la base maggiore del trapezio.

Possiamo facilmente trovare la base maggiore del trapezio se calcoliamo il segmento EO. È la linea mediana del triangolo ADB e AB=2∙EO.
Cosa abbiamo? Si dice che la linea mediana è uguale a 12 e la differenza tra i segmenti EO e ОF è uguale a 2. Possiamo scrivere due equazioni e risolvere il sistema:
![]()
È chiaro che in questo caso puoi selezionare una coppia di numeri senza calcoli, questi sono 5 e 7. Ma risolviamo comunque il sistema:

Quindi EO=12–5=7. Pertanto la base maggiore è uguale a AB=2∙EO=14.
27844. In un trapezio isoscele le diagonali sono perpendicolari. L'altezza del trapezio è 12. Trova la sua linea mediana.

Notiamo subito che l'altezza tracciata attraverso il punto di intersezione delle diagonali in un trapezio isoscele giace sull'asse di simmetria e divide il trapezio in due trapezi rettangolari uguali, cioè le basi di questa altezza sono divise a metà.
Sembrerebbe che per calcolare la linea di mezzo dobbiamo trovare delle ragioni. Qui si presenta un piccolo vicolo cieco... Come, conoscendo l'altezza, in questo caso calcolare le basi? Non c'è modo! Esistono molti di questi trapezi con un'altezza fissa e diagonali che si intersecano con un angolo di 90 gradi. Cosa dovrei fare?
Osserva la formula per la linea mediana di un trapezio. Dopotutto, non abbiamo bisogno di conoscere le ragioni stesse; è sufficiente conoscere la loro somma (o metà somma). Possiamo farcela.
Poiché le diagonali si intersecano ad angolo retto, si formano triangoli rettangoli isosceli di altezza EF:
Da quanto sopra segue che FO=DF=FC e OE=AE=EB. Ora scriviamo a quanto equivale l'altezza, espressa attraverso i segmenti DF e AE:

Quindi la linea di mezzo è 12.
*In generale, questo è un problema, come capisci, per il calcolo mentale. Ma sono sicuro che la spiegazione dettagliata fornita sia necessaria. E quindi... Se guardi la figura (a condizione che durante la costruzione venga rispettato l'angolo tra le diagonali), l'uguaglianza FO=DF=FC e OE=AE=EB attira immediatamente la tua attenzione.
I prototipi includono anche tipologie di compiti con trapezi. Si costruisce su un foglio di carta in un quadrato e bisogna trovare la linea di mezzo; il lato della cella solitamente è uguale a 1, ma può avere un valore diverso.
27848. Trova la linea mediana del trapezio ABCD, se i lati delle celle quadrate sono uguali a 1.

È semplice, calcola le basi per celle e usa la formula: (2+4)/2=3
Se le basi sono costruite ad angolo rispetto alla griglia cellulare, ci sono due modi. Per esempio!
Trapezio-un quadrilatero i cui due lati sono paralleli. I lati paralleli sono la base, i lati non paralleli sono i lati.
Esistono diversi tipi principali: curvilineo, isoscele, arbitrario, rettangolare. Il calcolo dell'area di un trapezio utilizzando la formula varia a seconda del tipo specifico di figura geometrica.
Cos'è un trapezio: tipi e differenze
Ne esistono quattro tipologie in totale, che differiscono non solo per la variabilità degli angoli, ma anche per l'eventuale presenza di segmenti curvi.

Area di un trapezio arbitrario
La variabilità nel calcolo dell'area di un trapezio arbitrario è piccola. Può essere calcolato rispetto alle dimensioni di base e all'altezza date; contare attraverso i quattro lati indicati della figura; risolvi l'esempio, conoscendo la lunghezza della linea centrale e l'altezza; lungo le diagonali indicate e l'angolo tra loro; calcolare attraverso le basi e due angoli.
La formula di base per calcolare questo metodo: 
Dove a e b sono lati paralleli e h è l'altezza del quadrilatero.
Compito di esempio: Data una figura geometrica piana, i cui lati paralleli corrispondono a lunghezze di 12 e 20 cm e l'altezza è di 10 cm, come trovare l'area?
Soluzione: Soluzione valida secondo la formula sopra S = (a + b)/2 x h: S = (12 + 20)/2 x 10 = 160 cm².
Conoscendo la lunghezza della linea mediana e l'altezza della figura piatta, puoi sempre trovare l'area del trapezio eseguendo letteralmente un'azione:

Dove h è l'altezza del quadrilatero e m è la linea mediana (linea retta che collega i punti medi dei lati).
Un esempio di risoluzione di un problema: Dato un trapezio in cui la lunghezza della linea mediana è 28 cm e l'altezza della figura è 19 cm, qual è l'area del quadrilatero piatto?
Soluzione: Usando la formula S = hm, sostituiamo i valori digitali delle condizioni problematiche invece delle lettere. Otteniamo S = 28 x 19 = 532 cm².
Questo metodo non è semplice come i precedenti. Qui vengono presi come base i teoremi di base della geometria, e quindi il principio per calcolare l'area di un trapezio è il seguente:

Dove a, b, c, d sono i quattro lati della figura, e il lato b deve necessariamente essere più lungo di a.
Esempio di calcolo: I lati sono dati: a = 2 cm, b = 4 cm, c = 8 cm, d = 7 cm Come trovare l'area di un trapezio?
Calcolo:
Puoi anche calcolare l'area di un trapezio conoscendo le dimensioni di entrambe le diagonali e l'angolo tra di loro. 
Designazioni: d₁ e d₂ sono la prima e la seconda diagonale, α è l'angolo tra le diagonali.
Esempio: Calcola l'area della figura per i seguenti valori noti: d₁ = 17 cm, d₂ = 25 cm, α = 35⁰.
La decisione giusta: S = ½ x 17 x 25 x sin35 = 212,5 x 0,57 = 121,125 cm².
Un'altra opzione di calcolo basata sul calcolo dell'area di un trapezio utilizzando le lunghezze di due basi e due angoli.

I significati delle lettere: b, a – lunghezze delle basi, α e β – angoli.
Soluzione:
Video di formazione
Un ottimo aiuto per apprendere i tipi base di calcolo delle aree sono i video con un linguaggio accessibile e facile da seguire, spiegazioni dettagliate ed esempi di risoluzione dei problemi.
Video “Trapezio: risoluzione dei problemi”
Video per principianti: informazioni presentate in modo chiaro contenenti formule di base per il calcolo dell'area di un trapezio.
Video “Area di un trapezio”
Il video contiene le informazioni più complete sui tipi di trapezi, le designazioni corrette delle lettere e le opzioni per risolvere vari problemi utilizzando tutti i metodi e principi di calcolo noti.
Tutte le formule e i metodi di calcolo elencati sono ampiamente applicabili quando si studia la geometria nelle scuole e nelle università. Studenti, scolari e candidati troveranno le informazioni fornite utili come promemoria online durante il periodo di preparazione intensiva per esami, test, scrittura di saggi, tesine e lavori simili.
- In contatto con 0
- Google+ 0
- OK 0
- Facebook 0