Ponieważ masa punktu jest stała, a jego przyspieszenie jest stałe, równanie wyrażające podstawową zasadę dynamiki można przedstawić w postaci

Równanie wyraża jednocześnie twierdzenie o zmianie pędu punktu w postaci różniczkowej: pochodna czasu pęd punktu jest równy suma geometryczna siły działające na punkt.

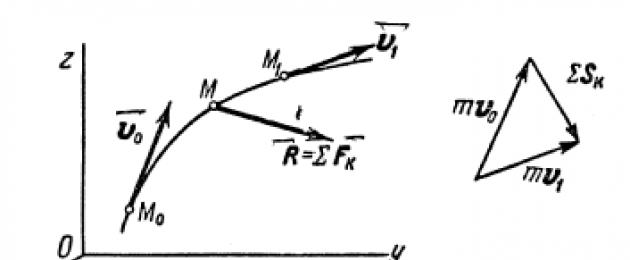
Całkujmy to równanie. Niech masa będzie punktowana M, poruszający się pod wpływem siły (ryc. 15), ma w tej chwili T=0 prędkości i w tej chwili T 1-biegowa.

Ryc.15

Następnie mnożymy obie strony równości przez i wyprowadzamy z nich całki oznaczone. W tym przypadku po prawej stronie, gdzie całkowanie zachodzi w czasie, granice całek będą wynosić 0 i T 1, a po lewej stronie, gdzie prędkość jest zintegrowana, granicami całki będą odpowiednie wartości prędkości i . Ponieważ całka z jest równa , wówczas w rezultacie otrzymujemy:

.

Całki po prawej stronie reprezentują impulsy działających sił. Dlatego ostatecznie będziemy mieli:

.

Równanie wyraża twierdzenie o zmianie pędu punktu w postaci końcowej: zmiana pędu punktu w pewnym okresie czasu jest równa sumie geometrycznej impulsów wszystkich sił działających na punkt w tym samym okresie czasu ( Ryż. 15).

Podczas rozwiązywania problemów zamiast równań wektorowych często stosuje się równania rzutowania.

W przypadku ruchu prostoliniowego występującego wzdłuż osi Oh twierdzenie wyraża pierwsze z tych równań.

Pytania autotestowe

Formułować podstawowe prawa mechaniki.

Jakie równanie nazywa się podstawowym równaniem dynamiki?

Jaka jest miara bezwładności ciał stałych podczas ruchu postępowego?

Czy masa ciała zależy od jego położenia na Ziemi?

Jaki układ odniesienia nazywa się inercyjnym?

Do jakiego ciała przyłożona jest siła bezwładności punktu materialnego oraz jaki jest jej moduł i kierunek?

Wyjaśnij różnicę między pojęciami „bezwładność” i „siła bezwładności”?

Do jakich ciał przykładana jest siła bezwładności, w jaki sposób jest ona skierowana i według jakiego wzoru można ją obliczyć?

Jaka jest zasada kinetostatyki?

Jakie są moduły i kierunki stycznych i normalnych sił bezwładności punktu materialnego?

Jak nazywa się masa ciała? Jaka jest jednostka masy w układzie SI?

Jaka jest miara bezwładności ciała?

Zapisz podstawowe zasady dynamiki w postaci wektorowej i różniczkowej?

NA punkt materialny działa stała siła. Jak porusza się punkt?

Jakie przyspieszenie uzyska punkt, jeśli zadziała na niego siła dwukrotnie większa od siły ciężkości?

Po zderzeniu dwóch punktów materialnych z masami M 1 = 6 kg i M 2 = 24 kg pierwszy punkt otrzymał przyspieszenie 1,6 m/s. Jakie przyspieszenie uzyska drugi punkt?

Przy jakim ruchu punktu materialnego jego styczna siła bezwładności jest równa zeru, a przy jakim ruchu jest normalna?

Jakie wzory stosuje się do obliczania modułów sił obrotowych i odśrodkowych bezwładności punktu należącego do ciało stałe, obracając się stała oś?

Jak sformułowane jest podstawowe prawo dynamiki punktowej?

Podaj sformułowanie prawa niezależności działania sił.

Zapisz to równania różniczkowe ruch punktu materialnego w postaci wektora i współrzędnych.

Sformułuj istotę pierwszego i drugiego głównego problemu dynamiki punktowej.

Podaj warunki, z których wyznaczane są stałe całkowania różniczkowych równań ruchu punktu materialnego.

Jakie równania dynamiki nazywane są naturalnymi równaniami ruchu punktu materialnego?

Jakie są dwa główne problemy dynamiki punktów rozwiązywane za pomocą ruchów różnicowych punktu materialnego?

Równania różniczkowe ruchu swobodnego punktu materialnego.

Jak wyznacza się stałe podczas całkowania różniczkowych równań ruchu punktu materialnego?

Wyznaczanie wartości dowolnych stałych pojawiających się podczas całkowania równań różniczkowych ruchu punktu materialnego.

Jakie są prawa swobodny spadek ciała?

Według jakich praw zachodzą poziome i pionowe ruchy ciała rzuconego w przestrzeni pod kątem do horyzontu? Jaka jest trajektoria jego ruchu i pod jakim kątem ciało ma największy zasięg lotu?

Jak obliczyć impuls zmiennej siły w skończonym okresie czasu?

Jak nazywa się pęd punktu materialnego?

Jak wyrazić podstawowa praca siłę przez elementarną ścieżkę punktu przyłożenia siły i jak poprzez przyrost współrzędnej łukowej tego punktu?

Przy jakich przemieszczeniach praca grawitacji jest: a) dodatnia, b) ujemna, c) zerowa?

Jak obliczyć moc siły przyłożonej do punktu materialnego obracającego się wokół ustalonej osi z prędkością kątową?

Sformułuj twierdzenie o zmianie pędu punktu materialnego.

W jakich warunkach pęd punktu materialnego się nie zmienia? W jakich warunkach jego rzut na określoną oś nie zmienia się?

Podaj sformułowanie twierdzenia o zmianie energia kinetyczna punkt materialny w postaci różniczkowej i skończonej.

Jak nazywa się moment pędu punktu materialnego względem: a) środka, b) osi?

Jak formułuje się twierdzenie o zmianie momentu pędu punktu względem środka i względem osi?

W jakich warunkach moment pędu punktu względem osi pozostaje niezmieniony?

Jak wyznacza się moment pędu punktu materialnego względem środka i względem osi? Jaki jest związek między nimi?

W jakim położeniu wektora pędu punktu materialnego jego moment względem osi jest równy zero?

Dlaczego trajektoria punktu materialnego poruszającego się pod wpływem siły centralnej leży w tej samej płaszczyźnie?

Jaki ruch punktu nazywamy prostoliniowym? Zapisz równanie różniczkowe ruchu prostoliniowego punktu materialnego.

Zapisz równania różniczkowe ruchu płaskiego punktu materialnego.

Jaki ruch punktu materialnego opisują równania różniczkowe Lagrange'a pierwszego rodzaju?

W jakich przypadkach punkt materialny nazywa się nieswobodnym i jakie są równania różniczkowe ruchu tego punktu?

Podaj definicje połączeń stacjonarnych i niestacjonarnych, holonomicznych i nieholonomicznych.

Jakie rodzaje połączeń nazywamy dwustronnymi? Jednostronny?

Jaka jest istota zasady wyzwolenia z więzów?

Jaką postać mają równania różniczkowe ruchu nieswobodnego punktu materialnego w postaci Lagrange'a? Co nazywa się mnożnikiem Lagrange’a?

Podaj sformułowanie dynamicznego twierdzenia Coriolisa.

Jaka jest istota zasady względności Galileo-Newtona?

Nazwij ruchy, w których siła bezwładności Coriolisa wynosi zero.

Jaki moduł i jaki kierunek ma przeniesienie i siły bezwładności Coriolisa?

Jaka jest różnica między równaniami różniczkowymi ruchu względnego i bezwzględnego punktu materialnego?

Jak wyznacza się przenoszenie i siły bezwładności Coriolisa w różnych przypadkach ruchu przenoszącego?

Jaka jest istota zasady względności mechaniki klasycznej?

Jakie układy odniesienia nazywane są inercyjnymi?

Jaki jest warunek względnego spoczynku punktu materialnego?

W jakich punktach powierzchnia ziemi Czy grawitacja ma największą i najmniejszą wartość?

Co wyjaśnia zbaczanie spadających ciał na wschód?

W jakim kierunku odchyla się ciało rzucone pionowo?

Łyżka jest opuszczana na wał z przyspieszeniem A=4 m/s 2. Ciężar łyżki G=2 kN. Wyznacz siłę naciągu liny podtrzymującej wannę?

Dwa punkty materialne poruszają się po linii prostej ze stałymi prędkościami 10 i 100 m/s. Czy możemy powiedzieć, że do tych punktów przyłożone są równoważne układy sił?

1) jest to niemożliwe;

Do dwóch punktów materialnych o masach 5 i 15 kg przykładane są jednakowe siły. Porównaj wartości liczbowe przyspieszenia tych punktów?

1) przyspieszenia są takie same;

2) przyspieszenie punktu o masie 15 kg jest trzykrotnie mniejsze niż przyspieszenie punktu o masie 5 kg.

Czy problemy dynamiki można rozwiązać za pomocą równań równowagi?

Wielkość ruchu punktu materialnego nazywana wielkością wektorową mV, równy iloczynowi masy punktu i jego wektora prędkości. Wektor mV zastosowany do ruchomego punktu.

Ilość ruchu systemu nazywana wielkością wektorową Q, równa sumie geometrycznej (wektorowi głównemu) wielkości ruchu wszystkich punktów układu:

Wektor Q jest wektorem swobodnym. W układzie jednostek SI moduł pędu mierzy się w kg m/s lub N s.

Z reguły prędkości wszystkich punktów układu są różne (patrz np. rozkład prędkości punktów toczącego się koła, pokazany na ryc. 6.21), dlatego też bezpośrednie sumowanie wektorów po prawej stronie równości (17.2) jest trudne. Znajdźmy wzór, za pomocą którego ilość Q dużo łatwiej policzyć. Z równości (16.4) wynika, że

Biorąc pochodną czasu obu stron, otrzymujemy Zatem biorąc pod uwagę równość (17.2), stwierdzamy, że

to znaczy pęd układu jest równy iloczynowi masy całego układu i prędkości jego środka masy.

Zauważ, że wektor Q, podobnie jak główny wektor sił w statyce, jest to jakaś uogólniona wektorowa charakterystyka ruchu całości układ mechaniczny. W ogólnym przypadku ruchu układu jego pęd wynosi Q można uznać za charakterystykę translacyjnej części ruchu układu wraz z jego środkiem masy. Jeżeli podczas ruchu układu (ciała) środek masy jest nieruchomy, wówczas wielkość ruchu układu będzie równa zeru. Jest to na przykład pęd ciała obracającego się wokół stałej osi przechodzącej przez jego środek masy.

Przykład. Określ wielkość ruchu układu mechanicznego (ryc. 17.1, A), składający się z ładunku A masa t A - 2 kg, jednorodny blok W o wadze 1 kg i kółkach D masa m D - 4 kg. Ładunek A porusza się z dużą prędkością V A - 2 m/s, koło D toczy się bez poślizgu, nić jest nierozciągliwa i nieważka. Rozwiązanie. Wielkość ruchu układu ciał

Ciało A idzie do przodu i Q ZA = m A V A(liczebnie Pytanie O= 4 kg m/s, kierunek wektorowy Pytanie O pokrywa się z kierunkiem V A). Blok W wykonuje ruch obrotowy wokół ustalonej osi przechodzącej przez środek masy; stąd, QB- 0. Koło D tworzy płaszczyznę równoległą

ruch; jego środek prędkości chwilowej znajduje się w punkcie DO, zatem prędkość jego środka masy (pkt MI) równy V mi = V A /2= 1 m/s. Wielkość ruchu koła Q D - m D V E - 4 kg m/s; wektor QD skierowany poziomo w lewo.

Przedstawiając wektory Pytanie O I QD na ryc. 17.1, B, znajdź wielkość ruchu Q układy według wzoru (a). Biorąc pod uwagę kierunki i wartości liczbowe wielkości, otrzymujemy Q ~^Q A +Q E=4l/2~ kg m/s, kierunek wektorowy Q pokazany na ryc. 17.1, B.

Biorąc pod uwagę, że a-dV/dt, równanie (13.4) podstawowej zasady dynamiki można przedstawić jako

Równanie (17.4) wyraża twierdzenie o zmianie pędu punktu w postaci różniczkowej: w każdej chwili czasu pochodna pędu punktu po czasie jest równa sile działającej na punkt. (W zasadzie jest to inne sformułowanie podstawowej zasady dynamiki, zbliżone do podanego przez Newtona.) Jeżeli na punkt działa kilka sił, to po prawej stronie równości (17.4) będzie wypadkowa przyłożonych sił do punktu materialnego.

Jeśli obie strony równości zostaną pomnożone przez dt, wtedy otrzymamy

Wielkość wektorowa po prawej stronie tej równości charakteryzuje działanie wywierane na ciało przez siłę w elementarnym okresie czasu dt ta wartość jest oznaczona dS i zadzwoń podstawowy impuls siły, tj.

Puls S wytrzymałość F przez skończony okres czasu /, - / 0 definiuje się jako granicę sumy całkowej odpowiednich impulsów elementarnych, tj.

W szczególnym przypadku, jeśli siła F jest wówczas stała pod względem wielkości i kierunku S = F(t| -/0) i S- F(t l -/ 0). Ogólnie rzecz biorąc, wielkość impulsu siły można obliczyć na podstawie jego rzutów na osie współrzędnych:

Teraz całkując obie strony równości (17.5) z T= const, otrzymujemy

Równanie (17.9) wyraża twierdzenie o zmianie pędu punktu w postaci skończonej (całkowej): zmiana pędu punktu w pewnym okresie czasu jest równa impulsowi siły działającej na punkt (lub impulsowi wypadkowej wszystkich sił przyłożonych do niego) w tym samym okresie czasu.

Rozwiązując problemy, używaj równań tego twierdzenia w rzutach na osie współrzędnych

Rozważmy teraz układ mechaniczny składający się z P punkty materialne. Następnie dla każdego punktu możemy zastosować twierdzenie o zmianie pędu w postaci (17.4), biorąc pod uwagę siły zewnętrzne i wewnętrzne przyłożone do punktów:

Sumując te równości i biorąc pod uwagę, że suma pochodnych jest równa pochodnej sumy, otrzymujemy

Ponieważ z natury sił wewnętrznych HF k=0 i z definicji pędu ^fn k V/ w = Q, to w końcu znajdziemy

Równanie (17.11) wyraża twierdzenie o zmianie pędu układu w postaci różniczkowej: w każdym momencie pochodna czasowa pędu układu jest równa sumie geometrycznej wszystkich sił zewnętrznych działających na układ.

Rzutując równość (17.11) na osie współrzędnych, otrzymujemy

Mnożenie obu stron (17.11) przez dt i całkując, otrzymujemy

gdzie 0, P 0 - wielkość ruchu układu w chwilach czasu odpowiednio i / 0.

Równanie (17.13) wyraża twierdzenie o zmianie pędu układu w postaci całkowej: zmiana pędu układu w dowolnym czasie jest równa sumie impulsów wszystkich sił zewnętrznych działających na układ w tym samym czasie.

W rzutach na osie współrzędnych otrzymujemy

Z twierdzenia o zmianie pędu układu można uzyskać następujące ważne konsekwencje, które wyrażają się prawo zachowania pędu układu.

• 1. Jeżeli suma geometryczna wszystkich sił zewnętrznych działających na układ wynosi zero (LF k=0), to z równania (17.11) wynika, że ​​w tym przypadku Q= const, tj. wektor pędu układu będzie stały pod względem wielkości i kierunku.
• 2. Jeżeli siły zewnętrzne działające na układ są takie, że suma ich rzutów na dowolną oś wynosi zero (np. Ja i kx = 0), to z równań (17.12) wynika, że ​​w tym przypadku Q x = const, czyli rzut pędu układu na tę oś pozostaje niezmieniony.

Należy zauważyć, że siły wewnętrzne układu nie biorą udziału w równaniu twierdzenia o zmianie pędu układu. Siły te, choć wpływają na pęd poszczególnych punktów układu, nie mogą zmienić pędu układu jako całości. Biorąc tę ​​okoliczność pod uwagę przy rozwiązywaniu problemów, zaleca się wybór rozważanego układu w taki sposób, aby nieznane siły (wszystkie lub część z nich) miały charakter wewnętrzny.

Prawo zachowania pędu jest wygodne do zastosowania w przypadkach, gdy zmieniając prędkość jednej części układu, konieczne jest określenie prędkości jego drugiej części.

Zadanie 17.1. DO ważenie wózka tx- 12 kg poruszających się w jednym punkcie po gładkiej poziomej płaszczyźnie A nieważki pręt jest przymocowany za pomocą cylindrycznego zawiasu OGŁOSZENIE długość /= 0,6 m z obciążeniem D masa t 2 - Na koniec 6 kg (ryc. 17.2). W momencie / 0 = 0, gdy prędkość wózka I () - 0,5 m/s, pręt OGŁOSZENIE zaczyna się obracać wokół osi A, prostopadle do płaszczyzny rysunku, zgodnie z prawem f = (tg/6)(3^2 - 1) rad (/-in sekund). Definiować: u=f.

§ 17 ust. 3. Twierdzenie o ruchu środka masy

Twierdzenie o zmianie pędu układu mechanicznego można wyrazić w innej formie, zwanej twierdzeniem o ruchu środka masy.

Podstawiając do równania (17.11) równość Q = MV C, dostajemy

Jeżeli masa M system jest stały, otrzymujemy

Gdzie i z - przyspieszenie środka masy układu.

Równanie (17.15) wyraża twierdzenie o ruchu środka masy układu: iloczyn masy układu i przyspieszenia jego środka masy jest równy sumie geometrycznej wszystkich sił zewnętrznych działających na układ.

Rzutując równość (17.15) na osie współrzędnych, otrzymujemy

Gdzie x do , y do , z do - współrzędne środka masy układu.

Równania te są równaniami różniczkowymi ruchu środka masy w rzutach na osie kartezjańskiego układu współrzędnych.

Omówmy uzyskane wyniki. Przypomnijmy najpierw, że środkiem masy układu jest punkt geometryczny, czasami znajdujący się poza geometrycznymi granicami ciała. Siły działające na układ mechaniczny (zewnętrzne i wewnętrzne) przykładane są do wszystkich punktów materialnych układu. Równania (17.15) pozwalają wyznaczyć ruch środka masy układu bez wyznaczania ruchu jego poszczególnych punktów. Porównując równania (17.15) twierdzenia o ruchu środka masy z równaniami (13.5) drugiej zasady Newtona dla punktu materialnego, dochodzimy do wniosku: środek masy układu mechanicznego porusza się jak punkt materialny, którego masa jest równa masie całego układu i tak jakby do tego punktu przyłożone były wszystkie siły zewnętrzne działające na układ. Zatem rozwiązania, które otrzymujemy poprzez rozważenie dane ciało jako punkt materialny wyznaczają prawo ruchu środka masy tego ciała.

W szczególności, jeśli ciało porusza się translacyjnie, wówczas charakterystyki kinematyczne wszystkich punktów ciała i jego środka masy są takie same. Dlatego ciało poruszające się translacyjnie można zawsze uznać za punkt materialny o masie równej masie całego ciała.

Jak widać z (17.15) siły wewnętrzne działające na punkty układu nie wpływają na ruch środka masy układu. Siły wewnętrzne mogą wpływać na ruch środka masy w przypadkach, gdy pod ich wpływem zmieniają się siły zewnętrzne. Przykłady tego zostaną podane poniżej.

Z twierdzenia o ruchu środka masy wynikają następujące ważne konsekwencje, które wyrażają prawo zachowania ruchu środka masy układu.

1. Jeżeli suma geometryczna wszystkich sił zewnętrznych działających na układ wynosi zero (LF k=0), to z równania (17.15) wynika,

a co z tym ac = 0 lub Vc = const, czyli środek masy tego układu

porusza się ze stałą prędkością pod względem wielkości i kierunku (innymi słowy równomiernie i prostoliniowo). W szczególnym przypadku, jeśli początkowo środek masy znajdował się w spoczynku ( Vc=0), to pozostanie w spoczynku; Gdzie

ścieżka Wiesz, że jego położenie w przestrzeni nie ulegnie zmianie, tj. r do = konst.

2. Jeżeli siły zewnętrzne działające na układ są takie, że suma ich rzutów na jakąś oś (np. oś X) równy zeru (?F e kx= 0), to z równania (17.16) wynika, że ​​w tym przypadku x s=0 lub VCx =x do = const, czyli rzut prędkości środka masy układu na tę oś jest wartością stałą. W szczególnym przypadku, jeśli w momencie początkowym Drażnić= 0, to w każdym kolejnym momencie wartość ta pozostanie taka sama, a co za tym idzie, współrzędna x sśrodek masy układu nie ulegnie zmianie, tj. x c - konst.

Rozważmy przykłady ilustrujące prawo ruchu środka masy.

Przykłady. 1. Jak zauważono, ruch środka masy zależy wyłącznie od sił zewnętrznych; siły wewnętrzne nie mogą zmienić położenia środka masy. Ale wewnętrzne siły systemu mogą powodować wpływy zewnętrzne. Zatem ruch człowieka po poziomej powierzchni odbywa się pod wpływem sił tarcia pomiędzy podeszwami jego butów a nawierzchnią drogi. Człowiek siłą swoich mięśni (sił wewnętrznych) odpycha się nogami od nawierzchni drogi, dlatego w punktach styku z jezdnią powstaje siła tarcia (zewnętrzna w stosunku do człowieka), skierowana w stronę jego ruch.

• 2. Samochód porusza się w podobny sposób. Wewnętrzne siły ciśnienia w silniku wymuszają obrót kół, ale ponieważ te ostatnie mają przyczepność do nawierzchni, powstałe siły tarcia „popychają” samochód do przodu (w rezultacie koła nie obracają się, ale poruszają się płasko równolegle). . Jeśli droga jest całkowicie gładka, wówczas środek masy samochodu będzie nieruchomy (przy zerowej prędkości początkowej), a koła przy braku tarcia będą się ślizgać, czyli wykonywać ruch obrotowy.
• 3. Ruch za pomocą śmigła, śmigła lub wioseł następuje w wyniku odrzucenia określonej masy powietrza (lub wody). Jeśli potraktujemy rzuconą masę i poruszające się ciało jako jeden układ, wówczas siły oddziaływania między nimi, jako siły wewnętrzne, nie są w stanie zmienić całkowitej wielkości ruchu tego układu. Jednak każda część tego układu będzie przesuwać np. łódkę do przodu, a wodę, którą wiosła będą odrzucać.
• 4. W pozbawionej powietrza przestrzeni, gdy rakieta się porusza, „wyrzuconą masę” należy „zabrać ze sobą”: silnik odrzutowy wprawia rakietę w ruch, odrzucając produkty spalania paliwa, którym rakieta jest wypełniona.
• 5. Podczas schodzenia na spadochronie można kontrolować ruch środka masy układu człowiek-spadochron. Jeżeli poprzez wysiłek mięśni osoba napręży liny spadochronu w taki sposób, że zmieni się kształt jego czaszy lub kąt natarcia strumienia powietrza, wówczas spowoduje to zmianę zewnętrznego wpływu strumienia powietrza, a tym samym wpłynie na ruch całego systemu.

Zadanie 17.2. W Zadanie 17.1 (patrz rys. 17.2) określ: 1) prawo ruchu wózka X (= /)(/), jeśli wiadomo, że w początkowym momencie czasu t 0 = O układ był w spoczynku i współrzędna x 10 = 0; 2) prawo zmiany w czasie całkowitej wartości reakcji normalnej N(N = N"+N") płaszczyzna pozioma, tj. N=f2(t).

Rozwiązanie. Tutaj, podobnie jak w zadaniu 17.1, rozważamy system składający się z wózka i ładunku D, w dowolnej pozycji pod działaniem przyłożonych do niego sił zewnętrznych (patrz ryc. 17.2). Osie współrzędnych Ooo narysuj go tak, aby oś x była pozioma, a oś Na przeszedł przez punkt 0, tj. położenie punktu A w pewnym momencie t-t 0 - 0.

1. Wyznaczenie prawa ruchu wózka. Aby wyznaczyć x, = /,(0, korzystamy z twierdzenia o ruchu środka masy układu. Utwórzmy równanie różniczkowe jego ruchu w rzucie na oś x:

Ponieważ wszystkie siły zewnętrzne są zatem pionowe T,F i kx = 0 i dlatego

Całkując to równanie, znajdujemy to Mx s = B, to znaczy rzut prędkości środka masy układu na oś x jest wartością stałą. Od początkowego momentu

Całkowanie równań Mx s= 0, otrzymujemy

tj. koordynować x sśrodek masy układu jest stały.

Zapiszmy wyrażenie Mx s dla dowolnego położenia układu (patrz rys. 17.2), biorąc pod uwagę to x A - x { , x D - x 2 I x 2 - x ( - I grzech ż. Zgodnie ze wzorem (16.5), który w tym przypadku wyznacza współrzędną środka masy układu Mx s - t ( x ( + t 2x2".

dla dowolnego punktu w czasie

dla chwili czasu / () = 0, X (= 0 i

Zgodnie z równością (b), współrzędna x sśrodek masy całego układu pozostaje niezmieniony, tj. xD^,) = xc(t). W konsekwencji przyrównując wyrażenia (c) i (d) otrzymujemy zależność współrzędnej x od czasu.

Odpowiedź: X - 0,2 m, gdzie T- w sekundy.

2. Definicja reakcji N. Do ustalenia N=f 2 (t) ułóżmy równanie różniczkowe ruchu środka masy układu w rzucie na oś pionową Na(patrz rys. 17.2):

Stąd oznaczenie N=N+N", dostajemy

Zgodnie ze wzorem wyznaczającym rzędną takśrodek masy układu, Mu s = t (yx + t 2 i 2, gdzie y, = w C1,o 2= i D = UA ~ 1 bo Ф” otrzymujemy

Różniczkując tę ​​równość dwukrotnie w czasie (biorąc pod uwagę, że w C1 I w A ilości są stałe i dlatego ich pochodne są równe zeru), znajdujemy

Podstawiając to wyrażenie do równania (e), wyznaczamy pożądaną zależność N z T.

Odpowiedź: N- 176,4 + 1,13,

gdzie f = (i/6)(3/ -1), T- w sekundy, N- w niutonach.

Zadanie 17.3. Masa silnika elektrycznego tx przymocowany do poziomej powierzchni fundamentu za pomocą śrub (ryc. 17.3). Nieważki pręt o długości l jest przymocowany na jednym końcu do wału silnika pod kątem prostym do osi obrotu, a na drugim końcu pręta zamontowany jest obciążnik punktowy. A masa t 2. Wał obraca się równomiernie z prędkością kątową c. Znajdź poziomy nacisk silnika na śruby. Rozwiązanie. Rozważmy układ mechaniczny składający się z silnika i obciążnika punktowego A, w dowolnej pozycji. Przedstawmy siły zewnętrzne działające na układ: grawitację Rx, R2, reakcja fundamentu w postaci siły pionowej N i siłę poziomą R. Narysujmy oś x poziomo.

Aby określić poziomy nacisk silnika na śruby (i będzie on liczbowo równy reakcji R i skierowany przeciwnie do wektora R ), ułożymy równanie twierdzenia o zmianie pędu układu w rzucie na poziomą oś x:

Dla rozważanego układu w jego dowolnym położeniu, biorąc pod uwagę, że pęd korpusu silnika wynosi zero, otrzymujemy Qx = - t 2 U A spol. Biorąc to pod uwagę V A = a z/, f = co/ (obrót silnika jest równomierny), otrzymujemy Q x - - m 2 co/cos co/. Różnicowanie Qx w czasie i podstawiając do równości (a), znajdujemy R- m 2 co 2 /sin co/.

Należy pamiętać, że to właśnie takie siły wymuszają (patrz § 14.3), gdy działają, powstają wymuszone wibracje konstrukcji.

Ćwiczenia dla niezależna praca

• 1. Co nazywa się pędem punktu i układu mechanicznego?
• 2. Jak zmienia się pęd punktu poruszającego się ruchem jednostajnym po okręgu?
• 3. Czym charakteryzuje się impuls siły?
• 4. Czy siły wewnętrzne układu wpływają na jego pęd? Na ruchu jego środka masy?
• 5. Jak pary przyłożonych do niego sił wpływają na ruch środka masy układu?
• 6. W jakich warunkach środek masy układu znajduje się w spoczynku? porusza się równomiernie i po linii prostej?

7. W łodzi stojącej, bez przepływu wody, osoba dorosła siedzi na rufie, a dziecko na dziobie łodzi. W jakim kierunku popłynie łódź, jeśli zamienią się miejscami?

W jakim przypadku moduł ruchu łodzi będzie duży: 1) jeśli dziecko przesunie się na rufę osoby dorosłej; 2) jeśli do dziecka na dziób łodzi podchodzi osoba dorosła? Jakie będzie przemieszczenie środka masy układu „łódź i dwie osoby” podczas tych ruchów?

W ten sam sposób, jak dla jednego punktu materialnego, wyprowadzimy twierdzenie o zmianie pędu układu w różnych postaciach.

Przekształćmy równanie (twierdzenie o ruchu środka masy układu mechanicznego)

w następujący sposób:

;

Otrzymane równanie wyraża twierdzenie o zmianie pędu układu mechanicznego w postaci różniczkowej: pochodna pędu układu mechanicznego po czasie jest równa wektorowi głównemu sił zewnętrznych działających na układ .

W rzutach na osie współrzędnych kartezjańskich:

; ; .

Biorąc całki obu stron ostatnich równań w czasie, otrzymujemy twierdzenie o zmianie pędu układu mechanicznego w postaci całkowej: zmiana pędu układu mechanicznego jest równa pędowi wektora głównego układu mechanicznego siły zewnętrzne działające na układ .

.

Lub w rzutach na osie współrzędnych kartezjańskich:

; ; .

Wnioski z twierdzenia (prawa zachowania pędu)

Prawo zachowania pędu otrzymuje się jako szczególne przypadki twierdzenia o zmianie pędu układu w zależności od charakterystyki układu sił zewnętrznych. Siły wewnętrzne mogą być dowolne, ponieważ nie wpływają na zmiany pędu.

Istnieją dwa możliwe przypadki:

1. Jeżeli suma wektorów wszystkich sił zewnętrznych przyłożonych do układu jest równa zeru, wówczas wielkość ruchu układu jest stała pod względem wielkości i kierunku

2. Jeżeli rzut wektora głównego sił zewnętrznych na dowolną oś współrzędnych i/lub i/lub jest równy zeru, to rzut pędu na te same osie ma wartość stałą, tj. i/lub i/lub odpowiednio.

Podobne wpisy można dokonać dla punktu materialnego i dla punktu materialnego.

Zadanie. Z broni, której masa M, pocisk o masie wylatuje w kierunku poziomym M z szybkością w. Znajdź prędkość V pistolety po strzale.

Rozwiązanie. Wszystkie siły zewnętrzne działające na mechaniczny układ broń-pocisk mają charakter pionowy. Oznacza to, że bazując na następstwie twierdzenia o zmianie pędu układu, mamy: .

Wielkość ruchu układu mechanicznego przed odpaleniem:

Wielkość ruchu układu mechanicznego po strzale:

.

Porównując prawe strony wyrażeń, otrzymujemy to

.

Znak „-” w otrzymanym wzorze wskazuje, że po oddaniu strzału działo cofnie się w kierunku przeciwnym do osi Wół.

PRZYKŁAD 2. Strumień cieczy o gęstości wypływa z prędkością V z rury o polu przekroju poprzecznego F i uderza pod kątem w pionową ściankę. Wyznacz ciśnienie płynu na ścianę.

ROZWIĄZANIE. Zastosujmy twierdzenie o zmianie pędu w postaci całkowej do objętości cieczy o masie M uderzanie w ścianę przez pewien czas T.

RÓWNANIE MESHCHERSKIEGO

(podstawowe równanie dynamiki ciała o zmiennej masie)

We współczesnej technologii zdarzają się przypadki, gdy masa punktu i układu nie pozostaje stała podczas ruchu, ale się zmienia. I tak np. podczas lotu rakiet kosmicznych, na skutek wyrzucenia produktów spalania i poszczególnych, niepotrzebnych części rakiety, zmiana masy osiąga 90-95% całkowitej wartości początkowej. Ale nie tylko technologia kosmiczna może być przykładem dynamiki zmiennego ruchu mas. W przemyśle tekstylnym przy nowoczesnych prędkościach roboczych maszyn i maszyn zachodzą znaczne zmiany masy różnych wrzecion, szpul i rolek.

Rozważmy główne cechy związane ze zmianami masy na przykładzie ruchu postępowego ciała o zmiennej masie. Podstawowej zasady dynamiki nie można bezpośrednio zastosować do ciała o zmiennej masie. Otrzymujemy zatem różniczkowe równania ruchu punktu o zmiennej masie, stosując twierdzenie o zmianie pędu układu.

Niech punkt będzie miał masę m+dm porusza się z dużą prędkością. Następnie od punktu oddziela się pewną cząstkę o masie dm poruszać się z dużą prędkością.

Wielkość ruchu ciała przed oderwaniem się cząstki:

Wielkość ruchu układu składającego się z ciała i oderwanej cząstki po jego oddzieleniu:

Następnie zmiana pędu:

Na podstawie twierdzenia o zmianie pędu układu:

Oznaczmy ilość - prędkość względna cząstki:

Oznaczmy

Rozmiar R zwaną siłą reakcji. Siła reakcji to ciąg silnika wywołany wyrzutem gazu z dyszy.

Wreszcie dostajemy

-

Wzór ten wyraża podstawowe równanie dynamiki ciała o zmiennej masie (wzór Meshchersky'ego). Z ostatniego wzoru wynika, że ​​równania różniczkowe ruchu punktu o zmiennej masie mają taką samą postać jak dla punktu o stałej masie, z wyjątkiem dodatkowej siły reakcji przyłożonej do punktu na skutek zmiany masy.

Podstawowe równanie dynamiki ciała o zmiennej masie wskazuje, że przyspieszenie tego ciała powstaje nie tylko pod wpływem sił zewnętrznych, ale także pod wpływem siły reakcji.

Siła reakcji to siła podobna do tej odczuwanej przez osobę strzelającą - przy strzelaniu z pistoletu wyczuwalna jest ona w dłoni; Strzelając z karabinu, jest on postrzegany przez ramię.

Pierwszy wzór Ciołkowskiego (na rakietę jednostopniową)

Niech punkt o zmiennej masie lub rakieta porusza się po linii prostej pod wpływem tylko jednej siły reakcji. Ponieważ dla wielu nowoczesnych silników odrzutowych , gdzie oznacza maksymalną siłę reakcji dopuszczoną przez konstrukcję silnika (ciąg silnika); - siła ciężkości działająca na silnik umieszczony na powierzchni ziemi. Te. powyższe pozwala pominąć składnik równania Meshchersky'ego i przyjąć to równanie w postaci do dalszej analizy: ,

Oznaczmy:

Rezerwa paliwa (dla silników odrzutowych na ciecz - sucha masa rakiety (jej masa pozostała po spaleniu całego paliwa);

Masa cząstek oddzielonych od rakiety; Widziany jako zmienna ilość, wahający się od do .

Zapiszmy równanie ruchu prostoliniowego punktu o zmiennej masie w postaci:

.

Ponieważ wzór na określenie zmiennej masy rakiety wynosi

Dlatego równania ruchu punktu Biorąc całki po obu stronach, otrzymujemy

Gdzie - charakterystyczna prędkość- jest to prędkość, jaką osiąga rakieta pod wpływem ciągu po wyrzuceniu z rakiety wszystkich cząstek (w przypadku silników odrzutowych na ciecz - po wypaleniu całego paliwa).

Wyjęty poza znak całki (co można zrobić na podstawie twierdzenia o wartości średniej znanego z wyższej matematyki) wynosi Średnia prędkość cząstki wyrzucone z rakiety.

Równanie różniczkowe ruchu punktu materialnego pod wpływem siły F można przedstawić w następującej postaci wektorowej:

Ponieważ masa punktu M przyjmuje się jako stałą, wówczas można ją wpisać pod znakiem pochodnej. Następnie

Wzór (1) wyraża twierdzenie o zmianie pędu punktu w postaci różniczkowej: pierwsza pochodna po czasie pędu punktu jest równa sile działającej na ten punkt.

W rzutach na osie współrzędnych (1) można przedstawić jako

Jeśli obie strony (1) zostaną pomnożone przez dt, wówczas otrzymujemy inną postać tego samego twierdzenia - twierdzenie o pędzie w postaci różniczkowej:

te. różnica pędu punktu jest równa elementarnemu impulsowi siły działającej na ten punkt.

Rzutując obie części (2) na osie współrzędnych otrzymujemy

Całkując obie części (2) od zera do t (ryc. 1), mamy

gdzie jest prędkość punktu w danej chwili T; - prędkość w T = 0;

S- impuls siły w czasie T.

Wyrażenie w postaci (3) jest często nazywane twierdzeniem o pędzie w postaci skończonej (lub całkowej): zmiana pędu punktu w dowolnym okresie czasu jest równa impulsowi siły w tym samym okresie.

W rzutach na osie współrzędnych twierdzenie to można przedstawić w następującej postaci:

W przypadku punktu materialnego twierdzenie o zmianie pędu w dowolnej postaci zasadniczo nie różni się od równań różniczkowych ruchu punktu.

Twierdzenie o zmianie pędu układu

Wielkość ruchu układu będzie nazywana wielkością wektorową Q, równa sumie geometrycznej (wektorowi głównemu) wielkości ruchu wszystkich punktów układu.

Rozważmy system składający się z N punkty materialne. Ułóżmy równania różniczkowe ruchu dla tego układu i dodajmy je wyraz po wyrazie. Następnie otrzymujemy:

Ostatnia suma, ze względu na właściwość sił wewnętrznych, jest równa zeru. Oprócz,

Wreszcie znajdujemy:

Równanie (4) wyraża twierdzenie o zmianie pędu układu w postaci różniczkowej: pochodna czasowa pędu układu jest równa sumie geometrycznej wszystkich sił zewnętrznych działających na układ.

Znajdźmy inne wyrażenie dla twierdzenia. Wpuść tę chwilę T= 0 oznacza wielkość ruchu układu Pytanie 0 i w danym momencie t 1 staje się równe Pytanie 1. Następnie mnożąc obie strony równości (4) przez dt i całkując otrzymujemy:

Czy gdzie:

(S-impuls siły)

ponieważ całki po prawej stronie dają impulsy sił zewnętrznych,

równanie (5) wyraża twierdzenie o zmianie pędu układu w postaci całkowej: zmiana pędu układu w pewnym okresie czasu jest równa sumie impulsów sił zewnętrznych działających na układ w tym samym czasie.

W rzutach na osie współrzędnych będziemy mieli:

Prawo zachowania pędu

Z twierdzenia o zmianie pędu układu można wyciągnąć następujące istotne konsekwencje:

1. Niech suma wszystkich sił zewnętrznych działających na układ będzie równa zero:

Zatem z równania (4) wynika, że ​​w tym przypadku Q = stała

Zatem, jeśli suma wszystkich sił zewnętrznych działających na układ jest równa zeru, wówczas wektor pędu układu będzie stały pod względem wielkości i kierunku.

2. 01Niech siły zewnętrzne działające na układ będą takie, że suma ich rzutów na jakąś oś (np. Ox) będzie równa zeru:

Zatem z równań (4`) wynika, że ​​w tym przypadku Q = stała

Zatem, jeżeli suma rzutów wszystkich działających sił zewnętrznych na dowolną oś jest równa zeru, to rzut wielkości ruchu układu na tę oś jest wartością stałą.

Te wyniki wyrażają prawo zachowania pędu układu. Wynika z nich, że siły wewnętrzne nie mogą zmienić całkowitej wielkości ruchu układu.

Spójrzmy na kilka przykładów:

· Zjawisko powrotu rolki. Jeśli potraktujemy karabin i kulę jako jeden układ, wówczas ciśnienie gazów proszkowych podczas strzału będzie siłą wewnętrzną. Siła ta nie może zmienić całkowitego pędu układu. Ponieważ jednak gazy prochowe, działając na kulę, nadają jej pewien ruch skierowany do przodu, muszą jednocześnie nadać karabinowi taki sam ruch w odwrotny kierunek. Spowoduje to cofnięcie się karabinu, tj. tzw powrót. Podobne zjawisko występuje podczas strzelania z broni (cofanie).

· Działanie śmigła (śmigła). Śmigło wprawia w ruch pewną masę powietrza (lub wody) wzdłuż osi śmigła, odrzucając tę ​​masę z powrotem. Jeżeli potraktujemy masę rzuconą i samolot (lub statek) jako jeden układ, wówczas siły oddziaływania śmigła z otoczeniem, jako siły wewnętrzne, nie są w stanie zmienić całkowitej wielkości ruchu tego układu. Dlatego też, gdy masa powietrza (wody) zostanie odrzucona, samolot (lub statek) uzyskuje odpowiednią prędkość do przodu, taką, że całkowity ruch rozważanego układu pozostaje równy zeru, ponieważ był zerowy przed rozpoczęciem ruchu .

Podobny efekt uzyskuje się poprzez działanie wioseł lub kół łopatkowych.

· Napęd rekt iwny W rakiecie (rakietze) gazowe produkty spalania paliwa wyrzucane są z dużą prędkością przez otwór w ogonie rakiety (z dyszy silnika odrzutowego). Siły ciśnienia działające w tym przypadku będą siłami wewnętrznymi i nie mogą zmienić całkowitego pędu układu gazy rakietowo-proszkowe. Ponieważ jednak uciekające gazy mają pewien ruch skierowany do tyłu, rakieta otrzymuje odpowiednią prędkość do przodu.

Twierdzenie o momentach względem osi.

Rozważ materialny punkt masy M, poruszając się pod wpływem siły F. Znajdźmy dla niego zależność pomiędzy momentami wektorów mV I F względem pewnej ustalonej osi Z.

m z (F) = xF - yF (7)

Podobnie dla wartości m(mV), jeśli zostanie wyjęty M będzie poza nawiasami

M z (mV) = m(xV - yV)(7`)

Biorąc pochodne po czasie z obu stron tej równości, znajdujemy

Po prawej stronie wynikowego wyrażenia pierwszy nawias jest równy 0, ponieważ dx/dt=V i dу/dt = V, drugi nawias według wzoru (7) jest równy

mz(F), gdyż zgodnie z podstawową zasadą dynamiki:

Wreszcie będziemy mieli (8)

Otrzymane równanie wyraża twierdzenie o momentach wokół osi: pochodna po czasie momentu pędu punktu względem dowolnej osi jest równa momentowi siła działająca o tej samej osi. Podobne twierdzenie obowiązuje dla chwil wokół dowolnego środka O.

Niech punkt materialny porusza się pod wpływem siły F. Wymagane jest określenie ruchu tego punktu względem poruszającego się układu Oksyz(patrz ruch złożony punktu materialnego), który porusza się w znany sposób względem układu stacjonarnego O 1 X 1 y 1 z 1 .

Podstawowe równanie dynamiki układu stacjonarnego

Zapiszmy bezwzględne przyspieszenie punktu, korzystając z twierdzenia Coriolisa

Gdzie A abs– przyspieszenie bezwzględne;

A wzgl– przyspieszenie względne;

A uliczka– akceleracja przenośna;

A rdzeń– Przyspieszenie Coriolisa.

Przepiszmy (25) biorąc pod uwagę (26)

Wprowadźmy notację
- przenośna siła bezwładności,
- Siła bezwładności Coriolisa. Wtedy równanie (27) przyjmuje postać

Podstawowe równanie dynamiki do studiowania ruch względny(28) zapisuje się analogicznie jak dla ruchu absolutnego, z tym że do sił działających na punkt należy dodać jedynie siły przeniesienia i bezwładności Coriolisa.

Ogólne twierdzenia o dynamice punktu materialnego

Rozwiązując wiele problemów, możesz użyć gotowych półfabrykatów uzyskanych na podstawie drugiego prawa Newtona. W tej sekcji zestawiono takie metody rozwiązywania problemów.

Twierdzenie o zmianie pędu punktu materialnego

Przedstawmy następujące charakterystyki dynamiczne:

1. Pęd punktu materialnego– wielkość wektora równa iloczynowi masy punktu i jego wektora prędkości

. (29)

2. Impuls siły

Elementarny impuls siły– wielkość wektora równa iloczynowi wektora siły i elementarnego przedziału czasu

(30).

Następnie pełny impuls

. (31)

Na F=stała, którą otrzymujemy S=Ft.

Impuls całkowity w skończonym czasie można obliczyć tylko w dwóch przypadkach, gdy siła działająca na punkt jest stała lub zależy od czasu. W innych przypadkach konieczne jest wyrażenie siły w funkcji czasu.

Równość wymiarów impulsu (29) i pędu (30) pozwala ustalić między nimi związek ilościowy.

Rozważmy ruch punktu materialnego M pod działaniem dowolna siła F po dowolnej trajektorii.

O U:
. (32)

Rozdzielamy zmienne w (32) i całkujemy

. (33)

W rezultacie, biorąc pod uwagę (31), otrzymujemy

. (34)

Równanie (34) wyraża następujące twierdzenie.

Twierdzenie: Zmiana pędu punktu materialnego w pewnym okresie czasu jest równa impulsowi siły działającej na ten punkt w tym samym przedziale czasu.

Podczas rozwiązywania problemów równanie (34) należy rzutować na osie współrzędnych

Twierdzenie to jest wygodne w użyciu, gdy wśród danych i nieznanych wielkości znajduje się masa punktu, jego prędkość początkowa i końcowa, siły i czas ruchu.

Twierdzenie o zmianie momentu pędu punktu materialnego

M
moment pędu punktu materialnego względem środka jest równy iloczynowi modułu pędu punktu i ramienia, tj. najkrótsza odległość (prostopadła) od środka do linii pokrywającej się z wektorem prędkości

, (36)

. (37)

Związek między momentem siły (przyczyną) a momentem pędu (skutkiem) ustala następujące twierdzenie.

Niech punkt M danej masy M porusza się pod wpływem siły F.

,
,

, (38)

. (39)

Obliczmy pochodną (39)

. (40)

Łącząc (40) i (38) ostatecznie otrzymujemy

. (41)

Równanie (41) wyraża następujące twierdzenie.

Twierdzenie: Pochodna po czasie wektora pędu punktu materialnego względem jakiegoś środka jest równa momentowi siły działającej na punkt względem tego samego środka.

Podczas rozwiązywania problemów równanie (41) należy rzutować na osie współrzędnych

W równaniach (42) momenty pędu i siły obliczane są względem osi współrzędnych.

Z (41) wynika prawo zachowania momentu pędu (prawo Keplera).

Jeżeli moment siły działający na punkt materialny względem jakiegoś środka wynosi zero, wówczas moment pędu punktu względem tego środka zachowuje swoją wielkość i kierunek.

Jeśli
, To
.

Twierdzenie i prawo zachowania są stosowane w zagadnieniach związanych z ruchem krzywoliniowym, szczególnie pod działaniem sił centralnych.