ruch obrotowy ciało stałe wokół stałej osi nazywamy taki ruch, w którym dowolne dwa punkty należące do ciała (lub niezmiennie z nim związane) pozostają nieruchome przez cały ruch(Rys. 2.2) .
Rysunek 2.2
przejazd przez punkty stałe ALE I W nazywa się linia prosta oś obrotu. Ponieważ odległość między punktami bryły sztywnej musi pozostać niezmieniona, oczywiste jest, że podczas ruchu obrotowego wszystkie punkty należące do osi będą nieruchome, a cała reszta będzie opisywała okręgi, których płaszczyzny są prostopadłe do osi obrotu, a centra leżą na tej osi. Aby określić położenie obracającego się ciała, rysujemy przez oś obrotu, wzdłuż której jest skierowana oś Az, pół samolot І - stały i półpłaszczyznowy ІІ osadzony w samym ciele i obracający się wraz z nim. Wtedy pozycja ciała w dowolnym momencie jest jednoznacznie określona przez kąt wzięty z odpowiednim znakiem φ między tymi samolotami, które nazwiemy kąt ciała. Rozważymy kąt φ pozytywne, jeśli opóźnione z ustalonej płaszczyzny w kierunku przeciwnym do ruchu wskazówek zegara (dla obserwatora patrzącego od dodatniego końca osi Az), ale ujemny, jeśli jest zgodny z ruchem wskazówek zegara. zmierzyć kąt φ będzie w radianach. Aby w dowolnym momencie poznać pozycję ciała, musisz znać zależność kąta φ od czasu T, tj.
|
|
To równanie wyraża prawo ruch obrotowy ciało sztywne wokół stałej osi.
Główną cechą kinematyczną ruchu obrotowego ciała sztywnego jest jego prędkość kątowa ω i przyspieszenie kątowe ε.
9.2.1. Prędkość kątowa i przyspieszenie kątowe ciała
Wielkość charakteryzująca szybkość zmian kąta obrotu φ w czasie nazywana jest prędkością kątową.
Jeśli przez jakiś czas  ciało robi zwrot
ciało robi zwrot  , to średnia liczbowo prędkość kątowa ciała dla tego okresu wyniesie
, to średnia liczbowo prędkość kątowa ciała dla tego okresu wyniesie  . W limicie w
. W limicie w  dostajemy
dostajemy
W ten sposób, wartość liczbowa prędkości kątowej ciała w danej chwili jest równa pierwszej pochodnej kąta obrotu względem czasu.
Zasada znaków: gdy obrót jest przeciwny do ruchu wskazówek zegara, ω> 0, a gdy zgodnie z ruchem wskazówek zegara, to ω< 0.
 lub ponieważ radian jest wielkością bezwymiarową,
lub ponieważ radian jest wielkością bezwymiarową,  .
.
W obliczeniach teoretycznych wygodniej jest używać wektora prędkości kątowej  , którego moduł jest równy
, którego moduł jest równy  i który jest skierowany wzdłuż osi obrotu korpusu w kierunku, z którego obrót jest widoczny w kierunku przeciwnym do ruchu wskazówek zegara. Wektor ten natychmiast określa moduł prędkości kątowej, oś obrotu i kierunek obrotu wokół tej osi.
i który jest skierowany wzdłuż osi obrotu korpusu w kierunku, z którego obrót jest widoczny w kierunku przeciwnym do ruchu wskazówek zegara. Wektor ten natychmiast określa moduł prędkości kątowej, oś obrotu i kierunek obrotu wokół tej osi.
Wielkość charakteryzująca tempo zmian prędkości kątowej w czasie nazywana jest przyspieszeniem kątowym ciała.
Jeśli przez jakiś czas  przyrost prędkości kątowej jest równy
przyrost prędkości kątowej jest równy  , to stosunek
, to stosunek  , tj. określa wartość średniego przyspieszenia wirującego ciała w czasie
, tj. określa wartość średniego przyspieszenia wirującego ciała w czasie  .
.
Kiedy starasz się  otrzymujemy wartość przyspieszenia kątowego w danej chwili T:
otrzymujemy wartość przyspieszenia kątowego w danej chwili T:
W ten sposób, wartość liczbowa przyspieszenia kątowego ciała w danej chwili jest równa pierwszej pochodnej prędkości kątowej lub drugiej pochodnej kąta obrotu ciała w czasie.
Jednostką miary jest zwykle  lub, co też jest
lub, co też jest  .
.
Jeśli moduł prędkości kątowej rośnie z czasem, nazywamy rotację ciała przyśpieszony, a jeśli się zmniejszy, - powolny. Kiedy ilości ω
I ε
mają te same znaki, wtedy obrót zostanie przyspieszony, gdy inny - spowolniony.  Przez analogię do prędkości kątowej przyspieszenie kątowe można również przedstawić jako wektor
Przez analogię do prędkości kątowej przyspieszenie kątowe można również przedstawić jako wektor  skierowane wzdłuż osi obrotu. W której
skierowane wzdłuż osi obrotu. W której
 .
.
Jeśli ciało obraca się w przyspieszonym kierunku  zbiega się z
zbiega się z  i przeciwnie
i przeciwnie  podczas powolnego obracania.
podczas powolnego obracania.
Jeżeli prędkość kątowa ciała pozostaje stała podczas ruchu ( ω= stały), wtedy nazywa się obrót ciała mundur.
Od  mamy
mamy  . Zakładając więc, że w początkowym momencie czasu
. Zakładając więc, że w początkowym momencie czasu  zastrzyk
zastrzyk  i biorąc całki na lewo od
i biorąc całki na lewo od  zanim
zanim  , a po prawej od 0 do T, w końcu dostajemy
, a po prawej od 0 do T, w końcu dostajemy
|
|
Z równomierną rotacją, kiedy  =0,
=0, I
I  .
.
Szybkość równomiernego obrotu jest często określana przez liczbę obrotów na minutę, oznaczając tę wartość jako n obr/min Znajdźmy związek między n obr./min i ω 1/s. Z jednym obrotem ciało obróci się o 2π, a przy n obroty na 2π n; ta tura jest wykonywana w 1 min, tj. T= 1min=60s. Wynika, że
|
|
Jeśli przyspieszenie kątowe ciała pozostaje stałe w trakcie ruchu (ε = stały), wtedy rotacja jest nazywana równie zmienne.
W początkowym momencie czasu T=0 kąt  , a prędkość kątowa
, a prędkość kątowa  (
( - początkowa prędkość kątowa).
- początkowa prędkość kątowa).  ;
; =ε
=ε  . Integracja lewej strony
. Integracja lewej strony  zanim
zanim  , a właściwa od 0 do T, znajdować
, a właściwa od 0 do T, znajdować
Prędkość kątowa ω tego obrotu  . Jeśli ω i ε mają te same znaki, rotacja będzie równomiernie przyspieszony, a jeśli jest inny równie wolno.
. Jeśli ω i ε mają te same znaki, rotacja będzie równomiernie przyspieszony, a jeśli jest inny równie wolno.
Kąt skrętu, prędkość kątowa i przyspieszenie kątowe
Obrót ciała sztywnego wokół stałej osi nazywa się takim ruchem, w którym dwa punkty ciała pozostają nieruchome przez cały czas ruchu. W tym przypadku wszystkie punkty ciała znajdujące się na linii prostej przechodzącej przez jego punkty stałe również pozostają stałe. Ta linia nazywa się oś obrotu ciała.
Jeśli ALE I W- stałe punkty korpusu (rys. 15 ), wtedy oś obrotu jest osią Oz, który może mieć dowolny kierunek w przestrzeni, niekoniecznie pionowy. Kierunek jednej osi Oz traktowane jako pozytywne.
Narysuj stałą płaszczyznę przez oś obrotu Przez i mobilny P, przymocowany do obracającego się korpusu. Niech obie płaszczyzny zbiegają się w początkowym momencie czasu. Wtedy w tym czasie T położenie poruszającej się płaszczyzny i samego obracającego się korpusu można określić za pomocą kąta dwuściennego między płaszczyznami i odpowiedniego kąta liniowego φ pomiędzy liniami prostymi znajdującymi się w tych płaszczyznach i prostopadłymi do osi obrotu. Zastrzyk φ nazywa się kąt ciała.
Pozycja ciała względem wybranego układu odniesienia jest całkowicie określona w dowolnym
punkt w czasie, jeśli podane jest równanie φ =f(t) (5)
gdzie f(t)- dowolna, dwukrotnie różniczkowalna funkcja czasu. To równanie nazywa się równanie obrotu ciała sztywnego wokół stałej osi.
Ciało obracające się wokół stałej osi ma jeden stopień swobody, ponieważ jego położenie jest określane przez ustawienie tylko jednego parametru - kąta φ .
Zastrzyk φ jest uważany za dodatni, jeśli jest wykreślany w kierunku przeciwnym do ruchu wskazówek zegara, a ujemny, jeśli jest wykreślany w przeciwnym kierunku, patrząc od dodatniego kierunku osi Oz. Trajektorie punktów ciała podczas jego obrotu wokół stałej osi to okręgi znajdujące się w płaszczyznach prostopadłych do osi obrotu.
Aby scharakteryzować ruch obrotowy ciała sztywnego wokół stałej osi, wprowadzamy pojęcia prędkości kątowej i przyspieszenia kątowego. Algebraiczna prędkość kątowa ciała w dowolnym momencie wywoływana jest pierwsza pochodna czasowa kąta obrotu w tym momencie, tj. dφ/dt = . Jest to wartość dodatnia, gdy ciało obraca się w kierunku przeciwnym do ruchu wskazówek zegara, ponieważ kąt obrotu wzrasta z czasem, a ujemna - gdy ciało obraca się zgodnie z ruchem wskazówek zegara, ponieważ kąt obrotu maleje.
Oznaczono moduł prędkości kątowej ω. Następnie ω= ׀dφ/dt׀= ׀φ ׀ (6)
Wymiar prędkości kątowej ustala się zgodnie z (6)
[ω] = kąt/czas = rad/s = s -1.
W inżynierii prędkość kątowa to prędkość obrotowa wyrażona w obrotach na minutę. Za 1 minutę ciało obróci się pod kątem 2πp, Jeśli P- liczba obrotów na minutę. Dzieląc ten kąt przez liczbę sekund na minutę otrzymujemy: (7)
Algebraiczne przyspieszenie kątowe ciała wywołaj pierwszą pochodną prędkości algebraicznej, tj. druga pochodna kąta obrotu d 2 φ / dt 2 \u003d ω. Oznaczamy moduł przyspieszenia kątowego ε , następnie ε=|φ| (8)
Wymiar przyspieszenia kątowego otrzymujemy z (8):
[ε ] = prędkość kątowa/czas = rad/s 2 = s -2
Jeśli φ’’>0 w φ’>0 , to algebraiczna prędkość kątowa wzrasta z czasem i w konsekwencji ciało wiruje z przyspieszeniem w rozważanym momencie czasu w pozytywna strona(zgodnie z ruchem wskazówek zegara). Na φ’’<0 I φ’<0 ciało obraca się szybko w kierunku ujemnym. Jeśli φ’’<0 w φ’>0 , wtedy mamy powolny obrót w kierunku dodatnim. Na φ’’>0 I φ’<0 , tj. powolny obrót jest w kierunku ujemnym. Prędkość kątowa i przyspieszenie kątowe na rysunkach są reprezentowane przez strzałki łukowe wokół osi obrotu. Strzałka łukowa prędkości kątowej wskazuje kierunek obrotu ciał;
Dla przyspieszonego obrotu strzałki łukowe dla prędkości kątowej i przyspieszenia kątowego mają te same kierunki dla wolnego obrotu - ich kierunki są przeciwne.
Szczególne przypadki obrotu ciała sztywnego
Mówi się, że rotacja jest jednolita, jeśli ω=const, φ= φ't
Obrót będzie jednolity, jeśli ε=stała. φ'= φ' 0 + φ''t i
Ogólnie, jeśli φ’’ nie zawsze,
![]()
Prędkości i przyspieszenia punktów ciała
Znane jest równanie obrotu ciała sztywnego wokół stałej osi φ= f(t)(rys. 16). Dystans s zwrotnica m w poruszającym się samolocie P po łuku koła (trajektorii punktu), liczone od punktu M oh znajduje się w stałej płaszczyźnie, jest wyrażona przez kąt φ nałóg s=hφ, gdzie h jest promieniem okręgu, po którym porusza się punkt. Jest to najkrótsza odległość od punktu m do osi obrotu. Czasami nazywa się to promieniem obrotu punktu. W każdym punkcie ciała promień obrotu pozostaje niezmieniony, gdy ciało obraca się wokół stałej osi.
 Algebraiczna prędkość punktowa m określony przez formułę v τ =s'=hφ Moduł prędkości punktowej: v=hω(9)
Algebraiczna prędkość punktowa m określony przez formułę v τ =s'=hφ Moduł prędkości punktowej: v=hω(9)
Prędkości punktów ciała podczas obrotu wokół stałej osi są proporcjonalne do ich najkrótszych odległości do tej osi. Współczynnik proporcjonalności to prędkość kątowa. Prędkości punktów są skierowane wzdłuż stycznych do trajektorii, a zatem są prostopadłe do promieni obrotu. Prędkości punktów ciała znajdujących się na odcinku linii prostej OM, zgodnie z (9) rozkładają się zgodnie z prawem liniowym. Są one do siebie równoległe, a ich końce leżą na jednej prostej przechodzącej przez oś obrotu. Rozkładamy przyspieszenie punktu na składowe styczne i normalne, tj. a=a τ + a nτ Przyspieszenia styczne i normalne obliczane są ze wzorów (10)
ponieważ dla okręgu promień krzywizny p=h(Rys. 17 ). W ten sposób,
 Przyspieszenia styczne, normalne i pełne punktów oraz prędkości również rozkładają się zgodnie z zasadą liniową. Zależą one liniowo od odległości punktów od osi obrotu. Przyspieszenie normalne jest skierowane wzdłuż promienia koła do osi obrotu. Kierunek przyspieszenia stycznego zależy od znaku algebraicznego przyspieszenia kątowego. Na φ’>0
I φ’’>0
lub φ’<0
I φ’<0
mamy przyspieszony obrót ciała i kierunek wektorów τ I v mecz. Jeśli φ’
I φ’"
mają różne znaki (wolna rotacja), to τ I v skierowane przeciwnie do siebie.
Przyspieszenia styczne, normalne i pełne punktów oraz prędkości również rozkładają się zgodnie z zasadą liniową. Zależą one liniowo od odległości punktów od osi obrotu. Przyspieszenie normalne jest skierowane wzdłuż promienia koła do osi obrotu. Kierunek przyspieszenia stycznego zależy od znaku algebraicznego przyspieszenia kątowego. Na φ’>0
I φ’’>0
lub φ’<0
I φ’<0
mamy przyspieszony obrót ciała i kierunek wektorów τ I v mecz. Jeśli φ’
I φ’"
mają różne znaki (wolna rotacja), to τ I v skierowane przeciwnie do siebie.
Oznaczanie α mamy kąt między pełnym przyspieszeniem punktu a jego promieniem obrotu
tanα = | a τ |/a n = ε/ω 2 (11)
od normalnego przyspieszenia a p zawsze pozytywny. Zastrzyk ale to samo dla wszystkich punktów ciała. Powinno być przesunięte od przyspieszenia do promienia obrotu w kierunku strzałki łuku przyspieszenia kątowego, niezależnie od kierunku obrotu bryły sztywnej.
Wektory prędkości kątowej i przyspieszenia kątowego
![]()
Wprowadźmy pojęcia wektorów prędkości kątowej i przyspieszenia kątowego ciała. Jeśli DO to wersor osi obrotu skierowanej w jej kierunku dodatnim, to wektory prędkości kątowej ώ i przyspieszenie kątowe ε określony przez wyrażenia (12)
Dlatego k-stała wektorowa w wartości bezwzględnej i kierunku, to z (12) wynika, że
ε=dώ/dt(13)

Na φ’>0 I φ’’>0 kierunki wektorowe ώ I ε mecz. Oba są skierowane w dodatnim kierunku osi obrotu. Oz(Rys. 18.a) Jeśli φ’>0 I φ’’<0 , następnie są skierowane w przeciwnych kierunkach (ryc. 18.b ). Wektor przyspieszenia kątowego pokrywa się w kierunku z wektorem prędkości kątowej podczas przyspieszonego obrotu i jest przeciwny do niego podczas wolnego obrotu. Wektory ώ I ε można narysować w dowolnym punkcie na osi obrotu. Są to przesuwające się wektory. Własność ta wynika z wzorów wektorowych na prędkości i przyspieszenia punktów ciała.
Złożony ruch punktowy
Podstawowe koncepcje
Aby zbadać niektóre, bardziej złożone typy ruchów ciała sztywnego, wskazane jest rozważenie najprostszego złożonego ruchu punktu. W wielu problemach ruch punktu należy rozpatrywać w odniesieniu do dwóch (lub więcej) układów odniesienia poruszających się względem siebie. Zatem ruch statku kosmicznego poruszającego się w kierunku Księżyca należy rozpatrywać zarówno względem Ziemi, jak i względem Księżyca, który porusza się względem Ziemi. Każdy ruch punktu można uznać za złożony, składający się z kilku ruchów. Na przykład ruch statku wzdłuż rzeki względem Ziemi można uznać za złożony, składający się z ruchu na wodzie i wraz z płynącą wodą.
W najprostszym przypadku złożony ruch punktu składa się z ruchów względnych i translacyjnych. Zdefiniujmy te ruchy. Niech mamy dwa układy odniesienia poruszające się względem siebie. Jeśli jeden z tych systemów O l x 1 r 1 z 1(Rys. 19 ) należy przyjąć jako główną lub stałą (jej ruch względem innych układów odniesienia nie jest brany pod uwagę), to drugi układ odniesienia Oxyz przesunie się względem pierwszego. Ruch punktu względem ruchomego układu odniesienia Oxyz nazywa się względny. Charakterystyki tego ruchu, takie jak trajektoria, prędkość i przyspieszenie, są nazywane względny. Oznaczono je indeksem r; dla prędkości i przyspieszenia v r , r r . Ruch punktu względem głównego lub stałego układu odniesienia O 1 x 1 r 1 z 1 nazywa się absolutny(lub trudne ). Jest też czasami nazywany złożony ruch. Trajektoria, prędkość i przyspieszenie tego ruchu nazywane są absolutnymi. Prędkość i przyspieszenie ruchu bezwzględnego oznaczono literami v, a bez indeksów.
 |
Ruch przenośny punktu to ruch, który wykonuje wraz z ruchomym układem odniesienia, jako punkt sztywno przymocowany do tego układu w rozważanym momencie. Ze względu na ruch względny, poruszający się punkt w różnym czasie zbiega się z różnymi punktami ciała S, do którego przymocowany jest ruchomy układ odniesienia. Przenośna prędkość i przenośne przyspieszenie to prędkość i przyspieszenie tego punktu ciała S, z którym w tej chwili zbiega się ruchomy punkt. Przenośna prędkość i przyspieszenie oznaczają v e i e.
Jeśli trajektorie wszystkich punktów ciała S, mocowane za pomocą ruchomego układu odniesienia, przedstawionego na rysunku (ryc. 20), wówczas otrzymujemy rodzinę linii - rodzinę trajektorii ruchu ruchomego punktu M. Ze względu na ruch względny punktu m w każdej chwili znajduje się na jednej z trajektorii ruchu przenośnego. Kropka m może pokrywać się tylko z jednym punktem każdej z trajektorii tej rodziny trajektorii przenośnych. W związku z tym czasami uważa się, że nie ma trajektorii ruchu postępowego, ponieważ linie, w których tylko jeden punkt jest faktycznie punktem trajektorii, należy traktować jako trajektorie ruchu ruchomego.
W kinematyce punktu badano ruch punktu względem dowolnego układu odniesienia, niezależnie od tego, czy ten układ odniesienia porusza się względem innych układów, czy nie. Uzupełnijmy to studium o uwzględnienie ruchu złożonego, w najprostszym przypadku składającego się z ruchu względnego i figuratywnego. Jeden i ten sam ruch bezwzględny, wybierający różne ruchome układy odniesienia, można uznać za składający się z różnych ruchów przenośnych i odpowiednio względnych.
Dodawanie prędkości
 Wyznaczmy prędkość ruchu bezwzględnego punktu, jeśli znane są prędkości ruchu względnego i figuratywnego tego punktu. Niech punkt wykona tylko jeden ruch względny względem ruchomego układu odniesienia Oxyz iw chwili t zajmie pozycję M na trajektorii ruchu względnego (rys. 20). W chwili czasu t+ t z powodu ruchu względnego punkt znajdzie się w położeniu M1, po przemieszczeniu MM1 wzdłuż trajektorii ruchu względnego. Załóżmy, że chodzi o punkt Oxyz i względną trajektorię przesunie się po pewnym łuku do MM 2. Jeżeli punkt uczestniczy jednocześnie w ruchach względnych i figuratywnych, to w czasie A; ona przeprowadzi się do MM" wzdłuż trajektorii ruchu absolutnego i w chwili czasu t+w zajmuje stanowisko M". Jeśli czas Na mały, a następnie przejść do limitu o Na, dążąc do zera, wówczas niewielkie przemieszczenia wzdłuż krzywych można zastąpić odcinkami cięciw i przyjąć jako wektory przemieszczeń. Dodając przemieszczenia wektorów, otrzymujemy
Wyznaczmy prędkość ruchu bezwzględnego punktu, jeśli znane są prędkości ruchu względnego i figuratywnego tego punktu. Niech punkt wykona tylko jeden ruch względny względem ruchomego układu odniesienia Oxyz iw chwili t zajmie pozycję M na trajektorii ruchu względnego (rys. 20). W chwili czasu t+ t z powodu ruchu względnego punkt znajdzie się w położeniu M1, po przemieszczeniu MM1 wzdłuż trajektorii ruchu względnego. Załóżmy, że chodzi o punkt Oxyz i względną trajektorię przesunie się po pewnym łuku do MM 2. Jeżeli punkt uczestniczy jednocześnie w ruchach względnych i figuratywnych, to w czasie A; ona przeprowadzi się do MM" wzdłuż trajektorii ruchu absolutnego i w chwili czasu t+w zajmuje stanowisko M". Jeśli czas Na mały, a następnie przejść do limitu o Na, dążąc do zera, wówczas niewielkie przemieszczenia wzdłuż krzywych można zastąpić odcinkami cięciw i przyjąć jako wektory przemieszczeń. Dodając przemieszczenia wektorów, otrzymujemy
![]() W związku z tym małe ilości wyższego rzędu są odrzucane, dążąc do zera przy Na, dążenie do zera. Dochodząc do granicy, mamy (14)
W związku z tym małe ilości wyższego rzędu są odrzucane, dążąc do zera przy Na, dążenie do zera. Dochodząc do granicy, mamy (14)
Dlatego (14) przyjmuje postać (15)
Otrzymano tak zwane twierdzenie o dodawaniu prędkości: prędkość bezwzględnego ruchu punktu jest równa sumie wektorowej prędkości ruchomego i względnego ruchu tego punktu. Ponieważ w ogólnym przypadku prędkości ruchu postępowego i względnego nie są prostopadłe, to (15')
Podobne informacje.
Ruch obrotowy ciała sztywnego. Obrotowy to ruch ciała sztywnego, w którym wszystkie jego punkty leżące na pewnej linii prostej, zwanej osią obrotu, pozostają nieruchome.
Podczas ruchu obrotowego wszystkie inne punkty ciała poruszają się w płaszczyznach prostopadłych do osi obrotu i zakreślają okręgi, których środki leżą na tej osi.
Aby określić położenie wirującego ciała, rysujemy przez oś z dwie półpłaszczyzny: półpłaszczyzna I - nieruchoma i półpłaszczyzna II - połączona z ciałem pełnym i obracająca się z nim (rys. 2.4). Wtedy pozycja ciała w dowolnym momencie będzie jednoznacznie określona przez kąt J między tymi półpłaszczyznami, wziętymi z odpowiednim znakiem, zwanym kątem obrotu ciała.
Gdy ciało się obraca, kąt obrotu j zmienia się w zależności od czasu, czyli jest funkcją czasu t:
To równanie nazywa się równanie ruch obrotowy ciała sztywnego.
Głównymi cechami kinematycznymi ruchu obrotowego ciała sztywnego są jego prędkość kątowa w oraz przyspieszenie kątowe e.
Jeśli w czasie D T= t1 + T ciało wykonuje skręt o Dj = j1 –j, to średnia prędkość kątowa ciała dla tego okresu będzie równa
 (1.16)
(1.16)
Aby określić wartość prędkości kątowej ciała w określonym czasie T znaleźć granicę stosunku przyrostu kąta obrotu Dj do przedziału czasu D T ponieważ ta ostatnia dąży do zera:
 (2.17)
(2.17)
Zatem prędkość kątowa ciała w danym momencie czasu jest liczbowo równa pierwszej pochodnej kąta obrotu względem czasu. Znak prędkości kątowej w pokrywa się ze znakiem kąta obrotu ciała j: w > 0 dla j > 0 i odwrotnie, jeśli j < 0. wtedy w < 0. Jednostką prędkości kątowej jest zwykle 1/s, więc radian jest wielkością bezwymiarową.
Prędkość kątową można przedstawić jako wektor w , którego wartość liczbowa jest równa dj/dt, która jest skierowana wzdłuż osi obrotu ciała w kierunku, z którego obserwuje się obrót w kierunku przeciwnym do ruchu wskazówek zegara.
Zmiana prędkości kątowej ciała w czasie charakteryzuje przyspieszenie kątowe e. Analogicznie do wyznaczania wartości średniej prędkości kątowej znajdujemy wyrażenie na wyznaczenie wartości średniego przyspieszenia:
 (2.18)
(2.18)
Następnie z wyrażenia . wyznaczane jest przyspieszenie ciała sztywnego w danym czasie
 (2.19)
(2.19)
tzn. przyspieszenie kątowe ciała w danej chwili jest równe pierwszej pochodnej prędkości kątowej lub drugiej pochodnej kąta obrotu ciała względem czasu. Wymiar przyspieszenia kątowego wynosi 1/s 2 .
Przyspieszenie kątowe ciała sztywnego, podobnie jak prędkość kątowa, można przedstawić jako wektor. Wektor przyspieszenia kątowego pokrywa się w kierunku z wektorem prędkości kątowej podczas przyspieszonego ruchu litego blatu i jest skierowany w przeciwnym kierunku podczas ruchu spowolnionego.
Ustaliwszy charakterystyki ruchu ciała sztywnego jako całości, przejdźmy do badania ruchu jego poszczególnych punktów. Zastanów się nad pewnym punktem m sztywny korpus znajdujący się w odległości h od osi obrotu r (rys. 2.3).
Gdy ciało się obraca, punkt M opisuje punkt na obwodzie o promieniu h wyśrodkowany na osi obrotu i leżący w płaszczyźnie prostopadłej do tej osi. Jeżeli w czasie dt następuje elementarny obrót ciała pod kątem dj , następnie wskaż m jednocześnie wykonuje elementarne przemieszczenie wzdłuż swojej trajektorii dS = h * dj ,. Następnie prędkość punktu M została wyznaczona z wyrażenia
![]() (2.20)
(2.20)
Prędkość nazywana jest prędkością liniową lub obwodową punktu M.
Zatem prędkość liniowa punktu wirującego ciała sztywnego jest liczbowo równa iloczynowi prędkości kątowej ciała i odległości od tego punktu do osi obrotu. Ponieważ dla wszystkich punktów ciała prędkość kątowa w; ma taką samą wartość, to ze wzoru na prędkość liniową wynika, że prędkości liniowe punktów wirującego ciała są proporcjonalne do ich odległości od osi obrotu. Prędkość liniowa punktu ciała sztywnego jest wektorem n skierowanym stycznie do okręgu opisanego przez punkt M.
Biały to odległość od osi obrotu popiołu stałego do określonego punktu m rozpatrywać jako wektor promienia h punktu M, to wektor prędkości liniowej punktu v można przedstawić jako iloczyn wektorowy wektora prędkości kątowej w wektor promienia h:
V = w * w (2/21)
Rzeczywiście, wynikiem iloczynu wektorowego (2.21) jest wektor równy w wartości bezwzględnej iloczynowi w * h i skierowany (rys. 2.5) prostopadle do płaszczyzny, w której leżą oba czynniki, w kierunku, z którego najbliższa kombinacja pierwszego czynnika, przy czym drugi występuje przeciwnie do ruchu wskazówek zegara, czyli stycznie do trajektorii punktu M.
Zatem wektor wynikający z iloczynu poprzecznego (2.21) odpowiada w wartości bezwzględnej i kierunku wektorowi prędkości liniowej punktu M.

Ryż. 2,5
Aby znaleźć wyrażenie na przyspieszenie ale punkt M wykonujemy zróżnicowanie czasowe wyrażenia (2.21) dla prędkości punktu
 (2.22)
(2.22)
Biorąc pod uwagę, że dj/dt=e oraz dh/dt = v, zapisujemy wyrażenie (2.22) jako
gdzie a r i an, odpowiednio, są składowymi stycznymi i normalnymi całkowitego przyspieszenia punktu ciała podczas ruchu obrotowego, wyznaczonymi z wyrażeń
Składowa styczna pełnego przyspieszenia punktu ciała (przyspieszenie styczne) w charakteryzuje zmianę wektora prędkości modulo i jest skierowana stycznie do trajektorii punktu ciała w kierunku wektora prędkości podczas ruchu przyspieszonego lub w kierunku przeciwnym w zwolnionym tempie. Moduł wektora przyspieszenia stycznego punktu ciała podczas ruchu obrotowego ciała sztywnego określa wyrażenie
![]() (2,25)
(2,25)
Normalna składowa pełnego przyspieszenia (normalne przyspieszenie) ale" powstaje w wyniku zmiany kierunku wektora prędkości punktu podczas barwienia ciała stałego. Jak wynika z wyrażenia (2.24) dla normalnego przyspieszenia, przyspieszenie to jest skierowane wzdłuż promienia h do środka okręgu, po którym porusza się punkt. Moduł wektora przyspieszenia normalnego punktu podczas ruchu obrotowego ciała sztywnego określa się z uwzględnieniem (2.20) za pomocą wyrażenia
W przyrodzie i technice często spotykamy się z przejawem ruchu obrotowego ciał stałych, takich jak wały i koła zębate. Jak ten rodzaj ruchu jest opisany w fizyce, jakie wzory i równania są do tego wykorzystywane, te i inne kwestie są omówione w tym artykule.
Czym jest rotacja?
Każdy z nas intuicyjnie wyobraża sobie, o jakim ruchu mówimy. Rotacja to proces, w którym ciało lub punkt materialny porusza się po torze kołowym wokół pewnej osi. Z geometrycznego punktu widzenia ciało sztywne to linia prosta, której odległość pozostaje niezmienna podczas ruchu. Odległość ta nazywana jest promieniem obrotu. W dalszej części oznaczymy go literą r. Jeśli oś obrotu przechodzi przez środek masy ciała, nazywa się ją własną osią. Przykładem obrotu wokół własnej osi jest odpowiedni ruch planet Układu Słonecznego.
Aby nastąpił obrót, musi wystąpić przyspieszenie dośrodkowe, które powstaje dzięki sile dośrodkowej. Siła ta kierowana jest od środka masy ciała do osi obrotu. Charakter siły dośrodkowej może być bardzo różny. Tak więc w skali kosmicznej grawitacja odgrywa swoją rolę, jeśli ciało jest przymocowane nitką, wówczas siła napięcia tego ostatniego będzie dośrodkowa. Kiedy ciało obraca się wokół własnej osi, rolę siły dośrodkowej odgrywa wewnętrzne oddziaływanie elektrochemiczne między pierwiastkami (cząsteczkami, atomami) tworzącymi ciało.
Należy rozumieć, że bez obecności siły dośrodkowej ciało porusza się po linii prostej.
Wielkości fizyczne opisujące obrót

Po pierwsze są to cechy dynamiczne. Obejmują one:
- moment pędu L;
- moment bezwładności I;
- moment siły M.
Po drugie, są to charakterystyki kinematyczne. Wymieńmy je:
- kąt obrotu θ;
- prędkość kątowa ω;
- przyspieszenie kątowe α.
Opiszmy krótko każdą z tych wielkości.
Moment pędu określa wzór:
Gdzie p jest liniowym momentem pędu, m masą punktu materialnego, v jest jego prędkością liniową.
Moment bezwładności punktu materialnego oblicza się za pomocą wyrażenia:
Dla dowolnego ciała o złożonym kształcie wartość I oblicza się jako całkowitą sumę momentów bezwładności punktów materialnych.
Moment siły M oblicza się w następujący sposób:
Tutaj F jest siłą zewnętrzną, d jest odległością od punktu jej przyłożenia do osi obrotu.
Fizyczne znaczenie wszystkich wielkości, w imię których występuje słowo „moment”, jest podobne do znaczenia odpowiadających im wielkości liniowych. Na przykład moment siły pokazuje możliwość przyłożonej siły do informowania układu wirujących ciał.
Charakterystyki kinematyczne są matematycznie zdefiniowane za pomocą następujących wzorów:
Jak widać z tych wyrażeń, charakterystyki kątowe mają podobne znaczenie do liniowych (prędkości v i przyspieszenie a), tylko mają zastosowanie do trajektorii kołowej.
Dynamika rotacji
W fizyce badanie ruchu obrotowego ciała sztywnego odbywa się za pomocą dwóch gałęzi mechaniki: dynamiki i kinematyki. Zacznijmy od dynamiki.
Dynamika bada siły zewnętrzne działające na układ ciał wirujących. Natychmiast zapiszemy równanie ruchu obrotowego ciała sztywnego, a następnie przeanalizujemy jego części składowe. Więc to równanie wygląda tak:
Działający na układ, który ma moment bezwładności I, powoduje pojawienie się przyspieszenia kątowego α. Im mniejsza wartość I, tym łatwiej za pomocą określonego momentu M rozkręcić układ do dużych prędkości w krótkich odstępach czasu. Na przykład metalowy pręt łatwiej obraca się wzdłuż własnej osi niż prostopadle do niego. Jednak ten sam pręt łatwiej obraca się wokół osi prostopadłej do niego i przechodzącej przez środek masy niż przez jego koniec.
Prawo zachowania L
Wielkość ta została wprowadzona powyżej i nazywana jest momentem pędu. Przedstawione w poprzednim akapicie równanie ruchu obrotowego bryły sztywnej jest często zapisywane w innej postaci:
Jeżeli moment sił zewnętrznych M działa na układ w czasie dt, to powoduje zmianę momentu pędu układu o dL. Odpowiednio, jeśli moment sił jest równy zero, to L = const. Jest to prawo zachowania wartości L. W tym celu wykorzystując zależność między prędkością liniową i kątową możemy napisać:
L \u003d m * v * r \u003d m * ω * r 2 \u003d I * ω.
Zatem przy braku momentu sił iloczyn prędkości kątowej i momentu bezwładności jest wartością stałą. To prawo fizyczne jest używane przez łyżwiarzy figurowych w ich występach lub przez sztuczne satelity, które muszą być obracane wokół własnej osi w przestrzeni kosmicznej.

przyspieszenie dośrodkowe
Powyżej, badając ruch obrotowy ciała sztywnego, wielkość ta została już opisana. Zwrócono również uwagę na charakter sił dośrodkowych. Tutaj tylko uzupełnimy te informacje i podamy odpowiednie wzory do obliczenia tego przyspieszenia. Oznaczmy to a c .
Ponieważ siła dośrodkowa jest skierowana prostopadle do osi i przechodzi przez nią, nie tworzy momentu. Oznacza to, że siła ta nie ma absolutnie żadnego wpływu na kinematyczną charakterystykę obrotu. Tworzy jednak przyspieszenie dośrodkowe. Oto dwie formuły jego definicji:
Zatem im większa prędkość kątowa i promień, tym większa siła musi być przyłożona, aby utrzymać ciało na torze kołowym. Uderzającym przykładem tego fizycznego procesu jest poślizg samochodu podczas skrętu. Poślizg występuje, gdy siła dośrodkowa, której rolę odgrywa siła tarcia, staje się mniejsza niż siła odśrodkowa (charakterystyka bezwładności).

Trzy główne cechy kinematyczne zostały wymienione powyżej w artykule. ciało stałe jest opisane następującymi wzorami:
θ = ω*t => ω = const., α = 0;
θ = ω 0 *t + α*t 2 /2 => ω = ω 0 + α*t, α = const.
W pierwszym wierszu znajdują się wzory na obrót jednostajny, który zakłada brak zewnętrznego momentu sił działających na układ. Drugi wiersz zawiera wzory na ruch jednostajnie przyspieszony po okręgu.

Zauważ, że obrót może wystąpić nie tylko przy przyspieszeniu dodatnim, ale także przy ujemnym. W takim przypadku we wzorach drugiego rzędu należy umieścić znak minus przed drugim terminem.
Przykład rozwiązania problemu
Moment siły 1000 N*m działał na metalowy wałek przez 10 sekund. Wiedząc, że moment bezwładności wału wynosi 50 kg*m2, należy wyznaczyć prędkość kątową, jaką ten moment siły nadał wałowi.

Stosując podstawowe równanie obrotu obliczamy przyspieszenie wału:
Ponieważ to przyspieszenie kątowe działało na wał w czasie t = 10 sekund, do obliczenia prędkości kątowej wykorzystujemy wzór na ruch jednostajnie przyspieszony:
ω = ω 0 + α*t = M/I*t.
Tutaj ω 0 = 0 (wał nie obracał się do momentu wystąpienia sił M).
Podstawiamy wartości liczbowe wielkości do równości, otrzymujemy:
ω \u003d 1000/50 * 10 \u003d 200 rad / s.
Aby przetłumaczyć tę liczbę na zwykłe obroty na sekundę, musisz podzielić ją przez 2 * pi. Po wykonaniu tej czynności otrzymujemy, że wał będzie się obracał z częstotliwością 31,8 obr/min.
DEFINICJA: Ruch obrotowy ciała sztywnego nazwiemy taki ruch, w którym wszystkie punkty ciała poruszają się po okręgach, których środki leżą na tej samej linii prostej, zwanej osią obrotu.
Aby zbadać dynamikę rotacji, do znanych wielkości kinematycznych dodajemy więcej dwie ilości: moment mocy(M) i moment bezwładności(J).
1. Z doświadczenia wiadomo: przyspieszenie ruchu obrotowego zależy nie tylko od wielkości siły działającej na ciało, ale także od odległości od osi obrotu do linii, wzdłuż której działa siła. Aby scharakteryzować tę okoliczność, wielkość fizyczna zwana moment siły.
Rozważmy najprostszy przypadek.
DEFINICJA: Moment siły względem pewnego punktu „O” jest wielkością wektorową zdefiniowaną przez wyrażenie , gdzie jest wektorem promienia narysowanym od punktu „O” do punktu przyłożenia siły.
Z definicji wynika, że jest to wektor osiowy. Jego kierunek dobiera się tak, aby obrót wektora wokół punktu „O” w kierunku siły i wektora tworzył układ prawoskrętny. Moduł momentu siły wynosi , gdzie a jest kątem między kierunkami wektorów i , oraz ja= r grzech a to długość prostopadłej opuszczonej od punktu „O” do prostej, wzdłuż której działa siła (zwana ramię siły względem punktu „O”) (rys. 4.2).
2. Dane doświadczalne pokazują, że na wielkość przyspieszenia kątowego wpływa nie tylko masa wirującego ciała, ale także rozkład masy względem osi obrotu. Wielkość, która uwzględnia tę okoliczność, nazywa się moment bezwładności wokół osi obrotu.
DEFINICJA: Ściśle mówiąc, moment bezwładności ciało względem pewnej osi obrotu nazywamy wartością J, równą sumie iloczynów mas elementarnych przez kwadraty ich odległości od danej osi.
Sumowanie dokonuje się po wszystkich elementarnych masach, na które zostało podzielone ciało. Należy pamiętać, że wielkość ta (J) istnieje niezależnie od obrotu (chociaż pojęcie momentu bezwładności wprowadzono przy rozpatrywaniu obrotu ciała sztywnego).
Każde ciało, niezależnie od tego, czy jest w spoczynku, czy obraca się, ma pewien moment bezwładności wokół dowolnej osi, tak jak ciało ma masę, niezależnie od tego, czy jest w ruchu, czy w spoczynku.
Biorąc pod uwagę, że moment bezwładności można przedstawić jako: . Ten stosunek jest przybliżony i będzie tym dokładniejszy, im mniejsze są objętości elementarne i odpowiadające im elementy masy. Dlatego problem znajdowania momentów bezwładności sprowadza się do całkowania: . Tutaj integracja odbywa się na całej objętości ciała.
Zapiszmy momenty bezwładności niektórych ciał o regularnym kształcie geometrycznym.
| 1. Jednorodna długa wędka. | |
| Ryż. 4.3 | Moment bezwładności wokół osi prostopadłej do pręta i przechodzący przez jej środek wynosi |
| 2. Solidny cylinder lub dysk. | |
| Ryż. 4.4 | Moment bezwładności wokół osi pokrywającej się z osią geometryczną wynosi . |
| 3. Cienkościenny cylinder o promieniu R. | |
| Ryż. 4,5 | |
| 4. Moment bezwładności kuli o promieniu R wokół osi przechodzącej przez jej środek | |
| Ryż. 4,6 | |
| 5. Moment bezwładności cienkiego dysku (grubość b< | |
| Ryż. 4,7 | |
| 6. Moment bezwładności pręta | |
| Ryż. 4,8 | |
| 7. Moment bezwładności pierścienia | |
| Ryż. 4,9 |
Obliczenia momentu bezwładności są tutaj dość proste, ponieważ przyjmuje się, że ciało jest jednorodne i symetryczne, a moment bezwładności wyznaczany jest względem osi symetrii.
Aby wyznaczyć moment bezwładności ciała względem dowolnej osi, musisz skorzystać z twierdzenia Steinera.
DEFINICJA: Moment bezwładności J względem dowolnej osi równa się sumie momentu bezwładności Jc wokół osi równoległej do danej i przechodzącego przez środek bezwładności ciała oraz iloczynu masy ciała pomnożonego przez kwadrat odległości między osiami (rys. 4.10).
- W kontakcie z 0
- Google+ 0
- ok 0
- Facebook 0

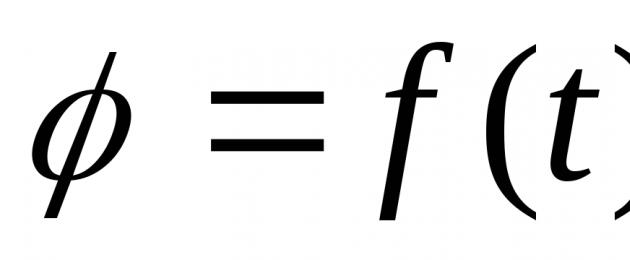
 .
. .
. .
.





