Stopień i jego właściwości. Określenie stopnia

Formuły stopni wykorzystywane w procesie redukcji i upraszczania złożone wyrażenia, w rozwiązywaniu równań i nierówności.

Numer C Jest N-ta potęga liczby A Gdy:

Operacje na stopniach.

1. Mnożąc stopnie o tej samej podstawie, dodaje się ich wskaźniki:

jestem·a n = za m + n .

2. Dzieląc stopnie o tej samej podstawie, ich wykładniki odejmuje się:

3. Moc iloczynu 2 lub więcej czynniki są równe iloczynowi potęg tych czynników:

(abc…) n = za n · b n · do n …

4. Stopień ułamka jest równy stosunkowi stopni dywidendy i dzielnika:

(a/b) n = za n /b n .

5. Podnosząc potęgę do potęgi, wykładniki mnoży się:

(a m) n = za m n .

Każdy powyższy wzór jest prawdziwy w kierunkach od lewej do prawej i odwrotnie.

Na przykład. (2 3 5/15)² = 2² 3² 5²/15² = 900/225 = 4.

Operacje z korzeniami.

1. Pierwiastek iloczynu kilku czynników jest równy iloczynowi pierwiastków tych czynników:

2. Pierwiastek stosunku jest równy stosunkowi dywidendy i dzielnika pierwiastków:

3. Podnosząc pierwiastek do potęgi, wystarczy podnieść liczbę pierwiastkową do tej potęgi:

4. Jeśli zwiększysz stopień zakorzenienia N raz i jednocześnie wbudować N potęga jest liczbą radykalną, wówczas wartość pierwiastka nie ulegnie zmianie:

5. Jeśli zmniejszysz stopień zakorzenienia N jednocześnie wyodrębnij korzeń N-ta potęga liczby pierwiastkowej, wówczas wartość pierwiastka nie ulegnie zmianie:

Stopień z wykładnikiem ujemnym. Potęgę pewnej liczby o wykładniku niedodatnim (całkowitym) definiuje się jako podzieloną przez potęgę tej samej liczby o wykładniku równym wartości bezwzględnej wykładnika niedodatniego:

Formuła jestem:a n = a m - n można używać nie tylko do M> N, ale także z M< N.

Na przykład. A4:a 7 = a 4 - 7 = a -3.

Do formuły jestem:a n = a m - n stało się sprawiedliwe, kiedy m=n, wymagana jest obecność stopnia zerowego.

Stopień z indeksem zerowym. Potęga dowolnej liczby różnej od zera z wykładnikiem zerowym jest równa jeden.

Na przykład. 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Stopień z wykładnikiem ułamkowym. Aby podnieść liczbę rzeczywistą A do stopnia m/n, musisz wyodrębnić root N stopień M-ta potęga tej liczby A.

Jeśli zignorujemy potęgę ósmą, co tutaj zobaczymy? Przypomnijmy program dla klasy 7. Pamiętasz? To jest wzór na skrócone mnożenie, czyli różnicę kwadratów! Otrzymujemy:

Ale jak to zrobić? Okazuje się, że jest to bardzo proste: pomaga nam tutaj parzysty stopień mianownika.

W magiczny sposób terminy zmieniły miejsca. To „zjawisko” dotyczy w równym stopniu każdego wyrażenia: łatwo możemy zmienić znaki w nawiasach.

Ale ważne jest, aby pamiętać: wszystkie znaki zmieniają się w tym samym czasie!

Wróćmy do przykładu:

I znowu formuła:

Cały nazywamy liczby naturalne, ich przeciwieństwa (to znaczy wzięte ze znakiem „ ”) i liczbę.

Dodatnia liczba całkowita i nie różni się niczym od naturalnego, wtedy wszystko wygląda dokładnie tak, jak w poprzedniej sekcji.

Przyjrzyjmy się teraz nowym przypadkom. Zacznijmy od wskaźnika równego.

Każda liczba do potęgi zerowej jest równa jeden:

Jak zawsze zadajmy sobie pytanie: dlaczego tak jest?

Rozważmy pewien stopień z podstawą. Weźmy na przykład i pomnóżmy przez:

Więc pomnożyliśmy liczbę przez i otrzymaliśmy to samo, co było - . Przez jaką liczbę należy pomnożyć, aby nic się nie zmieniło? Zgadza się, dalej. Oznacza.

To samo możemy zrobić z dowolną liczbą:

Powtórzmy regułę:

Każda liczba do potęgi zerowej jest równa jeden.

Ale są wyjątki od wielu zasad. I tutaj też jest - to jest liczba (jako podstawa).

Z jednej strony musi być równy dowolnemu stopniowi - bez względu na to, ile pomnożysz zero przez samo, nadal otrzymasz zero, to jasne. Ale z drugiej strony, jak każda liczba do potęgi zerowej, musi być równa. Ile w tym prawdy? Matematycy postanowili się nie angażować i odmówili podniesienia zera do potęgi zerowej. Oznacza to, że teraz nie możemy nie tylko podzielić przez zero, ale także podnieść go do potęgi zerowej.

Przejdźmy dalej. Z wyjątkiem liczby naturalne a liczby na liczby całkowite obejmują liczby ujemne. Aby zrozumieć, czym jest potęga ujemna, zróbmy to samo, co poprzednio: pomnóż jakąś liczbę normalną przez tę samą liczbę do potęgi ujemnej:

Stąd łatwo jest wyrazić to, czego szukasz:

Rozszerzmy teraz otrzymaną regułę w dowolnym stopniu:

Sformułujmy więc regułę:

Liczba o potędze ujemnej jest odwrotnością tej samej liczby o potędze dodatniej. Ale w tym samym czasie Podstawa nie może mieć wartości null:(ponieważ nie można dzielić przez).

Podsumujmy:

I. Wyrażenie nie jest w tym przypadku zdefiniowane. Jeśli następnie.

II. Dowolna liczba do potęgi zerowej jest równa jeden: .

III. Liczba różna od zera do potęgi ujemnej jest odwrotnością tej samej liczby do potęgi dodatniej: .

Zadania do samodzielnego rozwiązania:

Cóż, jak zwykle przykłady niezależnych rozwiązań:

Analiza problemów w celu samodzielnego rozwiązania:

Wiem, wiem, liczby przerażają, ale na Unified State Exam trzeba być przygotowanym na wszystko! Rozwiąż te przykłady lub przeanalizuj ich rozwiązania, jeśli nie mogłeś ich rozwiązać, a na egzaminie nauczysz się łatwo sobie z nimi radzić!

Kontynuujmy poszerzanie zakresu liczb „odpowiednich” jako wykładnik.

Teraz rozważmy liczby wymierne. Jakie liczby nazywamy wymiernymi?

Odpowiedź: wszystko, co można przedstawić jako ułamek, gdzie i są liczbami całkowitymi, i.

Aby zrozumieć, co to jest „stopień ułamkowy”, rozważ ułamek:

Podnieśmy obie strony równania do potęgi:

Przypomnijmy sobie teraz zasadę dot „stopień do stopnia”:

Jaką liczbę należy podnieść do potęgi, aby otrzymać?

To sformułowanie jest definicją pierwiastka stopnia VII.

Przypomnę: pierwiastek z potęgi liczby () to liczba, która podniesiona do potęgi jest równa.

Oznacza to, że pierwiastkiem potęgi th jest odwrotna operacja podniesienia do potęgi: .

Okazało się, że. Oczywiście to szczególny przypadek można rozszerzyć: .

Teraz dodajemy licznik: co to jest? Odpowiedź jest łatwa do uzyskania, korzystając z reguły mocy do potęgi:

Ale czy podstawa może być dowolną liczbą? W końcu nie można wyodrębnić pierwiastka ze wszystkich liczb.

Nic!

Pamiętajmy o zasadzie: każda liczba podniesiona do potęgi parzystej jest liczbą dodatnią. Oznacza to, że nie można wyodrębnić pierwiastków parzystych z liczb ujemnych!

Oznacza to, że takich liczb nie można podnieść do potęgi ułamkowej o parzystym mianowniku, to znaczy wyrażenie nie ma sensu.

A co z wyrażeniem?

Ale tutaj pojawia się problem.

Liczbę można przedstawić w postaci innych, redukowalnych ułamków, na przykład lub.

I okazuje się, że istnieje, ale nie istnieje, ale to tylko dwa różne zapisy o tej samej liczbie.

Albo inny przykład: raz, potem możesz to zapisać. Jeśli jednak zapiszemy wskaźnik inaczej, znów wpadniemy w kłopoty: (czyli otrzymaliśmy zupełnie inny wynik!).

Aby uniknąć takich paradoksów, zastanawiamy się tylko dodatni wykładnik podstawowy z wykładnikiem ułamkowym.

Więc jeśli:

- Liczba naturalna;
- liczba całkowita;

Przykłady:

Wymierne wykładniki są bardzo przydatne do przekształcania wyrażeń z pierwiastkami, na przykład:

5 przykładów do przećwiczenia

Analiza 5 przykładów do szkolenia

1. Nie zapomnij o zwykłych właściwościach stopni:

2. . Tutaj pamiętamy, że zapomnieliśmy nauczyć się tabeli stopni:

w końcu - to jest lub. Rozwiązanie zostanie znalezione automatycznie: .

Cóż, teraz najtrudniejsza część. Teraz się o tym przekonamy stopień z niewymiernym wykładnikiem.

Wszystkie zasady i właściwości stopni tutaj są dokładnie takie same jak dla stopnia z wymiernym wykładnikiem, z wyjątkiem

Przecież z definicji liczby niewymierne to liczby, których nie można przedstawić w postaci ułamka zwykłego, gdzie i są liczbami całkowitymi (tzn. wszystkie liczby niewymierne są liczbami rzeczywistymi z wyjątkiem wymiernych).

Badając stopnie z wykładnikami naturalnymi, całkowitymi i wymiernymi, za każdym razem tworzyliśmy pewien „obraz”, „analogię” lub opis w bardziej znanych terminach.

Na przykład stopień z wykładnikiem naturalnym to liczba pomnożona przez siebie kilka razy;

...liczbę do potęgi zerowej- jest to jakby liczba pomnożona raz przez siebie, to znaczy nie zaczęli jej jeszcze mnożyć, co oznacza, że sama liczba jeszcze się nawet nie pojawiła - dlatego wynikiem jest tylko pewna „pusta liczba” , czyli liczba;

...stopień ujemnej liczby całkowitej- to tak, jakby nastąpił jakiś „proces odwrotny”, to znaczy liczba nie została pomnożona przez siebie, ale podzielona.

Nawiasem mówiąc, w nauce często stosuje się stopień ze złożonym wykładnikiem, to znaczy wykładnik nie jest nawet liczbą rzeczywistą.

Ale w szkole nie myślimy o takich trudnościach; będziesz miał okazję zrozumieć te nowe koncepcje w instytucie.

GDZIE JESTEŚMY NA PEWNO, ŻE DOJEDZIESZ! (jeśli nauczysz się rozwiązywać takie przykłady :))

Na przykład:

Zdecyduj sam:

Analiza rozwiązań:

1. Zacznijmy od zwykłej zasady podnoszenia potęgi do potęgi:

Teraz spójrz na wskaźnik. Czy on ci niczego nie przypomina? Przypomnijmy sobie wzór na skrócone mnożenie różnicy kwadratów:

W tym przypadku,

Okazało się, że:

Odpowiedź: .

2. Ułamki zwykłe w wykładnikach redukujemy do tej samej postaci: albo oba ułamki dziesiętne, albo oba zwykłe. Otrzymujemy na przykład:

Odpowiedź: 16

3. Nic specjalnego, używamy zwykłych właściwości stopni:

POZIOM ZAAWANSOWANY

Określenie stopnia

Stopień jest wyrażeniem postaci: , gdzie:

— podstawa stopnia;
- wykładnik.

Stopień ze wskaźnikiem naturalnym (n = 1, 2, 3,...)

Podniesienie liczby do potęgi naturalnej n oznacza pomnożenie liczby przez nią samą razy:

Stopień z wykładnikiem całkowitym (0, ±1, ±2,...)

Jeśli wykładnik jest Dodatnia liczba całkowita numer:

Budowa do stopnia zerowego:

Wyrażenie jest nieokreślone, ponieważ z jednej strony w dowolnym stopniu jest to, a z drugiej strony dowolna liczba do th stopnia jest tym.

Jeśli wykładnik jest ujemna liczba całkowita numer:

(ponieważ nie można dzielić przez).

Jeszcze raz o zerach: wyrażenie nie jest zdefiniowane w przypadku. Jeśli następnie.

Przykłady:

Potęga z wykładnikiem wymiernym

- Liczba naturalna;
- liczba całkowita;

Przykłady:

Właściwości stopni

Aby ułatwić rozwiązywanie problemów, spróbujmy zrozumieć: skąd wzięły się te właściwości? Udowodnijmy je.

Zobaczmy: co jest i?

Priorytet A:

Zatem po prawej stronie tego wyrażenia otrzymujemy następujący iloczyn:

Ale z definicji jest to potęga liczby z wykładnikiem, czyli:

co było do okazania

Przykład : Uprość wyrażenie.

Rozwiązanie : .

Przykład : Uprość wyrażenie.

Rozwiązanie : Ważne jest, aby pamiętać, że w naszej regule Koniecznie muszą być te same powody. Dlatego łączymy moce z bazą, ale pozostaje to osobnym czynnikiem:

Kolejna ważna uwaga: ta zasada - tylko dla iloczynu mocy!

W żadnym wypadku nie możesz tak pisać.

Podobnie jak w przypadku poprzedniej własności, przejdźmy do definicji stopnia:

Przegrupujmy tę pracę w następujący sposób:

Okazuje się, że wyrażenie mnoży się przez siebie razy, czyli zgodnie z definicją jest to potęga liczby:

Zasadniczo można to nazwać „wyjęciem wskaźnika z nawiasów”. Ale nigdy nie możesz tego zrobić w całości: !

Przypomnijmy sobie skrócone wzory na mnożenie: ile razy chcieliśmy pisać? Ale to w końcu nieprawda.

Moc o podstawie ujemnej.

Do tego momentu omawialiśmy jedynie, jak to powinno wyglądać indeks stopni. Ale co powinno być podstawą? W uprawnieniach naturalny wskaźnik może być podstawa Jakikolwiek numer .

Rzeczywiście, możemy pomnożyć przez siebie dowolne liczby, niezależnie od tego, czy są one dodatnie, ujemne, czy nawet. Zastanówmy się, które znaki („” lub „”) będą miały potęgę liczb dodatnich i ujemnych?

Na przykład, czy liczba jest dodatnia czy ujemna? A? ?

W przypadku pierwszego wszystko jest jasne: niezależnie od tego, ile liczb dodatnich pomnożymy przez siebie, wynik będzie dodatni.

Ale te negatywne są trochę bardziej interesujące. Pamiętamy prostą zasadę z szóstej klasy: „minus za minus daje plus”. To znaczy, lub. Ale jeśli pomnożymy przez (), otrzymamy - .

I tak w nieskończoność: przy każdym kolejnym mnożeniu znak będzie się zmieniał. Można sformułować następujące proste zasady:

nawet stopień, - liczba pozytywny.
Liczba ujemna podniesiona do dziwne stopień, - liczba negatywny.
Liczba dodatnia w dowolnym stopniu jest liczbą dodatnią.
Zero do dowolnej potęgi jest równe zero.

Ustal sam, jaki znak będą miały następujące wyrażenia:

1.	2.	3.
4.	5.	6.

Czy udało Ci się? Oto odpowiedzi:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

Mam nadzieję, że w pierwszych czterech przykładach wszystko jest jasne? Po prostu patrzymy na podstawę i wykładnik i stosujemy odpowiednią regułę.

W przykładzie 5) wszystko też nie jest tak straszne, jak się wydaje: w końcu nie ma znaczenia, jaka jest podstawa - stopień jest równy, co oznacza, że wynik zawsze będzie dodatni. No chyba, że podstawa wynosi zero. Podstawa nie jest równa, prawda? Oczywiście, że nie, ponieważ (ponieważ).

Przykład 6) nie jest już takie proste. Tutaj musisz dowiedzieć się, co jest mniejsze: lub? Jeśli o tym pamiętamy, staje się jasne, co oznacza, że podstawa jest mniejsza od zera. Oznacza to, że stosujemy zasadę 2: wynik będzie ujemny.

I znowu używamy definicji stopnia:

Wszystko jest jak zwykle - zapisujemy definicję stopni i dzielimy je między sobą, dzielimy na pary i otrzymujemy:

Zanim przyjrzymy się ostatniej regule, rozwiążmy kilka przykładów.

Oblicz wyrażenia:

Rozwiązania :

Jeśli zignorujemy potęgę ósmą, co tutaj zobaczymy? Przypomnijmy program dla klasy 7. Pamiętasz? To jest wzór na skrócone mnożenie, czyli różnicę kwadratów!

Otrzymujemy:

Przyjrzyjmy się uważnie mianownikowi. Wygląda bardzo podobnie do jednego z czynników licznikowych, ale co jest nie tak? Kolejność terminów jest niewłaściwa. Gdyby zostały odwrócone, miałaby zastosowanie zasada 3. Ale w jaki sposób? Okazuje się, że jest to bardzo proste: pomaga nam tutaj parzysty stopień mianownika.

Jeśli pomnożysz to przez, nic się nie zmieni, prawda? Ale teraz okazuje się, że jest tak:

W magiczny sposób terminy zmieniły miejsca. To „zjawisko” dotyczy w równym stopniu każdego wyrażenia: łatwo możemy zmienić znaki w nawiasach. Ale ważne jest, aby pamiętać: Wszystkie znaki zmieniają się w tym samym czasie! Nie da się tego zastąpić, zmieniając tylko jedną wadę, która nam się nie podoba!

Wróćmy do przykładu:

I znowu formuła:

A teraz ostatnia zasada:

Jak to udowodnimy? Oczywiście jak zwykle: rozwińmy pojęcie stopnia i uprośćmy je:

Cóż, teraz otwórzmy nawiasy. Ile jest w sumie liter? razy przez mnożniki – o czym ci to przypomina? To nic innego jak definicja operacji mnożenie: Były tam tylko mnożniki. Oznacza to, że z definicji jest to potęga liczby z wykładnikiem:

Przykład:

Stopień z irracjonalnym wykładnikiem

Oprócz informacji o stopniach dla poziomu średniego przeanalizujemy stopień z irracjonalnym wykładnikiem. Wszystkie zasady i właściwości stopni są tutaj dokładnie takie same, jak w przypadku stopnia z wymiernym wykładnikiem, z wyjątkiem - wszak z definicji liczby niewymierne to liczby, których nie można przedstawić w postaci ułamka, gdzie i są liczbami całkowitymi (czyli , liczby niewymierne są liczbami rzeczywistymi z wyjątkiem liczb wymiernych).

Badając stopnie z wykładnikami naturalnymi, całkowitymi i wymiernymi, za każdym razem tworzyliśmy pewien „obraz”, „analogię” lub opis w bardziej znanych terminach. Na przykład stopień z wykładnikiem naturalnym to liczba pomnożona przez siebie kilka razy; liczba do potęgi zerowej jest jakby liczbą pomnożoną raz przez siebie, to znaczy nie zaczęli jej jeszcze mnożyć, co oznacza, że sama liczba jeszcze się nawet nie pojawiła - dlatego wynik jest tylko pewnym „pusta liczba”, czyli liczba; stopień z wykładnikiem całkowitym ujemnym - to tak, jakby nastąpił jakiś „proces odwrotny”, to znaczy liczba nie została pomnożona przez siebie, ale podzielona.

Niezwykle trudno jest wyobrazić sobie stopień z irracjonalnym wykładnikiem (tak jak trudno wyobrazić sobie przestrzeń 4-wymiarową). Jest to raczej obiekt czysto matematyczny, który matematycy stworzyli, aby rozszerzyć pojęcie stopnia na całą przestrzeń liczb.

Nawiasem mówiąc, w nauce często stosuje się stopień ze złożonym wykładnikiem, to znaczy wykładnik nie jest nawet liczbą rzeczywistą. Ale w szkole nie myślimy o takich trudnościach; będziesz miał okazję zrozumieć te nowe koncepcje w instytucie.

Co więc zrobimy, jeśli zobaczymy irracjonalny wykładnik? Robimy wszystko, żeby się tego pozbyć! :)

Na przykład:

Zdecyduj sam:

Odpowiedzi:

Pamiętajmy o różnicy we wzorze kwadratów. Odpowiedź: .
Sprowadzamy ułamki zwykłe do tej samej postaci: albo oba ułamki dziesiętne, albo oba zwykłe. Otrzymujemy np.: .
Nic specjalnego, używamy zwykłych właściwości stopni:

PODSUMOWANIE ROZDZIAŁU I PODSTAWOWE WZORY

Stopień zwane wyrażeniem postaci: , gdzie:

Stopień z wykładnikiem całkowitym

stopień, którego wykładnikiem jest liczba naturalna (tj. liczba całkowita i dodatnia).

Potęga z wykładnikiem wymiernym

stopień, którego wykładnikiem są liczby ujemne i ułamkowe.

Stopień z irracjonalnym wykładnikiem

stopień, którego wykładnik jest nieskończony dziesiętny lub root.

Właściwości stopni

Cechy stopni.

Liczba ujemna podniesiona do nawet stopień, - liczba pozytywny.
Liczba ujemna podniesiona do dziwne stopień, - liczba negatywny.
Liczba dodatnia w jakimkolwiek stopniu jest liczbą dodatnią.
Zero jest równe dowolnej potędze.
Każda liczba do potęgi zerowej jest równa.

TERAZ MASZ SŁOWO...

Jak podoba Ci się artykuł? Napisz poniżej w komentarzu, czy Ci się podobało, czy nie.

Opowiedz nam o swoich doświadczeniach z używaniem właściwości stopnia.

Być może masz pytania. Lub sugestie.

Napisz w komentarzach.

I powodzenia na egzaminach!

Temat lekcji: Podniesienie do potęgi iloczynu, ilorazu i mocy

Typ lekcji: Lekcja uogólniania i systematyzacji wiedzy

Wygenerowane wyniki:

Temat. Utrwalenie umiejętności wykorzystania właściwości stopni z wykładnikami naturalnymi

Osobisty. Rozwijaj umiejętność planowania swoich działań zgodnie z zadaniem edukacyjnym

Metatemat. Rozwijać zrozumienie istoty recept algebraicznych i umiejętność działania zgodnie z proponowanym algorytmem

Oczekiwane rezultaty: Studenci nauczą się wykorzystywać właściwości wykładników z wykładnikami naturalnymi do obliczania znaczenia wyrażeń oraz konwertowania wyrażeń zawierających wykładniki.

Sprzęt: karty, projektor multimedialny, karty sygnałowe do refleksji.

Struktura organizacyjna lekcji:

1 . Organizowanie czasu.

Witam, drodzy ludzie! Bardzo się cieszę, że cię widzę. Zacznijmy lekcję matematyki

Jakie trudności napotkałeś podczas wykonywania zadania?

Odbicie.

Przed każdym uczniem stoją kubki w trzech kolorach: czerwonym, zielonym, niebieskim.

Opowiedz mi o swoim nastroju za pomocą kolorowych kółek (czerwony– radosna, jestem pewna, że na lekcji nauczę się wielu nowych rzeczy, jestem pewna swojej wiedzy.

Zielony -spokój; Jestem pewien swojej wiedzy.

Niebieski– niepokojące; nie jestem pewien siebie).

Pocieszę Cię trochę słowami Poissona: „Życie upiększają dwie rzeczy: uprawianie matematyki i jej nauczanie”.

Udekorujmy nasze życie!

2. Określenie tematu i celu lekcji.

Dzisiaj będziemy kontynuować naukę tematu: „Potęgowanie iloczynu ilorazu i stopnia”,

skonsolidujemy wszystkie wyuczone działania ze stopniami,

Nauczymy się rozumować, myśleć logicznie i udowadniać swój punkt widzenia.

3. Ankieta błyskawiczna zgodnie z zasadami tematu.

Jak pomnożyć potęgi o tych samych podstawach? Daj przykłady.

Jak podzielić stopnie o tej samej podstawie?

Jaka jest potęga liczby a, różnej od 0, z wykładnikiem zerowym?

Jak podnieść iloczyn do potęgi?

Jak podnieść stopień do potęgi?

4. Liczenie ustne.

Kto jest właścicielem tych słów?

„Wśród wszystkich nauk, które otwierają człowiekowi drogę do zrozumienia praw natury, najpotężniejszą i największą nauką jest matematyka”.

/Zofia Wasiliewna Kowalewska/

Pierwsza kobieta jest matematyczką.

Dowiesz się, wykonując zadania obliczeń mentalnych.

K – Jaki jest bok kwadratu, jeśli jego pole wynosi 49 cm 2. (7cm)

O – Kwadrat jakiej liczby jest równy? ()

B – x 3 x 4 (x 7)

A – x 6 : x 2 (x 4)

L – (x 3) 3 (x 9)

E-
(M 3 )

W -
(M 8 )

Z -
(M 10 )

K – (- 2) 3 (-8)

A - - 2 2 (-4)

Ja - 2 0 (1)

5. Konsolidacja zdobytej wiedzy.

Powtórzyliśmy zasady podnoszenia iloczynu do potęgi i potęgi do potęgi.

Skupmy się teraz na zadaniach praktycznych.

Opieką zajmie się kilka osóbbadania. (Slajd)

Pracujcie w parach.

1) Udowodnić, że kwadraty przeciwnych liczb są równe.

2) Udowodnić, że kostki przeciwnych liczb są przeciwne.

3) Jak zmieni się powierzchnia kwadratu, jeśli jego bok zostanie podwojony; 3 razy; 10 razy; n razy?

4) Jak zmieni się objętość sześcianu, jeśli jego krawędź zostanie podwojona; 3 razy; 10 razy; n razy?

6. Refleksja: pokaż mi swój nastrój.

7. Ćwiczenia fizyczne: „Zgadzam się – nie zgadzam się”

Potrząsnij głową, jeśli się ze mną zgadzasz, czy nie.

1) (y 2) 3 = y 5 (nie)

2) (-3) 3 = -27 (tak)

3) (-x) 2 = -x 2 (nie)

4) Wykres funkcji y = 1,3x przechodzi przez początek. (Tak)

3 · () 2 – 0,5 2

a) -1; b) - 1 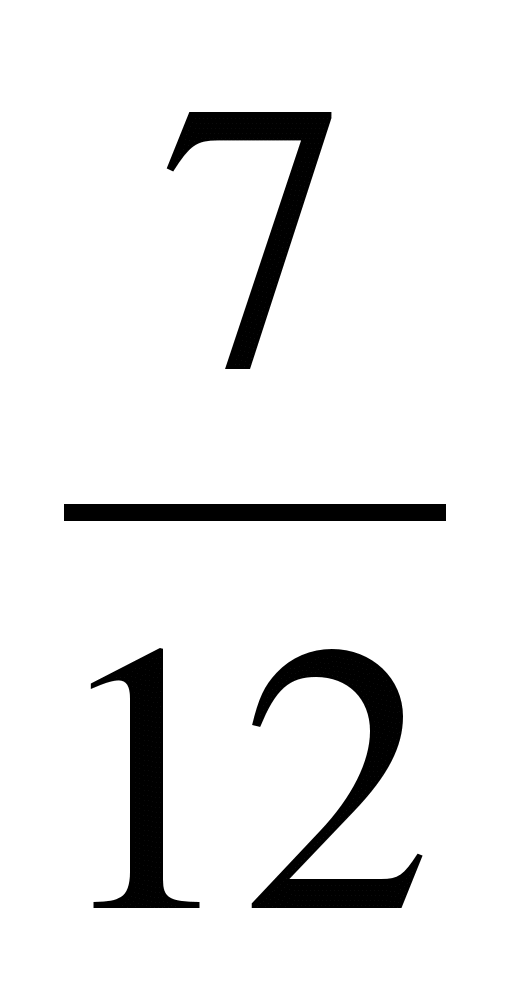; w 1 ; d) 1

2) Uprość wyrażenie:

a) m 10; b)m 4; c) m 2; d) m 8.

3) Oblicz:

A) 3; b) 9; płyta CD)

4) Jakie wyrażenie należy zastąpić zamiast (*), aby uzyskać tożsamość:

X 8 : (*) = x 4

A) x 4; b) x 2; c) x 8; d) x 12

Sprawdzanie testu slajdów:

9. Zagrajmy w „Znajdź błąd!”

1) 15 : za 3 = za 5

2) –z · z 5 · z 0 = - z 6 - Prawidłowy

3)
=

4)(y 4 y) 2 = y 10 - prawda

Zapisz błędne zadania i rozwiąż je poprawnie.

10. Podsumowanie lekcji.

Czego nauczyłeś się na lekcji?

11. D/z

nr 458, 457 (slajd)

Doniesienia o S.V. Kowalewskiej.

12. Refleksja.

Pokaż mi, jak się czujesz, kiedy wychodzisz z lekcji?

Slajd: Powodzenia!

FI:

Niezależna praca. (test)

1) Znajdź znaczenie wyrażenia:

3· () 2 – 0,5 2

a) -1; b) - 1 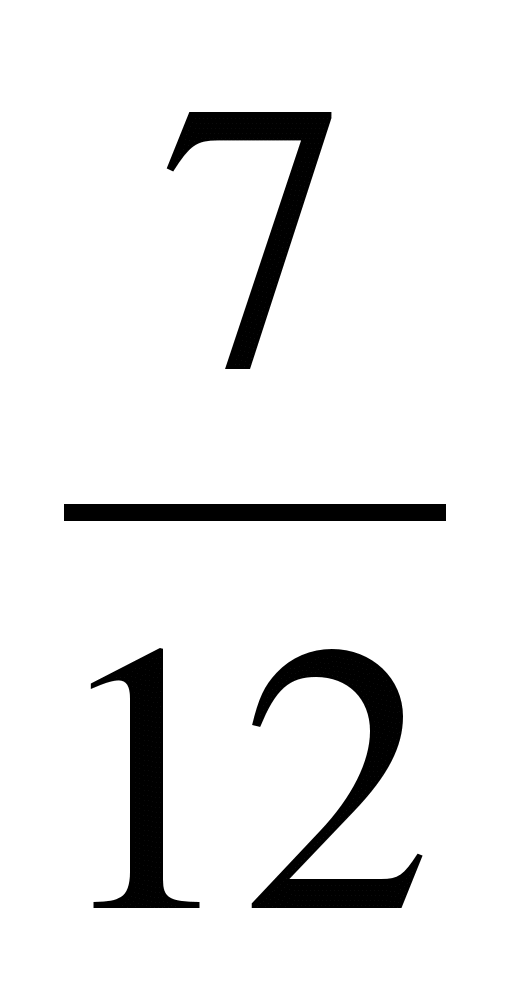; w 1 ; d) 1

2) Uprość wyrażenie:

a) m 10; b)m 4; c) m 2; d) m 8.

3) Oblicz:

a) 3; b) 9; płyta CD)

4) Jakie wyrażenie należy zastąpić zamiast (*), aby uzyskać tożsamość:

x 8 : (*) = x 4

a) x 4; b) x 2; c) x 8; d) x 12

Stopień:

Niezależna praca. (test)

1) Znajdź znaczenie wyrażenia:

3· () 2 – 0,5 2

a) -1; b) - 1 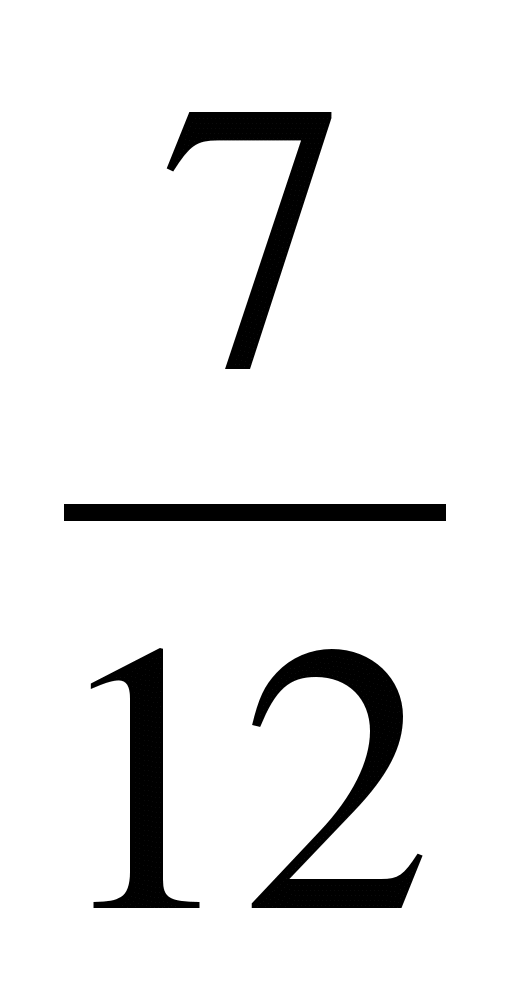; w 1 ; d) 1

2) Uprość wyrażenie:

główny cel

Zapoznanie studentów z właściwościami stopni z wykładnikami naturalnymi i nauczenie ich wykonywania operacji na stopniach.

Temat „Stopień i jego właściwości” zawiera trzy pytania:

Oznaczanie stopnia za pomocą wskaźnika naturalnego.
Mnożenie i dzielenie potęg.
Potęgowanie iloczynu i stopnia.

Pytania kontrolne

Sformułuj definicję stopnia z wykładnikiem naturalnym większym niż 1. Podaj przykład.
Sformułuj definicję stopnia z wykładnikiem 1. Podaj przykład.
Jaka jest kolejność działań przy obliczaniu wartości wyrażenia zawierającego potęgi?
Sformułuj główną właściwość stopnia. Daj przykład.
Sformułuj zasadę mnożenia potęg o tych samych podstawach. Daj przykład.
Sformułuj regułę dzielenia potęg o tych samych podstawach. Daj przykład.
Sformułuj regułę potęgowania iloczynu. Daj przykład. Udowodnij tożsamość (ab) n = a n b n .
Sformułuj regułę podnoszenia potęgi do potęgi. Daj przykład. Udowodnij tożsamość (a m) n = a m n .

Definicja stopnia.

Potęga liczby A z naturalnym wskaźnikiem N, większe niż 1, jest iloczynem n czynników, z których każdy jest równy A. Potęga liczby A z wykładnikiem 1 jest samą liczbą A.

Stopień z podstawą A i wskaźnik N jest napisane tak: oraz n. Brzmi: „ A do pewnego stopnia N”; „ n-ta potęga liczby A ”.

Z definicji stopnia:

za 4 = a a a a

. . . . . . . . . . . .

Znajdowanie wartości potęgi nazywa się przez potęgowanie .

1. Przykłady potęgowania:

3 3 = 3 3 3 = 27

0 4 = 0 0 0 0 = 0

(-5) 3 = (-5) (-5) (-5) = -125

25 ; 0,09 ;

25 = 5 2 ; 0,09 = (0,3) 2 ; .

27 ; 0,001 ; 8 .

27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .

4. Znajdź znaczenie wyrażeń:

a) 3 10 3 = 3 10 10 10 = 3 1000 = 3000

b) -2 4 + (-3) 2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7

opcja 1

a) 0,3 0,3 0,3

c) b b b b b b

d) (-x) (-x) (-x) (-x)

e) (ab) (ab) (ab)

2. Przedstaw liczbę w postaci kwadratu:

3. Przedstaw liczby w postaci sześcianu:

4. Znajdź znaczenie wyrażeń:

c) -1 4 + (-2) 3

d) -4 3 + (-3) 2

e) 100 - 5 2 4

Mnożenie potęg.

Dla dowolnej liczby a i dowolnych liczb m i n obowiązuje:

za m za n = za m + n .

Dowód:

Reguła : Przy mnożeniu potęg o tych samych podstawach podstawy pozostają takie same, a wykładniki potęg są dodawane.

za m za n za k = za m + n za k = za (m + n) + k = za m + n + k

a) x 5 x 4 = x 5 + 4 = x 9

b) y 6 = y 1 y 6 = y 1 + 6 = y 7

c) b 2 b 5 b 4 = b 2 + 5 + 4 = b 11

d) 3 4 9 = 3 4 3 2 = 3 6

e) 0,01 0,1 3 = 0,1 2 0,1 3 = 0,1 5

a) 2 3 2 = 2 4 = 16

b) 3 2 3 5 = 3 7 = 2187

opcja 1

1. Obecny jako stopień:

a) x 3 x 4 e) x 2 x 3 x 4

b) a 6 a 2 g) 3 3 9

c) y 4 y h) 7 4 49

d) a a 8 i) 16 2 7

e) 2 3 2 4 j) 0,3 3 0,09

2. Przedstaw jako stopień i znajdź wartość z tabeli:

a) 2 2 2 3 c) 8 2 5

b) 3 4 3 2 d) 27 243

Podział stopni.

Dla dowolnej liczby a0 i dowolnych liczb naturalnych m i n takich, że m>n zachodzi:

za m: za n = za m - n

Dowód:

za m - n za n = za (m - n) + n = za m - n + n = za m

z definicji ilorazu:

za m: za n = za m - n .

Reguła: Przy dzieleniu potęg o tej samej podstawie podstawę pozostawia się taką samą, a wykładnik dzielnika odejmuje się od wykładnika dzielnej.

Definicja: Potęga liczby a, różnej od zera, z wykładnikiem zerowym, jest równa jeden:

ponieważ za n: za n = 1 w a0.

a) x 4: x 2 = x 4 - 2 = x 2

b) r 8: r 3 = r 8 - 3 = r 5

c) za 7:a = za 7:za 1 = za 7 - 1 = za 6

d) od 5:od 0 = od 5:1 = od 5

a) 5 7:5 5 = 5 2 = 25

b) 10 20:10 17 = 10 3 = 1000

V)

G)

D)

opcja 1

1. Przedstaw iloraz w postaci potęgi:

2. Znajdź znaczenie wyrażeń:

Podniesienie do potęgi produktu.

Dla dowolnego a i b oraz dowolnej liczby naturalnej n:

(ab) n = za n b n

Dowód:

Z definicji stopnia

(ab)n=

Grupując oddzielnie czynniki a i b, otrzymujemy:

Sprawdzona właściwość mocy iloczynu rozciąga się na moc iloczynu trzech lub więcej czynników.

Na przykład:

(a b do) n = za n b n do n ;

(za b do re) n = za n b n do n re n .

Reguła: Podnosząc iloczyn do potęgi, każdy czynnik jest podnoszony do tej potęgi, a wynik jest mnożony.

1. Podnieś do potęgi:

a) (a b) 4 = za 4 b 4

b) (2 x y) 3 =2 3 x 3 y 3 = 8 x 3 y 3

c) (3 a) 4 = 3 4 za 4 = 81 za 4

d) (-5 lat) 3 = (-5) 3 lat 3 = -125 lat 3

e) (-0,2 x y) 2 = (-0,2) 2 x 2 y 2 = 0,04 x 2 y 2

e) (-3 za b do) 4 = (-3) 4 za 4 b 4 do 4 = 81 za 4 b 4 do 4

2. Znajdź wartość wyrażenia:

a) (2 10) 4 = 2 4 10 4 = 16 1000 = 16000

b) (3 5 20) 2 = 3 2 100 2 = 9 10000= 90000

c) 2 4 5 4 = (2 5) 4 = 10 4 = 10000

d) 0,25 11 4 11 = (0,25 4) 11 = 1 11 = 1

D)

opcja 1

1. Podnieś do potęgi:

b) (2 a c) 4

e) (-0,1 x y) 3

2. Znajdź wartość wyrażenia:

b) (5 7 20) 2

Podniesienie do potęgi potęgi.

Dla dowolnej liczby a i dowolnych liczb naturalnych m i n:

(a m) n = za m n

Dowód:

Z definicji stopnia

(a m) n =

Reguła: Przy podnoszeniu potęgi do potęgi podstawa pozostaje taka sama, a wykładniki są mnożone.

1. Podnieś do potęgi:

(za 3) 2 = za 6 (x 5) 4 = x 20

(y 5) 2 = r 10 (b 3) 3 = b 9

2. Uprość wyrażenia:

a) za 3 (za 2) 5 = za 3 za 10 = za 13

b) (b 3) 2 b 7 = b 6 b 7 = b 13

c) (x 3) 2 (x 2) 4 = x 6 x 8 = x 14

d) (y 7) 3 = (y 8) 3 = r 24

A)

B)

opcja 1

1. Podnieś do potęgi:

a) (a 4) 2 b) (x 4) 5

c) (y 3) 2 d) (b 4) 4

2. Uprość wyrażenia:

a) 4 (za 3) 2

b) (b 4) 3 b 5+

c) (x 2) 4 (x 4) 3

d) (y 9) 2

3. Znajdź znaczenie wyrażeń:

Aplikacja

Definicja stopnia.

Opcja 2

1. Zapisz iloczyn w postaci potęgi:

a) 0,4 0,4 0,4

c) a a a a a a a

d) (-y) (-y) (-y) (-y)

e) (bс) (bс) (bс)

2. Przedstaw liczbę w postaci kwadratu:

3. Przedstaw liczby w postaci sześcianu:

4. Znajdź znaczenie wyrażeń:

c) -1 3 + (-2) 4

d) -6 2 + (-3) 2

e) 4 5 2 – 100

Opcja 3

1. Zapisz iloczyn w postaci potęgi:

a) 0,5 0,5 0,5

c) z z z z z z z z z

d) (-x) (-x) (-x) (-x)

e) (ab) (ab) (ab)

2. Przedstaw liczbę w postaci kwadratu: 100; 0,49; .

3. Przedstaw liczby w postaci sześcianu:

4. Znajdź znaczenie wyrażeń:

c) -1 5 + (-3) 2

d) -5 3 + (-4) 2

e) 5 4 2 - 100

Opcja 4

1. Zapisz iloczyn w postaci potęgi:

a) 0,7 0,7 0,7

c) x x x x x x

d) (-a) (-a) (-a)

e) (bс) (bс) (bс) (bc)

2. Przedstaw liczbę w postaci kwadratu:

3. Przedstaw liczby w postaci sześcianu:

4. Znajdź znaczenie wyrażeń:

c) -1 4 + (-3) 3

d) -3 4 + (-5) 2

e) 100 - 3 2 5

Mnożenie potęg.

Opcja 2

1. Obecny jako stopień:

a) x 4 x 5 e) x 3 x 4 x 5

b) a 7 a 3 g) 2 3 4

c) y 5 y h) 4 3 16

d) a a 7 i) 4 2 5

e) 2 2 2 5 j) 0,2 3 0,04

2. Przedstaw jako stopień i znajdź wartość z tabeli:

a) 3 2 3 3 c) 16 2 3

b) 2 4 2 5 d) 9 81

Opcja 3

1. Obecny jako stopień:

a) za 3 za 5 f) y 2 y 4 y 6

b) x 4 x 7 g) 3 5 9

c) b 6 b h) 5 3 25

d) y 8 i) 49 7 4

e) 2 3 2 6 j) 0,3 4 0,27

2. Przedstaw jako stopień i znajdź wartość z tabeli:

a) 3 3 3 4 c) 27 3 4

b) 2 4 2 6 d) 16 64

Opcja 4

1. Obecny jako stopień:

a) a 6 a 2 e) x 4 x x 6

b) x 7 x 8 g) 3 4 27

c) y 6 y h) 4 3 16

d) x x 10 i) 36 6 3

e) 2 4 2 5 j) 0,2 2 0,008

2. Przedstaw jako stopień i znajdź wartość z tabeli:

a) 2 6 2 3 c) 64 2 4

b) 3 5 3 2 d) 81 27

Podział stopni.

Opcja 2

1. Przedstaw iloraz w postaci potęgi:

2. Znajdź znaczenie wyrażeń:

Przypominamy, że na tej lekcji zrozumiemy właściwości stopni z naturalnymi wskaźnikami i zerem. Stopnie z racjonalne wskaźniki i ich właściwości będą omawiane na lekcjach dla klasy 8.

Potęga z wykładnikiem naturalnym ma kilka ważnych właściwości, które pozwalają uprościć obliczenia na przykładach z potęgami.

Nieruchomość nr 1
Produkt mocy

Pamiętać!

Przy mnożeniu potęg o tych samych podstawach podstawa pozostaje niezmieniona, a wykładniki potęg są dodawane.

a m · a n = a m + n, gdzie „a” to dowolna liczba, a „m”, „n” to dowolne liczby naturalne.

Ta właściwość potęg ma zastosowanie również do iloczynu trzech lub więcej potęg.

Uprość wyrażenie.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
Przedstaw to jako stopień.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
Przedstaw to jako stopień.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Ważny!

Należy pamiętać, że we wskazanej własności mówiliśmy jedynie o mnożeniu potęg na tej samej podstawie . Nie dotyczy to ich dodawania.

Nie można zastąpić sumy (3 3 + 3 2) liczbą 3 5. Jest to zrozumiałe, jeśli
oblicz (3 3 + 3 2) = (27 + 9) = 36 i 3 5 = 243

Nieruchomość nr 2
Częściowe stopnie

Pamiętać!

Przy dzieleniu potęg o tej samej podstawie podstawa pozostaje niezmieniona, a wykładnik dzielnika odejmuje się od wykładnika dzielnej.

= 11 3 - 2 4 2 - 1 = 11 4 = 44

Przykład. Rozwiązać równanie. Korzystamy z własności potęg ilorazowych.
3 8: t = 3 4

T = 3 8 - 4

Odpowiedź: t = 3 4 = 81

Korzystając z właściwości nr 1 i nr 2, można łatwo upraszczać wyrażenia i wykonywać obliczenia.

Przykład. Uprość wyrażenie.
4 5 m + 6 4 m + 2: 4 4 m + 3 = 4 5 m + 6 + m + 2: 4 4 m + 3 = 4 6 m + 8 - 4 m - 3 = 4 2 m + 5
Przykład. Znajdź wartość wyrażenia, korzystając z właściwości wykładników.
= = = 2 9 + 2
2 5
= 2 11
2 5
= 2 11 − 5 = 2 6 = 64
Ważny!
Proszę zauważyć, że we własności 2 mówiliśmy tylko o dzieleniu potęg o tych samych podstawach.

Nie możesz zastąpić różnicy (4 3 −4 2) liczbą 4 1. Jest to zrozumiałe, jeśli liczyć (4 3 −4 2) = (64 − 16) = 48 i 4 1 = 4

Bądź ostrożny!

Nieruchomość nr 3
Podnoszenie stopnia do potęgi

Pamiętać!
Podnosząc stopień do potęgi, podstawa stopnia pozostaje niezmieniona, a wykładniki są mnożone.
(a n) m = a n · m, gdzie „a” jest dowolną liczbą, a „m”, „n” są dowolnymi liczbami naturalnymi.

Właściwości 4
Moc produktu

Pamiętać!
Podnosząc iloczyn do potęgi, każdy z czynników podnosi się do potęgi. Otrzymane wyniki następnie mnoży się.
(a b) n = a n b n, gdzie „a”, „b” są dowolnymi liczbami wymiernymi; „n” jest dowolną liczbą naturalną.
- Przykład 1.
  (6 za 2 b 3 do) 2 = 6 2 za 2 2 b 3 2 do 1 2 = 36 za 4 b 6 do 2
- Przykład 2.
  (-x 2 y) 6 = ((-1) 6 x 2 6 y 1 6) = x 12 y 6
Ważny!
Należy pamiętać, że właściwość nr 4, podobnie jak inne właściwości stopni, również stosuje się w odwrotnej kolejności.
(a n · b n)= (a · b) n
Oznacza to, że aby pomnożyć potęgi o tych samych wykładnikach, można pomnożyć podstawy, ale pozostawić wykładnik bez zmian.
- Przykład. Oblicz.
  2 4 5 4 = (2 5) 4 = 10 4 = 10 000
- Przykład. Oblicz.
  0,5 16 2 16 = (0,5 2) 16 = 1
W więcej złożone przykłady Może się zdarzyć, że mnożenie i dzielenie będzie konieczne w przypadku potęg o różnych podstawach i różnych wykładnikach. W takim przypadku zalecamy wykonanie następujących czynności.

Na przykład, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

Przykład podnoszenia ułamka dziesiętnego do potęgi.
4 21 (-0,25) 20 = 4 4 20 (-0,25) 20 = 4 (4 (-0,25)) 20 = 4 (-1) 20 = 4 1 = 4
Właściwości 5
Potęga ilorazu (ułamka)

Pamiętać!
Aby podnieść iloraz do potęgi, możesz oddzielnie podnieść dzielną i dzielnik do tej potęgi i podzielić pierwszy wynik przez drugi.
(a: b) n = a n: b n, gdzie „a”, „b” to dowolne liczby wymierne, b ≠ 0, n jest dowolną liczbą naturalną.
- Przykład. Przedstaw wyrażenie jako iloraz potęg.
  (5: 3) 12 = 5 12: 3 12
Przypominamy, że iloraz można przedstawić jako ułamek. Dlatego bardziej szczegółowo omówimy temat podnoszenia ułamka do potęgi na następnej stronie.