Suma pracy wykonanej przez siły zewnętrzne. Twierdzenie o zmianie energii kinetycznej

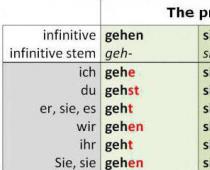
Energia zwany skalarem wielkość fizyczna, który jest pojedynczą miarą różnych form ruchu materii i miarą przejścia ruchu materii z jednej formy do drugiej.

Aby scharakteryzować różne formy ruchu materii, wprowadza się odpowiednie rodzaje energii, na przykład: mechaniczną, wewnętrzną, energię oddziaływań elektrostatycznych, wewnątrzjądrowych itp.

Energia podlega prawu zachowania, które jest jednym z najważniejszych praw natury.

Energia mechaniczna E charakteryzuje ruch i wzajemne oddziaływanie ciał oraz jest funkcją prędkości i względnego położenia ciał. Jest równa sumie energii kinetycznej i potencjalnej.

Energia kinetyczna

Rozważmy przypadek, gdy ciało ma masę M istnieje stała siła \(~\vec F\) (może być wypadkową kilku sił) i wektory siły \(~\vec F\) i przemieszczenia \(~\vec s\) są skierowane wzdłuż jednego linię prostą w jednym kierunku. W tym przypadku pracę wykonaną przez siłę można zdefiniować jako A = F∙S. Moduł siły zgodnie z drugim prawem Newtona jest równy F = m∙a i moduł przemieszczenia S w równomiernie przyspieszonym ruchu prostoliniowym jest powiązany z modułami początkowymi υ 1 i ostateczny υ 2 prędkości i przyspieszenia A wyrażenie \(~s = \frac(\upsilon^2_2 - \upsilon^2_1)(2a)\) .

Stąd zabieramy się do pracy

\(~A = F \cdot s = m \cdot a \cdot \frac(\upsilon^2_2 - \upsilon^2_1)(2a) = \frac(m \cdot \upsilon^2_2)(2) - \frac (m \cdot \upsilon^2_1)(2)\) . (1)

Wielkość fizyczna równa połowie iloczynu masy ciała i kwadratu jego prędkości nazywa się energia kinetyczna ciała.

Energię kinetyczną reprezentuje litera mi k.

\(~E_k = \frac(m \cdot \upsilon^2)(2)\) . (2)

Wówczas równość (1) można zapisać następująco:

\(~A = E_(k2) - E_(k1)\) . (3)

Twierdzenie o energii kinetycznej

praca wypadkowych sił przyłożonych do ciała jest równa zmianie energii kinetycznej ciała.

Ponieważ zmiana energii kinetycznej jest równa pracy siły (3), energię kinetyczną ciała wyraża się w tych samych jednostkach co praca, czyli w dżulach.

Jeżeli początkowa prędkość ruchu ciała masowego M wynosi zero, a ciało zwiększa prędkość do tej wartości υ , to praca wykonana przez tę siłę jest równa końcowej wartości energii kinetycznej ciała:

\(~A = E_(k2) - E_(k1)= \frac(m \cdot \upsilon^2)(2) - 0 = \frac(m \cdot \upsilon^2)(2)\) . (4)

Fizyczne znaczenie energii kinetycznej

Energia kinetyczna ciała poruszającego się z prędkością v pokazuje, jaką pracę musi wykonać siła działająca na ciało w spoczynku, aby nadać mu tę prędkość.

Energia potencjalna

Energia potencjalna jest energią oddziaływania pomiędzy ciałami.

Energia potencjalna ciała uniesionego nad Ziemią to energia oddziaływania ciała z Ziemią za pomocą sił grawitacyjnych. Energia potencjalna ciała odkształconego sprężyście jest energią oddziaływania poszczególne części ciała między sobą siłami sprężystości.

Potencjał są nazywane wytrzymałość, którego działanie zależy wyłącznie od położenia początkowego i końcowego ruchomego punkt materialny lub ciała i nie zależy od kształtu trajektorii.

Na trajektorii zamkniętej praca wykonana przez siłę potencjalną jest zawsze równa zeru. Potencjalne siły obejmują siły grawitacyjne, siły sprężystości, siły elektrostatyczne i niektóre inne.

Uprawnienie, których praca zależy od kształtu trajektorii, nazywane są niepotencjalny. Kiedy punkt materialny lub ciało porusza się po zamkniętej trajektorii, praca wykonana przez siłę niepotencjalną nie jest równa zeru.

Energia potencjalna oddziaływania ciała z Ziemią

Znajdźmy pracę wykonaną przez grawitację F t podczas przesuwania ciała o masie M pionowo w dół z pewnej wysokości H 1 nad powierzchnią Ziemi na wysokość H 2 (ryc. 1). Jeśli różnica H 1 – H 2 jest znikomy w porównaniu do odległości do środka Ziemi, a następnie siły ciężkości F t podczas ruchu ciała można uznać za stałe i równe mg.

Ponieważ przemieszczenie pokrywa się w kierunku z wektorem grawitacji, praca wykonana przez grawitację jest równa

\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)

Rozważmy teraz ruch ciała po pochyłej płaszczyźnie. Podczas przesuwania ciała w dół po nachylonej płaszczyźnie (ryc. 2) siła ciężkości F t = m∙g działa

\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)

Gdzie H– wysokość płaszczyzny pochyłej, S– moduł przemieszczenia równy długości pochyłej płaszczyzny.

Ruch ciała z punktu W Dokładnie Z po dowolnej trajektorii (ryc. 3) można sobie wyobrazić jako składające się z ruchów wzdłuż odcinków pochyłych płaszczyzn o różnych wysokościach H’, H'' itp. Praca A grawitacja na całej długości W V Z równa sumie pracy na poszczególnych odcinkach trasy:

\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\), (7)

Gdzie H 1 i H 2 – wysokości od powierzchni Ziemi, na których znajdują się odpowiednio punkty W I Z.

Z równości (7) wynika, że ​​praca grawitacji nie zależy od toru ruchu ciała i jest zawsze równa iloczynowi modułu grawitacji i różnicy wysokości w położeniu początkowym i końcowym.

Podczas ruchu w dół praca grawitacji jest dodatnia, podczas ruchu w górę jest ujemna. Praca wykonana przez grawitację na zamkniętej trajektorii wynosi zero.

Równość (7) można przedstawić w następujący sposób:

\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)

Wielkość fizyczna równa iloczynowi masy ciała i modułu przyspieszenia swobodny spadek i nazywa się wysokość, na jaką ciało unosi się nad powierzchnię Ziemi energia potencjalna interakcja pomiędzy ciałem a Ziemią.

Praca wykonana przez grawitację podczas przemieszczania ciała o masie M z punktu położonego na dużej wysokości H 2, do punktu znajdującego się na wysokości H 1 od powierzchni Ziemi, wzdłuż dowolnej trajektorii, jest równa zmianie energia potencjalna oddziaływanie ciała i Ziemi, ujęte za pomocą znaku przeciwnego.

\(~A = - (E_(p2) - E_(p1))\) . (9)

Energia potencjalna jest oznaczona literą mi P.

Wartość energii potencjalnej ciała wzniesionego nad Ziemię zależy od wyboru poziomu zerowego, czyli wysokości, na której przyjmuje się, że energia potencjalna wynosi zero. Zwykle przyjmuje się, że energia potencjalna ciała na powierzchni Ziemi wynosi zero.

Przy tym wyborze poziomu zerowego, energia potencjalna mi p ciała znajdującego się na wysokości H nad powierzchnią Ziemi jest równa iloczynowi masy m ciała przez moduł przyspieszenia grawitacyjnego G i dystans H to z powierzchni Ziemi:

\(~E_p = m \cdot g \cdot h\) . (10)

Fizyczne znaczenie energii potencjalnej oddziaływania ciała z Ziemią

energia potencjalna ciała, na które działa grawitacja, jest równa pracy wykonanej przez grawitację podczas przemieszczania ciała do poziomu zerowego.

W przeciwieństwie do energii kinetycznej ruch do przodu, które mogą mieć tylko wartości dodatnie, energia potencjalna ciała może być zarówno dodatnia, jak i ujemna. Masa ciała M, położony na wysokości H, Gdzie H < H 0 (H 0 – wysokość zerowa), ma ujemną energię potencjalną:

\(~E_p = -m \cdot g \cdot h\) .

Energia potencjalna oddziaływania grawitacyjnego

Energia potencjalna oddziaływania grawitacyjnego układu dwóch punktów materialnych z masami M I M, położony w pewnej odległości R jedno od drugiego jest równe

\(~E_p = G \cdot \frac(M \cdot m)(r)\) . (jedenaście)

Gdzie G jest stałą grawitacji i zerem energii potencjalnej odniesienia ( mi p = 0) przyjęte o godz R = ∞.

Energia potencjalna oddziaływania grawitacyjnego ciała z masą M z Ziemią, gdzie H– wysokość ciała nad powierzchnią ziemi, M e – masa Ziemi, R e jest promieniem Ziemi i wybiera się zero odczytu energii potencjalnej H = 0.

\(~E_e = G \cdot \frac(M_e \cdot m \cdot h)(R_e \cdot (R_e +h))\) . (12)

Pod tym samym warunkiem wyboru zera odniesienia jest energia potencjalna oddziaływania grawitacyjnego ciała z masą M z Ziemią na małych wysokościach H (H « R e) równe

\(~E_p = m \cdot g \cdot h\) ,

gdzie \(~g = G \cdot \frac(M_e)(R^2_e)\) jest wielkością przyspieszenia grawitacyjnego w pobliżu powierzchni Ziemi.

Energia potencjalna ciała odkształconego sprężyście

Obliczmy pracę wykonaną przez siłę sprężystości, gdy odkształcenie (wydłużenie) sprężyny zmienia się od określonej wartości początkowej X 1 do wartości końcowej X 2 (ryc. 4, b, c).

Siła sprężystości zmienia się wraz z odkształceniem sprężyny. Aby obliczyć pracę wykonaną przez siłę sprężystości, można przyjąć średnią wartość modułu siły (ponieważ siła sprężystości zależy liniowo od X) i pomnóż przez moduł przemieszczenia:

\(~A = F_(upr-cp) \cdot (x_1 - x_2)\) , (13)

gdzie \(~F_(upr-cp) = k \cdot \frac(x_1 - x_2)(2)\) . Stąd

\(~A = k \cdot \frac(x_1 - x_2)(2) \cdot (x_1 - x_2) = k \cdot \frac(x^2_1 - x^2_2)(2)\) lub \(~A = -\left(\frac(k \cdot x^2_2)(2) - \frac(k \cdot x^2_1)(2) \right)\) . (14)

Nazywa się wielkość fizyczną równą połowie iloczynu sztywności ciała przez kwadrat jego odkształcenia energia potencjalna ciało odkształcone sprężyście:

\(~E_p = \frac(k \cdot x^2)(2)\) . (15)

Ze wzorów (14) i (15) wynika, że ​​praca siły sprężystej jest równa zmianie energii potencjalnej ciała odkształconego sprężyście, przyjętej ze znakiem przeciwnym:

\(~A = -(E_(p2) - E_(p1))\) . (16)

Jeśli X 2 = 0 i X 1 = X, zatem, jak widać ze wzorów (14) i (15),

\(~E_p = A\) .

Fizyczne znaczenie energii potencjalnej ciała odkształconego

energia potencjalna ciała odkształconego sprężyście jest równa pracy wykonanej przez siłę sprężystości, gdy ciało przechodzi do stanu, w którym odkształcenie wynosi zero.

Energia potencjalna charakteryzuje ciała oddziałujące, a energia kinetyczna charakteryzuje ciała poruszające się. Zarówno energia potencjalna, jak i kinetyczna zmieniają się jedynie w wyniku takiego oddziaływania ciał, w którym siły działające na ciała wykonują pracę różną od zera. Rozważmy kwestię zmian energii podczas oddziaływań ciał tworzących układ zamknięty.

Zamknięty system- jest to układ, na który nie działają siły zewnętrzne lub działanie tych sił jest kompensowane. Jeżeli kilka ciał oddziałuje ze sobą tylko za pomocą sił grawitacyjnych i sprężystych i nie działają na nie żadne siły zewnętrzne, to dla wszelkich interakcji ciał praca sił sprężystych lub grawitacyjnych jest równa zmianie energii potencjalnej ciał, przyjętej z przeciwnym znakiem:

\(~A = -(E_(p2) - E_(p1))\) . (17)

Zgodnie z twierdzeniem o energii kinetycznej praca wykonana przez te same siły jest równa zmianie energii kinetycznej:

\(~A = E_(k2) - E_(k1)\) . (18)

Z porównania równości (17) i (18) wynika, że ​​zmiana energii kinetycznej ciał w układzie zamkniętym jest w wartości bezwzględnej równa zmianie energii potencjalnej układu ciał i ma przeciwny znak:

\(~E_(k2) - E_(k1) = -(E_(p2) - E_(p1))\) lub \(~E_(k1) + E_(p1) = E_(k2) + E_(p2) \) . (19)

Prawo zachowania energii w procesach mechanicznych:

suma energii kinetycznej i potencjalnej ciał tworzących układ zamknięty i oddziałujących ze sobą siłami grawitacji i sprężystości pozostaje stała.

Nazywa się sumą energii kinetycznej i potencjalnej ciał całkowita energia mechaniczna.

Dajmy najprostsze doświadczenie. Rzućmy stalową kulę w górę. Podając prędkość początkową υ inch, nadamy mu energię kinetyczną, dlatego zacznie rosnąć w górę. Działanie grawitacji prowadzi do zmniejszenia prędkości piłki, a co za tym idzie, jej energii kinetycznej. Ale piłka wznosi się coraz wyżej i zdobywa coraz więcej energii potencjalnej ( mi p = m∙g∙h). Zatem energia kinetyczna nie znika bez śladu, ale zamienia się w energię potencjalną.

W momencie osiągnięcia najwyższego punktu trajektorii ( υ = 0) piłka jest całkowicie pozbawiona energii kinetycznej ( mi k = 0), ale jednocześnie jego energia potencjalna staje się maksymalna. Następnie piłka zmienia kierunek i porusza się w dół ze zwiększającą się prędkością. Teraz energia potencjalna jest zamieniana z powrotem na energię kinetyczną.

Ujawnia prawo zachowania energii znaczenie fizyczne koncepcje praca:

praca sił grawitacyjnych i sprężystych jest z jednej strony równa wzrostowi energii kinetycznej, a z drugiej strony spadkowi energii potencjalnej ciał. Dlatego praca jest równa energii przetworzonej z jednego rodzaju na drugi.

Prawo zmiany energii mechanicznej

Jeżeli układ oddziałujących ze sobą ciał nie jest zamknięty, to jego energia mechaniczna nie jest zachowana. Zmiana energii mechanicznej takiego układu jest równa działaniu sił zewnętrznych:

\(~A_(vn) = \Delta E = E - E_0\) . (20)

Gdzie mi I mi 0 – sumaryczna energia mechaniczna układu odpowiednio w stanie końcowym i początkowym.

Przykładem takiego układu jest układ, w którym wraz z siłami potencjalnymi działają siły niepotencjalne. Siły niepotencjalne obejmują siły tarcia. W większości przypadków, gdy kąt pomiędzy siłą tarcia F R ciało jest π radianów, praca wykonana przez siłę tarcia jest ujemna i równa

\(~A_(tr) = -F_(tr) \cdot s_(12)\) ,

Gdzie S 12 – ścieżka ciała pomiędzy punktami 1 i 2.

Siły tarcia podczas ruchu układu zmniejszają jego energię kinetyczną. W rezultacie energia mechaniczna zamkniętego układu niekonserwatywnego zawsze maleje, zamieniając się w energię niemechanicznych form ruchu.

Przykładowo samochód poruszający się po poziomym odcinku drogi po wyłączeniu silnika pokonuje pewien dystans i zatrzymuje się pod wpływem sił tarcia. Energia kinetyczna ruchu do przodu samochodu stała się równa zeru, a energia potencjalna nie wzrosła. Kiedy samochód hamował, klocki hamulcowe, opony samochodowe i asfalt nagrzewały się. W rezultacie w wyniku działania sił tarcia energia kinetyczna samochodu nie zanikła, ale zamieniła się w energię wewnętrzną ruch termiczny Cząsteczki

Prawo zachowania i przemiany energii

W każdej interakcji fizycznej energia ulega przemianie z jednej formy w drugą.

Czasami kąt pomiędzy siłą tarcia F tr i przemieszczenie elementarne Δ R jest równa zeru, a praca siły tarcia jest dodatnia:

\(~A_(tr) = F_(tr) \cdot s_(12)\) ,

Przykład 1. Niech siła zewnętrzna F działa na blok W, który można przesuwać na wózku D(ryc. 5). Jeśli wózek przesunie się w prawo, wówczas praca wykonana przez siłę tarcia ślizgowego F tr2 działający na wózek od strony bloku jest dodatni:

Przykład 2. Kiedy koło się toczy, jego siła tarcia tocznego skierowana jest wzdłuż ruchu, ponieważ punkt styku koła z powierzchnią poziomą porusza się w kierunku przeciwnym do kierunku ruchu koła, a praca siły tarcia jest dodatnia (ryc. 6):

Literatura

1. Kabardin O.F. Fizyka: Odniesienia. materiały: podręcznik. podręcznik dla studentów. – M.: Edukacja, 1991. – 367 s.
2. Kikoin I.K., Kikoin A.K. Fizyka: Podręcznik. dla 9 klasy. średnio szkoła – M.: Prosveshchenie, 1992. – 191 s.
3. Podręcznik do fizyki elementarnej: Proc. dodatek. W 3 tomach / wyd. G.S. Landsberg: tom 1. Mechanika. Ciepło. Fizyka molekularna. – M.: Fizmatlit, 2004. – 608 s.
4. Yavorsky B.M., Seleznev Yu.A. Podręcznik informacyjny po fizyce dla osób rozpoczynających naukę na uniwersytetach i samokształceniu. – M.: Nauka, 1983. – 383 s.

2.4.1. Energia kinetyczna układ mechaniczny. Energia kinetyczna materialnego punktu masy poruszającego się z prędkością nazywa się ilością

Energia kinetyczna układu mechanicznego jest sumą energii kinetycznych punktów materialnych wchodzących w skład tego układu:

W przypadkach, gdy masa układu jest rozłożona w sposób ciągły, sumowanie w wyrażeniu (7) zastępuje się całkowaniem po obszarze rozkładu.

Zależność pomiędzy wartościami energii kinetycznej układu mechanicznego w dwóch układach odniesienia, z których jeden jest nieruchomy, a drugi porusza się translacyjnie z prędkością , gdzie punkt C jest środkiem masy układu mechanicznego, wyraża się wzorem Twierdzenie Koeniga:

. (8)

Tutaj - energia kinetyczna układu mechanicznego w ruchomym układzie współrzędnych.

Korzystanie z wyrażeń (6, 7, 8) pozwala na pisanie wzorów do obliczania energii kinetycznej solidny:

Kiedy ciało o masie porusza się do przodu z dużą prędkością

Podczas obrotu z prędkością kątową wokół ustalonej osi ciała z momentem bezwładności

w ruchu płasko-równoległym ciała sztywnego z prędkością kątową przy wartości centralnego momentu bezwładności względem osi prostopadłej do płaszczyzny ruchu oraz wartości momentu bezwładności względem chwilowej osi obrotu

. (11)

2.4.2. Charakterystyka energetyczna. Charakterystyka energetyczna siły obejmuje jej moc, pracę i energię potencjalną.

Moc siła, której punkt przyłożenia porusza się z prędkością, nazywa się wielkością

Stanowisko wytrzymałość w przedziale elementarnym czasu, a elementarne przesunięcie punktu przyłożenia odpowiadające temu okresowi czasu określa reguła

Praca wytrzymałość w skończonym odstępie czasu czas i odpowiednia zmiana promienia - wektor punktu przyłożenia tej siły od do - nazywa się wielkością

. (14)

W podobny sposób oblicza się pracę wykonaną przez moment pary sił.

Energię potencjalną definiuje się tylko w przypadkach, gdy wyrażenie (13) jest różniczką całkowitą:

Gdy warunek (15) jest spełniony, mówimy, że siła jest potencjalna. Relacje łączące rzuty siły na oś wybranego układu współrzędnych z funkcją:

Jeżeli punkt przyłożenia siły przesunął się z położenia na położenie , to całkując (15) możemy otrzymać

. (17)

Uwaga: energię potencjalną określa się do stałego terminu; Zaobserwowana cecha pozwala nam przyjąć, że energia potencjalna jest równa zeru w wybranym przez nas punkcie (np. w początku współrzędnych).

W przypadku, gdy dla zbioru sił działających na układ mechaniczny można zapisać wyrażenie na energię potencjalną, układ mechaniczny nazywa się konserwatywny. Takie układy mechaniczne mają ważne cechy - działanie siły aktywne nie zależy od rodzaju trajektorii i prawa ruchu po niej; pracować w ruchu pętla zamknięta równy zeru.

Warunki, w jakich istnieje funkcja:

2.4.3. Twierdzenie o zmianie energii kinetycznej. Zapisanie twierdzenia o zmianie energii kinetycznej układu mechanicznego w postaci różniczkowej:

Pochodna czasowa energii kinetycznej układu mechanicznego jest równa mocy sił zewnętrznych i wewnętrznych.

Całkowa postać zapisu twierdzenia o zmianie energii kinetycznej

, (20)

Gdzie ; ; ; .

W szczególnym przypadku, gdy wyrażenie na energię potencjalną można zapisać na sumę sił zewnętrznych i wewnętrznych układu, spełniona jest zasada zachowania całkowitej energii mechanicznej

a sam system okazuje się konserwatywny.

PRZYKŁAD 3. Dla układu mechanicznego pokazanego na rys. 2 otrzymaj równanie różniczkowe ruch ładunku.

ROZWIĄZANIE. Skorzystajmy z twierdzenia o zmianie energii kinetycznej w postaci różniczkowej (19). Uwolnijmy się mentalnie od połączeń, stosując odpowiednie reakcje na ciała układu mechanicznego (patrz rys. 2). Uwaga: siły przyłożone do nieruchomego środka masy bloku współosiowego nie są przedstawione, ponieważ ich moc wynosi zero.

Utwórzmy wyrażenie na energię kinetyczną układu mechanicznego.

Forma integralna (ostateczna).. Twierdzenie o zmianie energii kinetycznej punktu materialnego: zmiana energii kinetycznej punktu materialnego przy pewnym jego przemieszczeniu jest równa sumie algebraicznej pracy wszystkich sił działających na ten punkt przy tym samym przemieszczeniu.

Sformułowano twierdzenie o zmianie energii kinetycznej układu mechanicznego: zmiana energii kinetycznej układu mechanicznego podczas przemieszczania się z jednego położenia do drugiego jest równa sumie pracy wszystkich sił zewnętrznych i wewnętrznych przyłożonych do układu podczas tego ruchu:

W przypadku układu niezmiennego suma pracy wykonanej przez siły wewnętrzne przy dowolnym przemieszczeniu jest równa zeru (), wówczas

Prawo zachowania energii mechanicznej. Gdy układ mechaniczny porusza się pod wpływem sił posiadających potencjał, zmiany energii kinetycznej układu wyznaczają zależności:

Gdzie ,

Suma energii kinetycznej i potencjalnej układu nazywa się całkowita energia mechaniczna systemy.

Zatem, Kiedy układ mechaniczny porusza się w stacjonarnym polu potencjalnym, całkowita energia mechaniczna układu podczas ruchu pozostaje niezmieniona.

Zadanie. Układ mechaniczny pod wpływem grawitacji wchodzi w ruch ze stanu spoczynku. Biorąc pod uwagę tarcie ślizgowe ciała 3, pomijając inne siły oporu oraz masy nitek przyjęte za nierozciągliwe, wyznacz prędkość i przyspieszenie ciała 1 w chwili, gdy droga przez nie przebyta stanie się równa S(ryc. 3.70).

W zadaniu zaakceptuj:

Rozwiązanie. Na układ mechaniczny działają siły czynne , , . Stosując zasadę uwolnienia układu od ograniczeń, pokażemy reakcje podpory przegubowo-nieruchomej 2 i chropowatej, nachylonej powierzchni. Przedstawiamy kierunki prędkości ciał układu biorąc pod uwagę fakt, że ciało 1 maleje.

Rozwiążmy problem stosując twierdzenie o zmianie energii kinetycznej układu mechanicznego:

Gdzie T i jest energią kinetyczną układu w położeniu początkowym i końcowym; - algebraiczna suma pracy wykonanej przez siły zewnętrzne przyłożone do układu w celu przemieszczenia układu z położenia początkowego do położenia końcowego; - suma pracy wykonanej przez siły wewnętrzne układu przy tym samym przemieszczeniu.

Dla rozważanego układu składającego się z absolutnie sztywnych ciał połączonych nierozciągliwymi gwintami:

Ponieważ układ znajdował się w spoczynku w położeniu początkowym, wówczas . Stąd:

Energia kinetyczna układu jest sumą energii kinetycznych ciał 1, 2, 3:

Energia kinetyczna ładunku 1 poruszającego się do przodu jest równa:

Energia kinetyczna bloku 2 obracającego się wokół osi Oz, prostopadle do płaszczyzny rysunku:

Energia kinetyczna ciała 3 w ruchu do przodu:

Zatem,

Wyrażenie na energię kinetyczną zawiera nieznane prędkości wszystkich ciał w układzie. Definicja musi zaczynać się od . Pozbądźmy się niepotrzebnych niewiadomych tworząc równania połączeń.

Równania więzów to nic innego jak zależności kinematyczne pomiędzy prędkościami i ruchami punktów w układzie. Tworząc równania więzów, wyrazimy wszystkie nieznane prędkości i ruchy ciał układu poprzez prędkość i ruch obciążenia 1.

Prędkość dowolnego punktu na obrzeżu o małym promieniu jest równa prędkości ciała 1 oraz iloczynowi prędkości kątowej ciała 2 i promienia obrotu R:

Stąd wyrażamy prędkość kątową ciała 2:

Prędkość obrotowa dowolnego punktu na krawędzi klocka o dużym promieniu jest z jednej strony równa iloczynowi prędkości kątowej klocka i promienia obrotu, a z drugiej strony prędkości ciała 3 :

Podstawiając wartość prędkości kątowej, otrzymujemy:

Całkując wyrażenia (a) i (b) w warunkach początkowych, zapisujemy stosunek przemieszczeń punktów układu:

Znając podstawowe zależności prędkości punktów układu wracamy do wyrażenia energii kinetycznej i podstawiamy do niej równania (a) i (b):

Moment bezwładności ciała 2 jest równy:

Podstawiając wartości mas ciał i moment bezwładności ciała 2 piszemy:

Wyznaczenie sumy pracy wszystkich sił zewnętrznych układu przy zadanym przemieszczeniu.

Teraz, zgodnie z twierdzeniem o zmianie energii kinetycznej układu mechanicznego, przyrównujemy wartości T I

Prędkość ciała 1 obliczamy z wyrażenia (g)

Przyspieszenie ciała 1 można wyznaczyć różniczkując równość (g) ze względu na czas.

Energia kinetyczna układu mechanicznego jest sumą energii kinetycznych wszystkich jego punktów materialnych:

Obliczmy różnicę na podstawie wyrażenia energii kinetycznej i wykonajmy kilka prostych przekształceń:

Opuszczenie wartości pośrednie i korzystając z wprowadzonego wcześniej symbolu dla oznaczenia pracy elementarnej piszemy:

Zatem różnica energii kinetycznej układu mechanicznego równa sumie prace elementarne wszystkich sił zewnętrznych i wewnętrznych działających na punkty układu. Taka jest treść twierdzenia o zmianie energii kinetycznej.

Należy zauważyć, że w ogólnym przypadku suma pracy wykonanej przez siły wewnętrzne układu nie jest równa zeru. Zanika ono tylko w niektórych szczególnych przypadkach: gdy układ jest ciałem absolutnie sztywnym; układ ciał absolutnie sztywnych współdziałających za pomocą elementów nieodkształcalnych (idealne zawiasy, absolutnie sztywne pręty, nierozciągliwe gwinty itp.). Z tego powodu twierdzenie o zmianie energii kinetycznej jest jedynym z ogólnych twierdzeń dynamiki, które uwzględnia wpływ sił wewnętrznych.

Można interesować się zmianą energii kinetycznej nie w nieskończenie małym okresie czasu, jak to zrobiono powyżej, ale w pewnym skończonym okresie czasu. Następnie stosując integrację możemy otrzymać:

Tutaj - odpowiednio wartości energii kinetycznej w momentach czasu - suma całkowitej pracy sił zewnętrznych i wewnętrznych w rozpatrywanym okresie czasu.

Otrzymana równość wyraża twierdzenie o zmianie energii kinetycznej w postaci końcowej (całkowej), które można sformułować w następujący sposób: zmiana energii kinetycznej podczas przejścia układu mechanicznego z jednego położenia do drugiego jest równa sumie całkowita praca wszystkich sił zewnętrznych i wewnętrznych.

Wykład 5. Twierdzenie o zmianie energii kinetycznej

5. 1. Praca siły

Niech moc – wypadkowa wszystkich sił układu, przyłożona do punktu P, oraz ( dx, dy, dz) – elementarny ruch punktu P po trajektorii P 1 P 2 (rys. 5.1). Praca podstawowa DA siły się nazywają produkt skalarny

Praca elementarna jest wielkością skalarną. Jeśli jest kątem między siłą a kierunkiem przemieszczenia , wówczas wyrażenie (5.1) można przedstawić jako

gdzie jest rzutem siły na kierunek elementarnego przemieszczenia (lub kierunek prędkości punktowej).

Znak pracy elementarnej zależy od znaku funkcji. Jeśli jest kątem ostrym, to , Jeśli jest kątem rozwartym, to , Jeśli , to .

Niech chodzi R wykonuje ostateczny ruch z pozycji do pozycji, opisując łuk. Podzielmy łuk na N dowolne małe sekcje, wskazując długość sekcji z numerem k Poprzez . Następnie elementarna praca siły na k- przekrój będzie równy , a od do - ilości pracy w poszczególnych przekrojach

Dokładną wartość pracy uzyskujemy przechodząc do limitu pod warunkiem podania ilości odcinków N rośnie w nieskończoność, a długość każdej sekcji maleje:

.

Taka granica nazywana jest całką krzywoliniową pierwszego rodzaju wzdłuż łuku i jest zapisywana w następujący sposób

. (5.3)

Rezultatem integracji jest dzieło kompletne A wytrzymałość F na rozważanym skończonym przemieszczeniu wzdłuż ścieżki.

5. 1. 1. Praca ciężkości

Pozwalać M – masa punktowa, G- przyśpieszenie grawitacyjne. Następnie

Obliczając pracę za pomocą wzorów (5.1) i (5.3), mamy

gdzie jest wysokość opadania punktu.

Kiedy zatem punkt wzrośnie, .

5. 1. 2. Praca liniowej siły sprężystej

Niech materialny punkt R porusza się wzdłuż osi Oh(Rys. 5.3) pod działaniem sprężyny, do której jest przymocowany. Jestem gruby , , wówczas sprężyna ulega odkształceniu i dla małych odchyleń punktu można przyjąć, że działa na nią siła sprężysta od strony sprężyny. Następnie praca siły sprężystości przy przemieszczeniu X 0 X 1 będzie równe

. (5.5)

Praca siły sprężystej jest równa połowie iloczynu współczynnika sztywności i różnicy kwadratów początkowego i końcowego wydłużenia (lub ściskania) sprężyny.

5. 1. 3. Elementarna praca sił przyłożonych do ciała stałego

Rozważmy ruch ciała w płaszczyźnie. Pozwalać O– dowolnie wybrany punkt na ciele bryłowym (rys. 5.4). Nazwijmy to słupem. Wówczas ruch ciała w płaszczyźnie można przedstawić jako sumę najprostszego ruchu postępowego wraz z biegunem oraz obrotu ciała wokół bieguna. Następnie prędkość punktu względem ustalonego układu współrzędnych zostanie wyznaczona jako suma geometryczna dwóch prędkości

gdzie jest prędkością bieguna, jest wektorem prędkości kątowej ciała sztywnego, jest prędkością Eulera, czyli prędkością punktu obracającego się wokół bieguna.

Będziemy przedstawiać ciało stałe jako układ mechaniczny składający się z N poszczególne punkty, których wzajemna odległość nie ulega zmianie.

Obliczmy przemieszczenie punktu pod wpływem siły:

Następnie .

Praca elementarna, zgodnie z (5.1), zostanie zapisana w następujący sposób

Wykorzystanie właściwości iloczynu mieszanego wektorów , przepisujemy ostatnie wyrażenie w formularzu

Niech będzie wypadkową wszystkich sił zewnętrznych i wewnętrznych (ryc. 5.4), przyłożonych w pewnym punkcie ciała, tj.

.

Wtedy (a) zostanie zapisane w ten sposób

Zgodnie z (3.1 i 3.2), wektor główny a główny moment sił wewnętrznych układu jest równy zeru, otrzymujemy

Tutaj: – wektor główny, – główny moment sił zewnętrznych względem punktu O.

Specjalne przypadki

A. Ruch postępowy ciała sztywnego. Wszystkie punkty ciała mają takie same przemieszczenia (ryc. 5.5, a) zarówno pod względem wielkości, jak i kierunku, wówczas z (5.6) otrzymujemy (tutaj):

. (5.7)

B. Obrót ciała sztywnego wokół ustalonej osi. Niech oś z przechodzi przez słup O(Rys. 5.5b). Następnie , ; z (5.6) otrzymujemy

. (5.8)

Przykład. Masa cewki M i promień R napędzany stałą siłą F, zastosowany w tym punkcie A(ryc. 5.6). Kołowrotek toczy się w prawo bez poślizgu na nierównej powierzchni.

Oblicz pracę wszystkich sił zewnętrznych, jeśli środek cewki przesunął się o pewną odległość, - współczynnik tarcia tocznego, - siłę tarcia, r - promień rdzenia cewki, na który przyłożona jest ta siła.

Rozwiązanie. Cewka porusza się ruchem płaskim. Ponieważ toczenie odbywa się bez poślizgu, chwilowy środek prędkości znajduje się w punkcie styku cewki z płaszczyzną, tj. w tym punkcie R(ryc. 5.6). Skierujmy oś S poziomo w prawo. Zgodnie z kierunkiem ruchu przyjmiemy dodatni kierunek kąta obrotu w kierunku przeciwnym do ruchu wskazówek zegara.

Niech środek cewki Z przeniesie się do. W takim przypadku cewka będzie obracać się pod kątem. Więc skąd

Po zaakceptowaniu tego punktu R dla chwilowej osi obrotu pracę elementarną obliczamy ze wzoru (5.8):

(A)

Tutaj: linie działania sił i mg przecinają zatem oś obrotu; dalej, gdzie N– siła reakcji normalnej.

Aby określić wymaganą pracę, pozostaje przyjąć całkę oznaczoną z (a) w zakresie od 0 do SA. Dostajemy

5. 2. Pole siłowe. Funkcja zasilania. Energia potencjalna

Załóżmy, że punkt porusza się w jakiejś przestrzeni i działa na niego siła z przestrzeni, która zależy od położenia punktu w tej przestrzeni, ale nie zależy od prędkości ruchu punktu. W tym przypadku mówią, że przestrzeń jest dana pole siłowe, a także, że punkt porusza się w polu siłowym. Odpowiednie koncepcje układu punktów materialnych są podobne.

W mechanice często spotyka się siły zależne od położenia punktów ich przyłożenia. Na przykład siła sprężystości przyłożona do punktu materialnego, który porusza się wzdłuż linii poziomej pod działaniem sprężyny. Najważniejszym przykładem pola siłowego w przyrodzie jest pole grawitacyjne: działanie Słońca na planetę o danej masie jest określone w każdym punkcie przestrzeni przez prawo uniwersalna grawitacja.

Pole siłowe nazywa się potencjał, jeśli istnieje funkcja skalarna U, zależnie tylko od współrzędnych , , punkt – punkt układu materialnego (ewentualnie także od czasu), taki, że

Funkcja nazywa się funkcja zasilania.

Rozważmy właściwości funkcji siły.

Praca elementarna (5.1) jest powiązana z funkcją siły w następujący sposób

Zatem, elementarna praca siły w potencjalnym polu siłowym jest równa pełny mechanizm różnicowy z funkcji mocy II.

Pełna praca siły w obszarze od punktu do momentu (Rys.5.1)

te. . (5.10)

Z uzyskanych wyrażeń wynika, że

1. praca wykonana przez siłę w potencjalnym polu siłowym wzdłuż dowolnej zamkniętej ścieżki wynosi zero;

2. działanie siły w potencjalnym polu siłowym zależy jedynie od położenia siły końcowej i początkowej punkty, ale sama ścieżka ruchu nie ma znaczenia.

Energia potencjalna. Energia potencjalna P w rozważanym punkcie pola siłowego R jest pracą wykonaną przez siły pola działające na punkt materialny, gdy ten przemieszcza się z punktu R V punkt wyjścia 1, tj.

P= lub P=

Połączmy funkcję siły U z energią potencjalną. Mamy

Przykłady obliczeń energii potencjalnej

1. Jednolite pole grawitacyjne. Pozwalać M– masa punktowa; G - przyśpieszenie grawitacyjne. Następnie (ryc. 5.2)

2. Elastyczne pole siłowe sprężyny. Niech punkt materialny porusza się wzdłuż osi Oh(Rys. 5.3) pod działaniem sprężyny, do której jest przymocowany. Jeśli sprężyna nie jest odkształcona, to zakładając we wzorze (5.5) otrzymujemy

.

5. 3. Energia kinetyczna

5. 3. 1. Energia kinetyczna układu. Twierdzenie Koeniga

Energia kinetyczna punktu materialnego jest połową iloczynu masy punktu i kwadratu jego prędkości, tj. . Energia kinetyczna jest dodatnią wielkością skalarną. W układzie SI jednostką energii kinetycznej jest dżul: .

Energia kinetyczna układu mechanicznego jest sumą energii kinetycznych wszystkich punktów wchodzących w skład układu:

(5.11)

Prędkości punktów układu (5.1) wyznaczane są względem ustalonego układu odniesienia.

Wyrównajmy początek współrzędnych ze środkiem masy układu. Załóżmy, że układ mechaniczny wraz z układem współrzędnych porusza się translacyjnie względem ustalonego układu współrzędnych (rys. 5.7). Punkt – punkt układu.

Następnie, na podstawie twierdzenia o dodawaniu prędkości, prędkość bezwzględna punktu Rk. zostanie zapisany jako suma wektorów prędkości przenośnej i względnej:

, (A)

gdzie jest prędkością początku poruszającego się układu współrzędnych ( prędkość przenośna, tj. prędkość środka masy układu); – prędkość punktowa Rk względem poruszającego się układu współrzędnych Oooz (prędkość względna).

Podstawiając (a) do wzoru (5.11) otrzymujemy

(5.12)

Oto masa całego układu.

Promień wektora środka masy układu w ruchomym układzie współrzędnych wyznacza się zgodnie z (2.1), – , Gdzie , tj. . Od pochodzenia O jest środkiem masy układu, a następnie , to, tj. druga suma w wyrażeniu (5.12) jest równa zero.

Zatem energia kinetyczna układu (5.12) ma postać

(5.13)

Ta równość decyduje Twierdzenie Koeniga.

Twierdzenie. Energia kinetyczna układu jest równa sumie energii kinetycznej, jaką miałby punkt materialny położony w środku masy układu i mający masę równą masie układu, oraz energię kinetyczną ruchu układu układu względem środka masy.

5. 3. 2. Energia kinetyczna ciała stałego

Ciało sztywne jest szczególnym przypadkiem układu mechanicznego i jest traktowane jako masa o ciągłym rozkładzie, wtedy wszystkie sumy zawarte w wyrażeniu na energię kinetyczną układu zamieniają się w całki. Zatem dla ciała stałego wzór (5.11) przyjmie postać

. (5.14)

1. Energia kinetyczna ciała sztywnego poruszającego się do przodu.

Przy tego rodzaju ruchu prędkości we wszystkich punktach ciała są takie same (ryc. 5.8). Wyjmując znak całki ze wzoru (5.14), otrzymujemy

. (5.15)

Energia kinetyczna ciała sztywnego poruszającego się postępowo jest równa połowie iloczynu masy ciałaMprzez kwadrat jego prędkości.

2. Energia kinetyczna ciała sztywnego obracającego się wokół ustalonej osi

Moduł prędkości V dowolnego punktu ciała sztywnego obracającego się wokół ustalonej osi jest równe , gdzie jest modułem prędkości kątowej ciała sztywnego, jest odległością punktu od osi obrotu z(ryc. 5.9). Podstawiając do wzoru (5.14), otrzymujemy

Tutaj – moment bezwładności ciała stałego względem osi z.

Energia kinetyczna ciała sztywnego obracającego się wokół ustalonej osi jest równa połowie iloczynu momentu bezwładności ciała względem osi obrotu i kwadratu prędkości kątowej ciała.

3. Energia kinetyczna ciała sztywnego podczas ruchu płasko-równoległego

W ruchu płasko-równoległym prędkość dowolnego punktu na ciele składa się z suma geometryczna prędkość bieguna i prędkość punktu podczas obrotu wokół bieguna. Pozwól ciału poruszać się płasko w płaszczyźnie Oksy, Następnie

|| . Jako biegun wybieramy środek masy ciała, wówczas we wzorze (5.13) prędkość jest prędkością punktu k ciało podczas jego obrotu względem bieguna (środka masy) i jest równe , gdzie jest odległość k- och, wskaż słup. Następnie (5.13) zostanie przepisany

Mając na uwadze – moment bezwładności ciała względem osi z przechodząc przez słup Z, ostatnie wyrażenie można przepisać jako

, (5.17)

w ruchu płasko-równoległym energia kinetyczna jest sumą energii kinetycznej ruchu postępowego wraz ze środkiem masy oraz energii kinetycznej obrotu wokół osi przechodzącej przez środek masy i prostopadłej do płaszczyzny ruchu.

5. 4. Twierdzenie o zmianie energii kinetycznej

5. 4. 1. Twierdzenie o zmianie energii kinetycznej punktu

Znajdźmy związek między pracą a zmianą prędkości. Niech punkt materialny ma masę M porusza się wzdłuż osi Oh pod wpływem siły, np. ściśniętej lub rozprężonej sprężyny, ustalonej w początku współrzędnych - punkt O(ryc. 5.10). Równanie ruchu punktu ma postać

Pomnóżmy obie strony tego równania przez , i, biorąc to pod uwagę , otrzymujemy

. (5.19)

Po prawej stronie tej równości zastępujemy Vx przez i pomnożyć przez dt prawą i lewą stronę. Następnie

. (5.20)

W tej formie równość ma bardzo jasne znaczenie: kiedy punkt zostanie przesunięty o dx, siła działa, w wyniku czego zmienia się jej ilość energia kinetyczna punktu, charakteryzujący ruch punktu, a w szczególności moduł jego prędkości. Jeżeli punkt przemieszcza się z położenia do , a jego prędkość zmienia się z do , to całkując (5.20) otrzymujemy

. (5.21)

Biorąc pod uwagę, że , w końcu znajdujemy

. (5.22)

Zmiana energii kinetycznej punktu materialnego podczas dowolnego ruchu jest równa pracy wykonanej przez siłę działającą na punkt podczas tego samego ruchu.

Wykonując wszystkie poprzednie procedury, otrzymujemy

,

tutaj jest łuk, po którym porusza się punkt (ryc. 5.11).

5. 4. 2. Twierdzenie o zmianie energii kinetycznej układu

Niech punkty układu mas przesuną się tak, aby ich wektory promieni w inercjalnym układzie odniesienia otrzymały przyrost. Sprawdźmy jak zmieniła się energia kinetyczna T systemy.

Zgodnie z (5.11) energią kinetyczną układu

.

Obliczmy różnicę energii kinetycznej układu i przekształćmy otrzymane wyrażenie

Tutaj

Biorąc to pod uwagę , gdzie jest przyspieszeniem punktu a i są wypadkową sił zewnętrznych i wewnętrznych przyłożonych do punktu, ostatnią równość zapisujemy w postaci

Zatem,

. (5.23)

Ostatnia równość wyraża twierdzenie o zmianie energii kinetycznej układu mechanicznego w postaci różniczkowej: różnica energii kinetycznej układu jest równa podstawowa praca wszystkie siły układu.

Szczególny przypadek. Dla ciała absolutnie sztywnego suma pracy wszystkich sił wewnętrznych układu jest równa zeru:

.

W konsekwencji twierdzenie o zmianie energii kinetycznej (5.23) ciała sztywnego można zapisać w postaci

Zmiana energii kinetycznej ciała stałego podczas dowolnego elementarnego przemieszczenia jest równa elementarnej pracy sił zewnętrznych działających na ciało.

Jeżeli scałkujemy obie strony (5.24) pomiędzy dwoma położeniami – początkowym i końcowym, w których odpowiednio energia kinetyczna i wynoszą, otrzymamy

. (5.25)

Przykład 1. Masa dysku M= 5 kg a promień wprawiany jest w ruch pod wpływem stałej siły przyłożonej w tym punkcie A(ryc. 5.6). Dysk toczy się po nierównej powierzchni w prawo bez poślizgu. Wyznacz prędkość środka masy Z cewka w chwili przebycia drogi, współczynnik tarcia ślizgowego, promień bezwładności tarczy

Rozwiązanie. Dysk porusza się ruchem płaskim. Zapiszmy twierdzenie o zmianie energii kinetycznej ciała stałego

Obliczmy energię kinetyczną dysku. W początkowej chwili dysk znajdował się w spoczynku, tj. . Energia kinetyczna w końcowym położeniu dysku