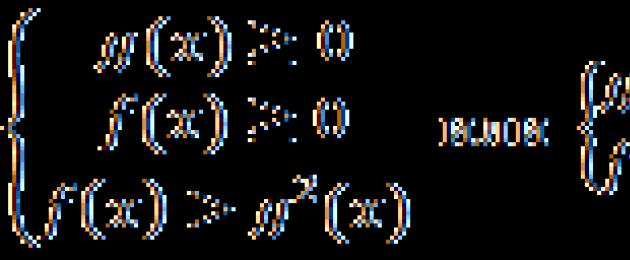Ojämlikheter med kvadratrötter. Att lösa irrationella ojämlikheter

I den här lektionen kommer vi att titta på att lösa irrationella ojämlikheter och ge olika exempel.

Ämne: Ekvationer och ojämlikheter. System av ekvationer och ojämlikheter

Lektion:Irrationella ojämlikheter

När man löser irrationella ojämlikheter är det ganska ofta nödvändigt att lyfta båda sidor av ojämlikheten till viss del, detta är en ganska ansvarsfull operation. Låt oss komma ihåg funktionerna.

Båda sidorna av ojämlikheten kan kvadreras om båda är icke-negativa, först då får vi en sann ojämlikhet från en sann ojämlikhet.

Båda sidorna av ojämlikheten kan kuberas i alla fall, om den ursprungliga ojämlikheten var sann, så får vi den korrekta olikheten när den kuberas.

Betrakta en ojämlikhet i formen:

Det radikala uttrycket måste vara icke-negativt. Funktionen kan ha vilka värden som helst, två fall måste beaktas.

I det första fallet är båda sidorna av ojämlikheten icke-negativa, vi har rätt att kvadrera den. I det andra fallet höger delär negativ, och vi har ingen rätt att göra det. I det här fallet är det nödvändigt att titta på innebörden av ojämlikheten: här är det positiva uttrycket (kvadratroten) större än det negativa uttrycket, vilket innebär att ojämlikheten alltid uppfylls.

Så vi har följande lösningsschema:

I det första systemet skyddar vi inte det radikala uttrycket separat, eftersom när systemets andra ojämlikhet är uppfylld måste det radikala uttrycket automatiskt vara positivt.

Exempel 1 - lösa ojämlikhet:

Enligt diagrammet går vi vidare till en likvärdig uppsättning av två system av ojämlikheter:

Låt oss illustrera:

Ris. 1 - illustration av lösningen till exempel 1

Som vi ser, när vi blir av med irrationalitet, till exempel vid kvadrering, får vi en uppsättning system. Ibland kan denna komplexa design förenklas. I den resulterande uppsättningen har vi rätt att förenkla det första systemet och få en motsvarande uppsättning:

Som en oberoende övning är det nödvändigt att bevisa att dessa uppsättningar är likvärdiga.

Betrakta en ojämlikhet i formen:

I likhet med den tidigare ojämlikheten överväger vi två fall:

I det första fallet är båda sidorna av ojämlikheten icke-negativa, vi har rätt att kvadrera den. I det andra fallet är den högra sidan negativ, och vi har ingen rätt att kvadrera den. I det här fallet är det nödvändigt att titta på innebörden av ojämlikheten: här är det positiva uttrycket (kvadratroten) mindre än det negativa uttrycket, vilket betyder att ojämlikheten är motsägelsefull. Det finns inget behov av att överväga det andra systemet.

Vi har ett likvärdigt system:

Ibland kan irrationella ojämlikheter lösas grafiskt. Denna metod är tillämplig när motsvarande grafer ganska lätt kan konstrueras och deras skärningspunkter kan hittas.

Exempel 2 - lösa ojämlikheter grafiskt:

A)

b)

Vi har redan löst den första ojämlikheten och vet svaret.

För att lösa ojämlikheter grafiskt behöver du konstruera en graf över funktionen på vänster sida och en graf över funktionen på höger sida.

Ris. 2. Grafer över funktioner och

För att plotta en graf för en funktion är det nödvändigt att omvandla parabeln till en parabel (spegla den i förhållande till y-axeln), och flytta den resulterande kurvan 7 enheter åt höger. Grafen bekräftar det denna funktion minskar monotont i sin definitionsdomän.

Grafen för en funktion är en rät linje och är lätt att konstruera. Skärningspunkten med y-axeln är (0;-1).

Den första funktionen minskar monotont, den andra ökar monotont. Om ekvationen har en rot, så är den den enda, det är lätt att gissa det från grafen: .

När värdet på argumentet är mindre än roten är parabeln ovanför den räta linjen. När värdet på argumentet är mellan tre och sju, passerar den räta linjen ovanför parabeln.

Vi har svaret:

Effektiv metod Metoden med intervaller används för att lösa irrationella ojämlikheter.

Exempel 3 - lös ojämlikheter med intervallmetoden:

A)

b)

Enligt intervallmetoden är det nödvändigt att tillfälligt gå bort från ojämlikhet. För att göra detta, flytta allt i den givna olikheten till vänster sida (få noll till höger) och introducera en funktion lika med vänster sida:

Nu måste vi studera den resulterande funktionen.

ODZ:

Vi har redan löst denna ekvation grafiskt, så vi uppehåller oss inte vid att bestämma roten.

Nu är det nödvändigt att välja intervall med konstant tecken och bestämma tecknet för funktionen på varje intervall:

Ris. 3. Konstantintervall för tecken till exempel 3

Låt oss komma ihåg att för att bestämma tecknen på ett intervall är det nödvändigt att ta en testpunkt och ersätta den i funktionen; funktionen kommer att behålla det resulterande tecknet under hela intervallet.

Låt oss kontrollera värdet vid gränspunkten:

Svaret är uppenbart:

Tänk på följande typ av ojämlikheter:

Låt oss först skriva ner ODZ:

Rötterna finns, de är icke-negativa, vi kan kvadrera båda sidor. Vi får:

Vi har ett likvärdigt system:

Det resulterande systemet kan förenklas. När den andra och tredje ojämlikheten uppfylls är den första sann automatisk. Vi har::

Exempel 4 - lösa ojämlikhet:

Vi agerar enligt schemat - vi får ett likvärdigt system.

Varje olikhet som inkluderar en funktion under roten kallas irrationell. Det finns två typer av sådana ojämlikheter:

I det första fallet är roten mindre än funktionen g(x), i det andra är den större. Om g(x) - konstant, är ojämlikheten avsevärt förenklad. Observera: till det yttre är dessa ojämlikheter väldigt lika, men deras lösningssystem är fundamentalt olika.

Idag kommer vi att lära oss hur man löser irrationella ojämlikheter av den första typen - de är de enklaste och mest begripliga. Ojämlikhetstecknet kan vara strikt eller icke-strikt. Följande påstående är sant för dem:

Sats. Varje irrationell ojämlikhet i formen

Motsvarar systemet av ojämlikheter:

Inte svag? Låt oss titta på var detta system kommer ifrån:

1. f (x) ≤ g 2 (x) - allt är klart här. Detta är den ursprungliga ojämlikheten i kvadrat;
2. f (x) ≥ 0 är ODZ för roten. Låt mig påminna dig: den aritmetiska kvadratroten existerar endast från icke-negativ tal;
3. g(x) ≥ 0 är rotens område. Genom att kvadrera ojämlikheten bränner vi bort det negativa. Som ett resultat kan extra rötter dyka upp. Olikheten g(x) ≥ 0 skär bort dem.

Många elever ”hänger sig” på systemets första olikhet: f (x) ≤ g 2 (x) - och glömmer helt bort de andra två. Resultatet är förutsägbart: fel beslut, förlorade poäng.

Eftersom irrationella ojämlikheter är ett ganska komplext ämne, låt oss titta på fyra exempel samtidigt. Från grundläggande till riktigt komplext. Alla problem är tagna från inträdesprov Moscow State University uppkallad efter M.V. Lomonosov.

Exempel på problemlösning

Uppgift. Lös ojämlikheten:

Före oss är en klassiker irrationell ojämlikhet: f(x) = 2x + 3; g(x) = 2 - konstant. Vi har:

Av de tre ojämlikheterna återstod endast två i slutet av lösningen. Eftersom ojämlikheten 2 ≥ 0 alltid gäller. Låt oss korsa de återstående ojämlikheterna:

Så, x ∈ [−1,5; 0,5]. Alla punkter är skuggade eftersom ojämlikheterna är inte strikta.

Uppgift. Lös ojämlikheten:

Vi tillämpar satsen:

Låt oss lösa den första ojämlikheten. För att göra detta kommer vi att avslöja kvadraten på skillnaden. Vi har:

2x 2 − 18x + 16< (x − 4) 2 ;
2x 2 − 18x + 16< x 2 − 8x + 16:
x 2 - 10x< 0;
x (x - 10)< 0;
x ∈ (0; 10).

Låt oss nu lösa den andra ojämlikheten. Där med kvadratisk trinomial:

2x 2 - 18x + 16 ≥ 0;
x 2 - 9x + 8 ≥ 0;
(x - 8) (x - 1) ≥ 0;
x ∈ (−∞; 1]∪∪∪∪)