Контрольная работа для заочного отделения
Данко, П. Е. Высшая математика в упражнениях и задачах: в 2 ч. / П.Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 5-е изд., испр. - М.: Высшая школа.Ч.1.-1998.-304с.
Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. -12-е издание. – СПб.: Лань, 2005.- 736 с
Б.М. Владимирский, А.Б. Горстко, Я.М. Ерусалимский. Математика: общий курс. – СПб.: Изд-во «Лань», 2002. – 954 с.
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - 5-е изд., стереотип. - М.: Наука, 1978. - 632с.
Демидович Б.П. Краткий курс высшей матетматики: Учебное пособие для вузов - M.: OOO «Издательство Астрель»: OOO «Издательство АСТ», 2001. - 656с.
Пискунов Н.С. Дифференциальные и интегральные исчисления: Учеб. для втузов. В 2-ч т. Т.II: - М.: Интеграл–Пресс, 2004. -544 с.
Введение.
Выполнять контрольную работу следует строго по графику. Каждый студент выполняет контрольную работу под вариантом, номер которого совпадает с его порядковым номером в групповом журнале. Решение задач нужно предоставить в письменном виде на отдельных листах (формата А 4, в скрепленном виде). Сдавать работу можно как в печатном, так и в письменном виде. Выполняя к.р. , студент должен переписать условие соответствующей задачи, написать подробное решение, выделив ответ. Там, где это необходимо, дать краткие пояснения по ходу решения.
«ЧИСЛОВЫЕ и ФУНКЦИОНАЛЬНЫЕ РЯДЫ»
Числовые ряды. Достаточные признаки их сходимости
Пусть u 1 , u 2 , u 3 , … , u n , …, где u n = f (n ), –– бесконечная числовая последовательность. Выражение u 1 + u 2 + u 3 + … + u n + … называется бесконечным числовым рядом , а числа u 1 , u 2 , u 3 , … , u n , … –– членами ряда; u n = f (n ) называется общим членом . Ряд часто записывают в виде .
Сумму первых n членов числового ряда обозначают через S n и называют n -й частичной суммой ряда :
Ряд называется сходящимся , если его n -я частичная сумма S n при неограниченном возрастании n стремится к конечному пределу, т.е. если . Число S называют суммой ряда . Если же n -я частичная сумма ряда при не стремится к конечному пределу, то ряд называют расходящимся .
Ряд , составленный из членов любой убывающей геометрической прогрессии, является сходящимся и имеет сумму .
Ряд , называемый гармоническим , расходится.
Необходимый признак сходимости. Если ряд сходится, то , т.е. при предел общего члена сходящегося ряда равен нулю.
Таким образом, если , то ряд расходится.
Перечислим важнейшие признаки сходимости и расходимости рядов с положительными членами.
Первый признак сравнения. Пусть даны два ряда
причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. . Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).
Этот признак остается в силе, если неравенства выполняются не при всех n , а лишь начиная с некоторого номера n = N .
Второй признак сравнения. Если существует конечный отличный от нуля предел , то ряды и одновременно сходятся или расходятся.
Радикальный признак Коши. Если для ряда
существует , то этот ряд сходится при , расходится при .
Признак Даламбера. Если для ряда существует , то этот ряд сходится при , расходится при .
Интегральный признак Коши. Если f (x ) при –– непрерывная положительная и монотонно убывающая функция, то ряд , где сходится или расходится в зависимости от того, сходится или расходится интеграл .
Рассмотрим теперь ряды, члены которых имеют чередующиеся знаки, т.е. ряды вида , где .
Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, а общий член стремится к нулю. То есть, если выполняются следующие два условия: 1) и 2) .
Возьмем n -ю частичную сумму сходящегося знакочередующегося ряда, для которого выполняется признак Лейбница:
Пусть –– n -й остаток ряда. Его можно записать как разность между суммой ряда S и n -й частичной суммой S n , т.е. . Нетрудно видеть, что
Величина оценивается с помощью неравенства .
Остановимся теперь на некоторых свойствах знакопеременных рядов (т.е. знакочередующихся рядов и рядов с произвольным чередованием знаков своих членов).
Знакопеременный ряд сходится, если сходится ряд .
В этом случае исходный ряд называется абсолютно сходящимся .
Сходящийся ряд называется условно сходящимся , если ряд расходится.
Пример 1. Исследовать сходимость ряда
Решение. Данный ряд составлен из членов бесконечно убывающей геометрической прогрессии и поэтому сходится. Найдем его сумму. Здесь , (знаменатель прогрессии). Следовательно,
Пример 2. Исследовать сходимость ряда .
Решение. Данный ряд получен из гармонического отбрасыванием первых десяти членов. Следовательно, он расходится.
Пример 3. Исследовать сходимость ряда . , –– ряд сходится.
$\sum \limits _{n=1}^{\infty }a_{n} $, члены которого удовлетворяют трём условиям:
- $a_{n} >0,\, \, \, n\ge 1$, т.е. исходный ряд с положительными членами;
- члены ряда монотонно убывают, т.е. $a_{1} >a_{2} >\ldots >a_{n-1} >a_{n} >\ldots >0$;
- общий член ряда стремится к нулю: $\mathop{\lim }\limits_{n\to \infty } a_{n} =0$.
Пусть существует непрерывная, монотонно убывающая, определ ённая при $x\ge 1$ функция f(x), такая что $f\left(1\right)=a_{1} ,\, \, \, f\left(2\right)=a_{2} ,\, \, \, \ldots ;\, \, \, f\left(n\right)=a_{n} ,\, \, \, \ldots $, т.е. $\sum \limits _{n=1}^{\infty }a_{n} =\sum \limits _{n=1}^{\infty }f(n) $. Тогда, если несобственный интеграл $\int \limits _{1}^{+\infty }f\left(x\right){\rm d}x $ сходится, то ряд $\sum \limits _{n=1}^{\infty }a_{n} $ тоже сходится; если указанный интеграл расходится, то этот ряд расходится.
Замечание 1
Теорема остаётся верной и тогда, когда её условия выполняются не для всех членов ряда, а лишь начиная с k-го ($n\ge k$), в таком случае рассматривается интеграл $\int \limits _{k}^{+\infty }f\left(x\right)\, {\rm d}x $.
Замечание 2
Интегральный признак Коши существенно облегчает исследование сходимости ряда, так как позволяет свести этот вопрос к выяснению сходимости интеграла от удачно подобранной соответствующей функции $f(x)$, что легко выполняется, применяя методы интегрального исчисления.
Теорема 2 (радикальный признак Коши)
Пусть дан ряд с положительными членами $\sum \limits _{n=1}^{\infty }a_{n} ,\, \, \, a_{n} >0$ и пусть существует конечный предел $\mathop{\lim }\limits_{n\to \infty } \sqrt[{n}]{a_{n} } =l.$Тогда:
- если $l
- если $l>1$, ряд расходится,
- если $l=1$, то для выяснения сходимости ряда радикальный признак Коши не применим.
Доказательство
- Пусть существует $\mathop{\lim }\limits_{n\to \infty } \sqrt[{n}]{a_{n} } =l0$, то $l\ge 0$. Рассмотрим число q такое, что $l 0$ существует $N=N({\rm \varepsilon })\in $N, начиная с которого $\forall n \ge N$ выполняется неравенство $\left|\sqrt[{n}]{a_{n} } -l\right|
$\sum \limits _{n=1}^{\infty }a_{n} =\, a_{1} +\, a_{2} +\ldots +\, a_{N} +\, a_{N+1} +a_{N+2} +...$ . (1)
Составим новый ряд
$\sum \limits _{k=0}^{\infty }q^{N+k} =q^{N} +\, q^{N+1} +q^{N+2} +\ldots $ (2)
Ряд (2) представляет собой ряд геометрической прогрессии со знаменателем $q$: $0\le q
- Пусть существует $\mathop{\lim }\limits_{n\to \infty } \sqrt[{n}]{a_{n} } =l>1$. Начиная с некоторого $N=N({\rm \varepsilon })\in {\rm N}$ $\forall n\ge N$, $\, \, \sqrt[{n}]{a_{n} } >1\, \, \, \Rightarrow \, \, \, \, a_{n} >1$, т.е. $\mathop{\lim }\limits_{n\to \infty } a_{n} \ne 0$, тогда исходный ряд расходится по необходимому признаку сходимости.
- Если $\mathop{\lim }\limits_{n\to \infty } \sqrt[{n}]{a_{n} } =l=1$ (или не существует), то для выяснения сходимости ряда радикальный признак Коши не применим.
Теорема доказана.
Теорема 3 (признак Даламбера)
Пусть дан ряд с положительными членами $\sum \limits _{n=1}^{\infty }a_{n} \, \, \, (a_{n} >0) $, и существует конечный предел $\mathop{\lim }\limits_{n\to \infty } \frac{a_{n+1} }{a_{n} } =l$, тогда:
- ряд $\sum \limits _{n=1}^{\infty }a_{n} $ сходится, если $l
- ряд $\sum \limits _{n=1}^{\infty }a_{n} $ расходится, если $l>1$,
- если $l=1$, то для выяснения сходимости ряда признак Даламбера не применим.
Доказательство
- Пусть предел $\mathop{\lim }\limits_{n\to \infty } \frac{a_{n+1} }{a_{n} } =l$ существует и $0\le l 0$ существует $N({\rm \varepsilon })\in $N, начиная с которого $\forall n\ge N=N({\rm \varepsilon })$ выполняется неравенство $\left|\frac{a_{n+1}} {a_n}-l\right|
Запишем исходный ряд $\sum \limits _{n=1}^{\infty }a_{n} \, \, \, (a_{n} >0) $ в виде: $\sum \limits _{n=1}^{\infty }a_{n} =a_{1} +a_{2} +\ldots +a_{N} +a_{N+1} +a_{N+2} \, +...$. Рассмотрим новый ряд $\sum \limits _{k=0}^{\infty }a_{N} \cdot q^{k} =a_{N} +qa_{N} +q^{2} a_{N} +\ldots $ . Этот ряд есть ряд геометрической прогрессии с $b_{1} =a_{N} $ и $0
- Пусть $\mathop{\lim }\limits_{n\to \infty } \frac{a_{n+1} }{a_{n} } =l>1$. Рассмотрим число q такое, что $l>q>1$. ${\rm \varepsilon }=l-q>0$, из определения предела следует:$-{\rm \varepsilon } q > 1.$Таким образом, $a_{n+1} >a_n > 0$ и при $n\to \infty $ общий член ряда $a_{n} $ не стремится к 0, т.е. ряд $\sum \limits _{n=1}^{\infty }a_n $ расходится, так как не выполняется необходимое условие сходимости ряда. Вторая часть теоремы доказана.
- Если $l=1$,$\mathop{\lim }\limits_{n\to \infty } \frac{a_{n+1} }{a_{n} } $ равен единице или не существует, в этом случае для выяснения сходимости ряда признак Даламбера не применим.
Пример 1
Исследовать на сходимость ряд $\sum \limits _{n=1}^{\infty }\, \frac{n}{2^{n} } $.
Решение. Обозначим $\frac{n}{2^{n} } =a_{n} $, $a_{n} >0$; найдём $a_{n+1} =\frac{n+1}{2^{n+1} } $. Составим предел $l=\mathop{\lim }\limits_{n\to \infty } \frac{a_{n+1} }{a_{n} } =\mathop{\lim }\limits_{n\to \infty } \frac{(n+1)\cdot 2^{n} }{2^{n} \cdot 2\cdot n} =\frac{1}{2} \mathop{\lim }\limits_{n\to \infty } \frac{n+1}{n} =\frac{1}{2}
Ответ: ряд $\sum \limits _{n=1}^{\infty }\, \frac{n}{2^{n} } $сходится.
Пример 2
Исследовать на сходимость ряд $\sum \limits _{n=1}^{\infty }\, \frac{n!}{5^{n} } $.
Решение. Обозначим $\frac{n!}{5^{n} } =a_{n} ,a_{n} >0$; найдём $a_{n+1} =\frac{(n+1)!}{5^{n+1} } $. Составим предел
т.е. по признаку Даламбера ряд расходится.
Ответ: ряд $\sum \limits _{n=1}^{\infty }\, \frac{n!}{5^{n} } $ расходится.
Пример 3
Исследовать на сходимость ряд $\sum \limits _{n=1}^{\infty }\, \left(\frac{n}{2n+1} \right)^{n} $
Решение. Обозначим $\left(\frac{n}{2n+1} \right)^{n} =a_{n} ,^{} a_{n} >0$. Составим предел:
$l=\mathop{\lim }\limits_{n\to \infty } \sqrt[{n}]{a_{n} } =\mathop{\lim }\limits_{n\to } \frac{n}{2n+1} =\frac{1}{2}
Ответ: ряд $\sum \limits _{n=1}^{\infty }\, \left(\frac{n}{2n+1} \right)^{n} $сходится.
ВЫСШАЯ МАТЕМАТИКА
Числовые ряды
Лекция. Числовые ряды
1. Определение числового ряда. Сходимость
2. Основные свойства числовых рядов
3. Ряды с положительными членами. Признаки сходимости
4. Знакочередующиеся ряды. Признак сходимости Лейбница
5. Знакопеременные ряды
Вопросы для самопроверки
Литература
Лекция. ЧИСЛОВЫЕ РЯДЫ
1. Определение числового ряда. Сходимость.
2. Основные свойства числовых рядов.
3. Ряды с положительными членами. Признаки сходимости.
4. Знакочередующиеся ряды. Признак сходимости Лейбница.
5. Знакопеременные ряды.
1. Определение числового ряда. Сходимость
В математических приложениях, а также при решении некоторых задач в экономике, статистике и других областях рассматриваются суммы с бесконечным числом слагаемых. Здесь мы дадим определение того, что понимается под такими суммами.
Пусть задана бесконечная числовая последовательность
, , …, , …Определение 1.1 . Числовым рядом или просто рядом называется выражение (сумма) вида
. (1.1) называются членами ряда , – общим или n – м членом ряда.Чтобы задать ряд (1.1) достаточно задать функцию натурального аргумента
вычисления -го члена ряда по его номеруПример 1.1 . Пусть
. Ряд (1.2)называется гармоническим рядом .
Пример 1.2 . Пусть
, Ряд (1.3)называется обобщенным гармоническим рядом . В частном случае при
получается гармонический ряд.Пример 1.3 . Пусть
= . Ряд (1.4)называется рядом геометрической прогрессии .
Из членов ряда (1.1) образуем числовую последовательность частичных сумм где
– сумма первых членов ряда, которая называется n -й частичной суммой , т. е. , , ,…………………………….
, (1.5)…………………………….
Числовая последовательность
при неограниченном возрастании номера может:1) иметь конечный предел;
2) не иметь конечного предела (предел не существует или равен бесконечности).
Определение 1.2 . Ряд (1.1) называется сходящимся, если последовательность его частичных сумм (1.5) имеет конечный предел, т. е.
В этом случае число
называется суммой ряда (1.1) и пишется .Определение 1.3. Ряд (1.1) называется расходящимся, если последовательность его частичных сумм не имеет конечного предела .
Расходящемуся ряду не приписывают никакой суммы.
Таким образом, задача нахождения суммы сходящегося ряда (1.1) равносильна вычислению предела последовательности его частичных сумм.
Рассмотрим несколько примеров.
Пример 1.4. Доказать, что ряд
сходится, и найти его сумму.
Найдем n - ю частичную сумму данного ряда
.Общий член
ряда представим в виде .Отсюда имеем:
. Следовательно, данный ряд сходится и его сумма равна 1:Пример 1.5 . Исследовать на сходимость ряд
(1.6)Для этого ряда
. Следовательно, данный ряд расходится.Замечание. При
ряд (1.6) представляет собой сумму бесконечного числа нулей и является, очевидно, сходящимся.Пример 1.6. Исследовать на сходимость ряд
(1.7)Для этого ряда
В этом случае предел последовательности частичных сумм
не существует, и ряд расходится.Пример 1.7. Исследовать на сходимость ряд геометрической прогрессии (1.4):
Нетрудно показать, что n -я частичная сумма ряда геометрической прогрессии при
задается формулой .Рассмотрим случаи:
Тогда и .Следовательно, ряд сходится и его сумма равна
Определение числового ряда и его сходимости.
Необходимый признак сходимости
Пусть – бесконечная последовательность чисел.
Определение. Выражение
, (1)
или, что то же самое, , называется числовым рядом , а числа https://pandia.ru/text/79/302/images/image005_146.gif" width="53" height="31">– членами ряда. Член с произвольным номером называется n -м, или общим членом ряда .
Само по себе выражение (1) никакого определенного числового смысла не имеет, потому что, вычисляя сумму, мы каждый раз имеем дело лишь с конечным числом слагаемых. Определить смысл этого выражения наиболее естественно следующим образом.
Пусть дан ряд (1).
Определение. Сумма n первых членов ряда

называется n -й частичной суммой ряда. Образуем последовательность частичных сумм:
font-size:14.0pt">С неограниченным увеличением числа n в сумме учитывается все большее число членов ряда. Поэтому разумно дать такое определение.
Определение. Если при существует конечный предел последовательности частичных сумм https://pandia.ru/text/79/302/images/image011_76.gif" width="103" height="41"> называется его суммой .
Если последовательность https://pandia.ru/text/79/302/images/image013_77.gif" width="80" height="31">, 2) если колеблющаяся. В обоих случаях говорят, что ряд суммы не имеет.
Пример 1. Рассмотрим ряд, составленный из членов геометрической прогрессии:
 , (2)
, (2)
где – называется первым членом прогрессии, а font-size:14.0pt"> Частичная сумма этого ряда при font-size:14.0pt">font-size:14.0pt">Отсюда:
1) если , то
font-size:14.0pt">т. е. ряд геометрической прогрессии сходится и его сумма .
В частности, если  , ряд
, ряд  сходится и его сумма .
сходится и его сумма .
При https://pandia.ru/text/79/302/images/image026_42.gif" width="307" height="59 src="> также сходится и его сумма .
2) если , то  , т. е. ряд (2) расходится.
, т. е. ряд (2) расходится.
3) если , то ряд (2) принимает вид font-size:14.0pt"> и
![]() , т. е. ряд расходится
(при font-size:18.0pt">)
.
, т. е. ряд расходится
(при font-size:18.0pt">)
.
4) если https://pandia.ru/text/79/302/images/image036_32.gif" width="265" height="37"> . Для этого ряда
https://pandia.ru/text/79/302/images/image038_28.gif" width="253" height="31 src=">,
т. е..gif" width="67" height="41"> не существует, следовательно, ряд также расходится (при ) .
Вычисление суммы ряда непосредственно по определению очень неудобно из-за трудности явного вычисления частичных сумм font-size:14.0pt"> и нахождения предела их последовательности. Но, если установлено, что ряд сходится, его сумму можно вычислить приближенно, т. к. из определения предела последовательности следует, что при достаточно больших . Поэтому при исследовании рядов достаточно
1) знать приемы, позволяющие констатировать сходимость ряда без нахождения его суммы;
2) уметь определить font-size:14.0pt">.gif" width="16 height=24" height="24"> с определенной точностью.
Сходимость числовых рядов устанавливается с помощью теорем, которые называются признаками сходимости.
Необходимый признак сходимости
Если ряд сходится, то его общий член стремится к нулю, т. е. font-size:14.0pt">.gif" width="61 height=63" height="63"> расходится.
Пример 2. Доказать, что ряд 0 " style="border-collapse:collapse">
 ;
;
 ;
;
 ;
;
 .
.
Решение.
А) https://pandia.ru/text/79/302/images/image051_28.gif" width="176" height="81 src="> расходится.

и поэтому ряд расходится. При решении использовался второй замечательный
предел:
 (подробнее см. ).
(подробнее см. ).
В) font-size:14.0pt">, т. е. последовательность
 – бесконечно
– бесконечно
малая. Так как при font-size:14.0pt">~ (см. ), то
~ .Учитывая это, получим:
значит, ряд расходится.
Г) font-size:14.0pt">,
следовательно, ряд расходится.
Условие
![]() является необходимым,
но не достаточным
условием сходимости ряда: существует множество рядов, для которых
является необходимым,
но не достаточным
условием сходимости ряда: существует множество рядов, для которых
![]() , но которые тем не менее расходятся.
, но которые тем не менее расходятся.
Пример 3. Исследовать сходимость ряда font-size:14.0pt"> Решение. Заметим, что https://pandia.ru/text/79/302/images/image066_20.gif" width="119" height="59 src=">, т. е. необходимое условие сходимости выполнено. Частичная сумма
left">
– раз
поэтому font-size:14.0pt">, а это значит, что ряд расходится по определению.
Достаточные признаки сходимости знакоположительных рядов
Пусть . Тогда ряд font-size:14.0pt"> Признак сравнения
Пусть и – знакоположительные ряды. Если для всех выполняется неравенство , то из сходимости ряда следует сходимость ряда , а из расходимости ряда https://pandia.ru/text/79/302/images/image074_19.gif" width="55" height="60">.
Этот признак остается в силе, если неравенство https://pandia.ru/text/79/302/images/image072_18.gif" width="60" height="24">, а лишь начиная с некоторого номера . Его можно проинтерпретировать следующим образом: если больший ряд сходится, то меньший тем более сходится; если расходится меньший ряд, то больший также расходится.
Пример 4. Исследовать сходимость ряда 0 " style="margin-left:50.4pt;border-collapse:collapse">
 ;
;
Решение.
А) Заметим, что
font-size:14.0pt"> для всех ![]() . Ряд с общим членом
. Ряд с общим членом
 сходится по признаку сравнения.
сходится по признаку сравнения.
Б) Сравним ряд с рядом ..gif" width="91" height="29 src=">.gif" width="87" height="59"> расходится, значит, данный ряд также расходится.
Несмотря на простоту формулировки признака сравнения, на практике более удобна следующая теорема, являющаяся его следствием.
Предельный признак сравнения
Пусть https://pandia.ru/text/79/302/images/image071_17.gif" width="53" height="60 src="> – знакоположительные ряды. Если существует конечный и не равный нулю предел , то оба ряда и
одновременно сходятся или одновременно расходятся.
В качестве ряда, используемого для сравнения с данным, часто выбирают ряд вида  . Такой ряд называется рядом Дирихле
. В примерах 3 и 4 было показано, что ряд Дирихле с и расходится. Можно пока-
. Такой ряд называется рядом Дирихле
. В примерах 3 и 4 было показано, что ряд Дирихле с и расходится. Можно пока-

 .
.
Если , то ряд
 называется гармоническим
. Гармонический ряд расходится.
называется гармоническим
. Гармонический ряд расходится.
Пример 5. Исследовать на сходимость ряд с помощью предельного признака сравнения, если
|
|
|
Решение. а) Так как при достаточно больших https://pandia.ru/text/79/302/images/image101_9.gif" width="31" height="23 src=">, а
![]() ~ , то
~ , то  ~ font-size:14.0pt">сравнения с данным гармонический ряд
font-size:14.0pt">, т. е. .
~ font-size:14.0pt">сравнения с данным гармонический ряд
font-size:14.0pt">, т. е. .
font-size:14.0pt"> Поскольку предел конечен и отличен от нуля и гармонический ряд расходится, то расходится и данный ряд.
Б) При достаточно больших https://pandia.ru/text/79/302/images/image109_10.gif" width="111" height="31 src=">.gif" width="129" height="31 src=">.gif" width="132" height="64 src="> – общий член ряда, с которым будем сравнивать данный:
Font-size:14.0pt">Ряд сходится (ряд Дирихле с font-size:16.0pt">) , поэтому данный ряд также сходится.
В)  , поэтому бесконечно малую
font-size:14.0pt"> можно
, поэтому бесконечно малую
font-size:14.0pt"> можно
заменить на эквивалентную ей при величину (https://pandia.ru/text/79/302/images/image058_20.gif" width="13" height="21 src="> при font-size: 20.0pt">) . ;
 ;
;
 ;
;
г )
 ;
;
 .
.
На практике часто не столь важно найти сумму ряда, как ответить на вопрос о сходимости ряда. Для этой цели используются признаки сходимости, основанные на свойствах общего члена ряда.
Необходимый признак сходимости ряда
ТЕОРЕМА 1
Если
ряд
сходится, то его общий член
 стремится к нулю при
стремится к нулю при ,
т.е.
,
т.е.
 .
.
Кратко : если ряд сходится, то его общий член стремится к нулю.
Доказательство.
Пусть ряд сходится и его сумма равна
 .
Для любого
.
Для любого
 частичная сумма
частичная сумма


 .
.
Тогда .
Из
доказанного необходимого признака
сходимости вытекает достаточный
признак расходимости ряда:
если при
 общий член ряда не стремится к нулю, то
ряд расходится.
общий член ряда не стремится к нулю, то
ряд расходится.
Пример
4.

Для
этого ряда общий член
 и
и .
.
Следовательно, данный ряд расходится.
Пример
5.
Исследовать
на сходимость ряд

Очевидно,
что общий член этого ряда, вид которого
не указан ввиду громоздкости выражения,
стремится к нулю при
 ,
т.е. необходимый признак сходимости
ряда выполняется, однако этот ряд
расходится, так как его сумма
стремится к бесконечности.
,
т.е. необходимый признак сходимости
ряда выполняется, однако этот ряд
расходится, так как его сумма
стремится к бесконечности.
Знакоположительные числовые ряды
Числовой ряд, все члены которого положительны, называется знакоположительным.
ТЕОРЕМА 2 (Критерий сходимости знакоположительного ряда)
Для сходимости знакоположительного ряда необходимо и достаточно, чтобы все его частичные суммы были ограничены сверху одним и тем же числом.
Доказательство.
Так как для любого

 ,
то,
т.е. последовательность
,
то,
т.е. последовательность – монотонно возрастающая, поэтому для
существования предела необходимо и
достаточно ограничение последовательности
сверху каким-либо числом.
– монотонно возрастающая, поэтому для
существования предела необходимо и
достаточно ограничение последовательности
сверху каким-либо числом.
Эта теорема в большей степени имеет теоретическое, чем практическое значение. Далее приведены другие признаки сходимости, имеющие большее применение.
Достаточные признаки сходимости знакоположительных рядов
ТЕОРЕМА 3 (Первый признак сравнения)
Пусть даны два знакоположительных ряда:
 (1)
(1)
 (2)
(2)
причем,
начиная с некоторого номера
 ,
для любого
,
для любого выполняется неравенство
выполняется неравенство Тогда:
Тогда:

Схематическая запись первого признака сравнения:

сход.сход.
расх.расх.
Доказательство.
1) Так как отбрасывание конечного числа
членов ряда не влияет на его сходимость,
докажем теорему для случая
 .
Пусть для любого
.
Пусть для любого имеем
имеем
 , (3)
, (3)
где
 и
и
 -
соответственно частичные суммы рядов
(1) и (2).
-
соответственно частичные суммы рядов
(1) и (2).
Если
ряд (2) сходится, то существует число
 .
Поскольку
при этом последовательность
.
Поскольку
при этом последовательность
 - возрастающая, ее предел больше любого
из ее членов, т.е.
- возрастающая, ее предел больше любого
из ее членов, т.е. для
любого
для
любого
 .
Отсюда
из неравенства (3) следует
.
Отсюда
из неравенства (3) следует
 .
Таким
образом, все частичные суммы ряда (1)
ограничены сверху числом
.
Таким
образом, все частичные суммы ряда (1)
ограничены сверху числом
 .
Согласно
теореме 2 этот ряд сходится.
.
Согласно
теореме 2 этот ряд сходится.
2) Действительно, если бы ряд (2) сходился, то по признаку сравнения сходился бы и ряд (1).
Для применения этого признака часто используют такие ряды-эталоны, сходимость или расходимость которых известна заранее, например:

3)
 -
ряд
Дирихле (он сходится при
-
ряд
Дирихле (он сходится при
 и расходится при
и расходится при ).
).
Кроме этого часто используют ряды, которые можно получить с помощью следующих очевидных неравенств:

 ,
,

 ,
, ,
, .
.
Рассмотрим на конкретных примерах схему исследования знакоположительного ряда на сходимость с помощью первого признака сравнения.
Пример
6.
Исследовать
ряд
 на сходимость.
на сходимость.
Шаг
1. Проверим знакоположительность ряда:
 для
для
Шаг
2. Проверим выполнение необходимого
признака сходимости ряда:
 .
Так как
.
Так как ,
то
,
то
(если вычисление предела вызывает трудности, то этот шаг можно пропустить).
Шаг
3. Используем первый признак сравнения.
Для этого подберем для данного ряда
ряд-эталон. Так как
 ,
то в качестве эталона можно взять ряд
,
то в качестве эталона можно взять ряд ,
т.е. ряд Дирихле. Этот ряд сходится, так
как показатель степени
,
т.е. ряд Дирихле. Этот ряд сходится, так
как показатель степени .
Следовательно, согласно первому признаку
сравнения сходится и исследуемый ряд.
.
Следовательно, согласно первому признаку
сравнения сходится и исследуемый ряд.
Пример
7.
Исследовать ряд
 на сходимость.
на сходимость.
1)
Данный ряд знакоположительный, так как
 для
для
2) Необходимый признак сходимости ряда выполняется, ибо
3)
Подберем ряд-эталон. Так как
 ,
то в качестве эталона можно взять
геометрический ряд
,
то в качестве эталона можно взять
геометрический ряд

 .
Этот ряд сходится, следовательно,
сходится и исследуемый ряд.
.
Этот ряд сходится, следовательно,
сходится и исследуемый ряд.
ТЕОРЕМА 4 (Второй признак сравнения)
Если
для знакоположительных рядов
 и
и
 существует отличный от нуля конечный
предел
существует отличный от нуля конечный
предел
 ,
то
ряды
сходятся или расходятся одновременно.
,
то
ряды
сходятся или расходятся одновременно.
Доказательство.
Пусть ряд (2) сходится; докажем, что тогда
сходится и ряд (1). Выберем какое-нибудь
число
 ,
большее,
чем
,
большее,
чем
 .
Из
условия
.
Из
условия
 вытекает
существование такого номера
вытекает
существование такого номера
 ,
что для всех
,
что для всех
 справедливо неравенство
справедливо неравенство ,
или,
что то же,
,
или,
что то же,
 (4)
(4)
Отбросив
в рядах (1) и (2) первые
 членов (что не влияет на сходимость),
можно считать, что неравенство (4)
справедливо для всех
членов (что не влияет на сходимость),
можно считать, что неравенство (4)
справедливо для всех
 Но ряд с общим членом
Но ряд с общим членом сходится
в силу сходимости ряда (2). Согласно
первому признаку сравнения, из неравенства
(4) следует сходимость ряда (1).
сходится
в силу сходимости ряда (2). Согласно
первому признаку сравнения, из неравенства
(4) следует сходимость ряда (1).
Пусть теперь сходится ряд (1); докажем сходимость ряда (2). Для этого следует просто поменять ролями заданные ряды. Так как

то, по доказанному выше, из сходимости ряда (1) должна следовать сходимость ряда (2).
Если
 при
при (необходимый признак сходимости), то из
условия
(необходимый признак сходимости), то из
условия ,
следует, что
,
следует, что и
и – бесконечно малые одного порядка
малости (эквивалентные при
– бесконечно малые одного порядка
малости (эквивалентные при ).
Следовательно, если дан ряд
).
Следовательно, если дан ряд
 ,
где
,
где
 при
при ,
то для этого ряда можно брать ряд-эталон
,
то для этого ряда можно брать ряд-эталон
 ,
где общий член
,
где общий член
 имеет тот же порядок малости, что и общий
член данного ряда.
имеет тот же порядок малости, что и общий
член данного ряда.
При
выборе ряда-эталона можно пользоваться
следующей таблицей эквивалентных
бесконечно малых при
 :
:
1)
 ; 4)
; 4) ;
;
2)
 ; 5)
; 5) ;
;
3)
 ; 6)
; 6) .
.
Пример 8. Исследовать на сходимость ряд
 .
.
 для любого
для любого .
.

Так
как
 ,
то возьмем в качестве ряда-эталона
гармонический расходящийся ряд
,
то возьмем в качестве ряда-эталона
гармонический расходящийся ряд .
Поскольку предел отношения общих членов
.
Поскольку предел отношения общих членов и
и конечен и отличен от нуля (он равен 1),
то на основании второго признака
сравнения данный ряд расходится.
конечен и отличен от нуля (он равен 1),
то на основании второго признака
сравнения данный ряд расходится.
Пример
9.
 по двум признакам сравнения.
по двум признакам сравнения.
Данный
ряд знакоположительный, так как
 ,
и
,
и .
Поскольку
.
Поскольку ,
то в качестве ряда-эталона можно брать
гармонический ряд
,
то в качестве ряда-эталона можно брать
гармонический ряд .
Этот ряд расходится и следовательно,
по первому признаку сравнения, исследуемый
ряд также расходится.
.
Этот ряд расходится и следовательно,
по первому признаку сравнения, исследуемый
ряд также расходится.
Так
как для данного ряда и ряда-эталона
выполняется условие
 (здесь использован 1-й замечательный
предел), то на основании второго признака
сравнения ряд
(здесь использован 1-й замечательный
предел), то на основании второго признака
сравнения ряд – расходится.
– расходится.
ТЕОРЕМА 5 (Признак Даламбера)
 существует конечный предел
существует конечный предел
 ,
то ряд сходится при
,
то ряд сходится при и расходится при
и расходится при .
.
Доказательство.
Пусть
 .
Возьмем какое-либо число
.
Возьмем какое-либо число ,
заключенное
между
,
заключенное
между
 и
1:
и
1:
 .
Из условия
.
Из условия
 следует,
что начиная с некоторого номера
следует,
что начиная с некоторого номера
 выполняется
неравенство
выполняется
неравенство
 ;
;
 ;
; (5)
(5)
Рассмотрим ряд
Согласно
(5) все члены ряда (6) не превосходят
соответствующих членов бесконечной
геометрической прогрессии
 Поскольку
Поскольку ,
эта прогрессия является сходящейся.
Отсюда в силу первого признака сравнения
вытекает сходимость ряда
,
эта прогрессия является сходящейся.
Отсюда в силу первого признака сравнения
вытекает сходимость ряда
Случай
 рассмотрите самостоятельно.
рассмотрите самостоятельно.
Замечания :

следует,
что остаток ряда

 .
.
Признак Даламбера удобен на практике тогда, когда общий член ряда содержит показательную функцию или факториал.
Пример
10.
Исследовать на сходимость ряд
 по признаку Даламбера.
по признаку Даламбера.
Данный ряд знакоположительный и
 .
.
(Здесь при вычислении дважды применено правило Лопиталя).

то по признаку Даламбера данный ряд сходится.
Пример
11.
 .
.
Данный
ряд знакоположительный и
 .
Поскольку
.
Поскольку
то данный ряд сходится.
ТЕОРЕМА 6 (Признак Коши)
Если
для знакоположительного ряда
 существует
конечный предел
существует
конечный предел
 ,
то при
,
то при ряд сходится, а при
ряд сходится, а при ряд расходится.
ряд расходится.
Доказательство аналогично теореме 5.
Замечания :

Пример
12.
Исследовать
на сходимость ряд
 .
.
Данный
ряд знакоположительный, так как
 для любого
для любого .
Поскольку вычисление предела
.
Поскольку вычисление предела вызывает определенные трудности, то
проверку выполнимости необходимого
признака сходимости ряда опускаем.
вызывает определенные трудности, то
проверку выполнимости необходимого
признака сходимости ряда опускаем.
то по признаку Коши данный ряд расходится.
ТЕОРЕМА 7 (Интегральный признак сходимости Маклорена - Коши)
Пусть дан ряд
члены которого положительны и не возрастают:

Пусть,
далее
 -
функция, которая определена для всех
вещественных
-
функция, которая определена для всех
вещественных
 ,
непрерывна, не возрастает и
,
непрерывна, не возрастает и

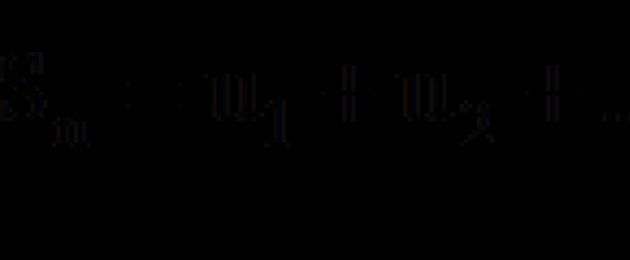
 ;
;
 ;
;
 ;
;