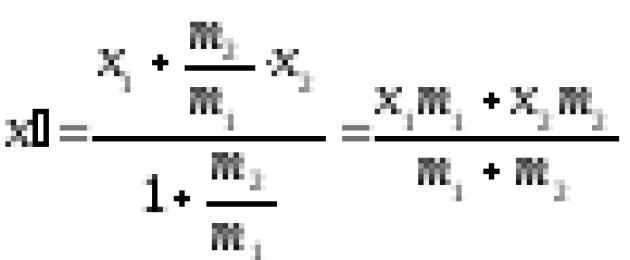Method of coordinates in space: formulas and comments of the tutor. Method of coordinates in space presentation for a lesson in geometry (Grade 11) on the topic Method of coordinates in space rectangular coordinate system

To use the preview of presentations, create a Google account (account) and sign in: https://accounts.google.com

Slides captions:

Rectangular coordinate system in space. Vector coordinates.

Rectangular coordinate system

If three pairwise perpendicular lines are drawn through a point in space, a direction is chosen on each of them and a unit of measurement of segments is chosen, then they say that a rectangular coordinate system is set in space

Straight lines, with directions chosen on them, are called coordinate axes, and their common point is called the origin of coordinates. It is usually denoted by the letter O. The coordinate axes are denoted as follows: Ox, Oy, O z - and have names: the abscissa axis, the y-axis, the applicate axis.

The entire coordinate system is denoted Oxy z . The planes passing through the coordinate axes Ox and Oy, Oy and O z , O z and Ox, respectively, are called coordinate planes and are denoted Oxy, Oy z , O z x.

Point O divides each of the coordinate axes into two beams. The ray whose direction coincides with the direction of the axis is called the positive semi-axis, and the other ray is the negative semi-axis.

In a rectangular coordinate system, each point M of space is associated with a triple of numbers, which are called its coordinates.

The figure shows six points A (9; 5; 10), B (4; -3; 6), C (9; 0; 0), D (4; 0; 5), E (0; 3; 0) , F(0; 0; -3).

Vector coordinates

Any vector can be decomposed into coordinate vectors, that is, it can be represented in the form where the expansion coefficients x, y, z are uniquely determined.

The coefficients x, y and z in the expansion of a vector in terms of coordinate vectors are called the coordinates of the vector in the given coordinate system.

Consider the rules that allow us to find the coordinates of their sum and difference, as well as the coordinates of the product of a given vector by the coordinates of these vectors. given number.

10 . Each coordinate of the sum of two or more vectors is equal to the sum of the corresponding coordinates of these vectors. In other words, if a (x 1, y 1, z 1) and b (x 2, y 2, z 2 ) are given vectors, then the vector a + b has coordinates (x 1 + x 2, y 1 + y 2 , z 1 + z 2 ).

twenty . Each coordinate of the difference of two vectors is equal to the difference of the corresponding coordinates of these vectors. In other words, if a (x 1, y 1, z 1) and b (x 2 y 2; z 2) are given vectors, then the vector a - b has coordinates (x 1 - x 2, y 1 - y 2, z 1 - z 2 ).

thirty . Each coordinate of the product of a vector by a number is equal to the product of the corresponding coordinate of the vector by that number. In other words, if a (x; y; x) is a given vector, α is a given number, then the vector α a has coordinates (αx; αy; α z).

On the topic: methodological developments, presentations and notes

Didactic Handout"A set of notes for students on the topic "Method of coordinates in space" for conducting lessons in the form of lectures. Geometry grade 10-11 ....

The purpose of the lesson: To test the knowledge, skills and abilities of students on the topic "Using the method of coordinates in space to solve tasks C2 USE." Planned educational results: Students demonstrate: ...

Lesson test in geometry in grade 11

Topic: " Method of coordinates in space”.

Target: Check the theoretical knowledge of students, their skills and abilities to apply this knowledge in solving problems in vector, vector-coordinate ways.

Tasks:

1 .Create conditions for control (self-control, mutual control) of the assimilation of knowledge and skills.

2. Develop mathematical thinking, speech, attention.

3. Promote activity, mobility, communication skills, common culture students.

Conduct form: work in groups.

Equipment and sources of information: screen, multimedia projector, spreadsheet, credit cards, tests.

During the classes

1. Mobilizing moment.

Lesson using CSR; students are divided into 3 dynamic groups, in which students with an acceptable, optimal and advanced level. Each group has a coordinator who manages the work of the entire group.

2 . Self-determination of students on the basis of anticipation.

Task:goal-setting according to the scheme: remember-learn-be able.

Entrance test - Fill in the blanks (on printouts)

entrance test

Fill the gaps…

1.Three pairwise perpendicular lines are drawn through a point in space

we, on each of them, the direction and unit of measurement of the segments are selected,

then they say that it is set …………. in space.

2. Straight lines with directions chosen on them are called ……………..,

and their common point is …………. .

3. In a rectangular coordinate system, each point M of space is associated with a triple of numbers that call it ………………..

4. The coordinates of a point in space are called ………………..

5. A vector whose length is equal to one is called …………..

6. Vectors iykare called………….

7. Odds xyz in decomposition a= xi + yj + zk called

……………vector a .

8. Each coordinate of the sum of two or more vectors is equal to ……………..

9. Each coordinate of the difference of two vectors is equal to ……………….

10. Each coordinate of the product of a vector and a number is equal to………………..

11.Each coordinate of the vector is equal to…………….

12. Each coordinate of the middle of the segment is equal to……………….

13. Vector length a { xyz) is calculated by the formula ……………………

14. Distance between points M 1(x 1 ; y 1; z 1) and M 2 (x 2; y 2 ; z2) is calculated by the formula …………………

15. The scalar product of two vectors is called……………..

16. The scalar product of non-zero vectors is equal to zero………………..

17. Dot product of vectorsa{ x 1; y 1; z 1} b { x 2 ; y 2 ; z 2) in expressed by the formula…………………

Mutual verification of the entrance test. Answers to the tasks of the test on the screen.

Evaluation criteria:

1-2 mistakes - "5"

3-4 errors - "4"

5-6 errors - "3"

In other cases - "2"

3. Doing work. (for cards).

Each card contains two tasks: No. 1 - theoretical with proof, No. 2 includes tasks.

Explain the level of difficulty of the tasks included in the work. The group performs one task, but having 2 parts. The group coordinator manages the work of the entire group. Discussion of the same information with several partners increases responsibility not only for one's own success, but also for the results of collective work, which has a positive effect on the microclimate in the team.

CARD #1

1. Derive formulas expressing the coordinates of the middle of the segment in terms of the coordinates of its ends.

2. Task: 1) Points A (-3; 1; 2) and B (1; -1; 2) are given

Find:

a) the coordinates of the midpoint of the segment AB

b) coordinates and length of the vector AB

2) The cube ABCDA1 B1 C1 D1 is given. Using the coordinate method, find the angle

between lines AB1 and A1 D.

CARD#2

Derive a formula for calculating the length of a vector from its coordinates.

Task: 1) Given points M(-4; 7; 0),N(0; -1; 2). Find the distance from the origin of coordinates to the middle of the segment MN.

→ → → → →

2) Vector data a and b. Find b(a+b), if a(-2;3;6),b=6i-8k

CARD #3

Derive a formula for calculating the distance between points with given coordinates.

Task: 1) Points A(2;1;-8), B(1;-5;0), C(8;1;-4) are given.

Prove that ∆ABC is isosceles and find the length middle line triangle connecting the midpoints of the sides.

2) Calculate the angle between straight lines AB and SD if A(1;1;0),

B(3;-1;2), D(0;1;0).

CARD#4

Derive formulas for the cosine of the angle between non-zero vectors with given coordinates.

Task: 1) The coordinates of three vertices of the parallelogram ABCD are given:

A(-6;-;4;0), B(6;-6;2), C(10;0;4). Find the coordinates of point D.

2) Find the angle between the lines AB and CD, if A (1; 1; 2), B (0; 1; 1), C (2; -2; 2), D (2; -3; 1).

CARD#5

Tell us how to calculate the angle between two lines in space using the direction vectors of these lines. →→

Task: 1) Find the scalar product of vectorsa and b, if:

→ → → ^ →

a) | a| =4; | b| =√3 (ab)=30◦

b) a {2 ;-3; 1}, b = 3 i +2 k

2) Points A(0;4;0), B(2;0;0), C(4;0;4) and D(2;4;4) are given. Prove that ABCD is a rhombus.

4. Verification of works dynamic groups by cards.

We listen to the speeches of the representatives of the groups. The work of the groups is evaluated by the teacher with the participation of students.

5. Reflection. Grades for credit.

Final test with a choice of answers (in printouts).

1) Vectors are given a {2 ;-4 ;3} b(-3; ─ ; 1). Find vector coordinates

→ 2

c = a+ b

a) (-5; 3 −; 4); b) (-1; -3.5; 4) c) (5; -4 −; 2) d) (-1; 3.5; -4)

2) Vectors are given a(4; -3; 5) and b(-3; 1; 2). Find vector coordinates

C=2 a – 3 b

a) (7;-2;3); b) (11; -7; 8); c) (17; -9; 4); d) (-1; -3; 4).

→ → → → → →

3) Calculate the scalar product of vectorsm and n, if m = a + 2 b- c

→ → → → →^ → → → → →

n= 2 a - b if | a|=2 , ‌| b |=3, (ab‌)=60°, c ┴ a , c ┴ b.

a)-1; b) -27; in 1; d) 35.

4) Vector length a { xyz) is equal to 5. Find the coordinates of the vector a ifx=2, z=-√5

a) 16; b) 4 or -4; at 9; d) 3 or -3.

5) Find the area ∆ABC if A(1;-1;3); B(3;-1;1) and C(-1;1;-3).

a) 4√3; b) √3; c) 2√3; d) √8.

Cross-validation test. Response codes to test tasks on the screen: 1(b); 2(c);

3(a); 4(b); 5(c).

Evaluation criteria:

Everything is correct - "5"

1 mistake - "4"

2 errors - "3"

In other cases - "2"

Student knowledge table

Work on

cards

final

test

Credit score

Tasks

theory

practice

1 group

2 group

3 group

Evaluation of students' preparation for the test.

The position of any point in space can be uniquely determined using a rectangular coordinate system. This system includes three mutually perpendicular axes intersecting at one point O is the origin of coordinates. One of the axes is called x-axis(axis Oh), the other y-axis (OU), the third applicate axis (Oz). planes XOY, XOZ and YOZ are called coordinate planes. Any segment is taken as scale unit for all three axes . The positive directions on the axes are chosen so that the rotation by 90 0 that combines the positive beam OX with positive beam OY, seemed to go counter-clockwise when viewed from the beam oz. This coordinate system is called right.

Position of any point M in space can be defined by three coordinates as follows . AcrossMdraw planes parallel to planesXOY, XOZ and YOZ. At the intersection with the axes, we get points, for example, P, Q and R respectively. Numbers X (abscissa), at(ordinate), z (applique), measuring segmentsOP, OQandORon the chosen scale are calledrectangular coordinatespoints M. They are taken positive or negative depending on whether the corresponding segments lie on the positive or negative semiaxis. Each triple of numbers ( X; at; z) corresponds to one and only one point in space, and vice versa.

Distance between two points and is calculated by the formula: (1.6)

Coordinates (x; y; z) pointsM dividing in a given ratio section AB, (,) are determined by the formulas:

In particular, at (point M divides the segment AB in half), formulas are obtained for determining the coordinates of the midpoint of the segment:

Example 4: on axle OU find a point equidistant from two points and .

Solution: Dot M lying on the axis OU, has coordinates . According to the task |AM| = |VM|. Let's find distances |AM| and |VM|, using formula (1.6):

We get the equation: .

Hence we find that 4 at= 16, i.e. y= 4. The desired point is M(0; 4; 0).

Example 5: Section AB divided into 3 equal parts. Find the coordinates of the division points, if the points are known and .

Solution:

Denote the points of division of the segment AB in the following order: WITH and D. According to the task |AC| = |CD| = |DB|. Therefore, the point WITH divides the segment AB in a relationship . Using formulas (1.7), we find the coordinates of the point C:

By formulas (1.8) we find the coordinates of the point D- the middle of the segment SW:

That is, point D has coordinates: .

Example 6: At points , ,, masses are concentrated accordingly m 1 , m 2 , m 3 , m 4 . Find the coordinates of the center of gravity of the system of these masses.

Solution:

As is known from the course of physics, the center of gravity of masses m 1 and m 2 placed at points A and V, divides the segment AB into parts inversely proportional to the masses concentrated at the ends of the segment (). Based on this, we first find the center of gravity of the system of two masses m 1 and m 2 placed at points A 1 and A 2 :

, ,.

Center of gravity of a three-mass system m 1 and m 2 and m 3 () we find similarly:

, ,.

We finally find the center of gravity of the system of three massesm 1 , m 2 , m 3 andm 4 :

, ,.

Questions to control:

Describe a rectangular coordinate system in the plane and all its components.

How are the coordinates of an arbitrary point on a plane determined?

Write a formula to find pdistance between two points on the plane .

How to findcoordinates of a point dividing a segment in a given ratio?

Write the formulas for the coordinates of the midpoint of the segment.

Write a formula that calculates the area of ​​a triangle if the coordinates of its vertices are known .

Describe the polar coordinate system.

What is the polar radius? To what extent is it measured?

What is a polar angle? Limits of its measurement?

How find the rectangular coordinates of a point for which polar coordinates?

How find the polar coordinates of a point for which the rectangular coordinates are known?

How to find distance between points in polar coordinate system?

Describe a rectangular coordinate system in space and all its components.

How to determine the coordinates of a point in space?

Write down the formula for finding the distance between two points in space.

Write formulas to find point coordinates, dividing the segment in a given ratio for a three-dimensional coordinate system.

The essence of the coordinate method for solving geometric problems

The essence of solving problems using the coordinate method is to introduce a coordinate system that is convenient for us in one case or another and rewrite all the data using it. After that, all unknown quantities or proofs are held using this system. How to enter the coordinates of points in any coordinate system was discussed by us in another article - we will not dwell on this here.

Let us introduce the main assertions that are used in the coordinate method.

Statement 1: The vector coordinates will be determined by the difference between the corresponding coordinates of the end of this vector and its beginning.

Statement 2: The midpoint coordinates of the segment will be defined as half the sum of the corresponding coordinates of its boundaries.

Statement 3: The length of any vector $\overline(δ)$ with given coordinates $(δ_1,δ_2,δ_3)$ will be determined by the formula

$|\overline(δ)|=\sqrt(δ_1^2+δ_2^2+δ_3^2)$

Statement 4: The distance between any two points given by the coordinates $(δ_1,δ_2,δ_3)$ and $(β_1,β_2,β_3)$ will be determined by the formula

$d=\sqrt((δ_1-β_1)^2+(δ_2-β_2)^2+(δ_3-β_3)^2)$

Scheme for solving geometric problems using the coordinate method

To solve geometric problems using the coordinate method, it is best to use this scheme:

Analyze what is given in the problem:

• Set the most appropriate coordinate system for the task;
• Mathematically, the condition of the problem, the question of the problem are written down, a drawing is built for this problem.

1. Write down all data of the problem in the coordinates of the selected coordinate system.

2. Compose the necessary relations from the conditions of the problem, and also connect these relations with what needs to be found (proved in the problem).
3. The result obtained is translated into the language of geometry.

Examples of problems solved by the coordinate method

The following tasks can be singled out as the main tasks leading to the coordinate method (their solutions will not be given here):

1. Tasks for finding the coordinates of a vector at its end and beginning.
2. Tasks related to the division of a segment in any respect.
3. Proof that three points lie on the same line or that four points lie on the same plane.
4. Tasks to find the distance between two given points.
5. Problems for finding volumes and areas of geometric shapes.

The results of solving the first and fourth problems are presented by us as the main statements above and are quite often used to solve other problems using the coordinate method.

Examples of tasks for applying the coordinate method

Example 1

Find the side of a regular pyramid whose height is $3$ cm if the side of the base is $4$ cm.

Let us be given a regular pyramid $ABCDS$, whose height is $SO$. Let's introduce a coordinate system, as in Figure 1.

Since the point $A$ is the center of the coordinate system we have constructed, then

Since the points $B$ and $D$ belong to the axes $Ox$ and $Oy$, respectively, then

$B=(4,0,0)$, $D=(0,4,0)$

Since the point $C$ belongs to the plane $Oxy$, then

Since the pyramid is regular, then $O$ is the midpoint of the segment $$. According to statement 2, we get:

$O=(\frac(0+4)(2),\frac(0+4)(2),\frac(0+0)(2))=(2,2,0)$

Since the height $SO$