Solving problems in mathematics is often accompanied by many difficulties for students. Helping the student cope with these difficulties, as well as teach them to apply their existing theoretical knowledge when solving specific problems in all sections of the course in the subject “Mathematics” is the main purpose of our site.
When starting to solve problems on the topic, students should be able to construct a point on a plane using its coordinates, as well as find the coordinates of a given point.
Calculation of the distance between two points A(x A; y A) and B(x B; y B) taken on a plane is performed using the formula d = √((x A – x B) 2 + (y A – y B) 2), where d is the length of the segment that connects these points on the plane.
If one of the ends of the segment coincides with the origin of coordinates, and the other has coordinates M(x M; y M), then the formula for calculating d will take the form OM = √(x M 2 + y M 2).
1. Calculation of the distance between two points based on the given coordinates of these points
Example 1.
Find the length of the segment that connects the coordinate plane points A(2; -5) and B(-4; 3) (Fig. 1).
Solution.
The problem statement states: x A = 2; x B = -4; y A = -5 and y B = 3. Find d.
Applying the formula d = √((x A – x B) 2 + (y A – y B) 2), we get:
d = AB = √((2 – (-4)) 2 + (-5 – 3) 2) = 10.
2. Calculation of the coordinates of a point that is equidistant from three given points
Example 2.
Find the coordinates of point O 1, which is equidistant from three points A(7; -1) and B(-2; 2) and C(-1; -5).
Solution.
From the formulation of the problem conditions it follows that O 1 A = O 1 B = O 1 C. Let the desired point O 1 have coordinates (a; b). Using the formula d = √((x A – x B) 2 + (y A – y B) 2) we find:
O 1 A = √((a – 7) 2 + (b + 1) 2);
O 1 B = √((a + 2) 2 + (b – 2) 2);
O 1 C = √((a + 1) 2 + (b + 5) 2).
Let's create a system of two equations:
(√((a – 7) 2 + (b + 1) 2) = √((a + 2) 2 + (b – 2) 2),
(√((a – 7) 2 + (b + 1) 2) = √((a + 1) 2 + (b + 5) 2).
After squaring the left and right parts we write the equations:
((a – 7) 2 + (b + 1) 2 = (a + 2) 2 + (b – 2) 2,
((a – 7) 2 + (b + 1) 2 = (a + 1) 2 + (b + 5) 2.
Simplifying, let's write
(-3a + b + 7 = 0,
(-2a – b + 3 = 0.
Having solved the system, we get: a = 2; b = -1.
Point O 1 (2; -1) is equidistant from the three points specified in the condition that do not lie on the same straight line. This point is the center of a circle passing through three given points (Fig. 2).
3. Calculation of the abscissa (ordinate) of a point that lies on the abscissa (ordinate) axis and is at a given distance from a given point
Example 3.
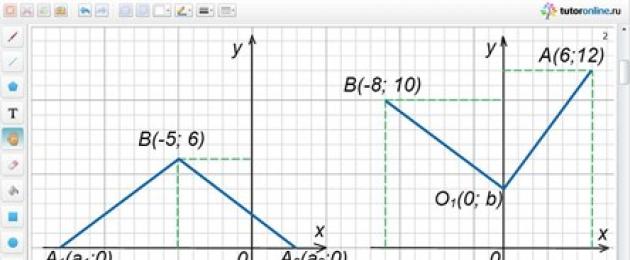
The distance from point B(-5; 6) to point A lying on the Ox axis is 10. Find point A.
Solution.
From the formulation of the problem conditions it follows that the ordinate of point A is equal to zero and AB = 10.
Denoting the abscissa of point A by a, we write A(a; 0).
AB = √((a + 5) 2 + (0 – 6) 2) = √((a + 5) 2 + 36).
We get the equation √((a + 5) 2 + 36) = 10. Simplifying it, we have
a 2 + 10a – 39 = 0.
The roots of this equation are a 1 = -13; and 2 = 3.
We get two points A 1 (-13; 0) and A 2 (3; 0).
Examination:
A 1 B = √((-13 + 5) 2 + (0 – 6) 2) = 10.
A 2 B = √((3 + 5) 2 + (0 – 6) 2) = 10.
Both obtained points are suitable according to the conditions of the problem (Fig. 3).
4. Calculation of the abscissa (ordinate) of a point that lies on the abscissa (ordinate) axis and is at the same distance from two given points
Example 4.
Find a point on the Oy axis that is at the same distance from points A (6, 12) and B (-8, 10).
Solution.
Let the coordinates of the point required by the conditions of the problem, lying on the Oy axis, be O 1 (0; b) (at the point lying on the Oy axis, the abscissa is zero). It follows from the condition that O 1 A = O 1 B.
Using the formula d = √((x A – x B) 2 + (y A – y B) 2) we find:
O 1 A = √((0 – 6) 2 + (b – 12) 2) = √(36 + (b – 12) 2);
O 1 B = √((a + 8) 2 + (b – 10) 2) = √(64 + (b – 10) 2).
We have the equation √(36 + (b – 12) 2) = √(64 + (b – 10) 2) or 36 + (b – 12) 2 = 64 + (b – 10) 2.
After simplification we get: b – 4 = 0, b = 4.
Point O 1 (0; 4) required by the conditions of the problem (Fig. 4).
5. Calculation of the coordinates of a point that is located at the same distance from the coordinate axes and some given point
Example 5.
Find point M located on the coordinate plane at the same distance from the coordinate axes and from point A(-2; 1).
Solution.
The required point M, like point A(-2; 1), is located in the second coordinate angle, since it is equidistant from points A, P 1 and P 2 (Fig. 5). The distances of point M from the coordinate axes are the same, therefore, its coordinates will be (-a; a), where a > 0.
From the conditions of the problem it follows that MA = MR 1 = MR 2, MR 1 = a; MP 2 = |-a|,
those. |-a| = a.
Using the formula d = √((x A – x B) 2 + (y A – y B) 2) we find:
MA = √((-a + 2) 2 + (a – 1) 2).
Let's make an equation:
√((-а + 2) 2 + (а – 1) 2) = а.
After squaring and simplification we have: a 2 – 6a + 5 = 0. Solve the equation, find a 1 = 1; and 2 = 5.
We obtain two points M 1 (-1; 1) and M 2 (-5; 5) that satisfy the conditions of the problem. 
6. Calculation of the coordinates of a point that is located at the same specified distance from the abscissa (ordinate) axis and from the given point
Example 6.
Find a point M such that its distance from the ordinate axis and from point A(8; 6) is equal to 5.
Solution.
From the conditions of the problem it follows that MA = 5 and the abscissa of point M is equal to 5. Let the ordinate of point M be equal to b, then M(5; b) (Fig. 6).
According to the formula d = √((x A – x B) 2 + (y A – y B) 2) we have:
MA = √((5 – 8) 2 + (b – 6) 2).
Let's make an equation:
√((5 – 8) 2 + (b – 6) 2) = 5. Simplifying it, we get: b 2 – 12b + 20 = 0. The roots of this equation are b 1 = 2; b 2 = 10. Consequently, there are two points that satisfy the conditions of the problem: M 1 (5; 2) and M 2 (5; 10).
It is known that many students, when solving problems independently, need constant consultations on techniques and methods for solving them. Often, a student cannot find a way to solve a problem without the help of a teacher. The student can receive the necessary advice on solving problems on our website.
Still have questions? Don't know how to find the distance between two points on a plane?
To get help from a tutor, register.
The first lesson is free!
website, when copying material in full or in part, a link to the source is required.
Let , (Figure 2.3). Required to find.
Figure 2.3. The distance between two points.
From the rectangular according to the Pythagorean theorem we have
That is ,
This formula is valid for any location of points and .
II. Division of a segment in this respect:
Let , . It is required to find , lying on the segment and dividing it in a given ratio (Figure 2.4.).
Figure 2.4. Division of a segment in this respect.
From the similarity ~, that is, from where. Likewise.
Thus,
– formula for dividing a segment in relation to .
If , then
– coordinates of the middle of the segment.
Comment. The derived formulas can be generalized to the case of a spatial rectangular Cartesian coordinate system. Let the points , . Then
- formula for finding the distance between points and .
Formula for dividing a segment in relation.
In addition to Cartesian ones on the plane and in space, you can construct big number other coordinate systems, that is, ways to characterize the position of a point on a plane or in space using two or three numerical parameters (coordinates). Let's look at some of the existing systems coordinates
On a plane it is possible to determine polar coordinate system , which is used, in particular, in the study of rotational movements.
Figure 2.5. Polar coordinate system.
Let us fix a point on the plane and a half-line emerging from it, and also select a scale unit (Figure 2.5). The point is called pole , half-line – polar axis . Let us assign two numbers to an arbitrary point:
– polar radius , equal to the distance from point M to pole O;
– polar angle , equal to angle between the polar axis and the half-line.
Measured in radians, the positive direction of the values is counted from counterclockwise, usually assumed.
The polar radius corresponds to the pole; the polar angle is not defined for it.
Let's find the relationship between rectangular and polar coordinates (Figure 2.6).
Figure 2.6. Relationship between rectangular and polar coordinate systems.
We will consider the origin of the rectangular coordinate system to be a pole, and take the ray to be the polar axis. Let - in a rectangular Cartesian coordinate system and - in a polar coordinate system. Let's find the relationship between rectangular and polar coordinates.
From rectangular, and from rectangular. Thus, the formulas
express the rectangular coordinates of a point in terms of its polar coordinates.
The inverse relationship is expressed by the formulas
Comment. The polar angle can also be determined from the formula, having previously determined from rectangular coordinates in which quadrant the point lies.
Example 1. Find the polar coordinates of a point.
Solution. We calculate ; The polar angle is found from the conditions:
Therefore, , therefore.
Example 2. Find the rectangular coordinates of the point.
Solution. We calculate
We get.
In three-dimensional space, in addition to the rectangular Cartesian coordinate system, cylindrical and spherical coordinate systems are often used.
Cylindrical coordinate system is a polar coordinate system in the plane, to which is added a spatial axis perpendicular to this plane (Figure 2.7). The position of any point is characterized by three numbers - its cylindrical coordinates: , where and are the polar coordinates (polar radius and polar angle) of the projection of the point onto the plane in which the polar coordinate system is chosen - the applicate, which is equal to the distance from the point to the specified plane.
Figure 2.7. Cylindrical coordinate system
To establish the relationship between the rectangular Cartesian coordinate system and the cylindrical one, we position them relative to each other as in Figure 2.8 (we place the plane in the plane, and the polar axis coincides with the positive direction of the axis, the axis is common in both coordinate systems).
Let be the rectangular coordinates of the point, be the cylindrical coordinates of this point, and be the projection of the point onto the plane. Then
formulas connecting rectangular and cylindrical coordinates of a point.
Figure 2.8. The relationship between the rectangular Cartesian
and cylindrical coordinate systems
Comment. Cylindrical coordinates are often used when considering bodies of rotation, with the axis located along the axis of rotation.
Spherical coordinate system can be constructed as follows. Let us choose the polar axis in the plane. Through the point we draw a straight line perpendicular to the plane (normal). Then any point in space can be associated with three real numbers, where is the distance from the point to, is the angle between the axis and the projection of the segment onto the plane, and is the angle between the normal and the segment. Notice, that , , .
If we position the plane in the plane, and choose the polar axis to coincide with the positive direction of the axis, and select the axis as the normal (Figure 2.9), we obtain formulas connecting these two coordinate systems
Figure 2.9. Relationship between spherical and rectangular Cartesian
coordinate systems
Scalar quantities, or scalars are completely characterized by their numerical value in the chosen system of units. Vector quantities or vectors, in addition to their numerical value, also have a direction. For example, if we say that the wind is blowing at a speed of 10 m/sec, then we will introduce a scalar value of wind speed, but if we say that the southwest wind is blowing at a speed of 10 m/sec, then in this case the wind speed will be already a vector.
Vector called a directed segment having a certain length, i.e. a segment of a certain length, in which one of the limiting points is taken as the beginning, and the second - as the end. We will denote the vector either or (Figure 2.10).
The length of a vector is denoted by the symbol or and is called the modulus of the vector. A vector whose length is 1 is called single . The vector is called zero , if its beginning and end coincide, and is denoted by θ or . The null vector has no specific direction and has a length equal to zero. Vectors and located on the same line or on parallel lines are called collinear . The two vectors are called equal , if they are collinear, have the same length and the same direction. All zero vectors are considered equal.
Two collinear vector, different from zero, having equal modules, but in the opposite direction, are called opposite . The vector opposite is denoted by , for the opposite vector.
To the number linear operations over vectors include the operations of addition, subtraction of vectors and multiplication of a vector by a number, i.e. operations whose result is a vector.
Let us define the indicated operations on vectors. Let two vectors and be given. Let's take an arbitrary point O and construct a vector, and plot the vector from point A. Then the vector connecting the beginning of the first term of the vector with the end of the second is called amount these vectors are denoted by . The considered rule for finding the sum of vectors is called triangle rules (Figure 2.11).
The same sum of vectors can be obtained in another way (Figure 2.12). Let us set aside the vector and the vector from the point. Let's construct a parallelogram on these vectors as on the sides. The vector, which is the diagonal of the parallelogram drawn from the vertex, will be the sum. This rule for finding the sum is called parallelogram rules .
The sum of any finite number of vectors can be obtained using the broken line rule (Figure 2.13). From an arbitrary point we plot a vector, then we plot a vector, etc. The vector connecting the beginning of the first to the end of the last is the sum
| |
By difference two vectors and is called such a vector, the sum of which with the subtracted vector gives the vector. From here rule for constructing a difference vector(Figure 2.14). From the point we plot the vector and the vector . The vector connecting the ends of the minuend vector and the subtrahend vector and directed from the subtrahend to the minuend vector is the difference.
Product of a vector for a real number λ is a vector that is collinear to the vector, has length and the same direction as the vector if , and the opposite direction to the vector if .
Entered linear operations over vectors have properties :
10 . Commutativity of addition: .
20 . Addition associativity: .
thirty . Existence of a neutral element by addition: .
4 0 . Existence of the opposite element by addition:
50 . Distributivity of multiplication by a number relative to addition of vectors: .
6 0 . Distributivity of multiplying a vector by the sum of two numbers:
7 0 . The associativity property regarding multiplication of a vector by a product of numbers: .
Let a system of vectors be given:
The expression where λ i (i = 1,2,…, n) are some numbers is called linear combination systems of vectors (2.1). The system of vectors (2.1) is called linearly dependent , if their linear combination is equal to zero, provided that not all numbers λ 1, λ 2, ..., λ n are equal to zero. The system of vectors (2.1) is called linearly independent , if their linear combination is equal to zero only if all numbers λ i = 0 (). Another definition can be given linear dependence vectors. The system of vectors (2.1) is called linearly dependent , if any vector of this system is linearly expressed in terms of the others, otherwise the system of vectors (2.1) linearly independent .
For vectors lying in the plane, the following statements are true.
10 . Any three vectors on a plane are linearly dependent.
20 . If the number of these vectors on the plane is more than three, then they are also linearly dependent.
thirty . In order for two vectors on a plane to be linearly independent, it is necessary and sufficient that they are non-collinear.
Thus, the maximum number of linearly independent vectors on the plane is two.
The vectors are called coplanar , if they lie in the same plane or are parallel to the same plane. The following statements are true for space vectors.
10 . Every four vectors of space are linearly dependent.
20 . If the number of these vectors in space is more than four, then they are also linearly dependent.
thirty . In order for three vectors to be linearly independent, it is necessary and sufficient that they be non-coplanar.
Thus, the maximum number of linearly independent vectors in space is three.
Any maximal subsystem of linearly independent vectors through which any vector of this system is expressed is called basis the one under consideration vector systems . It is easy to conclude that the basis on the plane consists of two non-collinear vectors, and the basis in space consists of three non-coplanar vectors. The number of basis vectors is called rank vector systems. The coefficients of expansion of a vector into basis vectors are called vector coordinates in this basis.
Let the vectors form a basis and let , then the numbers λ 1, λ 2, λ 3 are the coordinates of the vector in the basis. In this case, write It can be shown that the decomposition of the vector in the basis is unique. The main meaning of the basis is that linear operations on vectors become ordinary linear operations on numbers - the coordinates of these vectors. Using the properties of linear operations on vectors, we can prove the following theorem.
Theorem. When two vectors are added, their corresponding coordinates are added. When a vector is multiplied by a number, all its coordinates are multiplied by that number.
Thus, if and , then , where , and where , λ is a certain number.
Typically, the set of all vectors in the plane, reduced to a common origin, with introduced linear operations, is denoted by V 2, and the set of all vectors in space, reduced to a common origin, is denoted by V 3. The sets V 2 and V 3 are called spaces of geometric vectors.
Angle between vectors and is called the smallest angle () by which one of the vectors must be rotated until it coincides with the second after bringing these vectors to a common origin.
Dot product two vectors is a number equal to the product of the moduli of these vectors and the cosine of the angle between them. The scalar product of vectors and is denoted by , or
If the angle between the vectors and is equal to , then
From a geometric point of view scalar product of vectors is equal to the product of the modulus of one vector and the projection onto it of another vector. From equality (2.2) it follows that
From here condition of orthogonality of two vectors: two vectors And are orthogonal if and only if their scalar product is equal to zero, i.e. .
The dot product of vectors is not a linear operation because its result is a number, not a vector.
Properties of the scalar product.
1º. – commutativity.
2º. – distributivity.
3º. – associativity with respect to a numerical factor.
4º. - property of a scalar square.
From property 4º follows the definition vector length :
Let a basis be given in the space V 3, where the vectors are unit vectors (they are called unit vectors), the direction of each of them coincides with the positive direction of the coordinate axes Ox, Oy, Oz of the rectangular Cartesian coordinate system.
Let us expand the space vector V 3 according to this basis (Figure 2.15):
Vectors are called vector components along the coordinate axes, or components, numbers a x , a y , a z– rectangular Cartesian coordinates of the vector A. The direction of the vector is determined by the angles α, β, γ formed by it with the coordinate lines. The cosine of these angles is called the direction vector. Then the direction cosines are determined by the formulas:
It is easy to show that
Let us express the scalar product in coordinate form.
Let it be. Multiplying these vectors as polynomials and taking into account that we obtain an expression for finding dot product in coordinate form:
those. the scalar product of two vectors is equal to the sum of paired products of coordinates of the same name.
From (2.6) and (2.4) follows the formula for finding vector length :
From (2.6) and (2.7) we obtain a formula for determining angle between vectors:
A triple of vectors is called ordered if it is indicated which of them is considered the first, which is considered the second, and which is considered the third.
Ordered three vectors called right , if after bringing them to a common origin from the end of the third vector, the shortest turn from the first to the second vector is made counterclockwise. Otherwise, the triple of vectors is called left . For example, in Figure 2.15, the vectors , , form the right triple of vectors, and the vectors , , form the left triple of vectors.
In a similar way, the concept of right and left coordinate systems in three-dimensional space is introduced.
Vector artwork vector by vector is a vector (another notation) that:
1) has length , where is the angle between the vectors and ;
2) perpendicular to the vectors and (), i.e. is perpendicular to the plane in which the vectors and ;
By definition, we find the vector product of the coordinate unit vectors , , :
If , , then the coordinates of the vector product of a vector and a vector are determined by the formula:
From the definition it follows geometric meaning vector product : vector modulus equal to area parallelogram built on vectors and .
Properties of a vector product:
4 0 . , if the vectors and are collinear, or one of these vectors is zero.
Example 3. The parallelogram is built on the vectors and , where , , . Calculate the length of the diagonals of this parallelogram, the angle between the diagonals and the area of the parallelogram.
Solution. The construction of vectors and is shown in Figure 2.16, the construction of a parallelogram on these vectors is shown in Figure 2.17.
Let us carry out an analytical solution to this problem. Let us express the vectors defining the diagonals of the constructed parallelogram through the vectors and , and then through and . We find , . Next, we find the lengths of the diagonals of the parallelogram as the lengths of the constructed vectors
The angle between the diagonals of the parallelogram is denoted by . Then from the formula for the scalar product of vectors we have:
Hence, .
Using the properties of the vector product, we calculate the area of the parallelogram:
Let three vectors , and , be given. Let's imagine that the vector is multiplied vectorially by and the vector and the resulting vector is multiplied scalarly by the vector, thereby determining the number. It is called vector-scalar or mixed work three vectors , and . Denoted by or.
Let's find out geometric meaning of mixed product (Figure 2.18). Let , , not be coplanar. Let's build a parallelepiped on these vectors as on edges. The cross product is a vector whose modulus is equal to the area of the parallelogram (base of the parallelepiped), built on the vectors and and is directed perpendicular to the plane of the parallelogram.
Dot product (equal to the product of the modulus of the vector and the projection onto ). The height of the constructed parallelepiped is the absolute value of this projection. Consequently, the absolute value of the mixed product of three vectors is equal to the volume of the parallelepiped built on the vectors , and , i.e. .
Hence the volume triangular pyramid, built on the vectors , and , is calculated by the formula .
Let's note some more properties of a mixed product vectors.
1 o. The sign of the product is positive if the vectors , , and form a system of the same name as the main one, and negative otherwise.
Really, the scalar product is positive if the angle between and is acute and negative if the angle is obtuse. With an acute angle between and , the vectors and are located on one side relative to the base of the parallelepiped, and therefore, from the end of the vector, the rotation from to will be visible in the same way as from the end of the vector, i.e. in a positive direction (counterclockwise).
At an obtuse angle, both the vectors and are located on different sides relative to the plane of the parallelogram lying at the base of the parallelepiped, and therefore, from the end of the vector, the rotation from to is visible in the negative direction (clockwise).
2 o A mixed product does not change when its factors are rearranged circularly: .
3 o When any two vectors are rearranged, the mixed product changes only the sign. For example, , . , . - unknown systems.
System(3.1) is called homogeneous , if all members are free . System (3.1) is called heterogeneous , if at least one of the free members .
System solution is called a set of numbers, when substituting them into the equations of the system instead of the corresponding unknowns, each equation of the system turns into an identity. A system that has no solution is called incompatible, or controversial . A system that has at least one solution is called joint .
The joint system is called certain , if it has a unique solution. If a consistent system has more than one solution, then it is called uncertain . Homogeneous system is always joint, since it has, according to at least, zero solution. An expression for the unknowns from which any specific solution of the system can be obtained is called general decision , and any specific solution of the system is its private solution . Two systems with the same unknowns equivalent (equivalent ), if each solution of one of them is a solution of the other or both systems are inconsistent.
Let's consider methods for solving systems linear equations.
One of the main methods for solving systems of linear equations is Gauss method, or sequential method exclusion of unknowns. The essence of this method is to reduce a system of linear equations to a stepwise form. In this case, the following equations have to be carried out: elementary transformations :
1. Rearranging the equations of the system.
2. Adding another equation to one equation.
3. Multiplying both sides of the equation by a number other than zero.
As a result, the system will take the form:
Continuing this process further, we eliminate the unknown from all equations, starting with the third. To do this, multiply the second equation by numbers and add to the 3rd, ..., to -th equation of the system. The following steps of the Gauss method are carried out similarly. If as a result of the transformations we obtain an identical equation, then we delete it from the system. If at some step of the Gaussian method an equation of the form is obtained:
then the system under consideration is inconsistent and its further solution ceases. If an equation of the form (3.2) is not encountered when fulfilling elementary transformations, then in no more than - steps system (3.1) will be transformed to a stepwise form:
To obtain a particular solution of the system, it will be necessary to assign specific values to the free variables in (3.4).
Note that since in the Gauss method all transformations are performed on the coefficients at unknown equations and free terms, then in practice this method is usually applied to a matrix composed of coefficients of unknowns and a column of free terms. This matrix is called extended. Using elementary transformations, this matrix is reduced to a stepwise form. Then, using the resulting matrix, the system is reconstructed and all previous reasoning is applied to it.
Example 1. Solve the system:
Solution. We create an extended matrix and reduce it to a stepwise form:
~ *) ~ **) ~ ***)
*) - the second line was multiplied by and the third line was crossed out.
In §§5, 6 and 10 of this chapter we will consider some of the simplest problems of analytical geometry, to which many more complex problems are often reduced. One such problem is the problem of the distance between two points.
Let two points be given in a rectangular coordinate system chosen on a plane. Let us express the distance d between these two points through their coordinates.
Let's find the projections of points A and B onto the coordinate axes (Fig. 8). Will have:

Through one of these points, for example A, we draw a straight line parallel to the abscissa axis until it intersects with the straight line at point C
From the right triangle ACB we get:
![]()
(here AC and CB are the lengths of the sides of triangle ACB). But since
(Chapter 1, § 3), then
It is clear that here we need to take arithmetic value root
Thus, the distance between two given points is equal to the square root of the sum of the squares of the differences between the same coordinates of these points.
Comment. If the given points A to B are located on a straight line parallel coordinate axis, then we will not get triangle ABC, but formula (3) will be valid in this case as well. Indeed, if, for example, points A to B lie on a straight line parallel to the Ox axis, then, obviously, (Chapter I, § 3). The same can be obtained from formula (3), since in this case
Calculating distances between points based on their coordinates on a plane is elementary; on the Earth’s surface it is a little more complicated: we will consider measuring the distance and initial azimuth between points without projection transformations. First, let's understand the terminology.
Introduction
Great circle arc length– the shortest distance between any two points located on the surface of a sphere, measured along the line connecting these two points (such a line is called orthodromy) and passing along the surface of the sphere or other surface of revolution. Spherical geometry is different from normal Euclidean geometry and the distance equations also take a different form. In Euclidean geometry, the shortest distance between two points is a straight line. On a sphere, there are no straight lines. These lines on the sphere are part of great circles - circles whose centers coincide with the center of the sphere. Initial azimuth- azimuth, taking which when starting to move from point A, following the great circle for the shortest distance to point B, the end point will be point B. When moving from point A to point B along the great circle line, the azimuth from the current position is end point B is constantly changing. The initial azimuth is different from a constant one, following which the azimuth from the current point to the final point does not change, but the route followed is not the shortest distance between two points.Through any two points on the surface of a sphere, if they are not directly opposite to each other (that is, they are not antipodes), a unique great circle can be drawn. Two points divide a large circle into two arcs. The length of a short arc is the shortest distance between two points. An infinite number of large circles can be drawn between two antipodal points, but the distance between them will be the same on any circle and equal to half the circumference of the circle, or π*R, where R is the radius of the sphere.

On a plane (in a rectangular coordinate system), large circles and their fragments, as mentioned above, represent arcs in all projections except the gnomonic one, where large circles are straight lines. In practice, this means that airplanes and other air transport always use the route of the minimum distance between points to save fuel, that is, the flight is carried out along a great circle distance, on a plane it looks like an arc.

The shape of the Earth can be described as a sphere, so great circle distance equations are important for calculating the shortest distance between points on the Earth's surface and are often used in navigation. Calculating distance by this method is more efficient and in many cases more accurate than calculating it for projected coordinates (in rectangular coordinate systems), since, firstly, it does not require translation geographical coordinates into a rectangular coordinate system (carry out projection transformations) and, secondly, many projections, if incorrectly selected, can lead to significant length distortions due to the characteristics of projection distortions. It is known that it is not a sphere, but an ellipsoid that describes the shape of the Earth more accurately, however, this article discusses the calculation of distances specifically on a sphere; for calculations, a sphere with a radius of 6,372,795 meters is used, which can lead to an error in calculating distances of the order of 0.5%.
Formulas
There are three ways to calculate the great circle spherical distance. 1. Spherical cosine theorem In the case of small distances and small calculation depth (number of decimal places), the use of the formula can lead to significant rounding errors. φ1, λ1; φ2, λ2 - latitude and longitude of two points in radians Δλ - difference in coordinates in longitude Δδ - angular difference Δδ = arccos (sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ) To convert the angular distance to metric, you need to multiply the angular difference by the radius Earth (6372795 meters), the units of the final distance will be equal to the units in which the radius is expressed (in this case, meters). 2. Haversine formula Used to avoid problems with short distances. 3. Modification for the antipodes The previous formula is also subject to the problem of antipodal points; to solve it, the following modification is used.My implementation on PHP
// Earth radius define("EARTH_RADIUS", 6372795); /* * Distance between two points * $φA, $λA - latitude, longitude of the 1st point, * $φB, $λB - latitude, longitude of the 2nd point * Written based on http://gis-lab.info/ qa/great-circles.html * Mikhail Kobzarev< >* */ function calculateTheDistance ($φA, $λA, $φB, $λB) ( // convert coordinates to radians $lat1 = $φA * M_PI / 180; $lat2 = $φB * M_PI / 180; $long1 = $λA * M_PI / 180; $long2 = $λB * M_PI / 180; // cosines and sines of latitudes and longitudes $cl1 = cos($lat1); ; $sl2 = sin($lat2); $delta = $long2 - $long1; $cdelta = cos($delta); $sdelta = sin($delta); $cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2)); $x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta; $ad = atan2($y, $x); $dist = $ad * EARTH_RADIUS; return $dist; Example of a function call: $lat1 = 77.1539; $long1 = -139.398; $lat2 = -77.1804; $long2 = -139.55; echo calculateTheDistance($lat1, $long1, $lat2, $long2) . "meters"; // Return "17166029 meters"Article taken from the site
Theorem 1. For any two points and a plane, the distance between them is expressed by the formula:
For example, if points and are given, then the distance between them is:
2. Area of a triangle.
Theorem 2.
For any points
not lying on the same straight line, the area of a triangle is expressed by the formula:
For example, let's find the area of the triangle formed by the points , and.
Comment. If the area of a triangle is zero, this means that the points lie on the same line.
3. Division of a segment in a given ratio.
Let an arbitrary segment be given on the plane and let
– any point of this segment other than the end points. The number defined by equality is called attitude, at which the point divides the segment.
The problem of dividing a segment in a given relation is to: for a given relation and given coordinates of points
and find the coordinates of the point.
Theorem 3.
If a point divides a segment
in a relationship
,
then the coordinates of this point are determined by the formulas: ![]() (1.3), where are the coordinates of the point, and are the coordinates of the point.
(1.3), where are the coordinates of the point, and are the coordinates of the point.
Consequence: If is the midpoint of the segment
, where and, then (1.4) (since).
For example. Points and are given. Find the coordinates of a point that is twice closer to than to
Solution: The required point divides the segment
in relation to since ![]() , Then
, Then ![]() ,
,![]() , got
, got
Polar coordinates
The most important after the rectangular coordinate system is the polar coordinate system. It consists of a certain point called pole, and the ray emanating from it - polar axis. In addition, the scale unit for measuring the lengths of segments is set. 
Let a polar coordinate system be given and let be an arbitrary point on the plane. Let be the distance from the point
to the point ; – the angle by which the polar axis must be rotated to align with the beam.
Polar coordinates of a point are called numbers. In this case, the number is considered the first coordinate and is called polar radius, the number is the second coordinate and is called polar angle.
Denoted by . The polar radius can have any non-negative value:. It is usually believed that the polar angle varies within the following limits:. However, in some cases it is necessary to determine angles measured from the polar axis clockwise.
The relationship between the polar coordinates of a point and its rectangular coordinates.
We will assume that the origin of the rectangular coordinate system is at the pole, and the positive semi-axis of the abscissa coincides with the polar axis. 
Let – in a rectangular coordinate system and – in a polar coordinate system. Defined– right triangle With. Then(1.5). These formulas express rectangular coordinates in terms of polar ones.
On the other hand, according to the Pythagorean theorem and
![]() (1.6) – these formulas express polar coordinates through rectangular ones.
(1.6) – these formulas express polar coordinates through rectangular ones.
Note that the formula defines two values of the polar angle, since. From these two angle values, choose the one at which the equalities are satisfied.
For example, let's find the polar coordinates of the point ..or, because I quarter.
Example 1: Find a point symmetrical to a point 
Relative to the bisector of the first coordinate angle.
Solution:
Let's draw through the point A direct l 1, perpendicular to the bisector l first coordinate angle. Let . On a straight line l 1 put aside the segment SA 1 , equal to the segment AC. Right Triangles ASO And A 1 CO equal to each other (on two sides). It follows that | OA| = |O.A. 1 |. Triangles ADO And OEA 1 are also equal to each other (by hypotenuse and acute angle). We conclude that |AD| = |OE| = 4,|OD| = |EA 1 | = 2, i.e. the point has coordinates x = 4, y = -2, those. A 1 (4;-2).
Note that there is a general statement: point A 1, symmetrical to the point relative to the bisector of the first and third coordinate angles, has coordinates, that is .
Example 2: Find the point at which a line passing through the points and , will intersect the axis Oh.
Solution:
Coordinates of the desired point WITH There is ( x; 0). And since the points A,IN And WITH lie on the same straight line, then the condition must be satisfied (x 2 -x 1 )(y 3 -y 1 )-(x 3 -x 1 )(y 2 -y 1 ) = 0 (formula (1.2), area of the triangle ABC equal to zero!), where are the coordinates of the point A, – points IN, – points WITH. We get, i.e., , . Therefore, the point WITH has coordinates ,, i.e..
Example 3: In the polar coordinate system, points are given. Find: A) distance between points and ; b) area of the triangle OM 1 M 2 (ABOUT– pole).
Solution:
a) Let us use formulas (1.1) and (1.5):
that is, .
b) using the formula for the area of a triangle with sides A And b and the angle between them (), we find the area of the triangle OM 1 M 2 . .
- In contact with 0
- Google+ 0
- OK 0
- Facebook 0