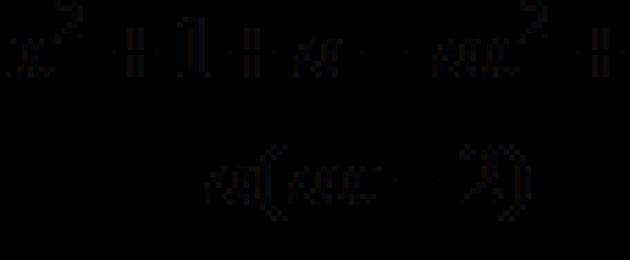Ejemplos de sistemas de ecuaciones con un parámetro. Resolver sistemas de ecuaciones lineales con parámetros.

A veces, en las ecuaciones, algunos coeficientes no vienen dados por valores numéricos específicos, sino que se indican con letras.

Ejemplo: hacha+b=c.

En esta ecuación X- desconocido, a B C– coeficientes que pueden tomar diferentes valores numéricos. Los coeficientes especificados de esta manera se llaman parámetros.

Una ecuación con parámetros define muchas ecuaciones (para todos los valores de parámetros posibles).

Ejemplo: –5 X+10=– 1;

X+4y= 0;

–102–1000y=; etc.

estas son todas las ecuaciones que están especificadas por la ecuación con parámetros hacha+b=c.

Resolver una ecuación con parámetros significa:

1. Indique en qué valores de parámetros tiene raíces la ecuación y cuántas hay para diferentes valores de parámetros.

2. Encuentre todas las expresiones para las raíces e indique para cada una de ellas los valores de los parámetros en los que esta expresión determina la raíz de la ecuación.

Pasemos a la ecuación ya dada con parámetros. hacha+b=c y lo solucionaremos.

Si A¹0, luego https://pandia.ru/text/80/014/images/image002_67.gif" width="63" height="41">;

en a=0 Y b=c,x– cualquier número real;

en a=0 Y b¹ C, la ecuación no tiene raíces.

En el proceso de resolución de esta ecuación, aislamos el valor del parámetro a=0, en el que se produce un cambio cualitativo en la ecuación, llamaremos a este valor del parámetro "control". Dependiendo de qué ecuación tengamos, los valores de “control” del parámetro se encuentran de manera diferente. Veamos diferentes tipos de ecuaciones e indiquemos cómo encontrar los valores de "control" del parámetro.

I. Ecuaciones lineales con parámetro y ecuaciones reducibles a lineales

En tales ecuaciones, los valores de "control" de los parámetros, por regla general, son los valores que hacen que los coeficientes sean cero. X.

Ejemplo 1. : 2A(A–2)x=a– 2

1. Los valores de “control” son valores que satisfacen la condición:

2A(A–2)=0

Resolvamos esta ecuación para la variable. A.

2un = 0 o A–2= 0, desde donde un = 0, un = 2.

2. Resolvamos la ecuación inicial para los valores de “control” del parámetro.

En un = 0 tenemos 0× x=– 2, pero este no es el caso para ningún valor real X, es decir, en este caso la ecuación no tiene raíces.

En un = 2 tenemos 0× x= 0, esto es cierto para cualquier valor X, lo que significa que la raíz de la ecuación es cualquier número real X.

3. Resolvamos la ecuación original en el caso en que A¹ 0 y A¹ 2 luego 2 A(A–2)¹ 0 y ambos lados de la ecuación se pueden dividir por 2 A(A–2), obtenemos:

Porque A¹ 2, entonces la fracción se puede reducir en ( A–2), entonces tenemos .

Respuesta: en un = 0, sin raíces;

en un = 2, raíz – cualquier número real;

en A¹ 0, A¹ 2, .

Se puede imaginar un algoritmo para resolver este tipo de ecuación.

1. Determine los valores de "control" del parámetro.

2. Resuelve la ecuación para X, en los valores de los parámetros de control.

3. Resuelve la ecuación para X, a valores distintos a los de “control”.

4. Escribe la respuesta en el formulario:

Respuesta: 1) para valores de parámetros..., la ecuación tiene raíces...;

2) para valores de parámetros..., la ecuación tiene raíces...;

3) para valores del parámetro..., la ecuación no tiene raíces.

Ejemplo 2. Resolver ecuación con parámetro.

(A 2–2A+1)x=un 2+2A- 3

1. Encuentre los valores de control del parámetro.

A 2–2A+1=0 Û ( A–1)2=0 Û A=1

2. Resuelve la ecuación para un = 1

0× x=(1+2×1–3) Û 0× x= 0 Þ X– cualquier número real.

3. Resuelve la ecuación para A¹ 1

A 2–2A+1¹ 0 Þ https://pandia.ru/text/80/014/images/image006_39.gif" width="115" height="45 src=">

porque A¹ 1, la fracción se puede reducir

https://pandia.ru/text/80/014/images/image007_35.gif" width="64" height="41 src=">.

Ejemplo 3. Resolver ecuación con parámetro.

https://pandia.ru/text/80/014/images/image009_29.gif" width="72" height="41 src=">.

4. Respuesta: 1) en un = 2, sin raíces;

2) cuando A¹ 0,A¹ 2, ;

3) cuando un = 0 la ecuación no tiene sentido.

Ejemplo 4. Resolver ecuación con parámetro.

https://pandia.ru/text/80/014/images/image011_28.gif" width="135" height="45 src=">

https://pandia.ru/text/80/014/images/image013_25.gif" width="175" height="45 src=">

porque X¹ 0 y A¹ – 2, la ecuación es equivalente a la ecuación

(A+3)x= 2A–1

Encontremos los valores de control del parámetro.

A+3= 0 Þ un=– 3.

2. Resuelve la ecuación para un=– 3.

0× x=– 7

a cualquiera X no hay igualdad

3. Resuelve la ecuación para A¹ – 3, un+ 3¹ 0.

https://pandia.ru/text/80/014/images/image015_21.gif" width="69" height="41 src="> Û ,

por lo tanto, para que la ecuación tenga sentido https://pandia.ru/text/80/014/images/image016_21.gif" width="40" height="41 src=">, no hay raíces;

2) cuando A¹ – 2, A¹ – 3, , .

II. Ecuaciones cuadráticas con un parámetro y ecuaciones reducibles a cuadráticas.

En tales ecuaciones, los valores del parámetro que hacen que el coeficiente sea cero generalmente se toman como "control". X 2, ya que en este caso la ecuación se vuelve lineal, al igual que el valor del parámetro, lo que hace que el discriminante de la ecuación desaparezca, ya que el número de raíces reales de la ecuación cuadrática depende del valor del discriminante.

Ejemplo 5. Resolver ecuación con parámetro.

(A–1)X 2+2(2A+1)X+(4A+3)= 0

1. Encontremos los valores de los parámetros que hacen que el coeficiente sea cero. X

A- 1=0 Û un = 1

2. Resuelve la ecuación para un = 1

0× X 2+2(2×1+1) X+4×1+3=0 Û 6 X+7=0Û.

3. Encontremos los valores del parámetro que hacen desaparecer el discriminante de la ecuación.

D=(2(2A+1))2–4(A–1)(4A+3)=(4A+1)2–(4A–4)(4A+3)=4(5A+4)

4(5A+4)=0 Û .

4. Resolvamos la ecuación para, en este caso la ecuación tendrá una raíz real

https://pandia.ru/text/80/014/images/image021_15.gif" width="133" height="41"> Û

9X 2+6X+1=0 Û (3 X+1)2=0 Û https://pandia.ru/text/80/014/images/image023_15.gif" width="51" height="41 src=">. En este caso D<0, поэтому уравнение действительных корней не имеет.

6. Resuelve la ecuación para A No. 1, https://pandia.ru/text/80/014/images/image025_12.gif" width="341" height="49 src=">

7. Respuesta: 1) con https://pandia.ru/text/80/014/images/image022_14.gif" width="51" height="41 src=">;

2) cuando un = 1, ;

3) para , no existen raíces reales;

4) en y A No. 1, https://pandia.ru/text/80/014/images/image027_10.gif" width="144" height="44 src=">

1. Desde A está en el denominador de la fracción, entonces la ecuación tiene sentido sólo cuando A#0. El denominador también contiene las expresiones. a2x– 2A y 2- Oh, que también debe ser distinto de cero

a2x– 2A¹0 Û A(Oh–2)¹0 Û A¹0, Oh–2¹0 Û A¹0, ;

2–Oh¹0 Û https://pandia.ru/text/80/014/images/image028_9.gif" width="41" height="41 src=">.

2. Resuelve la ecuación para A¹0, https://pandia.ru/text/80/014/images/image029_9.gif" width="169" height="47 src="> Û Û

(1–A)X 2+2X+1+A=0 ...................(*)

3. Encontremos los valores de los parámetros que hacen que el coeficiente sea cero. X 2

1–A=0 Û A=1

4. Resuelve la ecuación (*) para A=1

0× X 2+2X+2=0 Û 2 x=– 2Û x=–1

Comprobemos de inmediato si coincide. X de https://pandia.ru/text/80/014/images/image032_8.gif" width="72" height="41 src=">, lo que significa que cuando A=1, x=– 1.

Objetivo:

• repetir la resolución de sistemas de ecuaciones lineales con dos variables
• definir un sistema de ecuaciones lineales con parámetros
• Te enseñará a resolver sistemas de ecuaciones lineales con parámetros.

durante las clases

1. Organizar el tiempo
2. Repetición
3. Explicación de un nuevo tema.
4. Consolidación
5. Resumen de la lección
6. Tarea

2. Repetición:

I. Ecuación lineal con una variable:

1. Definir una ecuación lineal con una variable.

[Una ecuación de la forma ax=b, donde x es una variable, a y b son algunos números, se llama ecuación lineal con una variable]

2. ¿Cuántas raíces puede tener una ecuación lineal?

[- Si a=0, b0, entonces la ecuación no tiene soluciones, x

Si a=0, b=0, entonces x R

Si a0, entonces la ecuación tiene una solución única, x =

3. Descubre cuántas raíces tiene la ecuación (según opciones)

II. Ecuación lineal con 2 variables y sistema de ecuaciones lineales con 2 variables.

1. Definir una ecuación lineal en dos variables. Dar un ejemplo.

[Una ecuación lineal con dos variables es una ecuación de la forma ax + by = c, donde xey son variables, a, byc son algunos números. Por ejemplo, x-y=5]

2. ¿Cómo se llama resolver una ecuación con dos variables?

[Una solución a una ecuación con dos variables es un par de valores de variables que convierte la ecuación en una verdadera igualdad.]

3. ¿El par de valores de las variables x = 7, y = 3 es una solución a la ecuación 2x ​​+ y = 17?

4. ¿Cómo se llama la gráfica de una ecuación en dos variables?

[La gráfica de una ecuación con dos variables es el conjunto de todos los puntos en el plano coordenado cuyas coordenadas son soluciones a esta ecuación.]

5. Descubre cuál es la gráfica de la ecuación:

[Expresemos la variable y a través de x: y=-1.5x+3

La fórmula y=-1,5x+3 es una función lineal, cuya gráfica es una línea recta. Dado que las ecuaciones 3x+2y=6 e y=-1.5x+3 son equivalentes, esta recta también es una gráfica de la ecuación 3x+2y=6]

6. ¿Cuál es la gráfica de la ecuación ax+bу=c con variables x e y, donde a0 o b0?

[La gráfica de una ecuación lineal con dos variables en la que al menos uno de los coeficientes de las variables no es cero es una línea recta.]

7. ¿Cómo se llama resolver un sistema de ecuaciones con dos variables?

[Una solución a un sistema de ecuaciones con dos variables es un par de valores de variables que convierte cada ecuación del sistema en una verdadera igualdad]

8. ¿Qué significa resolver un sistema de ecuaciones?

[Resolver un sistema de ecuaciones significa encontrar todas sus soluciones o demostrar que no hay soluciones.]

9. Averigüe si dicho sistema siempre tiene soluciones y, de ser así, cuántas (gráficamente).

10. ¿Cuántas soluciones puede tener un sistema de dos ecuaciones lineales con dos variables?

[La única solución es si las líneas se cruzan; no tiene soluciones si las rectas son paralelas; infinitos si las lineas coinciden]

11. ¿Qué ecuación suele definir una línea recta?

12. Establezca una conexión entre coeficientes de ángulos y términos libres:

Opción I: y=-x+2 y= -x-3, k 1 = k 2 , b 1 b 2, sin soluciones;

Opción II: y=-x+8 y=2x-1, k 1 k 2 , una solución;

Opción III: y=-x-1 y=-x-1, k 1 = k 2, b 1 = b 2, muchas soluciones.

Conclusión:

1. Si los coeficientes angulares de las rectas que son gráficas de estas funciones son diferentes, entonces estas rectas se cruzan y el sistema tiene una solución única.
2. Si los coeficientes angulares de las rectas son iguales y los puntos de intersección con el eje y son diferentes, entonces las rectas son paralelas y el sistema no tiene soluciones.
3. Si los coeficientes angulares y los puntos de intersección con el eje y son iguales, entonces las rectas coinciden y el sistema tiene infinitas soluciones.

Hay una tabla en la pizarra que el profesor y los alumnos van rellenando poco a poco.

III. Explicación de un nuevo tema.

Definición: Ver sistema

• A 1 x+B 1 y=C
• A 2 x+B 2 y=C 2

donde A 1, A 2, B 1, B 2, C 1 C 2 son expresiones que dependen de los parámetros, y x e y son incógnitas, se denomina sistema de dos ecuaciones algebraicas lineales con dos incógnitas en los parámetros.

Son posibles los siguientes casos:

1) Si , entonces el sistema tiene una solución única

2) Si , entonces el sistema no tiene soluciones.

3) Si , entonces el sistema tiene infinitas soluciones.

IV. Consolidación

Ejemplo 1.

¿A qué valores del parámetro a funciona el sistema?

• 2x - 3y = 7
• Ah - 6 años = 14

a) tiene un número infinito de soluciones;

b) tiene una solución única

Respuesta:

a) si a=4, entonces el sistema tiene un número infinito de soluciones;

b) si un4, entonces sólo hay una solución.

Ejemplo 2.

Resuelve el sistema de ecuaciones.

• x+(m+1)y=1
• x+2y=n

Solución: a), es decir para m1 el sistema tiene una solución única.

b), es decir para m=1 (2=m+1) y n1 el sistema original no tiene soluciones

c) , para m=1 y n=1 el sistema tiene infinitas soluciones.

Respuesta: a) si m=1 y n1, entonces no hay soluciones

b) m=1 y n=1, entonces la solución es un conjunto infinito

• y - cualquiera
• x=n-2y

c) si m1 y n son cualquiera, entonces

Ejemplo 3.

• akh-3ау=2а+3
• x+ay=1

Solución: De la ecuación II encontramos x = 1-аy y sustituimos la ecuación I en la ecuación

a(1-ау)-3ау=2а+3

a-a 2 y-3ау=2а+3

A 2 y-3ау=а+3

A(a+3)y=a+3

Posibles casos:

1) a=0. Entonces la ecuación queda así 0*y=3 [y]

Por lo tanto, para a=0 el sistema no tiene soluciones.

2) a=-3. Entonces 0*y=0.

Por tanto, y. En este caso x=1-ау=1+3у

3) a0 y a-3. Entonces y=-, x=1-a(-=1+1=2

Respuesta:

1) si a=0, entonces (x; y)

2) si a=-3, entonces x=1+3y, y

3) si un0 y a?-3, entonces x=2, y=-

Consideremos el segundo método para resolver el sistema (1).

Resolvamos el sistema (1) usando el método de la suma algebraica: primero multiplicamos la primera ecuación del sistema por B 2, la segunda por B 1 y sumamos estas ecuaciones término por término, eliminando así la variable y:

Porque A 1 B 2 -A 2 B 1 0, entonces x =

Ahora eliminemos la variable x. Para ello se multiplica la primera ecuación del sistema (1) por A 2, y la segunda por A 1, y se suman ambas ecuaciones término a término:

• A 1 A 2 x +A 2 B 1 y=A 2 C 1
• -A 1 A 2 x-A 1 B 2 y=-A 1 C 2
• y(A 2 B 1 -A 1 B 2) = A 2 C 1 -A 1 C 2

porque A 2 B 1 -A 1 B 2 0 y =

Para facilitar la resolución del sistema (1), introducimos la siguiente notación:

- determinante principal

Ahora la solución al sistema (1) se puede escribir usando determinantes:

Las fórmulas dadas se llaman fórmulas de Cramer.

Si , entonces el sistema (1) tiene una solución única: x=; y=

Si , o , entonces el sistema (1) no tiene soluciones

Si , , , , entonces el sistema (1) tiene un número infinito de soluciones.

En este caso, es necesario investigar más a fondo el sistema. En este caso, por regla general, se reduce a una ecuación lineal. En este caso, suele ser conveniente estudiar el sistema de la siguiente manera: resolviendo la ecuación, encontramos valores específicos de los parámetros o expresamos uno de los parámetros en términos de los demás y sustituimos estos valores de los parámetros en el sistema. Entonces obtenemos un sistema con coeficientes numéricos específicos o con un número menor de parámetros, que deben ser estudiados.

Si los coeficientes A 1 , A 2 , B 1 , B 2 del sistema dependen de varios parámetros, entonces es conveniente estudiar el sistema utilizando determinantes del sistema.

Ejemplo 4.

Para todos los valores del parámetro a, resuelva el sistema de ecuaciones.

• (a+5)x+(2a+3)y=3a+2
• (3a+10)x+(5a+6)y=2a+4

Solución: Encontremos el determinante del sistema:

= (a+5)(5a+6) – (3a+10) (2a+3)= 5a 2 +31a+30-6a 2 -29a-30=-a 2 +2a=a(2-a)

= (3a+2) (5a+6) –(2a+4)(2a+3)=15a 2 +28a+12-4a 2 -14a-12=11a 2 +14a=a(11a+14)

=(a+5) (2a+4)-(3a+10)(3a+2)=2a 2 +14a+20-9a 2 -36a-20=-7a 2 -22a=-a(7a+22)

Resolvamos un sistema de ecuaciones con un parámetro (A. Larin, opción 98)

Encuentre todos los valores del parámetro, para cada uno de los cuales el sistema

tiene exactamente una solución.

Echemos un vistazo más de cerca al sistema. En la primera ecuación del sistema, el lado izquierdo es y el lado derecho no depende del parámetro. Es decir, podemos considerar esta ecuación como la ecuación de la función

y podemos trazar esta función.

Segunda ecuación del sistema.

Depende del parámetro, y al seleccionar un cuadrado completo en el lado izquierdo de la ecuación, obtenemos la ecuación de un círculo.

Por lo tanto, tiene sentido trazar gráficas de cada ecuación y ver en qué valor del parámetro estas gráficas tienen un punto de intersección.

Comencemos con la primera ecuación. Primero, abramos los módulos. Para hacer esto, igualamos cada expresión submodular a cero para encontrar los puntos en los que cambia el signo.

La primera expresión submodular cambia de signo en , la segunda en .

Tracemos estos puntos en la línea de coordenadas y encontremos los signos de cada expresión submodular en cada intervalo:

Tenga en cuenta que para y la ecuación no tiene sentido, por lo que puncionamos estos puntos.

Ahora expandamos los módulos en cada intervalo. (Recuerde: si una expresión submodular es mayor o igual a cero, entonces expandimos el módulo con el mismo signo, y si es menor que cero, entonces con el signo opuesto).

Ambas expresiones submodulares son negativas, por lo tanto, expandimos ambos módulos con signo opuesto:

Es decir, cuando la función original tiene la forma

En este intervalo, la primera expresión submodular es negativa y la segunda es positiva, por lo tanto obtenemos:

- la función no existe en este intervalo.

3. título="x>2">!}

En este intervalo, ambas expresiones submodulares son positivas; expandimos ambos módulos con el mismo signo. Obtenemos:

Es decir, con title="x>2"> исходная функция имеет вид !}

Entonces, obtuvimos la gráfica de la función.

Ahora veamos la segunda ecuación:

Seleccionemos un cuadrado completo en el lado izquierdo de la ecuación, para ello sumamos el número 4 a ambos lados de la ecuación:

Para un valor específico del parámetro, la gráfica de esta ecuación es un círculo con centro en un punto con coordenadas, cuyo radio es 5. Para diferentes valores, tenemos una serie de círculos:

Moveremos el círculo de abajo hacia arriba hasta que toque el lado izquierdo de la gráfica de la primera función. En la imagen este círculo es rojo. El centro de este círculo es el punto, sus coordenadas son (-2;-3). Además, cuando se mueve hacia arriba, el círculo tiene un punto de intersección con el lado izquierdo de la gráfica de la función, es decir, el sistema tiene una solución única.

Seguimos moviendo el círculo hacia arriba hasta que toque el lado derecho de la gráfica de la primera función. Esto sucederá cuando el centro del círculo esté en el punto con coordenadas (-2;0); en la figura, este círculo es azul.

Al moverse más hacia arriba, el círculo cruzará las partes izquierda y derecha de la gráfica de la primera función, es decir, el círculo tendrá dos puntos de intersección con la gráfica de la primera función y el sistema tendrá dos soluciones. Esta situación continúa hasta que el centro del círculo está en el punto con coordenadas (-2; 5); este círculo es verde. En este punto, el círculo toca el lado izquierdo del gráfico y se cruza con el derecho. Es decir, el sistema tiene una solución.

Entonces, el sistema tiene una solución única cuando(-3;0]; si los valores del parámetro a son más de uno, entonces la ecuación tendrá dos raíces.

¿Aún tienes preguntas? ¿No sabes cómo resolver ecuaciones con un parámetro?
Para obtener ayuda de un tutor -.
¡La primera lección es gratis!

blog.site, al copiar material total o parcialmente, se requiere un enlace a la fuente original.

1. Sistemas de ecuaciones lineales con parámetro.

Los sistemas de ecuaciones lineales con un parámetro se resuelven mediante los mismos métodos básicos que los sistemas de ecuaciones ordinarios: el método de sustitución, el método de suma de ecuaciones y el método gráfico. El conocimiento de la interpretación gráfica de sistemas lineales facilita responder a la pregunta sobre el número de raíces y su existencia.

Ejemplo 1.

Encuentre todos los valores del parámetro a para los cuales el sistema de ecuaciones no tiene soluciones.

(x + (a 2 – 3)y = a,
(x + y = 2.

Solución.

Veamos varias formas de resolver esta tarea.

1 vía. Usamos la propiedad: el sistema no tiene soluciones si la razón de los coeficientes delante de x es igual a la razón de los coeficientes delante de y, pero no igual a la razón de los términos libres (a/a 1 = b /b 1 ≠ c/c 1). Entonces nosotros tenemos:

1/1 = (a 2 – 3)/1 ≠ a/2 o sistema

(y 2 – 3 = 1,
(un ≠ 2.

De la primera ecuación a 2 = 4, por tanto, teniendo en cuenta la condición de que a ≠ 2, obtenemos la respuesta.

Respuesta: a = -2.

Método 2. Resolvemos por el método de sustitución.

(2 – y + (a 2 – 3)y = a,
(x = 2 – y,

((a 2 – 3)y – y = a – 2,
(x = 2 – y.

Después de quitar el factor común y entre paréntesis en la primera ecuación, obtenemos:

((a 2 – 4)y = a – 2,
(x = 2 – y.

El sistema no tiene soluciones si la primera ecuación no tiene soluciones, es decir

(y 2 – 4 = 0,
(un – 2 ≠ 0.

Obviamente, a = ±2, pero teniendo en cuenta la segunda condición, la respuesta sólo viene con un resultado negativo.

Respuesta: a = -2.

Ejemplo 2.

Encuentre todos los valores del parámetro a para los cuales el sistema de ecuaciones tiene un número infinito de soluciones.

(8x + ay = 2,
(ax + 2y = 1.

Solución.

Según la propiedad, si la razón de los coeficientes de x e y es la misma y es igual a la razón de los miembros libres del sistema, entonces tiene un número infinito de soluciones (es decir, a/a 1 = b/ segundo 1 = c/c 1). Por lo tanto 8/a = a/2 = 2/1. Resolviendo cada una de las ecuaciones resultantes, encontramos que a = 4 es la respuesta en este ejemplo.

Respuesta: un = 4.

2. Sistemas de ecuaciones racionales con parámetro.

Ejemplo 3.

(3|x| + y = 2,
(|x| + 2y = a.

Solución.

Multipliquemos la primera ecuación del sistema por 2:

(6|x| + 2y = 4,
(|x| + 2y = a.

Restando la segunda ecuación de la primera, obtenemos 5|x| = 4 – una. Esta ecuación tendrá una solución única para a = 4. En otros casos, esta ecuación tendrá dos soluciones (para a< 4) или ни одного (при а > 4).

Respuesta: a = 4.

Ejemplo 4.

Encuentre todos los valores del parámetro a para los cuales el sistema de ecuaciones tiene una solución única.

(x + y = a,
(y – x 2 = 1.

Solución.

Resolveremos este sistema utilizando el método gráfico. Por tanto, la gráfica de la segunda ecuación del sistema es una parábola elevada a lo largo del eje Oy hacia arriba en un segmento unitario. La primera ecuación especifica un conjunto de rectas paralelas a la recta y = -x (Foto 1). En la figura se ve claramente que el sistema tiene solución si la recta y = -x + a es tangente a la parábola en un punto de coordenadas (-0,5, 1,25). Sustituyendo estas coordenadas en la ecuación de la línea recta en lugar de x e y, encontramos el valor del parámetro a:

1,25 = 0,5 + a;

Respuesta: a = 0,75.

Ejemplo 5.

Usando el método de sustitución, averigüe en qué valor del parámetro a, el sistema tiene una solución única.

(ax – y = a + 1,
(ax + (a + 2)y = 2.

Solución.

De la primera ecuación expresamos y y la sustituimos en la segunda:

(y = hacha – a – 1,
(ax + (a + 2)(ax – a – 1) = 2.

Reduzcamos la segunda ecuación a la forma kx = b, que tendrá una solución única para k ≠ 0. Tenemos:

hacha + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;

a 2 x + 3ax = 2 + a 2 + 3a + 2.

Representamos el trinomio cuadrado a 2 + 3a + 2 como producto de paréntesis

(a + 2)(a + 1), y a la izquierda quitamos x de paréntesis:

(a 2 + 3a)x = 2 + (a + 2)(a + 1).

Obviamente, a 2 + 3a no debe ser igual a cero, por lo tanto,

a 2 + 3a ≠ 0, a(a + 3) ≠ 0, lo que significa a ≠ 0 y ≠ -3.

Respuesta: un ≠ 0; ≠ -3.

Ejemplo 6.

Usando el método de solución gráfica, determine en qué valor del parámetro a el sistema tiene una solución única.

(x 2 + y 2 = 9,
(y – |x| = a.

Solución.

Con base en la condición construimos una circunferencia con centro en el origen y radio de 3 segmentos unitarios; esto es lo que especifica la primera ecuación del sistema

x 2 + y 2 = 9. La segunda ecuación del sistema (y = |x| + a) es una línea discontinua. Mediante el uso Figura 2 Consideramos todos los casos posibles de su ubicación con respecto al círculo. Es fácil ver que a = 3.

Respuesta: a = 3.

¿Aún tienes preguntas? ¿No sabes cómo resolver sistemas de ecuaciones?
Para obtener ayuda de un tutor -.
¡La primera lección es gratis!

blog.site, al copiar material total o parcialmente, se requiere un enlace a la fuente original.