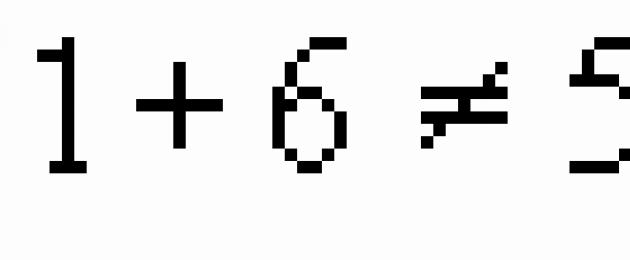Ejemplos del teorema de Vieta. Teorema de Vieta para ecuaciones cuadráticas y otras

Casi cualquiera ecuación cuadrática\se puede convertir a la forma \ Sin embargo, esto es posible si inicialmente divides cada término por un coeficiente \ antes \ Además, puedes introducir una nueva notación:

\[(\frac (b)(a))= p\] y \[(\frac (c)(a)) = q\]

Debido a esto, tendremos una ecuación\llamada en matemáticas ecuación cuadrática reducida. Las raíces de esta ecuación y los coeficientes están interrelacionados, lo que confirma el teorema de Vieta.

Teorema de Vieta: La suma de las raíces de la ecuación cuadrática reducida \ es igual al segundo coeficiente \ tomado con el signo opuesto, y el producto de las raíces es el término libre \

Para mayor claridad, resolvamos la siguiente ecuación:

Resolvamos esta ecuación cuadrática usando las reglas escritas. Analizados los datos iniciales, podemos concluir que la ecuación tendrá dos raíces diferentes, ya que:

Ahora, de todos los factores del número 15 (1 y 15, 3 y 5), seleccionamos aquellos cuya diferencia es igual a 2. Bajo esta condición caen los números 3 y 5. Ponemos un signo menos delante del más pequeño. número. Así, obtenemos las raíces de la ecuación \

Respuesta: \[ x_1= -3 y x_2 = 5\]

¿Dónde puedo resolver una ecuación usando el teorema de Vieta en línea?

Puedes resolver la ecuación en nuestro sitio web https://site. Un solucionador en línea gratuito te permitirá resolver la ecuación en línea cualquiera complejidad en segundos. Todo lo que necesitas hacer es simplemente ingresar tus datos en el solucionador. También puedes ver instrucciones en vídeo y aprender a resolver la ecuación en nuestro sitio web. Y si aún tienes preguntas, puedes hacerlas en nuestro grupo VKontakte http://vk.com/pocketteacher. Únete a nuestro grupo, siempre estaremos encantados de ayudarte.

En octavo grado, a los estudiantes se les presentan las ecuaciones cuadráticas y cómo resolverlas. Al mismo tiempo, como muestra la experiencia, la mayoría de los estudiantes utilizan solo un método para resolver ecuaciones cuadráticas completas: la fórmula de las raíces de una ecuación cuadrática. Para los estudiantes que tienen buenas habilidades de cálculo mental, este método es claramente irracional. Los estudiantes a menudo tienen que resolver ecuaciones cuadráticas incluso en la escuela secundaria, y allí es una lástima perder tiempo calculando el discriminante. En mi opinión, al estudiar ecuaciones cuadráticas, se debe prestar más tiempo y atención a la aplicación del teorema de Vieta (según el programa Álgebra-8 de A.G. Mordkovich, solo se planean dos horas para estudiar el tema “Teorema de Vieta. Descomposición de una ecuación cuadrática trinomio en factores lineales”).

En la mayoría de los libros de texto de álgebra, este teorema se formula para la ecuación cuadrática reducida y establece que si la ecuación tiene raíces y , entonces las igualdades , , se satisfacen para ellas. Luego se formula un enunciado inverso al teorema de Vieta y se ofrecen varios ejemplos para practicar este tema.

Echemos ejemplos específicos y trazar la lógica de la solución utilizando el teorema de Vieta.

Ejemplo 1. Resuelve la ecuación.

Digamos que esta ecuación tiene raíces, es decir, y . Entonces, según el teorema de Vieta, las igualdades deben cumplirse simultáneamente:

Tenga en cuenta que el producto de raíces es un número positivo. Esto significa que las raíces de la ecuación son del mismo signo. Y como la suma de las raíces también es un número positivo, concluimos que ambas raíces de la ecuación son positivas. Volvamos de nuevo al producto de las raíces. Supongamos que las raíces de la ecuación son números enteros positivos. Entonces la primera igualdad correcta sólo se puede obtener de dos maneras (hasta el orden de los factores): o . Comprobemos para los pares de números propuestos la viabilidad del segundo enunciado del teorema de Vieta: . Por tanto, los números 2 y 3 satisfacen ambas igualdades y, por tanto, son las raíces de la ecuación dada.

Respuesta: 2; 3.

Resaltemos las principales etapas del razonamiento al resolver la ecuación cuadrática anterior usando el teorema de Vieta:

Escribe el enunciado del teorema de Vieta.

(*)

determine los signos de las raíces de la ecuación (si el producto y la suma de las raíces son positivos, entonces ambas raíces son números positivos. Si el producto de las raíces es un número positivo y la suma de las raíces es negativa, entonces ambas raíces son números negativos. Si el producto de las raíces es un numero negativo, entonces las raíces tienen signos diferentes. Además, si la suma de las raíces es positiva, entonces la raíz con un módulo mayor es un número positivo, y si la suma de las raíces es menor que cero, entonces la raíz con un módulo mayor es un número negativo);
seleccione pares de números enteros cuyo producto dé la primera igualdad correcta en la notación (*);
de los pares de números encontrados, seleccione el par que, cuando se sustituya en la segunda igualdad en la notación (*), dará la igualdad correcta;
indica en tu respuesta las raíces encontradas de la ecuación.

Pongamos más ejemplos.

Ejemplo 2: resolver la ecuación .

Solución.

Sean y las raíces de la ecuación dada. Luego, según el teorema de Vieta, observamos que el producto es positivo y la suma es un número negativo. Esto significa que ambas raíces son números negativos. Seleccionamos pares de factores que dan un producto de 10 (-1 y -10; -2 y -5). El segundo par de números suma -7. Esto significa que los números -2 y -5 son las raíces de esta ecuación.

Respuesta: -2; -5.

Ejemplo 3: resolver la ecuación .

Solución.

Sean y las raíces de la ecuación dada. Luego, según el teorema de Vieta, observamos que el producto es negativo. Esto significa que las raíces son de diferentes signos. La suma de las raíces también es un número negativo. Esto significa que la raíz con el módulo mayor es negativa. Seleccionamos pares de factores que dan el producto -10 (1 y -10; 2 y -5). El segundo par de números suma -3. Esto significa que los números 2 y -5 son las raíces de esta ecuación.

Respuesta: 2; -5.

Tenga en cuenta que el teorema de Vieta puede, en principio, formularse para una ecuación cuadrática completa: si ecuación cuadrática tiene raíces y , entonces las igualdades , , se satisfacen para ellas. Sin embargo, la aplicación de este teorema es bastante problemática, ya que en una ecuación cuadrática completa al menos una de las raíces (si existe alguna, por supuesto) es un número fraccionario. Y trabajar seleccionando fracciones es largo y difícil. Pero todavía hay una salida.

Considere la ecuación cuadrática completa . Multiplica ambos lados de la ecuación por el primer coeficiente. A y escribe la ecuación en la forma . Introduzcamos una nueva variable y obtengamos la ecuación cuadrática reducida, cuyas raíces y (si están disponibles) se pueden encontrar usando el teorema de Vieta. Entonces las raíces de la ecuación original serán . Tenga en cuenta que es muy sencillo crear la ecuación reducida auxiliar: el segundo coeficiente se conserva y el tercer coeficiente es igual al producto. C.A. Con cierta habilidad, los estudiantes crean inmediatamente una ecuación auxiliar, encuentran sus raíces usando el teorema de Vieta e indican las raíces de la ecuación completa dada. Pongamos ejemplos.

Ejemplo 4: resolver la ecuación .

Creemos una ecuación auxiliar. y usando el teorema de Vieta encontraremos sus raíces. Esto significa que las raíces de la ecuación original .

Respuesta: .

Ejemplo 5: resolver la ecuación .

La ecuación auxiliar tiene la forma. Según el teorema de Vieta, sus raíces son . Encontrar las raíces de la ecuación original. .

Respuesta: .

Y un caso más en el que la aplicación del teorema de Vieta permite encontrar verbalmente las raíces de una ecuación cuadrática completa. No es difícil demostrar que el número 1 es la raíz de la ecuación , si y solo si. La segunda raíz de la ecuación se encuentra mediante el teorema de Vieta y es igual a. Una declaración más: de modo que el número –1 es la raíz de la ecuación necesario y suficiente para. Entonces la segunda raíz de la ecuación según el teorema de Vieta es igual a . Se pueden formular afirmaciones similares para la ecuación cuadrática reducida.

Ejemplo 6: Resuelve la ecuación.

Tenga en cuenta que la suma de los coeficientes de la ecuación es cero. Entonces, las raíces de la ecuación. .

Respuesta: .

Ejemplo 7. Resuelve la ecuación.

Los coeficientes de esta ecuación satisfacen la propiedad. (de hecho, 1-(-999)+(-1000)=0). Entonces, las raíces de la ecuación. .

Respuesta: ..

Ejemplos de aplicación del teorema de Vieta

Tarea 1. Resuelve la ecuación cuadrática dada usando el teorema de Vieta.

1. 6. 11. 16.
2. 7. 12. 17.
3. 8. 13. 18.
4. 9. 14. 19.
5. 10. 15. 20.

Tarea 2. Resuelve la ecuación cuadrática completa pasando a la ecuación cuadrática reducida auxiliar.

1. 6. 11. 16.
2. 7. 12. 17.
3. 8. 13. 18.
4. 9. 14. 19.
5. 10. 15. 20.

Tarea 3. Resuelve una ecuación cuadrática usando la propiedad.

Primero, formulemos el teorema en sí: Tengamos una ecuación cuadrática reducida de la forma x^2+b*x + c = 0. Digamos que esta ecuación contiene las raíces x1 y x2. Entonces, según el teorema, las siguientes afirmaciones son válidas:

1) La suma de las raíces x1 y x2 será igual al valor negativo del coeficiente b.

2) El producto de estas mismas raíces nos dará el coeficiente c.

Pero ¿cuál es la ecuación dada?

Una ecuación cuadrática reducida es una ecuación cuadrática cuyo coeficiente de mayor grado es igual a uno, es decir esta es una ecuación de la forma x^2 + b*x + c = 0. (y la ecuación a*x^2 + b*x + c = 0 no está reducida). En otras palabras, para llevar la ecuación a la forma dada, debemos dividir esta ecuación por el coeficiente de la potencia más alta (a). La tarea es llevar esta ecuación a la siguiente forma:

3*x^2 12*x + 18 = 0;

−4*x^2 + 32*x + 16 = 0;

1,5*x^2 + 7,5*x + 3 = 0; 2*x^2 + 7*x − 11 = 0.

Dividiendo cada ecuación por el coeficiente de mayor grado, obtenemos:

X^2 4*x + 6 = 0; X^2 8*x − 4 = 0; X^2 + 5*x + 2 = 0;

X^2 + 3,5*x − 5,5 = 0.

Como puedes ver en los ejemplos, incluso las ecuaciones que contienen fracciones se pueden reducir a la forma dada.

Usando el teorema de Vieta

X^2 5*x + 6 = 0 ⇒ x1 + x2 = − (−5) = 5; x1*x2 = 6;

obtenemos las raíces: x1 = 2; x2 = 3;

X^2 + 6*x + 8 = 0 ⇒ x1 + x2 = −6; x1*x2 = 8;

como resultado obtenemos las raíces: x1 = -2 ; x2 = -4;

X^2 + 5*x + 4 = 0 ⇒ x1 + x2 = −5; x1*x2 = 4;

obtenemos las raíces: x1 = −1; x2 = −4.

El significado del teorema de Vieta.

El teorema de Vieta nos permite resolver cualquier ecuación cuadrática reducida en casi segundos. A primera vista, esto parece una tarea bastante difícil, pero después de 5 10 ecuaciones, puedes aprender a ver las raíces de inmediato.

De los ejemplos dados, y usando el teorema, queda claro cómo se puede simplificar significativamente la solución de ecuaciones cuadráticas, porque usando este teorema, puedes resolver una ecuación cuadrática prácticamente sin cálculos complejos y sin calcular el discriminante, y como sabes, el Cuantos menos cálculos, más difícil es cometer un error, lo cual es importante.

En todos los ejemplos, utilizamos esta regla basándonos en dos suposiciones importantes:

La ecuación dada, es decir el coeficiente del grado más alto es igual a uno (esta condición es fácil de evitar. Puede usar la forma no reducida de la ecuación, entonces las siguientes afirmaciones serán válidas x1+x2=-b/a; x1*x2=c/ a, pero suele ser más difícil de resolver :))

Cuando una ecuación tiene dos raíces diferentes. Suponemos que la desigualdad es verdadera y el discriminante es estrictamente mayor que cero.

Por tanto, podemos crear un algoritmo de solución general utilizando el teorema de Vieta.

Algoritmo de solución general utilizando el teorema de Vieta.

Reducimos una ecuación cuadrática a su forma reducida si la ecuación se nos da en forma no reducida. Cuando los coeficientes de la ecuación cuadrática, que presentamos anteriormente como dados, resultan ser fraccionarios (no decimales), entonces, en este caso, nuestra ecuación debe resolverse mediante el discriminante.

También hay casos en los que volver a la ecuación inicial nos permite trabajar con números “convenientes”.

François Viète (1540-1603) – matemático, creador de las famosas fórmulas de Viète

teorema de vieta necesitado para solución rápida ecuaciones cuadráticas (en palabras simples).

Más detalladamente, entonces El teorema de Vieta es que la suma de las raíces de una ecuación cuadrática dada es igual al segundo coeficiente, que se toma con el signo opuesto, y el producto es igual al término libre. Cualquier ecuación cuadrática reducida que tenga raíces tiene esta propiedad.

Usando el teorema de Vieta, puedes resolver fácilmente ecuaciones cuadráticas mediante selección, así que digamos "gracias" a este matemático con una espada en sus manos por nuestro feliz séptimo grado.

Prueba del teorema de Vieta

Para demostrar el teorema, puedes utilizar fórmulas de raíces conocidas, gracias a las cuales componeremos la suma y el producto de las raíces de una ecuación cuadrática. Sólo después de esto podemos asegurarnos de que sean iguales y, en consecuencia, .

Digamos que tenemos una ecuación: . Esta ecuación tiene las siguientes raíces: y . Demostremos que , .

Según las fórmulas para las raíces de una ecuación cuadrática:

1. Encuentra la suma de las raíces:

Veamos esta ecuación, cómo la obtuvimos exactamente así:

= .

Paso 1. Reduciendo las fracciones a un denominador común, resulta:

= = .

Paso 2. Tenemos una fracción donde necesitamos abrir los corchetes:

Reducimos la fracción a 2 y obtenemos:

Hemos demostrado la relación para la suma de las raíces de una ecuación cuadrática usando el teorema de Vieta.

2. Encuentra el producto de las raíces:

= = = = = .

Probemos esta ecuación:

Paso 1. Existe una regla para multiplicar fracciones, según la cual multiplicamos esta ecuación:

Ahora recordemos la definición. raíz cuadrada y considera:

= .

Paso 3. Recordemos el discriminante de la ecuación cuadrática: . Por lo tanto, en lugar de D (discriminante), sustituimos en la última fracción, entonces resulta:

= .

Etapa 4. Abrimos los corchetes y reducimos términos semejantes a la fracción:

Paso 5. Acortamos “4a” y obtenemos .

Entonces hemos demostrado la relación para el producto de raíces usando el teorema de Vieta.

¡IMPORTANTE!Si el discriminante es cero, entonces la ecuación cuadrática tiene una sola raíz.

Teorema inverso al teorema de Vieta

Usando el teorema inverso al teorema de Vieta, podemos comprobar si nuestra ecuación se resuelve correctamente. Para comprender el teorema en sí, es necesario considerarlo con más detalle.

Si los números son así:

Y luego son las raíces de la ecuación cuadrática.

Prueba del teorema inverso de Vieta

Paso 1.Sustituyamos expresiones por sus coeficientes en la ecuación:

Paso 2.Transformemos el lado izquierdo de la ecuación:

Paso 3. Encontremos las raíces de la ecuación, y para ello usamos la propiedad de que el producto es igual a cero:

O . De dónde viene: o .

Ejemplos con soluciones usando el teorema de Vieta.

Ejemplo 1

Ejercicio

Encuentra la suma, producto y suma de cuadrados de las raíces de una ecuación cuadrática sin encontrar las raíces de la ecuación.

Solución

Paso 1. Recordemos la fórmula discriminante. Sustituimos nuestros números por las letras. Es decir, – esto reemplaza a , y . Esto implica:

Resulta:

Título="Representado por QuickLaTeX.com" height="13" width="170" style="vertical-align: -1px;">. Если дискриминант больше нуля, тогда у уравнения есть корни. По теореме Виета их сумма , а произведение . !}

Expresemos la suma de los cuadrados de las raíces mediante su suma y producto:

Respuesta

7; 12; 25.

Ejemplo 2

Ejercicio

Resuelve la ecuación. Sin embargo, no utilice fórmulas de ecuaciones cuadráticas.

Solución

Esta ecuación tiene raíces cuyo discriminante (D) es mayor que cero. En consecuencia, según el teorema de Vieta, la suma de las raíces de esta ecuación es 4 y el producto es 5. Primero, determinamos los divisores del número cuya suma es 4. Estos son los números " 5” y “-1”. Su producto es igual a 5 y su suma es 4. Esto significa que, según el teorema inverso al teorema de Vieta, son las raíces de esta ecuación.

Respuesta

Y Ejemplo 4

Ejercicio

Escribe una ecuación donde cada raíz sea el doble de la raíz correspondiente de la ecuación:

Solución

Según el teorema de Vieta, la suma de las raíces de esta ecuación es igual a 12 y el producto = 7. Esto significa que dos raíces son positivas.

La suma de las raíces de la nueva ecuación será igual a:

Y el trabajo.

Por el teorema inverso al teorema de Vieta, la nueva ecuación tiene la forma:

Respuesta

El resultado es una ecuación cuya raíz es el doble de grande:

Entonces, vimos cómo resolver la ecuación usando el teorema de Vieta. Es muy conveniente utilizar este teorema si resuelves problemas que involucran los signos de las raíces de ecuaciones cuadráticas. Es decir, si el término libre en la fórmula es un número positivo y si la ecuación cuadrática tiene raíces reales, entonces ambos pueden ser negativos o positivos.

Y si el término libre es un número negativo, y si la ecuación cuadrática tiene raíces reales, entonces ambos signos serán diferentes. Es decir, si una raíz es positiva, entonces la otra raíz sólo será negativa.

Fuentes útiles:

Dorofeev G.V., Suvorova S.B., Bunimovich E.A. Álgebra octavo grado: “Ilustración” de Moscú, 2016 – 318 p.
Rubin A.G., Chulkov P.V. – libro de texto Álgebra 8º grado: Moscú “Balass”, 2015 – 237 p.
Nikolsky S. M., Potopav M. K., Reshetnikov N. N., Shevkin A. V. – Álgebra 8º grado: “Ilustración” de Moscú, 2014 – 300

teorema de vieta fórmula inversa Vieta y ejemplos con soluciones para tontos. actualizado: 22 de noviembre de 2019 por: Artículos científicos.Ru

Uno de los métodos para resolver una ecuación cuadrática es usar Fórmulas VIET, que lleva el nombre de FRANCOIS VIETTE.

Fue un famoso abogado que sirvió al rey francés en el siglo XVI. En su tiempo libre estudió astronomía y matemáticas. Estableció una conexión entre las raíces y los coeficientes de una ecuación cuadrática.

Ventajas de la fórmula:

1 . Al aplicar la fórmula, podrá encontrar rápidamente una solución. Debido a que no es necesario ingresar el segundo coeficiente en el cuadrado, luego restarle 4ac, encontrar el discriminante y sustituir su valor en la fórmula para encontrar las raíces.

2 . Sin solución, puede determinar los signos de las raíces y seleccionar los valores de las raíces.

3 . Habiendo resuelto un sistema de dos registros, no es difícil encontrar las raíces mismas. En la ecuación cuadrática anterior, la suma de las raíces es igual al valor del segundo coeficiente con un signo menos. El producto de las raíces en la ecuación cuadrática anterior es igual al valor del tercer coeficiente.

4 . Usando estas raíces, escribe una ecuación cuadrática, es decir, resuelve el problema inverso. Por ejemplo, este método se utiliza para resolver problemas de mecánica teórica.

5 . Es conveniente utilizar la fórmula cuando el coeficiente principal es igual a uno.

Defectos:

1 . La fórmula no es universal.