Calcolo dell'area di una figura Questo è forse uno dei problemi più difficili nella teoria dell'area. Nella geometria della scuola, viene insegnato loro a trovare le aree delle forme geometriche di base come, ad esempio, un triangolo, un rombo, un rettangolo, un trapezio, un cerchio, ecc. Tuttavia, spesso si ha a che fare con il calcolo delle aree di figure più complesse. È nel risolvere tali problemi che è molto conveniente utilizzare il calcolo integrale.
Definizione.
Trapezio curvilineo si chiama una qualche figura G, delimitata dalle rette y = f(x), y = 0, x = a e x = b, e la funzione f(x) è continua sul segmento [a; b] e non cambia il suo segno su di esso (Fig. 1). L'area di un trapezio curvilineo può essere indicata con S(G).
L'integrale definito ʃ a b f(x)dx per la funzione f(x), che è continua e non negativa sul segmento [a; b], ed è l'area del corrispondente trapezio curvilineo.
Cioè, per trovare l'area della figura G, delimitata dalle linee y \u003d f (x), y \u003d 0, x \u003d a e x \u003d b, è necessario calcolare il integrale definito ʃ abf (x) dx.
In questo modo, S(G) = ʃ a b f(x)dx.
Se la funzione y = f(x) non è positiva su [a; b], quindi l'area del trapezio curvilineo può essere trovata dalla formula S(G) = -ʃ a b f(x)dx.
Esempio 1
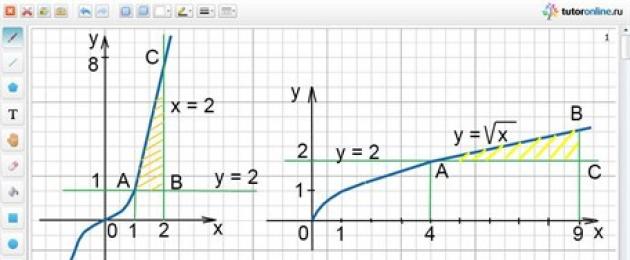
Calcola l'area della figura delimitata dalle linee y \u003d x 3; y = 1; x = 2.
Soluzione.
Le linee date formano la figura ABC, che viene mostrata tratteggiando Riso. 2.
L'area desiderata è uguale alla differenza tra le aree del trapezio curvilineo DACE e del quadrato DABE.
Utilizzando la formula S = ʃ a b f(x)dx = S(b) – S(a), troviamo i limiti di integrazione. Per fare ciò, risolviamo un sistema di due equazioni:
(y \u003d x 3,
(y = 1.
Pertanto, abbiamo x 1 \u003d 1 - il limite inferiore e x \u003d 2 - il limite superiore.
Quindi, S = S DACE - S DABE = ʃ 1 2 x 3 dx - 1 = x 4 /4| 1 2 - 1 \u003d (16 - 1) / 4 - 1 \u003d 11/4 (unità quadrate).
Risposta: 11/4 mq. unità

Esempio 2
Calcola l'area della figura delimitata dalle linee y \u003d √x; y = 2; x = 9.
Soluzione.
Le linee date formano la figura ABC, che è delimitata dall'alto dal grafico della funzione
y \u003d √x, e da sotto il grafico della funzione y \u003d 2. La figura risultante è mostrata tratteggiando Riso. 3.
L'area desiderata è uguale a S = ʃ a b (√x - 2). Troviamo i limiti di integrazione: b = 9, per trovare a risolviamo il sistema di due equazioni:
(y = √x,
(y = 2.
Quindi, abbiamo che x = 4 = a è il limite inferiore.
Quindi, S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√x| 4 9 - 2x| 4 9 \u003d (18 - 16/3) - (18 - 8) \u003d 2 2/3 (unità quadrate).
Risposta: S = 2 2/3 mq. unità
Esempio 3
Calcola l'area della figura delimitata dalle linee y \u003d x 3 - 4x; y = 0; x ≥ 0.
Soluzione.
Tracciamo la funzione y \u003d x 3 - 4x per x ≥ 0. Per fare ciò, troviamo la derivata y ':
y' = 3x 2 – 4, y' = 0 a х = ±2/√3 ≈ 1,1 sono punti critici.
Se disegniamo i punti critici sull'asse reale e posizioniamo i segni della derivata, otteniamo che la funzione decresce da zero a 2/√3 e aumenta da 2/√3 a più infinito. Allora x = 2/√3 è il punto minimo, il valore minimo della funzione y è min = -16/(3√3) ≈ -3.
Determiniamo i punti di intersezione del grafico con gli assi delle coordinate:
se x \u003d 0, allora y \u003d 0, il che significa che A (0; 0) è il punto di intersezione con l'asse Oy;
se y \u003d 0, allora x 3 - 4x \u003d 0 o x (x 2 - 4) \u003d 0 o x (x - 2) (x + 2) \u003d 0, da dove x 1 \u003d 0, x 2 \u003d 2, x 3 \u003d -2 (non adatto, perché x ≥ 0).
I punti A(0; 0) e B(2; 0) sono i punti di intersezione del grafico con l'asse Ox.
Le linee fornite formano la figura OAB, che viene mostrata tratteggiando Riso. 4.
Poiché la funzione y \u003d x 3 - 4x assume (0; 2) un valore negativo, allora
S = |ʃ 0 2 (x 3 – 4x)dx|.
Abbiamo: ʃ 0 2 (x 3 - 4x)dx = (x 4 /4 - 4x 2 /2)| 0 2 \u003d -4, da dove S \u003d 4 metri quadrati. unità
Risposta: S = 4 mq. unità

Esempio 4
Trova l'area della figura delimitata dalla parabola y \u003d 2x 2 - 2x + 1, le rette x \u003d 0, y \u003d 0 e la tangente a questa parabola nel punto con l'ascissa x 0 \u003d 2.
Soluzione.
Innanzitutto, componiamo l'equazione della tangente alla parabola y \u003d 2x 2 - 2x + 1 nel punto con l'ascissa x₀ \u003d 2.
Poiché la derivata y' = 4x - 2, allora per x 0 = 2 otteniamo k = y'(2) = 6.
Trova l'ordinata del punto di contatto: y 0 = 2 2 2 – 2 2 + 1 = 5.
Pertanto, l'equazione tangente ha la forma: y - 5 \u003d 6 (x - 2) o y \u003d 6x - 7.
Costruiamo una figura delimitata da linee:
y \u003d 2x 2 - 2x + 1, y \u003d 0, x \u003d 0, y \u003d 6x - 7.
Г y \u003d 2x 2 - 2x + 1 - parabola. Punti di intersezione con gli assi coordinati: A(0; 1) - con l'asse Oy; con l'asse Ox - non ci sono punti di intersezione, perché l'equazione 2x 2 - 2x + 1 = 0 non ha soluzioni (D< 0). Найдем вершину параболы:
x b \u003d 2/4 \u003d 1/2;
y b \u003d 1/2, ovvero il vertice del punto della parabola B ha coordinate B (1/2; 1/2).
Quindi, la figura la cui area deve essere determinata viene mostrata tratteggiando Riso. 5.
Abbiamo: S O A B D \u003d S OABC - S ADBC.
Trova le coordinate del punto D dalla condizione:
6x - 7 = 0, cioè x \u003d 7/6, quindi DC \u003d 2 - 7/6 \u003d 5/6.
Troviamo l'area del triangolo DBC usando la formula S ADBC = 1/2 · DC · BC. In questo modo,
S ADBC = 1/2 5/6 5 = 25/12 mq. unità
S OABC = ʃ 0 2 (2x 2 - 2x + 1)dx = (2x 3 /3 - 2x 2 /2 + x)| 0 2 \u003d 10/3 (unità quadrate).
Infine otteniamo: S O A B D \u003d S OABC - S ADBC \u003d 10/3 - 25/12 \u003d 5/4 \u003d 1 1/4 (unità quadrate).
Risposta: S = 1 1/4 mq. unità
Abbiamo esaminato degli esempi trovare le aree delle figure delimitate da linee date. Per risolvere con successo tali problemi, è necessario essere in grado di costruire linee e grafici di funzioni su un piano, trovare i punti di intersezione delle linee, applicare la formula per trovare l'area, il che implica la capacità e le abilità di calcolare determinati integrali.
sito, con copia integrale o parziale del materiale, è richiesto un link alla fonte.
In questa lezione impareremo a calcolare aree di figure piatte, che sono chiamati trapezi curvilinei .
Esempi di tali figure sono nella figura seguente.
Da un lato, trovare l'area di una figura piatta utilizzando un integrale definito è estremamente semplice. Stiamo parlando dell'area della figura, che è limitata dall'alto da una certa curva, dal basso - dall'asse delle ascisse ( Bue), e a sinistra e a destra ci sono alcune linee rette. La semplicità è quella l'integrale definito della funzione a cui è data la curva, e c'è l'area di tale figura(trapezio curvilineo).
Per calcolare l'area di una figura, abbiamo bisogno di:
- Integrale definito della funzione che definisce la curva , che limita il trapezio curvilineo dall'alto. Ed ecco che arriva la prima sfumatura significativa: un trapezio curvilineo può essere limitato da una curva non solo dall'alto, ma anche dal basso . Come agire in questo caso? Semplice ma importante da ricordare: l'integrale in questo caso è preso con un segno meno .
- Limiti di integrazione un e B, che troviamo dalle equazioni delle rette che delimitano la figura a sinistra e a destra: X = un , X = B, dove un e B- numeri.
Separatamente, alcune sfumature in più.
La curva che limita il trapezio curvilineo dall'alto (o dal basso) deve essere grafico di una funzione continua e non negativa y = F(X) .
I valori X devono appartenere al segmento [un, B] . Cioè, ad esempio, le linee come una sezione di un fungo non vengono prese in considerazione, in cui la gamba si adatta perfettamente a questo segmento e il cappello è molto più largo.
I segmenti laterali possono degenerare in punti . Se hai visto una figura del genere nel disegno, questo non dovrebbe confonderti, poiché questo punto ha sempre il suo valore sull'asse x. Quindi tutto è in ordine con i limiti dell'integrazione.
Ora puoi passare a formule e calcoli. Quindi la zona S il trapezio curvilineo può essere calcolato con la formula
Se F(X) ≤ 0 (il grafico della funzione si trova sotto l'asse Bue), poi area di un trapezio curvo può essere calcolato con la formula
Ci sono anche casi in cui entrambi i limiti superiore e inferiore della figura sono rispettivamente funzioni y = F(X) e y = φ (X) , quindi l'area di tale cifra viene calcolata dalla formula
![]() . (3)
. (3)
Risolviamo i problemi insieme
Iniziamo con i casi in cui l'area di una figura può essere calcolata utilizzando la formula (1).
Esempio 1Bue) e diretto X = 1 , X = 3 .

Soluzione. Perché y = 1/X> 0 sul segmento , quindi l'area del trapezio curvilineo si trova dalla formula (1):
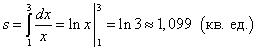 .
.
Esempio 2 Trova l'area della figura delimitata dal grafico della funzione, linea retta X= 1 e l'asse x ( Bue ).

Soluzione. Il risultato dell'applicazione della formula (1):
![]()
Se poi S= 1/2; se poi S= 1/3, ecc.
Esempio 3 Trova l'area della figura delimitata dal grafico della funzione, l'asse x ( Bue) e diretto X = 4 .

Soluzione. La figura corrispondente alla condizione del problema è un trapezio curvilineo, in cui il segmento sinistro è degenerato in un punto. I limiti di integrazione sono 0 e 4. Poiché, secondo la formula (1), troviamo l'area del trapezio curvilineo:
 .
.
Esempio 4 Trova l'area della figura delimitata dalle linee , , e situata nel 1° quarto.

Soluzione. Per usare la formula (1), rappresentiamo l'area della figura data dalle condizioni dell'esempio come somma delle aree di un triangolo OAB e trapezio curvilineo ABC. Quando si calcola l'area di un triangolo OAB i limiti dell'integrazione sono le ascisse dei punti o e UN, e per la figura ABC- ascisse di punti UN e C (UNè il punto di intersezione della retta OA e parabole, e C- punto di intersezione della parabola con l'asse Bue). Risolvendo congiuntamente (come sistema) le equazioni di una retta e di una parabola, otteniamo (l'ascissa del punto UN) e (l'ascissa di un altro punto di intersezione della retta e la parabola, che non serve per la soluzione). Allo stesso modo, otteniamo , (ascisse di punti C e D). Ora abbiamo tutto per trovare l'area della figura. Noi troviamo:

Esempio 5 Trova l'area di un trapezio curvilineo ACDB, se l'equazione della curva cd e ascisse UN e B rispettivamente 1 e 2.

Soluzione. Esprimiamo questa equazione della curva attraverso Y: L'area del trapezio curvilineo è trovata dalla formula (1):
 .
.
Passiamo ai casi in cui l'area di una figura può essere calcolata utilizzando la formula (2).
Esempio 6 Trova l'area della figura delimitata dalla parabola e dall'asse x ( Bue ).

Soluzione. Questa figura si trova sotto l'asse x. Pertanto, per calcolare la sua area, utilizziamo la formula (2). I limiti di integrazione sono le ascisse ei punti di intersezione della parabola con l'asse Bue. Quindi,

Esempio 7 Trova l'area tra l'asse x ( Bue) e due sinusoidi adiacenti.

Soluzione. L'area di questa figura può essere trovata dalla formula (2):
![]() .
.
Troviamo ogni termine separatamente:
 .
.
 .
.
Infine troviamo la zona:
![]() .
.
Esempio 8 Trova l'area della figura racchiusa tra la parabola e la curva.

Soluzione. Esprimiamo le equazioni delle rette in termini di Y:
L'area secondo la formula (2) sarà ottenuta come
![]() ,
,
dove un e B- ascisse di punti UN e B. Li troviamo risolvendo insieme le equazioni:

Infine troviamo la zona:

E, infine, ci sono casi in cui l'area di una figura può essere calcolata utilizzando la formula (3).
Esempio 9 Trova l'area della figura racchiusa tra le parabole ![]() e .
e .
Calcola l'area di una figura delimitata da linee.
Soluzione.
Troviamo i punti di intersezione delle rette date. Per fare ciò, risolviamo il sistema di equazioni:
Per trovare le ascisse dei punti di intersezione delle rette date, risolviamo l'equazione:
Noi troviamo: X 1 = -2, X 2 = 4.
Quindi, queste rette, che sono una parabola e una retta, si intersecano in punti UN(-2; 0), B(4; 6).

Queste linee formano una figura chiusa, l'area di cui viene calcolata utilizzando la formula sopra:



Secondo la formula di Newton-Leibniz, troviamo:



Trova l'area di un'area delimitata da un'ellisse.
Soluzione.

Dall'equazione dell'ellisse per il quadrante I abbiamo . Da qui, secondo la formula, otteniamo
Applichiamo la sostituzione X = un peccato T, dx = un cos T dt. Nuovi limiti di integrazione T = α e T = β sono determinati dalle equazioni 0 = un peccato T, un = un peccato T. Può essere messo α = 0 e β = π /2.
Troviamo un quarto dell'area richiesta
![]()
Da qui S = pab.
Trova l'area di una figura delimitata da lineey = - X 2 + X + 4 ey = - X + 1.
Soluzione.
Trova i punti di intersezione delle linee y = -X 2 + X + 4, y = -X+ 1, eguagliando le ordinate delle rette: - X 2 + X + 4 = -X+ 1 o X 2 - 2X- 3 = 0. Trova le radici X 1 = -1, X 2 = 3 e le loro ordinate corrispondenti y 1 = 2, y 2 = -2.

Usando la formula dell'area delle figure, otteniamo
Trova l'area racchiusa dalla parabolay = X 2 + 1 e direttoX + y = 3.
Soluzione.
Risolvere il sistema di equazioni
trova le ascisse dei punti di intersezione X 1 = -2 e X 2 = 1.

Supponendo y 2 = 3 - X e y 1 = X 2 + 1, in base alla formula che otteniamo
Calcola l'area contenuta all'interno del lemniscato di BernoulliR 2 = un 2 cos 2 φ .
Soluzione.

Nel sistema di coordinate polari, l'area della figura delimitata dall'arco della curva R = F(φ ) e due raggi polari φ 1 = ʅ e φ 2 = ʆ , è espresso dall'integrale
A causa della simmetria della curva, determiniamo prima un quarto dell'area desiderata
Pertanto, l'area totale è S = un 2 .
Calcola la lunghezza dell'arco di un astroideX 2/3 + y 2/3 = un 2/3 .
Soluzione.

Scriviamo l'equazione dell'astroide nella forma
(X 1/3) 2 + (y 1/3) 2 = (un 1/3) 2 .
Mettiamo X 1/3 = un 1/3 cos T, y 1/3 = un 1/3 peccato T.
Da qui otteniamo le equazioni parametriche dell'astroide
X = un cos 3 T, y = un peccato 3 T, (*)
dove 0 ≤ T ≤ 2π .
Data la simmetria della curva (*), basta trovare un quarto della lunghezza dell'arco l corrispondente alla modifica del parametro T da 0 a π /2.
Noi abbiamo
dx = -3un cos 2 T peccato t dt, dio = 3un peccato 2 T cos t dt.
Da qui troviamo
![]()
Integrazione dell'espressione risultante nell'intervallo da 0 a π /2, otteniamo
![]()
![]()
Da qui l = 6un.
Trova l'area delimitata dalla spirale di ArchimedeR = aφ e due vettori raggio che corrispondono agli angoli polariφ 1 eφ 2 (φ 1 < φ 2 ).
Soluzione.

Area delimitata da una curva R = F(φ ) è calcolato con la formula , dove α e β - limiti di variazione dell'angolo polare.
Così, otteniamo

 (*)
(*)
Da (*) segue che l'area delimitata dall'asse polare e il primo giro della spirale di Archimede ( φ 1 = 0; φ 2 = 2π ):
Allo stesso modo troviamo l'area delimitata dall'asse polare e il secondo giro della spirale di Archimede ( φ 1 = 2π ; φ 2 = 4π ):
![]()
L'area richiesta è uguale alla differenza di queste aree
Calcola il volume di un corpo ottenuto dalla rotazione attorno ad un asseBue figura delimitata da paraboley = X 2 eX = y 2 .
Soluzione.

Risolviamo il sistema di equazioni
e prendi X 1 = 0, X 2 = 1, y 1 = 0, y 2 = 1, da cui i punti di intersezione delle curve o(0; 0), B(undici). Come si vede in figura, il volume desiderato del corpo di rivoluzione è uguale alla differenza tra i due volumi formati dalla rotazione attorno all'asse Bue trapezi curvilinei OCBA e ODBA:

Calcola l'area delimitata dall'asseBue e sinusoidey = peccatoX sui segmenti: a); B) .
Soluzione.

a) Sul segmento, la funzione sin X conserva il segno, e quindi dalla formula , assumendo y= peccato X, noi troviamo


b) Sul segmento , funzione sin X cambia segno. Per la corretta soluzione del problema, è necessario dividere il segmento in due e [ π , 2π ], in ciascuno dei quali la funzione conserva il suo segno.
Secondo la regola dei segni, sul segmento [ π , 2π ] l'area è presa con un segno meno.
Di conseguenza, l'area desiderata è uguale a
![]()
![]()
![]()
![]()
![]()
Determinare il volume del corpo delimitato dalla superficie ottenuta dalla rotazione dell'ellisseattorno all'asse maggioreun .
Soluzione.

Dato che l'ellisse è simmetrica rispetto agli assi coordinati, basta trovare il volume formato dalla rotazione attorno all'asse Bue la zona OAB, pari a un quarto dell'area dell'ellisse, e raddoppiare il risultato.
Indichiamo il volume del corpo di rivoluzione attraverso V X; quindi, in base alla formula, abbiamo , dove 0 e un- ascisse di punti B e UN. Dall'equazione dell'ellisse troviamo . Da qui
Pertanto, il volume richiesto è pari a . (Quando l'ellisse ruota attorno all'asse minore B, il volume del corpo è )
Trova l'area delimitata dalle paraboley 2 = 2 px eX 2 = 2 pi .
Soluzione.

Per prima cosa troviamo le coordinate dei punti di intersezione delle parabole per determinare l'intervallo di integrazione. Trasformando le equazioni originali, otteniamo e . Uguagliando questi valori, otteniamo o X 4 - 8P 3 X = 0.
X 4 - 8P 3 X = X(X 3 - 8P 3) = X(X - 2P)(X 2 + 2px + 4P 2) = 0.
Troviamo le radici delle equazioni:
![]()
![]()
Considerando il fatto che il punto UN l'intersezione delle parabole è nel primo quarto, quindi i limiti di integrazione X= 0 e X = 2P.
L'area desiderata è trovata dalla formula
un)
Soluzione.
Il primo e più importante momento della decisione è la costruzione di un disegno.
Facciamo un disegno:
L'equazione y=0 imposta l'asse x;
- x=-2 e x=1 - rettilineo, parallelo all'asse UO;
- y \u003d x 2 +2 - una parabola i cui rami sono diretti verso l'alto, con un vertice nel punto (0;2).
Commento. Per costruire una parabola basta trovare i punti della sua intersezione con gli assi coordinati, cioè mettendo x=0 trova l'intersezione con l'asse UO e risolvendo l'equazione quadratica corrispondente, trova l'intersezione con l'asse Oh .
Il vertice di una parabola può essere trovato usando le formule:
Puoi disegnare linee e punto per punto.
Sull'intervallo [-2;1] il grafico della funzione y=x 2 +2 situato oltre l'asse Bue , Ecco perché:
Risposta: S \u003d 9 unità quadrate
Dopo che l'attività è stata completata, è sempre utile guardare il disegno e capire se la risposta è reale. In questo caso, "a occhio" contiamo il numero di celle nel disegno - beh, ne verranno digitate circa 9, sembra essere vero. È abbastanza chiaro che se avessimo, diciamo, la risposta: 20 unità quadrate, allora, ovviamente, è stato commesso un errore da qualche parte: 20 celle chiaramente non rientrano nella cifra in questione, al massimo una dozzina. Se la risposta si è rivelata negativa, anche il compito è stato risolto in modo errato.
Cosa fare se si trova il trapezio curvilineo sotto l'asse Oh?
B) Calcola l'area di una figura delimitata da linee y=-e x , x=1 e assi coordinati.
Soluzione.
Facciamo un disegno.
Se un trapezio curvilineo completamente sotto l'asse Oh , allora la sua area può essere trovata dalla formula:
Risposta: S=(e-1) mq" 1,72 mq
Attenzione! Non confondere i due tipi di attività:
1) Se ti viene chiesto di risolvere solo un integrale definito senza alcun significato geometrico, allora può essere negativo.
2) Se ti viene chiesto di trovare l'area di una figura usando un integrale definito, allora l'area è sempre positiva! Ecco perché nella formula appena considerata compare il meno.
In pratica, molto spesso la figura si trova sia nel semipiano superiore che in quello inferiore.
Con) Trova l'area di una figura piana delimitata da linee y \u003d 2x-x 2, y \u003d -x.
Soluzione.
Per prima cosa devi fare un disegno. In generale, quando si costruisce un disegno in problemi di area, siamo più interessati ai punti di intersezione delle linee. Troviamo i punti di intersezione della parabola e della retta, questo può essere fatto in due modi. Il primo modo è analitico.
Risolviamo l'equazione:
Quindi il limite inferiore di integrazione a=0 , il limite superiore di integrazione b=3 .
|
Costruiamo le rette date: 1. Parabola - vertice nel punto (1;1); intersezione degli assi Oh - punti(0;0) e (0;2). 2. Retta - la bisettrice del 2° e 4° angolo di coordinate. E ora Attenzione! Se nell'intervallo [ a;b] qualche funzione continua f(x) maggiore o uguale a qualche funzione continua g(x), quindi l'area della figura corrispondente può essere trovata dalla formula: . E non importa dove si trova la figura - sopra l'asse o sotto l'asse, ma è importante quale grafico è PIÙ ALTO (rispetto a un altro grafico) e quale è SOTTO. Nell'esempio in esame è ovvio che sul segmento la parabola si trova al di sopra della retta, e quindi è necessario sottrarre da |
È possibile costruire linee punto per punto, mentre i limiti dell'integrazione si scoprono come "da soli". Tuttavia, il metodo analitico per trovare i limiti a volte deve essere utilizzato se, ad esempio, il grafo è sufficientemente grande o la costruzione filettata non ha rivelato i limiti di integrazione (possono essere frazionari o irrazionali).
La figura desiderata è delimitata da una parabola dall'alto e da una retta dal basso.
Sul segmento , secondo la formula corrispondente:
Risposta: S \u003d Unità di 4,5 mq
Infatti, per trovare l'area di una figura, non è necessaria tanta conoscenza dell'integrale indefinito e definito. Il compito "calcolare l'area utilizzando un integrale definito" comporta sempre la costruzione di un disegno, quindi le tue conoscenze e abilità di disegno saranno una questione molto più rilevante. A questo proposito, è utile rinfrescare la memoria dei grafici delle principali funzioni elementari e, come minimo, essere in grado di costruire una retta, e un'iperbole.
Un trapezio curvilineo è una figura piatta delimitata da un asse, linee rette e un grafico di una funzione continua su un segmento che non cambia segno in questo intervallo. Lascia che questa figura sia localizzata non meno ascissa:
Poi l'area di un trapezio curvilineo è numericamente uguale a un certo integrale. Qualsiasi integrale definito (che esiste) ha un significato geometrico molto buono.
In termini di geometria, l'integrale definito è l'AREA.
Questo è, l'integrale definito (se esiste) corrisponde geometricamente all'area di qualche figura. Si consideri ad esempio l'integrale definito. L'integrando definisce una curva sul piano che si trova sopra l'asse (chi lo desidera può completare il disegno), e l'integrale definito stesso è numericamente uguale all'area del corrispondente trapezio curvilineo.
Esempio 1
Questa è una tipica dichiarazione di attività. Il primo e più importante momento della decisione è la costruzione di un disegno. Inoltre, il disegno deve essere costruito GIUSTO.
Quando si costruisce un progetto, consiglio il seguente ordine: primoè meglio costruire tutte le linee (se presenti) e solo Poi- parabole, iperboli, grafici di altre funzioni. I grafici delle funzioni sono più redditizi da costruire puntuale.
In questo problema, la soluzione potrebbe essere simile a questa.
Facciamo un disegno (notare che l'equazione definisce l'asse):
Sul segmento si trova il grafico della funzione oltre l'asse, Ecco perché:
Risposta:
Dopo che l'attività è stata completata, è sempre utile guardare il disegno e capire se la risposta è reale. In questo caso, "a occhio" contiamo il numero di celle nel disegno - beh, ne verranno digitate circa 9, sembra essere vero. È abbastanza chiaro che se avessimo, diciamo, la risposta: 20 unità quadrate, allora, ovviamente, è stato commesso un errore da qualche parte: 20 celle chiaramente non rientrano nella cifra in questione, al massimo una dozzina. Se la risposta si è rivelata negativa, anche il compito è stato risolto in modo errato.
Esempio 3
Calcola l'area della figura delimitata da linee e assi coordinati.
Soluzione: Facciamo un disegno:
Se si trova il trapezio curvilineo sotto l'asse(o quantomeno non superiore asse dato), allora la sua area può essere trovata dalla formula:
In questo caso:
Attenzione! Non confondere i due tipi di attività:
1) Se ti viene chiesto di risolvere solo un integrale definito senza alcun significato geometrico, allora può essere negativo.
2) Se ti viene chiesto di trovare l'area di una figura usando un integrale definito, allora l'area è sempre positiva! Ecco perché nella formula appena considerata compare il meno.
In pratica, il più delle volte la figura si trova sia nel semipiano superiore che in quello inferiore, e quindi, dai problemi scolastici più semplici, si passa ad esempi più significativi.
Esempio 4
Trova l'area di una figura piatta delimitata da linee , .
Soluzione: Per prima cosa devi completare il disegno. In generale, quando si costruisce un disegno in problemi di area, siamo più interessati ai punti di intersezione delle linee. Troviamo i punti di intersezione della parabola e della retta. Questo può essere fatto in due modi. Il primo modo è analitico. Risolviamo l'equazione:
Quindi, il limite inferiore di integrazione, il limite superiore di integrazione.
È meglio non utilizzare questo metodo, se possibile..
È molto più proficuo e veloce costruire le linee punto per punto, mentre i limiti dell'integrazione si scoprono come “da soli”. Tuttavia, il metodo analitico per trovare i limiti a volte deve essere utilizzato se, ad esempio, il grafo è sufficientemente grande o la costruzione filettata non ha rivelato i limiti di integrazione (possono essere frazionari o irrazionali). E considereremo anche un tale esempio.
Torniamo al nostro compito: è più razionale costruire prima una retta e solo dopo una parabola. Facciamo un disegno:
Ed ora la formula di lavoro: Se è presente una funzione continua sull'intervallo Maggiore o uguale qualche funzione continua, quindi l'area della figura delimitata dai grafici di queste funzioni e dalle rette, può essere trovata dalla formula:
Qui non è più necessario pensare a dove si trova la figura - sopra l'asse o sotto l'asse e, grosso modo, importa quale grafico è SOPRA(relativo a un altro grafico), e quale è SOTTO.
Nell'esempio in esame è ovvio che sul segmento la parabola si trova al di sopra della retta, e quindi è necessario sottrarre da
Il completamento della soluzione potrebbe essere simile a questo:
La figura desiderata è delimitata da una parabola dall'alto e da una retta dal basso.
Sul segmento , secondo la formula corrispondente:
Risposta:
Esempio 4
Calcola l'area della figura delimitata dalle linee , , , .
Soluzione: Facciamo prima un disegno:
La figura di cui dobbiamo trovare l'area è ombreggiata in blu.(guarda attentamente la condizione: come la cifra è limitata!). Ma in pratica, a causa della disattenzione, si verifica spesso un "glitch", che è necessario trovare l'area della figura che è ombreggiata in verde!
Questo esempio è utile anche in quanto in esso l'area della figura viene calcolata utilizzando due integrali definiti.
Veramente:
1) Sul segmento sopra l'asse c'è un grafico a linea retta;
2) Sul segmento sopra l'asse c'è un grafico dell'iperbole.
È abbastanza ovvio che le aree possono (e dovrebbero) essere aggiunte, quindi:
Come calcolare il volume di un corpo di rivoluzioneusando un integrale definito?
Immagina una figura piatta sul piano delle coordinate. Abbiamo già trovato la sua zona. Ma, in aggiunta, questa figura può anche essere ruotata e ruotata in due modi:
Intorno all'asse x;
Intorno all'asse y .
In questo articolo verranno discussi entrambi i casi. Il secondo metodo di rotazione è particolarmente interessante, causa le maggiori difficoltà, ma in realtà la soluzione è quasi la stessa della più comune rotazione attorno all'asse x.
Iniziamo con il tipo di rotazione più popolare.
- In contatto con 0
- Google+ 0
- ok 0
- Facebook 0