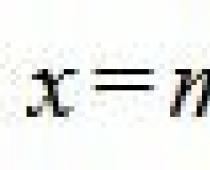В 8 классе школьники на уроках математики знакомятся с таким понятием, как «радикал» или, попросту говоря, «корень». Тогда же они впервые сталкиваются с такой проблемой, как упрощение сложных радикалов. Сложные радикалы – это такие выражения, в которых один корень находится под другим. Поэтому их ещё иногда называют вложенными радикалами. В данной статье репетитор по математике и физике подробно рассказывает о том, как упростить сложный радикал .
Методы упрощения сложных радикалов
Упростить сложный радикал — значит избавиться от внешнего корня. Правильнее всего начать изучение этой темы с упрощения двойных радикалов. Ведь если мы научимся упрощать двойные радикалы, то и более сложные тоже сумеем.
Как нам избавиться от внешнего корня? Понятно, что для этого нужно преобразовать подкоренное выражение, представив его в виде полного квадрата. Для этого воспользуемся известной формулой «Квадрат разности»:
Здесь, как видите, справа у отрицательного члена есть множитель . Поэтому и под корнем давайте получим этот множитель. Для этого представим в виде произведения на :
Тогда и . Осталось только обратить внимание на то, что ![]() . Теперь видно, что под корнем у нас получился квадрат разности:
. Теперь видно, что под корнем у нас получился квадрат разности:
Теперь вспоминаем, что . Именно модулю. Здесь это очень важно, потому что квадратный корень – положительное число. Тогда получаем:
![]()
Ну а поскольку title="Rendered by QuickLaTeX.com" height="21" width="61" style="vertical-align: -3px;">, модуль раскрывается со знаком минус. В результате в ответе получаем:
Вот так просто нам удалось упростить этот радикал. Но есть и более сложные случаи, когда не сразу удаётся догадаться, как представить подкоренное выражение в виде полного квадрата. Например, в следующем примере.
Чтобы долго не ломать голову, можно воспользоваться следующим способом.
Напоминаю, что наша цель состоит в том, чтобы представить выражение под корнем в виде полного квадрата. Конкретно в этом примере в виде квадрата суммы:
Ну а квадрат суммы раскрывается по известной формуле, которую мы сегодня уже писали:
Так вот, идея, собственно, состоит в том, чтобы за взять иррациональную часть подкоренного выражения, а за – рациональную. Тогда получается следующая система уравнений:

Понятно, что и . Иначе не выполняется второе уравнение системы. Тогда выражаем коэффициент из второго уравнения:
Знаменатель этой дроби не равен нулю, значит нулю равен её числитель. Получаем биквадратное уравнение, которое решается стандартным способом (подробнее смотрите в приложенном видео). Решая его, мы получаем аж 4 корня. Можно взять любой. Мне больше нравится . Тогда . Итак, получаем окончательно:
Вот такой способ, как упростить сложный радикал. Есть ещё один. Для любителей запоминать сложные формулы, коим я не являюсь. Но для полноты описания расскажу и о нём тоже.
Формула сложных радикалов
Вот так выглядит эта формула:
Довольно страшная, не правда ли? Но не бойтесь, её действительно можно успешно применять в некоторых случаях. Разберём на примере:
Подставляем в формулу соответствующие значения:
Вот такой получается ответ.
Итак, сегодня на занятии я рассказал о том, как упростить сложный радикал. Если вы не знали ранее методы, о которых сегодня шла речь, то скорее всего вам еще нужно очень многому научиться, чтобы чувствовать себя уверенным на ЕГЭ или на вступительном экзамене по математике. Но не переживайте, я могу вас всему этому научить. Вся необходимая информация о моих занятиях находится на . Удачи вам!
Материал подготовил , Сергей Валерьевич
Урок и презентация на тему: "Преобразование выражений, содержащих радикал"
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 11 класса
Интерактивное пособие для 9–11 классов "Тригонометрия"
Интерактивное пособие для 10–11 классов "Логарифмы"
Ребята, на прошлом уроке мы изучили свойства корня n-ой степени. Сегодня мы посмотрим, как их применять при решении различных задач которые могут встретиться на практике.
Давайте сделаем небольшую памятку из свойств наших корней:
1. ${(\sqrt[n]{a})}^n=a$; $\sqrt[n]{a^n}=a$.
2. $\sqrt[n]{a*b}=\sqrt[n]{a}*\sqrt[n]{b}$.
3. $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$, $b≠0$.
4. ${(\sqrt[n]{a})}^k=\sqrt[n]{a^k}$.
5. $\sqrt[n]{\sqrt[k]{a}}=\sqrt{a}$.
6. $\sqrt{a^{k*p}}=\sqrt[n]{a^{k}}$.
Используя наши формулы, мы можем преобразовывать выражения содержащие радикалы (операция извлечения корня), такие выражения называются иррациональными.
Пример.
Упростить выражение:
а) $\sqrt{48a^7}$.
б) ${(\sqrt{a^3})}^2$.
Решение.
а) Подкоренное выражение приведем к виду: $16*a^4*3a^3$.
Тогда, используя формулу 2 из нашей памятки, исходное выражение примет вид:
$\sqrt{48a^7}=\sqrt{16*a^4*3a^3}=\sqrt{16}*\sqrt{a^4}*\sqrt{3a^3}=2a*\sqrt{3a^3}$.
Полученное нами выражение считается более простым, так как под знаком корня более простое выражение.
Преобразование такого вида называется – вынесением множителя за знак радикала.
Б) Воспользуемся формулой 4: ${(\sqrt{a^3})}^2=\sqrt{{(a^3)}^2}=\sqrt{a^6}$.
Преобразуем полученное выражение тем же методом, что и в первом примере.
$\sqrt{a^6}=\sqrt{a^5*a}=\sqrt{a^5}*\sqrt{a}=a*\sqrt{a}$.
При вынесении множителя за знак радикала следует обратить особое внимание на знак выносимого множителя. В случае четных степеней он может быть как положительным, так и отрицательным.
Давайте рассмотрим пример: $\sqrt{x^6*y}$.
О знаке числа х мы ничего не знаем, преобразовав наше выражение получим: $x*\sqrt{y}$.
На самом деле эта запись неверная. Повторимся: о знаке числа х мы ничего не знаем. Как быть в этом случае?
Для того чтобы быть уверенным, что ответ правильный, лучше представить его виде: $|x|*\sqrt{y}$.
Обобщенная формула для корней с четным показателем будет выглядеть так: $\sqrt{a^{2n}}=|a|$.
Ребята, мы рассмотрели операцию вынесение множителя за знак радикала. Существует и обратная операция – внесение множителя под знак радикала.
Пример.
Сравнить числа $4\sqrt{2}$ и $2\sqrt{4}$.
Решение.
Мы знаем: $4=\sqrt{64}$ и $2=\sqrt{8}$.
Преобразуем исходное выражение:
$4\sqrt{2}=\sqrt{64}*\sqrt{2}=\sqrt{128}$.
$2\sqrt{4}=\sqrt{8}*\sqrt{4}=\sqrt{32}$.
Показатели корней обоих выражений одинаковые. Больше то число, у которого больше подкоренное выражение. В нашем случае: $\sqrt{128}>\sqrt{32}$.
Пример.
Упростить выражение: $\sqrt{x^3*\sqrt{x}}$.
Решение.
Внесем выражение, содержащее третью степень, под знак корня:
$x^3*\sqrt{x}=\sqrtx^{12}*\sqrt{x}=\sqrt{x^{13}}$.
Воспользуемся формулой 5. Исходное выражение можно представить в виде: $\sqrt{\sqrt{x^{13}}}=\sqrt{x^{13}}$.
Пример.
Выполнить действия:
а) $(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})$.
б) $(\sqrt{a}-\sqrt{b})(\sqrt{a^2}+\sqrt{ab}+\sqrt{b^2})$.
Решение:
а) Воспользуемся формулой разности квадратов:
$(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})=(\sqrt{a^2}+\sqrt{b^2})$.
Теперь давайте упростим полученное нами выражение, воспользуемся формулой 6 нашей памятки:
$(\sqrt{a^2}-\sqrt{b^2})=(\sqrt{a}-\sqrt{b})$ (показатель корня и степень подкоренного выражения разделили на 2.
Ответ: $(\sqrt{a^2}-\sqrt{b^2})(\sqrt{a^2}+\sqrt{b^2})=(\sqrt{a}-\sqrt{b})$.
Б) Давайте внимательно посмотрим на наше выражение. Оно похоже на формулу разности кубов, давайте ее и применим:
$(\sqrt{a}-\sqrt{b})(\sqrt{a^2}+\sqrt{ab}+\sqrt{b^2})={(\sqrt{a})}^3-{(\sqrt{b})}^3=a-b$.
Пример.
Выполнить действия:
а) $\sqrt{a^5}*\sqrt{a^3}$.
б) $\sqrt{3-\sqrt{3}}*\sqrt{12+6\sqrt{3}}$.
Решение.
Перемножать можно только корни одной и той же степени. Давайте приведем наши выражения к одинаковому показателю корня.
$\sqrt{a^5}=\sqrt{a^{10}}$ (домножили на 2).
$\sqrt{a^3}=\sqrt{a^{9}}$ (домножили на 3).
$\sqrt{a^5}*\sqrt{a^3}=\sqrt{a^{10}}*\sqrt{a^9}=\sqrt{a^{19}}$.
Упростим получившиеся выражение:
$\sqrt{a^{19}}=\sqrt{a^{12}*a^7}=|a|*\sqrt{a^7}$.
Обратим внимание на то, что показатель корня наших выражений – четный. Это значит, что подкоренное выражение содержит только положительные числа, то есть $a≥0$, но тогда $|a|=a$.
Ответ: $\sqrt{a^5}*\sqrt{a^3}=a*\sqrt{a^7}$.
Б)Этот пример можно решить двумя способами. Давайте рассмотрим каждый из способов:
1 способ. Приведем первый множитель к 4-ой степени:
$\sqrt{3-\sqrt{3}}=\sqrt{{(3-\sqrt{3})}^2}=\sqrt{9-6\sqrt{3}+3}=\sqrt{12-6\sqrt{3}}$.
Перемножим радикалы:
$\sqrt{12-6\sqrt{3}}*\sqrt{12+6\sqrt{3}}=\sqrt{{(12-6\sqrt{3})}*(12+6\sqrt{3})}=\sqrt{144-36*3}=\sqrt{144-108}=\sqrt{36}=\sqrt{6^2}=\sqrt{6}$.
2 способ. Посмотрим на подкоренное выражение во втором множителе:
$12+6\sqrt{3}=9+6\sqrt{3}+3=3^2+2*3*\sqrt{3}+{(\sqrt{3})}^2={(3+\sqrt{3})}^2$.
Мы можем преобразовать множитель в целом:
$\sqrt{12+6\sqrt{3}}=\sqrt{{(3+\sqrt3)}^2}=\sqrt{3+\sqrt{3}}$ (разделили на 2 показатели степеней).
Преобразуем всё выражение:
$\sqrt{3-\sqrt{3}}*\sqrt{12+\sqrt{3}}=\sqrt{3-\sqrt{3}}*\sqrt{3+\sqrt{3}}=\sqrt{(3-\sqrt{3})*(3+\sqrt{3})}=\sqrt{9-3}=\sqrt{6}$.
Пример.
Разложить на множители выражение:
$\sqrt{x^8}-2\sqrt{x^4y^2}+\sqrt{y^4}$.
Решение.
Перепишем исходное выражение в виде:
$\sqrt{x^8}-2\sqrt{x^4y^2}+\sqrt{y^4}={(\sqrt{x^4})}^2-2*\sqrt{x^4}*\sqrt{y^2}+{(\sqrt{y^2})}^2$ - это так называемый "квадрат разности".
$\sqrt{x^8}-2\sqrt{x^4y^2}+\sqrt{y^4}={(\sqrt{x^4}-\sqrt{y^2})}^2={(x\sqrt{x}-\sqrt{y^2})}^2$.
Пример.
Сократить дробь: $\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}-2\sqrt{xy}+\sqrt{y}}$.
Решение.
1 способ.
Рассмотрим числитель и знаменатель отдельно:
$\sqrt{x}-\sqrt{y}=\sqrt{x^2}-\sqrt{y^2}=(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})$.
$\sqrt{x}-2\sqrt{xy}+\sqrt{y}=\sqrt{x^2}-2\sqrt{xy}+\sqrt{y^2}={(\sqrt{x}-\sqrt{y})}^2$.
Сократим получившиеся выражение:
$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}-2\sqrt{xy}+\sqrt{y}}$=$\frac{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}{({\sqrt{x}-\sqrt{y})}^2}$=$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x}-\sqrt{y}}$.
2 способ.
Введем замену переменных.
Пусть $a=\sqrt{x}$, $b=\sqrt{y}$. Тогда $\sqrt{x}=a^2$ и $\sqrt{y}=b^2$.
$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}-2\sqrt{xy}+\sqrt{y}}=\frac{a^2-b^2}{{a^2-2ab+b}^2}=\frac{(a-b)(a+b)}{{(a-b)^2}}=\frac{(a+b)}{(a-b)}=\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x}-\sqrt{y}}$.
Замена переменных часто упрощает ход решения. Работать с рациональными выражениями гораздо проще и привычней, чем с иррациональными.
Задачи для самостоятельного решения
1. Упростить выражение:а) $\sqrt{162a^5}$.
б) ${(\sqrt{a^5})}^3$.
2. Сравнить числа: $3\sqrt{4}$ и $2\sqrt{5}$.
3. Упростить выражение: $\sqrt{{x^2}*\sqrt{x^2}}$.
4. Выполнить действия:
а) $\sqrt{a^7}*\sqrt{a^4}$.
б) $\sqrt{4-\sqrt{3}}*\sqrt{19+8\sqrt{3}}$.
5. Разложить на множители выражение: $\sqrt{x^6}-6\sqrt{x^3y^5}+9\sqrt{y^{10}}$.
6. Сократить дробь: $\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+2\sqrt{xy}+\sqrt{y}}$.
Свойства корней лежат в основе двух следующих преобразований, называемых внесением под знак корня и вынесением из-под знака корня, к рассмотрению которых мы и переходим.
Внесение множителя под знак корня
Внесение множителя под знак подразумевает замену выражения , где B и C – некоторые числа или выражения, а n – натуральное число, большее единицы, тождественно равным выражением, имеющим вид или .
Например, иррациональное выражение после внесения множителя 2 под знак корня принимает вид .
Теоретические основы этого преобразования, правила его проведения, а также решения всевозможных характерных примеров даны в статье внесение множителя под знак корня .
Вынесение множителя из-под знака корня
Преобразованием, в известном смысле обратным внесению множителя под знак корня, является вынесение множителя из-под знака корня. Оно состоит в представлении корня в виде произведения при нечетных n или в виде произведения при четных n , где B и C – некоторые числа или выражения.
За примером вернемся в предыдущий пункт: иррациональное выражение после вынесения множителя из-под знака корня принимает вид . Другой пример: вынесение множителя из-под знака корня в выражении дает произведение , которое можно переписать в виде .
На чем базируется это преобразование, и по каким правилам оно проводится, разберем в отдельной статье вынесение множителя из-под знака корня . Там же приведем решения примеров и перечислим способы приведения подкоренного выражения к виду, удобному для вынесения множителя.
Преобразование дробей, содержащих корни
Иррациональные выражения могут содержать дроби, в числителе и знаменателе которых присутствуют корни. С такими дробями можно проводить любые из основных тождественных преобразований дробей .
Во-первых, ничто не мешает работать с выражениями в числителе и знаменателе. В качестве примера рассмотрим дробь . Иррациональное выражение в числителе, очевидно, тождественно равно , а, обратившись к свойствам корней, выражение в знаменателе можно заменить корнем . В результате исходная дробь преобразуется к виду .
Во-вторых, можно изменить знак перед дробью, изменив знак числителя или знаменателя. Например, имеют место такие преобразования иррационального выражения:  .
.
В-третьих, иногда возможно и целесообразно провести сокращение дроби. К примеру, как отказать себе в удовольствии сократить дробь  на иррациональное выражение , в результате получаем
на иррациональное выражение , в результате получаем  .
.
Понятно, что во многих случаях, прежде чем выполнить сокращение дроби, выражения в ее числителе и знаменателе приходится раскладывать на множители, чего в простых случаях позволяют добиться формулы сокращенного умножения. А иногда сократить дробь помогает замена переменной, позволяющая от исходной дроби с иррациональностью перейти к рациональной дроби, работать с которой комфортнее и привычнее.
Для примера возьмем выражение . Введем новые переменные и , в этих переменных исходное выражение имеет вид . Выполнив в числителе
Тема урока :
«Преобразование выражений, содержащих радикалы»
Цель урока :
Образовательная:
Формирование умение решать задания на преобразование выражений, содержащих радикалы;
закрепить понятия свойства корня n -ой;
способствовать совершенствованию умений и навыков по работы в Microsoft Office Excel при обработки информации на производстве.
Развивающая:
развитие мыслительных умения: структурировать объекты (выделять составные части объекта и располагать их в иерархическом виде).
развивать творческое (продуктивное) мышление (в процессе составления ребуса),
Воспитательная:
воспитание общей и информационной культуры, трудолюбия, усидчивости, терпения, бережного отношения к компьютерной технике, привитие учащимся навыков самостоятельности в работе.
Тип урока : систематизация знаний
Вид урока: проблемный
Методические приемы: наглядно – иллюстративный: ребус, компьютерное тестирование, практический: выборочное решение примеров, задачи производственной направленности
Оборудование и наглядные средства обучения : компьютерный класс с ОС Windows XP и пакетом программ Microsoft Office 2003,мультимедийный проектор, презентация, компьютерный тест, раздаточный материал (ребус).
Межпредметные связи: математика- информатика- производственное обучение.
Ход урока:
I .Организационный момент : Подготовка учащихся к уроку
(проверка отсутствующих на уроке, наличие тетрадей), сообщение темы и целей
урока. Слайд1,2

Мотивация.
Слайд3,4


В связи с большим скоплением на производстве цифровых данных обработка информации не возможна без применения вычислительной техники. Операторы ЭВМ обрабатывают информацию с помощью информационных технологий. Сегодня на уроке мы применим ваши математические и профессиональные знания при решении задачи производственной направленности.
Задача:
Вычислите среднее значение коэффициента мощности по цеху, если показания счетчика активной энергии в начале и конце месяца были соответственно 2326 и 2476 Квтч, показания реактивной энергии в начале и конце месяца соответственно 1673 и 1773 КвАрч. Вычисления производить в программе Microsoft Office Excel 2003.
Слайд 5.

Но к решению задачи мы приступим немного позже.
Инструктаж по технике безопасности. Слайд 6.

II .Актуализация опорных знаний:
2.1 Компьютерное тестирование (6 человек, 10 минут)
Слайд 7.

2.2 Фронтальный опрос (с оставшейся группой):
2.2.1 Что такое радикал? Слайд 8.

2.2.3Перечислите:
а)свойства корня n -ой степени. Слайд 9.

б) корень из дроби. Слайд10.

в)Извлечение корня из корня. Слайд 11.

г)основное свойство корня. Слайд 12.

Проверка теста.(При необходимости разбор теста через мультимедиа проектор).
III . Практическая работа.
Слайд 13.

Решите примеры.По ответу в примере выберите соответствующую букву в ребусе, запишите ответ в таблицу. Полученный термин «----»- организованная последовательность действий.
IV .Закрепление пройденного материала.
Преподаватель разбирает решение задачи на доске.
Слайд 14.

Для того, чтобы вычислить среднее значение коэффициента мощности по цеху, которое не должно превышать 0,99-0,75 (только в этом случае нет простоя оборудования), нужно найти косинус угла. Вычисления производятся по Теореме Пифагора(так как треугольник прямоугольный).Первый катет – реактивная энергия, второй катет – активная энергия, гипотенуза – полная энергия. Косинус угла – это отношение активной энергии к полной. А полная энергия – это радикал второго порядка
Учащиеся используя инструкционную карту выполняют работу на компьютере, используя Microsoft Office Excel 2003.
V .Подведение итогов урока:
Сегодня на уроке мы с вами подтвердили слова русского ученого М.В. Ломоносова
“ Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь”. (М.В.Ломоносов) . Без радикалов не возможно вычислить затраты электроэнергии по предприятию.А обучаясь в данном лицее по профессии «Оператор ЭВМ» и получая на уроках производственного обучения информацию о работе на вычислительной - техникой вы можете обработать любую информацию, пользуясь информационными технологиями. Поэтому слова Натан Ротшильд «Кто владеет информацией, владеет миром» очень актуальны при работе по вашей профессии на любом предприятии или заводе.
Выставление оценок за урок.
VI .Домашнее задание: § 36. №36.17,№36.23