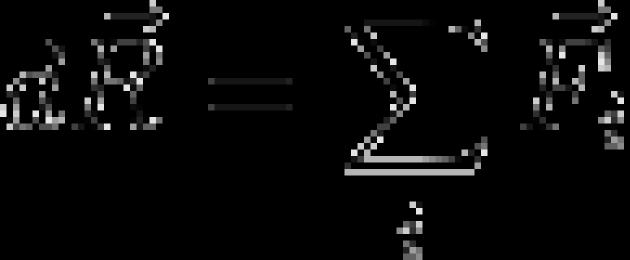Prawo zmiany pędu punktu. Zmiana pędu układu mechanicznego

Pogląd: ten artykuł został przeczytany 14066 razy

PDF Wybierz język... Rosyjski Ukraiński Angielski

Krótka recenzja

Całość materiału pobiera się powyżej, po wybraniu języka

Ilość ruchu

Pęd punktu materialnego - wielkość wektorowa równa iloczynowi masy punktu i jego wektora prędkości.

Jednostką miary pędu jest (kg m/s).

Ilość ruchu układ mechaniczny - wielkość wektora równa suma geometryczna(wektor główny) pędu układu mechanicznego jest równy iloczynowi masy całego układu i prędkości jego środka masy.

Kiedy ciało (lub układ) porusza się w taki sposób, że jego środek masy jest nieruchomy, wówczas wielkość ruchu ciała jest równa zeru (na przykład obrót ciała wokół stała oś przechodzi przez środek masy ciała).

W przypadku ruchu złożonego wielkość ruchu układu nie będzie charakteryzowała części obrotowej ruchu podczas obrotu wokół środka masy. Oznacza to, że wielkość ruchu charakteryzuje jedynie ruch translacyjny układu (wraz ze środkiem masy).

Siła impulsu

Impuls siły charakteryzuje działanie siły w pewnym okresie czasu.

Impuls siły w skończonym okresie czasu definiuje się jako całkowitą sumę odpowiednich impulsów elementarnych.

Twierdzenie o zmianie pędu punktu materialnego

(w formach różnicowych mi ):

Pochodna po czasie pędu punktu materialnego jest równa sumie geometrycznej sił działających na te punkty.

(V forma integralna ):

Zmiana pędu punktu materialnego w pewnym okresie czasu jest równa sumie geometrycznej impulsów sił przyłożonych do tego punktu w tym okresie.

Twierdzenie o zmianie pędu układu mechanicznego

(w formie różnicowej ):

Pochodna pędu układu po czasie jest równa sumie geometrycznej wszystkiego siły zewnętrzne, działając na system.

(w formie integralnej ):

Zmiana pędu układu w pewnym okresie czasu jest równa sumie geometrycznej impulsów sił zewnętrznych działających na układ w tym okresie.

Twierdzenie to pozwala wykluczyć z rozważań oczywiście nieznane siły wewnętrzne.

Twierdzenie o zmianie pędu układu mechanicznego i twierdzenie o ruchu środka masy to dwie różne formy tego samego twierdzenia.

Prawo zachowania pędu układu

1. Jeżeli suma wszystkich sił zewnętrznych działających na układ jest równa zeru, wówczas wektor pędu układu będzie stały pod względem kierunku i wielkości.
2. Jeżeli suma rzutów wszystkich działających sił zewnętrznych na dowolną oś jest równa zeru, to rzut pędu na tę oś jest wartością stałą.

wnioski:

1. Prawa zachowania wskazują, że siły wewnętrzne nie mogą zmienić całkowitego ruchu układu.
2. Twierdzenie o zmianie pędu układu mechanicznego nie charakteryzuje ruchu obrotowego układu mechanicznego, a jedynie ruch translacyjny.

Podano przykład: Określ pęd dysku o określonej masie, jeśli znana jest jego prędkość kątowa i rozmiar.

Przykład obliczeń koła zębatego czołowego
Przykład obliczenia koła zębatego czołowego. Dokonano doboru materiału, obliczenia dopuszczalnych naprężeń, obliczenia wytrzymałości stykowej i zginającej.

Przykład rozwiązania problemu zginania belki
W przykładzie zbudowane są diagramy siły ścinające i momentów zginających, odnaleziono niebezpieczny przekrój i wybrano dwuteownik. W problematyce analizowano konstrukcję diagramów z wykorzystaniem zależności różniczkowych, przeprowadzoną analiza porównawcza różne przekroje poprzeczne belki.

Przykład rozwiązania problemu skręcania wału
Zadanie polega na zbadaniu wytrzymałości wału stalowego przy zadanej średnicy, materiale i dopuszczalnym naprężeniu. Podczas rozwiązywania konstruowane są wykresy momentów obrotowych, naprężeń ścinających i kątów skręcenia. Ciężar własny wału nie jest brany pod uwagę

Przykład rozwiązania problemu rozciągania-ściskania pręta
Zadanie polega na badaniu wytrzymałości pręta stalowego przy określonych naprężeniach dopuszczalnych. Podczas rozwiązywania konstruowane są wykresy sił podłużnych, naprężeń normalnych i przemieszczeń. Ciężar własny wędki nie jest brany pod uwagę

Zastosowanie twierdzenia o zachowaniu energii kinetycznej
Przykład rozwiązania zadania z wykorzystaniem twierdzenia o zachowaniu energii kinetycznej układu mechanicznego

Wyznaczanie prędkości i przyspieszenia punktu za pomocą zadanych równań ruchu
Przykład rozwiązania zadania wyznaczenia prędkości i przyspieszenia punktu przy wykorzystaniu zadanych równań ruchu

Wyznaczanie prędkości i przyspieszeń punktów ciała sztywnego podczas ruchu płasko-równoległego
Przykład rozwiązania zadania wyznaczania prędkości i przyspieszeń punktów solidny w ruchu płasko-równoległym

Wyznaczanie sił w prętach kratownicy płaskiej
Przykład rozwiązania problemu wyznaczania sił w prętach kratownicy płaskiej metodą Rittera i metodą węzłów tnących

Zastosowanie twierdzenia o zmianie momentu pędu
Przykład rozwiązania problemu za pomocą twierdzenia o zmianie moment kinetyczny do wyznaczania prędkości kątowej ciała obracającego się wokół ustalonej osi.

Układem omawianym w twierdzeniu może być dowolny układ mechaniczny składający się z dowolnych ciał.

Stwierdzenie twierdzenia

Wielkość ruchu (impuls) układu mechanicznego jest wielkością równą sumie wielkości ruchu (impulsów) wszystkich ciał wchodzących w skład układu. Impuls sił zewnętrznych działających na ciała układu jest sumą impulsów wszystkich sił zewnętrznych działających na ciała układu.

( kg m/s)

Twierdzenie o zmianie pędu układu stwierdza

Zmiana pędu układu w pewnym okresie czasu jest równa impulsowi sił zewnętrznych działających na układ w tym samym czasie.

Prawo zachowania pędu układu

Jeżeli suma wszystkich sił zewnętrznych działających na układ wynosi zero, wówczas wielkość ruchu (pęd) układu jest wielkością stałą.

, otrzymujemy wyrażenie twierdzenia o zmianie pędu układu w postaci różniczkowej:

Po zintegrowaniu obu stron powstałej równości w dowolnie wybranym okresie czasu pomiędzy niektórymi i , otrzymujemy wyrażenie twierdzenia o zmianie pędu układu w postaci całkowej:

Prawo zachowania pędu (Prawo zachowania pędu) stwierdza, że ​​suma wektorów impulsów wszystkich ciał układu jest wartością stałą, jeśli suma wektorów sił zewnętrznych działających na układ jest równa zeru.

(moment pędu m 2 kg s −1)

Twierdzenie o zmianie momentu pędu względem środka

pochodna po czasie momentu pędu (momentu kinetycznego) punktu materialnego względem dowolnego ustalonego środka jest równa momentowi siły działającej na punkt względem tego samego środka.

nie wiem 0 /dt = M 0 (F ) .

Twierdzenie o zmianie momentu pędu względem osi

pochodna czasowa momentu pędu (momentu kinetycznego) punktu materialnego względem dowolnej ustalonej osi jest równa momentowi siły działającej na ten punkt względem tej samej osi.

nie wiem X /dt = M X (F ); nie wiem y /dt = M y (F ); nie wiem z /dt = M z (F ) .

Rozważmy punkt materialny M masa M , poruszając się pod wpływem siły F (Rysunek 3.1). Zapiszmy i skonstruujmy wektor momentu pędu (pędu kinetycznego) M 0 punktów materialnych względem środka O :

Rozróżnijmy wyrażenie na moment pędu (moment kinetyczny). k 0) według czasu:

Ponieważ dr /dt = V , a następnie iloczyn wektorowy V ⊗ M ⋅ V (wektory współliniowe V I M ⋅ V ) jest równe zeru. W tym samym czasie d(m ⋅ V) /dt = F zgodnie z twierdzeniem o pędzie punktu materialnego. Dlatego to otrzymujemy

nie wiem 0 /dt = R ⊗F , (3.3)

Gdzie R ⊗F = M 0 (F ) – wektorowy moment siły F względem stałego środka O . Wektor k 0 ⊥ płaszczyzna ( R , M ⊗V ) i wektor M 0 (F ) ⊥ samolot ( R ,F ), w końcu mamy

nie wiem 0 /dt = M 0 (F ) . (3.4)

Równanie (3.4) wyraża twierdzenie o zmianie momentu pędu (pędu pędu) punktu materialnego względem środka: pochodna czasowa momentu pędu (momentu kinetycznego) punktu materialnego względem dowolnego ustalonego środka jest równa momentowi siły działającej na punkt względem tego samego środka.

Rzutując równość (3.4) na osie współrzędnych kartezjańskich, otrzymujemy

nie wiem X /dt = M X (F ); nie wiem y /dt = M y (F ); nie wiem z /dt = M z (F ) . (3.5)

Równości (3.5) wyrażają twierdzenie o zmianie momentu pędu (pędu kinetycznego) punktu materialnego względem osi: pochodna czasowa momentu pędu (momentu kinetycznego) punktu materialnego względem dowolnej ustalonej osi jest równa momentowi siły działającej na ten punkt względem tej samej osi.

Rozważmy konsekwencje wynikające z twierdzeń (3.4) i (3.5).

Wniosek 1. Rozważmy przypadek, gdy siła F podczas całego ruchu punkt przechodzi przez nieruchomy środek O (przypadek siły centralnej), tj. Gdy M 0 (F ) = 0. Zatem z twierdzenia (3.4) wynika, że k 0 = konst ,

te. w przypadku siły centralnej moment pędu (moment kinetyczny) punktu materialnego względem środka tej siły pozostaje stały pod względem wielkości i kierunku (rysunek 3.2).

Rysunek 3.2

Od warunku k 0 = konst wynika z tego, że trajektoria poruszającego się punktu jest płaską krzywą, której płaszczyzna przechodzi przez środek tej siły.

Konsekwencja 2. Pozwalać M z (F ) = 0, tj. siła przecina oś z lub równolegle do niego. W tym przypadku, jak widać z trzeciego równania (3.5), k z = konst ,

te. jeżeli moment siły działający na punkt względem dowolnej ustalonej osi jest zawsze zerowy, to moment pędu (moment kinetyczny) punktu względem tej osi pozostaje stały.

Dowód twierdzenia o zmianie pędu

Niech układ składa się z punktów materialnych o masach i przyspieszeniach. Wszystkie siły działające na ciała układu dzielimy na dwa typy:

Siły zewnętrzne to siły działające od ciał nie wchodzących w skład rozpatrywanego układu. Wypadkowa sił zewnętrznych działających na punkt materialny o liczbie I oznaczmy

Siły wewnętrzne to siły, z którymi ciała samego układu oddziałują ze sobą. Siła z jaką działa na punkt z liczbą I punkt z numerem jest ważny k, będziemy oznaczać , oraz siłę wpływu I punkt dalej k punkt - . Jasne, kiedy więc

Korzystając z wprowadzonej notacji, piszemy drugie prawo Newtona dla każdego z rozważanych punktów materialnych w formie

Biorąc pod uwagę, że i podsumowując wszystkie równania drugiej zasady Newtona, otrzymujemy:

Wyrażenie reprezentuje sumę wszystkich sił wewnętrznych działających w układzie. Zgodnie z trzecim prawem Newtona w tej sumie każda siła odpowiada takiej sile, że zatem zachodzi Ponieważ cała suma składa się z takich par, sama suma wynosi zero. Dzięki temu możemy pisać

Korzystając z zapisu pędu układu, otrzymujemy

Poprzez uwzględnienie zmiany pędu sił zewnętrznych , otrzymujemy wyrażenie twierdzenia o zmianie pędu układu w postaci różniczkowej:

Zatem każde z ostatnich otrzymanych równań pozwala stwierdzić: zmiana pędu układu następuje jedynie w wyniku działania sił zewnętrznych, a siły wewnętrzne nie mogą mieć żadnego wpływu na tę wartość.

Całkując obie strony powstałej równości w dowolnie wybranym przedziale czasu pomiędzy pewnymi i , otrzymujemy wyrażenie twierdzenia o zmianie pędu układu w postaci całkowej:

gdzie i są wartościami wielkości ruchu układu w momentach czasu i, odpowiednio, i jest impulsem sił zewnętrznych w pewnym okresie czasu. Zgodnie z tym, co powiedziano wcześniej i wprowadzonymi oznaczeniami,

Niech punkt materialny porusza się pod wpływem siły F. Wymagane jest określenie ruchu tego punktu względem poruszającego się układu Oksyz(patrz ruch złożony punktu materialnego), który porusza się w znany sposób względem układu stacjonarnego O 1 X 1 y 1 z 1 .

Podstawowe równanie dynamiki układu stacjonarnego

Zapiszmy bezwzględne przyspieszenie punktu, korzystając z twierdzenia Coriolisa

Gdzie A abs– przyspieszenie bezwzględne;

A wzgl– przyspieszenie względne;

A uliczka– akceleracja przenośna;

A rdzeń– Przyspieszenie Coriolisa.

Przepiszmy (25) biorąc pod uwagę (26)

Wprowadźmy notację
- przenośna siła bezwładności,
- Siła bezwładności Coriolisa. Wtedy równanie (27) przyjmuje postać

Podstawowe równanie dynamiki do badania ruchu względnego (28) zapisuje się analogicznie jak dla ruchu absolutnego, z tym że do sił działających na punkt należy dodać jedynie przeniesienie i siły bezwładności Coriolisa.

Ogólne twierdzenia o dynamice punktu materialnego

Rozwiązując wiele problemów, możesz użyć gotowych półfabrykatów uzyskanych na podstawie drugiego prawa Newtona. W tej sekcji zestawiono takie metody rozwiązywania problemów.

Twierdzenie o zmianie pędu punktu materialnego

Wprowadźmy następujące charakterystyki dynamiczne:

1. Pęd punktu materialnego– wielkość wektora równa iloczynowi masy punktu i jego wektora prędkości

. (29)

2. Impuls siły

Elementarny impuls siły– wielkość wektora równa iloczynowi wektora siły i elementarnego przedziału czasu

(30).

Następnie pełny impuls

. (31)

Na F=stała, którą otrzymujemy S=Ft.

Impuls całkowity w skończonym czasie można obliczyć tylko w dwóch przypadkach, gdy siła działająca na punkt jest stała lub zależy od czasu. W innych przypadkach konieczne jest wyrażenie siły w funkcji czasu.

Równość wymiarów impulsu (29) i pędu (30) pozwala ustalić między nimi związek ilościowy.

Rozważmy ruch punktu materialnego M pod działaniem dowolna siła F po dowolnej trajektorii.

O U:
. (32)

Rozdzielamy zmienne w (32) i całkujemy

. (33)

W rezultacie, biorąc pod uwagę (31), otrzymujemy

. (34)

Równanie (34) wyraża następujące twierdzenie.

Twierdzenie: Zmiana pędu punktu materialnego w pewnym okresie czasu jest równa impulsowi siły działającej na ten punkt w tym samym przedziale czasu.

Podczas rozwiązywania problemów równanie (34) należy rzutować na osie współrzędnych

Twierdzenie to jest wygodne w użyciu, gdy wśród danych i nieznanych wielkości znajduje się masa punktu, jego prędkość początkowa i końcowa, siły i czas ruchu.

Twierdzenie o zmianie momentu pędu punktu materialnego

M
moment pędu punktu materialnego względem środka jest równy iloczynowi modułu pędu punktu i ramienia, tj. najkrótsza odległość (prostopadła) od środka do linii pokrywającej się z wektorem prędkości

, (36)

. (37)

Związek między momentem siły (przyczyną) a momentem pędu (skutkiem) ustala następujące twierdzenie.

Niech punkt M danej masy M porusza się pod wpływem siły F.

,
,

, (38)

. (39)

Obliczmy pochodną (39)

. (40)

Łącząc (40) i (38) ostatecznie otrzymujemy

. (41)

Równanie (41) wyraża następujące twierdzenie.

Twierdzenie: Pochodna po czasie wektora pędu punktu materialnego względem jakiegoś środka jest równa momentowi siły działającej na punkt względem tego samego środka.

Podczas rozwiązywania problemów równanie (41) należy rzutować na osie współrzędnych

W równaniach (42) momenty pędu i siły obliczane są względem osi współrzędnych.

Z (41) wynika prawo zachowania momentu pędu (prawo Keplera).

Jeżeli moment siły działający na punkt materialny względem dowolnego środka wynosi zero, wówczas moment pędu punktu względem tego środka zachowuje swoją wielkość i kierunek.

Jeśli
, To
.

Twierdzenie i prawo zachowania są stosowane w zagadnieniach związanych z ruchem krzywoliniowym, szczególnie pod działaniem sił centralnych.

Rozważmy system składający się z punktów materialnych. Komponujmy dla tego systemu równania różniczkowe ruchy (13) i sumuj je termin po terminie. Wtedy otrzymamy

Ostatnia suma, ze względu na właściwość sił wewnętrznych, jest równa zeru. Oprócz,

W końcu znajdujemy

Równanie (20) wyraża twierdzenie o zmianie pędu układu w postaci różniczkowej: pochodna czasowa pędu układu jest równa sumie geometrycznej wszystkich sił zewnętrznych działających na układ. W projekcjach na osie współrzędnych będzie:

Znajdźmy inne wyrażenie dla twierdzenia. Niech w danym momencie wielkość ruchu układu będzie równa i w tej chwili będzie równa . Następnie mnożąc obie strony równości (20) i całkując, otrzymujemy

ponieważ całki po prawej stronie dają impulsy sił zewnętrznych.

Równanie (21) wyraża twierdzenie o zmianie pędu układu w postaci całkowej: zmiana pędu układu w pewnym okresie czasu jest równa sumie impulsów działających na układ sił zewnętrznych przez ten sam okres czasu.

W rzutach na osie współrzędnych będą:

Wskażmy na związek pomiędzy udowodnionym twierdzeniem a twierdzeniem o ruchu środka masy. Ponieważ , podstawiając tę ​​wartość do równości (20) i biorąc pod uwagę, że otrzymujemy , czyli równanie (16).

W konsekwencji twierdzenie o ruchu środka masy i twierdzenie o zmianie pędu układu to zasadniczo dwa różne kształty to samo twierdzenie. W przypadkach, gdy badany jest ruch ciała sztywnego (lub układu ciał), można zastosować dowolną z tych postaci, a równanie (16) jest zwykle wygodniejsze w użyciu. W przypadku ośrodka ciągłego (ciecz, gaz) przy rozwiązywaniu problemów zwykle posługują się twierdzeniem o zmianie pędu układu. Twierdzenie to ma także ważne zastosowania w teorii zderzeń (patrz rozdział XXXI) oraz w badaniu ruchu strumieniowego (patrz § 114).

Równanie różniczkowe ruchu punktu materialnego pod wpływem siły F można przedstawić w następującej postaci wektorowej:

Ponieważ masa punktu M przyjmuje się jako stałą, wówczas można ją wpisać pod znakiem pochodnej. Następnie

Wzór (1) wyraża twierdzenie o zmianie pędu punktu w postaci różniczkowej: pierwsza pochodna po czasie pędu punktu jest równa sile działającej na ten punkt.

W rzutach na osie współrzędnych (1) można przedstawić jako

Jeśli obie strony (1) zostaną pomnożone przez dt, wówczas otrzymujemy inną postać tego samego twierdzenia - twierdzenie o pędzie w postaci różniczkowej:

te. różnica pędu punktu jest równa elementarnemu impulsowi siły działającej na ten punkt.

Rzutując obie części (2) na osie współrzędnych otrzymujemy

Całkując obie części (2) od zera do t (ryc. 1), mamy

gdzie jest prędkość punktu w danej chwili T; - prędkość w T = 0;

S- impuls siły w czasie T.

Wyrażenie w postaci (3) jest często nazywane twierdzeniem o pędzie w postaci skończonej (lub całkowej): zmiana pędu punktu w dowolnym okresie czasu jest równa impulsowi siły w tym samym okresie.

W rzutach na osie współrzędnych twierdzenie to można przedstawić w następującej postaci:

W przypadku punktu materialnego twierdzenie o zmianie pędu w dowolnej postaci zasadniczo nie różni się od równań różniczkowych ruchu punktu.

Twierdzenie o zmianie pędu układu

Wielkość ruchu układu będzie nazywana wielkością wektorową Q, równa sumie geometrycznej (wektorowi głównemu) wielkości ruchu wszystkich punktów układu.

Rozważmy system składający się z N punkty materialne. Ułóżmy równania różniczkowe ruchu dla tego układu i dodajmy je wyraz po wyrazie. Następnie otrzymujemy:

Ostatnia suma, ze względu na właściwość sił wewnętrznych, jest równa zeru. Oprócz,

Wreszcie znajdujemy:

Równanie (4) wyraża twierdzenie o zmianie pędu układu w postaci różniczkowej: pochodna czasowa pędu układu jest równa sumie geometrycznej wszystkich sił zewnętrznych działających na układ.

Znajdźmy inne wyrażenie dla twierdzenia. Wpuść tę chwilę T= 0 oznacza wielkość ruchu układu Pytanie 0 i w danym momencie t 1 staje się równe Pytanie 1. Następnie mnożąc obie strony równości (4) przez dt i całkując otrzymujemy:

Czy gdzie:

(S-impuls siły)

ponieważ całki po prawej stronie dają impulsy sił zewnętrznych,

równanie (5) wyraża twierdzenie o zmianie pędu układu w postaci całkowej: zmiana pędu układu w pewnym okresie czasu jest równa sumie impulsów sił zewnętrznych działających na układ w tym samym okresie czasu.

W rzutach na osie współrzędnych będziemy mieli:

Prawo zachowania pędu

Z twierdzenia o zmianie pędu układu można wyciągnąć następujące ważne wnioski:

1. Niech suma wszystkich sił zewnętrznych działających na układ będzie równa zero:

Zatem z równania (4) wynika, że ​​w tym przypadku Q = stała

Zatem, jeśli suma wszystkich sił zewnętrznych działających na układ jest równa zeru, wówczas wektor pędu układu będzie stały pod względem wielkości i kierunku.

2. 01Niech siły zewnętrzne działające na układ będą takie, że suma ich rzutów na jakąś oś (np. Ox) będzie równa zeru:

Zatem z równań (4`) wynika, że ​​w tym przypadku Q = stała

Zatem, jeżeli suma rzutów wszystkich działających sił zewnętrznych na dowolną oś jest równa zeru, to rzut wielkości ruchu układu na tę oś jest wartością stałą.

Te wyniki wyrażają prawo zachowania pędu układu. Wynika z nich, że siły wewnętrzne nie mogą zmienić całkowitej wielkości ruchu układu.

Spójrzmy na kilka przykładów:

· Zjawisko powrotu rolki. Jeśli potraktujemy karabin i kulę jako jeden układ, wówczas ciśnienie gazów proszkowych podczas strzału będzie siłą wewnętrzną. Siła ta nie może zmienić całkowitego pędu układu. Ponieważ jednak gazy prochowe, działając na kulę, nadają jej pewien ruch skierowany do przodu, muszą jednocześnie nadać karabinowi taki sam ruch w odwrotny kierunek. Spowoduje to cofnięcie się karabinu, tj. tzw powrót. Podobne zjawisko występuje podczas strzelania z broni (cofanie).

· Działanie śmigła (śmigła). Śmigło wprawia w ruch pewną masę powietrza (lub wody) wzdłuż osi śmigła, odrzucając tę ​​masę z powrotem. Jeżeli potraktujemy masę rzuconą i samolot (lub statek) jako jeden układ, wówczas siły oddziaływania śmigła z otoczeniem, jako siły wewnętrzne, nie są w stanie zmienić całkowitej wielkości ruchu tego układu. Dlatego też, gdy masa powietrza (wody) zostanie odrzucona, samolot (lub statek) uzyskuje odpowiednią prędkość do przodu, taką, że całkowity ruch rozważanego układu pozostaje równy zeru, ponieważ był zerowy przed rozpoczęciem ruchu .

Podobny efekt uzyskuje się poprzez działanie wioseł lub kół łopatkowych.

· Napęd rekt iwny W rakiecie (rakietze) gazowe produkty spalania paliwa wyrzucane są z dużą prędkością przez otwór w ogonie rakiety (z dyszy silnika odrzutowego). Siły ciśnienia działające w tym przypadku będą siłami wewnętrznymi i nie mogą zmienić całkowitego pędu układu gazy rakietowo-proszkowe. Ponieważ jednak uciekające gazy mają pewien ruch skierowany do tyłu, rakieta otrzymuje odpowiednią prędkość do przodu.

Twierdzenie o momentach względem osi.

Rozważ materialny punkt masy M, poruszając się pod wpływem siły F. Znajdźmy dla niego zależność pomiędzy momentami wektorów mV I F względem pewnej ustalonej osi Z.

m z (F) = xF - yF (7)

Podobnie dla wartości m(mV), jeśli zostanie wyjęty M będzie poza nawiasami

M z (mV) = m(xV - yV)(7`)

Biorąc pochodne po czasie z obu stron tej równości, znajdujemy

Po prawej stronie wynikowego wyrażenia pierwszy nawias jest równy 0, ponieważ dx/dt=V i dу/dt = V, drugi nawias według wzoru (7) jest równy

mz(F), gdyż zgodnie z podstawową zasadą dynamiki:

Wreszcie będziemy mieli (8)

Otrzymane równanie wyraża twierdzenie o momentach wokół osi: pochodna po czasie momentu pędu punktu względem dowolnej osi jest równa momentowi siła działająca o tej samej osi. Podobne twierdzenie obowiązuje dla chwil wokół dowolnego środka O.