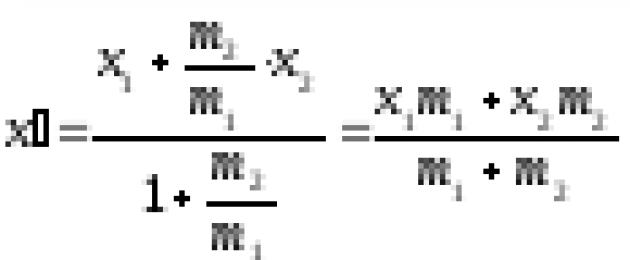Metod för koordinater i rymden: formler och kommentarer från handledaren. Koordinatmetod i rymdpresentation för en geometrilektion (årskurs 11) på ämnet Koordinatmetod i rymden rektangulärt koordinatsystem

För att använda presentationsförhandsvisningar, skapa ett Google-konto och logga in på det: https://accounts.google.com

Bildtexter:

Rektangulärt koordinatsystem i rymden. Vektorkoordinater.

Rektangulärt koordinatsystem

Om tre parvisa vinkelräta linjer dras genom en punkt i rymden, väljs en riktning på var och en av dem och en måttenhet för segmenten, då säger de att rektangulärt system koordinater i rymden

Raka linjer med riktningar valda på dem kallas koordinataxlar, och deras gemensamma punkt är ursprunget till koordinaterna. Det betecknas vanligtvis med bokstaven O. Koordinataxlarna betecknas enligt följande: Ox, Oy, O z - och har namn: abskissaxel, ordinataaxel, applikataxel.

Hela koordinatsystemet betecknas Oxy z. Planen som går genom koordinataxlarna Ox och Oy, Oy respektive O z, O z och Ox kallas koordinera plan och betecknas Oxy, Oy z, O z x.

Punkt O delar var och en av koordinataxlarna i två strålar. En stråle vars riktning sammanfaller med axelns riktning kallas en positiv halvaxel, och den andra strålen kallas en negativ halvaxel.

I ett rektangulärt koordinatsystem är varje punkt M i rymden associerad med en trippel av tal, som kallas dess koordinater.

Figuren visar sex punkter A (9; 5; 10), B (4; -3; 6), C (9; 0; 0), D (4; 0; 5), E (0; 3; 0) F (0; 0; -3).

Vektorkoordinater

Vilken vektor som helst kan expanderas till koordinatvektorer, det vill säga representerade i formen där expansionskoefficienterna x, y, z bestäms på ett unikt sätt.

Koefficienterna x, y och z i expansionen av en vektor till koordinatvektorer kallas koordinaterna för vektorn i ett givet koordinatsystem.

Låt oss överväga reglerna som tillåter oss att använda koordinaterna för dessa vektorer för att hitta koordinaterna för deras summa och skillnad, såväl som produktens koordinater given vektor på givet nummer.

10 . Varje koordinat av summan av två eller flera vektorer är lika med summan av motsvarande koordinater för dessa vektorer. Med andra ord, om a (x 1, y 1, z 1) och b (x 2, y 2, z 2) ges vektorer, så har vektorn a + b koordinater (x 1 + x 2, y 1 + y2, z1 + z2).

20 . Varje koordinat för skillnaden mellan två vektorer är lika med skillnaden mellan motsvarande koordinater för dessa vektorer. Med andra ord, om a (x 1, y 1, z 1) och b (x 2 y 2; z 2) ges vektorer, så har vektorn a - b koordinater (x 1 - x 2, y 1 - y 2, zl - z2).

trettio . Varje koordinat av produkten av en vektor och ett tal är lika med produkten av motsvarande koordinat för vektorn och detta tal. Med andra ord, om a (x; y; x) är en given vektor, är α ett givet tal, då har vektorn α a koordinater (αх; αу; α z).

På ämnet: metodologisk utveckling, presentationer och anteckningar

Didaktisk Handout"En uppsättning anteckningar för studenter på ämnet "Method of coordinates in space" för att genomföra lektioner i form av föreläsningar. Geometri årskurs 10-11....

Syfte med lektionen: Att testa elevernas kunskaper, färdigheter och förmågor i ämnet "Att använda metoden för koordinater i rymden för att lösa C2 Unified State Examination-uppgifter." Planerade pedagogiska resultat: Eleverna visar: ...

Lektionsprov i geometri i årskurs 11

Ämne: " Metod för koordinater i rymden."

Mål: Testa elevernas teoretiska kunskaper, deras färdigheter och förmåga att tillämpa denna kunskap för att lösa problem med vektor- och vektorkoordinatmetoder.

Uppgifter:

1 .Skapa förutsättningar för kontroll (självkontroll, ömsesidig kontroll) för inhämtande av kunskaper och färdigheter.

2. Utveckla matematiskt tänkande, tal, uppmärksamhet.

3. Främja aktivitet, rörlighet, kommunikationsförmåga, allmän kultur studenter.

Uppförandeform: jobba i grupper.

Utrustning och informationskällor: duk, multimediaprojektor, kunskapsbord, testkort, tester.

Under lektionerna

1.Mobiliserande ögonblick.

Lektion med CSR; eleverna är indelade i 3 dynamiska grupper, där eleverna har en acceptabel, optimal och avancerad nivå. Varje grupp väljer en koordinator som leder hela gruppens arbete.

2 . Elevernas självbestämmande baserat på förväntan.

Uppgift:målsättning enligt schemat: komma ihåg-lära-kunna.

Inträdesprov - Fyll i de tomma fälten (i utskrifter)

Inträdesprov

Fyll luckorna...

1.Tre par vinkelräta räta linjer ritas genom en punkt i rymden.

på var och en av dem väljs segmentens riktning och måttenhet,

då säger de att det är givet …………. i rymden.

2. Raka linjer med valda riktningar kallas ……………..,

och deras gemensamma poäng …………. .

3. I ett rektangulärt koordinatsystem är varje punkt M i rymden associerad med en trippel av tal som kallar den ………………..

4. Koordinaterna för en punkt i rymden kallas ………………..

5. En vektor vars längd är lika med ett kallas …………..

6. Vektorer iykkallas………….

7. Odds xyz i sönderdelning a= xi + yj + zk kallas

……………vektorer a .

8. Varje koordinat av summan av två eller flera vektorer är lika med …………………..

9. Varje koordinat för skillnaden mellan två vektorer är lika med ……………….

10. Varje koordinat av produkten av en vektor och ett tal är lika med………………..

11. Varje vektorkoordinat är lika med………………….

12. Varje koordinat i mitten av segmentet är lika med……………….

13. Vektorlängd a { xyz) beräknas med formeln …………………………

14. Avstånd mellan punkterna M 1(x 1 ; y 1; z 1) och M 2 (x 2; y 2 ; z2) beräknat med formeln …………………

15. Den skalära produkten av två vektorer kallas …………………..

16. Skalärprodukten av vektorer som inte är noll är lika med noll………………..

17. Prickprodukt av vektorera{ x 1; y 1; z 1} b { x 2 ; y 2 ; z 2) in uttryckt med formeln………………………

Peer review av inträdesprovet. Svar på testuppgifter på skärmen.

Evalutionskriterie:

1-2 fel – "5"

3-4 fel - "4"

5-6 fel - "3"

I andra fall – "2"

3. Att få jobbet gjort. (med kort).

Varje kort innehåller två uppgifter: nr 1 - teoretisk med bevis, nr 2 innehåller uppgifter.

Förklara komplexitetsnivån för de uppgifter som ingår i arbetet. Gruppen utför en uppgift, men har 2 delar. Gruppsamordnaren leder hela gruppens arbete. Att diskutera samma information med flera partners ökar ansvaret inte bara för ens egna framgångar, utan också för resultaten av kollektivt arbete, vilket har en positiv effekt på mikroklimatet i teamet.

KORT nr 1

1.Härled formler som uttrycker koordinaterna för mitten av ett segment genom koordinaterna för dess ändar.

2.Uppgift: 1) Givet punkterna A (-3; 1; 2) och B (1; -1; 2)

Hitta:

a) koordinater för mittpunkten av segment AB

b) koordinater och längd för vektor AB

2) Givet en kub ABCDA1 B1 C1 D1. Använd koordinatmetoden och hitta vinkeln

mellan räta linjer AB1 och A1 D.

KORT#2

Härled en formel för att beräkna längden på en vektor från dess koordinater.

Problem: 1) Givet poäng M(-4; 7; 0),N(0; -1; 2). Hitta avståndet från origo till mitten av segmentet MN.

→ → → → →

2) Vektorer ges a Och b. Hitta b(a+b), Om a (-2; 3; 6), b = 6i-8k

KORT nr 3

Härled en formel för att beräkna avståndet mellan punkter med givna koordinater.

Problem: 1) Givet poäng A(2;1;-8), B(1;-5;0), C(8;1;-4).

Bevisa att ∆ABC är likbent och hitta längden mittlinje triangel som förbinder sidornas mittpunkter.

2) Beräkna vinkeln mellan räta linjer AB och CD, om A(1;1;0),

B(3;-1;2), D(0;1;0).

KORT#4

Härled formler för cosinus för vinkeln mellan vektorer som inte är noll med givna koordinater.

Problem: 1) Givet koordinaterna för de tre hörnen i parallellogrammet ABCD:

A(-6;-;4;0), B(6;-6;2), C(10;0;4). Hitta koordinaterna för punkt D.

2) Hitta vinkeln mellan räta linjer AB och CD, om A(1;1;2), B(0;1;1), C(2;-2;2), D(2;-3;1) .

KORT#5

Berätta för oss hur man beräknar vinkeln mellan två linjer i rymden med hjälp av dessa linjers riktningsvektorer. →→

Uppgift: 1) Hitta skalär produkt vektorera Och b, Om:

→ → → ^ →

a) | a| =4; | b| =√3 (ab)=30◦

b) a {2 ;-3; 1}, b = 3 i +2 k

2) Givet punkterna A(0;4;0), B(2;0;0), C(4;0;4) och D(2;4;4). Bevisa att ABCD är en romb.

4. Kontroll av arbetet dynamiska grupper med kort.

Vi lyssnar på grupprepresentanternas framträdanden. Gruppernas arbete bedöms av läraren med deltagande av elever.

5. Reflektion. Provbetyg.

Slutprov med flerval (i utskrifter).

1) Vektorer ges a {2 ;-4 ;3} b(-3; ─ ; 1). Hitta vektorns koordinater

→ 2

c = a+ b

a) (-5; 3 -; 4); b) (-1; -3,5;4) c) (5; -4 -; 2) d) (-1; 3,5; -4)

2) Vektorer ges a(4; -3; 5) och b(-3; 1; 2). Hitta vektorns koordinater

C=2 a – 3 b

a) (7;-2;3); b) (11; -7; 8); c) (17; -9; 4); d) (-1; -3; 4).

→ → → → → →

3) Beräkna skalärprodukten av vektorerm Och n, Om m = a + 2 b- c

→ → → → →^ → → → → →

n= 2 a - b om | a|=2 , ‌| b |=3, (ab‌)=60°, c ┴ a , c ┴ b.

a)-1; b) -27; i 1; d) 35.

4) Vektorlängd a { xyz) är lika med 5. Hitta koordinaterna för vektor a ifx=2, z=-√5

a) 16; b) 4 eller -4; vid 9; d)3 eller -3.

5) Hitta arean ∆ABC om A(1;-1;3); B(3;-1;1) och C(-1;1;-3).

a) 4√3; b) √3; c)2√3; d)√8.

Peer review av testet. Svarskoder för testuppgifter på skärmen: 1(b); 2(c);

3(a); 4(b); 5(c).

Evalutionskriterie:

Allt är korrekt - "5"

1 fel - "4"

2 fel - "3"

I andra fall - "2"

Elevkunskapstabell

Jobba på

kort

Slutlig

testa

Bedömning för provet

Uppgifter

teori

öva

1 grupp

2:a gruppen

3 grupp

Bedöma elevernas förberedelser inför provet.

Positionen för vilken punkt som helst i rymden kan bestämmas unikt med hjälp av ett rektangulärt koordinatsystem. Detta system inkluderar tre ömsesidigt vinkelräta axlar som skär varandra i en punkt O – ursprung för koordinater. En av axlarna kallas x-axeln(axel Åh), annan - y-axeln (OU), tredje – axeltillämpning (Uns). Flygplan XOY, XOZ Och YOZ kallas koordinatplan. Varje segment tas som skalenhet för alla tre axlarna . Positiva riktningar på axlarna väljs så att en rotation på 90 0, kombinerar den positiva strålen OXE med positiv stråle OY, verkade passera moturs sett från strålen UNS. Detta koordinatsystem kallas höger.

Position för vilken punkt som helst M i rymden kan definieras av tre koordinater enligt följande . GenomMrita plan parallellt med planenXOY, XOZ Och YOZ. I skärningspunkten med axlarna får vi punkter, t.ex. P, F Och R respektive. Tal X (abskissa), på(ordinera), z (ansöka), mäta segmentOP, O QOchELLERpå en vald skala anropasrektangulära koordinaterpoäng M. De tas positiva eller negativa beroende på om motsvarande segment ligger på den positiva eller negativa halvaxeln. Varje trippel av siffror ( X; på; z) motsvarar en och endast en punkt i rymden, och vice versa.

Avstånd mellan två punkter och beräknas med formeln: (1.6)

Koordinater (x; y; z) poängM, dividerat i ett givet förhållande linjesegmentet AB, (,) bestäms av formlerna:

I synnerhet vid (punkt M delar upp ett segment AB på hälften), får vi formler för att bestämma koordinaterna för segmentets mittpunkt:

Exempel 4: På axeln OU hitta en punkt på samma avstånd från två punkter Och .

Lösning: Punkt M, liggande på axeln OU, har koordinater . Enligt förutsättningarna för problemet |AM| = |VM|. Låt oss hitta avstånden |AM| Och |VM|, med formeln (1.6):

Vi får ekvationen: .

Härifrån finner vi att 4 på= 16, dvs. y = 4. Den önskade punkten är där M(0; 4; 0).

Exempel 5: Linjesegmentet AB uppdelad i 3 lika delar. Hitta koordinaterna för divisionspunkterna om punkterna och .

Lösning:

Låt oss beteckna segmentets divisionspunkter AB i följande ordning: MED Och D. Enligt förutsättningarna för problemet |AC| = |CD| = |DB|. Därför peka MED delar upp ett segment AB i ett förhållande . Med hjälp av formler (1.7) hittar vi koordinaterna för punkt C:

Med hjälp av formler (1.8) hittar vi punktens koordinater D– segmentets mittpunkt NE:

Det vill säga, punkt D har koordinater: .

Exempel 6: På punkter , ,, massorna koncentreras därefter m 1 , m 2 , m 3 , m 4 . Hitta koordinaterna för tyngdpunkten för systemet med dessa massor.

Lösning:

Som du vet från en fysikkurs, massors tyngdpunkt m 1 och m 2 placerade på poäng A Och I, delar upp ett segment AB i delar omvänt proportionella mot massorna koncentrerade i ändarna av segmentet (). Utifrån detta hittar vi först tvåmasssystemets tyngdpunkt m 1 och m 2 placerade på poäng A 1 Och A 2 :

, ,.

Tyngdpunkten för ett tremasssystem m 1 och m 2 och m 3 () finner vi på liknande sätt:

, ,.

Vi hittar äntligen tremasssystemets tyngdpunktm 1 , m 2 , m 3 Ochm 4 :

, ,.

Frågor för kontroll:

Beskriv ett rektangulärt koordinatsystem på ett plan och alla dess komponenter.

Hur bestäms koordinaterna för en godtycklig punkt på planet?

Skriv en formel för att hitta sidavståndet mellan två punkter på plan .

Hur man hittarkoordinater för en punkt som delar ett segment i ett givet förhållande?

Skriv formler för koordinaterna för segmentets mittpunkt.

Skriv en formel som beräknar arean av en triangel om koordinaterna för dess hörn är kända .

Beskriv det polära koordinatsystemet.

Vad kallas polarradie? I vilken utsträckning mäts det?

Vad kallas en polär vinkel? Gränserna för dess mätning?

Hur hitta de rektangulära koordinaterna för en punkt för vilken de polära koordinaterna är kända?

Hur hitta de polära koordinaterna för en punkt för vilken rektangulära koordinater är kända?

Hur man hittar avstånd mellan punkter i polärt koordinatsystem?

Beskriv det rektangulära koordinatsystemet i rymden och alla dess komponenter.

Hur bestämmer man koordinaterna för en punkt i rymden?

Skriv ner en formel för att hitta avståndet mellan två punkter i rymden.

Skriv ner formlerna för att hitta punktkoordinater, dividera segmentet i ett givet förhållande för ett tredimensionellt koordinatsystem.

Kärnan i koordinatmetoden för att lösa geometriska problem

Kärnan i att lösa problem med koordinatmetoden är att införa ett koordinatsystem som är bekvämt för oss i ett visst fall och skriva om all data med hjälp av den. Därefter utförs alla okända kvantiteter eller bevis med detta system. Vi diskuterade hur man anger koordinaterna för punkter i vilket koordinatsystem som helst i en annan artikel - vi kommer inte att uppehålla oss vid detta här.

Låt oss presentera de viktigaste påståendena som används i koordinatmetoden.

Påstående 1: Koordinaterna för vektorn kommer att bestämmas av skillnaden mellan motsvarande koordinater för slutet av denna vektor och dess början.

Påstående 2: Koordinaterna för mitten av segmentet kommer att bestämmas som halva summan av motsvarande koordinater för dess gränser.

Påstående 3: Längden på en vektor $\overline(δ)$ med givna koordinater $(δ_1,δ_2,δ_3)$ kommer att bestämmas av formeln

$|\överlinje(δ)|=\sqrt(δ_1^2+δ_2^2+δ_3^2)$

Påstående 4: Avståndet mellan två valfria punkter som anges av koordinaterna $(δ_1,δ_2,δ_3)$ och $(β_1,β_2,β_3)$ bestäms av formeln

$d=\sqrt((δ_1-β_1)^2+(δ_2-β_2)^2+(δ_3-β_3)^2)$

Schema för att lösa geometriska problem med hjälp av koordinatmetoden

För att lösa geometriska problem med koordinatmetoden är det bäst att använda detta schema:

Analysera vad som ges i problemet:

Ställ in det koordinatsystem som passar bäst för uppgiften;
Problemets tillstånd, frågan om problemet skrivs ner matematiskt och en ritning för detta problem konstrueras.

Skriv ner all uppgiftsdata i koordinaterna för det valda koordinatsystemet.
Gör de nödvändiga relationerna från problemets villkor, och koppla även dessa relationer till det som behöver hittas (bevisas i problemet).
Översätt det erhållna resultatet till geometrins språk.

Exempel på problem lösta med koordinatmetoden

De huvudsakliga problemen som leder till koordinatmetoden kan identifieras enligt följande (vi kommer inte att ge deras lösningar här):

Problem med att hitta koordinaterna för en vektor baserat på dess slut och början.
Problem relaterade till att dela upp ett segment i något avseende.
Bevis att tre punkter ligger på samma linje eller att fyra punkter ligger på samma plan.
Problem att hitta avståndet mellan två givna punkter.
Problem med att hitta volymer och ytor för geometriska figurer.

Resultaten av att lösa det första och fjärde problemet presenteras av oss som de viktigaste påståendena ovan och används ganska ofta för att lösa andra problem med hjälp av koordinatmetoden.