Att resonera enbart baserat på exakta fakta och exakta slutsatser från dessa fakta kallas strikta resonemang. I de fall där osäkra fakta måste användas för att fatta beslut blir rigorösa resonemang olämpliga. Därför är en av de största styrkorna med alla expertsystem dess förmåga att forma resonemang under förhållanden av osäkerhet lika framgångsrikt som mänskliga experter gör. Sådana resonemang är inte rigorösa. Vi kan lugnt prata om närvaro rolig logik.
Osäkerhet, och som en konsekvens kan suddig logik betraktas som en brist på adekvat information för beslutsfattande. Osäkerhet blir ett problem eftersom det kan hindra skapandet av den bästa lösningen och till och med göra att en dålig lösning hittas. Det bör noteras att en högkvalitativ lösning som hittas i realtid ofta anses mer acceptabel än en bättre lösning som tar lång tid att beräkna. Att skjuta upp behandlingen för att tillåta ytterligare tester kan till exempel leda till att patienten dör innan den får behandling.
Orsaken till osäkerheten är förekomsten av olika fel i informationen. Förenklad klassificering Dessa fel kan presenteras i sin uppdelning i följande typer:
- tvetydighet i information, vars förekomst beror på att viss information kan tolkas på olika sätt;
- ofullständig information på grund av bristen på vissa uppgifter;
- otillräcklig information på grund av användning av data som inte överensstämmer med den verkliga situationen ( möjliga orsakerär subjektiva fel: lögner, felaktig information, utrustningsfel);
- mätfel som uppstår på grund av bristande överensstämmelse med kraven på korrekthet och noggrannhet av kriterierna för kvantitativ presentation av data;
- slumpmässiga fel, vars manifestation är slumpmässiga fluktuationer i data i förhållande till deras medelvärde (orsaken kan vara: utrustningens opålitlighet, Brownsk rörelse, termiska effekter etc.).
Idag har ett betydande antal teorier om osäkerhet utvecklats, som försöker eliminera några eller till och med alla fel och ge tillförlitliga logiska slutsatser under osäkerhetsförhållanden. De teorier som oftast används i praktiken är de som bygger på den klassiska definitionen av sannolikhet och på posterior sannolikhet.
Ett av de äldsta och viktigaste problemlösningsverktygen artificiell intelligensär sannolikhet. Sannolikhetär ett kvantitativt sätt att redovisa osäkerhet. Klassisk sannolikhet kommer från en teori som först föreslogs av Pascal och Fermat 1654. Sedan dess har mycket arbete gjorts inom området sannolikhet och implementeringen av många tillämpningar av sannolikhet inom vetenskap, teknik, företag, ekonomi och andra områden.
Klassisk sannolikhet
Klassisk sannolikhetäven kallad a priori sannolikhet, eftersom dess definition gäller idealiska system. Termen "a priori" betyder en sannolikhet som bestäms "till händelser", utan att ta hänsyn till många faktorer som inträffar i verkliga världen. Begreppet a priori-sannolikhet sträcker sig till händelser som inträffar i idealiska system som är benägna att slitas eller påverkas av andra system. I ett idealiskt system sker förekomsten av någon av händelserna på samma sätt, vilket gör deras analys mycket lättare.
Den grundläggande formeln för klassisk sannolikhet (P) definieras enligt följande:
I denna formel W- Antalet förväntade händelser, och N- det totala antalet händelser med lika sannolikheter som är möjliga resultat av ett experiment eller test. Till exempel sannolikheten att få någon hexagonal kant tärningarär 1/6, och att dra vilket kort som helst från en kortlek som innehåller 52 olika kort är 1/52.
Sannolikhetslärans axiom
En formell sannolikhetsteori kan skapas utifrån tre axiom:

Ovanstående axiom gjorde det möjligt att lägga grunden för sannolikhetsteorin, men de beaktar inte sannolikheten för att händelser inträffar i verkliga - icke-ideala system. I motsats till a priori-metoden, i verkliga system, att bestämma sannolikheten för någon händelse P(E), metoden som används för att bestämma experimentell sannolikhet som en frekvensfördelningsgräns:

Posterior sannolikhet
I denna formel f(E) anger frekvensen av förekomst av någon händelse mellan N-antal observationer av övergripande resultat. Denna typ av sannolikhet kallas också posterior sannolikhet, dvs. sannolikhet bestäms "efter händelserna". Grunden för att bestämma posterior sannolikhet är mätningen av den frekvens med vilken en händelse inträffar under ett stort antal försök. Till exempel att bestämma den sociala typen av en kreditvärdig bankklient baserat på empirisk erfarenhet.
Händelser som inte utesluter varandra kan påverka varandra. Sådana händelser klassas som komplexa. Sannolikheten för komplexa händelser kan beräknas genom att analysera deras motsvarande provrum. Dessa provutrymmen kan representeras med Venn-diagram, som visas i fig. 1

Fig. 1 Provutrymme för två evenemang som inte utesluter varandra
Sannolikheten för att händelse A inträffar, som bestäms med hänsyn till att händelse B har inträffat, kallas villkorad sannolikhet och betecknas P(A|B). Villkorlig sannolikhet definieras enligt följande:

Tidigare sannolikhet
I denna formel, sannolikheten P(B) får inte vara lika med noll och representerar a priori sannolikhet som bestäms innan annan ytterligare information är känd. Tidigare sannolikhet, som används i samband med användning av betingad sannolikhet, kallas ibland absolut sannolikhet.
Det finns ett problem som i huvudsak är motsatsen till problemet med att beräkna betingad sannolikhet. Den består i att bestämma den inversa sannolikheten, som visar sannolikheten för en tidigare händelse med hänsyn till de händelser som inträffade i framtiden. I praktiken förekommer denna typ av sannolikhet ganska ofta, till exempel under medicinsk diagnostik eller utrustningsdiagnostik, där vissa symtom identifieras, och uppgiften är att hitta en möjlig orsak.
För att lösa detta problem, använd Bayes sats, uppkallad efter den brittiske matematikern Thomas Bayes från 1700-talet. Bayesiansk teori används nu flitigt för att analysera beslutsträd inom ekonomi och samhällsvetenskap. Den Bayesianska lösningssökningsmetoden används också i PROSPECTORs expertsystem vid identifiering av lovande platser för mineralprospektering. PROSPECTOR-systemet fick stor popularitet som det första expertsystemet med hjälp av vilket en värdefull molybdenfyndighet upptäcktes, värd 100 miljoner dollar.
En slumpmässig händelse bedöms av ett tal som bestämmer intensiteten av manifestationen av denna händelse. Detta nummer kallas sannolikhet evenemang P()
. Sannolikhet för en elementär händelse –  . Sannolikheten för en händelse är ett numeriskt mått på graden av objektivitet, möjligheten för denna händelse. Ju högre sannolikhet, desto mer möjlig är händelsen.
. Sannolikheten för en händelse är ett numeriskt mått på graden av objektivitet, möjligheten för denna händelse. Ju högre sannolikhet, desto mer möjlig är händelsen.
Varje händelse som sammanfaller med hela resultatområdet S, ringde pålitlig händelse, dvs. en sådan händelse som som ett resultat av experimentet nödvändigtvis måste inträffa (till exempel förlust av valfritt antal poäng från 1 till 6 på en tärning). Om evenemanget inte tillhör uppsättningen S, då anses det omöjlig(till exempel kasta ett nummer större än 6 på en tärning). Sannolikheten för en omöjlig händelse är 0, sannolikheten för en viss händelse är 1. Alla andra händelser har en sannolikhet från 0 till 1.
evenemang E Och  kallas motsatt, Om E kommer när det inte kommer
kallas motsatt, Om E kommer när det inte kommer  . Till exempel händelse E– "rulla ett jämnt antal poäng", sedan händelsen
. Till exempel händelse E– "rulla ett jämnt antal poäng", sedan händelsen  - "rullar ett udda antal poäng." Två händelser E 1
Och E 2
kallas oförenlig, om det inte finns något gemensamt resultat för båda händelserna.
- "rullar ett udda antal poäng." Två händelser E 1
Och E 2
kallas oförenlig, om det inte finns något gemensamt resultat för båda händelserna.
För att bestämma sannolikheterna för slumpmässiga händelser används direkta eller indirekta metoder. Vid direkt beräkning av sannolikheten särskiljs a priori och a posteriori beräkningsscheman, när utföra observationer (experiment) eller a priori räkna antalet experiment m, där händelsen manifesterade sig, och det totala antalet utförda experiment n. Indirekta metoder bygger på axiomatisk teori. Eftersom händelser definieras som mängder, kan alla mängdteoretiska operationer utföras på dem. Mängdlära och funktionsanalys föreslogs av akademiker A.N. Kolmogorov och utgjorde grunden för den axiomatiska sannolikhetsteorin. Låt oss presentera sannolikhetsaxiomen.
Axiomjag. HändelsefältF(S) är en algebra av mängder.
Detta axiom pekar på analogin mellan mängdlära och sannolikhetsteori.
AxiomII.
Till varje set frånF(S) är associerad med ett reellt tal P(
frånF(S) är associerad med ett reellt tal P( ), kallad sannolikheten för händelsen
), kallad sannolikheten för händelsen :
:
givet att S 1 S 2 = (för oförenliga händelser S 1 Och S 2 ), eller för en uppsättning inkompatibla händelser
Var N– antalet elementära händelser (möjliga utfall).
Sannolikhet slumpmässig händelse
|
|
Var  – sannolikheter för elementära händelser
– sannolikheter för elementära händelser  ingår i delmängden
ingår i delmängden  .
.
Exempel 1.1. Bestäm sannolikheten att få varje nummer när du kastar en tärning, får ett jämnt tal, nummer 4 .
Lösning. Sannolikheten för att varje nummer faller ur mängden
S = (1, 2, 3, 4, 5, 6)
 1/6.
1/6.
Sannolikheten att rulla ett jämnt tal, dvs.  ={2,
4, 6},
baserat på (1.6) kommer det att vara P(
={2,
4, 6},
baserat på (1.6) kommer det att vara P(  )
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2
.
)
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2
.
Sannolikhet att få ett tal 4
, dvs.  =
{4, 5, 6 }
,
=
{4, 5, 6 }
,
P(  )
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
)
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
Arbetsuppgifter för självständigt arbete
1. Det finns 20 vita, 30 svarta och 50 röda bollar i en korg. Bestäm sannolikheten att den första bollen som dras från korgen kommer att vara vit; svart; röd.
2. Det finns 12 killar och 10 tjejer i elevgruppen. Vad är sannolikheten att följande uteblir från sannolikhetslära seminariet: 1) en ung man; 2) flicka; 3) två unga män?
3. Under året kännetecknades 51 dagar av att det dessa dagar regnade (eller snöade). Hur stor är sannolikheten att du riskerar att fastna i regn (eller snö): 1) gå till jobbet; 2) gå på en vandring i 5 dagar?
4. Skriv ett problem om ämnet för denna uppgift och lös det.
1.1.3. Definition av posterior sannolikhet (statistisk sannolikhet eller frekvens
slumpmässig händelse)
Vid fastställandet av sannolikheten a priori antogs att  lika troligt. Detta är inte alltid sant, oftare händer det
lika troligt. Detta är inte alltid sant, oftare händer det  på
på  . Antagande
. Antagande  leder till ett fel i a priori-bestämningen P(
leder till ett fel i a priori-bestämningen P(  )
enligt det etablerade systemet. För att bestämma
)
enligt det etablerade systemet. För att bestämma  och i det allmänna fallet P(
och i det allmänna fallet P(  )
genomföra riktade tester. Under sådana tester (till exempel testresultaten i exemplen 1.2, 1.3) under olika förhållanden av olika förhållanden, påverkan, orsaksfaktorer, d.v.s. likgiltig fall, olika resultat(olika manifestationer av informationen om objektet som studeras.) Varje testresultat motsvarar ett element
)
genomföra riktade tester. Under sådana tester (till exempel testresultaten i exemplen 1.2, 1.3) under olika förhållanden av olika förhållanden, påverkan, orsaksfaktorer, d.v.s. likgiltig fall, olika resultat(olika manifestationer av informationen om objektet som studeras.) Varje testresultat motsvarar ett element  eller en delmängd
eller en delmängd
 set S.Om vi definierar m som antalet gynnsamma evenemang A resultat till följd av n tester, sedan den bakre sannolikheten (statistisk sannolikhet eller frekvens av en slumpmässig händelse A)
set S.Om vi definierar m som antalet gynnsamma evenemang A resultat till följd av n tester, sedan den bakre sannolikheten (statistisk sannolikhet eller frekvens av en slumpmässig händelse A)
Baserat på lagen stora nummer För
 A
A
|
|
de där. när antalet försök ökar, tenderar frekvensen av en slumpmässig händelse (posterior, eller statistisk, sannolikhet) till sannolikheten för denna händelse.
Exempel 1.2. Bestämt av fallschemat är sannolikheten att landa huvuden när man kastar ett mynt 0,5. Du måste kasta ett mynt 10, 20, 30... gånger och bestämma frekvensen av den slumpmässiga händelsen av huvuden efter varje serie av tester.
Lösning. C. Poisson kastade ett mynt 24 000 gånger och landade på huvuden 11 998 gånger. Sedan, enligt formel (1.7), sannolikheten för landningshuvuden
 .
.
Arbetsuppgifter för självständigt arbete
Baserat på stort statistiskt material ( n ) värdena för sannolikheterna för utseendet av enskilda bokstäver i det ryska alfabetet och rymden () i texterna erhölls, som ges i tabell 1.1.
Tabell 1.1. Sannolikheten för att bokstäverna i alfabetet förekommer i text
|
| ||||||||
|
| ||||||||
|
| ||||||||
|
|
Ta en sida med valfri text och bestäm hur ofta olika bokstäver förekommer på den sidan. Öka längden på testerna till två sidor. Jämför de erhållna resultaten med uppgifterna i tabellen. Rita en sammanfattning.
Vid skjutning mot mål erhölls följande resultat (se tabell 1.2).
Tabell 1.2. Mål skjutresultat
Vad är sannolikheten att målet skulle träffas med det första skottet om det var mindre än "tio", "nio" etc.?
3. Planera och genomföra liknande tester för andra evenemang. Presentera deras resultat.
I. Villkorliga sannolikheter. Före och bakre sannolikhet. 3
II. Oberoende evenemang. 5
III. Testa statistiska hypoteser. Statistisk signifikans. 7
IV.Användning av chi-kvadrattestet 19
1. Bestämma tillförlitligheten av skillnaden mellan en uppsättning frekvenser och en uppsättning sannolikheter. 19
2. Bestämning av tillförlitligheten av skillnaden mellan flera uppsättningar av frekvenser. 26
OBEROENDE UPPGIFT 33
Lektion nr 2
Villkorliga sannolikheter. Före och bakre sannolikhet.
En slumpvariabel specificeras av tre objekt: en uppsättning elementära händelser, en uppsättning händelser och en sannolikhet för händelser. Värdena som en slumpvariabel kan ta kallas elementära händelser. Uppsättningar av elementära händelser kallas evenemang. För numeriska och andra inte särskilt komplexa slumpmässiga variabler varje specifikt given uppsättning elementära händelser är en händelse.
Låt oss ta ett exempel: kasta en tärning.
Det finns 6 elementära händelser totalt: "poäng", "2 poäng", "3 poäng"... "6 poäng". Händelse - vilken uppsättning elementära händelser som helst, till exempel "jämn" - summan av de elementära händelserna "2 poäng", "4 poäng" och "6 poäng".
Sannolikheten för en elementär händelse P(A) är 1/6:
sannolikheten för en händelse är antalet elementära händelser som ingår i den, dividerat med 6.
Ganska ofta, förutom den kända sannolikheten för en händelse, finns det ytterligare information som ändrar denna sannolikhet. Till exempel patientdödlighet. av de inlagda på sjukhuset med akut blödande magsår är cirka 10 %. Men om patienten är över 80 år är denna dödlighet 30 %.
För att beskriva sådana situationer, den sk betingade sannolikheter. De betecknas som P(A/B) och läses "sannolikheten för händelse A given händelse B." För att beräkna den villkorade sannolikheten används formeln:
Låt oss gå tillbaka till föregående exempel:
Antag att bland de patienter som lagts in på sjukhuset med akut blödande magsår är 20 % patienter över 80 år. Bland alla patienter är dessutom andelen avlidna patienter över 80 år 6 % (kom ihåg att andelen av alla dödsfall är 10 %). I detta fall
Vid definition av betingade sannolikheter används ofta termerna a priori(bokstavligen – före erfarenhet) och a posteriori(bokstavligen - efter erfarenhet) sannolikhet.
Med villkorade sannolikheter kan du använda en sannolikhet för att beräkna andra, till exempel byta en händelse och ett villkor.
Låt oss överväga denna teknik med hjälp av exemplet att analysera sambandet mellan risken för reumatisk feber (reumatisk feber) och ett av antigenerna som är en riskfaktor för det.
Förekomsten av reumatism är cirka 1 %. Låt oss beteckna närvaron av reumatism som R+, medan P(R+) = 0,01.
Närvaron av antigen kommer att betecknas som A+. Det finns hos 95 % av patienter med reumatism och hos 6 % av personer som inte lider av reumatism. I vår notation är dessa: villkorliga sannolikheter P(A + /R +) = 0,95 och P(A + /R -) = 0,06.
Baserat på dessa tre sannolikheter kommer vi successivt att bestämma andra sannolikheter.
För det första, om förekomsten av reumatism är P(R +) = 0,01, så är sannolikheten att inte bli sjuk P(R -) = 1-P(R +) = 0,99.
Från formeln för betingad sannolikhet finner vi det
P(A + ochR +) = P(A + /R +) * P(R +) = 0,95*0,01 = 0,0095, eller 0,95% av befolkningen både lider av reumatism och har antigenet.
likaså
P(A + ochR -) = P(A + /R -) * P(R -) = 0,06*0,99 = 0,0594, eller 5,94% av befolkningen bär antigenet, men lider inte av reumatism.
Eftersom alla som har antigenet antingen lider av reumatism eller inte lider av reumatism (men inte båda samtidigt), ger summan av de två sista sannolikheterna frekvensen av att antigenet bärs i befolkningen som helhet:
P(A +)= P(A + ochR +) + P(A + ochR -) = 0,0095 + 0,0594 = 0,0689
Följaktligen är andelen människor som inte har antigenet lika med
P(A-)=1-P(A+) = 0,9311
Eftersom förekomsten av reumatism är 1 %, och andelen personer som har antigenet och lider av reumatism är 0,95 %, är andelen personer som har reumatism och inte har antigenet lika med:
P(A - ochR +) = P(R +) - P(A + ochR +) = 0,01 – 0,0095 = 0,0005
Nu kommer vi att gå i motsatt riktning, från sannolikheterna för händelser och deras kombinationer till villkorade sannolikheter. Enligt den ursprungliga villkorliga sannolikhetsformeln kommer P(A + /R +) = P(R + och A +)/ P(A +) = 0,0095/0,06890,1379, eller ungefär 13,8 % av individerna som bär antigenet, att få reumatism . Eftersom förekomsten av befolkningen som helhet bara är 1%, ökar det faktum att identifiera ett antigen sannolikheten för att utveckla reumatism med 14 gånger.
På liknande sätt är P(R + /A -) = P(R + ochA -)/ P(A -) = 0,0005/0,93110,000054, det vill säga det faktum att inget antigen upptäcktes under testningen minskar sannolikheten för att utveckla reumatism. 19 gånger.
Låt oss formatera den här uppgiften i ett Excel-kalkylblad:
|
Förekomst av reumatism R+ | ||
|
Närvaro av antigen hos patienter med A+ | ||
|
Närvaro av antigen hos icke-sjuka A+-patienter | ||
|
Sannolikhet att inte bli sjuk |
P(R -)=1- P(R +) | |
|
Samtidigt lider de av reumatism och har antigenet |
P(A + och R +)= P(A + /R +) * P(R +) | |
|
De bär på antigenet, men blir inte sjuka av reumatism |
P(A + och R -)= P(A + /R -) * P(R -) | |
|
Frekvens av antigentransport i den allmänna befolkningen |
P(A +)= P(A + och R +) + P(A + och R -) | |
|
Andel människor utan antigen |
P(A -)=1- P(A +) | |
|
Andel personer med reumatism som inte har antigen |
P(A - och R +) = P(R +) - P(A + och R +) | |
|
Personer som bär antigenet kommer att utveckla reumatism |
P(A + /R +)= P(R + och A +)/ P(A +) | |
|
Personer som inte bär på antigenet kommer inte att utveckla reumatism |
P(R + /A -)=P(R + och A -)/ P(A -) |
Du kan se processen för att skapa en tabell picture2\p2-1.gif
Fråga nr 38. Komplett grupp av händelser. Formel för total sannolikhet. Bayes formler.
Två händelser. Oberoende i aggregatet. Formulering av multiplikationssatsen i detta fall.
Fråga nr 37. Villkorlig sannolikhet. Multiplikationssats. Definition av oberoende
Villkorlig sannolikhet är sannolikheten för en händelse givet att en annan händelse redan har inträffat.
P(A│B)= p(AB)/ p(B)
Villkorlig sannolikhet återspeglar inverkan av en händelse på sannolikheten för en annan.
Multiplikationssats.
Sannolikheten för att händelser ska inträffa bestäms av formeln P(A 1,A 2,....A n)= P(A 1)P(A 2/ A 1)...P(A n / A 1 A 2... A n -1)
För produkten av två händelser följer att
P(AB)=P(A/B)P(B)=P(B/A)P(A)
Om den ena händelsen inte beror på den andra, om förekomsten av en av dem inte påverkar sannolikheten för att den andra inträffar, så beror den senare inte heller på den första. Detta ger all anledning att kalla sådana evenemang oberoende. Matematiskt betyder oberoende att den villkorade sannolikheten för en händelse är densamma som dess sannolikhet (ovillkorlig sannolikhet).
1. De säger att händelse A inte beror på händelse B om
P(A│B)=P(A)
Om händelse A inte beror på händelse B, så beror händelse B inte på händelse A.
2. Om händelserna A och B är oberoende, så är P(AB) = P(A)P(B) - denna likhet används för att bestämma oberoende händelser.
Det är nödvändigt att skilja mellan parvis oberoende av händelser och oberoende i aggregatet.
Händelser A1, A2,...An kallas kollektivt oberoende om de är parvis oberoende och var och en av dem inte beror på produkten av någon uppsättning andra händelser.
Om händelserna A1, A2,….An är oberoende i sin helhet då
P(Ai,A2,...A n)=P(Ai)P(A2)...P(A n).
I varje grupp kommer någon händelse definitivt att inträffa som ett resultat av testet, och förekomsten av en av dem utesluter förekomsten av alla andra. Sådana händelser kallas en komplett händelsegrupp.
Definition: Om en grupp av händelser är sådan att minst en av dem måste inträffa som ett resultat av testet, och två av dem är inkompatibla, kallas denna grupp av händelser en komplett grupp.
Varje händelse från en hel grupp kallas en elementär händelse. Varje elementärt evenemang är lika möjligt, eftersom det finns ingen anledning att tro att någon av dem är mer möjlig än någon annan händelse i hela gruppen.
Två motstridiga händelser utgör en komplett grupp.
Den relativa frekvensen av händelse A är förhållandet mellan antalet experiment som ett resultat av vilken händelse A inträffade och Totala numret experiment.
Skillnaden mellan relativ frekvens och sannolikhet är att sannolikhet beräknas utan direkt experimentering, och relativ frekvens beräknas efter experiment.
Total sannolikhetsformel
(där A är någon händelse, H1, H2 ... Hi är parvis inkompatibla och bildar en komplett grupp, och A kan inträffa tillsammans med H1, H2 Hi)
P(A)=P(A|H1) P(Hl)+P(A|H2)P(H2)+P(A|H3)P(H3)+…+P(A| Hn)P(Hn)
Bayes formel
Kommentar. Händelser Hi kallas sannolikhetshypoteser, p(Hi) är a priori sannolikheter för hypoteser Hi, och sannolikheter P(Hi/A) är a posteriori sannolikheter för hypoteser Hi
Låt resultatet av experimentet vara känt, nämligen att händelse A inträffade. Detta faktum kan ändra a priori (det vill säga kända före experimentet) sannolikheter för hypoteserna. För att omvärdera sannolikheterna för hypoteser med ett känt experimentellt resultat, används Bayes formel:
Exempel. Efter två skott från två skyttar, vars träffsannolikheter var lika med 0,6 och 0,7, var det ett hål i målet. Hitta sannolikheten att den första skytten träffade.
Lösning. Låt händelse A vara en träff med två skott,
och hypoteser: H1 – den första träffen och den andra missad,
H2 – den första missade och den andra träffen,
H3 - båda träffade,
H4 – båda missade.
Sannolikheter för hypoteser:
р(Í1) = 0,6·0,3 = 0,18,
p(H2) = 0,4·0,7 = 0,28,
p(H3) = 0,6·0,7 = 0,42,
p(H4) = 0,4 0,3 = 0,12.
Då p(A/H1) = p(A/H2) = 1,
p(A/H3) = p(A/H4) = 0.
Därför är den totala sannolikheten p(A) = 0,18 1 + 0,28 1 + 0,42 0 + 0,12 0 = 0,46.
Den totala sannolikhetsformeln låter dig beräkna sannolikheten för en händelse av intresse genom de villkorade sannolikheterna för denna händelse under antagandet av vissa hypoteser, såväl som sannolikheterna för dessa hypoteser.
Definition 3.1. Låt händelse A endast inträffa tillsammans med en av händelserna H1, H2,..., Hn, vilket bildar en komplett grupp av inkompatibla händelser. Sedan kallas händelserna Н1, Н2,..., Нп hypoteser.
Sats 3.1. Sannolikheten för att händelse A inträffar tillsammans med hypoteserna H1, H2,..., Hn är lika med:
där p(Hi) är sannolikheten för den i:te hypotesen och p(A/Hi) är sannolikheten för händelse A, beroende på implementeringen av denna hypotes. Formeln (P(A)= ) kallas den totala sannolikhetsformeln
Fråga nr 39. Bernoulli-schema. Sannolikhet för m framgångar i en serie av n försök
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0

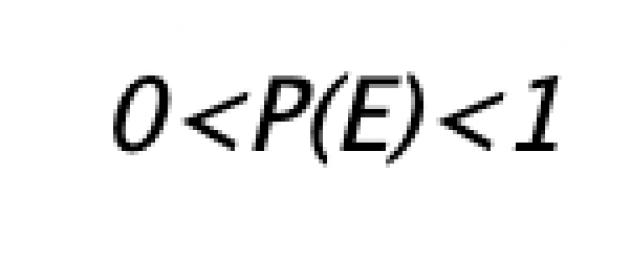
 ,
, ,
n
,
,
n
,









