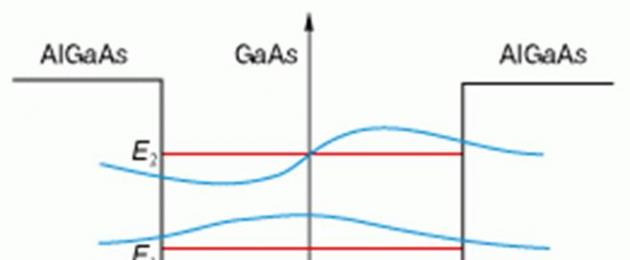
Ris. 2. Energiband vid gränsen mellan två halvledare - heterostruktur. E c Och E u- gränser för ledningsbandet och valensbandet, T.ex- bandgapets bredd. Elektron med mindre energi E c 2 (nivån visas i rött) kan bara vara till höger om gränsen

För elektroner som rör sig i en halvledare med smala gap och har mindre energi E c 2 kommer gränsen att spela rollen som en potentiell barriär. Två heterojunctions begränsar en elektrons rörelse på båda sidor och bildar så att säga en potentialbrunn.

Så skapas kvantbrunnar genom att placera ett tunt lager av halvledare med ett smalt bandgap mellan två lager av material med ett bredare bandgap. Som ett resultat blir elektronen låst i en riktning, vilket leder till kvantisering av transversell rörelseenergi.

Samtidigt kommer elektronernas rörelse i de andra två riktningarna att vara fri, så vi kan säga att elektrongasen i kvantbrunnen blir tvådimensionell.

På samma sätt kan en struktur innehållande en kvantbarriär framställas genom att placera ett tunt lager av en halvledare med bredbandsgap mellan två smalbandshalvledare.

Flera avancerade tekniska processer har utvecklats för produktion av sådana strukturer, men de bästa resultaten vid framställning av kvantstrukturer har uppnåtts med metoden molekylär strålepitaxi.

För att odla ett tunt lager av halvledare med denna metod måste du rikta en ström av atomer eller molekyler på ett noggrant rengjort substrat. Flera strömmar av atomer, som erhålls genom att förånga ett ämne från separata uppvärmda källor, flyger samtidigt på substratet.

För att undvika kontaminering odlas strukturen i högvakuum. Hela processen är datorstyrd, kemisk sammansättning och kristallstrukturen hos det odlade lagret kontrolleras under tillväxtprocessen.

Molecular beam epitaxi-metoden gör det möjligt att odla perfekta enkristallskikt med en tjocklek av endast ett fåtal gitterperioder (en gitterperiod är cirka 2).

Det är extremt viktigt att gitterperioderna för två intilliggande lager, som har olika kemisk sammansättning, är nästan lika. Då kommer skikten att följa varandra exakt och den odlade strukturens kristallgitter kommer inte att innehålla defekter.

Genom att använda molekylstråleepitaxmetoden är det möjligt att erhålla en mycket skarp (exakt till ett monolager) gräns mellan två intilliggande lager, och ytan är slät på atomnivå.

Kvantstrukturer kan odlas från olika material, men det mest framgångsrika paret för att odla kvantbrunnar är halvledaren GaAs - galliumarsenid och Al x Ga 1-x As fast lösning, där en del av galliumatomerna är ersatta av aluminiumatomer. Magnitud xär andelen galliumatomer som ersatts av aluminiumatomer; den varierar vanligtvis från 0,15 till 0,35. Bandgapet i galliumarsenid är 1,5 eV, och i Al x Ga 1-x As fast lösning ökar det med ökande x. Ja när x= 1, det vill säga i AlAs-föreningen är bandgapet 2,2 eV.

För att odla en kvantbrunn är det nödvändigt att ändra den kemiska sammansättningen av de atomer som flyger på det växande lagret under tillväxten.

Först måste du odla ett lager av halvledare med breda bandgap, det vill säga Al x Ga 1-x As, sedan ett lager av smalspalt GaAs-material och slutligen igen ett lager av Al x Ga 1-x As.

Energidiagrammet för en kvant som är väl förberedd på detta sätt visas i fig. 3. Brunnen har ett ändligt djup (flera tiondelar av en elektronvolt). Den innehåller bara två diskreta nivåer, och vågfunktionerna vid brunnsgränsen försvinner inte. Detta innebär att elektronen även kan detekteras utanför brunnen, i det område där den totala energin är mindre än potentialen. Naturligtvis kan detta inte hända i klassisk fysik, men i kvantfysik det är möjligt.

Ris. 3. Kvantbrunn bildad i ett lager av halvledare med ett smalt bandgap inklämt mellan två halvledare med ett bredare bandgap

Teknologer har utvecklat flera sätt att producera kvantprickar och trådar. Dessa strukturer kan exempelvis bildas vid gränsytan mellan två halvledare där en tvådimensionell elektrongas finns.

Detta kan göras genom att lägga till ytterligare barriärer som begränsar rörelsen av elektroner i ytterligare en eller två riktningar.

Kvanttrådar är bildade i botten av ett V-format spår bildat på halvledarsubstratet. Om en halvledare med ett mindre bandgap avsätts vid basen av detta spår, kommer elektronerna i denna halvledare att låsas i två riktningar.

I fig. Figur 4 visar kvantprickar skapade vid gränsytan mellan galliumarsenid och aluminium galliumarsenid. Under tillväxtprocessen infördes ytterligare föroreningsatomer i AlGaAs-halvledaren. Elektroner från dessa atomer går in i GaAs-halvledaren, det vill säga in i en region med lägre energi. Men de kan inte gå för långt, eftersom de attraheras av föroreningsatomerna de lämnade, som fick Positiv laddning. Nästan alla elektroner är koncentrerade vid själva heterogränssnittet på GaAs-sidan och bildar en tvådimensionell gas. Processen att bilda kvantprickar börjar med att deponera en serie masker på AlGaAs-ytan, som var och en är formad som en cirkel. Därefter utförs djupetsning, under vilken hela AlGaAs-skiktet och delvis GaAs-skiktet avlägsnas (i fig. 4).

Ris. 4. Kvantpunkter bildade i en tvådimensionell elektrongas vid gränsytan mellan två halvledare

Som ett resultat blir elektronerna låsta i de resulterande cylindrarna (i fig. 4 är området där elektronerna finns färgat rött). Cylindrarnas diametrar är i storleksordningen 500 nm.

I en kvantprick är rörelsen begränsad i tre riktningar och energispektrumet är helt diskret, precis som i en atom. Därför kallas kvantprickar också konstgjorda atomer, även om varje sådan prick består av tusentals eller till och med hundratusentals verkliga atomer.

Dimensionerna på kvantprickar (vi kan också prata om kvantlådor) är i storleksordningen flera nanometer. Liksom en riktig atom kan en kvantprick innehålla en eller flera fria elektroner. Om det finns en elektron så är det som en konstgjord väteatom, om det finns två är det en heliumatom osv.

Kvantprick- ett fragment av en ledare eller halvledare, begränsat i alla tre rumsliga dimensioner och som innehåller ledningselektroner. Poängen måste vara så liten att kvanteffekter är betydande. Detta uppnås om elektronens kinetiska energi , på grund av osäkerheten i dess rörelsemängd, kommer att vara märkbart större än alla andra energiskalor: först och främst högre än temperaturen uttryckt i energienheter ( d- karakteristisk punktstorlek, m- effektiv massa av en elektron vid en punkt).

Kvantprick Varje liten nog bit av metall eller halvledare kan tjäna. Historiskt sett var de första kvantprickarna förmodligen mikrokristaller av kadmiumselenid CdSe. En elektron i en sådan mikrokristall känns som en elektron i en tredimensionell potentialpotentialbrunn; den har många stationära energinivåer med ett karakteristiskt avstånd mellan dem (det exakta uttrycket för energinivåerna beror på spetsens form). I likhet med övergången mellan energinivåer för en atom, när en kvantpunkt övergår mellan energinivåer, kan en foton sändas ut. Det är också möjligt att kasta en elektron till en hög energinivå, och ta emot strålning från övergången mellan lägre liggande nivåer (luminescens). Dessutom, till skillnad från verkliga atomer, kan övergångsfrekvenser enkelt kontrolleras genom att ändra dimensionerna på kristallen. Egentligen fungerade observationen av luminescens i kadmiumselenidkristaller med en luminescensfrekvens bestämd av kristallens storlek som den första observationen av kvantprickar.

För närvarande ägnas många experiment åt kvantprickar som bildas i en tvådimensionell elektrongas. I en tvådimensionell elektrongas är rörelsen av elektroner vinkelrätt mot planet redan begränsad, och ett område på planet kan isoleras med hjälp av gatemetallelektroder placerade ovanpå heterostrukturen. Kvantpunkter i en tvådimensionell elektrongas kan anslutas genom tunnelkontakter till andra områden av den tvådimensionella gasen och ledning genom kvantpunkten kan studeras. I ett sådant system observeras fenomenet Coulomb-blockad.

Kvantprickar PbSe på PbTe-lager

Ris. 1a Kiselbaserad germanium quantum dot Si 001 (foto taget med ett elektronskanningmikroskop) (ritning från HP:s forskargrupp)

Ris. 1b Halvledare konisk fotonisk kanal som en kvantpunkt

Elektroner som fångas av kvantprickar beter sig likadant som om de fanns i en vanlig atom, även om den "konstgjorda atomen" inte har någon kärna. Vilken atom som representerar en sådan uppsättning elektroner beror på antalet elektroner i kvantpunkten.

Ris. Mått på en nanokristallkvantprick

Förutom att helt enkelt rita ett mönster på ytan av en halvledare och etsa, för att skapa kvantprickar, kan du använda materialets naturliga egenskap för att bilda små öar under tillväxtprocessen. Sådana öar kan till exempel spontant bildas på ytan av ett växande kristallint lager. Det finns andra tekniker för att förbereda kvantbrunnar, trådar och prickar, som vid första anblicken verkar väldigt enkla.

Kapitel 10. BEGREPPET BANDTEORI OM FASTämnen

Idén om valens som förmågan hos en atom att bilda kemiska bindningar med ett visst antal andra atomer när den appliceras på en fast kropp förlorar sin mening, eftersom här möjligheten till kollektiv interaktion realiseras. Så i en molekyl är atomernas valens lika med en, men i en kristall är varje atom omgiven av 6 atomer och vice versa.

Energispektrumet för en isolerad atom bestäms av interaktionen mellan elektroner och kärnan och är diskret till sin natur. Energitillstånden för elektroner i ett fast ämne bestäms av dess interaktion både med dess kärna och med kärnorna i andra atomer. I en kristall är atomkärnorna belägna periodiskt längs vilken riktning som helst (fig. 56). Därför rör sig elektronen i ett periodiskt elektriskt fält (nära kärnorna potentiell energi elektroner är mindre än i gapet mellan kärnorna). Detta leder till det faktum att istället för en diskret atomenerginivå i ett fast innehåll N atomer uppstår N energinivåer som ligger nära varandra, som bildar en energizon. I denna mening talar de om uppdelningen av energinivån i en energizon. Intilliggande energinivåer i zonen är separerade från varandra med 10 -23 eV. Som jämförelse påpekar vi att genomsnittet värmeenergi elektroner vid temperatur T= 300 K är ~ 10 -2 eV. Som ett resultat kan spektrumet av elektroner inuti bandet betraktas som kvasi-kontinuerligt.

Antalet tillstånd i en zon är lika med produkten av antalet atomer i kristallen och multipeln av atomenerginivån från vilken zonen bildades. Multipeln av en energinivå hänvisar till antalet elektroner som kan vara på denna nivå enligt Pauli-principen.

Zoner med tillåtna energier är åtskilda av zoner med förbjudna energier. Deras bredd är jämförbar med bredden på de tillåtna energibanden. Med ökande energi ökar bredden på de tillåtna banden, och bredden på de förbjudna banden minskar (fig. 57).

§2. Metaller, halvledare, dielektrika

Skillnader i elektriska egenskaper fasta ämnen förklaras av elektronernas olika fyllning av tillåtna energiband och bredden på bandgapen. För att kroppen ska kunna utföra elektricitet det är nödvändigt att ha fria energinivåer i tillåtna band till vilka elektroner kan röra sig under påverkan av ett elektriskt fält.

Metaller

Tänk på en natriumkristall. Dess elektroniska formel är. Energidiagrammet för natrium visas i fig. 58.

En isolerad atom har ett diskret energispektrum. När atomer närmar sig varandra, med start från ett visst interatomärt avstånd, delas energinivåerna i zoner. De yttre nivåerna delas först: lediga 3 R, sedan halvfylld nivå 3 s. När avståndet minskar r innan r 1 överlappning sker 3 R- och 3 s-zoner med tillåtna energier. På distans r = r 0 (r 0 är det interatomära jämviktsavståndet i kristallen), upphör atomernas närmande. Valens 3 s elektroner kan uppta vilket tillstånd som helst inom detta band. Nivå 1 s och 2 s kan bara dela när r< r 0 och in kemisk bindning delta inte. Anslutningen utförs av ett kollektiv av valenselektroner, vars energitillstånd bildar ett gemensamt band till följd av överlappning.

I zonen med tillåtna energier som bildas av valensnivåer kommer det att finnas 8 N stater (antal s-tillstånd 2 N; siffra R- stater 6 N). Atomen har en valenselektron, så denna zon kommer att innehålla N elektroner som upptar tillstånd i enlighet med Pauli-principen och principen om minsta energi. Följaktligen är vissa stater i zonen fria.

Kristaller i vilka zonen som bildas av nivåerna av valenselektroner är delvis fylld klassificeras som metaller Denna zon kallas ledningszonen.

Halvledare och dielektrika

Låt oss överväga energistrukturen för halvledare och dielektrika med hjälp av exemplet på ett typiskt halvledarkristallint kisel (Z = 14), vars elektroniska formel är . Under bildandet av ett kristallgitter, med början från ett visst interatomärt avstånd r 1 > r 0 (r 0 – jämviktsavstånd mellan atomer i kristallen) uppstår sp 3-hybridisering av elektroniska tillstånd av kisel, vilket inte bara leder till överlappning 3 s och 3 R zoner och deras sammanslagning och bildande av en enda 3 sp 3 hybridvalensband (fig. 59), där det maximala antalet elektroner är 8 N. I kristallint kisel bildar varje atom 4 tetraedriska bindningar, vilket kompletterar sitt valensskal med upp till åtta elektroner. Som ett resultat, i valensbandet alla 8 N stater är upptagna. Alltså för halvledare och dielektrika band som bildas av valenselektronnivåer- valensband (VB) - helt fyllt. Nästa lediga 4 s-bandet överlappar inte valensbandet på interatomärt avstånd r 0, och är skild från den av en zon av förbjudna energier (ZZ) . Elektroner som finns i valensbandet kan inte delta i ledning, eftersom alla tillstånd i bandet är upptagna. För att en ström ska uppstå i kristallen är det nödvändigt att överföra elektroner från valensbandet till nästa fria band av tillåtna energier. Den första fria tillåtna zonen ovanför valensband kallas ledningszon (CB). Energigapet mellan botten av ledningsbandet och toppen av valensbandet kallas bandgap Wg.

Beroende på bandgapet, allt kristallina kropparär indelade i tre klasser:

1. metaller - 0,1 eV;

2. halvledare -;

3. dielektrikum - 4 eV.

Följaktligen har kroppar följande resistivitetsvärden:

1. metaller - ρ = 10 -8 10 -6 Ohm m;

2. halvledare - ρ = 10 -6 10 8 Ohm m;

3. dielektrikum - ρ >10 8 Ohm m.

Vid en temperatur T= 0 halvledare är dielektriska, men med ökande temperatur minskar deras motstånd kraftigt. Vid upphettning smälter dielektrikum innan elektronisk ledningsförmåga uppstår.

Ett av de största problemen med solid state-teorin är att bestämma energispektrum och stationära tillstånd för elektroner i en kristall. En kvalitativ uppfattning om detta spektrum kan erhållas med hjälp av ungefärliga metoder och förenklingar. För det första tror man att undersystemet av kärnor praktiskt taget är i vila (i förhållande till elektronernas snabba rörelse) - den adiabatiska approximationen. För det andra antas det att varje elektron rör sig i ett fält skapat av andra elektroner och oberoende av den momentana positionen för en given elektron, vilket gör att varje elektrons rörelse kan betraktas oberoende av alla andra och beskrivas av en-elektronen Schrödinger ekvation.

Denna approximation kallas singelelektron.

Approximation av hårt bundna elektroner. I en isolerad atom kan elektroner endast ockupera diskreta energinivåer, som är åtskilda av intervaller av förbjudna energier. I det här fallet tenderar elektroner att ockupera de lägsta nivåerna, men under förutsättning att det inte finns fler än två elektroner på varje nivå (Pauli-principen).

Under bildandet av en kristall, på grund av sammanförandet av N identiska atomer, uppstår interaktionskrafter mellan dem: frånstötande krafter mellan kärnor och mellan elektroner från angränsande atomer och dragkrafter mellan alla kärnor och alla elektroner.

Den starkt bundna elektronapproximationen är baserad på idén att generaliserade elektroner bibehåller en tillräckligt stark bindning med atomer, och deras potentiella energi kan representeras i följande form.

, (4.20)

Var Ua– potentiell energi hos en elektron i en isolerad atom. För en kristall är det en periodisk funktion med en period lika med gitterparametern, eftersom elektronens energi upprepas när den passerar från en atom till en annan;
är en korrektionsterm som tar hänsyn till närliggande atomers inverkan på denna energi.

Om vi ​​i (4.20) försummar korrigeringstermen
,de där. anser den sk noll approximation, då som vågfunktion och energi för elektronen i kristallen ska vi ta vågfunktionen och energi E a för en elektron i en isolerad atom:
,
.

Skillnaden mellan en kristall och en individuell atom i detta fall är följande. Medan i en isolerad atom är denna energinivå E a unik, i en kristall som består av N atomer upprepas den N gånger. Med andra ord, varje nivå av en isolerad atom i en kristall visar sig vara N-multiplicera urarta.

Låt oss nu ta hänsyn till korrigeringstermen
i potentiell energi (4.20). När isolerade atomer kommer närmare varandra och bildar ett gitter, befinner sig varje atom i ett ständigt ökande fält av sina grannar som den interagerar med.

Inom området för dessa krafter avlägsnas degenerationen av atomära nivåer. Det är därför varje energinivå, inte urarta i en isolerad atom, delas i N nära undernivåer belägna från varandra och bildar en energizon. Denna zon består av mycket nära åtskilda energinivåer, vars densitet ökar med avståndet från zonens kanter enligt en parabolisk lag och når ett maximum i mitten av zonen. När atomerna kommer närmare delas de högsta energinivåerna först, sedan de lägre när atomerna kommer närmare.

Mekanismen för bildandet av energizoner visas i fig. 4.3.

Ris. 4.3. Schema för bildning av energiband i en kristall

Om energinivån hade i en atom (2 l+1) –multipel degeneration, då kommer motsvarande energiband att bestå av N(2 l+1) undernivåer. Således ger nivå s zonen s, bestående av N undernivåer och kapabel att ta emot 2 N elektroner: nivå p ger ett band p som består av 3 N undernivåer och kan hålla 6N elektroner, etc.

Eftersom en kristall med en volym på 1 m 3 innehåller cirka 10 28 atomer, och bredden på energibandet är cirka 1 eV, är avståndet mellan energinivåerna i bandet cirka 10–28 eV. Därför är en försumbar liten energipåverkan tillräcklig för att orsaka övergången av elektroner från en nivå till en annan inom bandet; vi kan anta att energibanden är kvasi-kontinuerliga.

Inverkan av gitterfältet på olika nivåer av atomen är inte densamma. Nivåerna av inre elektroner, som starkt interagerar med kärnan, upplever en så svag splittring att den kan försummas: när vi flyttar till fler och fler externa elektroner minskar energin från deras interaktion med kärnan, och påverkan av det yttre fältet ökar. Den starkaste förändringen under påverkan av fältet upplevs av nivåerna av yttre valenselektroner, som är relativt svagt associerade med kärnan, och energizoner, bildad av energinivåerna hos dessa elektroner, visa sig vara den bredaste. Detta bevisas av naturen hos valenselektronernas elektronmoln: de överlappar så mycket att de skapar ett resulterande moln med nästan likformig densitet. Detta motsvarar tillståndet för deras fullständiga socialisering i gallret. Sådana socialiserade elektroner brukar kallas fri, och deras helhet – elektronisk gas.

Inre elektroner, starkt bundna till kärnan, upplever endast en liten störning från närliggande atomer, som ett resultat av vilket deras energinivåer i kristallen förblir nästan lika smala som i isolerade atomer.

Således motsvarar varje energinivå för en isolerad atom i en kristall tillåten energizon: nivå 1 s – zon 1 s, nivå 2 R– zon 2 R etc. Zoner med tillåtna energier är åtskilda av områden med förbjudna energier – förbjudna zoner E g. När elektronenergin i en atom ökar, ökar bredden på de tillåtna banden, medan bredden på de förbjudna banden minskar.

I många fall kan det finnas överlappning mellan tillåtna områden. Liksom energinivåer i isolerade atomer kan energiband vara helt fyllda med elektroner, delvis fyllda eller tomma. Allt beror på strukturen hos de elektroniska skalen av isolerade atomer och interatomära avstånd i kristallen. Den översta zonen, delvis eller helt fylld med elektroner, kallas valensbandet, och den ofyllda zonen närmast den är ledningszon.

Approximation av fria elektroner. Låt oss betrakta fallet med rörelsen av en helt fri elektron längs X-axeln, beskriven enligt följande Schrödengers ekvation:

, (4.21)

, (4.22)

eftersom en fri elektron har kinetisk energi.

Formel (4.22) representerar dispersionsförhållande för fria elektroner, vilket uttrycker beroendet E(p). Det kan konverteras enligt följande. Enligt Louis de Broglies formel,

, (4.23)

där λ är elektronvåglängden, och

. (4.24)

Vektor k, i riktning som sammanfaller med elektronvågens utbredningsriktning, och i magnitud lika med 2π/λ, kallas vågvektor för elektronen. Genom att ersätta p från (4.23) till (4.22) får vi

. (4.25)

Från (4.22) och (4.24) är det tydligt att för fria elektroner är spridningslagen till sin natur kvadratisk och för endimensionell elektronrörelse uttrycks med en kvadratisk parabel som visas i Fig. 4.4.

Lösningen till ekvation (4.21) är en plan vandringsvåg:

, (4.26)

Var A– vågamplitud.

Fig.4.4. Dispersionslag för en fri elektron

Vågfunktionens kvadratiska modul är, som bekant, proportionell mot sannolikheten att detektera en elektron i ett särskilt område av rymden. Som framgår av (4.26), för en fri elektron beror denna sannolikhet inte på elektronkoordinaten, eftersom

Det betyder att för en fri elektron är alla punkter i rymden ekvivalenta och sannolikheten att hitta den i någon av dem är densamma.

Approximation av löst bundna elektroner. Låt oss gå över till fallet med elektronrörelse i ett periodiskt fält av en kristall som bildas av regelbundet placerade gitterjoner (fig. 4.5).

Fig. 4.5. Sannolikhet att detektera en elektron när man rör sig i ett fält av korrekt placerade joner

I denna approximation representeras den potentiella energin för en elektron som

;
, (4.28)

Var U 0 (x) – potentiell energi för en elektron i fältet för positiva joner, förutsatt att detta fält kompenseras av fältet för alla andra elektroner;

U 0 (x) - periodisk funktion med en period lika med gitterkonstanten;

- tar hänsyn till ofullständig lokal kompensation av jonfältet av elektroner. Sannolikheten att hitta en elektron på en given plats i kristallen måste vara en periodisk funktion av x-koordinaten, eftersom positioner skiljer sig från varandra med en mängd som är en multipel av gitterkonstanten A(till exempel bestämmelser A, A' Och I i fig. 4.5) för en elektron är lika sannolika. Endast positioner inom samma period kommer att vara olika A(till exempel inom ACA-perioden). Det betyder att vågfunktions amplitud
en elektron som rör sig i ett periodiskt fält förblir inte konstant, som en fri elektron, utan ändras periodiskt, eller, som de säger, modulerar med en period lika med gitterperioden a. Låt oss beteckna denna amplitud med u(x). Sedan vågfunktionen för en elektron som rör sig i ett periodiskt fält kristall i x-axelns riktning kan representeras i följande form:

, (4.29)

i detta fall u(x+na)=u(x), där n är vilket heltal som helst. Relation (4.29) kallas Bloch funktion. Den specifika formen av denna funktion bestäms av typen av potentiell energi U(x) som ingår i Schrödinger-ekvationen (4.9).

Följaktligen bör spridningsförhållandet för elektroner som rör sig i kristallens periodiska fält också ändras i jämförelse med fria elektroner. För det första får energispektrumet för sådana elektroner en bandkaraktär. Inuti varje zon visar sig elektronenergin vara en periodisk funktion av vågvektorn k och för en endimensionell kristall (atomkedja) med parametern A kan uttryckas med följande relation:

Var E A– energin på den atomnivå från vilken zonen bildades; MED– förskjutning av denna nivå under påverkan av fältet av angränsande atomer; A- så kallade utbytesintegral, med hänsyn till möjligheten av övergång från atom till atom som har dykt upp för elektronerna i kristallen på grund av överlappningen av deras vågfunktioner. Ju större överlappning mellan vågfunktionerna, d.v.s. desto större frekvens kan närliggande atomer byta ut sina elektroner med. För s-stater A s <0 , för p-tillstånd A sid >0 , därför är det tillrådligt att skriva relation (4.30) separat för s- och p-zonerna:

för r-zoner

Var
;
;,- absoluta värdet av utbytesintegraler för dessa stater.

I fig. 4.6. spridningskurvor visas E(k) för s- och p-zoner, konstruktion med hjälp av ekvationerna (4.31) och (4.32).

För s-tillstånd E s kl k=0 tar minimivärdet
. När k ökar, minskar det coska Och
växer och når sitt maximala värde
på
.

Fig.4.6. Missbruk E(k) i representationen av de givna zonerna

Ändrar på samma sätt E s (k) när det ändras k från 0 innan - π/a. Bredden på den tillåtna s-zonen sträcker sig från E s min innan E s Max, är jämställd

För p-tillstånd
ligger vid
, A
vid k=0. P-zonens bredd

bestäms fortfarande av värdet på utbytesintegralen A r. Som regel gäller att ju högre atomnivån är, desto mer överlappar vågfunktionerna för elektronerna på denna nivå i kristallen, desto större är utbytesintegralen och desto bredare är energibandet som bildas från denna nivå. Från höga atomnivåer bildas därför breda energiband, åtskilda av smala bandgap (se fig. 4.3).

Vågvektorområden k, inom vilken energin E(k) elektron, som en periodisk funktion k, upplever en hel cykel av sin förändring, kallad Brillouin-zoner. För en endimensionell kristall (atomkedja) sträcker sig den första Brillouin-zonen från
innan
och har en omfattning
(Fig. 4.6), två segment från
innan
och från
innan
representerar den andra Brillouin-zonen, etc. Med värderingar
, Var
energin genomgår ett avbrott, vilket leder till bildandet av bandgap med bredd, t.ex.

Alla möjliga energivärden i varje energizon kan erhållas genom att ändra k inom den första Brillouin-zonen, därför beroendet E(k) byggs ofta endast för den första zonen. Alla andra värden E kan föras in i denna zon. Detta sätt att avbilda E(k) kallad diagram över de givna zonerna(Fig. 4.6). En annan metod är möjlig, kallad det utökade zonschemat (Fig. 4.7).

Här finns de olika energizonerna i k-utrymme i olika Brillouin-zoner.

Fig.4.7. Representation av energiband i ett utökat banddiagram

I fig. 4.7 visar också det paraboliska beroendet E(k) för en fri elektron. Nära dispersionskurvans extrema, dvs. nära punkter k=0 Och
(mitten och gränsen till den första Brillouin-zonen),
kan ordnas i rad enligt ka (k räknat från 0 om extremumet är i mitten av Brillouin-zonen, och från
, om extremumet är på gränsen till Brillouin-zonen) och begränsa oss till de två första termerna av expansionen:

Genom att ersätta detta med (4.31) och (4.32) får vi:

Dispersionskurvans minimum E(k) kallas botten av energizonen, max – topp eller tak zoner. Därför kan de erhållna relationerna skrivas om i följande mer allmänna form:

För botten av zonen;

För takområdet.

Således, vid botten och toppen av energibandet, är elektronenergin proportionell mot kvadraten på vågvektorn, beräknad på ovanstående sätt, och mot utbytesintegralen, som bestämmer bredden på bandet. I fig. 4.6 visas parabolerna som motsvarar ekvationerna 4.35 och 4.36 med en streckad linje.

Låt oss betrakta den fysiska naturen hos diskontinuiteter i elektronens energispektrum vid gränserna för Brillouin-zonerna. Låt oss uttrycka k genom elektronvåglängden λ och skriv villkoret för funktionens diskontinuitet E(k):

eller
. (4.37)

Detta är det välkända Wulff-Bragg-tillståndet för en elektronvåg som infaller på ett gitter vinkelrätt mot atomplanen. Följaktligen uppstår diskontinuiteter i energispektrumet för en elektron i en kristall när Bragg-reflektionsvillkoret (4.37) är uppfyllt. Elektroner med denna våglängd genomgår reflektion och kan inte fortplanta sig i kristallen.

För riktiga kristaller är beroendet E(k) i regel mycket mer komplext än det som beskrivs av formel (4.30).

I fig. 4.8. Som ett exempel visas dispersionskurvor som begränsar ledningsbandet (kurva 1) och valensbandet (kurva 2) för kisel.

Ris. 4.8. Dispersionskurvor och banddiagram av kisel

För att underlätta presentationen kommer vi att fortsätta diskussionen med det speciella exemplet på en partikel med massa i närvaro av en skalär potential.Låt oss också anta att när funktionen beror på att vektorn fixerar partikelns position och Schrödinger-ekvationen , oberoende av

tid, kommer att skrivas i formuläret

På språket för teorin om partiella differentialekvationer kallas en ekvation som (36) en egenvärdesekvation. Lösningen på denna ekvation är en egenfunktion som motsvarar egenvärdet E för operatorn H.

Egenvärdesproblemet definieras i verkligheten endast om de "regularitets"-villkor och randvillkor som funktionen måste uppfylla anges, Villkoren som ställs på funktionen måste naturligtvis överensstämma med den allmänna tolkningen av vågfunktionen. Vi återkommer till detta ämne i kap. IV. Vi kräver här att funktionen och dess första ordningens partiella derivator är kontinuerliga och begränsade funktioner i hela utrymmet.

I det här fallet är det möjligt att bevisa giltigheten av följande resultat, som vi accepterar som data, men kommer att kunna verifiera dem med hjälp av många exempel.

a) Om då ekvation (36) har lösningar endast för vissa vissa värden av E, vilket bildar ett diskret spektrum. Egenfunktionen för valfritt egenvärde (eller varje funktion, om det finns flera av dem) försvinner i oändligheten. Mer exakt konvergerar integralen utsträckt till hela konfigurationsutrymmet. Enligt den statistiska tolkningen betyder detta att sannolikheten för att hitta en partikel i oändligheten är noll, partikeln förblir lokaliserad i ett ändligt område av rymden. Partikeln sägs vara i ett bundet tillstånd.

b) Om då ekvation (36) kan ha lösningar för alla positiva värden av E. De säger att positiva energier bildar ett kontinuerligt spektrum. Motsvarande egenfunktioner försvinner inte i oändligheten, deras asymptotiska beteende liknar det för en plan våg. Närmare bestämt tenderar modulen till en ändlig konstant eller oscillerar mellan värden, varav minst en skiljer sig från noll. Partikeln förblir inte lokaliserad i det finita området. Vågfunktioner av denna typ används för att beskriva kollisionsproblem; de säger att vi har att göra med en partikel i obundet tillstånd, eller i stationärt tillstånd spridning.

Således får vi det första fundamentala resultatet: kvantiseringen av energinivåer för bundna tillstånd, dvs en av de mest imponerande experimentella fakta,

orsakade kraschen klassisk teori. Att bestämma de kvantiserade energinivåerna presenteras här som ett problem med att hitta egenvärdena. Att lösa detta problem med högsta möjliga grad av noggrannhet är ett av vågmekanikens centrala problem. För vissa speciellt enkla former Det Hamiltonska problemet kan lösas rigoröst. Detta är just fallet med väteatomen (vi kommer att överväga det i detalj i kapitel XI), när energinivåerna visar sig vara operatörens egenvärden. Det resulterande spektrumet sammanfaller med det som förutspåddes av den gamla kvantteorin ; Vi har redan haft tillfälle att betona det fantastiska sammanträffandet av detta spektrum med experimentella data. I mer svåra situationer olika ungefärliga metoder bör användas. Men i alla fall där det var möjligt att beräkna energispektrumet med en tillräcklig grad av noggrannhet visade sig överensstämmelse med experiment vara så bra som man kunde förvänta sig av en icke-relativistisk teori.

Själva funktionen kan i viss mån utsättas för experimentell verifiering. Egenfunktioner för ett diskret spektrum används i själva verket vid beräkningen av olika observerbara storheter, till exempel sannolikheten för kvantövergångar. När det gäller egenfunktionerna för det kontinuerliga spektrumet är deras asymptotiska form direkt relaterad till de effektiva tvärsnitten som kännetecknar spridningsfenomen, vilket kommer att förtydligas i detalj senare. Inom området icke-relativistisk atomfysik har ännu inte ett enda fall av diskrepans mellan vågmekanikens förutsägelser och experimentella data upptäckts.

proportionell mot T: n ~T. Följaktligen bör den termiska konduktivitetskoefficienten vara omvänt proportionell mot temperaturen, vilket är i kvalitativ överensstämmelse med experimentet. Vid temperaturer under Debye-temperaturen är l praktiskt taget oberoende av T, och värmeledningsförmågan bestäms helt av beroendet av kristallens värmekapacitet på T, C V ~ T 3. Därför, vid låga temperaturer λ ~T 3. Det karakteristiska beroendet av värmeledningsförmåga på temperatur visas i figur 9.

I metaller, förutom gittervärmeledningsförmåga, är det också nödvändigt att ta hänsyn till värmeledningsförmåga på grund av värmeöverföring av fria elektroner. Detta förklarar den höga värmeledningsförmågan hos metaller jämfört med icke-metaller.

3. Elektronisk struktur av kristaller.

3.1.Rörelse av elektroner i ett periodiskt fält. Bandstruktur av energispektrumet för elektroner i en kristall. Bloch funktioner. Dispersionskurvor. Effektiv massa.

I ett fast ämne är avstånden mellan atomerna jämförbara med deras storlekar. Därför överlappar angränsande atomers elektronskal delvis varandra och åtminstone valenselektronerna för varje atom befinner sig i ett ganska starkt fält av angränsande atomer. En exakt beskrivning av alla elektroners rörelse, med hänsyn till Coulomb-interaktionen av elektroner med varandra och med atomkärnor, är en extremt svår uppgift även för en enskild atom. Därför används vanligtvis den självkonsistenta fältmetoden, där problemet reduceras till att beskriva varje enskild elektrons rörelse i det effektiva potentialfält som skapas av atomkärnor och medelfältet för de återstående elektronerna.

Låt oss först betrakta strukturen för energinivåerna för en kristall, baserat på den starka bindningsapproximationen, där det antas att bindningsenergin för en elektron med dess atom avsevärt överstiger rörelseenergi dess rörelse från atom till atom. På stora avstånd mellan atomerna har var och en av dem ett system med smala energinivåer motsvarande relaterade stater elektron med jon. När atomerna kommer närmare minskar bredden och höjden på de potentiella barriärerna mellan dem, och tack vare tunnlingseffekten kan elektroner röra sig från

en atom till en annan, vilket åtföljs av en expansion av energinivåer och deras omvandling till energizoner.(Fig. 10). Detta gäller särskilt för svagt bundna valenselektroner, som lätt kan röra sig genom kristallen från atom till atom, och i viss mån blir lik fria elektroner. Elektroner med djupare energinivåer är var och en mycket starkare bundna till sin egen atom. De bildar smala energiband med stora intervall av förbjudna energier. I fig. Figur 10 visar konventionellt potentiella kurvor och energinivåer för en Na-kristall. Den allmänna karaktären hos elektronenergispektrumet beroende på det interna nukleära avståndet, d, presenteras i figur 11. I ett antal fall breddas de övre nivåerna så mycket att intilliggande energiband överlappar varandra. I fig. 11 detta inträffar när d = d1.

Baserat på Heisenberg–Bohr-osäkerhetsrelationen är bredden på energibandet, ∆ε, relaterad till uppehållstiden τ för en elektron vid en viss gitterplats genom relationen: ∆ε τ > h. På grund av tunneleffekten kan en elektron läcka genom en potentialbarriär. Enligt uppskattningen, vid det interatomära avståndet d ~ 1Aτ ~ 10 -15 s, och därför ∆ε ~ h/τ ~ 10 -19 J ~ 1 eV, dvs. Bandgapet är i storleksordningen en eller flera eV. Om en kristall består av N atomer, så består varje energiband av N undernivåer. En kristall 1 cm3 stor innehåller N~ 1022 atomer. Följaktligen, med en bandbredd på ~ 1 eV, är avståndet mellan undernivåerna ~ 10 -22 eV, vilket är signifikant mindre energi termisk rörelse under normala förhållanden. Detta avstånd är så obetydligt att zonerna i de flesta fall kan anses vara praktiskt taget sammanhängande.

I en idealisk kristall är atomkärnorna belägna vid noderna av kristallgittret och bildar en strikt periodisk struktur. I enlighet med detta beror även den potentiella energin hos elektronen, V(r), periodvis på de rumsliga koordinaterna, d.v.s. har translationell symmetri:

gitter, a i (i = 1,2,3,...) – vektorer för huvudöversättningarna.

Vågfunktioner och energinivåer i ett periodiskt fält (1) bestäms genom att lösa Schrödinger-ekvationen

representerar produkten av ekvationen för en plan vandringsvåg, ei kr, med en periodisk faktor, u k (r) = u k (r + a n), med gitterperioden. Funktioner (3) kallas Bloch-funktioner.

Vid V(r) = 0 har ekvation (2) en lösning i form av en plan våg:

där m är partikelmassan. Energins E beroende av vågtalet visas spridningskurva. Enligt (5), i fallet med en fri elektron, är detta en parabel. I analogi med fri rörelse kallas vektork i ekvation (3) för vågvektorn, аp = h k – kvasi-momentum.

I den svaga kopplingsapproximationen beaktas rörelsen av nästan fria elektroner, som påverkas av det störande fältet för jonkärnornas periodiska potential. Till skillnad från fri rörelse, i ett periodiskt fält har V(r) ekvation (2) inte lösningar för alla värden av E. Områden med tillåtna energier växlar med områden med förbjudna energier. I den svaga kopplingsmodellen förklaras detta av Bragg-reflektionen av elektronvågor i kristallen.

Låt oss överväga denna fråga mer detaljerat. Villkoret för maximal reflektion av elektronvågor i en kristall (Wulff–Bragg-tillstånd) bestäms av formel (17) del I. Med tanke på att G = n g får vi:

Låt oss betrakta ett system av ändliga intervall som inte innehåller värden på k som uppfyller relationen (7):

( - n g /2

Området för förändring av k i tredimensionellt k - rymd, givet av formeln

(8) för alla möjliga riktningar, bestämmer gränserna för den n:e Brillouin-zonen. Inom varje Brillouin-zon (n= 1,2,3,...) är elektronenergin en kontinuerlig funktion av k, och vid zonernas gränser lider den av en diskontinuitet. Om villkor (7) är uppfyllt för incidentens amplitud,

ψ k (r) = uk (r) ei kr

och reflekterade

ψ -k (r) = u - k (r) e -i kr

vågorna blir desamma, u k (r) = u -k (r). Dessa vågor ger två lösningar till Schrödinger-ekvationen:

Denna funktion beskriver ackumuleringen av negativ laddning på positiva joner, där den potentiella energin är lägst. På samma sätt, från formel (9b) får vi:

ρ 2 (r) = |ψ 2 (r)|2 =4 u g/2 2 (r)sin 2 (gr/2)

Denna funktion beskriver en fördelning av elektroner där de är placerade övervägande i områden som motsvarar mitten av avstånden mellan joner. I detta fall kommer den potentiella energin att vara större. Funktionen ψ 2 kommer att motsvara energin E2 > E1.

bandgap av bredd T.ex. Energi E`1 bestämmer den övre gränsen för den första zonen, och energi E2 bestämmer den nedre gränsen för den andra zonen. Det betyder att när elektronvågor utbreder sig i kristaller uppstår energiområden för vilka det inte finns några lösningar på Schrödinger-ekvationen som har en vågnatur.

Eftersom naturen hos energiberoendet av vågvektorn avsevärt påverkar dynamiken hos elektroner i en kristall, är det av intresse att som ett exempel betrakta det enklaste fallet med en linjär kedja av atomer belägna på avstånd a från varandra längs x-axeln. I detta fall g = 2π /a. Figur 12 visar spridningskurvorna för de tre första endimensionella Brillouin-zonerna: (-

π/a< k <π /a), (-2π /a < k < -π /a; π/ a < k < 2π /a), (-3π/ a < k < -2π /a; 2π /a < k < 3π /a). К запрещенным зонам относятся области энергии Е`1 < E < E2 , E`2 <

E< E3 и т.д.

I fig. 12 presenteras utökad zonkrets, där olika energizoner är belägna i VC-rymden i olika Brillouin-zoner. Det är dock alltid möjligt, och ofta bekvämt, att välja en vågvektor så att dess ände ligger innanför den första Brillouin-zonen. Låt oss skriva Bloch-funktionen som:

ligga i den första Brillouin-zonen. Genom att ersätta k med formel (11) får vi:

har formen av en Bloch-funktion med Bloch-multiplikatorn (13). Indexet n anger nu numret på den energizon som den givna funktionen tillhör. Proceduren för att föra en godtycklig vågvektor till den första Brillouin-zonen kallas diagram över de givna zonerna. I detta schema tar vectork värdena -g/2< k < g/2 , но одному и тому же значениюк будут отвечать различные значения энергии, каждое из которых будет соответствовать одной из зон. На рисунке 13 представлена схема приведенных зон для одномерной решетки, соответствующая расширенной зонной схеме на рисунке 12.

Således beror förekomsten av energigap på Bragg-reflektion av de Broglie-elektronvågor från kristallplan. Brytpunkterna bestäms av villkoren för maximal vågreflektion.

Enligt kvantmekanikens lagar betraktas en elektrons translationsrörelse som rörelsen hos ett vågpaket med vågvektorer nära vektorn k. Grupphastigheten för vågpaketet, v , ges av