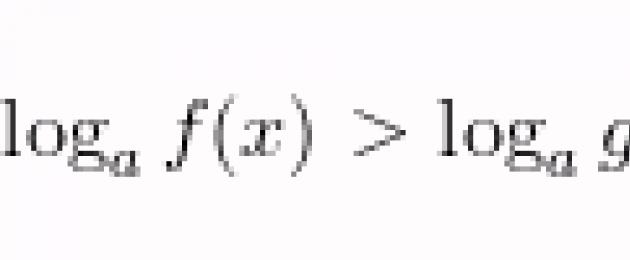LOGARITMISKA OJÄMLIKHETER I ANVÄNDNING
Sechin Mikhail Alexandrovich
Liten vetenskapsakademi för studenter i Republiken Kazakstan "Iskatel"
MBOU "Sovetskaya Secondary School No. 1", 11:e klass, stad. sovjetisk Sovetsky-distriktet
Gunko Lyudmila Dmitrievna, lärare för den kommunala budgetutbildningsinstitutionen "Sovetskaya Secondary School No. 1"
Sovetsky-distriktet
Målet med arbetet: studie av lösningsmekanismen logaritmiska ojämlikheter C3 använder icke-standardiserade metoder, identifierande intressanta fakta logaritm
Studieämne:
3) Lär dig att lösa specifika logaritmiska olikheter C3 med hjälp av icke-standardiserade metoder.
Resultat:
Innehåll
Inledning……………………………………………………………………………………………….4
Kapitel 1. Problemets historia…………………………………………………………………5
Kapitel 2. Insamling av logaritmiska ojämlikheter ………………………… 7
2.1. Ekvivalenta övergångar och den generaliserade metoden för intervall………………… 7
2.2. Rationaliseringsmetod……………………………………………………………… 15
2.3. Icke-standardiserad substitution……………………………………………… ............... 22
2.4. Uppgifter med fällor………………………………………………………………27
Slutsats……………………………………………………………………………………… 30
Litteratur……………………………………………………………………. 31
Introduktion
Jag går i 11:e klass och planerar att gå in på ett universitet där kärnämnet är matematik. Det är därför jag arbetar mycket med problem i del C. I uppgift C3 behöver jag lösa en icke-standardiserad ojämlikhet eller system av ojämlikheter, vanligtvis relaterat till logaritmer. När jag förberedde mig inför provet ställdes jag inför problemet med brist på metoder och tekniker för att lösa logaritmiska ojämlikheter i tentamen som erbjuds i C3. Metoder som studeras i Läroplanen om detta ämne, ge inte en grund för att lösa C3-uppgifter. Matteläraren föreslog att jag skulle arbeta med C3-uppgifter självständigt under hennes ledning. Dessutom var jag intresserad av frågan: möter vi logaritmer i våra liv?
Med detta i åtanke valdes ämnet:
"Logaritmiska ojämlikheter i Unified State Exam"
Målet med arbetet: studie av mekanismen för att lösa C3-problem med icke-standardiserade metoder, identifiera intressanta fakta om logaritmen.
Studieämne:
1) Hitta nödvändig information om icke-standardiserade metoder för att lösa logaritmiska ojämlikheter.
2) Hitta ytterligare information om logaritmer.
3) Lär dig att lösa specifika C3-problem med icke-standardiserade metoder.
Resultat:
Den praktiska betydelsen ligger i utbyggnaden av apparaten för att lösa C3-problem. Detta material kan användas i vissa lektioner, för klubbar och valfria lektioner i matematik.
Projektprodukten kommer att vara samlingen "C3 Logaritmiska olikheter med lösningar."
Kapitel 1. Bakgrund
Under hela 1500-talet ökade antalet ungefärliga beräkningar snabbt, främst inom astronomi. Att förbättra instrument, studera planetrörelser och annat arbete krävde kolossala, ibland många år, beräkningar. Astronomi var i verklig fara att drunkna i ouppfyllda beräkningar. Svårigheter uppstod inom andra områden, till exempel inom försäkringsverksamheten behövdes tabeller med sammansatt ränta för olika räntor. Den största svårigheten var multiplikation och division av flersiffriga tal, särskilt trigonometriska storheter.
Upptäckten av logaritmer baserades på egenskaperna hos progressioner som var välkända i slutet av 1500-talet. På sambandet mellan termerna för den geometriska progressionen q, q2, q3, ... och aritmetisk progression deras indikatorer är 1, 2, 3,... Arkimedes talade i sin "Psalmitis". En annan förutsättning var utvidgningen av gradbegreppet till negativa och fraktionerade exponenter. Många författare har påpekat att multiplikation, division, exponentiering och rotextraktion i geometrisk progression motsvarar i aritmetik - i samma ordning - addition, subtraktion, multiplikation och division.
Här var tanken på logaritmen som en exponent.
I historien om utvecklingen av läran om logaritmer har flera stadier passerat.
Steg 1
Logaritmer uppfanns senast 1594 oberoende av den skotske baronen Napier (1550-1617) och tio år senare av den schweiziske mekanikern Bürgi (1552-1632). Båda ville ge ett nytt bekvämt medel aritmetiska beräkningar, även om de närmade sig denna uppgift annorlunda. Napier uttryckte kinematiskt den logaritmiska funktionen och gick därigenom in i ett nytt funktionsteorifält. Bürgi stannade på grundval av att överväga diskreta progressioner. Definitionen av logaritmen för båda liknar dock inte den moderna. Termen "logaritm" (logaritmus) tillhör Napier. Det uppstod från en kombination av grekiska ord: logos - "relation" och ariqmo - "antal", vilket betydde "antal relationer". Inledningsvis använde Napier en annan term: numeri artificiella - "artificiella tal", i motsats till numeri naturalts - "naturliga tal".
År 1615, i ett samtal med Henry Briggs (1561-1631), en professor i matematik vid Gresh College i London, föreslog Napier att man skulle ta noll som logaritmen för ett och 100 som logaritmen för tio, eller vad som motsvarar samma sak, bara 1. Så här skrevs decimallogaritmer och De första logaritmiska tabellerna ut. Senare kompletterades Briggs tabeller av den holländska bokhandlaren och matematikentusiasten Adrian Flaccus (1600-1667). Napier och Briggs, även om de kom till logaritmer tidigare än alla andra, publicerade sina tabeller senare än de andra - 1620. Tecknen log och Log introducerades 1624 av I. Kepler. Termen "naturlig logaritm" introducerades av Mengoli 1659 och följdes av N. Mercator 1668, och Londonläraren John Speidel publicerade tabeller över naturliga logaritmer av tal från 1 till 1000 under namnet "Nya logaritmer".
De första logaritmiska tabellerna publicerades på ryska 1703. Men i alla logaritmiska tabeller fanns räknefel. De första felfria tabellerna publicerades 1857 i Berlin, bearbetade av den tyske matematikern K. Bremiker (1804-1877).
Steg 2
Ytterligare utveckling av teorin om logaritmer är förknippad med en bredare tillämpning av analytisk geometri och infinitesimalkalkyl. Vid den tiden hade sambandet mellan kvadraturen av en liksidig hyperbel och den naturliga logaritmen fastställts. Teorin om logaritmer från denna period är förknippad med namnen på ett antal matematiker.
Tysk matematiker, astronom och ingenjör Nikolaus Mercator i en uppsats
"Logarithmotechnics" (1668) ger en serie som ger expansionen av ln(x+1) i
potenser av x:
Detta uttryck överensstämmer exakt med hans tankegång, även om han naturligtvis inte använde tecknen d, ..., utan mer krånglig symbolik. Med upptäckten av den logaritmiska serien förändrades tekniken för att beräkna logaritmer: de började bestämmas med hjälp av oändliga serier. I sina föreläsningar "Elementary Mathematics from a Higher Point of View", som hölls 1907-1908, föreslog F. Klein att man skulle använda formeln som startpunkt konstruktion av logaritmteorin.
Steg 3
Definition av en logaritmisk funktion som en invers funktion
exponentiell, logaritm som en exponent för en given bas
formulerades inte omedelbart. Essä av Leonhard Euler (1707-1783)
"An Introduction to the Analysis of Infinitesimals" (1748) tjänade till ytterligare
utveckling av teorin om logaritmiska funktioner. Således,
134 år har gått sedan logaritmer först introducerades
(räknat från 1614), innan matematiker kom till definitionen
begreppet logaritm, som nu ligger till grund för skolkursen.
Kapitel 2. Insamling av logaritmiska olikheter
2.1. Ekvivalenta övergångar och den generaliserade metoden för intervaller.
Motsvarande övergångar
 , om en > 1
, om en > 1
 , om 0 <
а <
1
, om 0 <
а <
1

Generaliserad intervallmetod
Denna metod är den mest universella för att lösa ojämlikheter av nästan alla typer. Lösningsdiagrammet ser ut så här:
1. För ojämlikheten till en form där funktionen på vänster sida är  , och till höger 0.
, och till höger 0.
2. Hitta funktionens domän  .
.
3. Hitta nollorna för funktionen  , det vill säga lösa ekvationen
, det vill säga lösa ekvationen  (och att lösa en ekvation är vanligtvis lättare än att lösa en olikhet).
(och att lösa en ekvation är vanligtvis lättare än att lösa en olikhet).
4. Rita definitionsdomänen och nollor för funktionen på tallinjen.
5. Bestäm tecknen för funktionen  på de erhållna intervallen.
på de erhållna intervallen.
6. Välj intervall där funktionen tar de önskade värdena och skriv ner svaret.
Exempel 1.

Lösning:

Låt oss tillämpa intervallmetoden

var
För dessa värden är alla uttryck under de logaritmiska tecknen positiva.
Svar:
Exempel 2.
![]()
Lösning:
1:a sätt . ADL bestäms av ojämlikhet x> 3. Att ta logaritmer för sådana x i bas 10 får vi
Den sista ojämlikheten skulle kunna lösas genom att tillämpa expansionsregler, d.v.s. jämföra faktorer med noll. Men i det här fallet är det lätt att bestämma intervallen för konstant tecken för funktionen
därför kan intervallmetoden tillämpas.
Fungera f(x) = 2x(x- 3.5)lgǀ x- 3ǀ är kontinuerlig vid x> 3 och försvinner punktvis x 1 = 0, x 2 = 3,5, x 3 = 2, x 4 = 4. Således bestämmer vi intervallen för konstant tecken för funktionen f(x):

Svar:
2:a metoden . Låt oss direkt tillämpa idéerna om intervallmetoden på den ursprungliga ojämlikheten.
För att göra detta, kom ihåg att uttrycken a b- a c och ( a - 1)(b- 1) har ett tecken. Då vår ojämlikhet kl x> 3 motsvarar ojämlikhet
![]()
eller
Den sista ojämlikheten löses med intervallmetoden
Svar:
Exempel 3.
![]()
Lösning:



Låt oss tillämpa intervallmetoden

Svar:

Exempel 4.

Lösning:
Sedan 2 x 2 - 3x+ 3 > 0 på riktigt x, Den där


För att lösa den andra olikheten använder vi intervallmetoden

I den första ojämlikheten gör vi ersättningen

då kommer vi till ojämlikheten 2y 2 - y - 1 < 0 и, применив метод интервалов, получаем, что решениями будут те y, som uppfyller ojämlikheten -0,5< y < 1.

![]()
Varifrån, eftersom
vi får ojämlikheten

som genomförs när x, för vilken 2 x 2 - 3x - 5 < 0. Вновь применим метод интервалов

Nu, med hänsyn till lösningen på den andra ojämlikheten i systemet, får vi äntligen

Svar:
Exempel 5.
![]()
Lösning:
Ojämlikhet är likvärdig med en samling system


eller

Låt oss använda intervallmetoden eller

Svar:

Exempel 6.
![]()
Lösning:
Ojämlikhet är lika med system

Låta
Sedan y > 0,
![]()
och den första ojämlikheten
systemet tar formen
![]()
eller vecklar ut sig
kvadratisk trinomialfaktor,
![]()
Att tillämpa intervallmetoden på den sista ojämlikheten,

vi ser att dess lösningar uppfyller villkoret y> 0 kommer att vara allt y > 4.
Således är den ursprungliga ojämlikheten ekvivalent med systemet:

Så, lösningarna på ojämlikheten är alla
![]()
2.2. Rationaliseringsmetod.
Tidigare löstes inte ojämlikheten med rationaliseringsmetoden, det var inte känt. Detta är den "nya moderna" effektiv metod lösningar på exponentiella och logaritmiska ojämlikheter" (citat från boken av S.I. Kolesnikova)
Och även om läraren kände honom fanns det en rädsla – kände han honom? Expert på Unified State Exam, varför ger de det inte i skolan? Det fanns situationer när läraren sa till eleven: "Var fick du det? Sätt dig ner - 2."
Nu främjas metoden överallt. Och för experter finns det riktlinjer, associerad med den här metoden, och i de "Mest kompletta utgåvorna typiska alternativ..." Lösning C3 använder denna metod.
UNDERBAR METOD!
"Magiskt bord"

I andra källor
Om a >1 och b >1, sedan log a b >0 och (a -1)(b -1)>0;
Om a >1 och 0 om 0<a<1 и b
>1, logga sedan a b<0 и (a
-1)(b
-1)<0;
om 0<a<1 и 0O och (a-1)(b-1)>0. Resonemanget som förs är enkelt, men förenklar lösningen av logaritmiska ojämlikheter avsevärt. Exempel 4.
log x (x 2 -3)<0
Lösning:
Exempel 5.
log 2 x (2x 2 -4x +6)≤log 2 x (x 2 +x ) Lösning: Exempel 6.
För att lösa denna olikhet skriver vi istället för nämnaren (x-1-1)(x-1), och istället för täljaren skriver vi produkten (x-1)(x-3-9 + x). Exempel 7.
Exempel 8.
2.3. Icke-standardiserad substitution. Exempel 1.
Exempel 2.
Exempel 3.
Exempel 4.
Exempel 5.
Exempel 6.
Exempel 7.
log 4 (3 x -1) log 0,25 Låt oss ersätta y=3 x -1; då kommer denna ojämlikhet att ta formen Logg 4 log 0,25 Därför att log 0,25 Låt oss ersätta t =log 4 y och erhålla olikheten t 2 -2t +≥0, vars lösning är intervallen - För att hitta värdena för y har vi alltså en uppsättning av två enkla olikheter Därför är den ursprungliga ojämlikheten ekvivalent med mängden av två exponentiella olikheter, Lösningen på den första olikheten i denna uppsättning är intervallet 0<х≤1, решением второго – промежуток 2≤х<+ Exempel 8.
Lösning:
Ojämlikhet är lika med system Lösningen på den andra ojämlikheten som definierar ODZ kommer att vara uppsättningen av dessa x,
för vilka x > 0.
För att lösa den första ojämlikheten gör vi substitutionen Då får vi ojämlikheten eller Uppsättningen av lösningar på den sista ojämlikheten hittas av metoden intervaller: -1< t < 2. Откуда, возвращаясь к переменной x, vi får eller Många av dem x, som tillfredsställer den sista ojämlikheten tillhör ODZ ( x> 0), är därför en lösning på systemet, och därav den ursprungliga ojämlikheten. Svar: 2.4. Uppgifter med fällor. Exempel 1.
Lösning. Olikhetens ODZ är alla x som uppfyller villkoret 0 Exempel 2.
log 2 (2 x +1-x 2)>log 2 (2 x-1 +1-x)+1.





 Svar. (0; 0,5)U.
Svar. (0; 0,5)U.


 Svar :
(3;6)
Svar :
(3;6)









 .
.
 = -log 4
= -log 4  = -(log 4 y -log 4 16)=2-log 4 y , sedan skriver vi om den sista olikheten som 2log 4 y -log 4 2 y ≤.
= -(log 4 y -log 4 16)=2-log 4 y , sedan skriver vi om den sista olikheten som 2log 4 y -log 4 2 y ≤.
 Lösningen på denna uppsättning är intervallen 0<у≤2 и 8≤у<+
Lösningen på denna uppsättning är intervallen 0<у≤2 и 8≤у<+ .
.
 det vill säga aggregat
det vill säga aggregat 
 . Således är den ursprungliga olikheten uppfylld för alla värden på x från intervallen 0<х≤1 и 2≤х<+
. Således är den ursprungliga olikheten uppfylld för alla värden på x från intervallen 0<х≤1 и 2≤х<+ .
.


![]()
![]()
![]()


 .
.
 . Därför är alla x från intervallet 0
. Därför är alla x från intervallet 0
Slutsats
Det var inte lätt att hitta specifika metoder för att lösa C3-problem från ett stort överflöd av olika utbildningskällor. Under arbetets gång kunde jag studera icke-standardiserade metoder för att lösa komplexa logaritmiska ojämlikheter. Dessa är: ekvivalenta övergångar och den generaliserade metoden för intervaller, metoden för rationalisering , icke-standardiserad substitution , uppgifter med fällor på ODZ. Dessa metoder ingår inte i skolans läroplan.
Med olika metoder löste jag 27 ojämlikheter som föreslagits på Unified State Exam i del C, nämligen C3. Dessa ojämlikheter med lösningar genom metoder utgjorde grunden för samlingen "C3 Logaritmiska olikheter med lösningar", som blev en projektprodukt av min verksamhet. Hypotesen jag ställde upp i början av projektet bekräftades: C3-problem kan effektivt lösas om du känner till dessa metoder.
Dessutom upptäckte jag intressanta fakta om logaritmer. Det var intressant för mig att göra det här. Mina projektprodukter kommer att vara användbara för både elever och lärare.
Slutsatser:
Därmed har projektmålet uppnåtts och problemet är löst. Och jag fick den mest kompletta och varierande erfarenheten av projektverksamhet i alla skeden av arbetet. Under arbetet med projektet var min huvudsakliga utvecklingsinverkan på mental kompetens, aktiviteter relaterade till logiska mentala operationer, utveckling av kreativ kompetens, personligt initiativ, ansvar, uthållighet och aktivitet.
En garanti för framgång när man skapar ett forskningsprojekt för Jag fick: betydande skolerfarenhet, förmågan att få information från olika källor, kontrollera dess tillförlitlighet och rangordna den efter betydelse.
Förutom direkta ämneskunskaper i matematik utökade jag mina praktiska färdigheter inom datavetenskap, fick nya kunskaper och erfarenheter inom psykologiområdet, knöt kontakter med klasskamrater och lärde mig att samarbeta med vuxna. Under projektverksamheten utvecklades organisatoriska, intellektuella och kommunikativa allmänpedagogiska färdigheter.
Litteratur
1. Koryanov A. G., Prokofiev A. A. System av ojämlikheter med en variabel (standarduppgifter C3).
2. Malkova A. G. Förberedelse för Unified State Examen i matematik.
3. Samarova S. S. Lösa logaritmiska ojämlikheter.
4. Matematik. Samling av träningsverk redigerade av A.L. Semenov och I.V. Jasjtjenko. -M.: MTsNMO, 2009. - 72 s.-
Artikeln ägnas åt analysen av uppgifter 15 från profilen Unified State Examination i matematik för 2017. I denna uppgift uppmanas skolbarn att lösa ojämlikheter, oftast logaritmiska. Även om det kan finnas vägledande sådana. Den här artikeln ger en analys av exempel på logaritmiska olikheter, inklusive de som innehåller en variabel i basen av logaritmen. Alla exempel är hämtade från den öppna banken av Unified State Examination-uppgifter i matematik (profil), så sådana ojämlikheter kommer sannolikt att uppstå i provet som uppgift 15. Perfekt för dem som vill lära sig att lösa uppgift 15 från den andra delen av profilen Unified State Exam på kort tid i matematik för att få fler betyg på provet.
Analys av uppgifter 15 från profilen Unified State Examination i matematik
| Exempel 1. Lös ojämlikheten: |
I uppgifter 15 i Unified State Exam i matematik (profil) stöter man ofta på logaritmiska ojämlikheter. Att lösa logaritmiska olikheter börjar med att bestämma intervallet för acceptabla värden. I det här fallet finns det ingen variabel i basen för båda logaritmerna, det finns bara talet 11, vilket avsevärt förenklar problemet. Så den enda begränsningen vi har här är att båda uttrycken under logaritmtecknet är positiva:
Title="Renderd av QuickLaTeX.com">!}
Den första ojämlikheten i systemet är den kvadratiska ojämlikheten. För att lösa det skulle vi verkligen vilja faktorisera vänster sida. Jag tror att du vet att någon kvadratisk trinomial av formen ![]() faktoriseras enligt följande:
faktoriseras enligt följande:
var och är rötterna till ekvationen. I det här fallet är koefficienten 1 (detta är den numeriska koefficienten framför ). Koefficienten är också lika med 1, och koefficienten är blindtermen, den är lika med -20. Rötterna till ett trinomial bestäms lättast med hjälp av Vietas sats. Ekvationen vi har gett betyder att summan av rötterna blir lika med koefficienten med motsatt tecken, det vill säga -1, och produkten av dessa rötter kommer att vara lika med koefficienten, det vill säga -20. Det är lätt att gissa att rötterna blir -5 och 4.
Nu kan den vänstra sidan av ojämlikheten faktoriseras: title="Rendered by QuickLaTeX.com" height="20" width="163" style="vertical-align: -5px;"> Решаем это неравенство. График соответствующей функции — это парабола, ветви которой направлены вверх. Эта парабола пересекает ось !} X vid punkterna -5 och 4. Detta betyder att den nödvändiga lösningen på ojämlikheten är intervallet . För de som inte förstår vad som står här kan ni se detaljerna i videon, från och med nu. Där hittar du också en detaljerad förklaring av hur den andra ojämlikheten i systemet löses. Det håller på att lösas. Dessutom är svaret exakt detsamma som för den första ojämlikheten i systemet. Det vill säga uppsättningen som skrivits ovan är regionen med tillåtna värden för ojämlikheten.
Så, med hänsyn till faktorisering, tar den ursprungliga ojämlikheten formen:
Med hjälp av formeln lägger vi till 11 till styrkan av uttrycket under tecknet för den första logaritmen, och flyttar den andra logaritmen till vänster sida av olikheten och ändrar dess tecken till motsatt:
Efter reduktion får vi:
Den sista ojämlikheten, på grund av ökningen av funktionen, är likvärdig med ojämlikheten ![]() , vars lösning är intervallet
, vars lösning är intervallet ![]() . Allt som återstår är att skära den med regionen med acceptabla värden för ojämlikheten, och detta kommer att vara svaret på hela uppgiften.
. Allt som återstår är att skära den med regionen med acceptabla värden för ojämlikheten, och detta kommer att vara svaret på hela uppgiften.
Så det nödvändiga svaret på uppgiften ser ut så här:
Vi har tagit itu med denna uppgift, nu går vi vidare till nästa exempel på uppgift 15 i Unified State Exam i matematik (profil).
| Exempel 2. Lös ojämlikheten:
|
Vi börjar lösningen med att bestämma intervallet av acceptabla värden för denna ojämlikhet. I basen av varje logaritm måste det finnas ett positivt tal som inte är lika med 1. Alla uttryck under logaritmens tecken måste vara positiva. Bråkets nämnare får inte innehålla noll. Det sista villkoret motsvarar det faktum att eftersom bara annars båda logaritmerna i nämnaren försvinner. Alla dessa villkor bestämmer intervallet av tillåtna värden för denna ojämlikhet, givet av följande system av ojämlikheter:
Title="Renderd av QuickLaTeX.com">!}
Inom intervallet av acceptabla värden kan vi använda logaritmkonverteringsformler för att förenkla den vänstra sidan av ojämlikheten. Använder formel ![]() vi blir av med nämnaren:
vi blir av med nämnaren:
Nu har vi bara logaritmer med en bas. Detta är redan mer bekvämt. Därefter använder vi formeln, och även formeln för att få uttrycket värt ära till följande form:
I beräkningarna använde vi det som låg inom intervallet för acceptabla värden. Med hjälp av substitutionen kommer vi fram till uttrycket:
Låt oss använda ytterligare en ersättare: . Som ett resultat kommer vi fram till följande resultat:
Så vi återgår gradvis till de ursprungliga variablerna. Först till variabeln:
Avsnitt: Matematik
Ofta, när man löser logaritmiska olikheter, finns det problem med en variabel logaritmbas. Alltså en ojämlikhet i formen
är en vanlig skolojämlikhet. Som regel, för att lösa det, används en övergång till en likvärdig uppsättning system:
Nackdelen med denna metod är behovet av att lösa sju ojämlikheter, utan att räkna två system och en population. Redan med dessa kvadratiska funktioner kan det ta mycket tid att lösa populationen.
Det är möjligt att föreslå ett alternativt, mindre tidskrävande sätt att lösa denna standardojämlikhet. För att göra detta tar vi hänsyn till följande teorem.
Sats 1. Låt det finnas en kontinuerligt ökande funktion på en mängd X. Då kommer på denna mängd tecknet för funktionens inkrement att sammanfalla med tecknet för argumentets ökning, d.v.s. , Var ![]() .
.
Obs: om en kontinuerligt minskande funktion på ett set X, då .
Låt oss återgå till ojämlikheten. Låt oss gå vidare till decimallogaritmen (du kan gå vidare till vilken som helst med en konstant bas större än en).
Nu kan du använda satsen och lägga märke till ökningen av funktioner i täljaren ![]() och i nämnaren. Så det är sant
och i nämnaren. Så det är sant
Som ett resultat är antalet beräkningar som leder till svaret ungefär halverat, vilket inte bara sparar tid, utan också gör att du potentiellt kan göra färre aritmetiska och slarviga fel.
Exempel 1.
Jämför vi med (1) finner vi ![]() ,
, ![]() , .
, .
Om vi går vidare till (2) kommer vi att ha:
Exempel 2.
Jämför vi med (1) finner vi , , .
Om vi går vidare till (2) kommer vi att ha:
Exempel 3.
Eftersom den vänstra sidan av ojämlikheten är en ökande funktion som och ![]() , då blir svaret många.
, då blir svaret många.
De många exemplen där Tema 1 kan tillämpas kan enkelt utökas genom att ta hänsyn till Tema 2.
Släpp på uppsättningen X funktionerna , , , definieras, och på denna uppsättning sammanfaller tecknen och, d.v.s. , då blir det rättvist.
Exempel 4.
Exempel 5.
Med standardmetoden löses exemplet enligt följande schema: produkten är mindre än noll när faktorerna har olika tecken. De där. en uppsättning av två system av ojämlikheter betraktas, där, som indikeras i början, varje ojämlikhet delas upp i ytterligare sju.
Om vi tar hänsyn till sats 2, kan var och en av faktorerna, med hänsyn till (2), ersättas av en annan funktion som har samma tecken i detta exempel O.D.Z.
Metoden att ersätta ökningen av en funktion med en ökning av argument, med hänsyn till sats 2, visar sig vara mycket bekväm när man löser typiska C3 Unified State Examination-problem.
Exempel 6.
Exempel 7.
. Låt oss beteckna . Vi får
. Observera att ersättningen innebär: . Återgå till ekvationen, vi får
.
Exempel 8.
I de satser vi använder finns inga begränsningar för klasser av funktioner. I den här artikeln, som ett exempel, användes satserna för att lösa logaritmiska olikheter. Följande flera exempel kommer att visa löftet om metoden för att lösa andra typer av ojämlikheter.
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0