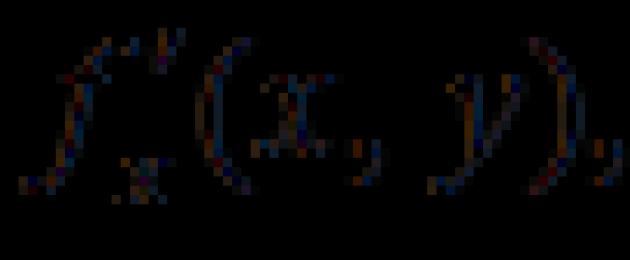Betrakta en funktion av två variabler:
Eftersom variablerna $x$ och $y$ är oberoende, för en sådan funktion kan vi introducera begreppet partiell derivata:
Den partiella derivatan av funktionen $f$ i punkten $M=\left(((x)_(0));((y)_(0)) \right)$ med avseende på variabeln $x$ är gränsen
\[(((f)")_(x))=\underset(\Delta x\till 0)(\mathop(\lim ))\,\frac(f\left(((x)_(0)) )+\Delta x;((y)_(0)) \right))(\Delta x)\]
På liknande sätt kan du definiera den partiella derivatan med avseende på variabeln $y$ :
\[(((f)")_(y))=\underset(\Delta y\to 0)(\mathop(\lim ))\,\frac(f\left(((x)_(0)) );((y)_(0))+\Delta y \right))(\Delta y)\]
Med andra ord, för att hitta den partiella derivatan av en funktion av flera variabler, måste du fixa alla andra variabler utom den önskade, och sedan hitta den vanliga derivatan med avseende på denna önskade variabel.
Detta leder till huvudtekniken för att beräkna sådana derivator: anta helt enkelt att alla variabler utom denna är en konstant, och differentiera sedan funktionen som du skulle differentiera en "vanlig" - med en variabel. Till exempel:
$\begin(align)& ((\left(((x)^(2))+10xy \right))_(x))^(\prime )=((\left(((x)^(2) )) \right))^(\prime ))_(x)+10y\cdot ((\left(x \right))^(\prime ))_(x)=2x+10y, \\& (( \left(((x)^(2))+10xy \right))_(y))^(\prime )=((\left(((x)^(2)) \right))^(\ prime ))_(y)+10x\cdot ((\left(y \right))^(\prime ))_(y)=0+10x=10x. \\\end(align)$
Uppenbarligen ger partiella derivator med avseende på olika variabler olika svar - detta är normalt. Det är mycket viktigare att förstå varför, säg, i det första fallet tog vi lugnt bort $10y$ från derivattecknet, och i det andra fallet nollställde vi helt den första termen. Allt detta händer på grund av det faktum att alla bokstäver, förutom variabeln genom vilken differentiering utförs, betraktas som konstanter: de kan tas ut, "brännas" etc.
Vad är "partiell derivata"?
Idag kommer vi att prata om funktioner för flera variabler och partiella derivator av dem. För det första, vad är en funktion av flera variabler? Hittills är vi vana vid att betrakta en funktion som $y\left(x \right)$ eller $t\left(x \right)$, eller vilken variabel som helst och en enda funktion av den. Nu kommer vi att ha en funktion, men flera variabler. När $y$ och $x$ ändras kommer värdet på funktionen att ändras. Till exempel, om $x$ fördubblas kommer värdet på funktionen att ändras, och om $x$ ändras, men $y$ inte ändras, kommer värdet på funktionen att ändras på samma sätt.
Naturligtvis kan en funktion av flera variabler, precis som en funktion av en variabel, differentieras. Men eftersom det finns flera variabler är det möjligt att differentiera efter olika variabler. I det här fallet uppstår specifika regler som inte fanns vid differentiering av en variabel.
Först och främst, när vi beräknar derivatan av en funktion från valfri variabel, måste vi ange för vilken variabel vi beräknar derivatan - detta kallas partiell derivata. Vi har till exempel en funktion av två variabler, och vi kan beräkna den både i $x$ och i $y$ - två partiella derivator för var och en av variablerna.
För det andra, så snart vi har fixat en av variablerna och börjar beräkna den partiella derivatan med avseende på den, betraktas alla andra som ingår i denna funktion som konstanter. Till exempel, i $z\left(xy \right)$, om vi betraktar den partiella derivatan med avseende på $x$, då varhelst vi stöter på $y$, betraktar vi den som en konstant och behandlar den som sådan. I synnerhet när vi beräknar derivatan av en produkt kan vi ta $y$ från parentes (vi har en konstant), och när vi beräknar derivatan av en summa, om vi någonstans får en derivata av ett uttryck som innehåller $y$ och inte innehåller $x$, då kommer derivatan av detta uttryck att vara lika med "noll" som derivatan av en konstant.
Vid första anblicken kan det verka som att jag pratar om något komplicerat, och många elever är först förvirrade. Det finns dock inget övernaturligt i partiella derivator, och nu kommer vi att se detta med exemplet med specifika problem.
Problem med radikaler och polynom
Uppgift nr 1
För att inte slösa tid, låt oss börja från början med allvarliga exempel.
Till att börja med, låt mig påminna dig om denna formel:
Detta är standardtabellvärdet som vi känner till från standardkursen.
I det här fallet beräknas derivatan $z$ enligt följande:
\[(((z)")_(x))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(x)=\frac( 1)(2\sqrt(\frac(y)(x)))((\left(\frac(y)(x) \right))^(\prime ))_(x)\]
Låt oss göra det igen, eftersom roten inte är $x$, utan något annat uttryck, i det här fallet $\frac(y)(x)$, så använder vi först standardtabellvärdet, och sedan, eftersom roten är inte $x $, och ett annat uttryck, måste vi multiplicera vår derivata med en annan av detta uttryck med avseende på samma variabel. Låt oss först beräkna följande:
\[((\left(\frac(y)(x) \right))^(\prime ))_(x)=\frac(((((y)"))_(x))\cdot x-y \cdot ((((x)"))_(x)))(((x)^(2)))=\frac(0\cdot x-y\cdot 1)(((x)^(2)) )=-\frac(y)(((x)^(2)))\]
Vi återgår till vårt uttryck och skriver:
\[(((z)")_(x))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(x)=\frac( 1)(2\sqrt(\frac(y)(x)))((\left(\frac(y)(x) \right))^(\prime ))_(x)=\frac(1) (2\sqrt(\frac(y)(x)))\cdot \left(-\frac(y)(((x)^(2))) \höger)\]
I grund och botten är det allt. Det är dock fel att lämna det i denna form: en sådan konstruktion är obekväm att använda för ytterligare beräkningar, så låt oss omvandla det lite:
\[\frac(1)(2\sqrt(\frac(y)(x)))\cdot \left(-\frac(y)((x)^(2))) \right)=\frac (1)(2)\cdot \sqrt(\frac(x)(y))\cdot \frac(y)(((x)^(2))))=\]
\[=-\frac(1)(2)\cdot \sqrt(\frac(x)(y))\cdot \sqrt(\frac(((y)^(2)))((x)^ (4))))=-\frac(1)(2)\sqrt(\frac(x\cdot ((y)^(2)))(y\cdot ((x)^(4)))) =-\frac(1)(2)\sqrt(\frac(y)(((x)^(3))))\]
Svaret har hittats. Låt oss nu ta itu med $y$:
\[(((z)")_(y))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot ((\left(\frac(y)(x) \right))^(\prime ))_(y)\]
Låt oss skriva ner det separat:
\[((\left(\frac(y)(x) \right))^(\prime ))_(y)=\frac(((((y)"))_(y))\cdot x-y \cdot ((((x)"))_(y)))(((x)^(2)))=\frac(1\cdot x-y\cdot 0)(((x)^(2)) )=\frac(1)(x)\]
Nu skriver vi ner:
\[(((z)")_(y))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot ((\left(\frac(y)(x) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot \frac(1)(x)=\]
\[=\frac(1)(2)\cdot \sqrt(\frac(x)(y))\cdot \sqrt(\frac(1)(((x)^(2))))=\frac (1)(2)\sqrt(\frac(x)(y\cdot ((x)^(2))))=\frac(1)(2\sqrt(xy))\]
Gjort.
Problem nr 2
Detta exempel är både enklare och mer komplext än det föregående. Det är mer komplicerat eftersom det finns fler åtgärder, men det är enklare eftersom det inte finns någon rot och dessutom är funktionen symmetrisk med avseende på $x$ och $y$, dvs. om vi byter $x$ och $y$ kommer formeln inte att ändras. Denna anmärkning kommer ytterligare att förenkla vår beräkning av den partiella derivatan, dvs. det räcker med att räkna en av dem, och i den andra byter du bara $x$ och $y$.
Låt oss komma till saken:
\[(((z)")_(x))=((\vänster(\frac(xy)(((x)^(2))+((y)^(2))+1) \höger ))^(\prime ))_(x)=\frac(((\left(xy \right))^(\prime ))_(x)\left(((x)^(2))+( (y)^(2))+1 \höger)-xy((\vänster(((x)^(2))+((y)^(2))+1 \höger))^(\prime ) )_(x))(((\vänster(((x)^(2))+((y)^(2))+1 \höger))^(2)))\]
Låt oss räkna:
\[((\left(xy \right))^(\prime ))_(x)=y\cdot ((\left(x \right))^(\prime ))=y\cdot 1=y\ ]
Men många elever förstår inte denna notation, så låt oss skriva det så här:
\[((\left(xy \right))^(\prime ))_(x)=((\left(x \right))^(\prime ))_(x)\cdot y+x\cdot ((\left(y \right))^(\prime ))_(x)=1\cdot y+x\cdot 0=y\]
Således är vi återigen övertygade om universaliteten hos den partiella derivativa algoritmen: oavsett hur vi beräknar dem, om alla regler tillämpas korrekt, kommer svaret att vara detsamma.
Låt oss nu titta på ytterligare en partiell derivata från vår stora formel:
\[((\vänster(((x)^(2))+((y)^(2))+1 \höger))^(\prime ))_(x)=((\vänster((( x)^(2)) \höger))^(\prime ))_(x)+((\left(((y)^(2)) \right))^(\prime ))_(x) +(((1)")_(x))=2x+0+0\]
Låt oss ersätta de resulterande uttrycken i vår formel och få:
\[\frac(((\left(xy \right))^(\prime ))_(x)\left(((x)^(2))+(y)^(2))+1 \ höger)-xy((\vänster(((x)^(2))+((y)^(2))+1 \höger))^(\prime ))_(x))(((\vänster) (((x)^(2))+((y)^(2))+1 \höger))^(2)))=\]
\[=\frac(y\cdot \left(((x)^(2))+((y)^(2))+1 \höger)-xy\cdot 2x)(((\left((( x)^(2))+((y)^(2))+1 \höger))^(2)))=\]
\[=\frac(y\vänster(((x)^(2))+((y)^(2))+1-2((x)^(2)) \höger))(((\ vänster(((x)^(2))+((y)^(2))+1 \höger))^(2)))=\frac(y\left(((y)^(2)) -((x)^(2))+1 \höger))(((\vänster(((x)^(2))+((y)^(2))+1 \höger))^(2) )))\]
Baserat på $x$ räknat. Och för att beräkna $y$ från samma uttryck, låt oss inte utföra samma sekvens av åtgärder, utan dra fördel av symmetrin i vårt ursprungliga uttryck - vi ersätter helt enkelt alla $y$ i vårt ursprungliga uttryck med $x$ och vice versa:
\[(((z)")_(y))=\frac(x\left(((x)^(2))-((y)^(2))+1 \höger))((( \left(((x)^(2))+((y)^(2))+1 \höger))^(2)))\]
På grund av symmetri beräknade vi detta uttryck mycket snabbare.
Nyanser av lösningen
För partiella derivator fungerar alla standardformler som vi använder för vanliga, nämligen derivatan av kvoten. Samtidigt uppstår dock specifika egenskaper: om vi betraktar den partiella derivatan av $x$, då när vi får den från $x$, betraktar vi den som en konstant, och därför kommer dess derivata att vara lika med "noll". .
Liksom i fallet med vanliga derivat kan partialen (detsamma) beräknas av flera olika sätt. Till exempel kan samma konstruktion som vi just beräknade skrivas om enligt följande:
\[((\left(\frac(y)(x) \right))^(\prime ))_(x)=y\cdot ((\left(\frac(1)(x) \right)) ^(\prime ))_(x)=-y\frac(1)(((x)^(2))))\]
\[((\left(xy \right))^(\prime ))_(x)=y\cdot (((x)")_(x))=y\cdot 1=y\]
Samtidigt kan man å andra sidan använda formeln från derivatsumman. Som vi vet är det lika med summan av derivator. Låt oss till exempel skriva följande:
\[((\vänster(((x)^(2))+((y)^(2))+1 \höger))^(\prime ))_(x)=2x+0+0=2x \]
Nu när vi vet allt detta, låt oss försöka arbeta med mer seriösa uttryck, eftersom reella partiella derivator inte är begränsade till bara polynom och rötter: det finns också trigonometri och logaritmer och exponentialfunktionen. Låt oss nu göra det här.
Problem med trigonometriska funktioner och logaritmer
Uppgift nr 1
Låt oss skriva följande standardformler:
\[((\left(\sqrt(x) \right))^(\prime ))_(x)=\frac(1)(2\sqrt(x))\]
\[((\left(\cos x \right))^(\prime ))_(x)=-\sin x\]
Beväpnade med denna kunskap, låt oss försöka lösa:
\[(((z)")_(x))=((\left(\sqrt(x)\cdot \cos \frac(x)(y) \right))^(\prime ))_(x )=((\left(\sqrt(x) \right))^(\prime ))_(x)\cdot \cos \frac(x)(y)+\sqrt(x)\cdot ((\left (\cos \frac(x)(y) \right))^(\prime ))_(x)=\]
Låt oss skriva ut en variabel separat:
\[((\left(\cos \frac(x)(y) \right))^(\prime ))_(x)=-\sin \frac(x)(y)\cdot ((\left( \frac(x)(y)\höger))^(\prime ))_(x)=-\frac(1)(y)\cdot \sin \frac(x)(y)\]
Låt oss återgå till vår design:
\[=\frac(1)(2\sqrt(x))\cdot \cos \frac(x)(y)+\sqrt(x)\cdot \left(-\frac(1)(y)\cdot \sin \frac(x)(y) \right)=\frac(1)(2\sqrt(x))\cdot \cos \frac(x)(y)-\frac(\sqrt(x))( y)\cdot \sin \frac(x)(y)\]
Det var allt, vi hittade det för $x$, låt oss nu göra beräkningarna för $y$:
\[(((z)")_(y))=((\left(\sqrt(x)\cdot \cos \frac(x)(y) \right))^(\prime ))_(y )=((\left(\sqrt(x) \right))^(\prime ))_(y)\cdot \cos \frac(x)(y)+\sqrt(x)\cdot ((\left (\cos \frac(x)(y) \right))^(\prime ))_(y)=\]
Återigen, låt oss beräkna ett uttryck:
\[((\left(\cos \frac(x)(y) \right))^(\prime ))_(y)=-\sin \frac(x)(y)\cdot ((\left( \frac(x)(y) \right))^(\prime ))_(y)=-\sin \frac(x)(y)\cdot x\cdot \left(-\frac(1)(( (y)^(2))) \höger)\]
Vi återgår till det ursprungliga uttrycket och fortsätter lösningen:
\[=0\cdot \cos \frac(x)(y)+\sqrt(x)\cdot \frac(x)(((y)^(2)))\sin \frac(x)(y) =\frac(x\sqrt(x))(((y)^(2)))\cdot \sin \frac(x)(y)\]
Gjort.
Problem nr 2
Låt oss skriva ner formeln vi behöver:
\[((\vänster(\ln x \höger))^(\prime ))_(x)=\frac(1)(x)\]
Låt oss nu räkna med $x$:
\[(((z)")_(x))=((\left(\ln \left(x+\ln y \right) \right))^(\prime ))_(x)=\frac( 1)(x+\ln y).((\vänster(x+\ln y \höger))^(\prime ))_(x)=\]
\[=\frac(1)(x+\ln y)\cdot \left(1+0 \right)=\frac(1)(x+\ln y)\]
Hittade för $x$. Vi räknar med $y$:
\[(((z)")_(y))=((\left(\ln \left(x+\ln y \right) \right))^(\prime ))_(y)=\frac( 1)(x+\ln y).((\left(x+\ln y \right))^(\prime ))_(y)=\]
\[=\frac(1)(x+\ln y)\left(0+\frac(1)(y) \right)=\frac(1)(y\left(x+\ln y \right))\ ]
Problemet är löst.
Nyanser av lösningen
Så, oavsett vilken funktion vi tar partialderivatan av, så förblir reglerna desamma, oavsett om vi arbetar med trigonometri, med rötter eller med logaritmer.
De klassiska reglerna för att arbeta med standardderivata förblir oförändrade, nämligen derivatan av en summa och en differens, en kvot och en komplex funktion.
Den sista formeln finns oftast när man löser problem med partiella derivator. Vi träffar dem nästan överallt. Det har aldrig funnits en enda uppgift där vi inte stött på den. Men oavsett vilken formel vi använder har vi fortfarande ett krav till, nämligen det speciella med att arbeta med partiella derivator. När vi fixar en variabel är alla andra konstanter. I synnerhet, om vi betraktar den partiella derivatan av uttrycket $\cos \frac(x)(y)$ med avseende på $y$, då är $y$ variabeln, och $x$ förblir konstant överallt. Samma sak fungerar tvärtom. Det kan tas ut ur derivattecknet, och derivatan av konstanten i sig kommer att vara lika med "noll".
Allt detta leder till att partiella derivator av samma uttryck, men med avseende på olika variabler, kan se helt olika ut. Låt oss till exempel titta på följande uttryck:
\[((\vänster(x+\ln y \höger))^(\prime ))_(x)=1+0=1\]
\[((\left(x+\ln y \right))^(\prime ))_(y)=0+\frac(1)(y)=\frac(1)(y)\]
Problem med exponentialfunktioner och logaritmer
Uppgift nr 1
Till att börja med, låt oss skriva följande formel:
\[((\vänster(((e)^(x)) \höger))^(\prime ))_(x)=((e)^(x))\]
Att känna till detta faktum, såväl som derivatan av en komplex funktion, låt oss försöka beräkna. Jag ska nu lösa det på två olika sätt. Den första och mest uppenbara är derivatan av produkten:
\[(((z)")_(x))=((\vänster(((e)^(x))\cdot ((e)^(\frac(x)(y))) \höger) )^(\prime ))_(x)=((\left(((e)^(x)) \right))^(\prime ))_(x)\cdot ((e)^(\frac (x)(y)))+((e)^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ) )_(x)=\]
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot ((\left(\frac(x)(y) \right))^(\prime ))_(x)=\]
Låt oss lösa följande uttryck separat:
\[((\left(\frac(x)(y) \right))^(\prime ))_(x)=\frac(((((x)"))_(x))\cdot y-x .((((y)"))_(x)))((y)^(2)))=\frac(1\cdot y-x\cdot 0)((y)^(2))) =\frac(y)((y)^(2)))=\frac(1)(y)\]
Vi återgår till vår ursprungliga design och fortsätter med lösningen:
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot \frac(1)(y)=((e)^(x))\cdot ((e)^(\frac(x)(y)))\left(1) +\frac(1)(y)\right)\]
Allt, $x$ beräknas.
Men som jag lovade kommer vi nu att försöka beräkna samma partiella derivata på ett annat sätt. För att göra detta, notera följande:
\[((e)^(x))\cdot ((e)^(\frac(x)(y)))=((e)^(x+\frac(x)(y))))\]
Låt oss skriva det så här:
\[((\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right))^(\prime ))_(x)=( (\vänster(((e)^(x+\frac(x)(y))) \höger))^(\prime ))_(x)=((e)^(x+\frac(x)(y )))\cdot ((\vänster(x+\frac(x)(y) \right))^(\prime ))_(x)=((e)^(x+\frac(x)(y)) )\cdot \left(1+\frac(1)(y) \right)\]
Som ett resultat fick vi exakt samma svar, men antalet beräkningar visade sig vara mindre. För att göra detta var det tillräckligt att notera att indikatorerna kan läggas till när du utför produkten.
Låt oss nu räkna med $y$:
\[(((z)")_(y))=((\vänster(((e)^(x))\cdot ((e)^(\frac(x)(y))) \höger) )^(\prime ))_(y)=((\left(((e)^(x)) \right))^(\prime ))_(y)\cdot ((e)^(\frac (x)(y)))+((e)^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ) )_(y)=\]
\[=0\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac(x)(y))) \cdot ((\left(\frac(x)(y) \right))^(\prime ))_(y)=\]
Låt oss lösa ett uttryck separat:
\[((\left(\frac(x)(y) \right))^(\prime ))_(y)=\frac(((((x)"))_(y))\cdot y-x \cdot ((((y)"))_(y)))((y)^(2)))=\frac(0-x\cdot 1)((y)^(2))) =-\frac(1)((y)^(2)))=-\frac(x)(((y)^(2))))\]
Låt oss fortsätta att lösa vår ursprungliga konstruktion:
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))\cdot \left(-\frac(x)(((y)^(2) )) \right)=-\frac(x)(((y)^(2)))\cdot ((e)^(x))\cdot ((e)^(\frac(x)(y) ))\]
Naturligtvis skulle samma derivata kunna beräknas på det andra sättet, och svaret skulle vara detsamma.
Problem nr 2
Låt oss räkna med $x$:
\[(((z)")_(x))=((\vänster(x \höger))_(x))\cdot \ln \vänster(((x)^(2))+y \höger )+x\cdot ((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\]
Låt oss beräkna ett uttryck separat:
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\frac(1)(((x) )^(2))+y)\cdot ((\vänster(((x)^(2))+y \höger))^(\prime ))_(x)=\frac(2x)((( x)^(2))+y)\]
Låt oss fortsätta att lösa den ursprungliga konstruktionen: $$
Detta är svaret.
Det återstår att hitta analogt med $y$:
\[(((z)")_(y))=((\vänster(x \höger))^(\prime ))_(y).\ln \left(((x)^(2)) +y \right)+x\cdot ((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(y)=\]
Som alltid beräknar vi ett uttryck separat:
\[((\left(((x)^(2))+y \right))^(\prime ))_(y)=((\left(((x)^(2)) \right) )^(\prime ))_(y)+(((y)")_(y))=0+1=1\]
Vi fortsätter att lösa den grundläggande designen:
Allt har beräknats. Som du kan se, beroende på vilken variabel som tas för differentiering, är svaren helt olika.
Nyanser av lösningen
Här är ett slående exempel på hur derivatan av samma funktion kan beräknas på två olika sätt. Titta här:
\[(((z)")_(x))=\vänster(((e)^(x))\cdot ((e)^(\frac(x)(y))) \höger)=( (\left(((e)^(x)) \right))^(\prime ))_(x)\cdot ((e)^(\frac(x)(y)))+((e) ^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ))_(x)=\]
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot \frac(1)(y)=((e)^(x))\cdot ((e)^(^(\frac(x)(y))))\ vänster(1+\frac(1)(y) \höger)\]
\[(((z)")_(x))=((\vänster(((e)^(x)).((e)^(\frac(x)(y))) \höger)) ^(\prime ))_(x)=((\left(((e)^(x+\frac(x)(y))) \höger))^(\prime ))_(x)=(( e)^(x+\frac(x)(y))).((\vänster(x+\frac(x)(y) \höger))^(\prime ))_(x)=\]
\[=((e)^(x))\cdot ((e)^(^(\frac(x)(y))))\left(1+\frac(1)(y) \right)\ ]
När man väljer olika vägar, mängden beräkningar kan vara olika, men svaret, om allt görs korrekt, kommer att vara detsamma. Detta gäller både klassiska och partiella derivator. Samtidigt påminner jag ännu en gång: beroende på vilken variabel derivatan tas, d.v.s. differentiering kan svaret bli helt annorlunda. Se:
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\frac(1)(((x) )^(2))+y)\cdot ((\vänster(((x)^(2))+y \höger))^(\prime ))_(x)=\frac(1)((( x)^(2))+y)\cdot 2x\]
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(y)=\frac(1)(((x) )^(2))+y)\cdot ((\vänster(((x)^(2))+y \höger))^(\prime ))_(y)=\frac(1)((( x)^(2))+y)\cdot 1\]
Sammanfattningsvis, för att konsolidera allt detta material, låt oss försöka beräkna ytterligare två exempel.
Problem med trigonometriska funktioner och funktioner med tre variabler
Uppgift nr 1
Låt oss skriva ner följande formler:
\[((\vänster(((a)^(x)) \höger))^(\prime ))=((a)^(x))\cdot \ln a\]
\[((\vänster(((e)^(x)) \höger))^(\prime ))=((e)^(x))\]
Låt oss nu lösa vårt uttryck:
\[(((z)")_(x))=((\vänster(((3)^(x\sin y)) \höger))^(\prime ))_(x)=((3) )^(x.\sin y))\cdot \ln 3\cdot ((\left(x\cdot \sin y \right))^(\prime ))_(x)=\]
Låt oss separat beräkna följande konstruktion:
\[((\left(x\cdot \sin y \right))^(\prime ))_(x)=(((x)")_(x))\cdot \sin y+x((\ vänster(\sin y \right))^(\prime ))_(x)=1\cdot \sin y+x\cdot 0=\sin y\]
Vi fortsätter att lösa det ursprungliga uttrycket:
\[=((3)^(x\sin y))\cdot \ln 3\cdot \sin y\]
Detta är det slutliga svaret för den privata variabeln på $x$. Låt oss nu räkna med $y$:
\[(((z)")_(y))=((\vänster(((3)^(x\sin y)) \höger))^(\prime ))_(y)=((3) )^(x\sin y))\cdot \ln 3\cdot ((\left(x\sin y \right))^(\prime ))_(y)=\]
Låt oss lösa ett uttryck separat:
\[((\left(x\cdot \sin y \right))^(\prime ))_(y)=(((x)")_(y))\cdot \sin y+x((\ vänster(\sin y \right))^(\prime ))_(y)=0\cdot \sin y+x\cdot \cos y=x\cdot \cos y\]
Låt oss lösa vår konstruktion till slutet:
\[=((3)^(x\cdot \sin y))\cdot \ln 3\cdot x\cos y\]
Problem nr 2
Vid första anblicken kan det här exemplet verka ganska komplicerat eftersom det finns tre variabler. Detta är faktiskt en av de mest enkla uppgifter i dagens videohandledning.
Hitta av $x$:
\[(((t)")_(x))=((\vänster(x((e)^(y))+y((e)^(z)) \höger))^(\prime ) )_(x)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(x)+((\left(y\cdot ((e)) ^(z)) \höger))^(\prime ))_(x)=\]
\[=((\left(x \right))^(\prime ))_(x)\cdot ((e)^(y))+x\cdot ((\left(((e)^(y) )) \right))^(\prime ))_(x)=1\cdot ((e)^(y))+x\cdot o=((e)^(y))\]
Låt oss nu ta itu med $y$:
\[(((t)")_(y))=((\vänster(x\cdot ((e)^(y))+y\cdot ((e)^(z)) \höger))^ (\prime ))_(y)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(y)+((\left(y\cdot) ((e)^(z)) \höger))^(\prime ))_(y)=\]
\[=x\cdot ((\vänster(((e)^(y)) \höger))^(\prime ))_(y)+((e)^(z))\cdot ((\vänster) (y \höger))^(\prime ))_(y)=x\cdot ((e)^(y))+((e)^(z))\]
Vi har hittat svaret.
Nu återstår bara att hitta med $z$:
\[(((t)")_(z))=((\vänster(x\cdot ((e)^(y)))+((y)^(z)) \höger))^(\prime ))_(z)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(z)+((\left(y\cdot ((e) )^(z)) \right))^(\prime ))_(z)=0+y\cdot ((\left((((e)^(z)) \right))^(\prime )) _(z)=y\cdot ((e)^(z))\]
Vi har beräknat den tredje derivatan, som kompletterar lösningen på det andra problemet.
Nyanser av lösningen
Som du kan se är det inget komplicerat i dessa två exempel. Det enda vi är övertygade om är att derivatan av en komplex funktion används ofta och beroende på vilken partiell derivata vi beräknar får vi olika svar.
I den sista uppgiften fick vi ta itu med en funktion av tre variabler samtidigt. Det är inget fel med det här, men i slutet var vi övertygade om att de alla är väsentligt olika varandra.
Nyckelord
De sista tipsen från dagens videohandledning är följande:
- Partiella derivator betraktas på samma sätt som vanliga, men för att beräkna den partiella derivatan med avseende på en variabel måste alla andra variabler som ingår i denna funktion, vi tar dem som konstanter.
- När vi arbetar med partiella derivator använder vi samma standardformler som med vanliga derivator: summa, differens, derivata av produkten och kvoten, och, naturligtvis, derivata av en komplex funktion.
Naturligtvis räcker det inte att bara titta på den här videolektionen för att helt förstå det här ämnet, så just nu på min hemsida finns det en uppsättning problem för den här videon specifikt tillägnad dagens ämne - gå in, ladda ner, lös dessa problem och kolla svaret . Och efter det inga problem med partiella derivator vare sig i tentor eller in självständigt arbete du kommer inte ha. Naturligtvis är detta inte den sista lektionen i högre matematik, så besök vår hemsida, lägg till VKontakte, prenumerera på YouTube, gilla och stanna hos oss!
Låt en funktion av två variabler ges. Låt oss ge argumentet en ökning och lämna argumentet oförändrat. Då kommer funktionen att få ett inkrement, som kallas ett partiellt inkrement av variabel och betecknas:
På liknande sätt, genom att fixa argumentet och ge ett inkrement till argumentet, får vi en partiell ökning av funktionen med variabel:
Kvantiteten kallas den totala ökningen av funktionen vid en punkt.
Definition 4. Den partiella derivatan av en funktion av två variabler med avseende på en av dessa variabler är gränsen för förhållandet mellan motsvarande partiella ökning av funktionen och ökningen av en given variabel när den senare tenderar till noll (om denna gräns existerar). Den partiella derivatan betecknas enligt följande: eller, eller.
Därför har vi per definition:
Partiella derivator av funktioner beräknas enligt samma regler och formler som en funktion av en variabel, med hänsyn till att när man differentierar med avseende på en variabel, anses den vara konstant, och när man differentierar med avseende på en variabel, anses den vara konstant .
Exempel 3. Hitta partiella derivator av funktioner:
Lösning. a) För att hitta, betraktar vi det som ett konstant värde och differentierar det som en funktion av en variabel:
På liknande sätt, om vi antar ett konstant värde, finner vi:

Definition 5. Den totala differentialen för en funktion är summan av produkterna av de partiella derivatorna av denna funktion med inkrementen av motsvarande oberoende variabler, d.v.s.
Med tanke på att differentialerna för de oberoende variablerna sammanfaller med deras inkrement, dvs. , formeln för den totala differentialen kan skrivas som

Exempel 4. Hitta full differential funktioner.

Lösning. Eftersom vi använder den totala differentialformeln

Partiella derivator av högre ordning
Partiella derivator kallas första ordningens partiella derivator eller första partiella derivator.
Definition 6. Andra ordningens partiella derivator av en funktion är partiella derivator av första ordningens partiella derivator.
Det finns fyra andra ordningens partiella derivator. De är betecknade enligt följande:




Partiella derivator av 3:e, 4:e och högre ordningen definieras på liknande sätt. Till exempel, för en funktion har vi:


Partiella derivator av sekund eller mer hög orderövertagna olika variabler kallas blandade partiella derivator. För en funktion är dessa derivator. Observera att i fallet när de blandade derivaten är kontinuerliga, så gäller likheten.
Exempel 5. Hitta andra ordningens partiella derivator av en funktion
Lösning. Den första ordningens partiella derivator för denna funktion finns i exempel 3:
Genom att differentiera med avseende på variablerna x och y får vi
Låt oss sammanfatta hur att hitta partiella derivator skiljer sig från att hitta "vanliga" derivator av en funktion av en variabel:
1) När vi hittar den partiella derivatan, Den där variabel anses vara en konstant.
2) När vi hittar den partiella derivatan, Den där variabel anses vara en konstant.
3) Reglerna och tabellen över derivator av elementära funktioner är giltiga och tillämpliga för alla variabler ( , eller någon annan) genom vilken differentiering utförs.
Steg två. Vi hittar andra ordningens partiella derivator. Det finns fyra av dem.
Beteckningar:
Eller – andraderivatan med avseende på "x"
Eller – andraderivatan med avseende på "Y"
Eller - blandad derivata "av x igrek"
Eller - blandad derivata "av igrek x"
Det är inget komplicerat med begreppet andraderivatan. Tala på ett enkelt språk, den andra derivatan är derivatan av den första derivatan.
För tydlighetens skull kommer jag att skriva om de redan hittade första ordningens partiella derivator:
![]()
Låt oss först hitta blandade derivat:
Som du kan se är allt enkelt: vi tar den partiella derivatan och differentierar den igen, men i det här fallet - den här gången enligt "Y".
Likaså:
För praktiska exempel, när alla partiella derivator är kontinuerliga, gäller följande likhet:
Genom andra ordningens blandade derivator är det alltså mycket bekvämt att kontrollera om vi har hittat första ordningens partiella derivator korrekt.
Hitta andraderivatan med avseende på "x".
Inga uppfinningar, låt oss ta det ![]() och särskilj det med "x" igen:
och särskilj det med "x" igen:
Likaså:
Det bör noteras att när du hittar måste du visa ökad uppmärksamhet, eftersom det inte finns några underbara jämlikheter att kontrollera.
Exempel 2
Hitta första och andra ordningens partiella derivator av funktionen
Detta är ett exempel för dig att lösa på egen hand (svar i slutet av lektionen).
Med viss erfarenhet kommer partiella derivator från exempel nr 1 och 2 att lösas muntligt av dig.
Låt oss gå vidare till mer komplexa exempel.
Exempel 3
Kolla det . Skriv ner första ordningens totala skillnad.
Lösning: Hitta första ordningens partiella derivator:

Var uppmärksam på underskriften: , bredvid "X" är det inte förbjudet att skriva inom parentes att det är en konstant. Den här anteckningen kan vara mycket användbar för nybörjare för att göra det lättare att navigera i lösningen.
Fler kommentarer:
(1) Vi tar alla konstanter utanför derivatans tecken. I det här fallet, och , och därför anses deras produkt vara ett konstant antal.
(2) Glöm inte hur man korrekt differentierar rötter.

(1) Vi tar bort alla konstanter från derivatans tecken; i detta fall är konstanten .
(2) Under primtal har vi produkten av två funktioner kvar, därför måste vi använda regeln för att differentiera produkten ![]() .
.
(3) Glöm inte att detta är en komplex funktion (om än den enklaste av komplexa). Vi använder motsvarande regel: ![]() .
.
Nu hittar vi blandade derivator av andra ordningen:


Det betyder att alla beräkningar utfördes korrekt.
Låt oss skriva ner den totala skillnaden. Inom ramen för den aktuella uppgiften är det meningslöst att säga vad den totala differentialen för en funktion av två variabler är. Det är viktigt att just denna skillnad mycket ofta behöver skrivas ner i praktiska problem.
Den totala differentialen av första ordningen för en funktion av två variabler har formen:
I detta fall:
Det vill säga, du behöver bara ersätta de redan hittade första ordningens partiella derivator i formeln. I denna och liknande situationer är det bäst att skriva differentialtecken i täljare:
Exempel 4
Hitta första ordningens partiella derivator av en funktion ![]() . Kolla det . Skriv ner första ordningens totala skillnad.
. Kolla det . Skriv ner första ordningens totala skillnad.
Detta är ett exempel för dig att lösa på egen hand. Den fullständiga lösningen och exemplet på problemet finns i slutet av lektionen.
Låt oss titta på en serie exempel som involverar komplexa funktioner.
Exempel 5
Hitta första ordningens partiella derivator av funktionen.
(1) Vi tillämpar regeln om differentiering av komplexa funktioner ![]() . Från klass Derivat av en komplex funktion en mycket viktig punkt bör komma ihåg: när vi förvandlar en sinus (extern funktion) till en cosinus med hjälp av tabellen, då har vi en inbäddning (intern funktion) ändras inte.
. Från klass Derivat av en komplex funktion en mycket viktig punkt bör komma ihåg: när vi förvandlar en sinus (extern funktion) till en cosinus med hjälp av tabellen, då har vi en inbäddning (intern funktion) ändras inte.
(2) Här använder vi rötters egenskap: , vi tar konstanten ur derivatans tecken, och vi presenterar roten i den form som är nödvändig för differentiering.
Likaså: 
Låt oss skriva ner första ordningens fullständiga differential:
Exempel 6
Hitta första ordningens partiella derivator av en funktion ![]() .
.
Skriv ner den totala skillnaden.
Detta är ett exempel för dig att lösa på egen hand (svar i slutet av lektionen). Jag kommer inte att ge dig en komplett lösning eftersom det är ganska enkelt.
Ganska ofta tillämpas alla ovanstående regler i kombination.
Exempel 7
Hitta första ordningens partiella derivator av en funktion ![]() .
.

(1) Vi använder regeln om differentiering av summan.
(2) Den första termen i detta fall anses vara en konstant, eftersom det inte finns något i uttrycket som beror på "x" - bara "y".
(Du vet, det är alltid trevligt när en bråkdel kan omvandlas till noll).
För den andra termen tillämpar vi produktdifferentieringsregeln. Förresten, ingenting hade förändrats i algoritmen om en funktion hade getts istället - det är viktigt att vi här har produkt av två funktioner, var och en av dem beror på "x", så du måste använda produktdifferentieringsregeln. För den tredje termen tillämpar vi regeln om differentiering av en komplex funktion.
Varje partiell derivata (av x och genom att y) av en funktion av två variabler är den vanliga derivatan av en funktion av en variabel för ett fast värde av den andra variabeln:
(Var y= konst),
(Var x= konst).
Därför beräknas partiella derivat med hjälp av formler och regler för beräkning av derivator av funktioner av en variabel, samtidigt som den andra variabelns konstant beaktas.
Om du inte behöver en analys av exempel och den minsta teori som krävs för detta, utan bara behöver en lösning på ditt problem, gå till online partiell derivatberäknare .
Om det är svårt att koncentrera sig för att hålla reda på var konstanten är i funktionen, så kan du i exemplets utkast till lösning istället för en variabel med ett fast värde ersätta vilket tal som helst - då kan du snabbt beräkna den partiella derivatan som den vanliga derivatan av en funktion av en variabel. Du behöver bara komma ihåg att returnera konstanten (en variabel med ett fast värde) till sin plats när du avslutar den slutliga designen.
Egenskapen hos partiella derivator som beskrivs ovan följer av definitionen av en partiell derivata, som kan förekomma i tentamensfrågor. Därför, för att bekanta dig med definitionen nedan, kan du öppna den teoretiska referensen.
Begreppet kontinuitet i funktion z= f(x, y) vid en punkt definieras på liknande sätt som detta koncept för en funktion av en variabel.
Fungera z = f(x, y) kallas kontinuerlig vid en punkt if
Skillnaden (2) kallas det totala ökningen av funktionen z(det erhålls som ett resultat av ökningar av båda argumenten).
Låt funktionen ges z= f(x, y) och period
Om funktionen ändras z inträffar när endast ett av argumenten ändras, t.ex. x, med ett fast värde för ett annat argument y, då kommer funktionen att få en ökning
kallas partiell funktionsökning f(x, y) Förbi x.
Överväger en funktionsändring z beroende på att endast ett av argumenten ändras, ändrar vi effektivt till en funktion av en variabel.
Om det finns en ändlig gräns
då kallas det för den partiella derivatan av funktionen f(x, y) genom argument x och indikeras av en av symbolerna
![]()
![]() (4)
(4)
Den partiella ökningen bestäms på liknande sätt z Förbi y:
och partiell derivat f(x, y) Förbi y:
![]() (6)
(6)
Exempel 1.
Lösning. Vi hittar den partiella derivatan med avseende på variabeln "x":
![]() (y fast);
(y fast);
Vi hittar den partiella derivatan med avseende på variabeln "y":
(x fast).
Som du kan se spelar det ingen roll i vilken utsträckning variabeln är fixerad: i det här fallet är det helt enkelt ett visst tal som är en faktor (som i fallet med den vanliga derivatan) till variabeln som vi hittar den partiella derivatan med . Om den fasta variabeln inte multipliceras med variabeln med vilken vi hittar partialderivatan, så försvinner denna ensamma konstant, oavsett i vilken utsträckning, som i fallet med den vanliga derivatan.
Exempel 2. Givet en funktion
Hitta partiella derivator
(med X) och (med Y) och beräkna deras värden vid punkten A (1; 2).
Lösning. Vid fast y derivatan av den första termen hittas som derivatan av potensfunktionen ( tabell över derivatfunktioner för en variabel):
![]() .
.
Vid fast x derivatan av den första termen återfinns som derivatan exponentiell funktion, och den andra – som en derivata av en konstant:
Låt oss nu beräkna värdena för dessa partiella derivator vid punkten A (1; 2):

Du kan kontrollera lösningen på partiella derivatproblem på online partiell derivatberäknare .
Exempel 3. Hitta partiella derivator av en funktion
Lösning. I ett steg finner vi
![]()
(y x, som om argumentet för sinus var 5 x: på samma sätt visas 5 före funktionstecknet);
![]()
(xär fast och är i detta fall en multiplikator vid y).
Du kan kontrollera lösningen på partiella derivatproblem på online partiell derivatberäknare .
De partiella derivatorna av en funktion av tre eller flera variabler definieras på liknande sätt.
Om varje uppsättning värden ( x; y; ...; t) oberoende variabler från uppsättningen D motsvarar ett specifikt värde u från många E, Den där u kallas en funktion av variabler x, y, ..., t och beteckna u= f(x, y, ..., t).
För funktioner av tre eller fler variabler finns ingen geometrisk tolkning.
Partiella derivator av en funktion av flera variabler bestäms och beräknas också under antagandet att endast en av de oberoende variablerna ändras, medan de andra är fasta.
Exempel 4. Hitta partiella derivator av en funktion
![]() .
.
Lösning. y Och z fast:
x Och z fast:
x Och y fast:
Hitta partiella derivator själv och titta sedan på lösningarna
Exempel 5.
Exempel 6. Hitta partiella derivator av en funktion.
Partialderivatan av en funktion av flera variabler har samma mekanisk betydelse är detsamma som derivatan av en funktion av en variabel, är förändringshastigheten för funktionen i förhållande till en förändring i ett av argumenten.
Exempel 8. Kvantitativt värde av flöde P passagerare järnvägar kan uttryckas med en funktion
Var P– antal passagerare, N– antal invånare i korrespondentpunkter, R– avstånd mellan punkter.
Partiell derivata av en funktion P Förbi R, likvärdig
visar att minskningen av passagerarflödet är omvänt proportionell mot kvadraten på avståndet mellan motsvarande punkter med samma antal invånare i poäng.
Partiell derivata P Förbi N, likvärdig
visar att ökningen av passagerarflödet är proportionell mot det dubbla antalet invånare avräkningar på samma avstånd mellan punkterna.
Du kan kontrollera lösningen på partiella derivatproblem på online partiell derivatberäknare .
Full differential
Produkten av en partiell derivata och ökningen av motsvarande oberoende variabel kallas en partiell differential. Partiella skillnader betecknas enligt följande:
![]()
Summan av partiella differentialer för alla oberoende variabler ger den totala differentialen. För en funktion av två oberoende variabler uttrycks den totala differentialen av likheten
![]() (7)
(7)
Exempel 9. Hitta den fullständiga differentialen för en funktion
Lösning. Resultatet av att använda formel (7):
![]()
En funktion som har en total differential vid varje punkt i en viss domän sägs vara differentierbar i den domänen.
Hitta den totala skillnaden själv och titta sedan på lösningen
Precis som i fallet med en funktion av en variabel, innebär differentierbarheten av en funktion i en viss domän dess kontinuitet i denna domän, men inte vice versa.
Låt oss formulera utan bevis tillräckligt skick funktionens differentierbarhet.
Sats. Om funktionen z= f(x, y) har kontinuerliga partiella derivator
i en given region är den differentierbar i denna region och dess differential uttrycks med formel (7).
Det kan visas att precis som i fallet med en funktion av en variabel är funktionens differential den huvudsakliga linjära delen av funktionens inkrement, så är den totala differentialen i fallet med en funktion av flera variabler. den huvudsakliga, linjära delen av inkrementen av oberoende några av variablerna full ökning av funktionen.
För en funktion av två variabler har den totala ökningen av funktionen formen
 (8)
(8)
där α och β är oändligt små vid och .
Partiella derivator av högre ordning
Partiella derivator och funktioner f(x, y) själva är några funktioner av samma variabler och kan i sin tur ha derivator med avseende på olika variabler, som kallas partiella derivator av högre ordning.
Begreppet en funktion av många variabler
Låt det finnas n-variabler och varje x 1, x 2 ... x n från en viss uppsättning av x tilldelas en definition. nummer Z, då ges funktionen Z = f (x 1, x 2 ... x n) för många variabler på mängden x.
X – område för funktionsdefinition
x 1, x 2 ... x n – oberoende variabel (argument)
Z – funktion Exempel: Z=P x 2 1 *x 2 (cylindervolym)
Betrakta Z=f(x;y) – funktionen av 2 variabler (x 1, x 2 ersatt av x,y). Resultaten överförs analogt till andra funktioner av många variabler. Området för att bestämma funktionen av 2 variabler är hela sladden (oh) eller en del av den. Antalet värden för funktionen av 2 variabler är en yta i det tredimensionella rummet.
Tekniker för att konstruera grafer: - Betrakta ytans tvärsnitt i kvadrater || koordinatrutor.
Exempel: x = x 0, zn. kvadrat X || 0уz y = y 0 0хz Typ av funktion: Z=f(x 0 ,y); Z=f(x,y 0)
Till exempel: Z=x2 +y2 -2y
Z= x 2 +(y-1) 2 -1 x=0 Z=(y-1) 2 -1 y=1 Z= x 2 -1 Z=0 x 2 +(y-1) 2 -1
Parabol surround(center(0,1)
Gränser och kontinuitet för funktioner för två variabler
Låt Z=f(x;y) ges, då är A gränsen för funktionen i t.(x 0 ,y 0), om för någon godtyckligt liten mängd. nummer E>0 är ett positivt tal b>0, som för alla x, y uppfyller |x-x 0 |<б; |y-y 0 |<б выполняется нерав-во |f(x,y)-A| Z=f(x;y) är kontinuerlig i en t. (x 0 , y 0) om: - den är definierad i denna t.; - har en final gräns vid x, tenderar till x 0 och y till y 0; - denna gräns = värde fungerar i t. (x 0 ,y 0), dvs. limf(x;y)=f(x 0 ,y 0) Om funktionen är kontinuerlig i varje t. mn-va X, då är den kontinuerlig i detta område Differentialfunktion, dess geombetydelse. Tillämpning av differential i ungefärliga värden. dy=f’(x)∆x – differentialfunktion dy=dx, dvs. dy=f ’(x)dx om y=x Ur en geologisk synvinkel är differentialen för en funktion ökningen av ordinatan för tangenten ritad till grafen för funktionen vid punkten med abskissan x 0 Dif-l används vid beräkning av ca. funktionsvärden enligt formeln: f(x 0 +∆x)~f(x 0)+f’(x 0)∆x Ju närmare ∆x är x, desto mer exakt blir resultatet Partiella derivator av första och andra ordningen Första ordningens derivata (som kallas partiell) A. Låt x, y vara inkrementen av de oberoende variablerna x och y någon gång från regionen X. Då kallas värdet lika med z = f(x+ x, y+ y) = f(x,y) totalen inkrement i punkten x 0, y 0. Om vi fixar variabeln x och ger inkrementet y till variabeln y, så får vi zу = f(x,y,+ y) – f(x,y) Den partiella derivatan av variabeln y bestäms på liknande sätt, dvs. Den partiella derivatan av en funktion av 2 variabler hittas med samma regler som för funktioner av en variabel. Skillnaden är att när man differentierar en funktion med avseende på variabeln x, betraktas y som const, och när man differentierar med avseende på y, x, betraktas det som const. Isolerade konst är kopplade till en funktion med hjälp av addition/subtraktion. Bundna konst är kopplade till en funktion genom multiplikation/divisionsoperationer. Derivata av isolerad const = 0 1.4.Komplett differentialfunktion av 2 variabler och dess tillämpningar
Låt z = f(x,y), då tz = 2:a ordningens partiell derivata För kontinuerliga funktioner av 2 variabler sammanfaller de blandade partiella derivatorna av 2:a ordningen. Tillämpningen av partiella derivator för bestämning av partiella derivator av max- och min-funktioner kallas extrema. A. Punkter kallas max eller min z = f(x,y) om det finns några segment så att för alla x och y från detta område f(x,y) T. Om en extremumpunkt för en funktion av 2 variabler ges, så är värdet av partiella derivator vid denna punkt lika med 0, d.v.s. , Punkterna där första ordningens partiella derivator kallas stationära eller kritiska. Därför, för att hitta extremumpunkterna för en funktion av 2 variabler, används tillräckliga extremumvillkor. Låt funktionen z = f(x,y) vara två gånger differentierbar, och en stationär punkt, 1) och maxA<0, minA>0. 1.4.(*)Full differential. Geometrisk betydelse av differential. Tillämpning av differential i ungefärliga beräkningar
A. Låt funktionen y = f(x) definieras i ett visst område vid punkterna. En funktion f(x) sägs vara differentierbar vid en punkt om dess inkrement vid denna punkt är Där A är ett konstant värde oberoende av , vid en fast punkt x, och är oändligt vid . En relativt linjär funktion A kallas differentialen för funktionen f(x) i en punkt och betecknas df() eller dy. Således kan uttryck (1) skrivas som Funktionens differential i uttryck (1) har formen dy = A. Liksom alla linjära funktioner är den definierad för vilket värde som helst För att underlätta att skriva differentialen betecknas inkrementet med dx och kallas differentialen för den oberoende variabeln x. Därför skrivs differentialen som dy = Adx. Om funktionen f(x) är differentierbar vid varje punkt i ett visst intervall, är dess differential en funktion av två variabler - punkten x och variabeln dx: T. För att funktionen y = g(x) ska vara differentierbar någon gång är det nödvändigt och tillräckligt att den har en derivata vid denna punkt, och (*)Bevis. Nödvändighet. Låt funktionen f(x) vara differentierbar vid punkten, dvs. Därför finns derivatan f’() och är lika med A. Därför dy = f’()dx Lämplighet. Låt det finnas en derivata f’(), dvs. = f'(). Då är kurvan y = f(x) ett tangentsegment. För att beräkna värdet av en funktion vid en punkt x, ta en punkt i någon granne av den, så att det inte är svårt att hitta f() och f’()/![]() - kallas fullt inkrement
- kallas fullt inkrement![]()
![]()
![]()
![]()
![]()
![]() , där den presenteras i formen (1)
, där den presenteras i formen (1)![]() ().
().![]() medan ökningen av funktionen endast måste beaktas för de för vilka + hör till definitionsdomänen för funktionen f(x).
medan ökningen av funktionen endast måste beaktas för de för vilka + hör till definitionsdomänen för funktionen f(x).![]() . Sedan
. Sedan![]()