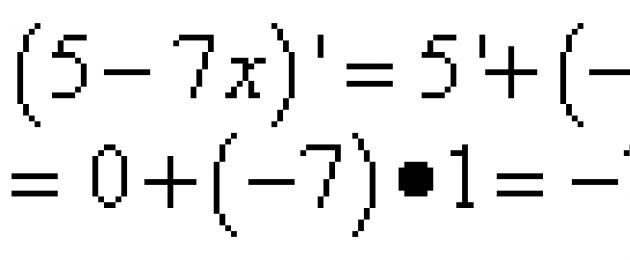Derivatan av funktionen y är roten till x. Hitta derivatan: algoritm och exempel på lösningar

Operationen att hitta en derivata kallas differentiering.

Som ett resultat av att lösa problem med att hitta derivator av de enklaste (och inte särskilt enkla) funktionerna genom att definiera derivatan som gränsen för förhållandet mellan ökningen och ökningen av argumentet, dök en tabell med derivator och exakt definierade regler för differentiering upp . Isaac Newton (1643-1727) och Gottfried Wilhelm Leibniz (1646-1716) var de första som arbetade med att hitta derivator.

Därför, i vår tid, för att hitta derivatan av någon funktion, är det inte nödvändigt att beräkna den ovan nämnda gränsen för förhållandet mellan ökningen av funktionen och ökningen av argumentet, utan behöver bara använda tabellen av derivat och reglerna för differentiering. Följande algoritm är lämplig för att hitta derivatan.

För att hitta derivatan, behöver du ett uttryck under strecktecknet bryta ner enkla funktioner och bestämma vilka åtgärder (produkt, summa, kvot) dessa funktioner är relaterade. Vidare hittar vi derivatorna av elementära funktioner i tabellen över derivator och formlerna för derivatorna av produkten, summan och kvoten - i differentieringsreglerna. Tabellen över derivat och differentieringsregler ges efter de två första exemplen.

Exempel 1 Hitta derivatan av en funktion

Lösning. Från reglerna för differentiering får vi reda på att derivatan av summan av funktioner är summan av derivator av funktioner, d.v.s.

Från tabellen med derivator får vi reda på att derivatan av "X" är lika med ett, och derivatan av sinus är cosinus. Vi ersätter dessa värden i summan av derivator och hittar den derivata som krävs av problemets tillstånd:

Exempel 2 Hitta derivatan av en funktion

Lösning. Differentiera som en derivata av summan, där den andra termen med en konstant faktor, den kan tas ur derivatans tecken:

Om det fortfarande finns frågor om var något kommer ifrån blir de som regel tydliga efter att ha läst derivattabellen och de enklaste reglerna för differentiering. Vi ska till dem just nu.

Tabell över derivator av enkla funktioner

1. Derivata av en konstant (tal). Valfritt tal (1, 2, 5, 200...) som finns i funktionsuttrycket. Alltid noll. Detta är mycket viktigt att komma ihåg, eftersom det krävs väldigt ofta
2. Derivata av den oberoende variabeln. Oftast "x". Alltid lika med ett. Detta är också viktigt att komma ihåg
3. Derivat av examen. När du löser problem måste du konvertera icke-kvadratrötter till en potens.
4. Derivata av en variabel i potensen -1
5. Derivata av kvadratroten
6. Sinusderivat
7. Cosinusderivat
8. Tangentderivat
9. Derivat av cotangens
10. Derivat av arcsine
11. Derivat av bågekosinus
12. Derivata av bågtangens
13. Derivata av den inversa tangenten
14. Derivata av naturlig logaritm
15. Derivata av en logaritmisk funktion
16. Exponentens derivata
17. Derivata av exponentialfunktion

Differentieringsregler

1. Derivata av summan eller skillnaden
2. Derivat av en produkt
2a. Derivat av ett uttryck multiplicerat med en konstant faktor
3. Derivat av kvoten
4. Derivata av en komplex funktion

Regel 1Om funktioner

är differentierbara vid något tillfälle, sedan vid samma punkt funktionerna

och

de där. derivatan av den algebraiska summan av funktioner är lika med den algebraiska summan av derivatorna av dessa funktioner.

Följd. Om två differentierbara funktioner skiljer sig åt med en konstant, är deras derivator det, dvs.

Regel 2Om funktioner

är differentierbara någon gång, då är deras produkt också differentierbar vid samma punkt

och

de där. derivatan av produkten av två funktioner är lika med summan av produkterna av var och en av dessa funktioner och derivatan av den andra.

Konsekvens 1. Den konstanta faktorn kan tas ur derivatans tecken:

Konsekvens 2. Derivatan av produkten av flera differentierbara funktioner är lika med summan av produkterna av derivatan av var och en av faktorerna och alla de andra.

Till exempel, för tre multiplikatorer:

Regel 3Om funktioner

differentierbar någon gång och , då är deras kvot vid denna tidpunkt också differentierbar.u/v, och

de där. derivatan av en kvot av två funktioner är lika med en bråkdel vars täljare är skillnaden mellan produkterna av nämnaren och derivatan av täljaren och täljaren och derivatan av nämnaren, och nämnaren är kvadraten på den tidigare täljaren .

Var man kan leta på andra sidor

När man hittar produktens derivata och kvoten i verkliga problem är det alltid nödvändigt att tillämpa flera differentieringsregler samtidigt, så fler exempel på dessa derivat finns i artikeln."Derivatet av en produkt och en kvot".

Kommentar. Du ska inte blanda ihop en konstant (det vill säga ett tal) som en term i summan och som en konstant faktor! När det gäller en term är dess derivata lika med noll, och i fallet med en konstant faktor tas den ur derivatans tecken. Detta är ett typiskt misstag som inträffar i det inledande skedet av att studera derivat, men eftersom den genomsnittliga studenten löser flera en-tvåkomponentsexempel gör detta misstag inte längre.

Och om du, när du särskiljer en produkt eller en kvot, har en term u"v, i vilken u- ett tal, till exempel 2 eller 5, det vill säga en konstant, då kommer derivatan av detta tal att vara lika med noll och därför kommer hela termen att vara lika med noll (ett sådant fall analyseras i exempel 10) .

Ett annat vanligt misstag är den mekaniska lösningen av derivatan av en komplex funktion som derivatan av en enkel funktion. Så derivata av en komplex funktionägnas åt en separat artikel. Men först ska vi lära oss att hitta derivator av enkla funktioner.

Längs vägen kan du inte klara dig utan omvandlingar av uttryck. För att göra detta kan du behöva öppna i nya Windows-manualer Handlingar med krafter och rötter och Åtgärder med bråk .

Om du letar efter lösningar på derivator med potenser och rötter, det vill säga när funktionen ser ut som , följ sedan lektionen "Derivat av summan av bråk med potenser och rötter".

Om du har en uppgift som , då är du inne på lektionen "Derivater av enkla trigonometriska funktioner".

Steg för steg exempel - hur man hittar derivatan

Exempel 3 Hitta derivatan av en funktion

Lösning. Vi bestämmer delarna av funktionens uttryck: hela uttrycket representerar produkten, och dess faktorer är summor, i den andra av vilka en av termerna innehåller en konstant faktor. Vi tillämpar produktdifferentieringsregeln: derivatan av produkten av två funktioner är lika med summan av produkterna för var och en av dessa funktioner och derivatan av den andra:

Därefter tillämpar vi regeln om differentiering av summan: derivatan av den algebraiska summan av funktioner är lika med den algebraiska summan av derivatorna av dessa funktioner. I vårt fall, i varje summa, den andra termen med ett minustecken. I varje summa ser vi både en oberoende variabel, vars derivata är lika med en, och en konstant (tal), vars derivata är lika med noll. Så, "x" förvandlas till ett och minus 5 - till noll. I det andra uttrycket multipliceras "x" med 2, så vi multiplicerar två med samma enhet som derivatan av "x". Vi får följande värden på derivat:

Vi ersätter de hittade derivatorna i summan av produkter och erhåller derivatan av hela funktionen som krävs av problemets tillstånd:

Och du kan kontrollera lösningen av problemet på derivatan på .

Exempel 4 Hitta derivatan av en funktion

Lösning. Vi måste hitta derivatan av kvoten. Vi tillämpar formeln för att differentiera en kvot: derivatan av en kvot av två funktioner är lika med en bråkdel vars täljare är skillnaden mellan produkterna av nämnaren och derivatan av täljaren och täljaren och derivatan av nämnaren, och nämnaren är kvadraten på den tidigare täljaren. Vi får:

Vi har redan hittat derivatan av faktorerna i täljaren i exempel 2. Låt oss inte heller glömma att produkten, som är den andra faktorn i täljaren, tas med ett minustecken i det aktuella exemplet:

Om du letar efter lösningar på sådana problem där du behöver hitta derivatan av en funktion, där det finns en kontinuerlig hög med rötter och grader, som t.ex. då välkommen till klassen "Derivatan av summan av bråk med potenser och rötter" .

Om du behöver lära dig mer om derivatorna av sinus, cosinus, tangenter och andra trigonometriska funktioner, det vill säga när funktionen ser ut som , då har du en lektion "Derivater av enkla trigonometriska funktioner" .

Exempel 5 Hitta derivatan av en funktion

Lösning. I denna funktion ser vi en produkt, vars en av faktorerna är kvadratroten av den oberoende variabeln, med den derivata som vi bekantade oss med i tabellen över derivator. Enligt produktdifferentieringsregeln och tabellvärdet för derivatan av kvadratroten får vi:

Du kan kontrollera lösningen av derivatproblemet på derivatkalkylator online .

Exempel 6 Hitta derivatan av en funktion

Lösning. I denna funktion ser vi kvoten, vars utdelning är kvadratroten av den oberoende variabeln. Enligt regeln om differentiering av kvoten, som vi upprepade och tillämpade i exempel 4, och tabellvärdet för derivatan av kvadratroten, får vi:

För att bli av med bråket i täljaren, multiplicera täljaren och nämnaren med .

1. Det allmänna fallet med formeln för derivatan av en rot av en godtycklig grad- ett bråk, vars täljare är ett, och nämnaren är ett tal lika med graden av roten för vilken derivatan beräknades, multiplicerad med roten av samma grad, vars rotuttryck är en variabel i graden av roten för vilken derivatan beräknades, reducerad med en
2. Derivat av kvadratroten- är ett specialfall av föregående formel. Derivat av kvadratroten ur xär ett bråktal vars täljare är ett och nämnaren är två gånger kvadratroten ur x
3. Kubrotsderivat, också ett specialfall av den allmänna formeln. Derivatan av kubroten är enheten dividerad med de tre kubrötterna x i kvadrat.

Nedan finns transformationer som förklarar varför formlerna för att hitta derivatan av kvadrat- och kubrötter är exakt som visas i figuren.

Naturligtvis kan dessa formler inte memoreras alls, om vi tar hänsyn till att att extrahera roten till en derivatgrad är detsamma som att höja en bråkdel till potensen, vars nämnare är lika med samma grad. Att sedan hitta derivatan av roten reduceras till att tillämpa formeln för att hitta derivatan av graden av motsvarande bråk.

Derivat av en variabel under kvadratroten

(√x)" = 1 / (2√x) eller 1/2 x -1/2

Förklaring:
(√x)" = (x 1/2)"

Kvadratroten är exakt samma operation som att höja till 1/2,detta betyder att för att hitta derivatan av roten kan du tillämpa formeln från regeln för att hitta derivatan av en variabel i en godtycklig grad:

(x 1/2)" \u003d 1/2 x -1/2 \u003d 1 / (2√x)

Derivat av kubroten (derivata av roten av tredje graden)

Derivatan av kubroten är exakt densamma som kvadratroten.

Föreställ dig kubroten som en potens av 1/3 och hitta derivatan enligt de allmänna reglerna för differentiering. En kort formel kan ses på bilden ovan, och nedan finns en förklaring till varför det är så.

Potensen -2/3 erhålls genom att subtrahera en från 1/3

Komplexa funktioner passar inte alltid definitionen av en komplex funktion. Om det finns en funktion av formen y \u003d sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, kan den inte betraktas som komplex, till skillnad från y \u003d sin 2 x.

Den här artikeln kommer att visa konceptet med en komplex funktion och dess identifiering. Låt oss arbeta med formler för att hitta derivatan med exempel på lösningar i slutsatsen. Användningen av tabellen över derivat och reglerna för differentiering minskar avsevärt tiden för att hitta derivatan.

Grundläggande definitioner

Definition 1

En komplex funktion är en funktion vars argument också är en funktion.

Det betecknas så här: f (g (x)) . Vi har att funktionen g (x) anses vara ett argument f (g (x)) .

Definition 2

Om det finns en funktion f och är en kotangensfunktion, så är g(x) = ln x den naturliga logaritmfunktionen. Vi får att den komplexa funktionen f (g (x)) kommer att skrivas som arctg (lnx). Eller en funktion f, som är en funktion upphöjd till 4:e potens, där g (x) \u003d x 2 + 2 x - 3 anses vara en hel rationell funktion, vi får att f (g (x)) \u003d (x 2 + 2 x - 3) 4 .

Uppenbarligen kan g(x) vara knepigt. Från exemplet y \u003d sin 2 x + 1 x 3 - 5, kan det ses att värdet på g har en kubrot med en bråkdel. Detta uttryck kan betecknas som y = f (f 1 (f 2 (x))) . Därav har vi att f är en sinusfunktion och f 1 är en funktion som ligger under kvadratroten, f 2 (x) \u003d 2 x + 1 x 3 - 5 är en rationell bråkfunktion.

Definition 3

Graden av kapsling definieras av vilket naturligt tal som helst och skrivs som y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))).

Definition 4

Begreppet funktionssammansättning hänvisar till antalet kapslade funktioner enligt problemformuleringen. För lösningen, formeln för att hitta derivatan av en komplex funktion av formen

(f(g(x)))"=f"(g(x)) g"(x)

Exempel

Exempel 1

Hitta derivatan av en komplex funktion av formen y = (2 x + 1) 2 .

Lösning

Enligt konventionen är f en kvadreringsfunktion och g(x) = 2 x + 1 anses vara en linjär funktion.

Vi använder derivatformeln för en komplex funktion och skriver:

f "(g (x)) = ((g (x)) 2)" = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1); g "(x) = (2x + 1)" = (2x)" + 1" = 2 x" + 0 = 2 1 x 1 - 1 = 2 ⇒ (f(g(x))) "=f" ( g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4

Det är nödvändigt att hitta en derivata med en förenklad initial form av funktionen. Vi får:

y = (2x + 1) 2 = 4x2 + 4x + 1

Därför har vi det

y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4

Resultaten stämde.

När man löser problem av detta slag är det viktigt att förstå var funktionen av formen f och g (x) kommer att ligga.

Exempel 2

Du bör hitta derivatorna av komplexa funktioner av formen y \u003d sin 2 x och y \u003d sin x 2.

Lösning

Den första posten i funktionen säger att f är kvadratfunktionen och g(x) är sinusfunktionen. Då får vi det

y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x)" = 2 sin x cos x

Den andra posten visar att f är en sinusfunktion, och g (x) = x 2 anger potensfunktionen. Det följer att produkten av en komplex funktion kan skrivas som

y " \u003d (sin x 2) " \u003d cos (x 2) (x 2) " \u003d cos (x 2) 2 x 2 - 1 \u003d 2 x cos (x 2)

Formeln för derivatan y \u003d f (f 1 (f 2 (f 3 (. . . (fn (x)))))) kommer att skrivas som y "= f" (f 1 (f 2 (f 3) (. . . ( fn (x)))))) f 1 "(f 2 (f 3 (. . . (fn (x))))) f 2" (f 3 (. . . (fn (x)) )) )) . . . f n "(x)

Exempel 3

Hitta derivatan av funktionen y = sin (ln 3 a r c t g (2 x)) .

Lösning

Det här exemplet visar komplexiteten i att skriva och bestämma funktionernas placering. Då betecknar y \u003d f (f 1 (f 2 (f 3 (f 4 (x))))), där f , f 1 , f 2 , f 3 , f 4 (x) är sinusfunktionen, funktionen av att höja till 3 grader, en funktion med en logaritm och bas e, en funktion av bågtangensen och en linjär.

Från formeln för definitionen av en komplex funktion har vi det

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x)

Får vad man ska hitta

1. f "(f 1 (f 2 (f 3 (f 4 (x))))) som derivatan av sinus i tabellen över derivator, sedan f "(f 1 (f 2 (f 3 (f 4 (x) ))))) ) = cos (ln 3 arctg (2 x)) .
2. f 1 "(f 2 (f 3 (f 4 (x)))) som en derivata av en potensfunktion, sedan f 1 "(f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 arctg (2 x) = 3 ln 2 arctg (2 x) .
3. f 2 "(f 3 (f 4 (x))) som en logaritmisk derivata, sedan f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 "(f 4 (x)) som en derivata av bågtangensen, sedan f 3 "(f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. När du hittar derivatan f 4 (x) \u003d 2 x, ta 2 från tecknet på derivatan med hjälp av formeln för derivatan av potensfunktionen med en exponent som är 1, sedan f 4 "(x) \u003d ( 2 x)" \u003d 2 x "\u003d 2 · 1 · x 1 - 1 = 2 .

Vi slår samman mellanresultaten och får det

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 arctan (2 x)) 3 ln 2 arctan (2 x) 1 arctan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arctan (2 x)) ln 2 arctan (2 x) arctan (2 x) (1 + 4 x 2)

Analysen av sådana funktioner liknar häckande dockor. Differentieringsregler kan inte alltid tillämpas explicit med hjälp av en derivattabell. Ofta behöver du använda formeln för att hitta derivator av komplexa funktioner.

Det finns vissa skillnader mellan en komplex syn och en komplex funktion. Med en tydlig förmåga att särskilja detta blir det extra lätt att hitta derivat.

Exempel 4

Det är nödvändigt att överväga att ta ett sådant exempel. Om det finns en funktion av formen y = tg 2 x + 3 tgx + 1 , så kan den betraktas som en komplex funktion av formen g (x) = tgx , f (g) = g 2 + 3 g + 1 . Uppenbarligen är det nödvändigt att tillämpa formeln för den komplexa derivatan:

f "(g (x)) \u003d (g 2 (x) + 3 g (x) + 1) " \u003d (g 2 (x)) " + (3 g (x)) " + 1 " == 2 g 2 - 1 (x) + 3 g "(x) + 0 \u003d 2 g (x) + 3 1 g 1 - 1 (x) \u003d \u003d 2 g (x) + 3 \u003d 2 tgx + 3; g " (x) = (tgx) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tanx + 3 cos 2 x

En funktion av formen y = t g x 2 + 3 t g x + 1 anses inte vara komplex, eftersom den har summan t g x 2 , 3 t g x och 1 . Men t g x 2 anses vara en komplex funktion, då får vi en potensfunktion av formen g (x) \u003d x 2 och f, som är en funktion av tangenten. För att göra detta måste du skilja efter mängden. Det förstår vi

y " = (tgx 2 + 3 tgx + 1) " = (tgx 2) " + (3 tgx) " + 1 " == (tgx 2) " + 3 (tgx) " + 0 = (tgx 2) " + 3 cos 2 x

Låt oss gå vidare till att hitta derivatan av en komplex funktion (t g x 2) ":

f "(g (x)) \u003d (tg (g (x))) " \u003d 1 cos 2 g (x) \u003d 1 cos 2 (x 2) g " (x) \u003d (x 2) " \u003d 2 x 2 - 1 \u003d 2 x ⇒ (tgx 2) " \u003d f " (g (x)) g " (x) \u003d 2 x cos 2 (x 2)

Vi får att y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Komplexa funktioner kan inkluderas i komplexa funktioner, och de komplexa funktionerna i sig kan vara sammansatta funktioner av den komplexa formen.

Exempel 5

Betrakta till exempel en komplex funktion av formen y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Denna funktion kan representeras som y = f (g (x)) , där värdet på f är en funktion av bas 3-logaritmen, och g (x) anses vara summan av två funktioner av formen h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 och k (x) = ln 2 x (x 2 + 1) . Uppenbarligen är y = f (h (x) + k (x)) .

Betrakta funktionen h(x) . Detta är förhållandet mellan l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 till m (x) = e x 2 + 3 3

Vi har att l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) är summan av två funktioner n (x) = x 2 + 7 och p ( x) \u003d 3 cos 3 (2 x + 1) , där p (x) \u003d 3 p 1 (p 2 (p 3 (x))) är en komplex funktion med en numerisk koefficient på 3, och p 1 är en kubfunktion, p 2 cosinusfunktion, p 3 (x) = 2 x + 1 - linjär funktion.

Vi fann att m (x) = ex 2 + 3 3 = q (x) + r (x) är summan av två funktioner q (x) = ex 2 och r (x) = 3 3 , där q (x) = q 1 (q 2 (x)) är en komplex funktion, q 1 är en funktion med en exponent, q 2 (x) = x 2 är en potensfunktion.

Detta visar att h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3) (x))) q 1 (q 2 (x)) + r (x)

När man går över till ett uttryck av formen k (x) \u003d ln 2 x (x 2 + 1) \u003d s (x) t (x), är det tydligt att funktionen representeras som ett komplext s (x) \ u003d ln 2 x \u003d s 1 ( s 2 (x)) med heltalsrationell t (x) = x 2 + 1, där s 1 är kvadratfunktionen och s 2 (x) = ln x är logaritmisk med basen e .

Det följer att uttrycket kommer att ha formen k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) .

Då får vi det

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Enligt funktionens strukturer blev det tydligt hur och vilka formler som måste tillämpas för att förenkla uttrycket när det är differentierat. För att bekanta dig med sådana problem och förstå deras lösning är det nödvändigt att hänvisa till punkten att differentiera en funktion, det vill säga att hitta dess derivata.

Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter

Härledning av formeln för derivatan av en potensfunktion (x till potensen av a). Derivat av rötter från x beaktas. Formeln för derivatan av en högre ordnings potensfunktion. Exempel på beräkning av derivat.

Innehåll

Se även: Potensfunktion och rötter, formler och graf
Power Function Plots

Grundläggande formler

Derivatan av x i potensen av a är a gånger x i potensen av en minus ett:
(1) .

Derivatan av den n:te roten av x till den m:te potensen är:
(2) .

Härledning av formeln för derivatan av en potensfunktion

Fall x > 0

Betrakta en potensfunktion av variabel x med exponent a :
(3) .
Här är a ett godtyckligt reellt tal. Låt oss överväga fallet först.

För att hitta derivatan av funktionen (3) använder vi egenskaperna för potensfunktionen och transformerar den till följande form:
.

Nu hittar vi derivatan genom att tillämpa:
;
.
Här .

Formel (1) är bevisad.

Härledning av formeln för derivatan av roten av graden n av x till graden m

Tänk nu på en funktion som är roten till följande form:
(4) .

För att hitta derivatan omvandlar vi roten till en potensfunktion:
.
Jämför vi med formel (3) ser vi det
.
Sedan
.

Med formel (1) hittar vi derivatan:
(1) ;
;
(2) .

I praktiken finns det inget behov av att memorera formel (2). Det är mycket bekvämare att först konvertera rötterna till potensfunktioner och sedan hitta deras derivator med formeln (1) (se exempel i slutet av sidan).

Fall x = 0

Om , då är exponentialfunktionen också definierad för värdet av variabeln x = 0 . Låt oss hitta derivatan av funktion (3) för x = 0 . För att göra detta använder vi definitionen av en derivata:
.

Ersätt x = 0 :
.
I det här fallet menar vi med derivata den högra gränsen för vilken .

Så vi hittade:
.
Av detta kan man se att vid , .
Vid , .
Vid , .
Detta resultat erhålls också med formel (1):
(1) .
Därför är formel (1) också giltig för x = 0 .

fall x< 0

Överväg funktion (3) igen:
(3) .
För vissa värden av konstanten a definieras den också för negativa värden för variabeln x . Låta nämligen a vara ett rationellt tal. Sedan kan det representeras som en irreducerbar bråkdel:
,
där m och n är heltal utan gemensam divisor.

Om n är udda, är exponentialfunktionen också definierad för negativa värden av variabeln x. Till exempel för n = 3 och m = 1 vi har kubroten av x :
.
Det är också definierat för negativa värden på x .

Låt oss hitta derivatan av potensfunktionen (3) för och för rationella värden av konstanten a , för vilken den är definierad. För att göra detta representerar vi x i följande form:
.
Sedan,
.
Vi hittar derivatan genom att ta konstanten ur derivatans tecken och tillämpa differentieringsregeln för en komplex funktion:

.
Här . Men
.
Sedan dess
.
Sedan
.
Det vill säga, formel (1) är också giltig för:
(1) .

Derivat av högre ordning

Nu hittar vi de högre ordningens derivator av potensfunktionen
(3) .
Vi har redan hittat första ordningens derivata:
.

Om vi ​​tar konstanten a från derivatans tecken, finner vi andra ordningens derivata:
.
På liknande sätt hittar vi derivator av tredje och fjärde ordningen:
;

.

Härifrån är det tydligt att derivata av en godtycklig n:te ordning har följande form:
.

Lägg märke till att om a är ett naturligt tal, , då är den n:e derivatan konstant:
.
Då är alla efterföljande derivator lika med noll:
,
kl.

Härledda exempel

Exempel

Hitta derivatan av funktionen:
.

Låt oss omvandla rötterna till makter:
;
.
Sedan tar den ursprungliga funktionen formen:
.

Vi hittar derivator av grader:
;
.
Derivatan av en konstant är noll:
.

Instruktion

Innan du hittar derivatan av roten, var uppmärksam på de andra funktionerna som finns i exemplet som löses. Om problemet har många radikala uttryck, använd då följande regel för att hitta derivatan av kvadratroten:

(√x)" = 1 / 2√x.

Och för att hitta derivatan av kubroten, använd formeln:

(³√x)" \u003d 1/3 (³√x)²,

där ³√x anger kubroten av x.

Om det, avsett för differentiering, finns en variabel i bråktal , konvertera sedan roten till en potensfunktion med lämplig exponent. För en kvadratrot kommer detta att vara en potens av ½, och för en kubrot blir det ⅓:

√x \u003d x ^ ½,
³√x = x ^ ⅓,

där ^ står för exponentiering.

För att hitta derivatan av en potensfunktion i allmänhet och x^1, x^⅓ i synnerhet, använd följande regel:

(x ^ n)" = n * x^(n-1).

För derivatan av roten innebär denna relation:

(x^½)" = ½ x ^ (-½) och
(x^⅓)" = ⅓ x ^ (-⅔).

Efter att ha differentierat allt, ta en närmare titt på resten av exemplet. Om du fick ett väldigt krångligt uttryck i ditt svar, så går det säkert att förenkla. De flesta skolexempel är utformade på ett sådant sätt att resultatet blir ett litet tal eller ett kompakt uttryck.

I många derivatproblem förekommer rötter (kvadrat och kub) tillsammans med andra funktioner. För att hitta derivatan av roten i det här fallet, tillämpa följande regler:
derivatan av en konstant (ett konstant tal, C) är lika med noll: C" = 0;
konstantfaktorn tas ur derivatans tecken: (k*f)" = k * (f)" (f är en godtycklig funktion) ;
derivatan av summan av flera funktioner är lika med summan av derivatorna: (f + g)" = (f)" + (g)";
derivatan av produkten av två funktioner är ... nej, inte produkten av derivatorna, utan följande uttryck: (fg)" = (f)"g + f (g)";
derivatan av kvoten är inte heller lika med kvoten av derivator, utan hittas enligt följande regel: (f / g)" = ((f)"g - f(g)") / g².

notera

På den här sidan kan du beräkna derivatan av en funktion online med en detaljerad lösning på problemet. Lösningen av derivatorna av en funktion görs med hjälp av de differentieringsregler som studenterna studerar under matematisk analys vid institutet. För att hitta derivatan av en funktion måste du ange en funktion för differentiering i fältet "Funktion" enligt datainmatningsreglerna.

Användbart råd

Derivatan av en funktion är gränsen för förhållandet mellan ökningen av funktionen och ökningen av argumentet när ökningen av argumentet tenderar till noll: Den matematiska innebörden av denna definition är inte särskilt lätt att förstå, eftersom i skolan algebra naturligtvis begreppet gränsen för en funktion studeras antingen inte alls eller studeras mycket ytligt. Men för att lära sig hur man hittar derivator av olika funktioner är detta inte nödvändigt.

Källor:

• rotderivata av x