Testa för korrespondensavdelning
Danko, P.E. Högre matematik i övningar och problem: på 2 timmar / P.E. Danko, A. G. Popov, T. Ya. Kozhevnikova. - 5:e uppl., rev. - M.: Högre skola. Del 1.-1998.-304 sid.
Bermant A.F., Aramanovich I.G. Kort kurs matematisk analys. -12:e upplagan. – St Petersburg: Lan, 2005.- 736 sid.
B.M. Vladimirsky, A.B. Gorstko, Ya.M. Jerusalemskij. Matematik: allmän kurs. – St Petersburg: Lan Publishing House, 2002. – 954 sid.
Kudryavtsev V.A., Demidovich B.P. Kort kurs i högre matematik. - 5:e upplagan, stereotyp. - M.: Nauka, 1978. - 632 sid.
Demidovich B.P. Kortkurs i högre matematik: Handledning för universitet - M.: OOO "Publishing House Astrel": OOO "Publishing House AST", 2001. - 656 sid.
Piskunov N.S. Differential- och integralkalkyl: Lärobok. för högskolor och universitet. I 2-timmarsvolym T.II: - M.: Integral-Press, 2004. -544 sid.
Introduktion.
Uppfylla testa följer strikt enligt schemat. Varje elev utför ett test under alternativet, vars nummer sammanfaller med dess löpnummer i gruppjournalen. Lösningar på problem ska lämnas skriftligen på separata ark (A4-format, häftat). Du kan lämna in arbete i antingen tryckt eller skriftlig form. Genomförande av k.r. , studenten måste skriva om tillståndet för motsvarande problem, skriv detaljerad lösning genom att markera svaret. Vid behov, ge korta förklaringar allt eftersom lösningen fortskrider.
"NUMERISK OCH FUNKTIONELL SERIE"
Nummerserie. Tillräckliga tecken på deras konvergens
Låta u 1 , u 2 , u 3 , … , u n, …, Var u n = f(n), är en oändlig talsekvens. Uttryck u 1 + u 2 + u 3 + … + u n+ ... kallas oändlig nummerserie , och siffrorna u 1 , u 2 , u 3 , … , u n, … – medlemmar i serien; u n = f(n) kallas gemensam medlem. En serie skrivs ofta i formen .
Summan av den första n medlemmar i en nummerserie betecknas med S n och ring n th delsumman av serien:
Serien heter konvergerande om det n-i delbelopp S n med obegränsad ökning n tenderar till den slutliga gränsen, dvs. Om . siffra S kallad summan av serien. Om n-th delsumman av serien när inte tenderar till en ändlig gräns, då kallas serien avvikande.
En serie som består av medlemmar av valfri fallande ordning geometrisk progression, är konvergent och har summan .
En serie som heter harmonisk, avviker.
Ett nödvändigt tecken på konvergens. Om serien konvergerar, då, dvs. vid gränsen för den gemensamma termen för den konvergenta serien är noll.
Således, om , då serien divergerar.
Låt oss lista de viktigaste tecknen på konvergens och divergens av serier med positiva termer.
Det första tecknet på jämförelse. Låt två rader ges
Dessutom överstiger inte varje medlem av serie (1) motsvarande medlem av serie (2), dvs. . Sedan om serie (2) konvergerar, då konvergerar serie (1) också; om serie (1) divergerar, så divergerar serie (2) också.
Detta kriterium förblir giltigt om ojämlikheterna inte är uppfyllda för alla n, men bara från ett visst antal n = N.
Det andra tecknet på jämförelse. Om det finns en ändlig gräns som inte är noll, då både konvergerar och divergerar serien.
Radikal Cauchy tecken. Om för en serie
existerar, då konvergerar denna serie vid och divergerar vid .
D'Alemberts tecken. Om det för en serie finns , då konvergerar denna serie vid och divergerar vid .
Integral Cauchy-test. Om f(x) för är en kontinuerlig positiv och monotont avtagande funktion, då serien där konvergerar eller divergerar beroende på om integralen konvergerar eller divergerar.
Låt oss nu betrakta serier vars medlemmar har alternerande tecken, dvs. serie av formuläret , där .
Ett test för konvergens av en alternerande serie (Leibniz-test). En alternerande serie konvergerar om de absoluta värdena för dess termer minskar monotont och den vanliga termen tenderar att bli noll. Det vill säga om följande två villkor är uppfyllda: 1) och 2).
Låt oss ta n den delsumma av en konvergent alternerande serie för vilken Leibniz-kriteriet gäller:
Låt -- n- resten av raden. Det kan skrivas som skillnaden mellan summan av serien S Och n delbeloppet S n, dvs. . Det är inte svårt att se det
Värdet uppskattas med hjälp av ojämlikhet.
Låt oss nu uppehålla oss vid några egenskaper hos alternerande serier (d.v.s. alternerande serier och serier med godtycklig alternering av deras medlemmars tecken).
En alternerande serie konvergerar om serien konvergerar.
I det här fallet kallas originalserien absolut konvergent.
En konvergent serie kallas villkorligt konvergent, om serien divergerar.
Exempel 1. Undersök konvergensen av en serie
Lösning. Denna serie är sammansatt av termer av en oändligt minskande geometrisk progression och konvergerar därför. Låt oss hitta summan. Här , (förloppets nämnare). Därav,
Exempel 2. Undersök seriens konvergens.
Lösning. Denna serie erhålls från den harmoniska serien genom att kassera de första tio termerna. Därför divergerar han.
Exempel 3. Undersök seriens konvergens., –– serien konvergerar.
$\sum \limits _(n=1)^(\infty )a_(n) $, vars medlemmar uppfyller tre villkor:
- $a_(n) >0,\, \, \, n\ge 1$, dvs. originalserie med positiva termer;
- seriens termer minskar monotont, d.v.s. $a_(1) >a_(2) >\ldots >a_(n-1) >a_(n) >\ldots >0$;
- den allmänna termen för serien tenderar till noll: $\mathop(\lim )\limits_(n\to \infty ) a_(n) =0$.
Låt det existera en kontinuerlig, monotont avtagande funktion f(x) definierad vid $x\ge 1$ så att $f\left(1\right)=a_(1) ,\, \, \, f\left(2 \ höger)=a_(2) ,\, \, \, \ldots ;\, \, \, f\left(n\right)=a_(n) ,\, \, \, \ldots $, d.v.s. $\summa \limits _(n=1)^(\infty )a_(n) =\summa \limits _(n=1)^(\infty )f(n) $. Sedan, om den felaktiga integralen $\int \limits _(1)^(+\infty )f\left(x\right)(\rm d)x $ konvergerar, då konvergerar serien $\sum \limits _(n= 1) ^(\infty )a_(n) $ konvergerar också; om den angivna integralen divergerar, så divergerar denna serie.
Anteckning 1
Satsen förblir sann även när dess villkor inte är uppfyllda för alla termer i serien, utan endast från kth ($n\ge k$), i vilket fall integralen $\int \limits _(k)^(+ \ infty )f\left(x\right)\, (\rm d)x $.
Anteckning 2
Det integrerade Cauchy-testet underlättar avsevärt studiet av konvergensen av en serie, eftersom det gör det möjligt att reducera denna fråga till att bestämma konvergensen av integralen för en väl vald motsvarande funktion $f(x)$, vilket enkelt görs med metoder av integralkalkyl.
Sats 2 (radikalt Cauchy-test)
Låt en serie med positiva termer $\summa \limits _(n=1)^(\infty )a_(n) ,\, \, \, a_(n) >0$ ges och låt det finnas en ändlig gräns $ \mathop(\ lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =l.$Då:
- om $l
- om $l>1$ divergerar serien,
- om $l=1$ är det radikala Cauchy-testet inte tillämpligt för att bestämma konvergensen av en serie.
Bevis
- Låt $\mathop(\lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =l0$ existera, sedan $l\ge 0$. Betrakta ett tal q så att $l 0$ det finns $N=N((\rm \varepsilon ))\i $N, från vilken $\forall n \ge N$ olikheten $\left|\sqrt[( n )](a_(n) ) -l\höger|
$\summa \limits _(n=1)^(\infty )a_(n) =\, a_(1) +\, a_(2) +\ldots +\, a_(N) +\, a_(N +1) +a_(N+2) +...$ . (1)
Låt oss skapa en ny rad
$\summa \limits _(k=0)^(\infty )q^(N+k) =q^(N) +\, q^(N+1) +q^(N+2) +\ldots $(2)
Serie (2) är en serie av geometrisk progression med nämnaren $q$: $0\le q
- Låt $\mathop(\lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =l>1$ existera. Med start från några $N=N((\rm \varepsilon ))\i (\rm N)$ $\forall n\ge N$, $\, \, \sqrt[(n)](a_(n) ) >1\, \, \, \Högerpil \, \, \, \, a_(n) >1$, dvs. $\mathop(\lim )\limits_(n\to \infty ) a_(n) \ne 0$, då divergerar den ursprungliga serien enligt det nödvändiga konvergenskriteriet.
- Om $\mathop(\lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =l=1$ (eller inte finns), då för att bestämma konvergensen av en serie , är det radikala Cauchy-testet inte tillämpligt.
Teoremet har bevisats.
Sats 3 (D'Alemberts test)
Låt en serie med positiva termer $\summa \limits _(n=1)^(\infty )a_(n) \, \, \, (a_(n) >0) $ ges, och det finns en ändlig gräns $\mathop( \lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) =l$, sedan:
- serien $\sum \limits _(n=1)^(\infty )a_(n) $ konvergerar om $l
- serien $\sum \limits _(n=1)^(\infty )a_(n) $ divergerar om $l>1$,
- om $l=1$ är d’Alemberts test inte tillämpligt för att bestämma konvergensen av en serie.
Bevis
- Låt gränsen $\mathop(\lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) =l$ existera och $0\le l 0$ existera $N( ( \rm \varepsilon ))\i $N, från vilken $\forall n\ge N=N((\rm \varepsilon ))$ olikheten $\left|\frac(a_(n+1)) ( a_n )-l\right|
Låt oss skriva den ursprungliga serien $\sum \limits _(n=1)^(\infty )a_(n) \, \, \, (a_(n) >0) $ i formen: $\sum \limits _(n= 1)^(\infty )a_(n) =a_(1) +a_(2) +\ldots +a_(N) +a_(N+1) +a_(N+2) \, + ...$ . Betrakta den nya serien $\sum \limits _(k=0)^(\infty )a_(N) \cdot q^(k) =a_(N) +qa_(N) +q^(2) a_(N) ) +\ldots $ . Denna serie är en serie av geometrisk progression med $b_(1) =a_(N) $ och $0
- Låt $\mathop(\lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) =l>1$. Betrakta ett tal q så att $l>q>1$. $(\rm \varepsilon )=l-q>0$, från definitionen av gränsen följer:$-(\rm \varepsilon ) q > 1.$ Alltså $a_(n+1) >a_n > 0$ och för $n \to \infty $ tenderar den vanliga termen i serien $a_(n) $ inte till 0, dvs. serien $\sum \limits _(n=1)^(\infty )a_n $ avviker eftersom den inte är uppfylld nödvändigt tillstånd konvergens av serien. Den andra delen av satsen är bevisad.
- Om $l=1$,$\mathop(\lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) $ är lika med en eller inte existerar, i detta fall för För att bestämma konvergensen av en serie är D'Alemberts test inte tillämpligt.
Exempel 1
Undersök serien $\sum \limits _(n=1)^(\infty )\, \frac(n)(2^(n) ) $ för konvergens.
Lösning. Låt oss beteckna $\frac(n)(2^(n) ) =a_(n) $, $a_(n) >0$; låt oss hitta $a_(n+1) =\frac(n+1)(2^(n+1) ) $. Låt oss sätta en gräns $l=\mathop(\lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) =\mathop(\lim )\limits_(n\ till \ infty ) \frac((n+1)\cdot 2^(n) )(2^(n) \cdot 2\cdot n) =\frac(1)(2) \mathop(\lim )\limits_ (n \till \infty ) \frac(n+1)(n) =\frac(1)(2)
Svar: serien $\sum \limits _(n=1)^(\infty )\, \frac(n)(2^(n) ) $konvergerar.
Exempel 2
Undersök serien $\sum \limits _(n=1)^(\infty )\, \frac(n) för konvergens{5^{n} } $.!}
Lösning. Låt oss beteckna $\frac(n{5^{n} } =a_{n} ,a_{n} >0$; найдём $a_{n+1} =\frac{(n+1)!}{5^{n+1} } $. Составим предел!}
de där. Enligt d'Alemberts kriterium skiljer sig serien åt.
Svar: serie $\summa \limits _(n=1)^(\infty )\, \frac(n{5^{n} } $ расходится.!}
Exempel 3
Undersök efter konvergens serien $\summa \limits _(n=1)^(\infty )\, \left(\frac(n)(2n+1) \right)^(n) $
Lösning. Låt oss beteckna $\left(\frac(n)(2n+1) \right)^(n) =a_(n) ,^() a_(n) >0$. Låt oss skapa en gräns:
$l=\mathop(\lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =\mathop(\lim )\limits_(n\to ) \frac(n) (2n+1) =\frac(1)(2)
Svar: serien $\sum \limits _(n=1)^(\infty )\, \left(\frac(n)(2n+1) \right)^(n) $konvergerar.
HÖGRE MATEMATIK
Nummerserie
Föreläsning.Nummerserie
1. Definition av en nummerserie. Konvergens
2. Grundläggande egenskaper för nummerserier
3. Serier med positiva termer. Tecken på konvergens
4. Omväxlande rader. Leibniz konvergenstest
5. Omväxlande serier
Självtestfrågor
Litteratur
Föreläsning. NUMERISK SERIE
1. Definition av en nummerserie. Konvergens.
2. Grundläggande egenskaper för nummerserier.
3. Serier med positiva termer. Tecken på konvergens.
4. Omväxlande rader. Leibniz konvergenstest.
5. Omväxlande serier.
1. Definition av en nummerserie. Konvergens
I matematiska tillämpningar, såväl som för att lösa vissa problem inom ekonomi, statistik och andra områden, beaktas summor med ett oändligt antal termer. Här kommer vi att ge en definition av vad som menas med sådana belopp.
Låt en oändlig talföljd ges
, , …, , …Definition 1.1. Nummerserie eller bara nära kallas ett uttryck (summa) av formen
. (1.1) kallas medlemmar av ett nummer, – allmän eller n – m medlem i serien.För att definiera serier (1.1) räcker det att specificera funktionen för det naturliga argumentet
beräkna den:e termen i en serie efter dess antalExempel 1.1. Låta
. Rad (1,2)kallad harmonisk serie .
Exempel 1.2. Låta
, Rad (1.3)kallad generaliserade harmoniska serier. I det speciella fallet när
en övertonsserie erhålls.Exempel 1.3. Låta
= . Rad (1,4)kallad nära geometrisk progression.
Från termerna för serie (1.1) bildar vi en numerisk sekvens av partierbelopp Var
– summan av de första termerna i serien, som kallas n-delbeloppet, dvs , , ,…………………………….
, (1.5)…………………………….
Nummerföljd
med en obegränsad ökning av antalet kan den:1) har en ändlig gräns;
2) har ingen ändlig gräns (gränsen finns inte eller är lika med oändlighet).
Definition 1.2. Serie (1.1) kallas konvergerande, om sekvensen av dess delsummor (1,5) har en ändlig gräns, dvs.
I det här fallet numret
kallad belopp serie (1.1) och skrivs .Definition 1.3.Serie (1.1) kallas avvikande, om sekvensen av dess delsummor inte har en ändlig gräns.
Ingen summa tilldelas den divergerande serien.
Således är problemet med att hitta summan av en konvergent serie (1.1) ekvivalent med att beräkna gränsen för sekvensen av dess delsummor.
Låt oss titta på några exempel.
Exempel 1.4. Bevisa att serien
konvergerar och hittar dess summa.
Vi hittar n- delsumman av denna serie
.Allmän medlem
Låt oss representera serien i formen .Härifrån har vi:
. Därför konvergerar denna serie och dess summa är lika med 1:Exempel 1.5. Undersök serien för konvergens
(1.6)För den här raden
. Därför skiljer sig denna serie.Kommentar. På
serie (1.6) är summan av ett oändligt antal nollor och är uppenbarligen konvergent.Exempel 1.6. Undersök serien för konvergens
(1.7)För den här raden
I det här fallet är gränsen för en sekvens av delsummor
existerar inte, och serien divergerar.Exempel 1.7. Undersök serien av geometrisk progression (1.4) för konvergens:
Det är lätt att visa det n-:e delsumman av en geometrisk progressionsserie vid
ges av formeln.Låt oss överväga fallen:
Sedan och.Därför konvergerar serien och dess summa är lika med
Definition av en talserie och dess konvergens.
Nödvändigt tecken på konvergens
Låta vara en oändlig talföljd.
Definition. Uttryck
, (1)
eller, vad är samma sak, kallas nummerserie, och siffrorna https://pandia.ru/text/79/302/images/image005_146.gif" width="53" height="31"> – medlemmar i serien. En medlem med ett godtyckligt nummer anropasn-m, eller vanlig medlem i serien.
I och för sig har uttrycket (1) ingen specifik numerisk betydelse, eftersom vi varje gång endast behandlar ett ändligt antal termer när vi beräknar summan. Det är mest naturligt att definiera innebörden av detta uttryck enligt följande.
Låt serie (1) ges.
Definition. Beloppnförsta medlemmarna i serien

kallad n delbeloppet rad. Låt oss bilda en sekvens av delsummor:
font-size:14.0pt">Med obegränsad antal ökningarnsumman tar hänsyn till allt större antal medlemmar i serien. Därför är det rimligt att ge en sådan definition.
Definition. Om det finns en ändlig gräns för sekvensen av delsummor https://pandia.ru/text/79/302/images/image011_76.gif" width="103" height="41"> kallas det belopp.
Om sekvensen är https://pandia.ru/text/79/302/images/image013_77.gif" width="80" height="31">, 2) om den är fluktuerande. I båda fallen säger de att serien har ingen summa.
Exempel 1. Betrakta en serie som består av termer för en geometrisk progression:
 , (2)
, (2)
där – kallas den första termen i progressionen, och font-size:14.0pt"> Delsumma av denna serie vid font-size:14.0pt">font-size:14.0pt">Härifrån:
1) om, då
font-size:14.0pt">dvs serien av geometrisk progression konvergerar och dess summa .
I synnerhet om  , rad
, rad  dess summa konvergerar också.
dess summa konvergerar också.
När https://pandia.ru/text/79/302/images/image026_42.gif" width="307" height="59 src="> konvergerar dess summa också.
2) om , då  serien (2) divergerar.
serien (2) divergerar.
3) om , då tar rad (2) formen font-size:14.0pt"> och![]() , dvs serien divergerar(vid font-size:18.0pt">) .
, dvs serien divergerar(vid font-size:18.0pt">) .
4) om https://pandia.ru/text/79/302/images/image036_32.gif" width="265" height="37">. För den här raden
https://pandia.ru/text/79/302/images/image038_28.gif" width="253" height="31 src=">,
dvs. gif" width="67" height="41"> existerar inte, därför divergerar serien också(vid ) .
Att beräkna summan av en serie direkt, per definition, är mycket obekvämt på grund av svårigheten att explicit beräkna delsummor font-size:14.0pt"> och hitta gränsen för deras sekvens. Men om det konstateras att serierna konvergerar, dess summa kan beräknas approximativt, eftersom gränsen för sekvensen bestäms följer att för tillräckligt stor. Därför räcker det när man studerar serier
1) känna till tekniker som låter dig ange konvergensen av en serie utan att hitta dess summa;
2) kunna avgörafont-size:14.0pt">.gif" width="16 height=24" height="24"> med en viss noggrannhet.
Konvergensen av talserier fastställs med hjälp av satser som kallas konvergenstest.
Obligatoriskt tecken konvergens
Om serien konvergerar tenderar dess vanliga term till noll, dvs. font-size:14.0pt">.gif" width="61 height=63" height="63"> divergerar.
Exempel 2. Bevisa att rad 0 " style="border-collapse:collapse">
 ;
;
 ;
;
 ;
;
 .
.
Lösning.
A) https://pandia.ru/text/79/302/images/image051_28.gif" width="176" height="81 src="> divergerar.

och därför divergerar serien. Lösningen använde den andra anmärkningsvärda
begränsa:  (se detaljer).
(se detaljer).
B) font-size:14.0pt">, dvs sekvens
 - oändligt
- oändligt
små Eftersom med font-size:14.0pt">~ (se), alltså
~ .Med hänsyn till detta får vi:
Detta betyder att serien divergerar.
D) font-size:14.0pt">,
därför skiljer sig serien åt.
Skick ![]() är nödvändig, Men inte tillräckligt villkor för konvergens av en serie: det finns många serier för vilka
är nödvändig, Men inte tillräckligt villkor för konvergens av en serie: det finns många serier för vilka![]() , men som ändå skiljer sig åt.
, men som ändå skiljer sig åt.
Exempel 3. Undersök konvergensen av serien font-size:14.0pt"> Lösning. Lägg märke till att https://pandia.ru/text/79/302/images/image066_20.gif" width="119" height="59 src="> d.v.s. det nödvändiga villkoret för konvergens är uppfyllt. Delbelopp
vänster">
- en gång
därför font-size:14.0pt">, vilket betyder att serien divergerar per definition.
Tillräckliga tecken på konvergens av positiva serier
Låt . Sedan serienfont-size:14.0pt"> Jämförelse tecken
Låta och är serier med positiva tecken. Om ojämlikheten är tillfredsställd för alla, följer från seriens konvergens seriens konvergens och från seriens divergens https://pandia.ru/text/79/302/images/image074_19.gif" width ="55" height="60">.
Detta tecken förblir i kraft om ojämlikheten https://pandia.ru/text/79/302/images/image072_18.gif" width="60" height="24">, men endast från ett visst antal. tolkas på följande sätt: om en större serie konvergerar så konvergerar den mindre än mer, om en mindre serie divergerar så divergerar den större också.
Exempel 4. Undersök konvergensen av serie 0 " style="margin-left:50.4pt;border-collapse:collapse">
 ;
;
Lösning.
A) Observera att font-size:14.0pt"> för alla ![]() . Serie med gemensam medlem
. Serie med gemensam medlem
 konvergerar i jämförelse.
konvergerar i jämförelse.
B) Jämför rad med rad ..gif" width="91" height="29 src=">.gif" width="87" height="59"> divergerar, vilket betyder att även denna serie divergerar.
Trots enkelheten i formuleringen av jämförelsekriteriet är i praktiken följande sats, som är dess följd, mer bekväm.
Jämförelsegräns
Låta https://pandia.ru/text/79/302/images/image071_17.gif" width="53" height="60 src="> – positiv teckenserie. Om det finns ändlig Och inte lika med noll limit, då både serier och
konvergera samtidigt eller divergera samtidigt.
Serien som används för jämförelse med data väljs ofta som en serie av formuläret  . En sådan serie kallas nära Dirichlet. I exempel 3 och 4 visades att Dirichlet-serien med och divergerar. Det är möjligt för nu
. En sådan serie kallas nära Dirichlet. I exempel 3 och 4 visades att Dirichlet-serien med och divergerar. Det är möjligt för nu

 .
.
Om , då serien  kallad harmonisk. Den harmoniska serien divergerar.
kallad harmonisk. Den harmoniska serien divergerar.
Exempel 5. Undersök serien för konvergensanvända det begränsande jämförelsekriteriet, if
|
|
|
Lösning. a) Eftersom för tillräckligt stora https://pandia.ru/text/79/302/images/image101_9.gif" width="31" height="23 src=">, och
![]() ~ då
~ då  ~ font-size:14.0pt">jämförelser med den givna övertonsserien font-size:14.0pt">, dvs.
~ font-size:14.0pt">jämförelser med den givna övertonsserien font-size:14.0pt">, dvs.
font-size:14.0pt"> Eftersom gränsen är finit och icke-noll och den harmoniska serien divergerar, divergerar denna serie också.
B) För tillräckligt stor https://pandia.ru/text/79/302/images/image109_10.gif" width="111" height="31 src=">.gif" width="129" height="31 src=">.gif" width="132" height="64 src="> – den allmänna medlemmen i serien som vi kommer att jämföra denna med:
Font-size:14.0pt">Serien konvergerar ( Dirichlet-serien med font-size:16.0pt">), så denna serie konvergerar också.
I)  , alltså oändligt liten font-size:14.0pt"> möjligt
, alltså oändligt liten font-size:14.0pt"> möjligt
ersätt med ett värde motsvarande det(https://pandia.ru/text/79/302/images/image058_20.gif" width="13" height="21 src="> med teckenstorlek: 20.0pt">). ;
 ;
;
 ;
;
G)
 ;
;
 .
.
I praktiken är det ofta inte så viktigt att hitta summan av en serie som att svara på frågan om seriens konvergens. För detta ändamål används konvergenskriterier baserade på egenskaperna hos den gemensamma termen i serien.
Ett nödvändigt tecken på konvergens av en serie
SAT 1
Om radenkonvergerar, då dess vanliga term  tenderar till noll som
tenderar till noll som  ,
de där.
,
de där.
 .
.
I korthet: Om en serie konvergerar tenderar dess vanliga term till noll.
Bevis. Låt serien konvergera och dess summa lika  . För vem som helst
. För vem som helst  delbelopp
delbelopp


 .
.
Sedan .
Av det bevisade nödvändiga kriteriet för konvergens följer det ett tillräckligt tecken på divergensen i en serie:
jag fet  Om den gemensamma termen för serien inte tenderar till noll, så divergerar serien.
Om den gemensamma termen för serien inte tenderar till noll, så divergerar serien.
Exempel 4.

För denna serie är den vanliga termen  Och
Och  .
.
Därför skiljer sig denna serie.
Exempel 5. Undersök serien för konvergens

Det är uppenbart att den allmänna termen för denna serie, vars form inte anges på grund av uttryckets besvärlighet, tenderar till noll som  , dvs. det nödvändiga kriteriet för konvergens av en serie är uppfyllt, men denna serie divergerar, eftersom dess summa
tenderar till oändligheten.
, dvs. det nödvändiga kriteriet för konvergens av en serie är uppfyllt, men denna serie divergerar, eftersom dess summa
tenderar till oändligheten.
Positiv nummerserie
En talserie där alla termer är positiva kallas positivt tecken.
SAT 2 (Kriterium för konvergens av en positiv serie)
För att en serie med positivt tecken ska konvergera är det nödvändigt och tillräckligt att alla dess delsummor avgränsas ovanifrån av samma tal.
Bevis. Sedan för vem som helst 
 , då, dvs. efterföljande
, då, dvs. efterföljande  – monotont ökande, därför är det nödvändigt och tillräckligt för att gränsen existerar att begränsa sekvensen uppifrån med ett visst antal.
– monotont ökande, därför är det nödvändigt och tillräckligt för att gränsen existerar att begränsa sekvensen uppifrån med ett visst antal.
Denna sats i i större utsträckning har snarare teoretisk än praktisk betydelse. Nedan finns andra konvergenstester som används mer allmänt.
Tillräckliga tecken på konvergens av positiva serier
SAT 3 (Första jämförelsetecken)
Låt två serier med positiva tecken ges:
 (1)
(1)
 (2)
(2)
och från ett visst antal  , för vem som helst
, för vem som helst  ojämlikheten håller
ojämlikheten håller  Sedan:
Sedan:

Schematisk notation av den första jämförelsefunktionen:

nedstigning.samlande.
exp.exp.
Bevis. 1) Eftersom att kassera ett ändligt antal termer i serien inte påverkar dess konvergens, bevisar vi satsen för fallet  . Låt det vara för vem som helst
. Låt det vara för vem som helst  vi har
vi har
 , (3)
, (3)
Var  Och
Och
 - delsummor av serie (1) respektive (2).
- delsummor av serie (1) respektive (2).
Om serie (2) konvergerar, så finns det ett tal  .
Eftersom i detta fall sekvensen
.
Eftersom i detta fall sekvensen  - ökar, dess gräns är större än någon av dess medlemmar, dvs.
- ökar, dess gräns är större än någon av dess medlemmar, dvs.  för vem som helst
för vem som helst  .
Av ojämlikhet (3) följer därför
.
Av ojämlikhet (3) följer därför
 .
Således begränsas alla delsummor av serie (1) ovanför av talet
.
Således begränsas alla delsummor av serie (1) ovanför av talet  .
Enligt sats 2 konvergerar denna serie.
.
Enligt sats 2 konvergerar denna serie.
2) I själva verket, om serie (2) konvergerade, då, i jämförelse, skulle serie (1) också konvergera.
För att tillämpa denna funktion används ofta sådana standardserier, vars konvergens eller divergens är känd i förväg, till exempel:

3)
 -
Dirichlet-serien (den konvergerar kl
-
Dirichlet-serien (den konvergerar kl  och avviker kl
och avviker kl  ).
).
Dessutom används ofta serier som kan erhållas med följande uppenbara ojämlikheter:

 ,
,

 ,
, ,
, .
.
Låt oss titta på specifika exempel ett schema för att studera en positiv serie för konvergens med användning av det första jämförelsekriteriet.
Exempel 6. Utforska rad  för konvergens.
för konvergens.
Steg 1. Låt oss kontrollera det positiva tecknet i serien:  För
För 
Steg 2. Låt oss kontrollera uppfyllandet av det nödvändiga kriteriet för konvergens av en serie:  . Därför att
. Därför att  , Den där
, Den där 
(om det är svårt att beräkna gränsen kan du hoppa över detta steg).
Steg 3. Använd det första jämförelsetecknet. För att göra detta kommer vi att välja en standardserie för denna serie. Därför att  , då kan vi ta serien som standard
, då kan vi ta serien som standard  , dvs. Dirichlet-serien. Denna serie konvergerar eftersom exponenten
, dvs. Dirichlet-serien. Denna serie konvergerar eftersom exponenten  . Följaktligen, enligt det första jämförelsekriteriet, konvergerar serierna som studeras också.
. Följaktligen, enligt det första jämförelsekriteriet, konvergerar serierna som studeras också.
Exempel 7. Utforska rad  för konvergens.
för konvergens.
1) Denna serie är positiv, eftersom  För
För 
2) Det nödvändiga kriteriet för konvergens av en serie är uppfyllt, eftersom
3) Låt oss välja en standardrad. Därför att  , då kan vi ta den geometriska serien som standard
, då kan vi ta den geometriska serien som standard

 . Denna serie konvergerar, och därför konvergerar serien som studeras också.
. Denna serie konvergerar, och därför konvergerar serien som studeras också.
SAT 4 (Andra jämförelsekriteriet)
Om för positiva serier
 Och
Och
 det finns en ändlig gräns som inte är noll
det finns en ändlig gräns som inte är noll  , Den där
raderna konvergerar eller divergerar samtidigt.
, Den där
raderna konvergerar eller divergerar samtidigt.
Bevis. Låt serie (2) konvergera; Låt oss bevisa att då också serie (1) konvergerar. Låt oss välja ett nummer  ,
mer än
,
mer än  .
Från tillståndet
.
Från tillståndet
 därav följer att ett sådant nummer existerar
därav följer att ett sådant nummer existerar
 det är för alla
det är för alla  ojämlikhet är sant
ojämlikhet är sant  ,
eller, vad är samma,
,
eller, vad är samma,
 (4)
(4)
Efter att ha kasserat de första på raderna (1) och (2)
 termer (som inte påverkar konvergens), kan vi anta att olikhet (4) gäller för alla
termer (som inte påverkar konvergens), kan vi anta att olikhet (4) gäller för alla  Men en serie med en gemensam medlem
Men en serie med en gemensam medlem  konvergerar på grund av konvergensen av serier (2). Enligt det första jämförelsekriteriet innebär olikhet (4) konvergens av serier (1).
konvergerar på grund av konvergensen av serier (2). Enligt det första jämförelsekriteriet innebär olikhet (4) konvergens av serier (1).
Låt nu serie (1) konvergera; Låt oss bevisa konvergensen av serier (2). För att göra detta, byt helt enkelt rollerna för de givna raderna. Därför att

då, enligt vad som bevisats ovan, bör konvergensen av serie (1) innebära konvergens av serie (2).
Om  på
på  (ett nödvändigt tecken på konvergens), sedan från villkoret
(ett nödvändigt tecken på konvergens), sedan från villkoret  , följer det
, följer det  Och
Och  – infinitesimals av samma storleksordning (motsvarande
– infinitesimals av samma storleksordning (motsvarande  ). Därför, om ges en serie
). Därför, om ges en serie
 , Var
, Var  på
på  , då för denna serie kan vi ta standardserien
, då för denna serie kan vi ta standardserien
 , var är den gemensamma termen
, var är den gemensamma termen  har samma litenhetsordning som den allmänna termen för den givna serien.
har samma litenhetsordning som den allmänna termen för den givna serien.
När du väljer en standardserie kan du använda följande tabell över ekvivalenta infinitesimaler vid  :
:
1)
 ; 4)
; 4) ;
;
2)
 ; 5)
; 5) ;
;
3)
 ; 6)
; 6) .
.
Exempel 8. Undersök serien för konvergens
 .
.
 för vem som helst
för vem som helst  .
.

Därför att  , då tar vi den harmoniska divergerande serien som en standardserie
, då tar vi den harmoniska divergerande serien som en standardserie  . Sedan gränsen för förhållandet mellan vanliga termer
. Sedan gränsen för förhållandet mellan vanliga termer  Och
Och  är ändlig och skiljer sig från noll (det är lika med 1), sedan baserat på det andra jämförelsekriteriet divergerar denna serie.
är ändlig och skiljer sig från noll (det är lika med 1), sedan baserat på det andra jämförelsekriteriet divergerar denna serie.
Exempel 9. enligt två jämförelsekriterier.
enligt två jämförelsekriterier.
Denna serie är positiv, eftersom  , Och
, Och  . Eftersom den
. Eftersom den  , då kan vi ta den harmoniska serien som en standardserie
, då kan vi ta den harmoniska serien som en standardserie  . Denna serie divergerar och därför, enligt det första tecknet på jämförelse, divergerar serien som studeras också.
. Denna serie divergerar och därför, enligt det första tecknet på jämförelse, divergerar serien som studeras också.
Eftersom för denna serie och standardserien är villkoret uppfyllt  (här används den 1:a anmärkningsvärda gränsen), sedan baserat på det andra jämförelsekriteriet serien
(här används den 1:a anmärkningsvärda gränsen), sedan baserat på det andra jämförelsekriteriet serien  – avviker.
– avviker.
SAT 5 (D'Alemberts test)
 det finns en ändlig gräns
det finns en ändlig gräns  , sedan konvergerar serien kl
, sedan konvergerar serien kl  och avviker kl
och avviker kl  .
.
Bevis. Låta  . Låt oss ta ett antal
. Låt oss ta ett antal  ,
slutit mellan
,
slutit mellan  och 1:
och 1:  . Från tillståndet
. Från tillståndet
 det följer att utgående från något nummer
det följer att utgående från något nummer  ojämlikheten håller
ojämlikheten håller
 ;
;
 ;
; (5)
(5)
Tänk på serien
Enligt (5) överskrider inte alla termer i serie (6) motsvarande termer för den oändliga geometriska progressionen  Eftersom den
Eftersom den  , är denna utveckling konvergent. Härifrån, på grund av det första jämförelsekriteriet, följer seriens konvergens
, är denna utveckling konvergent. Härifrån, på grund av det första jämförelsekriteriet, följer seriens konvergens
Happening  överväga själv.
överväga själv.
Anteckningar :

det följer att resten av serien 
 .
.
D'Alemberts test är praktiskt praktiskt när den vanliga termen i serien innehåller exponentiell funktion eller faktoriellt.
Exempel 10. Undersök serien för konvergens  enligt D'Alemberts tecken.
enligt D'Alemberts tecken.
Denna serie är positiv och
 .
.
(Här, i beräkningen, tillämpas L'Hopitals regel två gånger).

sedan, enligt d'Alemberts kriterium, konvergerar denna serie.
Exempel 11. .
.
Denna serie är positiv och  . Eftersom den
. Eftersom den
då konvergerar denna serie.
SAT 6 (Cauchy-test)
Om för en positiv serie
 det finns en ändlig gräns
det finns en ändlig gräns  , då när
, då när  serien konvergerar, och när
serien konvergerar, och när  raden divergerar.
raden divergerar.
Beviset liknar sats 5.
Anteckningar :

Exempel 12. Undersök serien för konvergens  .
.
Denna serie är positiv, eftersom  för vem som helst
för vem som helst  . Sedan beräkningen av gränsen
. Sedan beräkningen av gränsen  orsaker vissa svårigheter, då utelämnar vi att kontrollera genomförbarheten av det nödvändiga kriteriet för konvergens av en serie.
orsaker vissa svårigheter, då utelämnar vi att kontrollera genomförbarheten av det nödvändiga kriteriet för konvergens av en serie.
då, enligt Cauchy-kriteriet, divergerar denna serie.
SAT 7 (Integraltest för Maclaurin - Cauchy-konvergens)
Låt en serie ges
vars villkor är positiva och inte ökar:

Låt, vidare
 - en funktion som är definierad för alla verkliga
- en funktion som är definierad för alla verkliga  , är kontinuerlig, ökar inte och
, är kontinuerlig, ökar inte och
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0

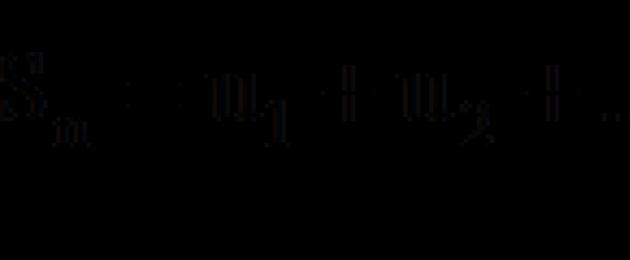
 ;
;
 ;
;
 ;
;