Balans i mekanik. Stabil och instabil jämvikt

DEFINITION

hållbar balans- detta är en jämvikt där kroppen, tagen ur jämvikt och lämnad åt sig själv, återgår till sin tidigare position.

Detta inträffar om, med en lätt förskjutning av kroppen i någon riktning från utgångsläget, resultatet av de krafter som verkar på kroppen blir icke-noll och riktas mot jämviktsläget. Till exempel en boll som ligger i botten av en sfärisk hålighet (Fig. 1a).

DEFINITION

Instabil jämvikt- detta är en jämvikt där kroppen, tagen ur jämviktspositionen och lämnad åt sig själv, kommer att avvika ännu mer från jämviktspositionen.

I detta fall, med en liten förskjutning av kroppen från jämviktspositionen, är resultanten av de krafter som appliceras på den inte noll och riktas från jämviktspositionen. Ett exempel är en kula placerad på toppen av en konvex sfärisk yta (Fig. 1 b).

DEFINITION

Likgiltig balans- detta är en jämvikt där kroppen, tagen ur jämvikt och lämnad åt sig själv, inte ändrar sin position (tillstånd).

I detta fall, med små förskjutningar av kroppen från dess ursprungliga position, förblir resultanten av de krafter som appliceras på kroppen lika med noll. Till exempel en boll som ligger på en plan yta (fig. 1, c).

Figur 1. Olika typer av kroppsbalans på ett stöd: a) stabil balans; b) instabil jämvikt; c) likgiltig jämvikt.

Statisk och dynamisk balans mellan kroppar

Om kroppen, som ett resultat av krafternas inverkan, inte får acceleration, kan den vara i vila eller röra sig jämnt i en rak linje. Därför kan vi prata om statisk och dynamisk jämvikt.

DEFINITION

Statisk balans- detta är en sådan jämvikt när kroppen är i vila under inverkan av applicerade krafter.

dynamisk balans- detta är en sådan jämvikt när kroppen inte ändrar sin rörelse under inverkan av krafter.

I ett tillstånd av statisk jämvikt är en lykta upphängd på kablar, vilken byggnadskonstruktion som helst. Som ett exempel på dynamisk jämvikt kan vi betrakta ett hjul som rullar på en plan yta i frånvaro av friktionskrafter.

Det följer att om den geometriska summan av alla yttre krafter appliceras på kroppen är lika med noll, då är kroppen i vila eller utför enhetlig rätlinjig rörelse. I det här fallet är det vanligt att säga att krafterna som appliceras på kroppen balanserar varandra. Vid beräkning av resultanten kan alla krafter som verkar på kroppen appliceras på massans centrum.

För att en icke-roterande kropp ska vara i jämvikt är det nödvändigt att resultanten av alla krafter som appliceras på kroppen är lika med noll.

$(\overrightarrow(F))=(\overrightarrow(F_1))+(\overrightarrow(F_2))+...= 0$

Om en kropp kan rotera kring någon axel, så räcker det för dess jämvikt inte att resultanten av alla krafter är lika med noll.

En krafts roterande verkan beror inte bara på dess storlek, utan också på avståndet mellan kraftens verkningslinje och rotationsaxeln.

Längden på vinkelrät draget från rotationsaxeln till kraftens verkningslinje kallas kraftens arm.

Produkten av kraftmodulen $F$ och armen d kallas kraftmomentet M. Momenten för de krafter som tenderar att rotera kroppen moturs anses vara positiva.

Momentregeln: en kropp med en fast rotationsaxel är i jämvikt om den algebraiska summan av momenten av alla krafter som appliceras på kroppen kring denna axel är noll:

I det allmänna fallet, när en kropp kan röra sig translationellt och rotera, måste båda villkoren vara uppfyllda för jämvikt: den resulterande kraften måste vara lika med noll och summan av alla kraftmoment måste vara lika med noll. Båda dessa villkor är inte tillräckliga för vila.

Figur 1. Indifferent jämvikt. Hjul som rullar på en horisontell yta. Den resulterande kraften och kraftmomentet är lika med noll

Ett hjul som rullar på en horisontell yta är ett exempel på likgiltig jämvikt (Fig. 1). Om hjulet stoppas vid något tillfälle kommer det att vara i jämvikt. Tillsammans med likgiltig jämvikt inom mekaniken urskiljs tillstånd av stabil och instabil jämvikt.

Ett jämviktstillstånd kallas stabilt om det med små avvikelser av kroppen från detta tillstånd uppstår krafter eller kraftmoment som tenderar att återföra kroppen till ett jämviktstillstånd.

Med en liten avvikelse hos kroppen från tillståndet av instabil jämvikt uppstår krafter eller kraftmoment som tenderar att avlägsna kroppen från jämviktspositionen. En boll som ligger på en plan horisontell yta är i ett tillstånd av likgiltig jämvikt.

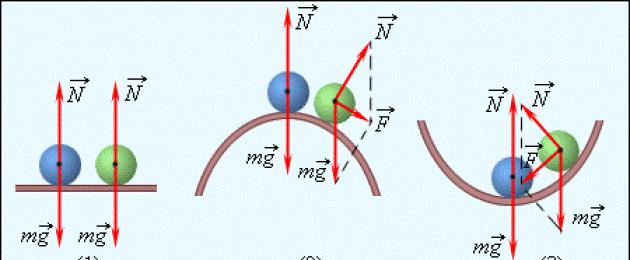
Figur 2. Olika typer av balans av en boll på ett stöd. (1) -- indifferent jämvikt, (2) -- instabil jämvikt, (3) -- stabil jämvikt

En boll som är placerad på toppen av en sfärisk avsats är ett exempel på en instabil jämvikt. Slutligen är kulan i botten av den sfäriska håligheten i ett tillstånd av stabil jämvikt (fig. 2).

För en kropp med en fast rotationsaxel är alla tre typer av jämvikt möjliga. Indifferent jämvikt uppstår när rotationsaxeln passerar genom masscentrum. I stabil och instabil jämvikt ligger massans centrum på en vertikal linje som går genom rotationsaxeln. I detta fall, om masscentrum ligger under rotationsaxeln, är jämviktstillståndet stabilt. Om masscentrum ligger ovanför axeln är jämviktstillståndet instabilt (fig. 3).

Figur 3. Stabil (1) och instabil (2) jämvikt för en homogen cirkulär skiva fixerad på O-axeln; punkt C är skivans masscentrum; $(\overrightarrow(F))_t\ $-- gravitation; $(\överhögerpil(F))_(y\ )$-- elastisk kraft för axeln; d -- axel

Ett specialfall är en kropps jämvikt på ett stöd. I detta fall appliceras inte stödets elastiska kraft på en punkt, utan fördelas över kroppens bas. Kroppen är i jämvikt om en vertikal linje dragen genom kroppens masscentrum passerar genom stödområdet, dvs innanför konturen som bildas av linjer som förbinder stödpunkterna. Om denna linje inte korsar stödområdet, välter kroppen.

Uppgift 1

Det lutande planet lutar i en vinkel på 30o mot horisonten (fig. 4). Det finns en kropp P på den, vars massa är m=2 kg. Friktion kan försummas. Gängan som kastas över blocket bildar en vinkel på 45o med det lutande planet. Vid vilken vikt av belastningen Q kommer kroppen P att vara i jämvikt?

Bild 4

Kroppen påverkas av tre krafter: tyngdkraften P, trådens spänning med belastningen Q och den elastiska kraften F från sidan av planet som trycker på den i riktning vinkelrät mot planet. Låt oss dekomponera kraften Р i komponenter: $\överhögerpil(Р)=(\överhögerpil(Р))_1+(\överhögerpil(Р))_2$. Villkor $(\overrightarrow(P))_2=$ För jämvikt, med hänsyn till dubbleringen av ansträngningen av det rörliga blocket, är det nödvändigt att $\overrightarrow(Q)=-(2\overrightarrow(P))_1$. Därav jämviktsvillkoret: $m_Q=2m(sin \widehat((\överhögerpil(P))_1(\överhögerpil(P))_2)\ )$. Om vi ​​ersätter värdena får vi: $m_Q=2\cdot 2(sin \left(90()^\circ -30()^\circ -45()^\circ \right)\ )=1,035\ kg$.

I vinden hänger den tjudrade ballongen över en annan punkt på jorden, till vilken kabeln är fäst (fig. 5). Kabelspänningen är 200 kg, vinkeln mot vertikalen är a=30$()^\circ$. Vad är vindtryckets kraft?

\[(\överhögerpil(F))_in=-(\överhögerpil(T))_1;\ \ \ \ \vänster|(\överhögerpil(F))_in\höger|=\vänster|(\överhögerpil(T)) _1\right|=Tg(sin (\mathbf \alpha )\ )\] \[\left|(\overrightarrow(F))_in\right|=\ 200\cdot 9.81\cdot (sin 30()^\circ \ )=981\ N\]

Denna föreläsning tar upp följande frågor:

1. Förutsättningar för jämvikt mellan mekaniska system.

2. Jämviktsstabilitet.

3. Ett exempel på att bestämma jämviktspositioner och studera deras stabilitet.

Studiet av dessa frågor är nödvändigt för att studera svängningsrörelserna hos ett mekaniskt system i förhållande till jämviktspositionen i disciplinen "Maskindelar", för att lösa problem i disciplinerna "Teori om maskiner och mekanismer" och "Materialstyrka".

Ett viktigt fall av rörelse hos mekaniska system är deras oscillerande rörelse. Oscillationer är upprepade rörelser av ett mekaniskt system med avseende på några av dess positioner, som inträffar mer eller mindre regelbundet i tiden. Kursen behandlar ett mekaniskt systems oscillerande rörelse i förhållande till jämviktspositionen (relativ eller absolut).

Ett mekaniskt system kan svänga under en tillräckligt lång tidsperiod endast nära en position med stabil jämvikt. Innan vi sammanställer ekvationerna för oscillerande rörelse är det därför nödvändigt att hitta jämviktspositionerna och undersöka deras stabilitet.

Jämviktsförhållanden för mekaniska system.

Enligt principen möjliga rörelser(statikens grundläggande ekvation), för att ett mekaniskt system, på vilket idealiska, stationära, begränsande och holonomiska begränsningar är pålagda, ska vara i jämvikt, är det nödvändigt och tillräckligt att alla generaliserade krafter i detta system är lika med noll:

var är den generaliserade kraft som motsvarar j-åh generaliserad koordinat;

s- antalet generaliserade koordinater i det mekaniska systemet.

Om differentialekvationer för rörelse kompilerades för det studerade systemet i form av Lagrangekvationer av det andra slaget, då för att bestämma de möjliga jämviktspositionerna, är det tillräckligt att likställa de generaliserade krafterna till noll och lösa de resulterande ekvationerna med avseende på generaliserade koordinater.

Om det mekaniska systemet är i jämvikt i ett potentiellt kraftfält, får vi från ekvation (1) följande jämviktsförhållanden:

Därför har den potentiella energin i jämviktsläget ett extremt värde. Inte varje jämvikt som definieras av ovanstående formler kan realiseras i praktiken. Beroende på systemets beteende när man avviker från jämviktspositionen talar man om stabiliteten eller instabiliteten i denna position.

Balansstabilitet

Definitionen av begreppet stabilitet i en jämviktsposition gavs i slutet av 1800-talet i den ryska vetenskapsmannen A. M. Lyapunovs verk. Låt oss titta på denna definition.

För att förenkla beräkningarna kommer vi vidare överens om de generaliserade koordinaterna q 1 , q 2 ,...,q s räkna från systemets jämviktsposition:

var

En jämviktsposition kallas stabil om för något godtyckligt litet taldu kan hitta ett annat nummer , det i fallet när de initiala värdena för de generaliserade koordinaterna och hastigheterna inte kommer att överskrida:

värden på generaliserade koordinater och hastigheter under ytterligare rörelse av systemet kommer inte att överstiga .

Med andra ord systemets jämviktsposition q 1 = q 2 = ...= q s= 0 kallas hållbar, om det alltid är möjligt att hitta sådana tillräckligt små initiala värden, vid vilken systemets rörelsekommer inte att lämna något givet godtyckligt litet område av jämviktspositionen. För ett system med en frihetsgrad kan systemets stabila rörelse visualiseras i fasplanet (fig. 1).För en stabil jämviktsposition, rörelsen av den representativa punkten, med början i området [ ] , kommer inte att gå utöver området i framtiden.

Figur 1

Jämviktspositionen kallas asymptotiskt stabil , om systemet med tiden kommer att närma sig jämviktspositionen, dvs

Att bestämma villkoren för stabiliteten i en jämviktsposition är en ganska svår uppgift, så vi begränsar oss till det enklaste fallet: studiet av stabiliteten i jämvikten hos konservativa system.

Tillräckliga villkor för stabiliteten av jämviktspositioner för sådana system definieras av Lagrange - Dirichlets sats : jämviktspositionen för ett konservativt mekaniskt system är stabil om, i jämviktspositionen, systemets potentiella energi har ett isolerat minimum .

Den potentiella energin för ett mekaniskt system bestäms upp till en konstant. Vi väljer denna konstant så att i jämviktsposition potentiell energi var lika med noll:

P(0)=0.

Då, för ett system med en frihetsgrad, är ett tillräckligt villkor för existensen av ett isolerat minimum, tillsammans med det nödvändiga villkoret (2), villkoret

Eftersom den potentiella energin i jämviktsläget har ett isolerat minimum och P(0)=0 , sedan i någon begränsad omgivning av denna position

П(q)=0.

Funktioner som har ett konstant tecken och är lika med noll endast när alla deras argument är noll anropas teckenbestämd. Därför, för att jämviktspositionen för ett mekaniskt system ska vara stabil, är det nödvändigt och tillräckligt att, i närheten av denna position, den potentiella energin är en positivt definierad funktion av generaliserade koordinater.

För linjära system och för system som kan reduceras till linjära för små avvikelser från jämviktspositionen (linjäriserad), kan den potentiella energin representeras som en kvadratisk form av generaliserade koordinater

var - generaliserade styvhetskoefficienter.

Generaliserade koefficienterär konstanta tal som kan bestämmas direkt från expansionen av den potentiella energin till en serie eller från värdena för den potentiella energins andraderivator med avseende på de generaliserade koordinaterna i jämviktspositionen:

Det följer av formel (4) att de generaliserade styvhetskoefficienterna är symmetriska med avseende på indexen

För det För att uppfylla tillräckliga villkor för jämviktspositionens stabilitet måste den potentiella energin vara en positiv bestämd kvadratisk form av dess generaliserade koordinater.

I matematik finns det Sylvesters kriterium , vilket ger nödvändiga och tillräckliga förutsättningar för den positiva bestämheten hos kvadratiska former: den kvadratiska formen (3) kommer att vara positiv definitiv om determinanten som består av dess koefficienter och alla dess huvudsakliga diagonala minorer är positiva, dvs. om koefficienterna kommer att uppfylla villkoren

.....

I synnerhet för linjärt system med två frihetsgrader kommer den potentiella energin och förutsättningarna för Sylvester-kriteriet att ha formen

På liknande sätt kan man studera positionerna för relativ jämvikt om man istället för potentiell energi tar hänsyn till det reducerade systemets potentiella energi.

P Ett exempel på att bestämma jämviktspositioner och studera deras stabilitet

Fig.2

Överväga mekaniskt system bestående av ett rör AB, som är pivoten OO 1 ansluten till den horisontella rotationsaxeln, och en kula som rör sig genom röret utan friktion och är ansluten till en punkt A rör med en fjäder (fig. 2). Låt oss bestämma systemets jämviktspositioner och utvärdera deras stabilitet för följande parametrar: rörlängd l 2 = 1 m , spö längd l 1 = 0,5 m . odeformerad fjäderlängd l 0 = 0,6 m, fjäderhastighet c= 100 N/m. Rörvikt m 2 = 2 kg, spö - m 1 = 1 kg och boll - m 3 = 0,5 kg. Distans OA lika l 3 = 0,4 m.

Låt oss skriva ett uttryck för den potentiella energin i det aktuella systemet. Den består av den potentiella energin hos tre kroppar i ett enhetligt gravitationsfält och den potentiella energin hos en deformerad fjäder.

En kropps potentiella energi i tyngdfältet är lika med produkten av kroppens vikt och höjden av dess tyngdpunkt över det plan där den potentiella energin anses vara noll. Låt den potentiella energin vara noll i planet som passerar genom stavens rotationsaxel OO 1, sedan för gravitationen

För den elastiska kraften bestäms den potentiella energin av mängden deformation

Låt oss hitta systemets möjliga jämviktspositioner. Koordinatvärdena i jämviktspositionerna är rötterna till följande ekvationssystem.

Ett liknande ekvationssystem kan sammanställas för vilket mekaniskt system som helst med två frihetsgrader. I vissa fall är det möjligt att få en exakt lösning av systemet. För system (5) existerar inte en sådan lösning, så rötterna måste sökas med numeriska metoder.

Genom att lösa systemet med transcendentala ekvationer (5) får vi två möjliga jämviktspositioner:

För att bedöma stabiliteten hos de erhållna jämviktspositionerna hittar vi alla andraderivator av den potentiella energin med avseende på de generaliserade koordinaterna och bestämmer de generaliserade styvhetskoefficienterna från dem.

En kropp är i vila (eller rör sig jämnt och i en rät linje) om vektorsumman av alla krafter som verkar på den är noll. Krafterna sägs balansera varandra. När vi har att göra med en kropp av en viss geometrisk form, när vi beräknar den resulterande kraften, kan alla krafter appliceras på kroppens masscentrum.

Villkoret för kropparnas jämvikt

För att en kropp som inte roterar ska vara i jämvikt är det nödvändigt att resultanten av alla krafter som verkar på den är lika med noll.

F → = F 1 → + F 2 → + . . + Fn → = 0 .

Bilden ovan visar balansen fast kropp. Blocket är i ett tillstånd av jämvikt under inverkan av tre krafter som verkar på det. Verkningslinjerna för krafterna F 1 → och F 2 → skär varandra i punkten O. Tillämpningspunkten för tyngdkraften är kroppens masscentrum C. Dessa punkter ligger på en rät linje och vid beräkning av den resulterande kraften reduceras F 1 → , F 2 → och mg → till punkt C .

Villkoret att resultanten av alla krafter är lika med noll är inte tillräckligt om kroppen kan rotera runt någon axel.

Kraftens d skuldra är längden av vinkelrät draget från kraftens verkningslinje till punkten för dess applicering. Kraftmomentet M är produkten av kraftens arm och dess modul.

Kraftmomentet tenderar att rotera kroppen runt sin axel. De ögonblick som roterar kroppen moturs anses vara positiva. Måttenheten för kraftmomentet i internationella systemet C - 1 N m e t r.

Definition. momentregel

Om den algebraiska summan av alla moment som appliceras på kroppen i förhållande till den fasta rotationsaxeln är lika med noll, är kroppen i jämvikt.

M1 + M2+. . + Mn = 0

Viktig!

I det allmänna fallet, för kroppars jämvikt, måste två villkor vara uppfyllda: den resulterande kraften är lika med noll och momentregeln iakttas.

Det finns olika typer av jämvikt inom mekanik. Därmed skiljer man mellan stabil och instabil, samt likgiltig jämvikt.

Ett typiskt exempel på en likgiltig jämvikt är ett rullande hjul (eller kula), som, om det stoppas vid någon punkt, kommer att vara i ett jämviktstillstånd.

Stabil jämvikt är en sådan jämvikt hos en kropp när det med sina små avvikelser uppstår krafter eller kraftmoment som tenderar att återföra kroppen till ett jämviktstillstånd.

Instabil jämvikt - ett tillstånd av jämvikt, med en liten avvikelse från vilken krafterna och kraftmomenten tenderar att få kroppen ur balans ännu mer.

I figuren ovan är kulans position (1) - indifferent jämvikt, (2) - instabil jämvikt, (3) - stabil jämvikt.

kropp med fast axel rotation kan vara i vilken som helst av de beskrivna jämviktspositionerna. Om rotationsaxeln passerar genom masscentrum uppstår en likgiltig jämvikt. I stabil och instabil jämvikt ligger masscentrum på en vertikal linje som går genom rotationsaxeln. När masscentrum ligger under rotationsaxeln är jämvikten stabil. Annars tvärtom.

Ett specialfall av jämvikt är jämvikten hos en kropp på ett stöd. I detta fall är den elastiska kraften fördelad över hela basen av kroppen och passerar inte genom en punkt. En kropp är i vila i jämvikt när en vertikal linje dragen genom massans centrum skär stödområdet. Annars, om linjen från massans centrum inte faller in i konturen som bildas av linjerna som förbinder stödpunkterna, välter kroppen.

Ett exempel på balansen hos en kropp på ett stöd är det berömda lutande tornet i Pisa. Enligt legenden tappade Galileo Galilei bollar från den när han utförde sina experiment på att studera fritt fall tel.

En linje dragen från tornets masscentrum skär basen cirka 2,3 m från dess centrum.

Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter

Klass: 10

Presentation för lektionen

Tillbaka framåt

Uppmärksamhet! Förhandsvisningen av bilden är endast i informationssyfte och representerar kanske inte hela omfattningen av presentationen. Om du är intresserad av detta arbete, ladda ner den fullständiga versionen.

Lektionens mål: Att studera kroppars jämviktstillstånd, att bekanta sig med olika typer av jämvikt; ta reda på de förhållanden under vilka kroppen är i jämvikt.

Lektionens mål:

• Träning: Att studera två jämviktsförhållanden, typer av jämvikt (stabil, instabil, likgiltig). Ta reda på under vilka förhållanden kroppar är mer stabila.
• Utvecklande: Att främja utvecklingen av kognitivt intresse för fysik. Utveckling av färdigheter för att jämföra, generalisera, lyfta fram det viktigaste, dra slutsatser.
• Pedagogisk: Att odla uppmärksamhet, förmågan att uttrycka sin åsikt och försvara den, att utveckla elevernas kommunikationsförmåga.

Lektionstyp: lektion lära nytt material med datorstöd.

Utrustning:

1. Diskett "Arbete och kraft" från "Elektroniska lektioner och tester.
2. Tabell "Jämviktsförhållanden".
3. Prisma lutande med ett lod.
4. Geometriska kroppar: cylinder, kub, kon, etc.
5. Dator, multimediaprojektor, interaktiv whiteboard eller skärm.
6. Presentation.

Under lektionerna

Idag i lektionen kommer vi att lära oss varför kranen inte faller, varför Roly-Vstanka-leksaken alltid återgår till sitt ursprungliga tillstånd, varför det lutande tornet i Pisa inte faller?

I. Upprepning och uppdatering av kunskap.

1. Formulera Newtons första lag. Vilken status har lagen?
2. Vilken fråga besvarar Newtons andra lag? Formel och formulering.
3. Vilken fråga besvarar Newtons tredje lag? Formel och formulering.
4. Vad är den resulterande kraften? Hur är hon?
5. Från skivan "Rörelse och interaktion av kroppar" slutför uppgift nr 9 "Resultanten av krafter med olika riktningar" (regeln för vektoraddition (2, 3 övningar)).

II. Att lära sig nytt material.

1. Vad kallas jämvikt?

Jämvikt är ett vilotillstånd.

2. Jämviktsförhållanden.(bild 2)

a) När är kroppen i vila? Vilken lag kommer detta ifrån?

Det första jämviktstillståndet: En kropp är i jämvikt om den geometriska summan av de yttre krafterna som appliceras på kroppen är noll. ∑ F = 0

b) Låt två lika krafter verka på brädan, som visas i figuren.

Kommer hon att vara i balans? (Nej, hon kommer att vända sig)

I vila är bara central punkt och resten rör på sig. Det betyder att för att kroppen ska vara i jämvikt är det nödvändigt att summan av alla krafter som verkar på varje element är lika med 0.

Det andra jämviktstillståndet: Summan av kraftmomenten som verkar medurs måste vara lika med summan av kraftmomenten som verkar moturs.

∑ M medurs = ∑ M moturs

Kraftmoment: M = F L

L - kraftaxel - det kortaste avståndet från stödpunkten till kraftens verkningslinje.

3. Kroppens tyngdpunkt och dess placering.(bild 4)

Kroppens tyngdpunkt- detta är den punkt genom vilken resultanten av alla parallella gravitationskrafter som verkar på enskilda delar av kroppen passerar (i vilken position som helst av kroppen i rymden).

Hitta tyngdpunkten för följande figurer:

4. Typer av balans.

men) (bilder 5-8)

Produktion: Jämvikten är stabil om det, med en liten avvikelse från jämviktspositionen, finns en kraft som tenderar att återföra den till detta läge.

Den position där dess potentiella energi är minimal är stabil. (bild 9)

b) Stabiliteten hos kroppar som är belägna på fulcrum eller på fulcrum.(bilder 10-17)

Produktion: För stabiliteten hos en kropp placerad på en punkt eller stödlinje är det nödvändigt att tyngdpunkten ligger under stödpunkten (linjen).

c) Stabiliteten av kroppar på en plan yta.

(bild 18)

1) Stödyta- det här är inte alltid en yta som är i kontakt med kroppen (men en som är begränsad av linjer som förbinder benen på bordet, stativet)

2) Analys av en bild från "Elektroniska lektioner och tester", skiva "Arbete och kraft", lektion "Typer av balans".

Bild 1.

1. Hur skiljer sig avföringen? (kvadratfot)
2. Vilken är mer stabil? (med större yta)
3. Hur skiljer sig avföringen? (Placering av tyngdpunkten)
4. Vilken är den mest stabila? (vilken tyngdpunkt är lägre)
5. Varför? (Eftersom den kan avledas till en större vinkel utan att välta)

3) Erfarenhet av ett avvikande prisma

1. Låt oss sätta ett prisma med ett lod på brädan och börja gradvis lyfta det över ena kanten. Vad ser vi?
2. Så länge lodet korsar ytan som begränsas av stödet, upprätthålls balansen. Men så snart den vertikala passagen genom tyngdpunkten börjar gå utanför stödytans gränser, välter bokhyllan.

Parsing bilder 19–22.

Slutsatser:

1. Kroppen med det största stödområdet är stabil.
2. Av två kroppar av samma område är kroppen vars tyngdpunkt är lägre stabil, eftersom den kan avledas utan att välta i stor vinkel.

Parsing bilder 23–25.

Vilka fartyg är mest stabila? Varför? (För vilken lasten är placerad i lastrummen och inte på däck)

Vilka bilar är mest stabila? Varför? (För att öka bilarnas stabilitet i svängar lutar vägbädden i svängens riktning.)

Slutsatser: Jämvikt kan vara stabilt, instabilt, likgiltigt. Kropparnas stabilitet är större, ju större stödytan är och ju lägre tyngdpunkten är.

III. Tillämpning av kunskap om kroppars stabilitet.

1. Vilka specialiteter behöver mest kunskap om kroppars balans?
2. Designers och designers av olika strukturer ( höghus, broar, TV-torn, etc.)
3. Cirkusartister.
4. Förare och andra proffs.

(bilder 28–30)

1. Varför återgår Roly-Vstanka till jämviktspositionen vid någon lutning av leksaken?
2. Varför lutar det lutande tornet i Pisa och faller inte?
3. Hur håller cyklister och motorcyklister balansen?

Lektionshämtmat:

1. Det finns tre typer av jämvikt: stabil, instabil, likgiltig.
2. Kroppens position är stabil, där dess potentiella energi är minimal.
3. Stabiliteten hos kroppar på en plan yta är större, ju större stödytan är och ju lägre tyngdpunkten är.

Läxa: § 54 – 56 (G.Ya. Myakishev, B.B. Bukhovtsev, N.N. Sotsky)

Använda källor och litteratur:

1. G.Ya. Myakishev, B.B. Bukhovtsev, N.N. Sotsky. Fysik. Årskurs 10.
2. Filmremsa "Stabilitet" 1976 (skannad av mig på en filmskanner).
3. Disk "Rörelse och interaktion av kroppar" från "Elektroniska lektioner och tester".
4. Diskett "Arbete och kraft" från "Elektroniska lektioner och tester".