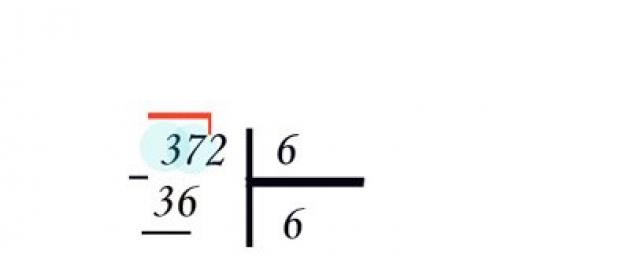Инструкция

Сначала проверьте навыки ребенка в умножении. Если ребенок нетвердо знает таблицу умножения, то с делением у него тоже могут быть проблемы. Тогда при объяснении деления можно разрешить подглядывать в шпаргалку, но таблицу все-таки придется выучить.

Запишите делимое и делитель через разделительную вертикальную черту. Под делителем вы будете записывать ответ - частное, отделив его горизонтальной чертой. Возьмите первую цифру числа 372 и спросите у ребенка, сколько раз число шесть «помещается» в тройке. Правильно, нисколько.

Тогда возьмите уже две цифры - 37. Для наглядности можно выделить их уголком. Снова повторите вопрос – сколько раз число шесть содержится в 37. Чтобы сосчитать быстро, пригодится . Подберите ответ вместе: 6*4 = 24 – совсем непохоже; 6*5 = 30 – близко к 37. Но 37-30 = 7 – шесть «поместится» еще раз. Наконец, 6*6 = 36, 37-36 = 1 – подходит. Первая цифра частного найдена – это 6. Напишите ее под делителем.

Запишите 36 под цифрой 37, подведите чертой. Для наглядности в записи можно использовать знак . Под чертой поставьте остаток – 1. Теперь «спустите» следующую цифру числа, двойку, к единице – получилось 12. Объясните ребенку, что цифры всегда «спускаются» по одной. Опять спросите, сколько «шестерок» содержит 12. Ответ – 2, на этот раз без остатка. Напишите вторую цифру частного рядом с первой. Окончательный результат – 62.

Также подробно рассмотрите случай деления . Например, 167/6 = 27, остаток 5. Скорее всего, ваш отпрыск про простые дроби пока ничего не слышал. Но если он будет задавать вопросы, что делать с остатком дальше, можно объяснить на примере яблок. 167 яблок разделили между шестью людьми. Каждому досталось 27 штук, и пять яблок остались неподеленными. Можно поделить и их, разрезав каждое на шесть долек и раздав поровну. Каждому человеку досталась одна долька от каждого яблока – 1/6. А так как яблок было пять штук, то и долек у каждого оказалось по пять – 5/6. То есть результат можно записать так: 27 5/6.

В этой статье мы разберем деление целых чисел с остатком . Начнем с общего принципа деления целых чисел с остатком, сформулируем и докажем теорему о делимости целых чисел с остатком, проследим связи между делимым, делителем, неполным частным и остатком. Дальше озвучим правила, по которым проводится деление целых чисел с остатком, и рассмотрим применение этих правил при решении примеров. После этого научимся выполнять проверку результата деления целых чисел с остатком.

Навигация по странице.

Общее представление о делении целых чисел с остатком

Деление целых чисел с остатком мы будем рассматривать как обобщение деления с остатком натуральных чисел . Это обусловлено тем, что натуральные числа являются составной частью целых чисел .

Начнем с терминов и обозначений, которые используются при описании.

По аналогии с делением натуральных чисел с остатком будем считать, что результатом деления с остатком двух целых чисел a и b (b не равно нулю) являются два целых числа c и d . Числа a и b называются делимым и делителем соответственно, число d – остатком от деления a на b , а целое число c называется неполным частным (или просто частным , если остаток равен нулю).

Условимся считать, что остаток есть целое неотрицательное число , и его величина не превосходит b , то есть, (подобные цепочки неравенств мы встречали, когда говорили о сравнении трех и большего количества целых чисел).

Если число c является неполным частным, а число d – остатком от деления целого числа a на целое число b , то этот факт мы будем кратко записывать как равенство вида a:b=c (ост. d) .

Отметим, что при делении целого числа a на целое число b остаток может быть равным нулю. В этом случае говорят, что a делится на b без остатка (или нацело ). Таким образом, деление целых чисел без остатка является частным случаем деления целых чисел с остатком.

Также стоит сказать, что при делении нуля на некоторое целое число мы всегда имеем дело с делением без остатка, так как в этом случае частное будет равно нулю (смотрите раздел теории деление нуля на целое число), и остаток также будет равен нулю.

С терминологией и обозначениями определились, теперь разберемся со смыслом деления целых чисел с остатком.

Делению целого отрицательного числа a на целое положительное число b тоже можно придать смысл. Для этого рассмотрим целое отрицательное число как долг . Представим такую ситуацию. Долг, который составляет предметов, должны погасить b человек, внеся одинаковый вклад. Абсолютная величина неполного частного c в этом случае будет определять величину долга каждого из этих людей, а остаток d покажет, какое количество предметов останется после уплаты долга. Приведем пример. Допустим 2 человека должны 7 яблок. Если считать, что каждый из них должен по 4 яблока, то после уплаты долга у них останется 1 яблоко. Этой ситуации отвечает равенство (−7):2=−4 (ост. 1) .

Делению с остатком произвольного целого числа a на целое отрицательное число мы не будем придавать никакого смысла, но оставим за ним право на существование.

Теорема о делимости целых чисел с остатком

Когда мы говорили о делении натуральных чисел с остатком, то выяснили, что делимое a , делитель b , неполное частное c и остаток d связаны между собой равенством a=b·c+d . Для целых чисел a , b , c и d характерна такая же связь. Эта связь утверждается следующей теоремой о делимости с остатком .

Теорема.

Любое целое число a возможно представить единственным образом через целое и отличное от нуля число b в виде a=b·q+r , где q и r – некоторые целые числа, причем .

Доказательство.

Сначала докажем возможность представления a=b·q+r .

Если целые числа a и b такие, что a делится на b нацело, то по определению существует такое целое число q , что a=b·q . В этом случае имеет место равенство a=b·q+r при r=0 .

Теперь будем считать, что b – целое положительное число. Выберем целое число q таким образом, чтобы произведение b·q не превышало числа a , а произведение b·(q+1) было уже больше, чем a . То есть, возьмем q таким, чтобы выполнялись неравенства b·q

Осталось доказать возможность представления a=b·q+r для отрицательных b .

Так как модуль числа b в этом случае является положительным числом, то для имеет место представление , где q 1 – некоторое целое число, а r – целое число, удовлетворяющее условиям . Тогда, приняв q=−q 1 , получаем нужное нам представление a=b·q+r для отрицательных b .

Переходим к доказательству единственности.

Предположим, что помимо представления a=b·q+r , q и r – целые числа и , существует еще одно представление a=b·q 1 +r 1 , где q 1 и r 1 – некоторые целые числа, причем q 1 ≠q и .

После вычитания из левой и правой части первого равенства соответственно левой и правой части второго равенства, получаем 0=b·(q−q 1)+r−r 1 , которое равносильно равенству r−r 1 =b·(q 1 −q) . Тогда должно быть справедливо и равенство вида , а в силу свойств модуля числа - и равенство .

Из условий и можно сделать вывод, что . Так как q и q 1 – целые и q≠q 1 , то , откуда заключаем, что . Из полученных неравенств и следует, что равенство вида невозможно при нашем предположении. Поэтому, не существует другого представления числа a , кроме a=b·q+r .

Связи между делимым, делителем, неполным частным и остатком

Равенство a=b·c+d позволяет находить неизвестное делимое a , если известны делитель b , неполное частное c и остаток d . Рассмотрим пример.

Пример.

Чему равно делимое, если при его делении на целое число −21 получилось неполное частное 5 и остаток 12 ?

Решение.

Нам требуется вычислить делимое a , когда известен делитель b=−21 , неполное частное c=5 и остаток d=12 . Обратившись к равенству a=b·c+d , получаем a=(−21)·5+12 . Соблюдая , сначала проводим умножение целых чисел −21 и 5 по правилу умножения целых чисел с разными знаками , после чего выполняем сложение целых чисел с разными знаками : (−21)·5+12=−105+12=−93 .

Ответ:

−93 .

Связи между делимым, делителем, неполным частным и остатком также выражаются равенствами вида b=(a−d):c , c=(a−d):b и d=a−b·c . Эти равенства позволяют вычислять делитель, неполное частное и остаток соответственно. Нам часто придется находить остаток от деления целого числа a на целое число b , когда известны делимое, делитель и неполное частное, используя формулу d=a−b·c . Чтобы в дальнейшем не возникало вопросов, разберем пример вычисления остатка.

Пример.

Найдите остаток от деления целого числа −19 на целое число 3 , если известно, что неполное частное равно −7 .

Решение.

Для вычисления остатка от деления воспользуемся формулой вида d=a−b·c . Из условия имеем все необходимые данные a=−19 , b=3 , c=−7 . Получаем d=a−b·c=−19−3·(−7)= −19−(−21)=−19+21=2 (разность −19−(−21) мы вычисляли по правилу вычитания целого отрицательного числа).

Ответ:

Деление с остатком целых положительных чисел, примеры

Как мы уже не раз отмечали, целые положительные числа представляют собой натуральные числа. Поэтому деление с остатком целых положительных чисел проводится по всем правилам деления с остатком натуральных чисел. Очень важно уметь с легкостью выполнять деление с остатком натуральных чисел , так как именно оно лежит в основе деления не только целых положительных чисел, но и в основе всех правил деления с остатком произвольных целых чисел.

С нашей точки зрения наиболее удобно выполнять деление столбиком , этот способ позволяет получить и неполное частное (или просто частное) и остаток. Рассмотрим пример деления с остатком целых положительных чисел.

Пример.

Выполните деление с остатком числа 14 671 на 54 .

Решение.

Выполним деление данных целых положительных чисел столбиком:

Неполное частное получилось равным 271 , а остаток равен 37 .

Ответ:

14 671:54=271 (ост. 37) .

Правило деления с остатком целого положительного числа на целое отрицательное, примеры

Сформулируем правило, позволяющее выполнять деление с остатком целого положительного числа на целое отрицательное число.

Неполное частное от деления целого положительного числа a на целое отрицательное число b представляет собой число, противоположное неполному частному от деления a на модуль числа b , а остаток от деления a на b равен остатку от деления на .

Из этого правила следует, что неполное частное от деления целого положительного числа на целое отрицательное число является целым неположительным числом .

Переделаем озвученное правило в алгоритм деления с остатком целого положительного числа на целое отрицательное:

• Делим модуль делимого на модуль делителя, получаем неполное частное и остаток. (Если при этом остаток получился равным нулю, то исходные числа делятся без остатка, и по правилу деления целых чисел с противоположными знаками искомое частное равно числу, противоположному частному от деления модулей.)
• Записываем число, противоположное полученному неполному частному, и остаток. Эти числа являются соответственно искомым частным и остатком от деления исходного целого положительного числа на целое отрицательное.

Приведем пример использования алгоритма деления целого положительного числа на целое отрицательное.

Пример.

Выполните деление с остатком целого положительного числа 17 на целое отрицательное число −5 .

Решение.

Воспользуемся алгоритмом деления с остатком целого положительного числа на целое отрицательное.

Разделив

Число, противоположное числу 3 , - это −3 . Таким образом, искомое неполное частное от деления 17 на −5 равно −3 , а остаток равен 2 .

Ответ:

17 :(−5)=−3 (ост. 2) .

Пример.

Разделите 45 на −15 .

Решение.

Модули делимого и делителя равны 45 и 15 соответственно. Число 45 делится на 15 без остатка, частное при этом равно 3 . Следовательно, целое положительное число 45 делится на целое отрицательное число −15 без остатка, частное при этом равно числу, противоположному 3 , то есть, −3 . Действительно, по правилу деления целых чисел с разными знаками имеем .

Ответ:

45:(−15)=−3 .

Деление с остатком целого отрицательного числа на целое положительное, примеры

Дадим формулировку правила деления с остатком целого отрицательного числа на целое положительное.

Чтобы получить неполное частное c от деления целого отрицательного числа a на целое положительное число b нужно взять число, противоположное неполному частному от деления модулей исходных чисел и вычесть из него единицу, после чего остаток d вычислить по формуле d=a−b·c .

Из данного правила деления с остатком следует, что неполное частное от деления целого отрицательного на целое положительное число является целым отрицательным числом.

Из озвученного правила вытекает алгоритм деления с остатком целого отрицательного числа a на целое положительное b :

• Находим модули делимого и делителя.
• Делим модуль делимого на модуль делителя, получаем неполное частное и остаток. (Если остаток равен нулю, то исходные целые числа делятся без остатка, и искомое частное равно числу, противоположному частному от деления модулей.)
• Записываем число, противоположное полученному неполному частному и вычитаем из него число 1 . Вычисленное число является искомым неполным частным c от деления исходного целого отрицательного числа на целое положительное.

Разберем решение примера, в котором воспользуемся записанным алгоритмом деления с остатком.

Пример.

Найдите неполное частное и остаток от деления целого отрицательного числа −17 на целое положительное число 5 .

Решение.

Модуль делимого −17 равен 17 , а модуль делителя 5 равен 5 .

Разделив 17 на 5 , получаем неполное частное 3 и остаток 2 .

Число, противоположное 3 , есть −3 . Вычитаем из −3 единицу: −3−1=−4 . Итак, искомое неполное частное равно −4 .

Осталось вычислить остаток. В нашем примере a=−17 , b=5 , c=−4 , тогда d=a−b·c=−17−5·(−4)= −17−(−20)=−17+20=3 .

Таким образом, неполное частное от деления целого отрицательного числа −17 на целое положительное число 5 равно −4 , а остаток равен 3 .

Ответ:

(−17):5=−4 (ост. 3) .

Пример.

Разделите целое отрицательное число −1 404 на целое положительное число 26 .

Решение.

Модуль делимого равен 1 404 , модуль делителя равен 26 .

Разделим 1 404 на 26 столбиком:

Так как модуль делимого разделился на модуль делителя без остатка, то исходные целые числа делятся без остатка, причем искомое частное равно числу, противоположному 54 , то есть, −54 .

Ответ:

(−1 404):26=−54 .

Правило деления с остатком целых отрицательных чисел, примеры

Сформулируем правило деления с остатком целых отрицательных чисел.

Чтобы получить неполное частное c от деления целого отрицательного числа a на целое отрицательное число b , нужно вычислить неполное частное от деления модулей исходных чисел и прибавить к нему единицу, после этого остаток d вычислить по формуле d=a−b·c .

Из этого правила следует, что неполное частное от деления целых отрицательных чисел является целым положительным числом.

Перепишем озвученное правило в виде алгоритма деления целых отрицательных чисел:

• Находим модули делимого и делителя.
• Делим модуль делимого на модуль делителя, получаем неполное частное и остаток. (Если остаток равен нулю, то исходные целые числа делятся без остатка, и искомое частное равно частному от деления модуля делимого на модуль делителя.)
• К полученному неполному частному прибавляем единицу, это число есть искомое неполное частное от деления исходных целых отрицательных чисел.
• Вычисляем остаток по формуле d=a−b·c .

Рассмотрим применение алгоритма деления целых отрицательных чисел при решении примера.

Пример.

Найдите неполное частное и остаток от деления целого отрицательного числа −17 на целое отрицательное число −5 .

Решение.

Воспользуемся соответствующим алгоритмом деления с остатком.

Модуль делимого равен 17 , модуль делителя равен 5 .

Деление 17 на 5 дает неполное частное 3 и остаток 2 .

К неполному частному 3 прибавляем единицу: 3+1=4 . Следовательно, искомое неполное частное от деления −17 на −5 равно 4 .

Осталось вычислить остаток. В этом примере a=−17 , b=−5 , c=4 , тогда d=a−b·c=−17−(−5)·4= −17−(−20)=−17+20=3 .

Итак, неполное частное от деления целого отрицательного числа −17 на целое отрицательное число −5 равно 4 , а остаток равен 3 .

Ответ:

(−17):(−5)=4 (ост. 3) .

Проверка результата деления целых чисел с остатком

После того, как выполнено деление целых чисел с остатком, полезно выполнить проверку полученного результата. Проверка проводится в два этапа. На первом этапе проверяется, является ли остаток d неотрицательным числом, а также проверяется выполнение условия . Если все условия первого этапа проверки выполнены, то можно приступать ко второму этапу проверки, в противном случае можно утверждать, что при делении с остатком где-то была допущена ошибка. На втором этапе проверяется справедливость равенства a=b·c+d . Если это равенство справедливо, то деление с остатком было проведено верно, в противном случае – где-то была допущена ошибка.

Рассмотрим решения примеров, в которых выполняется проверка результата деления целых чисел с остатком.

Пример.

При делении числа −521 на −12 было получено неполное частное 44 и остаток 7 , выполните проверку результата.

Решение. −2 при b=−3 , c=7 , d=1 . Имеем b·c+d=−3·7+1=−21+1=−20 . Таким образом, равенство a=b·c+d – неверное (в нашем примере a=−19 ).

Следовательно, деление с остатком было проведено неверно.

Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.

Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.

Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.

Приведем решение примера, так как понять суть метода проще всего на практике.

Пример 1. Как делить натуральные числа с остатком?

Разделим натуральное число 273844 на натуральное число 97 .

Проводим деление столбиком и записываем:

Результат: неполное частное от деления равно 2823 , а остаток равен 13 .

Деление чисел с остатком через последовательное вычитание

Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.

Пример 2. Деление с остатком через последовательное вычитание.

Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3 .

Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7 - 3 = 4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4 - 3 = 1 яблоко.

1 яблоко - это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:

7 ÷ 3 = 2 (остаток 1)

Это значит, что число 3 как бы умещается в числе 7 два раза, а единица - остаток, меньший чем 3 .

Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.

Пример 3. Деление с остатком через последовательное вычитание.

Вычислим: 145 ÷ 46 .

Число 99 больше, чем 46 , поэтому продолжаем последовательное вычитание делителя:

Повторяем эту операцию еще раз:

В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток - результат вычитания, который меньше делителя. В нашем случае остатком является число 7 .

145 ÷ 46 = 3 (остаток 7) .

Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.

Если a < b , то a ÷ b = 0 (остаток a) .

Например:

12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)

Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.

Метод подбора неполного частного

При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.

Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1 , 2 , 3 и т.д.

Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d = a - b · c . Здесь d - остаток от деления, a - делимое, b - делитель, с - неполное частное.

В-третьих, не будем забывать, что остаток всегда меньше делителя.

Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0 , 1 , 2 , 3 и т.д. Применяя формулу d = a - b · c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b . Число, взятое за с на этом шаге и будет неполным частным.

Разберем применение этого метода на примере.

Пример 4. Деление с остатком методом подбора

Разделим 267 на 21 .

a = 267 ; b = 21 . Подберем неполное частное.

Используем формулу d = a - b · c и будем последовательно перебирать c , придавая ему значения 0 , 1 , 2 , 3 и т.д.

Если с = 0 , имеем: d = a - b · c = 267 - 21 · 0 = 267 . Число 267 больше, чем 21 , поэтому продолжаем подстановку.

При с = 1 имеем: d = a - b · c = 267 - 21 · 1 = 246 . Т.к. 246 > 21 , снова повторяем процесс.

При с = 2 имеем: d = a - b · c = 267 - 21 · 2 = 267 - 42 = 225 ; 225 > 21 .

При с = 3 имеем: d = a - b · c = 267 - 21 · 3 = 267 - 63 = 204 ; 204 > 21 .

При с = 12 имеем: d = a - b · c = 267 - 21 · 12 = 267 - 252 = 15 ; 15 < 21 .

Алгоритм деления натуральных чисел с остатком

Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.

Вспомним, что в случае, когда a < b, неполное частное равно нулю, а остаток равен делимомому a . Мы будем рассматривать случай, когда a > b .

Сформулируем три вопроса и ответим на них:

1. Что там известно?
2. Что нам нужно найти?
3. Как мы будем это делать?

Изначально известными являются делимое и делитель: a и b .

Найти нужно неполное частное c и остаток d .

Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a = b · c + d . Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a = b · c + d , тогда мы найдем искомые величины.

Алгоритм деления, благодаря которому мы представим a в виде суммы a = b · c + d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47 .

1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе - два.

Запомним это число.

2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.

В нашем примере справа от 47 дописываем нуль. Так как 470 < 899 , запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.

3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10 . В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.

4. Будем последовательно умножать делитель на 1 , 2 , 3 . . и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.

Рабочий разряд в нашем примере - десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470 .

470 < 899 , поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47 · 20 = 940 ; 940 > 899 .

Число, которое мы получили на предпоследнем шаге (470 = 47 · 10) является первым из искомых слагаемых.

5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.

Шаги 1 - 5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1 - 5 , но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.

Обратимся к примеру. 899 - 470 = 429 , 429 > 47 . Повторяем шаги 1 - 5 алгоритма с числом 429 , взятым в качестве делимого.

1. В записи числа 429 на один знак больше, чем в записи числа 47 . Запоминаем разницу - число 1 .

2. В записи делимого справа дописываем один нуль. Получаем число 470 . Так как 470 > 429 , из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1 - 1 = 0 . Запоминаем 0 .

3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы

4. Последовательно умножим делитель 47 на 1 , 2 , 3 . . и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47 · 9 = 423 < 429 , 47 · 10 = 470 > 429 . Таким образом, второе искомое слагаемое - 47 · 9 = 423 .

5. Разность между 429 и 423 равна числу 6 . Так как 6 < 47 , это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.

6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899 = 470 + 423 + 6 . Вспоминаем, что 470 = 47 · 10 , 423 = 47 · 9 . Перепишем равенство:

899 = 47 · 10 + 47 · 9 + 6

Применим распределительное свойство умножения.

899 = 47 · 10 + 47 · 9 + 6 = 47 · (10 + 9) + 6

899 = 47 · 19 + 6 .

Таким образом, мы представили делимое в виде уже данной ранее формулы a = b · c + d .

Искомые неизвестные:неполное частное с = 19 , остаток d = 6 .

Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:

Пример 5. Деление натуральных чисел с остатком

Разделим числа 42252 и 68 .

Используем алгоритм. Первые пять шагов дают первое слагаемое - число 40800 = 68 · 600 .

Снова повторяем первые пять шагов алгоритма с числом 1452 = 42252 - 40800 и получаем второе слагаемое 1360 = 68 · 20

Третий раз проходим шаги аглоритма, но у же с новым числом 92 = 1452 - 1360 . Третье слагаемое равно 68 = 68 · 1 . Остаток равен 24 = 92 - 68 .

В результате получаем:

42252 = 40800 + 1360 + 68 + 24 = 68 · 600 + 68 · 20 + 68 · 1 + 24 = = 68 · (600 + 20 + 1) + 24 = 68 · 621 + 24

Неполное частное равно 621 , остаток равен 24 .

Деление натуральных чисел с остатком. Проверка результата

Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.

На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.

Важно!

Остаток всегда меньше делителя!

На втором этапе проверяется справедливость равенства a = b · c + d . Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.

Пример 6. Проверка результата деления натуральных чисел с остатком.

Проверим, верно ли, что 506 ÷ 28 = 17 (остаток 30) .

Сравниваем остаток и делитель: 30 > 28 .

Значит, деление выполнено неверно.

Пример 7. Проверка результата деления натуральных чисел с остатком.

Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5 . Правильно ли он сделал?

Чтобы узнать это, сначала сравниваем остаток и делитель: 5 < 13 .

Первый пункт проверки пройден, переходим ко второму.

Запишем формулу a = b · c + d . a = 121 ; b = 13 ; c = 9 ; d = 5 .

Подставляем значения и сравниваем результаты

13 · 9 + 5 = 117 + 5 = 122 ; 121 ≠ 122

Значит, в вычисления школьника где-то закралась ошибка.

Пример 8. Проверка результата деления натуральных чисел с остатком.

Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111 . В результате у него получилось число 54 с остатком 4 . Все ли правильно посчитано?

Проверим! Остаток 4 меньше, чем делитель 111 , поэтому переходим ко второму этапу проверки.

Используем формулу a = b · c + d , где a = 5998 ; b = 111 ; c = 54 ; d = 4 .

После подстановки, имеем:

5998 = 111 · 54 + 4 = 5994 + 4 = 5998 .

Равенство корректно, а значит, и деление выполнено верно.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.

• Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
• Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
• Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям

Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.

Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».

Итак, как объяснить ребенку деление столбиком :

• Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
• Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
• Пусть ребенок сам разделит другое число, например, более сложное: 24:4
• Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные

Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.

Начинайте с простого — деление на однозначное число:

Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.

Например, 256 разделить на 4:

• Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
• Спросите у малыша, сколько четверок помещается в двойке — нисколько
• Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
• Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
• Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
• Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
• Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»

Письменное деление на двузначное число

Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.

Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.

Выполните вместе такое простое действие: 184:23 — как нужно объяснять:

• Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
• Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8

Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.

Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:

• Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
• Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
• Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
• Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно

Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.

Например:

• Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
• Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
• Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
• Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
• Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
• Запишите 2864 под 2864, получается в разности 0. Ответ 204

Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.

Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.

Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.

Алгоритм деления чисел заключается в следующем:

• Сделать прикидку числа, которое будет стоять в ответе
• Найти первое неполное делимое
• Определить число цифр в частном
• Найти цифры в каждом разряде частного
• Найти остаток (если он есть)

По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).

Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:

• 1428:42
• 2924:68
• 30296:56
• 136576:64
• 16514:718

Для закрепления результата можно использовать такие игры на деление:

• «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.

Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.

Видео: Игра арифметика для детей сложение вычитание деление умножение

Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2

Видео: Знакомство с делением | Забавная МАТЕМАТИКА для малышей

Видео: Деление двузначного числа на однозначное

Когда ребенок дополнительно занимается дома, он закрепляет пройденный материал в школе. Благодаря этому ему легче учиться и он не будет отставать от сверстников. Поэтому помогайте своим детям, занимайтесь дома с ними вместе. и у малыша все получится!

Видео: Деление в столбик часть 1

Видео: Деление в столбик часть 2

Видео: Деление в столбик часть 3

Видео: Деление в столбик часть 4

Видео: Деление в столбик часть 5

Прочитайте тему урока: «Деление с остатком». Что вы уже знаете по этой теме?

Можете ли вы разложить 8 слив поровну на две тарелки (рис. 1)?

Рис. 1. Иллюстрация к примеру

В каждую тарелку можно положить по 4 сливы (рис. 2).

Рис. 2. Иллюстрация к примеру

Действие, которое мы выполнили, можно записать так.

8: 2 = 4

Как вы думаете, можно ли 8 слив поровну разложить на 3 тарелки (рис. 3)?

Рис. 3. Иллюстрация к примеру

Будем действовать так. Сначала в каждую тарелку положим по одной сливе, потом по второй сливе. У нас останется 2 сливы, но 3 тарелки. Значит, дальше поровну мы разложить не можем. Мы положили в каждую тарелку по 2 сливы, и 2 сливы у нас осталось (рис. 4).

Рис. 4. Иллюстрация к примеру

Продолжим наблюдение.

Прочитайте числа. Среди данных чисел найдите те, которые делятся на 3.

11, 12, 13, 14, 15, 16, 17, 18, 19

Проверьте себя.

Остальные числа (11, 13, 14, 16, 17, 19) на 3 не делятся, или говорят «делятся с остатком».

Найдем значение частного.

Узнаем, сколько раз по 3 содержится в числе 17 (рис. 5).

Рис. 5. Иллюстрация к примеру

Мы видим, что поместилось по 3 овала 5 раз и 2 овала осталось.

Выполненное действие можно записать так.

17: 3 = 5 (ост. 2)

Можно записать и в столбик (рис. 6)

Рис. 6. Иллюстрация к примеру

Рассмотрите рисунки. Объясните подписи к этим рисункам (рис. 7).

Рис. 7. Иллюстрация к примеру

Рассмотрим первый рисунок (рис. 8).

Рис. 8. Иллюстрация к примеру

Мы видим, что 15 овалов разделили по 2. По 2 повторилось 7 раз, в остатке - 1 овал.

Рассмотрим второй рисунок (рис. 9).

Рис. 9. Иллюстрация к примеру

На этом рисунке 15 квадратов разделили по 4. По 4 повторилось 3 раза, в остатке - 3 квадрата.

Рассмотрим третий рисунок (рис. 10).

Рис. 10. Иллюстрация к примеру

Можно сказать, что 15 овалов разделили по 3. По 3 повторилось 5 раз поровну. В таких случаях говорят, что остаток - 0.

Выполним деление.

Семь квадратов разделим по три. Получим две группы, и один квадрат останется. Запишем решение (рис. 11).

Рис. 11. Иллюстрация к примеру

Выполним деление.

Узнаем, сколько раз по четыре содержится в числе 10. Видим, что в числе 10 по четыре содержится 2 раза и 2 квадрата остаются. Запишем решение (рис. 12).

Рис. 12. Иллюстрация к примеру

Выполним деление.

Узнаем, сколько раз по два содержится в числе 11. Видим, что в числе 11 по два содержится 5 раз и 1 квадрат остается. Запишем решение (рис. 13).

Рис. 13. Иллюстрация к примеру

Сделаем вывод. Разделить с остатком - значит узнать, сколько раз делитель содержится в делимом и сколько единиц останется.

Деление с остатком можно выполнить и на числовом луче.

На числовом луче отметим отрезки по 3 деления и увидим, что по три деления оказалось три раза и одно деление осталось (рис. 14).

Рис. 14. Иллюстрация к примеру

Запишем решение.

10: 3 = 3 (ост.1)

Выполним деление.

На числовом луче отметим отрезки по 3 деления и увидим, что по три деления оказалось три раза и два деления осталось (рис. 15).

Рис. 15. Иллюстрация к примеру

Запишем решение.

11: 3 = 3 (ост.2)

Выполним деление.

На числовом луче отметим отрезки по 3 деления и увидим, что получили ровно 4 раза, остаток отсутствует (рис. 16).

Рис. 16. Иллюстрация к примеру

Запишем решение.

12: 3 = 4

Сегодня на уроке мы познакомились с делением с остатком, научились выполнять названное действие с помощью рисунка и числового луча, потренировались в решении примеров по теме урока.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. - М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. - М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. - М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. - М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. - М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. - М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. - М.: «Экзамен», 2012.

1. Nsportal.ru ().
2. Prosv.ru ().
3. Do.gendocs.ru ().

Домашнее задание

1. Выпиши числа, которые делятся на 2 без остатка.

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19

2. Выполни деление с остатком с помощью рисунка.

3. Выполни деление с остатком с помощью числового луча.

4. Составь задание для своих товарищей по теме урока.