In July 2020, NASA launches an expedition to Mars. The spacecraft will deliver to Mars an electronic carrier with the names of all registered members of the expedition.
If this post solved your problem or you just liked it, share the link to it with your friends on social networks.
One of these code options needs to be copied and pasted into the code of your web page, preferably between the tags
And or right after the tag . According to the first option, MathJax loads faster and slows down the page less. But the second option automatically tracks and loads the latest versions of MathJax. If you insert the first code, then it will need to be updated periodically. If you paste the second code, then the pages will load more slowly, but you will not need to constantly monitor MathJax updates.The easiest way to connect MathJax is in Blogger or WordPress: in the site control panel, add a widget designed to insert third-party JavaScript code, copy the first or second version of the load code presented above into it, and place the widget closer to the beginning of the template (by the way, this is not at all necessary , since the MathJax script is loaded asynchronously). That's all. Now learn the MathML, LaTeX, and ASCIIMathML markup syntax and you're ready to embed math formulas into your web pages.
Another New Year's Eve... frosty weather and snowflakes on the window pane... All this prompted me to write again about... fractals, and what Wolfram Alpha knows about it. On this occasion, there is an interesting article in which there are examples of two-dimensional fractal structures. Here we will consider more complex examples of three-dimensional fractals.
A fractal can be visually represented (described) as a geometric figure or body (meaning that both are a set, in this case, a set of points), the details of which have the same shape as the original figure itself. That is, it is a self-similar structure, considering the details of which, when magnified, we will see the same shape as without magnification. Whereas in the case of a regular geometric figure (not a fractal), when zoomed in, we will see details that have a simpler shape than the original figure itself. For example, at a sufficiently high magnification, part of an ellipse looks like a straight line segment. This does not happen with fractals: with any increase in them, we will again see the same complex shape, which with each increase will be repeated again and again.
Benoit Mandelbrot, the founder of the science of fractals, in his article Fractals and Art for Science wrote: "Fractals are geometric shapes that are as complex in their details as they are in their overall form. That is, if part of the fractal will be enlarged to the size of the whole, it will look like the whole, or exactly, or perhaps with a slight deformation.
. To do this, use graph paper or a graphical calculator. Select any number of numeric values for the independent variable x (\displaystyle x) and plug them into the function to calculate the values of the dependent variable y (\displaystyle y). Put the found coordinates of the points on the coordinate plane, and then connect these points to build a graph of the function.- Substitute positive numeric values into the function x (\displaystyle x) and corresponding negative numeric values. For example, given a function f (x) = 2 x 2 + 1 (\displaystyle f(x)=2x^(2)+1). Substitute the following values into it x (\displaystyle x):
Check if the graph of the function is symmetrical about the y-axis. Symmetry refers to the mirror image of the graph about the y-axis. If the part of the graph to the right of the y-axis (positive values of the independent variable) matches the part of the graph to the left of the y-axis (negative values of the independent variable), the graph is symmetrical about the y-axis. If the function is symmetrical about the y-axis, the function is even.
Check if the graph of the function is symmetrical about the origin. The origin is the point with coordinates (0,0). Symmetry about the origin means that a positive value y (\displaystyle y)(with a positive value x (\displaystyle x)) corresponds to a negative value y (\displaystyle y)(with a negative value x (\displaystyle x)), and vice versa. Odd functions have symmetry with respect to the origin.
Check if the graph of the function has any symmetry. The last type of function is a function whose graph does not have symmetry, that is, there is no mirror image both relative to the y-axis and relative to the origin. For example, given a function.
- Substitute several positive and corresponding negative values into the function x (\displaystyle x):
- According to the results obtained, there is no symmetry. Values y (\displaystyle y) for opposite values x (\displaystyle x) do not match and are not opposite. Thus, the function is neither even nor odd.
- Please note that the function f (x) = x 2 + 2 x + 1 (\displaystyle f(x)=x^(2)+2x+1) can be written like this: f (x) = (x + 1) 2 (\displaystyle f(x)=(x+1)^(2)). Written in this form, the function appears to be even because there is an even exponent. But this example proves that the form of a function cannot be quickly determined if the independent variable is enclosed in parentheses. In this case, you need to open the brackets and analyze the resulting exponents.
Function is one of the most important mathematical concepts. Function - variable dependency at from a variable x, if each value X matches a single value at. variable X called the independent variable or argument. variable at called the dependent variable. All values of the independent variable (variable x) form the domain of the function. All values that the dependent variable takes (variable y), form the range of the function.
Function Graph they call the set of all points of the coordinate plane, the abscissas of which are equal to the values of the argument, and the ordinates are equal to the corresponding values of the function, that is, the values of the variable are plotted along the abscissa x, and the values of the variable are plotted along the y-axis y. To plot a function, you need to know the properties of the function. The main properties of the function will be discussed below!
To plot a function graph, we recommend using our program - Graphing Functions Online. If you have any questions while studying the material on this page, you can always ask them on our forum. Also on the forum you will be helped to solve problems in mathematics, chemistry, geometry, probability theory and many other subjects!
Basic properties of functions.
1) Function scope and function range.
The scope of a function is the set of all valid valid values of the argument x(variable x) for which the function y = f(x) defined.
The range of a function is the set of all real values y that the function accepts.
In elementary mathematics, functions are studied only on the set of real numbers.
2) Function zeros.
Values X, at which y=0, is called function zeros. These are the abscissas of the points of intersection of the graph of the function with the x-axis.
3) Intervals of sign constancy of a function.
The intervals of sign constancy of a function are such intervals of values x, on which the values of the function y either only positive or only negative are called intervals of sign constancy of the function.

4) Monotonicity of the function.
Increasing function (in some interval) - a function in which a larger value of the argument from this interval corresponds to a larger value of the function.
Decreasing function (in some interval) - a function in which a larger value of the argument from this interval corresponds to a smaller value of the function.
5) Even (odd) functions.
An even function is a function whose domain of definition is symmetric with respect to the origin and for any X f(-x) = f(x). The graph of an even function is symmetrical about the y-axis.
An odd function is a function whose domain of definition is symmetric with respect to the origin and for any X from the domain of definition the equality f(-x) = - f(x). The graph of an odd function is symmetrical about the origin.
Even function
1) The domain of definition is symmetrical with respect to the point (0; 0), that is, if the point a belongs to the domain of definition, then the point -a also belongs to the domain of definition.
2) For any value x f(-x)=f(x)
3) The graph of an even function is symmetrical about the Oy axis.
odd function has the following properties:
1) The domain of definition is symmetrical with respect to the point (0; 0).
2) for any value x, which belongs to the domain of definition, the equality f(-x)=-f(x)
3) The graph of an odd function is symmetrical with respect to the origin (0; 0).
Not every function is even or odd. Functions general view are neither even nor odd.



6) Limited and unlimited functions.
A function is called bounded if there exists a positive number M such that |f(x)| ≤ M for all values of x . If there is no such number, then the function is unbounded.
7) Periodicity of the function.
A function f(x) is periodic if there exists a non-zero number T such that for any x from the domain of the function, f(x+T) = f(x). This smallest number is called the period of the function. All trigonometric functions are periodic. (Trigonometric formulas).
Function f is called periodic if there exists a number such that for any x from the domain of definition the equality f(x)=f(x-T)=f(x+T). T is the period of the function.
Every periodic function has an infinite number of periods. In practice, the smallest positive period is usually considered.
The values of the periodic function are repeated after an interval equal to the period. This is used when plotting graphs.

Even and odd functions are one of its main properties, and parity occupies an impressive part of the school course in mathematics. It largely determines the nature of the behavior of the function and greatly facilitates the construction of the corresponding graph.
Let us define the parity of the function. Generally speaking, the function under study is considered even if for opposite values of the independent variable (x) located in its domain, the corresponding values of y (function) are equal.
Let us give a more rigorous definition. Consider some function f (x), which is defined in the domain D. It will be even if for any point x located in the domain of definition:
- -x (opposite dot) also lies in the given scope,
- f(-x) = f(x).
From the above definition, the condition necessary for the domain of definition of such a function follows, namely, symmetry with respect to the point O, which is the origin of coordinates, since if some point b is contained in the domain of definition of an even function, then the corresponding point - b also lies in this domain. From the foregoing, therefore, the conclusion follows: an even function has a form that is symmetrical with respect to the ordinate axis (Oy).
How to determine the parity of a function in practice?
Let it be given using the formula h(x)=11^x+11^(-x). Following the algorithm that follows directly from the definition, we first of all study its domain of definition. Obviously, it is defined for all values of the argument, that is, the first condition is satisfied.
The next step is to substitute the argument (x) with its opposite value (-x).
We get:
h(-x) = 11^(-x) + 11^x.
Since addition satisfies the commutative (displacement) law, it is obvious that h(-x) = h(x) and the given functional dependence is even.
Let's check the evenness of the function h(x)=11^x-11^(-x). Following the same algorithm, we get h(-x) = 11^(-x) -11^x. Taking out the minus, as a result, we have
h(-x)=-(11^x-11^(-x))=- h(x). Hence h(x) is odd.
By the way, it should be recalled that there are functions that cannot be classified according to these criteria, they are called neither even nor odd.
Even functions have a number of interesting properties:
- as a result of the addition of similar functions, an even one is obtained;
- as a result of subtracting such functions, an even one is obtained;
- even, also even;
- as a result of multiplying two such functions, an even one is obtained;
- as a result of multiplication of odd and even functions, an odd one is obtained;
- as a result of dividing the odd and even functions, an odd one is obtained;
- the derivative of such a function is odd;
- If we square an odd function, we get an even one.
The parity of a function can be used in solving equations.
To solve an equation like g(x) = 0, where the left side of the equation is an even function, it will be enough to find its solutions for non-negative values of the variable. The obtained roots of the equation must be combined with opposite numbers. One of them is subject to verification.
The same is successfully used to solve non-standard problems with a parameter.
For example, is there any value for the parameter a that would make the equation 2x^6-x^4-ax^2=1 have three roots?
If we take into account that the variable enters the equation in even powers, then it is clear that replacing x with -x will not change the given equation. It follows that if a certain number is its root, then so is the opposite number. The conclusion is obvious: the roots of the equation, other than zero, are included in the set of its solutions in “pairs”.
It is clear that the number 0 itself is not, that is, the number of roots of such an equation can only be even and, naturally, for any value of the parameter it cannot have three roots.
But the number of roots of the equation 2^x+ 2^(-x)=ax^4+2x^2+2 can be odd, and for any value of the parameter. Indeed, it is easy to check that the set of roots of a given equation contains solutions in "pairs". Let's check if 0 is a root. When substituting it into the equation, we get 2=2. Thus, in addition to "paired" 0 is also a root, which proves their odd number.
Hide Show
Ways to set a function
Let the function be given by the formula: y=2x^(2)-3 . By assigning any value to the independent variable x , you can use this formula to calculate the corresponding values of the dependent variable y . For example, if x=-0.5 , then using the formula, we get that the corresponding value of y is y=2 \cdot (-0.5)^(2)-3=-2.5 .
Given any value taken by the x argument in the formula y=2x^(2)-3 , only one function value can be calculated that corresponds to it. The function can be represented as a table:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Using this table, you can figure out that for the value of the argument -1, the value of the function -3 will correspond; and the value x=2 will correspond to y=0, and so on. It is also important to know that each argument value in the table corresponds to only one function value.
More functions can be set using graphs. With the help of the graph, it is established which value of the function correlates with a certain value of x. Most often, this will be an approximate value of the function.
Even and odd function
The function is even function, when f(-x)=f(x) for any x from the domain. Such a function will be symmetrical about the Oy axis.
The function is odd function when f(-x)=-f(x) for any x in the domain. Such a function will be symmetrical about the origin O (0;0) .
The function is not even, nor odd and called general function when it does not have symmetry about the axis or origin.
We examine the following function for parity:
f(x)=3x^(3)-7x^(7)
D(f)=(-\infty ; +\infty) with a symmetrical domain of definition about the origin. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).
Hence, the function f(x)=3x^(3)-7x^(7) is odd.
Periodic function
The function y=f(x) , in the domain of which f(x+T)=f(x-T)=f(x) is true for any x, is called periodic function with period T \neq 0 .
Repetition of the graph of the function on any segment of the abscissa axis, which has length T .
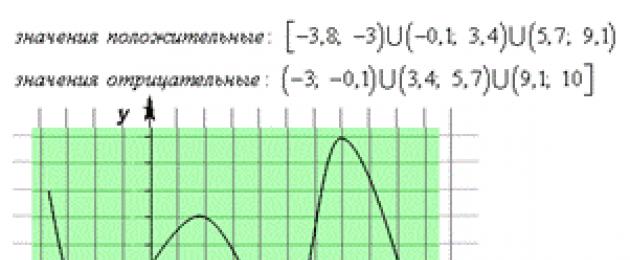
Intervals where the function is positive, that is, f (x) > 0 - segments of the abscissa axis, which correspond to the points of the graph of the function that lie above the abscissa axis.
f(x) > 0 on (x_(1); x_(2)) \cup (x_(3); +\infty)
Gaps where the function is negative, i.e. f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.
f(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))
Function limitation
bounded from below it is customary to call a function y=f(x), x \in X when there exists a number A for which the inequality f(x) \geq A holds for any x \in X .
An example of a function bounded below: y=\sqrt(1+x^(2)) since y=\sqrt(1+x^(2)) \geq 1 for any x .
bounded from above a function y=f(x), x \in X is called if there exists a number B for which the inequality f(x) \neq B holds for any x \in X .
An example of a function bounded below: y=\sqrt(1-x^(2)), x \in [-1;1] since y=\sqrt(1+x^(2)) \neq 1 for any x \in [-1;1] .
Limited it is customary to call a function y=f(x), x \in X when there exists a number K > 0 for which the inequality \left | f(x) \right | \neq K for any x \in X .
Example of a bounded function: y=\sin x is bounded on the whole number line because \left | \sin x \right | \neq 1.
Increasing and decreasing function
It is customary to speak of a function that increases on the interval under consideration as increasing function when a larger value of x will correspond to a larger value of the function y=f(x) . From here it turns out that taking from the considered interval two arbitrary values of the argument x_(1) and x_(2) , and x_(1) > x_(2) , it will be y(x_(1)) > y(x_(2)) .
A function that decreases on the interval under consideration is called decreasing function when a larger value of x will correspond to a smaller value of the function y(x) . From here it turns out that taking from the considered interval two arbitrary values of the argument x_(1) and x_(2) , and x_(1) > x_(2) , it will be y(x_(1))< y(x_{2}) .
Function roots it is customary to name the points at which the function F=y(x) intersects the abscissa axis (they are obtained as a result of solving the equation y(x)=0 ).
a) If an even function increases for x > 0, then it decreases for x< 0
b) When an even function decreases for x > 0, then it increases for x< 0
c) When an odd function increases for x > 0, then it also increases for x< 0
d) When an odd function decreases for x > 0, then it will also decrease for x< 0
Function extremes
Function minimum point y=f(x) it is customary to call such a point x=x_(0) , in which its neighborhood will have other points (except for the point x=x_(0) ), and then the inequality f(x) > f (x_(0)) . y_(min) - designation of the function at the point min.
Function maximum point y=f(x) it is customary to call such a point x=x_(0) , in which its neighborhood will have other points (except for the point x=x_(0) ), and then the inequality f(x) will be satisfied for them< f(x^{0}) . y_{max} - обозначение функции в точке max.
Necessary condition
According to Fermat's theorem: f"(x)=0, then when the function f(x) , which is differentiable at the point x_(0) , an extremum will appear at this point.
Sufficient condition
- When the sign of the derivative changes from plus to minus, then x_(0) will be the minimum point;
- x_(0) - will be a maximum point only when the derivative changes sign from minus to plus when passing through the stationary point x_(0) .
The largest and smallest value of the function on the interval
Calculation steps:
- Looking for derivative f"(x) ;
- Stationary and critical points of the function are found and those belonging to the interval are chosen;
- The values of the function f(x) are found at the stationary and critical points and ends of the segment. The smallest of the results will be the smallest value of the function, and more - greatest.
- In contact with 0
- Google Plus 0
- OK 0
- Facebook 0