Pöörlev liikumine tahkeümber fikseeritud telje nimetatakse selle liikumist, mille puhul kaks kehale kuuluvat (või sellega alati seotud punkti) jäävad kogu liikumise vältel liikumatuks.(joonis 2.2) .
Joonis 2.2
Fikseeritud punktide läbimine A ja V sirgjoont nimetatakse pöörlemistelg. Kuna jäiga keha punktide vaheline kaugus peab jääma muutumatuks, on ilmne, et pöörleva liikumise ajal on kõik teljele kuuluvad punktid liikumatud ja kõik ülejäänud kirjeldavad ringe, mille tasandid on risti pöörlemisteljega ja keskused asuvad sellel teljel. Pöörleva keha asukoha määramiseks joonistagem läbi pöörlemistelje, mida mööda telg on suunatud Az, poollennuk І - fikseeritud ja pooltasapinnaline ІІ põimitud kehasse endasse ja pöörleb koos sellega. Siis määrab keha asendi igal ajahetkel üheselt vastava märgiga võetud nurga järgi φ nende tasandite vahel, mida me nimetame keha pöördenurk. Vaatleme nurka φ edasilükkamise korral positiivne fikseeritud tasapinnalt vastupäeva (telje positiivsest otsast vaadates vaatleja jaoks Az) ja päripäeva negatiivselt. Mõõtke nurka φ on radiaanides. Et teada keha asendit igal ajahetkel, peate teadma nurga sõltuvust φ ajast t, st.
|
|
See võrrand väljendab seadus pöörlev liikumine jäik keha ümber fikseeritud telje.
Jäiga keha pöörleva liikumise peamised kinemaatilised omadused on selle nurkkiirus ω ja nurkkiirendus ε.
9.2.1. Keha nurkkiirus ja nurkiirendus
Suurust, mis iseloomustab pöördenurga φ muutumise kiirust ajas, nimetatakse nurkkiiruseks.
Kui teatud aja jooksul  keha pöörleb läbi nurga
keha pöörleb läbi nurga  , siis on keha arvuliselt keskmine nurkkiirus sellel ajavahemikul
, siis on keha arvuliselt keskmine nurkkiirus sellel ajavahemikul  ... Limiidis kl
... Limiidis kl  saada
saada
Sellel viisil, keha nurkkiiruse arvväärtus antud ajahetkel on võrdne pöördenurga esimese tuletisega ajas.
Märkide reegel: kui pöörlemine toimub vastupäeva, ω> 0 ja kui päripäeva, siis ω< 0.
 või kuna radiaanid on mõõtmeteta,
või kuna radiaanid on mõõtmeteta,  .
.
Teoreetilistes arvutustes on mugavam kasutada nurkkiiruse vektorit  , mille moodul on
, mille moodul on  ja mis on suunatud piki keha pöörlemistelge suunas, kust pöörlemist vaadatakse vastupäeva. See vektor määrab koheselt nurkkiiruse mooduli ja pöörlemistelje ning pöörlemissuuna ümber selle telje.
ja mis on suunatud piki keha pöörlemistelge suunas, kust pöörlemist vaadatakse vastupäeva. See vektor määrab koheselt nurkkiiruse mooduli ja pöörlemistelje ning pöörlemissuuna ümber selle telje.
Suurust, mis iseloomustab nurkkiiruse muutumise kiirust ajas, nimetatakse keha nurkkiirenduseks.
Kui teatud aja jooksul  nurkkiiruse juurdekasv on
nurkkiiruse juurdekasv on  , siis suhe
, siis suhe  , st. määrab pöörleva keha keskmise kiirenduse väärtuse ajas
, st. määrab pöörleva keha keskmise kiirenduse väärtuse ajas  .
.
Kui pingutada  saame nurkkiirenduse väärtuse hetkel t:
saame nurkkiirenduse väärtuse hetkel t:
Sellel viisil, keha nurkkiirenduse arvväärtus antud ajahetkel on võrdne keha nurkkiiruse esimese tuletise või teise pöördenurga tuletisega ajas.
Mõõtühik on tavaliselt  või mis on ka
või mis on ka  .
.
Kui nurkkiiruse moodul aja jooksul suureneb, nimetatakse keha pöörlemist kiirendatud ja kui see väheneb, - aeglustus. Kui kogused ω
ja ε
on samad märgid, siis pöörlemine kiireneb, kui erinev - aeglustunud.  Analoogiliselt nurkkiirusega saab nurkiirendust kujutada ka vektorina
Analoogiliselt nurkkiirusega saab nurkiirendust kujutada ka vektorina  suunatud piki pöörlemistelge. Kus
suunatud piki pöörlemistelge. Kus
 .
.
Kui keha pöörleb kiirendatud suunas  langeb kokku
langeb kokku  , ja vastupidi
, ja vastupidi  aeglasel pöörlemisel.
aeglasel pöörlemisel.
Kui keha nurkkiirus jääb liikumise ajal konstantseks ( ω= konst), siis nimetatakse keha pöörlemist ühtlane.
Alates  meil on
meil on  ... Seega, eeldades, et esialgsel ajahetkel
... Seega, eeldades, et esialgsel ajahetkel  süstimine
süstimine  , ja integraalid vasakule
, ja integraalid vasakule  enne
enne  ja paremal 0 kuni t, saame lõpuks
ja paremal 0 kuni t, saame lõpuks
|
|
Ühtlase pöörlemisega, millal  =0,
=0, ja
ja  .
.
Ühtlase pöörlemise kiirus määratakse sageli pöörete arvuga minutis, mida tähistatakse n p/min Leiame omavahelised suhted n rpm ja ω 1/s. Ühe pöördega pöörleb keha 2π võrra ja koos n pöördeid 2π võrra n; see pööre tehakse 1 minutiga, st. t= 1 min = 60 s. Sellest järeldub
|
|
Kui keha nurkiirendus jääb konstantseks kogu liikumise vältel (ε = konst), siis nimetatakse pöörlemist võrdselt muutlikud.
Algsel ajahetkel t= 0 nurk  ja nurkkiirus
ja nurkkiirus  (
( - algnurkkiirus).
- algnurkkiirus).  ;
; =ε
=ε  ... Integreerides vasaku külje
... Integreerides vasaku külje  enne
enne  , ja parempoolne 0 kuni t, leia
, ja parempoolne 0 kuni t, leia
Selle pöörlemise nurkkiirus ω  ... Kui ω ja ε märgid on samad, on pöörlemine ühtlaselt kiirendatud ja kui erinev - sama aeglane.
... Kui ω ja ε märgid on samad, on pöörlemine ühtlaselt kiirendatud ja kui erinev - sama aeglane.
Roolinurk, nurkkiirus ja nurkkiirendus
Jäiga keha pöörlemine ümber fikseeritud telje nimetatakse selle liikumist, mille puhul kaks kehapunkti jäävad kogu liikumisaja jooksul liikumatuks. Sel juhul jäävad liikumatuks ka kõik keha punktid, mis asuvad selle fikseeritud punkte läbival sirgel. Seda rida nimetatakse keha pöörlemistelg.
Kui A ja V- keha fikseeritud punktid (joon. 15 ), siis on pöörlemistelg telg Oz, millel võib olla mis tahes suund ruumis, mitte tingimata vertikaalne. Ühe telje suund Oz positiivseks võetud.
Joonistage fikseeritud tasapind läbi pöörlemistelje Kõrval ja mobiilne P, kinnitatud pöörleva korpuse külge. Laske mõlemad tasapinnad esialgsel ajahetkel kokku langeda. Siis ajahetkel t liigutatava tasandi ja pöörleva keha asendit saab määrata tasapindadevahelise kahetahulise nurga ja vastava joonnurga järgi φ nendel tasapindadel paiknevate ja pöördeteljega risti olevate sirgjoonte vahel. Süstimine φ helistas keha pöördenurk.
Keha asend valitud tugiraami suhtes on täielikult määratud mis tahes
ajahetk, kui võrrand on antud φ =f (t) (5)
kus f (t)- mis tahes, kaks korda diferentseeruv aja funktsioon. Seda võrrandit nimetatakse jäiga keha pöörlemise võrrand ümber fikseeritud telje.
Ümber fikseeritud telje pöörleval kehal on üks vabadusaste, kuna selle asukoht määratakse ainult ühe parameetri - nurga - määramisega. φ .
Süstimine φ peetakse positiivseks, kui see asetatakse vastupäeva, ja negatiivseks - vastupidises suunas, kui vaadata telje positiivsest suunast Oz. Keha punktide trajektoorid, kui see pöörleb ümber fikseeritud telje, on ringid, mis asuvad pöörlemisteljega risti olevatel tasapindadel.
Jäiga keha pöörleva liikumise iseloomustamiseks ümber fikseeritud telje tutvustame nurkkiiruse ja nurkkiirenduse mõisteid. Keha algebraline nurkkiirus suvalisel ajahetkel nimetatakse sellel hetkel pöördenurga esimest tuletist, st. dφ / dt = φ. See on positiivne väärtus, kui keha pöörleb vastupäeva, kuna pöördenurk aja jooksul suureneb, ja negatiivne, kui keha pöörleb päripäeva, kuna pöördenurk väheneb.
Nurkkiiruse moodul on ω. Siis ω= ׀dφ / dt׀= ׀φ ׀ (6)
Nurkkiiruse mõõde määratakse vastavalt punktile (6)
[ω] = nurk / aeg = rad / s = s -1.
Inseneriteaduses on nurkkiirus kiirus, mida väljendatakse pööretes minutis. 1 minuti pärast pöördub keha nurga all 2πп, kui P- pöörete arv minutis. Jagades selle nurga sekundite arvuga minutis, saame: (7)
Keha algebraline nurkiirendus nimetatakse algebralise kiiruse esimest tuletist, s.o. pöördenurga teine tuletis d 2 φ / dt 2 = ω... Nurkkiirenduse moodulit tähistatakse ε , siis ε=|φ| (8)
Nurkkiirenduse mõõde saadakse punktist (8):
[ε ] = nurkkiirus / aeg = rad / s 2 = s -2
Kui φ’’>0 juures φ’>0 , siis algebraline nurkkiirus suureneb ajaga ja seetõttu pöörleb keha kõnealusel hetkel kiirendatud kiirusega positiivne pool(vastupäeva). Kell φ’’<0 ja φ’<0 keha pöörleb kiiresti negatiivses suunas. Kui φ’’<0 juures φ’>0 , siis on meil positiivses suunas aeglasem pöörlemine. Kell φ’’>0 ja φ’<0 , st. aeglasem pöörlemine on negatiivses suunas. Joonistel kujutatud nurkkiirust ja nurkkiirendust on kujutatud kaarnooled ümber pöörlemistelje. Nurkkiiruse kaarnool näitab kehade pöörlemissuunda;
Kiirendatud pöörlemise korral on nurkkiiruse ja nurkkiirenduse kaare nooltel aeglustunud pöörlemisel samad suunad – nende suunad on vastupidised.
Jäiga keha pöörlemise erijuhud
Pöörlemist nimetatakse ühtlaseks, kui ω = const, φ = φ't
Pöörlemine on ühtlaselt muutuv, kui ε = konst. φ '= φ' 0 + φ''t ja
Üldiselt, kui φ’’ mitte alati,
![]()
Kehapunktide kiirused ja kiirendused
Jäiga keha ümber fikseeritud telje pöörlemise võrrand on teada φ = f (t)(joon. 16). Kaugus s punktid M liigutatavas tasapinnas P mööda ringjoont (punkti trajektoori), mõõdetuna punktist oi, paikneb fikseeritud tasapinnal, väljendatuna nurga kaudu φ sõltuvus s = hφ, kus h on ringi raadius, mida mööda punkt liigub. See on punktist lühim kaugus M pöörlemisteljele. Mõnikord nimetatakse seda punkti pöörlemise raadiuseks. Keha igas punktis jääb pöörlemisraadius muutumatuks, kui keha pöörleb ümber fikseeritud telje.
 Algebralise punkti kiirus M määratakse valemiga v τ = s ’= hφ Punkti kiiruse moodul: v = hω(9)
Algebralise punkti kiirus M määratakse valemiga v τ = s ’= hφ Punkti kiiruse moodul: v = hω(9)
Keha punktide kiirused pöörlemisel ümber fikseeritud telje on võrdelised nende lühima kaugusega selle teljega. Kuvasuhe on nurkkiirus. Punktide kiirused on suunatud piki trajektooride puutujat ja on seetõttu risti pöörderaadiusega. Sirgesegmendil paiknevate kehapunktide kiirused OM, punktile (9) vastavad jaotatakse vastavalt lineaarsele seadusele. Need on üksteisega paralleelsed ja nende otsad asuvad ühel sirgel, mis läbib pöörlemistelge. Jagame punkti kiirenduse puutuja- ja normaalkomponentideks, s.o. a = a τ + a nτ Tangentsiaalne ja normaalkiirendus arvutatakse valemitega (10)
kuna ringi puhul on kõverusraadius p = h(joon. 17 ). Sellel viisil,
 Lineaarse seaduse järgi jaotuvad ka punktide puutuja-, normaal- ja summaarsed kiirendused, samuti kiirused. Need sõltuvad lineaarselt punktide kaugustest pöörlemisteljest. Tavaline kiirendus on suunatud mööda ringi raadiust pöörlemisteljele. Tangentsiaalkiirenduse suund sõltub algebralise nurkkiirenduse märgist. Kell φ’>0
ja φ’’>0
või φ’<0
ja φ’<0
meil on keha kiirendatud pöörlemine ja vektorite suund a τ ja v kokku sobima. Kui φ’
ja φ’"
on erinevad märgid (aeglane pöörlemine), siis a τ ja v suunatud üksteisele vastakuti.
Lineaarse seaduse järgi jaotuvad ka punktide puutuja-, normaal- ja summaarsed kiirendused, samuti kiirused. Need sõltuvad lineaarselt punktide kaugustest pöörlemisteljest. Tavaline kiirendus on suunatud mööda ringi raadiust pöörlemisteljele. Tangentsiaalkiirenduse suund sõltub algebralise nurkkiirenduse märgist. Kell φ’>0
ja φ’’>0
või φ’<0
ja φ’<0
meil on keha kiirendatud pöörlemine ja vektorite suund a τ ja v kokku sobima. Kui φ’
ja φ’"
on erinevad märgid (aeglane pöörlemine), siis a τ ja v suunatud üksteisele vastakuti.
Määrates α nurk punkti kogukiirenduse ja selle pöörderaadiuse vahel on meil
tgα = | a τ | / a n = ε / ω 2 (11)
alates tavalisest kiirendusest a n alati positiivne. Süstimine a kõigi keha punktide jaoks sama. Seda tuleks edasi lükata kiirenduselt pöörderaadiusele nurkkiirenduse kaare noole suunas, sõltumata jäiga keha pöörlemissuunast.
Nurkkiiruse ja nurkkiirenduse vektorid
![]()
Tutvustame mõisteid keha nurkkiiruse ja nurkkiirenduse vektorid. Kui TO on selle positiivse poole suunas suunatud pöörlemistelje ühikvektor, siis nurkkiiruse vektorid ώ ja nurkkiirendus ε on määratud avaldistega (12)
Sest k on vektori suuruse ja suuna konstant, siis (12) järeldub, et
ε = dώ / dt(13)

Kell φ’>0 ja φ’’>0 suunavektorid ώ ja ε kokku sobima. Mõlemad on suunatud pöörlemistelje positiivsele poolele. Oz(Joon. 18.a) Kui φ’>0 ja φ’’<0 , siis on need suunatud vastassuundadesse (joonis 18.b ). Nurkkiirenduse vektor langeb kiirendatud pöörlemise ajal kokku nurkkiiruse vektoriga ja aeglustamisel vastupidine. Vektorid ώ ja ε saab joonistada mis tahes punkti pöörlemisteljel. Need on libisevad vektorid. See omadus tuleneb keha punktide kiiruste ja kiirenduste vektorvalemitest.
Kompleksne punkti liikumine
Põhimõisted
Mõne keerukama jäiga kehaliigutuse tüübi uurimiseks on soovitatav kaaluda punkti lihtsaimat keerulist liikumist. Paljude ülesannete puhul tuleb punkti liikumist vaadelda kahe (või enama) üksteise suhtes liikuva võrdluskaadri suhtes. Niisiis tuleb Kuu poole liikuva kosmoseaparaadi liikumist vaadelda samaaegselt nii Maa suhtes kui ka Kuu suhtes, mis liigub Maa suhtes. Iga punkti liikumist võib pidada keeruliseks, mis koosneb mitmest liigutusest. Näiteks võib pidada keeruliseks laeva liikumist mööda jõge Maa suhtes, mis seisneb liikumises mööda vett ja koos voolava veega.
Lihtsamal juhul koosneb punkti keeruline liikumine suhtelistest ja kujundlikest liikumistest. Määratleme need liikumised. Olgu meil kaks tugiraami, mis liiguvad üksteise suhtes. Kui üks neist süsteemidest O l x 1 y 1 z 1(joon. 19 ) võetakse põhi- või statsionaarseks (selle liikumist teiste tugiraamide suhtes ei võeta arvesse), siis teine tugiraam Oxyz liigub esimese suhtes. Punkti liikumine liikuva tugiraami suhtes Oxyz helistas sugulane. Nimetatakse selle liikumise tunnuseid, nagu trajektoor, kiirus ja kiirendus sugulane. Neid tähistatakse indeksiga r; kiiruse ja kiirenduse jaoks v r, a r. Punkti liikumine põhi- või statsionaarse tugisüsteemi suhtes O 1 x 1 y 1 z 1 helistas absoluutne(või keeruline ). Mõnikord nimetatakse seda ka komposiit liikumine. Selle liikumise trajektoori, kiirust ja kiirendust nimetatakse absoluutseks. Absoluutse liikumise kiirus ja kiirendus on tähistatud tähtedega v, a indekseid pole.
 |
Punkti ülekantavaks liikumiseks nimetatakse liikumist, mida see sooritab koos liikuva tugiraamiga, kui punkti, mis on antud ajahetkel jäigalt selle süsteemi külge kinnitatud. Suhtelise liikumise tõttu langeb erinevatel aegadel liikuv punkt kokku keha erinevate punktidega S, millega liigutatav tugiraam on kinnitatud. Transporditav kiirus ja transporditav kiirendus on keha selle punkti kiirus ja kiirendus. S, millega liikuv punkt hetkel ühtib. Kaasaskantav kiirus ja kiirendus tähendavad v e ja e.
Kui kõigi kehapunktide trajektoorid S, kinnitatud liikuvale tugiraamile, mis on kujutatud joonisel (joon. 20), siis saame joonte perekonna - punkti translatsioonilise liikumise trajektooride perekonna M. Punkti suhtelise liikumise tõttu M igal ajahetkel on see kaasaskantava liikumise ühel trajektooril. Punkt M võib kokku langeda ainult ühe punktiga selle ülekandetrajektooride perekonna trajektooridest. Sellega seoses arvatakse mõnikord, et ülekantava liikumise trajektoore pole, kuna on vaja arvestada joonte ülekantava liikumise trajektoore, milles ainult üks punkt on tegelikult trajektoori punkt.
Punkti kinemaatikas uuriti punkti liikumist mis tahes tugiraami suhtes, sõltumata sellest, kas see tugiraam liigub teiste kaadrite suhtes või mitte. Täiendame seda uurimust, võttes arvesse keerulist liikumist, mis kõige lihtsamal juhul koosneb suhtelisest ja kujundlikust. Ühte ja sama absoluutset liikumist, valides erinevaid liikuvaid tugiraame, võib pidada erinevatest kujundlikest ja vastavalt suhtelistest liikumistest koosnevaks.
Kiiruse lisamine
 Määrame punkti absoluutse liikumise kiiruse, kui selle punkti suhtelise ja kujundliku liikumise kiirused on teada. Las punkt sooritab liikuva tugiraami Oxyz suhtes ainult ühte suhtelist liikumist ja ajahetkel t hõivab suhtelise liikumise trajektooril positsiooni M (joonis 20). Ajahetkel t + t on suhtelise liikumise tõttu punkt asendis М 1, olles sooritanud ММ 1 liikumise mööda suhtelise liikumise trajektoori. Oletame, et sellega on seotud punkt Oxyz ja suhtelise trajektoori järgi liigub see mööda mõnda kõverat MM 2. Kui punkt osaleb samaaegselt nii suhtelises kui ka kujundlikus liikumises, siis aja jooksul A; ta kolib MM" mööda absoluutse liikumise trajektoori ja ajahetkel t + Kell positsiooni võtta M". Kui aeg Kell on väike ja seejärel minna piirini kell kell, kaldudes nulli, siis saab väikesed nihked piki kõveraid asendada akordide segmentidega ja võtta nihkevektoritena. Lisades vektorite nihked, saame
Määrame punkti absoluutse liikumise kiiruse, kui selle punkti suhtelise ja kujundliku liikumise kiirused on teada. Las punkt sooritab liikuva tugiraami Oxyz suhtes ainult ühte suhtelist liikumist ja ajahetkel t hõivab suhtelise liikumise trajektooril positsiooni M (joonis 20). Ajahetkel t + t on suhtelise liikumise tõttu punkt asendis М 1, olles sooritanud ММ 1 liikumise mööda suhtelise liikumise trajektoori. Oletame, et sellega on seotud punkt Oxyz ja suhtelise trajektoori järgi liigub see mööda mõnda kõverat MM 2. Kui punkt osaleb samaaegselt nii suhtelises kui ka kujundlikus liikumises, siis aja jooksul A; ta kolib MM" mööda absoluutse liikumise trajektoori ja ajahetkel t + Kell positsiooni võtta M". Kui aeg Kell on väike ja seejärel minna piirini kell kell, kaldudes nulli, siis saab väikesed nihked piki kõveraid asendada akordide segmentidega ja võtta nihkevektoritena. Lisades vektorite nihked, saame
![]() Sellega seoses jäetakse kõrvale väikesed kõrgema järgu kogused, mis kipuvad nulli minema kell, kipub nulli. Piirini üle minnes on meil (14)
Sellega seoses jäetakse kõrvale väikesed kõrgema järgu kogused, mis kipuvad nulli minema kell, kipub nulli. Piirini üle minnes on meil (14)
Seetõttu võtab (14) kuju (15)
Saadakse nn kiiruse liitmise teoreem: punkti absoluutse liikumise kiirus võrdub selle punkti kujundliku ja suhtelise liikumise kiiruste vektorsummaga. Kuna üldiselt ei ole kaasaskantavate ja suhteliste liikumiste kiirused risti, siis (15 ')
Sarnane teave.
Jäiga keha pöörlev liikumine. Pöörlemine on jäiga keha liikumine, mille käigus kõik selle punktid, mis asuvad kindlal sirgel, mida nimetatakse pöörlemisteljeks, jäävad liikumatuks.
Pöörleva liikumise ajal liiguvad kõik ülejäänud keha punktid pöörlemisteljega risti olevatel tasapindadel ja kirjeldavad ringe, mille keskpunktid asuvad sellel rõugel.
Pöörleva keha asukoha määramiseks joonistame läbi z-telje kaks pooltasapinda: pooltasapind I - statsionaarne ja pooltasapind II - mis on seotud jäiga kehaga ja pöörleb koos sellega (joon. 2.4). Siis määrab keha asendi igal ajahetkel üheselt nurk j nende pooltasandite vahel, võetud vastava märgiga, mida nimetatakse keha pöördenurgaks.
Kui keha pöörleb, muutub pöördenurk j ajaga, st see on aja t funktsioon:
Seda võrrandit nimetatakse võrrand jäiga keha pöörlev liikumine.
Jäiga keha pöörleva liikumise peamised kinemaatilised karakteristikud on selle nurkkiirus w nurkkiirendus e.
Kui õigel ajal D t= t1 + t keha teeb pöörde võrra Dj = j1 –j, siis on keha keskmine nurkkiirus sellel ajavahemikul võrdne
 (1.16)
(1.16)
Et määrata keha nurkkiiruse väärtus antud ajahetkel t leida pöördenurga Dj juurdekasvu ja ajavahemiku D suhte piir t kui viimane kipub nulli:
 (2.17)
(2.17)
Seega on keha nurkkiirus antud ajahetkel arvuliselt võrdne pöördenurga esimese tuletisega ajas. Nurkkiiruse w märk langeb kokku keha pöördenurga märgiga j: w > 0 j jaoks > 0 ja vastupidi, kui j < 0.siis w < 0. Nurkkiiruse mõõde on tavaliselt 1/s, kuna radiaan on dimensioonitu.
Nurkkiirust saab esitada vektorina w , mille arvväärtus on võrdne dj / dt-ga, mis on suunatud piki keha pöörlemistelge suunas, kust pöörlemist nähakse vastupäeva.
Keha nurkkiiruse muutumine ajas iseloomustab nurkkiirendust e. Analoogiliselt nurkkiiruse keskmise väärtuse leidmisega leiame avaldise keskmise kiirenduse väärtuse määramiseks:
 (2.18)
(2.18)
Siis määratakse avaldise järgi jäiga keha kiirendus antud ajahetkel
 (2.19)
(2.19)
ehk keha nurkkiirendus antud ajahetkel on võrdne keha nurkkiiruse esimese tuletise või keha pöördenurga teise tuletisega aja suhtes. Nurkkiirenduse mõõde on 1/s 2.
Jäiga keha nurkiirendust ja ka nurkkiirust saab esitada vektorina. Nurkkiirenduse vektor langeb suunaliselt kokku nurkkiiruse vektoriga jäiga keerise kiirendatud liikumise ajal ja on suunatud aeglustunud liikumise ajal vastupidises suunas.
Olles kindlaks teinud jäiga keha kui terviku liikumise omadused, uurime selle üksikute punktide liikumist. Mõelge mõnele punktile M jäik keha, mis asub pöördeteljest r kaugusel h (joonis 2.3).
Kui keha pöörleb, kirjeldab punkt M raadiusega h ümbermõõtu p, mille keskpunkt on pöörlemisteljel ja asub selle teljega risti. Kui ajas dt toimub keha elementaarne pöörlemine nurga dj all , punkt M samal ajal sooritab ta elementaarse liikumise mööda oma trajektoori dS = h * dj ,. Seejärel määrati avaldise järgi punkti M kiirus
![]() (2.20)
(2.20)
Kiirust nimetatakse punkti M lineaar- või perifeerseks kiiruseks.
Seega on pöörleva jäiga keha punkti joonkiirus arvuliselt võrdne keha nurkkiiruse korrutisega kaugusega sellest punktist pöörlemisteljeni. Kuna keha kõigi punktide nurkkiirus w; on sama väärtusega, siis joonkiiruse valemist järeldub, et pöörleva keha punktide joonkiirused on võrdelised nende kaugustega pöörlemisteljest. Jäiga keha punkti lineaarkiirus on vektor n, mis on suunatud punktiga kirjeldatud ringjoonele tangentsiaalselt M.
Kui kaugus tahke laulu pöörlemisteljest teatud punktini M vaadeldakse punkti M raadiusvektoriks h, siis punkti v lineaarkiiruse vektorit saab esitada nurkkiiruse vektori korrutisena w raadiuse vektor h:
V = w * h (2/21)
Tõepoolest, vektorkorrutise (2.21) tulemus on vektor, mille suurus on võrdne korrutisega w * h ja mis on suunatud (joonis 2.5) risti tasapinnaga, millel kaks tegurit asetsevad, suunas, millest lähtudes on kõige lähem kokkulangevus esimest tegurit koos teisega vaadeldakse liikumas vastupäeva, st mööda punkti M trajektoori puutujat.
Seega vektori korrutisest (2.21) tulenev vektor vastab suuruselt ja suunalt punkti M joonkiiruse vektorile.

Riis. 2.5
Kiirenduse väljenduse leidmiseks a punkt М, teostame avaldise (2.21) ajalise diferentseerimise punkti kiiruse jaoks
 (2.22)
(2.22)
Arvestades, et dj / dt = e, a dh / dt = v, kirjutame avaldise (2.22) kujul
kus a g ja an on keha punkti kogukiirenduse puutuja ja normaalkomponent pöörleva liikumise ajal, mis määratakse avaldiste põhjal
Keha punkti kogukiirenduse tangentsiaalne komponent (tangentsiaalne kiirendus) at iseloomustab kiirusvektori muutust absoluutväärtuses ja on kiirendamise ajal suunatud tangentsiaalselt keha punkti trajektoorile kiirusvektori suunas. liikumisel või vastupidises suunas aeglustunud liikumise ajal. Keha punkti tangentsiaalse kiirenduse vektori suurus jäiga keha pöörlemise ajal määratakse avaldisega
![]() (2,25)
(2,25)
Täiskiirenduse tavakomponent (tavaline kiirendus) a" tekib tahke aine värvimisel punkti kiirusvektori suuna muutumise tõttu. Nagu tavakiirenduse avaldisest (2.24) järeldub, on see kiirendus suunatud piki raadiust h ringi keskpunkti, mida mööda punkt liigub. Punkti normaalkiirenduse vektori moodul jäiga keha pöördliikumise ajal määratakse avaldisega (2.20) arvesse võttes.
Looduses ja tehnikas kohtame sageli jäikade kehade, näiteks võllide ja hammasrataste pöörleva liikumise avaldumist. Kuidas seda tüüpi liikumist füüsikas kirjeldatakse, milliseid valemeid ja võrrandeid selleks kasutatakse, neid ja muid küsimusi käsitletakse selles artiklis.
Mis on pöörlemine?
Igaüks meist esindab intuitiivselt, millist liikumist arutatakse. Pöörlemine on protsess, mille käigus keha või materjali punkt liigub mööda ringikujulist rada ümber teatud telje. Geomeetriliselt on jäik keha sirgjoon, mille kaugus jääb liikumise ajal muutumatuks. Seda kaugust nimetatakse pöörderaadiuseks. Järgnevalt tähistame seda r-tähega. Kui pöörlemistelg läbib keha massikeskme, siis nimetatakse seda oma teljeks. Ümber oma telje pöörlemise näide on Päikesesüsteemi planeetide vastav liikumine.
Selleks, et pöörlemine toimuks, peab toimuma tsentripetaalne kiirendus, mis tekib tsentripetaaljõu toimel. See jõud on suunatud keha massikeskmest pöörlemisteljele. Tsentripetaaljõu olemus võib olla väga erinev. Niisiis mängib kosmilisel skaalal oma rolli gravitatsioon, kui keha kinnitada niidiga, siis on viimase pingutusjõud tsentripetaalne. Kui keha pöörleb ümber oma telje, mängib tsentripetaaljõu rolli keha moodustavate elementide (molekulid, aatomid) vaheline sisemine elektrokeemiline interaktsioon.
On vaja mõista, et ilma tsentripetaaljõuta liigub keha sirgjooneliselt.
Pöörlemist kirjeldavad füüsikalised suurused

Esiteks on need dünaamilised omadused. Need sisaldavad:
- impulsi moment L;
- inertsimoment I;
- jõumoment M.
Teiseks on need kinemaatilised omadused. Loetleme need:
- pöördenurk θ;
- nurkkiirus ω;
- nurkkiirendus α.
Kirjeldame lühidalt iga nimetatud suurust.
Impulsi hetk määratakse järgmise valemiga:
Kui p on lineaarne impulss, m on materiaalse punkti mass, v on selle lineaarkiirus.
Materiaalse punkti inertsmoment arvutatakse avaldise abil:
Iga keeruka kujuga keha puhul arvutatakse I väärtus materiaalsete punktide inertsmomentide integraalsummana.
Jõumoment M arvutatakse järgmiselt:
Siin on F välisjõud, d on kaugus selle rakenduspunktist pöörlemisteljeni.
Kõigi suuruste füüsikaline tähendus, mille nimetus sisaldab sõna "hetk", on sarnane vastavate lineaarsete suuruste tähendusega. Näiteks näitab jõumoment rakendatud jõu võimet anda edasi pöörlevate kehade süsteem.
Kinemaatilised omadused määratakse matemaatiliselt järgmiste valemitega:
Nagu nendest avaldistest nähtub, on nurkkarakteristikud oma tähenduselt sarnased lineaarsetele (kiirused v ja kiirendus a), ainult need on rakendatavad ringtee jaoks.
Pöörlemise dünaamika
Füüsikas uuritakse jäiga keha pöörlevat liikumist kahe mehaanika osa abil: dünaamika ja kinemaatika. Alustame dünaamikast.
Dünaamika uurib pöörlevate kehade süsteemile mõjuvaid välisjõude. Paneme kohe kirja jäiga keha pöörlemisliikumise võrrandi ja seejärel analüüsime selle koostisosi. Niisiis, see võrrand näeb välja selline:
Mis mõjutab süsteemi, millel on inertsimoment I, põhjustab nurkkiirenduse α ilmnemise. Mida väiksem on I väärtus, seda lihtsam on teatud hetke M abil süsteem lühikese aja jooksul suurele kiirusele keerutada. Näiteks metallvarda on lihtsam pöörata mööda oma telge kui sellega risti. Sama varrast on aga lihtsam pöörata ümber temaga risti oleva ja massikeset läbiva telje kui läbi selle otsa.
Koguse L säilitusseadus
Seda väärtust tutvustati eespool, seda nimetatakse nurkmomendiks. Eelmises lõigus esitatud jäiga keha pöörlemisliikumise võrrand kirjutatakse sageli erineval kujul:
Kui süsteemile mõjub aja dt jooksul välisjõudude moment M, siis põhjustab see süsteemi nurkimpulsi muutuse väärtuse dL võrra. Seega, kui jõudude moment on null, siis L = const. See on suuruse L jäävuse seadus. Selle jaoks võime lineaar- ja nurkkiiruse seost kasutades kirjutada:
L = m * v * r = m * ω * r 2 = I * ω.
Seega on jõudude momendi puudumisel nurkkiiruse ja inertsmomendi korrutis konstantne. Seda füüsikaseadust kasutavad uisutajad oma esinemistel või tehissatelliitidel, mida tuleb avatud ruumis pöörata ümber oma telje.

Tsentripetaalne kiirendus
Eespool, uurides jäiga keha pöörlevat liikumist, on seda väärtust juba kirjeldatud. Samuti märgiti ära tsentripetaalsete jõudude olemus. Siin me ainult täiendame seda teavet ja esitame vastavad valemid selle kiirenduse arvutamiseks. Tähistame seda c-ga.
Kuna tsentripetaaljõud on suunatud teljega risti ja läbib seda, ei tekita see momenti. See tähendab, et see jõud ei mõjuta pöörlemise kinemaatilisi omadusi. See tekitab aga tsentripetaalse kiirenduse. Siin on selle määratluse jaoks kaks valemit:
Seega, mida suurem on nurkkiirus ja raadius, seda rohkem tuleb rakendada jõudu, et hoida keha ringteel. Selle füüsilise protsessi suurepärane näide on auto libisemine kurvides. Libisemine tekib siis, kui tsentripetaaljõud, mille rolli mängib hõõrdejõud, muutub väiksemaks tsentrifugaaljõust (inertsiaalkarakteristikust).

Eespool on artiklis loetletud kolm peamist kinemaatilist omadust. tahket keha kirjeldatakse järgmiste valemitega:
θ = ω * t => ω = konst., α = 0;
θ = ω 0 * t + α * t 2/2 => ω = ω 0 + α * t, α = konst.
Esimene rida sisaldab ühtlase pöörlemise valemeid, mis eeldab süsteemile mõjuvate jõudude välismomendi puudumist. Teine rida sisaldab valemeid ühtlaselt kiirendatud liikumiseks mööda ringi.

Pange tähele, et pöörlemine võib toimuda mitte ainult positiivse, vaid ka negatiivse kiirenduse korral. Sel juhul tuleks teise rea valemites teise liikme ette panna miinusmärk.
Näide probleemi lahendamisest
Pöördemoment 1000 N * m mõjutas metallvõlli 10 sekundit. Teades, et võlli inertsmoment on 50 kg * m 2, on vaja määrata nurkkiirus, mille nimetatud jõumoment võllile andis.

Pöörlemise põhivõrrandi abil arvutame võlli kiirenduse:
Kuna see nurkkiirendus mõjus võllile aja t = 10 sekundit, siis kasutame nurkkiiruse arvutamiseks ühtlaselt kiirendatud liikumise valemit:
ω = ω 0 + α * t = M / I * t.
Siin ω 0 = 0 (võll ei pöörlenud enne jõudude momendi M mõju).
Asendades suuruste arvväärtused võrdsusega, saame:
ω = 1000/50 * 10 = 200 rad / s.
Selle arvu teisendamiseks tavapärasteks pööreteks sekundis peate selle jagama 2 * pi-ga. Pärast selle toimingu sooritamist leiame, et võll pöörleb sagedusega 31,8 pööret minutis. / S.
MÄÄRATLUS: Jäiga keha pöörlev liikumine me nimetame sellist liikumist, mille käigus kõik keha punktid liiguvad ringidena, mille keskpunktid asuvad samal sirgel, mida nimetatakse pöörlemisteljeks.
Pöörlemise dünaamika uurimiseks lisatakse teadaolevatele kinemaatilistele suurustele veel kaks kogust: jõu hetk(M) ja inertsimoment(J).
1. Kogemustest on teada: pöörleva liikumise kiirendus ei sõltu mitte ainult kehale mõjuva jõu suurusest, vaid ka kaugusest pöörlemisteljelt jooneni, mida mööda jõud mõjub. Selle asjaolu iseloomustamiseks kasutatakse füüsikalist suurust nn jõu hetk.
Vaatleme kõige lihtsamat juhtumit.
MÄÄRATLUS: Jõumoment teatud punkti suhtes "O" on vektorsuurus, mis on määratud avaldisega, kus on punktist "O" jõu rakenduspunkti tõmmatud raadiuse vektor.
Definitsioonist järeldub, et see on telgvektor. Selle suund on valitud nii, et vektori pöörlemine ümber punkti “O” jõu suunas ja vektor moodustaks parempoolse süsteemi. Jõumomendi moodul on võrdne, kus a on nurk vektorite suundade ja ja l= r patt a - risti pikkus, mis langeb punktist "O" sirgjoonele, mida mööda jõud mõjub (nn. jõu õlg punkti "O" suhtes) (joonis 4.2).
2. Katseandmed näitavad, et nurkkiirenduse suurust ei mõjuta mitte ainult pöörleva keha mass, vaid ka massi jaotus pöörlemistelje suhtes. Väärtust, mis seda asjaolu arvesse võtab, nimetatakse inertsimoment pöörlemistelje ümber.
MÄÄRATLUS: rangelt võttes inertsimoment keha väärtust teatud pöörlemistelje suhtes nimetatakse väärtuseks J, mis võrdub elementaarmasside korrutistega nende kauguste ruutude võrra sellest teljest.
Summeerimine viiakse läbi kõigi elementaarsete masside kohta, milleks keha purustati. Tuleb meeles pidada, et see suurus (J) eksisteerib sõltumata pöörlemisest (kuigi jäiga keha pöörlemise käsitlemisel võeti kasutusele inertsmomendi mõiste).
Igal kehal, olenemata sellest, kas see on puhke- või pöörlemisasendis, on teatud inertsimoment mis tahes telje suhtes, nii nagu kehal on mass, olenemata sellest, kas see liigub või puhkab.
Arvestades seda, võib inertsmomenti esitada järgmiselt:. See suhe on ligikaudne ja mida väiksemad on elementaarmahud ja vastavad massielemendid, seda täpsem see on. Järelikult taandub inertsimomentide leidmise probleem integratsiooniks:. Siin toimub integreerimine kogu keha mahus.
Paneme kirja mõne korrapärase geomeetrilise kujuga keha inertsmomendid.
| 1. Ühtlane pikk võll. | |
| Riis. 4.3 | Inertsimoment vardaga risti oleva ja selle keskkohta läbiva telje suhtes on |
| 2. Tahke silinder või ketas. | |
| Riis. 4.4 | Inertsimoment geomeetrilise teljega kokku langeva telje suhtes on võrdne. |
| 3. Õhukeseseinaline silinder raadiusega R. | |
| Riis. 4.5 | |
| 4. Raadiusega kuuli inertsimoment selle keskpunkti läbiva telje suhtes | |
| Riis. 4.6 | |
| 5. Õhukese ketta inertsimoment (paksus b< | |
| Riis. 4.7 | |
| 6. Varda inertsimoment | |
| Riis. 4.8 | |
| 7. Rõnga inertsimoment | |
| Riis. 4.9 |
Inertsmomendi arvutused on siin üsna lihtsad, sest eeldatakse, et keha on homogeenne ja sümmeetriline ning inertsimoment määratakse sümmeetriatelje suhtes.
Keha inertsmomendi määramiseks mis tahes telje suhtes on vaja kasutada Steineri teoreemi.
MÄÄRATLUS: Inertsimoment J suvalise telje suhtes on võrdne antud inertsmomendi J summaga antud teljega paralleelse ja keha inertsikeskpunkti läbiva telje suhtes ning kehamassi korrutisega telgedevahelise kauguse ruuduga (joonis fig. 4.10).
- Kokkupuutel 0
- Google+ 0
- Okei 0
- Facebook 0

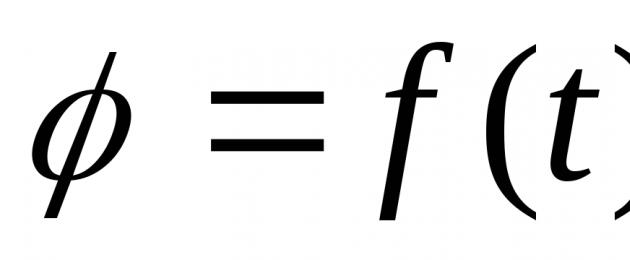
 .
. .
. .
.





