Մոդուլային աղյուսակ. Ֆունկցիայի գրաֆիկներ մոդուլով

Մոդուլն այն բաներից է, որի մասին կարծես թե բոլորը լսել են, բայց իրականում ոչ ոք իրականում չի հասկանում: Ուստի այսօր մեծ դաս է լինելու՝ նվիրված մոդուլներով հավասարումներ լուծելուն։

Անմիջապես կասեմ՝ դասը պարզ է լինելու։ Ընդհանուր առմամբ, մոդուլները, ընդհանուր առմամբ, համեմատաբար պարզ թեմա են: «Այո, իհարկե, հեշտ է! Դա ստիպում է իմ ուղեղը պայթել»: - Շատ ուսանողներ կասեն, բայց ուղեղի այս բոլոր ընդմիջումները պայմանավորված են նրանով, որ մարդկանց մեծամասնության գլխում ոչ թե գիտելիք կա, այլ ինչ-որ խելագարություն: Եվ այս դասի նպատակը հիմարությունը գիտելիքի վերածելն է: :)

Մի քիչ տեսություն

Ուրեմն գնանք։ Սկսենք ամենակարևորից՝ ի՞նչ է մոդուլը: Հիշեցնեմ, որ թվի մոդուլը պարզապես նույն թիվն է, բայց վերցված առանց մինուս նշանի։ Այսինքն, օրինակ, $\left| -5 \աջ|=5$. Կամ $\ձախ| -129.5\աջ|=129.5$.

Արդյո՞ք դա այդքան պարզ է: Այո, պարզ: Այդ դեպքում ո՞րն է դրական թվի մոդուլը: Այստեղ ավելի պարզ է. դրական թվի մոդուլը հավասար է հենց այս թվին. $\left| 5\աջ|=5$; $\ձախ| 129,5 \իրավունք|=129,5$ և այլն։

Հետաքրքիր բան է ստացվում. տարբեր թվեր կարող են ունենալ նույն մոդուլը: Օրինակ՝ $\left| -5 \աջ|=\ձախ| 5\աջ|=5$; $\ձախ| -129.5 \աջ|=\ձախ| 129,5 \աջ|=129,5$։ Հեշտ է տեսնել, թե ինչ թվեր են դրանք, որոնցում մոդուլները նույնն են. այս թվերը հակադիր են։ Այսպիսով, մենք ինքներս ենք նշում, որ հակադիր թվերի մոդուլները հավասար են.

\[\ձախ| -a \աջ|=\ձախ| ա\իրավունք|\]

Մեկ այլ կարևոր փաստ. մոդուլը երբեք բացասական չէ. Ինչ թիվ էլ վերցնենք՝ նույնիսկ դրական, նույնիսկ բացասական, նրա մոդուլը միշտ դրական է ստացվում (կամ ծայրահեղ դեպքերում՝ զրո): Այդ իսկ պատճառով մոդուլը հաճախ անվանում են թվի բացարձակ արժեք։

Բացի այդ, եթե միավորենք մոդուլի սահմանումը դրական և բացասական թվերի համար, մենք ստանում ենք բոլոր թվերի մոդուլի գլոբալ սահմանումը: Այսինքն՝ թվի մոդուլը հավասար է հենց այս թվին, եթե թիվը դրական է (կամ զրո), կամ հավասար է հակառակ թվին, եթե թիվը բացասական է։ Դուք կարող եք սա գրել որպես բանաձև.

Կա նաև զրոյի մոդուլ, բայց այն միշտ հավասար է զրոյի։ Բացի այդ, զրոն միակ թիվն է, որը չունի հակադիր:

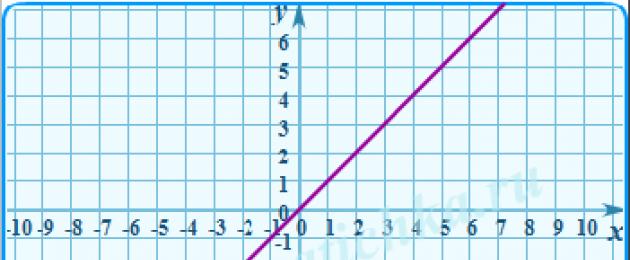
Այսպիսով, եթե դիտարկենք $y=\left| ֆունկցիան x \right|$ և փորձեք նկարել դրա գրաֆիկը, կստանաք այսպիսի «daw».

Մոդուլի գրաֆիկի և հավասարումների լուծման օրինակ

Այս նկարից անմիջապես կարող եք տեսնել, որ $\left| -m \աջ|=\ձախ| m \right|$, և մոդուլի սյուժեն երբեք չի ընկնում x առանցքից ցածր: Բայց սա դեռ ամենը չէ. կարմիր գիծը նշում է $y=a$ ուղիղ գիծը, որը դրական $a$-ով մեզ տալիս է միանգամից երկու արմատ՝ $((x)_(1))$ և $((x) _(2)) $, բայց մենք այդ մասին կխոսենք ավելի ուշ: :)

Բացի զուտ հանրահաշվական սահմանումից, կա նաև երկրաչափական սահմանում. Ենթադրենք, թվային տողի վրա կա երկու կետ՝ $((x)_(1))$ և $((x)_(2))$: Այս դեպքում $\left| արտահայտությունը ((x)_(1))-((x)_(2)) \right|$-ն ընդամենը նշված կետերի միջև եղած հեռավորությունն է: Կամ, եթե ցանկանում եք, այս կետերը միացնող հատվածի երկարությունը.

Մոդուլը թվային գծի կետերի միջև հեռավորությունն է

Այս սահմանումից նաև հետևում է, որ մոդուլը միշտ ոչ բացասական է։ Բայց բավական սահմանումներ և տեսություն. եկեք անցնենք իրական հավասարումների: :)

Հիմնական բանաձև

Լավ, մենք պարզեցինք սահմանումը: Բայց դա ավելի հեշտ չեղավ: Ինչպե՞ս լուծել այս մոդուլը պարունակող հավասարումները:

Հանգիստ, պարզապես հանգիստ: Սկսենք ամենապարզ բաներից։ Մտածեք այսպիսի մի բան.

\[\ձախ| x\աջ|=3\]

Այսպիսով, մոդուլ $x$-ը 3 է: Ինչի՞ կարող է հավասար լինել $x$-ը: Դե, դատելով սահմանումից, $x=3$-ը մեզ լավ կհամապատասխանի: Իրոք.

\[\ձախ| 3\աջ|=3\]

Այլ թվեր կա՞ն։ Կապը կարծես հուշում է, որ կա: Օրինակ՝ $x=-3$ — $\left| -3 \աջ|=3$, այսինքն. պահանջվող հավասարությունը բավարարված է.

Ուրեմն, միգուցե, եթե փնտրենք, մտածենք, ավելի շատ թվեր գտնե՞նք։ Բայց անջատիր. այլևս թվեր չկան: $\ձախ| x \right|=3$-ն ունի միայն երկու արմատ՝ $x=3$ և $x=-3$:

Հիմա մի փոքր բարդացնենք խնդիրը։ Թողեք $f\left(x \right)$ ֆունկցիան $x$ փոփոխականի փոխարեն մոդուլի նշանի տակ, իսկ աջ կողմում եռակի փոխարեն դրեցինք կամայական $a$ թիվը։ Մենք ստանում ենք հավասարումը.

\[\ձախ| f\ ձախ (x \աջ) \աջ|=a\]

Դե, ինչպես եք որոշում: Հիշեցնեմ՝ $f\left(x \right)$-ը կամայական ֆունկցիա է, $a$-ը՝ ցանկացած թիվ։ Նրանք. ընդհանրապես ցանկացած! Օրինակ:

\[\ձախ| 2x+1 \աջ|=5\]

\[\ձախ| 10x-5 \աջ|=-65\]

Դիտարկենք երկրորդ հավասարումը. Նրա մասին անմիջապես կարելի է ասել՝ նա արմատներ չունի։ Ինչո՞ւ։ Ճիշտ է, քանի որ դրա համար պահանջվում է, որ մոդուլը հավասար լինի բացասական թվին, ինչը երբեք չի լինում, քանի որ մենք արդեն գիտենք, որ մոդուլը միշտ դրական թիվ է կամ ծայրահեղ դեպքում՝ զրո։

Բայց առաջին հավասարմամբ ամեն ինչ ավելի զվարճալի է: Երկու տարբերակ կա՝ կա՛մ դրական արտահայտություն կա մոդուլի նշանի տակ, ապա՝ $\left| 2x+1 \right|=2x+1$, կամ այս արտահայտությունը դեռ բացասական է, որի դեպքում $\left| 2x+1 \աջ|=-\ձախ(2x+1 \աջ)=-2x-1$: Առաջին դեպքում մեր հավասարումը կվերագրվի հետևյալ կերպ.

\[\ձախ| 2x+1 \աջ|=5\Աջ սլաք 2x+1=5\]

Եվ հանկարծ պարզվում է, որ $2x+1$ ենթամոդուլային արտահայտությունն իսկապես դրական է՝ այն հավասար է 5 թվին։ Այսինքն՝ մենք կարող ենք ապահով կերպով լուծել այս հավասարումը. արդյունքում ստացված արմատը կլինի պատասխանի մի մասը.

Նրանք, ովքեր հատկապես անհավատ են, կարող են փորձել փոխարինել գտած արմատը սկզբնական հավասարման մեջ և համոզվել, որ մոդուլի տակ իսկապես դրական թիվ կլինի:

Հիմա եկեք նայենք բացասական ենթամոդուլային արտահայտության դեպքին.

\[\ձախ\( \սկիզբ(հավասարեցնել)& \ձախ| 2x+1 \աջ|=5 \\& 2x+1 \lt 0 \\\վերջ (հավասարեցնել) \աջ.\Աջ սլաք -2x-1=5 \Աջ սլաք 2x+1=-5\]

Վա՜յ Կրկին, ամեն ինչ պարզ է. մենք ենթադրեցինք, որ $2x+1 \lt 0$, և արդյունքում ստացանք $2x+1=-5$ - իսկապես, այս արտահայտությունը զրոյից փոքր է: Մենք լուծում ենք ստացված հավասարումը, մինչդեռ արդեն հաստատ գիտենք, որ հայտնաբերված արմատը կհամապատասխանի մեզ.

Ընդհանուր առմամբ կրկին երկու պատասխան ստացանք՝ $x=2$ և $x=3$։ Այո, հաշվարկների քանակը մի փոքր ավելի է ստացվել, քան շատ պարզ հավասարման $\left| x \right|=3$, բայց սկզբունքորեն ոչինչ չի փոխվել։ Այսպիսով, միգուցե կա ինչ-որ ունիվերսալ ալգորիթմ:

Այո, նման ալգորիթմ գոյություն ունի։ Եվ հիմա մենք կվերլուծենք այն:

Ազատվել մոդուլի նշանից

Եկեք մեզ տրվի $\left| հավասարումը f\left(x \right) \right|=a$, իսկ $a\ge 0$ (հակառակ դեպքում, ինչպես արդեն գիտենք, արմատներ չկան): Այնուհետև դուք կարող եք ազատվել մոդուլային նշանից հետևյալ կանոնի համաձայն.

\[\ձախ| f\ ձախ (x \աջ) \աջ|=a\Աջ սլաք f\ ձախ (x \աջ)=\pm a\]

Այսպիսով, մոդուլի հետ մեր հավասարումը բաժանվում է երկու մասի, բայց առանց մոդուլի: Դա ամբողջ տեխնոլոգիան է: Փորձենք լուծել մի քանի հավասարումներ։ Սկսենք սրանից

\[\ձախ| 5x+4 \աջ|=10\Աջ սլաք 5x+4=\pm 10\]

Առանձին-առանձին կքննարկենք, երբ աջ կողմում կա տասը գումարած, իսկ երբ այն մինուսով է։ Մենք ունենք:

\[\սկիզբ(հավասարեցնել)& 5x+4=10\Աջ սլաք 5x=6\Աջ սլաք x=\frac(6)(5)=1,2; \\& 5x+4=-10\Rightarrow 5x=-14\Rightarrow x=-\frac(14)(5)=-2.8: \\\վերջ (հավասարեցնել)\]

Այսքանը: Ստացանք երկու արմատ՝ $x=1,2$ և $x=-2,8$։ Ամբողջ լուծումը տառացիորեն երկու տող է վերցրել։

Լավ, հարց չկա, եկեք մի քիչ ավելի լուրջ բան նայենք.

\[\ձախ| 7-5x \աջ|=13\]

Կրկին բացեք մոդուլը գումարած և մինուսով.

\[\սկիզբ (հավասարեցնել)& 7-5x=13\Rightarrow -5x=6\Rightarrow x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Rightarrow -5x=-20\Rightarrow x=4. \\\վերջ (հավասարեցնել)\]

Կրկին մի քանի տող, և պատասխանը պատրաստ է: Ինչպես ասացի, մոդուլներում բարդ բան չկա։ Պարզապես պետք է հիշել մի քանի կանոն. Հետևաբար, մենք ավելի առաջ ենք գնում և անցնում իսկապես ավելի բարդ գործերով։

Աջ կողմի փոփոխական պատյան

Այժմ հաշվի առեք այս հավասարումը.

\[\ձախ| 3x-2 \աջ|=2x\]

Այս հավասարումը սկզբունքորեն տարբերվում է բոլոր նախորդներից։ Ինչպե՞ս: Իսկ այն, որ $2x$ արտահայտությունը հավասարության նշանից աջ է, և մենք չենք կարող նախապես իմանալ՝ դա դրական է, թե բացասական։

Ինչպե՞ս լինել այդ դեպքում: Նախ, մենք պետք է մեկընդմիշտ դա հասկանանք եթե հավասարման աջ կողմը բացասական է, ապա հավասարումը արմատներ չի ունենա- մենք արդեն գիտենք, որ մոդուլը չի ​​կարող հավասար լինել բացասական թվի:

Եվ երկրորդը, եթե աջ մասը դեռ դրական է (կամ հավասար է զրոյի), ապա կարող եք շարունակել ճիշտ նույն կերպ, ինչպես նախկինում. պարզապես բացեք մոդուլը առանձին՝ գումարած նշանով և առանձին՝ մինուս նշանով։

Այսպիսով, մենք ձևակերպում ենք կանոն $f\left(x \right)$ և $g\left(x \right)$ կամայական ֆունկցիաների համար:

\[\ձախ| f\ ձախ (x \աջ) \աջ|=g\ ձախ (x \աջ)\Աջ սլաք \ձախ\( \սկիզբ (հավասարեցնել)& f\ ձախ (x \աջ) =\pm g\ ձախ (x \աջ ), \\& g\ ձախ (x \աջ)\ge 0. \\\վերջ (հավասարեցնել) \աջ.\]

Ինչ վերաբերում է մեր հավասարմանը, մենք ստանում ենք.

\[\ձախ| 3x-2 \աջ|=2x\Աջ սլաք \ձախ\( \սկիզբ (հավասարեցնել)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\վերջ (հավասարեցնել) \աջ.\]

Դե, մենք կարող ենք ինչ-որ կերպ կարգավորել $2x\ge 0$ պահանջը: Ի վերջո, մենք կարող ենք հիմարաբար փոխարինել այն արմատները, որոնք ստանում ենք առաջին հավասարումից և ստուգել, ​​թե արդյոք անհավասարությունը պահպանվում է, թե ոչ:

Այսպիսով, եկեք լուծենք ինքնին հավասարումը.

\[\սկիզբ (հավասարեցնել)& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\Rightarrow 3x=0\Rightarrow x=0. \\\վերջ (հավասարեցնել)\]

Լավ, այս երկու արմատներից որն է բավարարում $2x\ge 0$ պահանջը: Այո՛, երկուսն էլ։ Հետևաբար պատասխանը կլինի երկու թիվ՝ $x=(4)/(3)\;$ և $x=0$: Սա է լուծումը: :)

Ես կասկածում եմ, որ ուսանողներից մեկն արդեն սկսել է ձանձրանալ: Դե, հաշվի առեք նույնիսկ ավելի բարդ հավասարումը.

\[\ձախ| ((x)^(3))-3((x)^(2))+x \աջ|=x-((x)^(3))\]

Թեև դա չար տեսք ունի, իրականում դա «մոդուլը հավասար է ֆունկցիայի» ձևի նույն հավասարումն է.

\[\ձախ| f\ ձախ (x \աջ) \աջ|=g\ ձախ (x \աջ)\]

Եվ դա լուծվում է նույն կերպ.

\[\ձախ| ((x)^(3))-3((x)^(2))+x \աջ|=x-((x)^(3))\Աջ սլաք \ձախ\( \սկիզբ (հավասարեցնել)& ( (x)^(3))-3((x)^(2))+x=\pm \ձախ(x-((x)^(3)) \աջ), \\& x-((x) )^(3))\ge 0. \\\վերջ (հավասարեցնել) \աջ.\]

Մենք ավելի ուշ կզբաղվենք անհավասարության հետ. այն ինչ-որ կերպ չափազանց արատավոր է (իրականում պարզ է, բայց մենք այն չենք լուծի): Առայժմ դիտարկենք ստացված հավասարումները: Դիտարկենք առաջին դեպքը. սա այն դեպքում, երբ մոդուլը ընդլայնվում է գումարած նշանով.

\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]

Դե, այստեղ անիմաստ է, որ դուք պետք է հավաքեք ամեն ինչ ձախ կողմում, բերեք նմանատիպերը և տեսեք, թե ինչ է տեղի ունենում: Եվ սա այն է, ինչ տեղի է ունենում.

\[\սկիզբ(հավասարեցնել)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\վերջ (հավասարեցնել)\]

$((x)^(2))$ ընդհանուր գործակիցը փակագծից դուրս հանելով՝ մենք ստանում ենք շատ պարզ հավասարում.

\[((x)^(2))\ձախ(2x-3 \աջ)=0\Աջ սլաք \ձախ[ \սկիզբ(հավասարեցնել)& ((x)^(2))=0 \\& 2x-3 =0 \\\վերջ (հավասարեցնել) \աջ:\]

\[((x)_(1))=0;\քառակուսի ((x)_(2))=\frac(3)(2)=1.5.\]

Այստեղ մենք օգտագործեցինք արտադրյալի կարևոր հատկությունը, որի համար գործոնավորեցինք սկզբնական բազմանդամը. արտադրյալը հավասար է զրոյի, երբ գործակիցներից գոնե մեկը հավասար է զրոյի։

Այժմ, նույն կերպ, մենք գործ կունենանք երկրորդ հավասարման հետ, որը ստացվում է ընդլայնելով մոդուլը մինուս նշանով.

\[\սկիզբ(հավասարեցնել)& ((x)^(3))-3((x)^(2))+x=-\ձախ(x-((x)^(3)) \աջ); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\ ձախ (-3x+2 \աջ)=0: \\\վերջ (հավասարեցնել)\]

Կրկին նույն բանը. արտադրյալը զրո է, երբ գործոններից գոնե մեկը զրո է: Մենք ունենք:

\[\ձախ[ \սկիզբ(հավասարեցնել)& x=0 \\& -3x+2=0 \\\վերջ (հավասարեցնել) \աջ:\]

Դե, ստացանք երեք արմատ՝ $x=0$, $x=1,5$ և $x=(2)/(3)\;$։ Դե, ի՞նչ կվերաբերվի այս հավաքածուի վերջնական պատասխանին: Դա անելու համար հիշեք, որ մենք ունենք լրացուցիչ անհավասարության սահմանափակում.

Ինչպե՞ս հաշվի առնել այս պահանջը: Եկեք պարզապես փոխարինենք գտնված արմատները և ստուգենք, արդյոք անհավասարությունը պահպանվում է այս $x$-ի համար, թե ոչ: Մենք ունենք:

\[\սկիզբ(հավասարեցնել)& x=0\Աջ սլաք x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Աջ սլաք x-((x)^(3))=1,5-((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Աջ սլաք x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\վերջ (հավասարեցնել)\]

Այսպիսով, $x=1,5$ արմատը մեզ չի համապատասխանում։ Եվ միայն երկու արմատ կգնա ի պատասխան.

\[((x)_(1))=0;\քառակուսի ((x)_(2))=\frac(2)(3).\]

Ինչպես տեսնում եք, նույնիսկ այս դեպքում դժվար բան չկար՝ մոդուլների հետ հավասարումները միշտ լուծվում են ըստ ալգորիթմի։ Պարզապես պետք է լավ հասկանալ բազմանդամներն ու անհավասարությունները: Հետևաբար, մենք անցնում ենք ավելի բարդ առաջադրանքների՝ արդեն կլինի ոչ թե մեկ, այլ երկու մոդուլ:

Հավասարումներ երկու մոդուլներով

Մինչ այժմ մենք ուսումնասիրել ենք միայն ամենապարզ հավասարումները՝ կար մեկ մոդուլ և մեկ այլ բան։ Մենք այս «ուրիշ բանն» ուղարկեցինք անհավասարության մեկ այլ մաս՝ մոդուլից հեռու, որպեսզի ի վերջո ամեն ինչ վերածվի $\left|-ի նման հավասարման։ f\left(x \right) \right|=g\left(x \աջ)$ կամ նույնիսկ ավելի պարզ $\left| f\left(x \աջ) \աջ|=a$.

Բայց մանկապարտեզն ավարտվել է. ժամանակն է մտածել ավելի լուրջ բանի մասին: Սկսենք հետևյալ հավասարումներից.

\[\ձախ| f\left(x \աջ) \աջ|=\ձախ| g\left(x \աջ) \աջ|\]

Սա «մոդուլը հավասար է մոդուլին» ձևի հավասարումն է։ Սկզբունքորեն կարևոր կետը այլ տերմինների և գործոնների բացակայությունն է. միայն մեկ մոդուլ ձախ կողմում, ևս մեկ մոդուլ աջ կողմում, և ոչ ավելին:

Հիմա կարելի է մտածել, որ նման հավասարումներ ավելի դժվար է լուծել, քան այն, ինչ մինչ այժմ ուսումնասիրել ենք: Բայց ոչ. այս հավասարումները ավելի հեշտ են լուծվում: Ահա բանաձեւը.

\[\ձախ| f\left(x \աջ) \աջ|=\ձախ| g\ ձախ (x \աջ) \աջ |\ Աջ սլաք f\ ձախ (x \աջ) =\pm g\ ձախ (x \աջ)\]

Ամեն ինչ! Մենք պարզապես հավասարեցնում ենք ենթամոդուլային արտահայտությունները՝ դրանցից մեկի նախածանցով գումարած կամ մինուս նշանով: Եվ հետո մենք լուծում ենք ստացված երկու հավասարումները, և արմատները պատրաստ են: Ոչ մի լրացուցիչ սահմանափակում, ոչ մի անհավասարություն և այլն: Ամեն ինչ շատ պարզ է.

Փորձենք լուծել այս խնդիրը.

\[\ձախ| 2x+3 \աջ|=\ձախ| 2x-7 \աջ|\]

Տարրական Ուոթսոն! Մոդուլների բացում.

\[\ձախ| 2x+3 \աջ|=\ձախ| 2x-7 \աջ|\Աջ սլաք 2x+3=\pm \ձախ(2x-7 \աջ)\]

Դիտարկենք յուրաքանչյուր դեպք առանձին.

\[\սկիզբ (հավասարեցնել)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\ձախ(2x-7 \աջ)\Աջ սլաք 2x+3=-2x+7: \\\վերջ (հավասարեցնել)\]

Առաջին հավասարումը արմատներ չունի։ Որովհետև ե՞րբ է $3=-7$: $x$-ի ի՞նչ արժեքների համար: «Ի՞նչ է դա $x$-ը: քեզ քարկոծե՞լ են։ $x$ ընդհանրապես չկա»,- ասում ես։ Եվ դուք ճիշտ կլինեք։ Մենք ստացել ենք հավասարություն, որը կախված չէ $x$ փոփոխականից, և միևնույն ժամանակ հավասարությունն ինքնին սխալ է։ Դրա համար էլ արմատներ չկան։

Երկրորդ հավասարման դեպքում ամեն ինչ մի փոքր ավելի հետաքրքիր է, բայց նաև շատ, շատ պարզ.

Ինչպես տեսնում եք, ամեն ինչ որոշվեց բառացիորեն մի քանի տողում. մենք այլ բան չէինք սպասում գծային հավասարումից: :)

Արդյունքում վերջնական պատասխանն է՝ $x=1$։

Դե, ինչպե՞ս: Դժվա՞ր: Իհարկե ոչ. Փորձենք մեկ այլ բան.

\[\ձախ| x-1 \աջ|=\ձախ| ((x)^(2))-3x+2 \աջ|\]

Կրկին մենք ունենք $\left| նման հավասարում f\left(x \աջ) \աջ|=\ձախ| g\left(x \աջ) \աջ|$. Հետևաբար, մենք անմիջապես վերագրում ենք այն՝ բացահայտելով մոդուլի նշանը.

\[((x)^(2))-3x+2=\pm \ձախ(x-1 \աջ)\]

Միգուցե ինչ-որ մեկը հիմա հարցնի. «Հեյ, ի՞նչ անհեթեթություն: Ինչու՞ գումարած-մինուսը աջ կողմում է, իսկ ձախ կողմում՝ ոչ: Հանգստացիր, ես ամեն ինչ կբացատրեմ: Իսկապես, լավ իմաստով, մենք պետք է վերագրեինք մեր հավասարումը հետևյալ կերպ.

Այնուհետև պետք է բացել փակագծերը, հավասար նշանից բոլոր տերմինները մեկ ուղղությամբ տեղափոխել (քանի որ հավասարումը, ակնհայտորեն, երկու դեպքում էլ քառակուսի է լինելու), ապա գտնել արմատները։ Բայց պետք է խոստովանեք. երբ «պլյուս-մինուս»-ը երեք տերմինի դիմաց է (հատկապես, երբ այս տերմիններից մեկը քառակուսի արտահայտություն է), ինչ-որ կերպ ավելի բարդ է թվում, քան այն իրավիճակը, երբ «պլյուս-մինուս»-ը միայն երկուսի դիմաց է: պայմանները.

Բայց ոչինչ չի խանգարում մեզ վերաշարադրել սկզբնական հավասարումը հետևյալ կերպ.

\[\ձախ| x-1 \աջ|=\ձախ| ((x)^(2))-3x+2 \աջ|\Աջ սլաք \ձախ| ((x)^(2))-3x+2 \աջ|=\ձախ| x-1 \ճիշտ|\]

Ինչ է պատահել? Այո, ոչ մի առանձնահատուկ բան. պարզապես փոխել են ձախ և աջ կողմերը: Մանրուք, որն ի վերջո մի փոքր կհեշտացնի մեր կյանքը։ :)

Ընդհանուր առմամբ, մենք լուծում ենք այս հավասարումը, հաշվի առնելով տարբերակները գումարած և մինուսով.

\[\սկիզբ(հավասարեցնել)& ((x)^(2))-3x+2=x-1\Աջ սլաք ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\ձախ(x-1 \աջ)\Աջ սլաք ((x)^(2))-2x+1=0: \\\վերջ (հավասարեցնել)\]

Առաջին հավասարումն ունի $x=3$ և $x=1$ արմատներ։ Երկրորդը, ընդհանուր առմամբ, ճշգրիտ քառակուսի է.

\[((x)^(2))-2x+1=((\ձախ(x-1 \աջ))^(2))\]

Հետևաբար, այն ունի մեկ արմատ՝ $x=1$։ Բայց այս արմատը մենք արդեն ստացել ենք ավելի վաղ։ Այսպիսով, վերջնական պատասխանի մեջ կմտնեն միայն երկու թվեր.

\[((x)_(1))=3;\քառակուսի ((x)_(2))=1.\]

Առաքելությունն ավարտված է: Կարող եք վերցնել դարակից և կարկանդակ ուտել։ Դրանցից 2-ն է՝ քո միջինը: :)

Կարևոր նշում. Միևնույն արմատների առկայությունը մոդուլի ընդլայնման տարբեր տարբերակների համար նշանակում է, որ սկզբնական բազմանդամները տարրալուծվում են գործոնների, և այդ գործոնների թվում անպայման կլինի ընդհանուր մեկը: Իրոք.

\[\սկիզբ(հավասարեցնել)& \ձախ| x-1 \աջ|=\ձախ| ((x)^(2))-3x+2 \աջ|; \\&\ձախ| x-1 \աջ|=\ձախ| \ձախ(x-1 \աջ)\ձախ(x-2 \աջ) \աջ|: \\\վերջ (հավասարեցնել)\]

Մոդուլի հատկություններից մեկը՝ $\left| a\cdot b \աջ|=\ձախ| a \աջ|\cdot \ձախ| b \right|$ (այսինքն, արտադրյալի մոդուլը հավասար է մոդուլի արտադրյալին), ուստի սկզբնական հավասարումը կարող է վերագրվել որպես.

\[\ձախ| x-1 \աջ|=\ձախ| x-1 \աջ|\cdot \ձախ| x-2 \ճիշտ|\]

Ինչպես տեսնում եք, մենք իսկապես ընդհանուր գործոն ունենք. Այժմ, եթե հավաքեք բոլոր մոդուլները մի կողմից, ապա կարող եք այս բազմապատկիչը հանել փակագծից.

\[\սկիզբ(հավասարեցնել)& \ձախ| x-1 \աջ|=\ձախ| x-1 \աջ|\cdot \ձախ| x-2 \աջ|; \\&\ձախ| x-1 \աջ|-\ձախ| x-1 \աջ|\cdot \ձախ| x-2 \աջ|=0; \\&\ձախ| x-1 \աջ|\cdot \left(1-\left| x-2 \աջ| \աջ)=0: \\\վերջ (հավասարեցնել)\]

Դե, հիմա մենք հիշում ենք, որ արտադրյալը հավասար է զրոյի, երբ գործոններից առնվազն մեկը հավասար է զրոյի.

\[\ձախ[ \սկիզբ(հավասարեցնել)& \ձախ| x-1 \աջ|=0, \\& \ձախ| x-2 \աջ|=1. \\\վերջ (հավասարեցնել) \աջ:\]

Այսպիսով, երկու մոդուլներով սկզբնական հավասարումը կրճատվել է երկու ամենապարզ հավասարումների, որոնց մասին մենք խոսեցինք դասի հենց սկզբում: Նման հավասարումները կարելի է լուծել ընդամենը մի քանի տողով: :)

Այս դիտողությունը կարող է անհարկի բարդ և գործնականում անկիրառելի թվալ։ Այնուամենայնիվ, իրականում դուք կարող եք հանդիպել շատ ավելի բարդ խնդիրների, քան նրանք, որոնք մենք այսօր վերլուծում ենք: Դրանցում մոդուլները կարող են համակցվել բազմանդամների, թվաբանական արմատների, լոգարիթմների և այլնի հետ։ Եվ նման իրավիճակներում հավասարման ընդհանուր աստիճանն իջեցնելու ունակությունը՝ ինչ-որ բան փակագծից դուրս դնելով, կարող է շատ, շատ հարմար լինել: :)

Այժմ ես կցանկանայի վերլուծել մեկ այլ հավասարում, որն առաջին հայացքից կարող է խելահեղ թվալ։ Շատ ուսանողներ «կպչում են» դրա վրա, նույնիսկ նրանք, ովքեր հավատում են, որ լավ են հասկանում մոդուլները:

Այնուամենայնիվ, այս հավասարումը նույնիսկ ավելի հեշտ է լուծել, քան այն, ինչ մենք դիտարկել ենք ավելի վաղ: Իսկ եթե հասկանաք ինչու, ապա կստանաք մոդուլներով հավասարումներ արագ լուծելու հերթական հնարք։

Այսպիսով, հավասարումը հետևյալն է.

\[\ձախ| x-((x)^(3)) \աջ|+\ձախ| ((x)^(2))+x-2 \աջ|=0\]

Ոչ, սա տառասխալ չէ. դա պլյուս է մոդուլների միջև: Եվ մենք պետք է գտնենք, թե $x$-ի համար երկու մոդուլների գումարը հավասար է զրոյի: :)

Ինչումն է խնդիրը? Եվ խնդիրն այն է, որ յուրաքանչյուր մոդուլ դրական թիվ է, կամ ծայրահեղ դեպքում՝ զրո։ Ի՞նչ է տեղի ունենում, երբ գումարում եք երկու դրական թիվ: Ակնհայտ է, որ կրկին դրական թիվ.

\[\սկիզբ (հավասարեցնել)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\վերջ (հավասարեցնել)\]

Վերջին տողը կարող է ձեզ պատկերացում տալ. միակ դեպքը, երբ մոդուլների գումարը զրո է, այն է, եթե յուրաքանչյուր մոդուլը հավասար է զրոյի.

\[\ձախ| x-((x)^(3)) \աջ|+\ձախ| ((x)^(2))+x-2 \աջ|=0\Աջ սլաք \ձախ\( \սկիզբ(հավասարեցնել)& \ձախ| x-((x)^(3)) \աջ|=0, \\& \ձախ|((x)^(2))+x-2 \աջ|=0. \\\վերջ (հավասարեցնել) \աջ.\]

Ե՞րբ է մոդուլը հավասար զրոյի: Միայն մեկ դեպքում, երբ ենթամոդուլի արտահայտությունը հավասար է զրոյի.

\[((x)^(2))+x-2=0\Աջ սլաք \ձախ(x+2 \աջ)\ձախ(x-1 \աջ)=0\Աջ սլաք \ձախ[ \սկիզբ (հավասարեցնել)& x=-2 \\& x=1 \\\վերջ (հավասարեցնել) \աջ.\]

Այսպիսով, մենք ունենք երեք կետ, որտեղ առաջին մոդուլը սահմանվում է զրոյի՝ 0, 1 և −1; ինչպես նաև երկու կետ, որտեղ երկրորդ մոդուլը զրոյացված է. −2 և 1: Այնուամենայնիվ, մեզ անհրաժեշտ է, որ երկու մոդուլները զրոյացվեն միաժամանակ, ուստի գտնված թվերից մենք պետք է ընտրենք դրանք, որոնք ներառված են երկու հավաքածուներում: Ակնհայտ է, որ կա միայն մեկ այդպիսի թիվ՝ $x=1$ – սա կլինի վերջնական պատասխանը։

պառակտման մեթոդ

Դե, մենք արդեն ծածկել ենք մի շարք առաջադրանքներ և սովորել ենք շատ հնարքներ: Կարծում եք՝ վե՞րջ: Բայց ոչ! Այժմ մենք կքննարկենք վերջնական տեխնիկան, և միևնույն ժամանակ ամենակարևորը: Մենք կխոսենք մոդուլով հավասարումների բաժանման մասին։ Ի՞նչ է քննարկվելու։ Եկեք մի փոքր հետ գնանք և դիտարկենք մի քանի պարզ հավասարում: Օրինակ՝ սա.

\[\ձախ| 3x-5\աջ|=5-3x\]

Սկզբունքորեն, մենք արդեն գիտենք, թե ինչպես լուծել նման հավասարումը, քանի որ դա ստանդարտ $\left| է f\left(x \right) \right|=g\left(x \աջ)$: Բայց եկեք փորձենք այս հավասարմանը նայել մի փոքր այլ տեսանկյունից: Ավելի ճիշտ, հաշվի առեք մոդուլի նշանի տակ գտնվող արտահայտությունը: Հիշեցնեմ, որ ցանկացած թվի մոդուլը կարող է հավասար լինել հենց թվին, կամ կարող է հակառակ լինել այս թվին.

\[\ձախ| a \աջ|=\ձախ\( \սկիզբ (հավասարեցնել)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\վերջ (հավասարեցնել) \աջ.\]

Իրականում այս երկիմաստությունն է ամբողջ խնդիրը. քանի որ մոդուլի տակ թիվը փոխվում է (դա կախված է փոփոխականից), մեզ համար պարզ չէ՝ դա դրական է, թե բացասական։

Բայց ի՞նչ, եթե մենք ի սկզբանե պահանջենք, որ այս թիվը լինի դրական: Օրինակ, եկեք պահանջենք $3x-5 \gt 0$ - այս դեպքում մեզ երաշխավորված է դրական թիվ ստանալ մոդուլի նշանի տակ, և մենք կարող ենք ամբողջությամբ ազատվել այս մոդուլից.

Այսպիսով, մեր հավասարումը կվերածվի գծայինի, որը հեշտությամբ լուծվում է.

Ճիշտ է, այս բոլոր նկատառումները իմաստ ունեն միայն $3x-5 \gt 0$ պայմանով - մենք ինքներս ենք ներկայացրել այս պահանջը, որպեսզի միանշանակ բացահայտենք մոդուլը: Այսպիսով, եկեք փոխարինենք գտնված $x=\frac(5)(3)$ այս պայմանով և ստուգենք.

Ստացվում է, որ $x$-ի նշված արժեքի համար մեր պահանջը չի բավարարվում, քանի որ արտահայտությունը հավասար է զրոյի, և մեզ անհրաժեշտ է, որ այն խիստ մեծ լինի զրոյից: Տխուր. :(

Բայց դա լավ է: Ի վերջո, կա ևս մեկ տարբերակ $3x-5 \lt 0$։ Ավելին. կա նաև $3x-5=0$ դեպք, սա նույնպես պետք է հաշվի առնել, այլապես լուծումը թերի կլինի։ Այսպիսով, հաշվի առեք $3x-5 \lt 0$ դեպքը.

Ակնհայտ է, որ մոդուլը կբացվի մինուս նշանով։ Բայց հետո մի տարօրինակ իրավիճակ է առաջանում. սկզբնական հավասարման մեջ նույն արտահայտությունը դուրս կգա և՛ ձախ, և՛ աջ կողմում.

Հետաքրքիր է, նման $x$-ի համար $5-3x$ արտահայտությունը հավասար կլինի $5-3x$ արտահայտությանը: Նման հավասարումներից նույնիսկ կապիտանն ակնհայտորեն կխեղդվի թուքով, բայց մենք գիտենք, որ այս հավասարումը ինքնություն է, այսինքն. դա ճշմարիտ է փոփոխականի ցանկացած արժեքի համար:

Եվ սա նշանակում է, որ ցանկացած $x$ կհամապատասխանի մեզ: Այնուամենայնիվ, մենք ունենք սահմանափակում.

Այլ կերպ ասած, պատասխանը կլինի ոչ թե մեկ թիվ, այլ ամբողջ ընդմիջում.

Վերջապես, մնում է ևս մեկ դեպք՝ $3x-5=0$: Այստեղ ամեն ինչ պարզ է. մոդուլի տակ կլինի զրո, և զրոյի մոդուլը նույնպես հավասար է զրոյի (սա ուղղակիորեն բխում է սահմանումից).

Բայց հետո սկզբնական հավասարումը $\left| 3x-5 \right|=5-3x$-ը կվերագրվի այսպես.

Մենք արդեն ստացել ենք այս արմատը վերևում, երբ դիտարկեցինք $3x-5 \gt 0$ դեպքը: Ավելին, այս արմատը $3x-5=0$ հավասարման լուծումն է. սա այն սահմանափակումն է, որը մենք ինքներս մտցրեցինք մոդուլը չեղարկելու համար: :)

Այսպիսով, բացի միջակայքից, մենք կբավարարվենք նաև այս միջակայքի ամենավերջում գտնվող թվով.

Արմատները հավասարումների մեջ համակցելով մոդուլով

Ընդհանուր վերջնական պատասխան՝ $x\in \left(-\infty ;\frac(5)(3) \right]$: Մոդուլով բավականին պարզ (ըստ էության գծային) հավասարման պատասխանում նման անհեթեթություն տեսնելը այնքան էլ սովորական չէ: Դե, սովորեք դրան. մոդուլի բարդությունը կայանում է նրանում, որ նման հավասարումների պատասխանները կարող են լիովին անկանխատեսելի լինել:

Շատ ավելի կարևոր է այլ բան. մենք հենց նոր ապամոնտաժեցինք համընդհանուր ալգորիթմը մոդուլով հավասարումը լուծելու համար: Եվ այս ալգորիթմը բաղկացած է հետևյալ քայլերից.

1. Հավասարման մեջ յուրաքանչյուր մոդուլ հավասարեցրու զրոյի: Եկեք մի քանի հավասարումներ ստանանք;
2. Լուծե՛ք այս բոլոր հավասարումները և նշե՛ք արմատները թվային տողի վրա։ Արդյունքում ուղիղ գիծը կբաժանվի մի քանի ընդմիջումների, որոնցից յուրաքանչյուրի վրա բոլոր մոդուլները եզակիորեն ընդլայնված են.
3. Լուծե՛ք յուրաքանչյուր միջակայքի սկզբնական հավասարումը և միավորե՛ք պատասխանները:

Այսքանը: Մնում է միայն մեկ հարց՝ ի՞նչ անել հենց 1-ին քայլում ստացված արմատների հետ։ Ենթադրենք՝ ունենք երկու արմատ՝ $x=1$ և $x=5$։ Նրանք թվային գիծը կկոտրեն 3 մասի.

Թվային գիծը բաժանելով ընդմիջումների՝ օգտագործելով կետերը

Այսպիսով, որո՞նք են միջակայքերը: Պարզ է, որ դրանք երեքն են.

1. Ձախ՝ $x \lt 1$ - միավորն ինքնին ներառված չէ միջակայքում;
2. Կենտրոնական՝ $1\le x \lt 5$ - այստեղ մեկը ներառված է միջակայքում, բայց հինգը ներառված չէ;
3. Ամենաաջը՝ $x\ge 5$ — հինգը ներառված է միայն այստեղ:

Կարծում եմ, դուք արդեն հասկանում եք օրինաչափությունը: Յուրաքանչյուր ինտերվալ ներառում է ձախ ծայրը և չի ներառում աջ ծայրը:

Առաջին հայացքից նման ռեկորդը կարող է անհարմար, անտրամաբանական և ընդհանրապես ինչ-որ խենթ թվալ։ Բայց հավատացեք ինձ, մի փոքր պրակտիկայից հետո դուք կգտնեք, որ սա ամենահուսալի մոտեցումն է և միևնույն ժամանակ չի խանգարում միանշանակ բացահայտվող մոդուլներին: Ավելի լավ է օգտագործել նման սխեման, քան ամեն անգամ մտածել. ձախ / աջ ծայրը տվեք ընթացիկ միջակայքին կամ «նետեք» այն հաջորդին:

Այստեղ ավարտվում է դասը։ Ներբեռնեք առաջադրանքները ինքնուրույն լուծելու համար, փորձեք, համեմատեք պատասխանների հետ և կտեսնենք ձեզ հաջորդ դասին, որը նվիրված կլինի մոդուլներով անհավասարություններին: :)

y=|x| ձևի ֆունկցիա:
Ֆունկցիայի գրաֆիկը միջակայքի վրա - y \u003d -x ֆունկցիայի գրաֆիկով:

Նախ դիտարկենք ամենապարզ դեպքը՝ y=|x| ֆունկցիան: Մոդուլի սահմանմամբ մենք ունենք.

Այսպիսով, x≥0-ի համար y=|x| ֆունկցիան համընկնում է y \u003d x ֆունկցիայի հետ, իսկ x-ի համար Օգտագործելով այս բացատրությունը՝ հեշտ է գծել y \u003d | x | ֆունկցիան (նկ. 1):

Հեշտ է տեսնել, որ այս գրաֆիկը y \u003d x ֆունկցիայի գրաֆիկի այն մասի միավորումն է, որը գտնվում է OX առանցքից ոչ ցած, և այն գիծը, որը ստացվում է հայելային արտացոլմամբ OX առանցքի շուրջ, դրա այդ հատվածը, որը գտնվում է OX առանցքի տակ:
Այս մեթոդը հարմար է նաև y=|kx+b| ֆունկցիայի գրաֆիկը գծելու համար։
Եթե ​​y=kx+b ֆունկցիայի գրաֆիկը ներկայացված է Նկար 2-ում, ապա y=|kx+b ֆունկցիայի գրաֆիկը: Նկար 3-ում ներկայացված գիծն է:

(!LANG:Օրինակ 1.Գծե՛ք y=||1-x 2 |-3| ֆունկցիան:
Կառուցենք y=1-x 2 ֆունկցիայի գրաֆիկը և դրա վրա կիրառենք «մոդուլ» գործողությունը (գրաֆիկի այն մասը, որը գտնվում է OX առանցքի տակ, արտացոլվում է սիմետրիկորեն OX առանցքի նկատմամբ)։

Եկեք գծապատկերը տեղափոխենք 3-ով ներքև:

Կիրառենք «մոդուլ» գործողությունը և ստացենք y=||1-x 2 |-3| ֆունկցիայի վերջնական գրաֆիկը:

Օրինակ 2Գծե՛ք y=||x 2 -2x|-3| ֆունկցիան:
Փոխակերպման արդյունքում ստանում ենք y=|x 2 -2x|=|(x-1) 2 -1|: Կառուցենք y=(x-1) 2 -1 ֆունկցիայի գրաֆիկը՝ կառուցենք y=x 2 պարաբոլա և 1-ով տեղափոխենք աջ և 1-ով ներքև:

Դրա վրա կիրառենք «մոդուլ» գործողությունը (գրաֆիկի այն մասը, որը գտնվում է OX առանցքի տակ, սիմետրիկ կերպով արտացոլվում է OX առանցքի նկատմամբ)։

Եկեք գրաֆիկը տեղափոխենք 3-ով ներքև և կիրառենք «մոդուլ» գործողությունը, արդյունքում կստանանք վերջնական գրաֆիկը։

Օրինակ 3Գրեք ֆունկցիան։
Մոդուլը ընդլայնելու համար մենք պետք է հաշվի առնենք երկու դեպք.
1)x>0, ապա մոդուլը կբացվի «+» = նշանով
2) x =

Կառուցենք գրաֆիկ առաջին դեպքի համար։

Եկեք դեն նետենք գրաֆիկի այն մասը, որտեղ x

Եկեք երկրորդ դեպքի համար կառուցենք գրաֆիկ և նույն կերպ դուրս գցենք այն մասը, որտեղ x>0, արդյունքում ստանում ենք:

Համատեղենք երկու գրաֆիկները և ստանանք վերջնականը։

Օրինակ 4Գրեք ֆունկցիան։
Նախ, եկեք կառուցենք ֆունկցիայի գրաֆիկը, դրա համար հարմար է ընտրել ամբողջական մասը, ստանում ենք. Հիմնվելով արժեքների աղյուսակի վրա՝ ստանում ենք գրաֆիկ։

Կիրառենք մոդուլի գործողությունը (գրաֆիկի այն մասը, որը գտնվում է OX առանցքի տակ, սիմետրիկորեն արտացոլվում է OX առանցքի նկատմամբ)։ Մենք ստանում ենք վերջնական աղյուսակը

Օրինակ 5Գրեք y=|-x 2 +6x-8| ֆունկցիան: Նախ, մենք պարզեցնում ենք ֆունկցիան y=1-(x-3) 2-ով և կառուցում դրա գրաֆիկը

Այժմ մենք կիրառում ենք «մոդուլ» գործողությունը և արտացոլում գրաֆիկի հատվածը OX առանցքի տակ՝ OX առանցքի համեմատ

Օրինակ 6Գծե՛ք y=-x 2 +6|x|-8 ֆունկցիան: Մենք նաև պարզեցնում ենք y=1-(x-3) 2 ֆունկցիան և կառուցում դրա գրաֆիկը

Այժմ մենք կիրառում ենք «մոդուլ» գործողությունը և արտացոլում գրաֆիկի հատվածը oY առանցքի աջ կողմում, ձախ կողմում:

Օրինակ 7Կազմեք ֆունկցիա . Եկեք գծագրենք ֆունկցիան

Եկեք գծագրենք ֆունկցիան

Կատարենք զուգահեռ փոխանցում 3 միավոր հատվածներով դեպի աջ և 2 վերև։ Գրաֆիկը նման կլինի.

Կիրառենք «մոդուլ» գործողությունը և գրաֆիկի x=3 ուղիղ գծից աջ հատվածն արտացոլենք ձախ կիսահարթության մեջ։

սղագրություն

1 6-11-րդ դասարանների աշակերտների կրթական և հետազոտական ​​աշխատանքի տարածաշրջանային գիտական ​​և գործնական կոնֆերանս «Մաթեմատիկայի կիրառական և հիմնարար հարցեր» Մաթեմատիկայի ուսումնասիրության մեթոդական ասպեկտները Գաբովա Անժելա Յուրիևնա մոդուլ պարունակող ֆունկցիաների գրաֆիկների կառուցում, դասարան 10, MOBU «Գիմնազիա 3» Կուդիմկար, Պիկուլևա Նադեժդա Իվանովնա, մաթեմատիկայի ուսուցիչ, MOBU «Գիմնազիա 3», Կուդիմկար, Պերմ, 2016 թ.

2 Բովանդակություն՝ Ներածություն...3 էջ I. Հիմնական մաս... 6 էջ 1.1Պատմական նախադրյալներ.. 6 էջ 2.Ֆունկցիաների հիմնական սահմանումները և հատկությունները էջ .8 էջ 2.3 Կոտորակային-ռացիոնալ ֆունկցիա 8 էջ. 3. 9 մոդուլով գրաֆիկների գծագրման ալգորիթմներ էջ 3.1 Մոդուլի որոշում .. 9 էջ «ներդիր մոդուլներ» բանաձևում 10 էջ 3.4 y = a 1 xx 1 + a 2 ձևի ֆունկցիաների գրաֆիկների կառուցման ալգորիթմ. xxanxxn + ax + b...13 էջ 3.5 Մոդուլով քառակուսի ֆունկցիայի գրաֆիկի կառուցման ալգորիթմ.14 էջ 3.6 Ալգորիթմ՝ կոտորակային ռացիոնալ ֆունկցիայի գծապատկեր մոդուլով: 15 p. 4. Քառակուսային ֆունկցիայի գրաֆիկի փոփոխություններ՝ կախված բացարձակ արժեքի նշանի տեղակայությունից ..17str. II. Եզրակացություն ... 26 էջ III. Հղումների և աղբյուրների ցանկ...27 էջ IV. Դիմում....28p. 2

3 Ներածություն Գրաֆիկական ֆունկցիաները դպրոցական մաթեմատիկայի ամենահետաքրքիր թեմաներից են: Մեր ժամանակների ամենամեծ մաթեմատիկոս Իսրայել Մոիսեևիչ Գելֆանդը գրել է. Այս գծապատկերը միջոց է՝ տեսնելու բանաձևերը և ֆունկցիաները և տեսնելու, թե ինչպես են փոխվում այդ ֆունկցիաները: Օրինակ, եթե գրված է y \u003d x 2, ապա դուք անմիջապես տեսնում եք պարաբոլա. եթե y = x 2-4, դուք տեսնում եք պարաբոլա իջեցված չորս միավորով; եթե y \u003d - (x 2 4), ապա տեսնում եք, որ նախորդ պարաբոլան շրջված է: Բանաձևը միանգամից տեսնելու այս ունակությունը և դրա երկրաչափական մեկնաբանությունը կարևոր է ոչ միայն մաթեմատիկայի, այլև այլ առարկաների ուսումնասիրության համար։ Դա մի հմտություն է, որը ձեզ հետ է մնում ողջ կյանքի ընթացքում, օրինակ՝ սովորել հեծանիվ վարել, մեքենա գրել կամ մեքենա վարել»: Մոդուլներով հավասարումների լուծման հիմունքները ստացվել են 6-րդ 7-րդ դասարանում։ Ես ընտրեցի այս թեման, քանի որ կարծում եմ, որ այն պահանջում է ավելի խորը և մանրակրկիտ ուսումնասիրություն: Ես ուզում եմ ավելի շատ գիտելիքներ ստանալ թվի մոդուլի, բացարձակ արժեքի նշան պարունակող գրաֆիկների գծագրման տարբեր եղանակների մասին։ Երբ ուղիղների, պարաբոլների, հիպերբոլաների «ստանդարտ» հավասարումները ներառում են մոդուլի նշանը, դրանց գրաֆիկները դառնում են անսովոր և նույնիսկ գեղեցիկ: Որպեսզի սովորեք, թե ինչպես կառուցել նման գրաֆիկներ, դուք պետք է տիրապետեք հիմնական թվերի կառուցման տեխնիկային, ինչպես նաև հաստատապես իմանաք և հասկանաք թվի մոդուլի սահմանումը: Դպրոցական մաթեմատիկայի դասընթացում մոդուլով գրաֆիկները բավականաչափ խորը չեն դիտարկվում, այդ իսկ պատճառով ես ցանկացա ընդլայնել իմ գիտելիքները այս թեմայի վերաբերյալ, կատարել իմ սեփական հետազոտությունը։ Առանց մոդուլի սահմանման մասին իմանալու՝ անհնար է կառուցել անգամ բացարձակ արժեք պարունակող ամենապարզ գրաֆիկը։ Մոդուլի նշանով արտահայտություններ պարունակող ֆունկցիաների գրաֆիկների բնորոշ հատկանիշը, 3

4-ը ոլորումների առկայությունն է այն կետերում, որտեղ մոդուլի նշանի տակ արտահայտությունը փոխում է նշանը: Աշխատանքի նպատակը՝ դիտարկել մոդուլի նշանի տակ փոփոխական պարունակող գծային, քառակուսի և կոտորակային ֆունկցիաների գրաֆիկի կառուցումը։ Առաջադրանքներ՝ 1) Ուսումնասիրել գծային, քառակուսի և կոտորակային-ռացիոնալ ֆունկցիաների բացարձակ արժեքի հատկությունների վերաբերյալ գրականությունը. 2) Հետազոտել ֆունկցիաների գրաֆիկների փոփոխությունները՝ կախված բացարձակ արժեքի նշանի տեղակայությունից. 3) Սովորեք գծել հավասարումների գրաֆիկները: Ուսումնասիրության առարկա՝ գծային, քառակուսի և կոտորակային ֆունկցիաների գրաֆիկներ։ Ուսումնասիրության առարկա՝ գծային, քառակուսի և կոտորակային ֆունկցիաների գրաֆիկի փոփոխություններ՝ կախված բացարձակ արժեքի նշանի տեղակայությունից։ Իմ աշխատանքի գործնական նշանակությունը կայանում է նրանում, որ. 2) հետագա ուսումնական գործունեության մեջ հետազոտական ​​հմտությունների կիրառման մեջ. Համապատասխանություն. գրաֆիկական առաջադրանքները ավանդաբար մաթեմատիկայի ամենադժվար թեմաներից են: Մեր շրջանավարտների առջեւ խնդիր է դրվել հաջողությամբ հանձնել ԳԱԳ եւ միասնական պետական ​​քննությունը։ Հետազոտական ​​խնդիր. GIA-ի երկրորդ մասից մոդուլի նշան պարունակող ֆունկցիաների գծագրում: Հետազոտության վարկած. GIA-ի երկրորդ մասի առաջադրանքների լուծման մեթոդաբանության կիրառումը, որը մշակվել է մոդուլի նշան պարունակող ֆունկցիաների գրաֆիկների կառուցման ընդհանուր մեթոդների հիման վրա, թույլ կտա ուսանողներին լուծել այդ խնդիրները 4

5 գիտակցված հիմունքներով ընտրեք լուծման առավել ռացիոնալ մեթոդը, կիրառեք լուծման տարբեր մեթոդներ և ավելի հաջող անցեք GIA-ն: Աշխատանքում կիրառված հետազոտական ​​մեթոդները. 1. Այս թեմայով մաթեմատիկական գրականության և ինտերնետային ռեսուրսների վերլուծություն: 2. Ուսումնասիրվող նյութի վերարտադրողական վերարտադրումը. 3. Ճանաչողական-որոնողական գործունեություն. 4. Տվյալների վերլուծություն և համեմատություն խնդիրների լուծման որոնման համար: 5. Վարկածների շարադրում և դրանց ստուգում. 6. Մաթեմատիկական փաստերի համեմատություն և ընդհանրացում. 7. Ստացված արդյունքների վերլուծություն. Այս աշխատանքը գրելիս օգտագործվել են հետևյալ աղբյուրները՝ ինտերնետ ռեսուրսներ, OGE թեստեր, մաթեմատիկական գրականություն։ 5

6 I. Հիմնական մաս 1.1 Պատմական նախադրյալներ. 17-րդ դարի առաջին կեսին ֆունկցիա հասկացությունը սկսեց ձևավորվել որպես մի փոփոխականի կախվածություն մյուսից։ Այսպիսով, ֆրանսիացի մաթեմատիկոսներ Պիեռ Ֆերմատը () և Ռենե Դեկարտը () ֆունկցիան պատկերացնում էին որպես կորի կետի օրդինատի կախվածություն դրա աբսցիսից: Իսկ անգլիացի գիտնական Իսահակ Նյուտոնը () ֆունկցիան հասկացել է որպես շարժվող կետի կոորդինատ, որը փոխվում է կախված ժամանակից։ «Ֆունկցիա» տերմինը (լատիներեն ֆունկցիայի կատարում, հանձնաժողով) առաջին անգամ ներմուծել է գերմանացի մաթեմատիկոս Գոթֆրիդ Լայբնիցը (): Նա ֆունկցիան կապեց երկրաչափական պատկերի հետ (ֆունկցիայի գրաֆիկ)։ Հետագայում շվեյցարացի մաթեմատիկոս Յոհան Բեռնուլին () և Սանկտ Պետերբուրգի Գիտությունների ակադեմիայի անդամ, 18-րդ դարի հայտնի մաթեմատիկոս Լեոնարդ Էյլերը () ֆունկցիան դիտարկեցին որպես վերլուծական արտահայտություն։ Էյլերը նաև ընդհանուր պատկերացում ունի ֆունկցիայի մասին՝ որպես մեկ փոփոխականի կախվածություն մյուսից։ «Մոդուլ» բառը առաջացել է լատիներեն «modulus» բառից, որը թարգմանաբար նշանակում է «չափել»։ Սա բազմարժեք բառ է (հոմանիշ), որն ունի բազմաթիվ իմաստներ և օգտագործվում է ոչ միայն մաթեմատիկայի, այլև ճարտարապետության, ֆիզիկայի, ճարտարագիտության, ծրագրավորման և այլ ճշգրիտ գիտությունների մեջ։ Ճարտարապետության մեջ սա չափման սկզբնական միավորն է, որը հաստատվել է տվյալ ճարտարապետական ​​կառույցի համար և օգտագործվում է դրա բաղկացուցիչ տարրերի բազմակի հարաբերակցություններն արտահայտելու համար։ Ճարտարագիտության մեջ սա տերմին է, որն օգտագործվում է տեխնոլոգիայի տարբեր ոլորտներում, որը չունի համընդհանուր նշանակություն և ծառայում է տարբեր գործակիցներ և քանակություններ նշելու համար, օրինակ՝ ներգրավման մոդուլը, առաձգականության մոդուլը և այլն։ 6

7 Զանգվածային մոդուլը (ֆիզիկայում) նյութի նորմալ լարվածության հարաբերակցությունն է հարաբերական երկարացմանը: 2. Ֆունկցիաների հիմնական սահմանումները և հատկությունները Ֆունկցիան մաթեմատիկական ամենակարևոր հասկացություններից է: Ֆունկցիան y փոփոխականի այնպիսի կախվածությունն է x փոփոխականից, որում x փոփոխականի յուրաքանչյուր արժեք համապատասխանում է y փոփոխականի մեկ արժեքին։ Ֆունկցիան սահմանելու եղանակներ. 1) վերլուծական մեթոդ (ֆունկցիան սահմանվում է մաթեմատիկական բանաձևով); 2) աղյուսակային մեթոդ (գործառույթը նշված է աղյուսակի միջոցով); 3) նկարագրական մեթոդ (գործառույթը տրվում է բանավոր նկարագրությամբ). 4) գրաֆիկական մեթոդ (գործառույթը սահմանվում է գրաֆիկի միջոցով): Ֆունկցիայի գրաֆիկը կոորդինատային հարթության բոլոր կետերի բազմությունն է, որոնց աբսցիսները հավասար են փաստարկի արժեքին, իսկ օրդինատները՝ ֆունկցիայի համապատասխան արժեքներին։ 2.1 Քառակուսային ֆունկցիա y=ax 2 +in+c բանաձևով սահմանված ֆունկցիան, որտեղ x և y փոփոխականներ են, իսկ a, b և c պարամետրերը՝ ցանկացած իրական թվեր, իսկ a = 0, կոչվում է քառակուսի։ y \u003d ax 2 + in + c ֆունկցիայի գրաֆիկը պարաբոլա է. պարաբոլայի համաչափության առանցքը y \u003d ax 2 + in + c ուղիղ գիծ է, a> 0-ի համար պարաբոլայի «ճյուղերը» ուղղված են դեպի վեր, a.<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7

8 (մեկ փոփոխականի ֆունկցիաների համար): Գծային ֆունկցիաների հիմնական հատկությունն այն է, որ ֆունկցիայի աճը համաչափ է փաստարկի աճին։ Այսինքն՝ ֆունկցիան ուղիղ համեմատականության ընդհանրացում է։ Գծային ֆունկցիայի գրաֆիկը ուղիղ գիծ է, այստեղից էլ նրա անունը։ Սա վերաբերում է մեկ իրական փոփոխականի իրական ֆունկցիային: 1) ժամը, ուղիղ գիծը կազմում է սուր անկյուն x առանցքի դրական ուղղությամբ: 2) Երբ, ուղիղը կազմում է բութ անկյուն x առանցքի դրական ուղղությամբ: 3) y առանցքի հետ ուղիղի հատման կետի օրդինատի ցուցիչն է. 4) Երբ, գիծն անցնում է սկզբնակետով: , 2.3 Կոտորակի ռացիոնալ ֆունկցիան այն կոտորակն է, որի համարիչը և հայտարարը բազմանդամներ են։ Այն ունի ձև, որտեղ, բազմանդամներ ցանկացած թվով փոփոխականներում: Մեկ փոփոխականի ռացիոնալ ֆունկցիաները հատուկ դեպք են՝ որտեղ և են բազմանդամներ: 1) Ցանկացած արտահայտություն, որը կարելի է ստանալ փոփոխականներից՝ օգտագործելով չորս թվաբանական գործողություններ, ռացիոնալ ֆունկցիա է: ութ

9 2) Ռացիոնալ ֆունկցիաների բազմությունը փակված է թվաբանական գործողությունների և կազմության գործողության ներքո. 3) Ցանկացած ռացիոնալ ֆունկցիա կարող է ներկայացվել որպես պարզ կոտորակների գումար. սա օգտագործվում է վերլուծական ինտեգրման մեջ .., 3. Մոդուլով գրաֆիկական ալգորիթմներ, եթե a-ն բացասական է: a = 3.2 Մոդուլով գծային ֆունկցիայի գրաֆիկ կառուցելու ալգորիթմ y= x ֆունկցիաների գրաֆիկները գծելու համար պետք է իմանալ, որ դրական x-ի համար մենք ունենք x = x: Սա նշանակում է, որ արգումենտի դրական արժեքների համար y=x գրաֆիկը համընկնում է y=x գրաֆիկի հետ, այսինքն՝ գրաֆիկի այս հատվածը ծագումից 45 աստիճան անկյան տակ x-ի նկատմամբ ծագող ճառագայթ է։ առանցք. x-ի համար< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9

10 Շինարարության համար մենք վերցնում ենք (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2) միավորները: Այժմ կառուցենք y= x-1 գրաֆիկ, եթե A-ն y= x կոորդինատներով գրաֆիկական կետն է, ապա Y օրդինատի նույն արժեքով գրաֆիկի կետը y= x-1 կլինի A1 կետը։ (a+1; a). Երկրորդ գրաֆիկի այս կետը կարելի է ստանալ առաջին գրաֆիկի A(a; a) կետից՝ Ox առանցքի զուգահեռ շարժվելով դեպի աջ: Սա նշանակում է, որ y= x-1 ֆունկցիայի ամբողջ գրաֆիկը ստացվում է y= x ֆունկցիայի գրաֆիկից՝ Ox առանցքին զուգահեռ աջ տեղափոխելով 1-ով: Կառուցենք գրաֆիկներ՝ y= x-1 Կառուցելու համար. վերցնում ենք (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1) միավորները: 3.3 «Ներդրված մոդուլներ» պարունակող ֆունկցիաների գրաֆիկների կառուցում բանաձևում Դիտարկենք կառուցման ալգորիթմը՝ օգտագործելով կոնկրետ օրինակ:

11 y \u003d i-2-ix + 5ii 1. Մենք կառուցում ենք ֆունկցիայի գրաֆիկը: 2. Ստորին կիսահարթության գրաֆիկը OX առանցքի նկատմամբ սիմետրիկ կերպով ցուցադրում ենք դեպի վեր և ստանում ֆունկցիայի գրաֆիկը։ տասնմեկ

12 3. Ֆունկցիայի գրաֆիկը սիմետրիկ կերպով ցուցադրում ենք OX առանցքի նկատմամբ և ստանում ֆունկցիայի գրաֆիկը։ 4. Ֆունկցիայի գրաֆիկը սիմետրիկ կերպով ցուցադրում ենք OX առանցքի նկատմամբ և ստանում 5 ֆունկցիայի գրաֆիկը։ Ցուցադրում ենք ֆունկցիայի գրաֆիկը OX առանցքի նկատմամբ և ստանում գրաֆիկը։ 12

13 6. Արդյունքում ֆունկցիայի գրաֆիկն այսպիսի տեսք ունի 3.4. y = a 1 x x 1 + a 2 x x a n x x n + ax + b ձևի ֆունկցիաների գրաֆիկների կառուցման ալգորիթմ: Նախորդ օրինակում բավական հեշտ էր ընդլայնել մոդուլի նշանները: Եթե ​​մոդուլների ավելի շատ գումարներ կան, ապա խնդրահարույց է դիտարկել ենթամոդուլային արտահայտությունների նշանների բոլոր հնարավոր համակցությունները: Ինչպե՞ս կարող ենք գծապատկերել ֆունկցիան այս դեպքում: Նկատի ունեցեք, որ գրաֆիկը բազմագիծ է, որտեղ գագաթները ունեն -1 և 2 աբսցիսներ: x = -1 և x = 2-ի համար ենթամոդուլի արտահայտությունները հավասար են զրոյի: Գործնականորեն մենք մոտեցանք նման գրաֆիկներ կառուցելու կանոնին. y \u003d a 1 x x 1 + a 2 x x a n x x n + ax + b ձևի ֆունկցիայի գրաֆիկը անսահման ծայրահեղ կապերով բազմագիծ է: Նման պոլիգիծ կառուցելու համար բավական է իմանալ նրա բոլոր գագաթները (գագաթային աբսցիսները ենթամոդուլային արտահայտությունների զրոներն են) և մեկական կառավարման կետ ձախ և աջ անսահման կապերի վրա։ տասներեք

14 Առաջադրանք. Գծե՛ք y = x + x 1 + x + 1 ֆունկցիան և գտե՛ք դրա ամենափոքր արժեքը: Լուծում՝ 1. Ենթամոդուլային արտահայտությունների զրոներ՝ 0; - մեկ; Polyline vertices (0; 2); (-տասներեք); (1; 3) (ենթամոդուլի արտահայտությունների զրոները փոխարինվում են հավասարման մեջ) Կառուցում ենք գրաֆիկ (նկ. 7), ֆունկցիայի ամենափոքր արժեքն է Քառակուսային ֆունկցիայի գրաֆիկի գծագրման ալգորիթմ մոդուլով Դարձել ալգորիթմներ ֆունկցիաների գրաֆիկները փոխակերպելու համար։ 1.y= f(x) ֆունկցիայի գրաֆիկի կառուցում։ Մոդուլի սահմանման համաձայն՝ այս ֆունկցիան տարրալուծվում է երկու ֆունկցիաների մի շարքի։ Հետևաբար, y= f(x) ֆունկցիայի գրաֆիկը բաղկացած է երկու գրաֆիկից՝ y= f(x) աջ կիսահարթությունում, y= f(-x) ձախ կիսհարթում։ Դրա հիման վրա մենք կարող ենք ձևակերպել կանոն (ալգորիթմ): y= f(x) ֆունկցիայի գրաֆիկը ստացվում է y= f(x) ֆունկցիայի գրաֆիկից հետևյալ կերպ՝ x 0-ում գրաֆիկը պահպանվում է, իսկ x-ում.< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14

15 3. Y= f(x) ֆունկցիայի գրաֆիկը կառուցելու համար նախ պետք է y= f(x) ֆունկցիան x> 0-ի համար, ապա x-ի համար:< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15

16 Այս գրաֆիկը ստանալու համար բավական է միայն նախկինում ստացված գրաֆիկը երեք միավորով տեղափոխել աջ։ Նկատի ունեցեք, որ եթե կոտորակի հայտարարը լիներ x + 3, ապա մենք կտեղափոխեինք գրաֆիկը ձախ. Այժմ մենք պետք է երկուսով բազմապատկենք բոլոր օրդինատները, որպեսզի ստանանք ֆունկցիայի գրաֆիկը: Վերջին բանը, որ մեզ մնում է անել, տրված ֆունկցիան գծելն է, եթե այն պարփակված է մոդուլի նշանի տակ: Դա անելու համար մենք սիմետրիկորեն դեպի վեր արտացոլում ենք գրաֆիկի ամբողջ մասը, որի օրդինատները բացասական են (այն մասը, որը գտնվում է x առանցքի տակ). Նկ.4 16

17 4. Քառակուսային ֆունկցիայի գրաֆիկի փոփոխություններ՝ կախված բացարձակ արժեքի նշանի տեղակայությունից: Գրեք y \u003d x 2 - x -3 ֆունկցիան 1) Քանի որ x \u003d x x 0-ում, պահանջվող գրաֆիկը համընկնում է պարաբոլի հետ y \u003d 0,25 x 2 - x - 3: Եթե x<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. բ) Հետևաբար, ես լրացնում եմ x-ի համար<0 часть графика, симметричную построенной относительно оси ОУ. 17

18 Նկ. 4 y \u003d f (x) ֆունկցիայի գրաֆիկը համընկնում է y \u003d f (x) ֆունկցիայի գրաֆիկի հետ արգումենտի ոչ բացասական արժեքների բազմության վրա և սիմետրիկ է դրան y-ի նկատմամբ։ - առանցք փաստարկի բացասական արժեքների բազմության վրա: Ապացույց. Եթե x 0, ապա f (x) = f (x), այսինքն. Փաստարկի ոչ բացասական արժեքների բազմության վրա y = f (x) և y = f (x) ֆունկցիաների գրաֆիկները համընկնում են: Քանի որ y \u003d f (x) զույգ ֆունկցիա է, ապա դրա գրաֆիկը սիմետրիկ է ՕՀ-ի նկատմամբ: Այսպիսով, y \u003d f (x) ֆունկցիայի գրաֆիկը կարելի է ստանալ y \u003d f (x) ֆունկցիայի գրաֆիկից հետևյալ կերպ. 2. x-ի համար<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. x-ի համար<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х

19 Եթե x 2 - x -6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 և սիմետրիկորեն արտացոլված մասը y \u003d f (x) y-ում<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, ապա f (x) \u003d f (x), ինչը նշանակում է, որ այս մասում y \u003d f (x) ֆունկցիայի գրաֆիկը համընկնում է բուն y \u003d f (x) ֆունկցիայի գրաֆիկի հետ: Եթե ​​f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19

20 Նկ.5 Եզրակացություն. y= f(x) ֆունկցիան գծագրել 1. Գծել y=f(x) ֆունկցիան; 2. Այն տարածքներում, որտեղ գրաֆիկը գտնվում է ստորին կիսահարթության մեջ, այսինքն՝ որտեղ f (x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20

21 Հետազոտական ​​աշխատանք ֆունկցիայի գրաֆիկների գծագրման վերաբերյալ y \u003d f (x) Կիրառելով բացարձակ արժեքի սահմանումը և նախկինում դիտարկված օրինակները՝ մենք գծագրելու ենք ֆունկցիայի գրաֆիկները՝ y \u003d 2 x - 3 y \u003d x 2-5 xy \ u003d x 2-2 և եզրակացություններ արեց: y = f (x) ֆունկցիայի գրաֆիկը կառուցելու համար անհրաժեշտ է՝ 1. Կառուցեք y = f (x) ֆունկցիայի գրաֆիկ x>0-ի համար։ 2. Կառուցեք գրաֆիկի երկրորդ մասը, այսինքն՝ կառուցված գրաֆիկը սիմետրիկ կերպով արտացոլեք ՕՀ-ի նկատմամբ, քանի որ. այս ֆունկցիան հավասար է: 3. Ստացված գծապատկերի հատվածները, որոնք գտնվում են ստորին կիսահարթությունում, պետք է վերին կիսահարթության վերածել OX առանցքի սիմետրիկ կերպով: Կառուցեք y \u003d 2 x - 3 ֆունկցիայի գրաֆիկ (մոդուլը որոշելու 1-ին մեթոդ) X< -1,5 и х>1,5 ա) y = 2x - 3, x>0-ի համար բ) x-ի համար<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 բ) x-ի համար<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) Մենք կառուցում ենք ուղիղ գիծ, ​​որը սիմետրիկ է կառուցվածին OS առանցքի նկատմամբ: 3) Գրաֆիկի այն հատվածները, որոնք գտնվում են ներքևի կես հարթությունում, ցուցադրվում են սիմետրիկորեն OX առանցքի նկատմամբ: Համեմատելով երկու գրաֆիկները՝ տեսնում ենք, որ դրանք նույնն են։ 21

22 Խնդիրների օրինակներ Օրինակ 1. Դիտարկենք y = x 2 6x +5 ֆունկցիայի գրաֆիկը: Քանի որ x-ը քառակուսի է, ապա անկախ x թվի նշանից քառակուսուց հետո այն դրական կլինի։ Սրանից հետևում է, որ y \u003d x 2-6x +5 ֆունկցիայի գրաֆիկը նույնական կլինի y \u003d x 2-6x +5 ֆունկցիայի գրաֆիկին, այսինքն. բացարձակ արժեքի նշան չպարունակող ֆունկցիայի գրաֆիկ (նկ. 2): Նկ.2 Օրինակ 2. Դիտարկենք y \u003d x 2 6 x +5 ֆունկցիայի գրաֆիկը: Օգտագործելով թվի մոդուլի սահմանումը, մենք փոխարինում ենք y \u003d x 2 6 x +5 բանաձևը Այժմ մենք գործ ունենք մաս-մաս կախվածության նշանակման հետ, որը մեզ քաջ հայտնի է: Մենք կկառուցենք այսպիսի գրաֆիկ. 1) կկառուցենք պարաբոլա y \u003d x 2-6x +5 և շրջագծիր դրա այն մասը, որը 22 է.

23-ը համապատասխանում է ոչ բացասական x արժեքներին, այսինքն. y առանցքի աջ կողմում գտնվող մասը։ 2) նույն կոորդինատային հարթությունում մենք կառուցում ենք պարաբոլա y \u003d x 2 +6x +5 և շրջում ենք դրա այն հատվածը, որը համապատասխանում է x-ի բացասական արժեքներին, այսինքն. y առանցքից ձախ կողմում գտնվող մասը: Պարաբոլների շրջանաձև մասերը միասին կազմում են y \u003d x 2-6 x +5 ֆունկցիայի գրաֆիկը (նկ. 3): Նկ.3 Օրինակ 3. Դիտարկենք y \u003d x 2-6 x +5 ֆունկցիայի գրաֆիկը: Որովհետեւ y \u003d x 2 6x +5 հավասարման գրաֆիկը նույնն է, ինչ ֆունկցիայի գրաֆիկն առանց մոդուլի նշանի (դիտված օրինակ 2-ում), հետևում է, որ y \u003d x 2 6 x +5 ֆունկցիայի գրաֆիկը նույնական է y \u003d x 2 6 x +5 ֆունկցիայի գրաֆիկին, որը դիտարկված է օրինակ 2-ում (նկ. 3): Օրինակ 4. Կառուցենք y \u003d x 2 6x +5 ֆունկցիայի գրաֆիկը: Դա անելու համար մենք կառուցում ենք y \u003d x 2-6x ֆունկցիայի գրաֆիկը: Դրանից y \u003d x 2-6x ֆունկցիայի գրաֆիկը ստանալու համար հարկավոր է պարաբոլայի յուրաքանչյուր կետ փոխարինել բացասական օրդինատով միևնույն աբսցիսով կետով, բայց հակառակ (դրական) օրդինատով: Այլ կերպ ասած, պարաբոլայի այն մասը, որը գտնվում է x առանցքի տակ, պետք է փոխարինվի x առանցքի նկատմամբ սիմետրիկ գծով։ Որովհետեւ մենք պետք է կառուցենք y \u003d x 2-6x +5 ֆունկցիայի գրաֆիկը, այնուհետև այն ֆունկցիայի գրաֆիկը, որը մենք համարել ենք y \u003d x 2-6x, պարզապես պետք է բարձրացնենք y առանցքի երկայնքով 5 միավորով (նկ. 4). 23

24 Նկ.4 Օրինակ 5. Կառուցենք y \u003d x 2-6x + 5 ֆունկցիայի գրաֆիկը: Դա անելու համար մենք օգտագործում ենք հայտնի piecewise ֆունկցիան։ Գտեք y \u003d 6x +5 6x + 5 \u003d 0 at ֆունկցիայի զրոները: Դիտարկենք երկու դեպք. 1) Եթե, ապա հավասարումը ստանում է y = x 2 6x -5 ձևը: Եկեք կառուցենք այս պարաբոլան և շրջենք դրա այն հատվածը, որտեղ: 2) Եթե, ապա հավասարումը վերցնում է y \u003d x 2 + 6x +5 ձևը: Կառուցենք այս պարաբոլան և կլորացնենք դրա այն հատվածը, որը գտնվում է կետից ձախ կոորդինատներով (նկ. 5): 24

25 Նկ.5 Օրինակ6. Եկեք գծենք y \u003d x 2 6 x +5 ֆունկցիան: Դա անելու համար մենք գծագրում ենք y \u003d x 2-6 x +5 ֆունկցիան: Մենք գծեցինք այս գրաֆիկը Օրինակ 3-ում: Քանի որ մեր ֆունկցիան ամբողջությամբ գտնվում է մոդուլի նշանի տակ, ֆունկցիայի գրաֆիկը գծելու համար y \u003d x 2 6 x +5, ձեզ անհրաժեշտ է y \u003d x 2 6 x ֆունկցիայի գրաֆիկի յուրաքանչյուր կետ: + 5 ժխտական ​​օրդինատով, փոխարինել նույն աբսցիսով կետով, բայց հակառակ (դրական) օրդինատով, այսինքն. Ox առանցքի տակ գտնվող պարաբոլայի մասը պետք է փոխարինվի Ox առանցքի նկատմամբ սիմետրիկ գծով (նկ. 6): Նկ.6 25

26 II. Եզրակացություն «Մաթեմատիկական տեղեկատվությունը կարելի է հմտորեն և շահավետ օգտագործել միայն ստեղծագործական յուրացման դեպքում, որպեսզի ուսանողն ինքը տեսնի, թե ինչպես կարելի է ինքնուրույն հասնել դրան»: Ա.Ն. Կոլմոգորովը. Այս առաջադրանքները մեծ հետաքրքրություն են ներկայացնում իններորդ դասարանի աշակերտների համար, քանի որ դրանք շատ տարածված են OGE թեստերում: Գործառույթների այս գրաֆիկները կառուցելու ունակությունը թույլ կտա ավելի հաջող հանձնել քննությունը: Ֆրանսիացի մաթեմատիկոսներ Պիեռ Ֆերման () և Ռենե Դեկարտը () ֆունկցիան պատկերացնում էին որպես կորի կետի օրդինատի կախվածություն դրա աբսցիսից։ Իսկ անգլիացի գիտնական Իսահակ Նյուտոնը () ֆունկցիան հասկացել է որպես շարժվող կետի կոորդինատ, որը փոխվում է կախված ժամանակից։ 26

27 III. Հղումների և աղբյուրների ցանկ 1. Galitsky M. L., Goldman A. M., Zvavich L. I. Հանրահաշվի խնդիրների ժողովածու 8 9-րդ դասարանների համար. Proc. նպաստ դպրոցի աշակերտների համար. և խորացումով պարապմունքներ։ ուսումնասիրություն Մաթեմատիկա 2-րդ հրտ. Մ .: Լուսավորություն, Դորոֆեև Գ.Վ. Մաթեմատիկա. Հանրահաշիվ. Գործառույթներ. Տվյալների վերլուծություն. Դասարան 9: m34 Պրոց. հանրակրթական ուսումնասիրությունների համար։ մենեջեր 2-րդ հրատ., կարծրատիպ. M .: Bustard, Solomonik V.S. Մաթեմատիկայի հարցերի և առաջադրանքների ժողովածու M .: «Բարձրագույն դպրոց», Յաշչենկո Ի.Վ. GIA. Մաթեմատիկա. տիպիկ քննության տարբերակներ. տարբերակների մասին.մ .. «Ազգային կրթություն», էջ. 5. Յաշչենկո Ի.Վ. OGE. Մաթեմատիկա. տիպիկ քննության տարբերակներ. տարբերակների մասին.մ .. «Ազգային կրթություն», էջ. 6. Յաշչենկո Ի.Վ. OGE. Մաթեմատիկա. տիպիկ քննության տարբերակներ. տարբերակների մասին.մ .. «Ազգային կրթություն», էջ.

28 Հավելված 28

29 Օրինակ 1. Գրեք y = x 2 8 x Լուծում ֆունկցիան: Եկեք սահմանենք ֆունկցիայի հավասարությունը: y(-x)-ի արժեքը նույնն է, ինչ y(x-ի), ուստի այս ֆունկցիան զույգ է: Այնուհետև նրա գրաֆիկը սիմետրիկ է Oy առանցքի նկատմամբ։ Մենք կառուցում ենք y \u003d x 2 8x + 12 ֆունկցիայի գրաֆիկ x 0-ի համար և ցուցադրում ենք գրաֆիկը սիմետրիկորեն Oy-ի նկատմամբ բացասական x-ի համար (նկ. 1): Օրինակ 2. y \u003d x 2 8x ձևի հետևյալ գրաֆիկը Սա նշանակում է, որ ֆունկցիայի գրաֆիկը ստացվում է հետևյալ կերպ. նրանք y \u003d x 2 8x + 12 ֆունկցիայի գրաֆիկ են կառուցում, թողնում են գրաֆիկի մասը։ որը գտնվում է Ox առանցքի վերևում անփոփոխ, և գրաֆիկի այն մասը, որը գտնվում է աբսցիսայի առանցքի տակ, ցուցադրվում է սիմետրիկորեն Ox առանցքի նկատմամբ (նկ. 2): Օրինակ 3. y \u003d x 2 8 x + 12 ֆունկցիան գծագրելու համար կատարվում է փոխակերպումների համակցություն՝ y \u003d x 2 8x + 12 y \u003d x 2 8 x + 12 y \u003d x 2 8 x Պատասխան Նկար 3. Օրինակ 4 Մոդուլի նշանի տակ գտնվող արտահայտությունը փոխում է նշանը x=2/3 կետում: Ժամը x<2/3 функция запишется так: 29

30 x>2/3-ի դեպքում ֆունկցիան կգրվի հետևյալ կերպ. Այսինքն՝ x=2/3 կետը մեր կոորդինատային հարթությունը բաժանում է երկու շրջանի, որոնցից մեկում (աջից) կառուցում ենք ֆունկցիան և մյուսը (ձախից) ֆունկցիայի գրաֆիկը, որը մենք կառուցում ենք. Օրինակ 5 Հաջորդը, գրաֆիկը նույնպես կոտրված է, բայց ունի երկու ընդմիջման կետ, քանի որ այն պարունակում է երկու արտահայտություն մոդուլի նշանների տակ.

31 Ընդարձակեք մոդուլները առաջին ինտերվալի վրա. Երկրորդ ինտերվալում. Երրորդ ինտերվալում. Այսպիսով, (- ; 1.5] միջակայքում մենք ունենք առաջին հավասարմամբ գրված գրաֆիկը, իսկ ինտերվալի վրա՝ երկրորդ հավասարմամբ գրված գրաֆիկը, և ընդմիջումով)