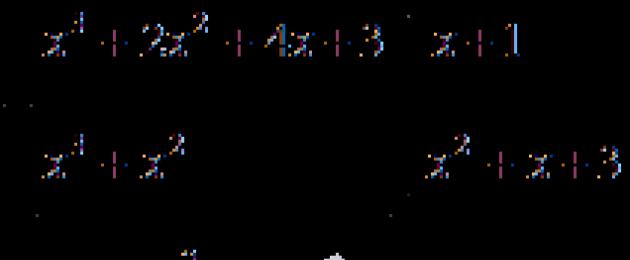5-րդ աստիճանի հավասարման լուծում ռադիկալներով. Բարձրագույն աստիճանի հավասարումների լուծում

Մեր կայքի youtube-ի ալիքում՝ բոլոր նոր տեսադասերին տեղյակ պահելու համար։

Սկզբից եկեք հիշենք աստիճանների հիմնական բանաձևերը և դրանց հատկությունները:

Թվի արտադրանք ապատահում է ինքն իրեն n անգամ, մենք կարող ենք այս արտահայտությունը գրել որպես a ... a = a n

1.a 0 = 1 (a ≠ 0)

3.a n a m = a n + m

4. (a n) m = a nm

5.a n b n = (ab) n

7.a n / a m = a n - m

Հզորություն կամ էքսպոնենցիալ հավասարումներ - սրանք հավասարումներ են, որոնցում փոփոխականները գտնվում են հզորություններով (կամ ցուցիչներով), իսկ հիմքը թիվ է:

Էքսպոնենցիալ հավասարումների օրինակներ.

Այս օրինակում 6 թիվը հիմքն է, այն միշտ կանգնած է ներքևում, իսկ փոփոխականը xաստիճան կամ ցուցանիշ:

Ահա էքսպոնենցիալ հավասարումների ևս մի քանի օրինակ:
2 x * 5 = 10
16 x - 4 x - 6 = 0

Հիմա տեսնենք, թե ինչպես են լուծվում էքսպոնենցիալ հավասարումները։

Եկեք մի պարզ հավասարում վերցնենք.

2 x = 2 3

Նման օրինակը կարելի է լուծել նույնիսկ մտքում։ Երևում է, որ x = 3: Ի վերջո, որպեսզի ձախ և աջ կողմերը հավասար լինեն, պետք է x-ի փոխարեն դնել 3 թիվը։
Հիմա տեսնենք, թե ինչպես պետք է այս լուծումը ձևակերպվի.

2 x = 2 3
x = 3

Նման հավասարումը լուծելու համար մենք հանեցինք նույնական հիմքեր(այսինքն՝ երկուսի) և գրի առավ այն, ինչ մնացել էր, սրանք աստիճաններ են։ Մենք ստացանք ցանկալի պատասխանը.

Հիմա ամփոփենք մեր որոշումը.

Էքսպոնենցիալ հավասարման լուծման ալգորիթմ.
1. Պետք է ստուգել նույնըարդյոք հավասարումը ունի աջ և ձախ հիմքեր: Եթե հիմքերը նույնը չեն, մենք տարբերակներ ենք փնտրում այս օրինակը լուծելու համար։
2. Այն բանից հետո, երբ հիմքերը նույնն են. հավասարեցնելաստիճանը և լուծիր ստացված նոր հավասարումը:

Այժմ լուծենք մի քանի օրինակ.

Սկսենք պարզ.

Ձախ և աջ կողմերի հիմքերը հավասար են 2 թվին, ինչը նշանակում է, որ մենք կարող ենք հրաժարվել հիմքից և հավասարեցնել դրանց աստիճանները:

x + 2 = 4 Սա ամենապարզ հավասարումն է:
x = 4 - 2
x = 2
Պատասխան՝ x = 2

Հետևյալ օրինակում կարող եք տեսնել, որ հիմքերը տարբեր են, դրանք 3 և 9 են:

3 3x - 9x + 8 = 0

Սկզբից մենք ինը տեղափոխում ենք աջ կողմ, ստանում ենք.

Այժմ դուք պետք է պատրաստեք նույն հիմքերը: Մենք գիտենք, որ 9 = 3 2: Եկեք օգտագործենք աստիճանների բանաձևը (a n) m = a nm:

3 3x = (3 2) x + 8

Մենք ստանում ենք 9 x + 8 = (3 2) x + 8 = 3 2x + 16

3 3x = 3 2x + 16 այժմ դուք կարող եք տեսնել, որ ձախ և աջ կողմերի հիմքերը նույնն են և հավասար են երեքի, ուստի մենք կարող ենք դրանք մերժել և հավասարեցնել աստիճանները:

3x = 2x + 16 ստացել է ամենապարզ հավասարումը
3x - 2x = 16
x = 16
Պատասխան՝ x = 16:

Տես հետևյալ օրինակը.

2 2x + 4 - 10 4 x = 2 4

Առաջին հերթին մենք նայում ենք հիմքերին, հիմքերը տարբերվում են երկուից և չորսից: Եվ մեզ պետք է, որ նրանք նույնը լինեն: Չորսը փոխարկեք (a n) m = a nm բանաձևով:

4 x = (2 2) x = 2 2x

Եվ մենք նաև օգտագործում ենք մեկ բանաձև a n a m = a n + m.

2 2x + 4 = 2 2x 2 4

Ավելացնել հավասարմանը.

2 2x 2 4 - 10 2 2x = 24

Մենք օրինակը բերել ենք նույն հիմքերի վրա։ Բայց մեզ խանգարում են 10-րդ և 24-րդ համարները: Ի՞նչ անել դրանց հետ: Եթե ուշադիր նայեք, կտեսնեք, որ ձախ կողմում մենք կրկնում ենք 2 2x, ահա պատասխանը՝ 2 2x կարող ենք հանել փակագծերից.

2 2x (2 4 - 10) = 24

Հաշվարկենք փակագծերում տրված արտահայտությունը.

2 4 — 10 = 16 — 10 = 6

Ամբողջ հավասարումը բաժանեք 6-ի.

Եկեք պատկերացնենք 4 = 2 2:

2 2x = 2 2 հիմքերը նույնն են, դեն նետեք դրանք և հավասարեցրեք հզորությունները:
2x = 2 մենք ստանում ենք ամենապարզ հավասարումը: Բաժանում ենք 2-ի, ստանում ենք
x = 1
Պատասխան՝ x = 1:

Եկեք լուծենք հավասարումը.

9 x - 12 * 3 x + 27 = 0

Եկեք փոխակերպենք.
9 x = (3 2) x = 3 2x

Մենք ստանում ենք հավասարումը.
3 2x - 12 3x +27 = 0

Մեր հիմքերը հավասար են 3-ի: Այս օրինակում դուք կարող եք տեսնել, որ առաջին երեքի աստիճանը երկու անգամ (2x) է, քան երկրորդը (ուղղակի x): Այս դեպքում դուք կարող եք լուծել փոխարինման մեթոդ... Թիվը փոխարինիր ամենափոքր աստիճանով.

Այնուհետեւ 3 2x = (3x) 2 = t 2

Բոլոր հզորությունները փոխարինեք x-ով հավասարման մեջ t-ով.

t 2 - 12t + 27 = 0
Մենք ստանում ենք քառակուսի հավասարում. Մենք լուծում ենք դիսկրիմինանտի միջոցով, ստանում ենք.
D = 144-108 = 36
t 1 = 9
t 2 = 3

Վերադառնալով փոփոխականին x.

Մենք վերցնում ենք t 1:
t 1 = 9 = 3 x

Այն է,

3 x = 9
3 x = 3 2
x 1 = 2

Գտնվել է մեկ արմատ: Մենք փնտրում ենք երկրորդը, t 2-ից:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Պատասխան՝ x 1 = 2; x 2 = 1.

Կայքում կարող եք հետաքրքրող հարցեր տալ ՕԳՆՈՒԹՅՈՒՆ ԼՈՒԾԵԼՈՒ բաժնում, մենք ձեզ անպայման կպատասխանենք։

Միացեք խմբին

Ընդհանուր առմամբ, 4-ից բարձր աստիճան ունեցող հավասարումը չի կարող լուծվել ռադիկալներով: Բայց երբեմն մենք դեռ կարող ենք գտնել ձախ կողմում գտնվող բազմանդամի արմատները ամենաբարձր աստիճանի հավասարման մեջ, եթե այն ներկայացնենք որպես առավելագույնը 4 աստիճանով բազմանդամների արտադրյալ։ Նման հավասարումների լուծումը հիմնված է բազմանդամը գործոնների վերածելու վրա, ուստի խորհուրդ ենք տալիս կրկնել այս թեման այս հոդվածն ուսումնասիրելուց առաջ:

Ամենից հաճախ պետք է գործ ունենալ ամբողջ թվային գործակիցներով ավելի բարձր աստիճանի հավասարումների հետ: Այս դեպքերում մենք կարող ենք փորձել գտնել ռացիոնալ արմատներ, և այնուհետև բազմանդամը գործակցեք, որպեսզի այն վերածվի ավելի ցածր աստիճանի հավասարման, որը հեշտ կլինի լուծել: Այս նյութի շրջանակներում մենք կդիտարկենք հենց այդպիսի օրինակներ։

Ամենաբարձր աստիճանի հավասարումներ ամբողջ թվային գործակիցներով

a n x n + a n - 1 x n - 1 + ձևի բոլոր հավասարումները: ... ... + a 1 x + a 0 = 0, մենք կարող ենք կրճատել նույն աստիճանի հավասարման՝ երկու կողմերը բազմապատկելով n n - 1-ով և փոխելով y = a n x ձևի փոփոխականը.

a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 +… + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 +… + b 1 y + b 0 = 0

Ստացված գործակիցները նույնպես ամբողջական կլինեն։ Այսպիսով, մեզ անհրաժեշտ կլինի n-րդ աստիճանի կրճատված հավասարումը լուծել ամբողջ թվային գործակիցներով, որն ունի x n + a n x n - 1 +… + a 1 x + a 0 = 0 ձևը:

Մենք հաշվարկում ենք հավասարման ամբողջ արմատները: Եթե հավասարումն ունի ամբողջական արմատներ, ապա պետք է դրանք փնտրել a 0-ի ազատ անդամի բաժանարարների մեջ: Եկեք դրանք գրենք և հերթով փոխարինենք սկզբնական հավասարության մեջ՝ ստուգելով արդյունքը։ Երբ մենք ինքնություն ձեռք բերենք և գտնենք հավասարման արմատներից մեկը, այն կարող ենք գրել x - x 1 · P n - 1 (x) = 0 ձևով: Այստեղ x 1-ը հավասարման արմատն է, իսկ P n - 1 (x)-ը x n + a n x n - 1 +… + a 1 x + a 0-ը x - x 1-ի բաժանման գործակիցն է:

Փոխարինեք մնացած բաժանարարները, որոնք գրված են P n - 1 (x) = 0-ով, սկսած x 1-ով, քանի որ արմատները կարող են կրկնվել: Ինքնությունը ստանալուց հետո x 2 արմատը համարվում է գտնված, և հավասարումը կարելի է գրել որպես (x - x 1) (x - x 2) P n - 2 (x) = 0: Այստեղ P n - 2 (x) կլինի P n - 1 (x) x - x 2-ի բաժանման գործակիցը։

Մենք շարունակում ենք կրկնել բաժանարարների շուրջ: Գտե՛ք բոլոր ամբողջ արմատները և նշանակե՛ք դրանց թիվը որպես m: Դրանից հետո սկզբնական հավասարումը կարող է ներկայացվել x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0: Այստեղ P n - m (x) n - m աստիճանի բազմանդամ է: Հաշվելու համար հարմար է օգտագործել Հորների սխեման։

Եթե մեր սկզբնական հավասարումն ունի ամբողջ թվային գործակիցներ, մենք չենք կարող կոտորակային արմատներ ունենալ:

Արդյունքում ստացանք P n - m (x) = 0 հավասարումը, որի արմատները կարելի է գտնել ցանկացած հարմար եղանակով։ Նրանք կարող են լինել իռացիոնալ կամ բարդ:

Եկեք ցույց տանք կոնկրետ օրինակինչպես է կիրառվում լուծման նման սխեման:

Օրինակ 1

Վիճակը:գտե՛ք x 4 + x 3 + 2 x 2 - x - 3 = 0 հավասարման լուծումը:

Լուծում

Սկսենք ամբողջական արմատներ գտնելուց:

Մենք ունենք ազատ անդամ, որը հավասար է մինուս երեքին: Այն ունի 1, - 1, 3 և - 3 բաժանարարներ։ Եկեք դրանք փոխարինենք սկզբնական հավասարման մեջ և տեսնենք, թե դրանցից որն է հանգեցնելու ինքնության:

Եթե x-ը հավասար է մեկի, մենք ստանում ենք 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, ինչը նշանակում է, որ մեկը կլինի այս հավասարման արմատը:

Այժմ մենք կատարում ենք x 4 + x 3 + 2 x 2 - x - 3 բազմանդամի բաժանումը (x - 1) սյունակում.

Այսպիսով, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3:

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Մենք ստացել ենք նույնականություն, ինչը նշանակում է, որ մենք գտել ենք հավասարման մեկ այլ արմատ, որը հավասար է -1-ի:

x 3 + 2 x 2 + 4 x + 3 բազմանդամը բաժանեք (x + 1) սյունակում.

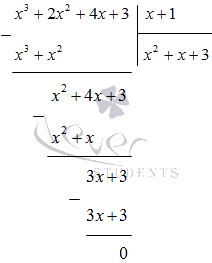
Մենք դա հասկանում ենք

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Հաջորդ բաժանարարը փոխարինեք x 2 + x + 3 = 0 հավասարությամբ, սկսած - 1-ով:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Ստացված հավասարությունները սխալ կլինեն, ինչը նշանակում է, որ հավասարումն այլևս չունի ինտեգրալ արմատներ։

Մնացած արմատները կլինեն x 2 + x + 3 արտահայտության արմատները:

D = 1 2 - 4 1 3 = - 11< 0

Այստեղից հետևում է, որ այս քառակուսի եռանկյունը չունի իրական արմատներ, այլ ունի բարդ խոնարհվածներ՝ x = - 1 2 ± i 11 2:

Պարզաբանենք, որ երկար բաժանման փոխարեն կարող ենք օգտագործել Հորների սխեման։ Դա արվում է այսպես՝ հավասարման առաջին արմատը որոշելուց հետո լրացնում ենք աղյուսակը։

Գործակիցների աղյուսակում մենք անմիջապես կարող ենք տեսնել բազմանդամների բաժանման գործակիցների գործակիցները, ինչը նշանակում է, որ x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x. + 3.

Հաջորդ - 1-ի հավասար արմատը գտնելուց հետո ստանում ենք հետևյալը.

Պատասխան. x = - 1, x = 1, x = - 1 2 ± i 11 2:

Օրինակ 2

Վիճակը:Լուծե՛ք x 4 - x 3 - 5 x 2 + 12 = 0 հավասարումը:

Լուծում

Ազատ անդամն ունի 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12 բաժանարարներ։

Մենք ստուգում ենք դրանք հերթականությամբ.

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Այսպիսով, x = 2 կլինի հավասարման արմատը: Բաժանեք x 4 - x 3 - 5 x 2 + 12 x - 2-ի վրա՝ օգտագործելով Հորների սխեմա.

Արդյունքում մենք ստանում ենք x - 2 (x 3 + x 2 - 3 x - 6) = 0:

2 3 + 2 2 - 3 2 - 6 = 0

Այսպիսով, 2-ը կրկին արմատ կլինի: Բաժանել x 3 + x 2 - 3 x - 6 = 0 x - 2:

Արդյունքում մենք ստանում ենք (x - 2) 2 (x 2 + 3 x + 3) = 0:

Մնացած բաժանարարները ստուգելն անիմաստ է, քանի որ x 2 + 3 x + 3 = 0 հավասարությունն ավելի արագ և հարմար է լուծելու համար՝ օգտագործելով տարբերակիչ:

Լուծենք քառակուսի հավասարումը.

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Ստանում ենք արմատների բարդ զուգակցված զույգ՝ x = - 3 2 ± i 3 2:

Պատասխանել x = - 3 2 ± i 3 2:

Օրինակ 3

Վիճակը:գտե՛ք x 4 + 1 2 x 3 - 5 2 x - 3 = 0 հավասարման իրական արմատները:

Լուծում

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Մենք իրականացնում ենք հավասարման երկու կողմերի 2 3 բազմապատկում.

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Փոխարինեք փոփոխականները y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Արդյունքում ստացանք ստանդարտ 4-րդ աստիճանի հավասարում, որը կարելի է լուծել ըստ ստանդարտ սխեմայի։ Ստուգենք բաժանարարները, բաժանենք և արդյունքում ստանանք, որ ունի 2 իրական արմատ y = - 2, y = 3 և երկու բարդ արմատ։ Ամբողջական լուծումն այստեղ չենք ներկայացնի։ Փոխարինման շնորհիվ այս հավասարման իրական արմատները կլինեն x = y 2 = - 2 2 = - 1 և x = y 2 = 3 2:

Պատասխան. x 1 = - 1, x 2 = 3 2

Եթե տեքստում սխալ եք նկատում, խնդրում ենք ընտրել այն և սեղմել Ctrl + Enter

16-րդ դարում մաթեմատիկոսները գրեթե պատահաբար հանդիպեցին բարդ թվերի (տե՛ս Գլուխ 11): TO XVIII դԿոմպլեքս թվերը համարվում էին իրական թվերի տիրույթի ընդլայնում, բայց դրանց հետ աշխատելը դեռևս հանգեցրեց հավասարության սխալի, քանի որ Լեոնարդ E-ի մեծ աշխատության մեջ թվերի տեսության վերաբերյալ՝ թվաբանական հետազոտություններ (1801), նա խուսափեց այսպես կոչված «երևակայականի» օգտագործումից։ թվեր»։ Ինձ թվում է, որ այս աշխատանքի ամենակարևոր մասը հանրահաշվի հիմնարար թեորեմի առաջին ապացույցն է։ Գաուսը հասկացավ, թե որքան կարևոր է այս թեորեմը՝ տարիների ընթացքում ստեղծելով մի քանի լրացուցիչ ապացույցներ։ 1849 թվականին նա վերանայեց առաջին տարբերակը՝ այս անգամ օգտագործելով բարդ թվեր։ Օգտագործելով ժամանակակից տերմինները՝ կարող ենք ասել, որ իրական կամ բարդ գործակիցներով ցանկացած վերջավոր բազմանդամ հավասարման համար նրա բոլոր արմատները կլինեն իրական կամ բարդ թվեր։ Այսպիսով, մենք բացասական պատասխան ենք ստանում այն երկարատև հարցին, թե արդյոք ավելի բարձր կարգի բազմանդամ հավասարումների լուծումը պահանջում է ավելի բարձր կարգի թվերի ստեղծում, քան բարդերը։

Այն ժամանակվա հանրահաշվի ամենադժվար խնդիրներից մեկն այն հարցն էր, թե արդյոք հինգերորդ կարգի բազմանդամը՝ քվինտիկը, լուծելի է հանրահաշվական մեթոդներով, այսինքն՝ վերջավոր թվով հանրահաշվական քայլերի օգնությամբ։ Այժմ դպրոցում սովորեցնում են քառակուսի հավասարումների լուծման բանաձեւը, իսկ 16-րդ դարից հայտնի են երրորդ և չորրորդ աստիճանի հավասարումների լուծման նմանատիպ մեթոդներ (գլուխ 11): Բայց Quintics-ի համար ոչ մի մեթոդ չի գտնվել։ Կարող է թվալ, որ հանրահաշվի հիմնարար թեորեմը պարունակում է հաստատական պատասխանի հեռանկար, բայց իրականում այն պարզապես երաշխավորում է լուծումների գոյությունը, ոչինչ չի ասում ճշգրիտ լուծումներ տվող բանաձևերի գոյության մասին (այդ ժամանակ արդեն մոտավոր թվեր կային. և գրաֆիկական մեթոդներ): Եվ հետո կային երկու մաթեմատիկական հանճարներ՝ ողբերգական ճակատագրով։

Նիլս Հենրիկ Աբելը (1802–1829) ծնվել է մեծ աղքատ ընտանիքում, որն ապրում էր Նորվեգիայի մի փոքրիկ գյուղում, մի երկրում, որը ավերված էր Անգլիայի և Շվեդիայի հետ երկար տարիների պատերազմից: Ուսուցիչը, բարյացակամորեն տրամադրված տղայի նկատմամբ, նրան մասնավոր դասեր է տվել, բայց հոր մահից հետո, տասնութ տարեկանում, չնայած. երիտասարդ տարիքև փխրուն առողջությամբ Աբելը ստիպված էր պահել իր ընտանիքը: 1824 թվականին նա հրատարակեց գիտական հոդված, որտեղ նա հայտարարեց, որ քվինտիկը լուծելի չէ հանրահաշվական միջոցներով, ինչպես, իսկապես, ավելի բարձր կարգի ցանկացած բազմանդամ։ Աբելը կարծում էր, որ այս հոդվածը կծառայի որպես իր ուղեցույց դեպի գիտական աշխարհ, և այն ուղարկեց Գյոթինգենի համալսարան Գաուսին: Ցավոք, Գաուսը չէր պատրաստվում դանակով կտրել էջերը (այդ ժամանակ ցանկացած ընթերցող պետք է դա աներ) և հոդվածը չկարդաց։ 1826 թվականին Նորվեգիայի կառավարությունը վերջապես միջոցներ հատկացրեց Աբելի Եվրոպա մեկնելու համար։ Վախենալով, որ Գաուսի հետ անձնական շփումը նրան մեծ ուրախություն չի պատճառի, մաթեմատիկոսը որոշեց չայցելել Գյոթինգեն և փոխարենը գնաց Բեռլին։ Այնտեղ նա ընկերացավ Օգյուստ Լեոպոլդ Կրելի (1780–1855) հետ՝ մաթեմատիկոս, ճարտարապետ և ինժեներ, ով մաթեմատիկայի վերաբերյալ խորհուրդ էր տալիս Պրուսիայի կրթության նախարարությանը։ Կրելը պատրաստվում էր հիմնել Journal of Clean-ը և կիրառական մաթեմատիկա«. Այսպիսով, Աբելը հնարավորություն ստացավ տարածելու իր աշխատանքը և շատ բան հրապարակեց, հատկապես «Journal»-ի վաղ համարներում, որն անմիջապես սկսեց համարվել շատ հեղինակավոր և հեղինակավոր գիտական հրատարակություն։ Նորվեգացին այնտեղ հրապարակեց իր ապացույցի ընդլայնված տարբերակը, որ քվինտիկն անորոշ է հանրահաշվական մեթոդներով: Իսկ հետո նա մեկնեց Փարիզ։ Այս ճամփորդությունը շատ վրդովեցրեց Աբելին, քանի որ նա գործնականում չստացավ ֆրանսիացի մաթեմատիկոսների աջակցությունը, որն այդքան անհրաժեշտ էր։ Նա մտերմացավ Օգյուստին Լուի Կոշիի (1789-1857) հետ, ով այդ ժամանակ գլխավոր լուսատուն էր։ մաթեմատիկական վերլուծություն, բայց ուներ շատ բարդ բնավորություն։ Ինչպես ինքն է ասել Աբելը, «Կոշին խելագար է, և ոչինչ չի կարելի անել դրա դեմ, թեև ներկայումս նա միակն է, ով ունակ է ամեն ինչի մաթեմատիկայի մեջ»: Եթե փորձենք արդարացումներ գտնել անպատկառության և արհամարհանքի դրսևորումների համար, որոնք բխում էին Գաուսից և Կոշիից, ապա կարող ենք ասել, որ քվինտիկը որոշակի համբավ ձեռք բերեց և գրավեց ինչպես հարգված մաթեմատիկոսների, այնպես էլ բնօրինակների ուշադրությունը: Աբելը վերադարձավ Նորվեգիա, որտեղ ավելի ու ավելի էր տառապում տուբերկուլյոզից։ Նա շարունակեց իր աշխատանքները ուղարկել Կրելլ, բայց մահացավ 1829 թվականին՝ չիմանալով, թե որքան է մեծացել իր հեղինակությունը։ գիտական աշխարհը... Նրա մահից երկու օր անց Աբելը Բեռլինում գիտական պաշտոն ստանձնելու առաջարկ ստացավ։

Աբելը ցույց տվեց, որ չորրորդ կարգից բարձր ցանկացած բազմանդամ չի կարող լուծվել ռադիկալների միջոցով, ինչպիսիք են քառակուսի, խորանարդ կամ ավելի բարձր արմատները: Այնուամենայնիվ, հստակ պայմանները, որոնց դեպքում այս բազմանդամները կարող էին լուծվել հատուկ դեպքերում և դրանց լուծման մեթոդը, ձևակերպվել են Գալուայի կողմից: Էվարիստ Գալուան (1811-1832) ապրեց կարճ և իրադարձություններով լի կյանք: Նա անհավանական շնորհալի մաթեմատիկոս էր: Գալուան անհաշտ էր նրանց հանդեպ, ում իրենից պակաս տաղանդավոր էր համարում, և միևնույն ժամանակ չէր կարող հանդուրժել սոցիալական անարդարությունը։ Նա մաթեմատիկայի տաղանդ չցուցաբերեց մինչև Լեժանդրի Երկրաչափության սկզբունքները կարդալը (հրատարակվել է 1794 թվականին, այս գիրքը հաջորդ հարյուր տարվա հիմնական դասագիրքն էր)։ Հետո նա բառացիորեն կուլ տվեց Լեժանդրի, իսկ ավելի ուշ՝ Աբելի մնացած գործերը։ Նրա ոգևորությունը, ինքնավստահությունը և անհանդուրժողականությունը հանգեցրին իսկապես սարսափելի հետևանքների ուսուցիչների և քննիչների հետ հարաբերություններում: Գալուան մասնակցել է ֆրանսիական մաթեմատիկայի բնօրրան՝ Ecole Polytechnique-ի ընդունելության մրցույթին, սակայն նախապատրաստված չլինելու պատճառով չի հանձնվել քննությանը: Նոր ուսուցչի հետ ծանոթանալուց հետո, ով ճանաչեց նրա տաղանդը, որոշ ժամանակ նրան հաջողվեց զսպել իր խառնվածքը։ 1829 թվականի մարտին Գալուան հրատարակեց իր առաջին հոդվածը շարունակվող կոտորակների մասին, որը նա համարեց իր ամենանշանակալի աշխատանքը։ Նա իր հայտնագործությունների մասին հաղորդագրություն է ուղարկել Գիտությունների ակադեմիա, իսկ Կոշին խոստացել է դրանք ներկայացնել, բայց մոռացել է։ Ավելին, նա պարզապես կորցրեց ձեռագիրը։

Գալուայի երկրորդ անհաջողությունը, երբ ընդունվեց պոլիտեխնիկական դպրոց, մտավ մաթեմատիկական ֆոլկլոր: Նա այնքան սովոր էր անընդհատ բարդ մաթեմատիկական գաղափարներ ունենալ իր գլխում, որ զայրանում էր քննողների մանր զրպարտություններից։ Քանի որ քննիչները դժվարությամբ էին հասկանում նրա բացատրությունը, նա գրատախտակի կտորը նետեց նրանցից մեկի երեսին։ Շուտով մահանում է նրա հայրը, ով ինքնասպան է լինում եկեղեցական ինտրիգների արդյունքում։ Նրա հուղարկավորության ժամանակ քիչ էր մնում խռովություն սկսվեր։ 1830 թվականի փետրվարին Գալուան գրեց հետևյալ երեք հոդվածները՝ դրանք ուղարկելով Գիտությունների ակադեմիա մաթեմատիկայի գլխավոր մրցանակի համար։ Ժոզեֆ Ֆուրիեն, որն այն ժամանակ ակադեմիայի քարտուղարն էր, մահացավ առանց դրանք կարդալու, իսկ մահից հետո նրա թղթերի մեջ հոդվածներ չգտնվեցին։ Հիասթափությունների նման հեղեղը կթափեր որևէ մեկին։ Գալուան ապստամբեց իշխանություն ունեցողների դեմ, քանի որ զգում էր. նրանք չճանաչեցին նրա արժանիքները և կործանեցին հորը։ Նա գլխապտույտ ընկավ քաղաքականության մեջ՝ դառնալով եռանդուն հանրապետական, որը 1830-ին Ֆրանսիայի ամենաիմաստուն որոշումը չէր: Վերջին հուսահատ փորձի ժամանակ նա գիտական հոդված ուղարկեց ֆրանսիացի հայտնի ֆիզիկոս և մաթեմատիկոս Սիմեոն Դենիս Պուասոնին (1781-1840), որն ի պատասխան լրացուցիչ ապացույցներ պահանջեց։

Սա վերջին կաթիլն էր: 1831 թվականին Գալուան երկու անգամ ձերբակալվեց՝ առաջին անգամ՝ իբր թագավոր Լուի Ֆիլիպի սպանության կոչ անելու համար, իսկ հետո նրան պաշտպանելու համար՝ իշխանությունները վախենում էին հանրապետական ապստամբությունից: Այս անգամ նա դատապարտվել է վեց ամսվա ազատազրկման՝ իրեն միացած լուծարված հրետանային գումարտակի համազգեստը ապօրինի կերպով կրելու շինծու մեղադրանքով։ Ազատվելով իր պատվի խոսքի վրա՝ նա սկսեց մի աշխատանք, որը նրան նույն զզվանքն էր պատճառում, ինչ կյանքում մնացած ամեն ինչ։ Իր նվիրված ընկեր Շևալիեին ուղղված նամակներում կարելի է զգալ նրա հիասթափությունը։ 1832 թվականի մայիսի 29-ին նա ընդունեց մենամարտի մարտահրավերը, որի պատճառները լիովին հասկանալի չեն։ «Ես անպատվաբեր կոկետի զոհ եմ դարձել. Իմ կյանքը մարել է ողորմելի վիճաբանության մեջ»,- գրում է նա իր նամակում բոլոր հանրապետականներին։ Առավելագույնը հայտնի ստեղծագործությունԳալուան զորակոչվել է ճակատագրական մենամարտի նախորդ գիշերը։ Բողոքները ցրված են դաշտերում՝ «Այլեւս ժամանակ չունեմ, այլեւս ժամանակ չունեմ». Նա ստիպված էր ուրիշներին թողնել միջանկյալ քայլերի մանրամասն ներկայացումը, որոնք էական չէին հիմնական գաղափարը հասկանալու համար։ Նրան անհրաժեշտ էր թղթի վրա շաղ տալ իր հայտնագործությունների հիմքերը՝ այն, ինչ այժմ կոչվում է Գալուայի թեորեմի ակունքները: Նա ավարտեց իր կտակը Շևալիեին խնդրելով «խնդրել Յակոբիին և Գաուսին հրապարակայնորեն արտահայտել իրենց կարծիքը ոչ թե այդ թեորեմների ճիշտության, այլ կարևորության մասին»։ Վաղ առավոտյան Գալուան գնաց իր մրցակցին դիմավորելու։ Նրանք պետք է կրակեին 25 քայլ հեռավորությունից։ Գալուան վիրավորվել է և հաջորդ առավոտյան մահացել հիվանդանոցում։ Նա ընդամենը քսան տարեկան էր։

Գալուան ապավինում էր Լագրանժի և Կոշիի աշխատանքին, բայց նա մշակեց ավելի ընդհանուր մեթոդ։ Դա ծայրահեղ էր կարևոր ձեռքբերումքվինտիկների լուծման բնագավառում։ Գիտնականն ավելի քիչ ուշադրություն է դարձրել սկզբնական հավասարումների կամ գրաֆիկական մեկնաբանության վրա և ավելի շատ մտածել է հենց արմատների բնույթի մասին: Պարզեցնելու համար Գալուան դիտարկել է միայն այսպես կոչված անկրճատելի քվինտիկները, այսինքն՝ նրանք, որոնք չեն կարող գործոնացվել ավելի ցածր կարգի բազմանդամների տեսքով (ինչպես ասացինք, մինչև չորրորդ կարգի ցանկացած բազմանդամ հավասարումների համար կան գտնելու բանաձևեր. նրանց արմատները): Ընդհանուր առմամբ, ռացիոնալ գործակիցներով անկրճատելի բազմանդամը այն բազմանդամն է, որը չի կարող քայքայվել ռացիոնալ գործակիցներով ավելի պարզ բազմանդամների։ Օրինակ, (x 5 - 1) կարող է ֆակտորիզացվել (x-1) (x 4 + x 3 + x 2 + x + 1),մինչդեռ (x 5 - 2)անկրճատելի. Գալուայի նպատակն էր սահմանել պայմաններ, որոնց դեպքում ընդհանուր անկրճատելի բազմանդամ հավասարման բոլոր լուծումները կարելի է գտնել ռադիկալներով։

Լուծման բանալին կայանում է նրանում, որ ցանկացած անկրճատելի հանրահաշվական հավասարման արմատները անկախ չեն, դրանք կարող են արտահայտվել մեկը մյուսի միջոցով: Այս հարաբերությունները ձևակերպվել են բոլոր հնարավոր փոխարկումների խմբի մեջ, այսպես կոչված, արմատային սիմետրիայի խումբ. քվինտիկի համար այս խումբը պարունակում է 5: = 5 x 4 x 3 x 2 x 1 = 120 տարր: Գալուայի տեսության մաթեմատիկական ալգորիթմները շատ բարդ են, և, ամենայն հավանականությամբ, մասամբ դրա պատճառով դրանք սկզբում հասկացվել են մեծ դժվարությամբ: Բայց այն բանից հետո, երբ աբստրակցիայի մակարդակը հնարավորություն տվեց հավասարումների հանրահաշվական լուծումներից անցնել նրանց հետ կապված խմբերի հանրահաշվական կառուցվածքին, Գալուան կարողացավ կանխատեսել հավասարման լուծելիությունը՝ հիմնվելով նման խմբերի հատկությունների վրա։ Ավելին, նրա տեսությունը տրամադրեց նաև մեթոդ, որով կարելի էր գտնել այս արմատները։ Ինչ վերաբերում է քվինտիկներին, ապա մաթեմատիկոս Ժոզեֆ Լյուվիլը (1809-1882), որը 1846 թ. մեծ մասըԳալուայի աշխատություններում իր «Մաքուր և կիրառական մաթեմատիկայի ամսագրում» նշվում է, որ երիտասարդ գիտնականն ապացուցել է «գեղեցիկ թեորեմ», և որպեսզի «սկզբնական աստիճանի անկրճատելի հավասարումը լուծելի լինի ռադիկալների առումով, անհրաժեշտ է և Բավական է, որ նրա բոլոր արմատները ռացիոնալ ֆունկցիաներ են, որոնցից երկուսը »: Քանի որ դա անհնար է քվինտիկի համար, այն հնարավոր չէ լուծել ռադիկալների օգնությամբ։

Երեք տարվա ընթացքում մաթեմատիկական աշխարհը կորցրեց իր ամենապայծառ նոր աստղերից երկուսը: Մեղադրանքներն ու արժեքների վերագնահատումը հետևեցին, և Աբելն ու Գալուան հասան իրենց արժանի ճանաչմանը, բայց միայն հետմահու: 1829 թվականին Կարլ Յակոբին Լեժանդրի միջոցով իմացել է Աբելի «կորած» ձեռագրի մասին, իսկ 1830 թվականին դիվանագիտական սկանդալ է ծագել, երբ Փարիզում Նորվեգիայի հյուպատոսը պահանջել է գտնել իր հայրենակցի հոդվածը։ Ի վերջո, Քոշին գտավ հոդվածը, բայց այն նորից կորավ Ակադեմիայում: Նույն թվականին Աբելին շնորհվեց մաթեմատիկայի գլխավոր մրցանակ (Ջակոբիի հետ միասին), բայց նա արդեն մահացած էր։ Նրա կենսագրությունը հրատարակվել է 1841 թվականին։ 1846 թվականին Լիուվիլը խմբագրեց Գալուայի որոշ ձեռագրեր և ներածությունում ափսոսանք հայտնեց, որ ակադեմիան ի սկզբանե մերժել էր Գալուայի աշխատանքը դրա բարդության պատճառով. »: Նա շարունակում է. «Գալուան չկա։ Եկեք չտրվենք անօգուտ քննադատությունների. Եկեք մի կողմ դնենք թերությունները և նայենք արժանիքներին»։ Մրգեր կարճ կյանքԳալուան տեղավորվում էր ընդամենը վաթսուն էջ: Ecole Normal-ի և École Polytechnique-ի թեկնածուների մաթեմատիկական ամսագրի խմբագիրը Galois-ի գործը մեկնաբանել է հետևյալ կերպ. Barbarus hic ego sum, quia non intelligor illis »:

Նախ, այս աշխատության երկրորդ էջը ծանրաբեռնված չէ անուններով, ազգանուններով, հասարակության մեջ տիրող իրավիճակի նկարագրություններով, տիտղոսներով և էլեգիաներով՝ ի պատիվ ինչ-որ խղճուկ արքայազնի, որի դրամապանակը կբացվի այդ խնկերի օգնությամբ՝ սպառնալիքով. այն փակելու, երբ գովեստներն ավարտվեն: Այստեղ դուք չեք տեսնի հարգալից գովեստներ՝ գրված տեքստից երեք անգամ մեծ տառերով՝ ուղղված գիտության մեջ բարձր դիրք ունեցողներին, ինչ-որ իմաստուն հովանավորին. ով ուզում է ինչ-որ բան գրել. Ես այստեղ ոչ մեկին չեմ ասում, որ ես պարտական եմ նրանց խորհուրդներին և աջակցությանը այն ամենին, ինչ լավ է իմ աշխատանքում։ Ես սա չեմ ասում, որովհետև դա սուտ կլինի։ Եթե ստիպված լինեի հիշատակել հասարակության կամ գիտության մեծերից որևէ մեկին (ներկայումս մարդկանց երկու խավերի միջև տարբերությունը գրեթե աննկատ է), երդվում եմ, դա երախտագիտության նշան չէր լինի։ Ես նրանց պարտական եմ այն փաստի համար, որ այս երկու հոդվածներից առաջինն այդքան ուշ եմ հրապարակել, և որ այդ ամենը գրել եմ բանտում, մի վայրում, որը հազիվ թե հարմար համարվի գիտական մտորումների համար, և ես հաճախ զարմանում եմ իմ ինքնազսպման վրա և. կարողություն պահել իմ բերանը ամրոցի վրա հիմար և արատավոր զոիլների հետ կապված: Ինձ թվում է, որ ես կարող եմ օգտագործել «զոյլես» բառը՝ չվախենալով, որ ինձ մեղադրեն անպարկեշտության մեջ, քանի որ ես այդպես եմ անվանում իմ հակառակորդներին։ Ես չեմ պատրաստվում այստեղ գրել, թե ինչպես և ինչու են ինձ բանտ ուղարկել, բայց պետք է ասեմ, որ իմ ձեռագրերը ամենից հաճախ պարզապես կորչում էին ակադեմիայի անդամների պարոնայք թղթապանակներում, թեև, իրականում, ես չեմ կարող պատկերացնել նման անխոհեմություն. մարդկանց այն մասը, ում խղճի վրա Աբելի մահը. Իմ կարծիքով, ցանկացած մարդ կցանկանար համեմատվել այս փայլուն մաթեմատիկոսի հետ։ Բավական է ասել, որ հավասարումների տեսության մասին իմ աշխատությունը 1830 թվականի փետրվարին ուղարկվել է Գիտությունների ակադեմիա, որից քաղվածքներ ուղարկվել են 1829 թվականի փետրվարին, և դրանցից ոչ մեկը չի տպվել, և նույնիսկ ձեռագիրը անհնար է վերադարձնել:

Գալուա, անտիպ նախաբան, 1832 թ

Դասարան: 9

Հիմնական նպատակները.

Համախմբել ամբողջ ռացիոնալ հավասարման երրորդ աստիճանի հայեցակարգը:
Ձևակերպեք ավելի բարձր աստիճանի հավասարումների լուծման հիմնական մեթոդները (n > 3).
Ուսուցանել բարձրագույն աստիճանի հավասարումների լուծման հիմնական մեթոդները:
Սովորեցնել ըստ տեսակի հավասարումների որոշել առավելագույնը արդյունավետ մեթոդիր որոշումները։

Ձևերը, մեթոդները և մանկավարժական տեխնիկաորոնք օգտագործվում են ուսուցչի կողմից դասում.

Դասախոսություն-սեմինարների վերապատրաստման համակարգ (դասախոսություններ - նոր նյութի բացատրություն, սեմինարներ - խնդիրների լուծում).
Տեղեկատվական և հաղորդակցական տեխնոլոգիաներ (ճակատային հարցում, բանավոր աշխատանք դասարանի հետ).
Տարբերակված ուսուցում, խմբակային և անհատական ձևեր.
Հետախուզական ուսուցում զարգացնող ուսուցման մեջ մաթեմատիկական ապարատև յուրաքանչյուր աշակերտի մտածողության կարողությունները:
Տպագիր նյութ - դասի անհատական կարճ ամփոփում (հիմնական հասկացությունները, բանաձևերը, հայտարարությունները, դասախոսական նյութը սեղմված է դիագրամների կամ աղյուսակների տեսքով):

Դասի պլան:

Կազմակերպման ժամանակ.
Փուլի նպատակը՝ ուսանողներին ընդգրկել ուսումնական գործունեություն, որոշել դասի բովանդակալից շրջանակը։
Ուսանողների գիտելիքների թարմացում.
Փուլի նպատակը` թարմացնել ուսանողների գիտելիքները նախկինում ուսումնասիրված հարակից թեմաների վերաբերյալ
Նոր թեմայի ուսումնասիրություն (դասախոսություն). Փուլի նպատակը. ձևակերպել ավելի բարձր աստիճանի հավասարումների լուծման հիմնական մեթոդները (n > 3)
Ամփոփելով.
Բեմի նպատակը՝ ևս մեկ անգամ ընդգծել դասի ընթացքում ուսումնասիրված նյութի առանցքային կետերը:
Տնային աշխատանք.
Բեմական նպատակը՝ ձևակերպել Տնային աշխատանքուսանողների համար.

Դասի ամփոփում

1. Կազմակերպչական պահ.

Դասի թեմայի ձևակերպում «Ամենաբարձր աստիճանի հավասարումներ. Դրանց լուծման մեթոդները»:

2. Սովորողների գիտելիքների ակտուալացում.

Տեսական հարցում - զրույց. Նախկինում ուսումնասիրված որոշ տեղեկությունների կրկնություն տեսությունից: Ուսանողները ձևակերպում են հիմնական սահմանումներ և ձևակերպում անհրաժեշտ թեորեմներ: Բերվում են օրինակներ՝ ավելի վաղ ձեռք բերված գիտելիքների մակարդակը ցույց տալու համար:

Հավասարման հայեցակարգը մեկ փոփոխականում:
Հավասարման արմատ հասկացությունը, հավասարման լուծումը։
Հայեցակարգ գծային հավասարումմեկ փոփոխականով, քառակուսի հավասարման հասկացությունը մեկ փոփոխականում:
Հավասարումների համարժեքության հայեցակարգը, հավասարում-հետևանքը (կողմնակի արմատների հասկացությունը), անցումը ոչ հետևանքով (արմատների կորստի դեպք):
Մեկ փոփոխականով ամբողջ ռացիոնալ արտահայտության հայեցակարգը:
Ամբողջ ռացիոնալ հավասարման հայեցակարգը n-րդ աստիճան. Ամբողջ ռացիոնալ հավասարման ստանդարտ ձևը: Կրճատված ամբողջ ռացիոնալ հավասարումը:
Անցում ավելի ցածր աստիճանի հավասարումների բազմության՝ սկզբնական հավասարումը գործոնների վերածելով:
Բազմանդամ հասկացություն n-րդ աստիճանից x... Բեզուտի թեորեմա. Բեզութի թեորեմի հետևանքները. Արմատային թեորեմներ ( Զ-արմատներ և Ք-արմատներ) մի ամբողջ ռացիոնալ հավասարման՝ ամբողջ թվային գործակիցներով (համապատասխանաբար կրճատված և չկրճատված):
Հորների սխեման.

3. Նոր թեմայի ուսումնասիրություն.

Մենք կդիտարկենք ողջ ռացիոնալ հավասարումը n- մեկ անհայտ փոփոխականով ստանդարտ ձևի երրորդ աստիճան x: P n (x)= 0, որտեղ P n (x) = a n x n + a n-1 x n-1 + a 1 x + a 0- բազմանդամ n-րդ աստիճանից x, ա n ≠ 0. Եթե ա n = 1, ապա նման հավասարումը կոչվում է կրճատված ամբողջ ռացիոնալ հավասարում n-րդ աստիճան. Դիտարկենք նման հավասարումներ տարբեր արժեքների համար nև թվարկեք դրանց լուծման հիմնական մեթոդները:

n= 1 - գծային հավասարում.

n= 2 - քառակուսի հավասարում:Խտրական բանաձեւ. Արմատները հաշվարկելու բանաձև. Վիետայի թեորեմա. Ընտրելով ամբողջական քառակուսի:

n= 3 - խորանարդ հավասարում:

Խմբավորման մեթոդ.

Օրինակ: x 3 - 4x 2 - x+ 4 = 0 (x - 4) (x 2– 1) = 0 x 1 = 4 , x 2 = 1,x 3 = -1.

Ձևի հակառակ խորանարդ հավասարումը կացին 3 + bx 2 + bx + ա= 0. Լուծե՛ք նույն գործակիցներով անդամները համակցելով:

Օրինակ: x 3 – 5x 2 – 5x + 1 = 0 (x + 1)(x 2 – 6x + 1) = 0 x 1 = -1, x 2 = 3 + 2, x 3 = 3 – 2.

Թեորեմի հիման վրա Z-արմատների ընտրություն. Հորների սխեման. Այս մեթոդը կիրառելիս պետք է ընդգծել, որ որոնումն այս դեպքում վերջավոր է, և արմատները ընտրում ենք որոշակի ալգորիթմի համաձայն՝ համաձայն թեորեմի. Զ- ամբողջ թվային գործակիցներով կրճատված ամբողջ ռացիոնալ հավասարման արմատները:

Օրինակ: x 3 – 9x 2 + 23x- 15 = 0. Տրված հավասարումը. Եկեք գրենք ազատ անդամի բաժանարարները ( + 1; + 3; + 5; + 15): Եկեք կիրառենք Հորների սխեման.

	x 3	x 2	x 1	x 0	եզրակացություն
	1	-9	23	-15
1	1	1 x 1 - 9 = -8	1 x (-8) + 23 = 15	1 x 15 - 15 = 0	1 - արմատ
	x 2	x 1	x 0

մենք ստանում ենք ( x – 1)(x 2 – 8x + 15) = 0 x 1 = 1, x 2 = 3, x 3 = 5.

Հավասարում ամբողջ թվային գործակիցներով. Թորեմի հիման վրա Q-արմատների ընտրություն. Հորների սխեման. Այս մեթոդը կիրառելիս անհրաժեշտ է ընդգծել, որ այս դեպքում թվարկումը վերջավոր է, և մենք արմատներն ընտրում ենք որոշակի ալգորիթմի համաձայն՝ համաձայն թեորեմի. Ք- անկրճատելի ամբողջ ռացիոնալ հավասարման արմատները ամբողջ թվային գործակիցներով:

Օրինակ՝ 9 x 3 + 27x 2 – x- 3 = 0. Հավասարումը չի կրճատվում: Եկեք գրենք ազատ անդամի բաժանարարները ( + 1; + 3). Գրենք անհայտի ամենաբարձր հզորության գործակիցի բաժանարարները: ( + 1; + 3; + 9) Հետևաբար, մենք արմատներ կփնտրենք արժեքների մեջ ( + 1; + ; + ; + 3). Եկեք կիրառենք Հորների սխեման.

	x 3	x 2	x 1	x 0	եզրակացություն
	9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 - 1 = 35	1 x 35 - 3 = 32 ≠ 0	1 - ոչ արմատ
-1	9	-1 x 9 + 27 = 18	-1 x 18 - 1 = -19	-1 x (-19) - 3 = 16 ≠ 0	-1 - ոչ արմատ
	9	x 9 + 27 = 30	x 30 - 1 = 9	x 9 - 3 = 0	արմատ
	x 2	x 1	x 0

մենք ստանում ենք ( x – )(9x 2 + 30x + 9) = 0 x 1 = , x 2 = - , x 3 = -3.

Ք-ն ընտրելիս հաշվարկի հարմարության համար - արմատներըհարմար է փոփոխականի փոփոխություն կատարել, գնալ կրճատված հավասարմանը և ընտրել Z - արմատները.

Եթե ազատ ժամկետը 1 է

.

Եթե կարող եք օգտագործել ձևի փոխարինում y = kx

.

Formula Cardano. Գոյություն ունի խորանարդային հավասարումների լուծման ունիվերսալ մեթոդ՝ սա Կարդանոյի բանաձևն է։ Այս բանաձեւը կապված է իտալացի մաթեմատիկոսներ Ջերոլամո Կարդանոյի (1501-1576), Նիկոլո Տարտալիայի (1500-1557), Սկիպիոնե դել Ֆերոյի (1465-1526) անունների հետ։ Այս բանաձեւը դուրս է մեր դասընթացի շրջանակներից:

n= 4 - չորրորդ աստիճանի հավասարում:

Խմբավորման մեթոդ.

Օրինակ: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 (x 4 + 2x 3) + (5x 2 + 10x) – (6x + 12) = 0 (x + 2)(x 3 + 5x - 6) = 0 (x + 2)(x– 1)(x 2 + x + 6) = 0 x 1 = -2, x 2 = 1.

Փոփոխական փոխարինման մեթոդ.

Ձևի երկքառակուսի հավասարում կացին 4 + bx 2 + վ = 0 .

Օրինակ: x 4 + 5x 2 - 36 = 0. Փոխարինում y = x 2. Այստեղից y 1 = 4, y 2 = -9: Այսպիսով x 1,2 = + 2 .

Ձևի չորրորդ աստիճանի հակառակ հավասարումը կացին 4 + bx 3 + գ x 2 + bx + ա = 0.

Մենք լուծում ենք՝ համադրելով նույն գործակիցներով տերմինները՝ փոխարինելով ձևը

կացին 4 + bx 3 + cx 2 – bx + ա = 0.

Ձևի չորրորդ աստիճանի վերադարձի ընդհանրացված հավասարում կացին 4 + bx 3 + cx 2 + kbx + k 2 a = 0.

Ընդհանուր տեսարանի փոխարինում. Որոշ ստանդարտ փոխարինումներ:

Օրինակ 3 . Ընդհանուր տեսքի փոխարինում(հետևում է կոնկրետ հավասարման ձևից):

n = 3.

Հավասարում ամբողջ թվային գործակիցներով. Q-արմատների տեղադրում n = 3.

Ընդհանուր բանաձև. Չորրորդ աստիճանի հավասարումների լուծման ունիվերսալ մեթոդ կա։ Այս բանաձեւը կապված է Լյուդովիկո Ֆերարիի (1522-1565) անվան հետ։ Այս բանաձեւը դուրս է մեր դասընթացի շրջանակներից:

n > 5 - հինգերորդ և ավելի բարձր աստիճանների հավասարումներ:

Հավասարում ամբողջ թվային գործակիցներով. Թեորեմի հիման վրա Z-արմատների ընտրություն. Հորների սխեման. Ալգորիթմը նման է վերը նշված ալգորիթմին n = 3.

Հավասարում ամբողջ թվային գործակիցներով. Q-արմատների տեղադրումթեորեմի հիման վրա. Հորների սխեման. Ալգորիթմը նման է վերը նշված ալգորիթմին n = 3.

Սիմետրիկ հավասարումներ. Կենտ աստիճանի ցանկացած վերադարձի հավասարում ունի արմատ x= -1 և այն գործոնների վերածելուց հետո մենք ստանում ենք, որ մեկ գործոնն ունի ձևը ( x+ 1), իսկ երկրորդ գործոնը հավասար աստիճանի վերադարձի հավասարումն է (դրա աստիճանը մեկով պակաս է սկզբնական հավասարման աստիճանից): Զույգ աստիճանի ցանկացած վերադարձի հավասարում ձևի արմատի հետ միասին x = φպարունակում է տեսակի արմատը. Օգտագործելով այս պնդումները՝ մենք խնդիրը լուծում ենք՝ իջեցնելով ուսումնասիրվող հավասարման աստիճանը։

Փոփոխական փոխարինման մեթոդ. Միատեսակության օգտագործումը.

Հինգերորդ աստիճանի (սա ցույց են տվել իտալացի մաթեմատիկոս Պաոլո Ռուֆինին (1765-1822) և նորվեգացի մաթեմատիկոս Նիլս Հենրիկ Աբելը (1802-1829)) և ավելի բարձր աստիճանների (սա ցույց են տվել իտալացի մաթեմատիկոս Պաոլո Ռուֆինին (1765-1822)) և ավելի բարձր աստիճանի հավասարումներ լուծելու ընդհանուր բանաձև չկա: Ֆրանսիացի մաթեմատիկոս Էվարիստ Գալուա (1811-1832)):

Կրկին հիշեցնենք, որ գործնականում հնարավոր է օգտագործել համակցություններվերը թվարկված մեթոդները: Հարմար է անցնել ավելի ցածր աստիճանի հավասարումների մի շարք սկզբնական հավասարման ֆակտորիզացիա.
Գործնականում լայնորեն կիրառվածը դուրս մնաց մեր այսօրվա քննարկման շրջանակներից։ գրաֆիկական մեթոդներլուծել հավասարումներ և լուծման մոտավոր մեթոդներավելի բարձր աստիճանի հավասարումներ.

Կան իրավիճակներ, երբ հավասարումը չունի R-արմատներ:

Օգտագործելով ֆունկցիաների միապաղաղության հատկությունը

4. Ամփոփում.

Համառոտ. Այժմ մենք յուրացրել ենք ավելի բարձր աստիճանի տարբեր հավասարումների լուծման հիմնական մեթոդները (n-ի համար > 3). Մեր խնդիրն է սովորել, թե ինչպես արդյունավետ օգտագործել վերը թվարկված ալգորիթմները: Կախված հավասարման տեսակից՝ մենք պետք է սովորենք որոշել, թե այս դեպքում լուծման որ մեթոդն է ամենաարդյունավետը, ինչպես նաև ճիշտ կիրառել ընտրված մեթոդը։

5. Տնային աշխատանք.

՝ էջ 7, էջ 164-174, թիվ 33-36, 39-44, 46.47։

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Այս թեմայի վերաբերյալ զեկույցների կամ ռեֆերատների հնարավոր թեմաները.

Formula Cardano
Հավասարումների լուծման գրաֆիկական մեթոդ. Լուծման օրինակներ.
Հավասարումների մոտավոր լուծման մեթոդներ.

Նյութի յուրացման և թեմայի նկատմամբ ուսանողների հետաքրքրության վերլուծություն.

Փորձը ցույց է տալիս, որ ուսանողներին առաջին հերթին հետաքրքրում է համալրման հնարավորությունը Զ-արմատներ և Ք-հավասարումների արմատները՝ օգտագործելով բավականին պարզ ալգորիթմ՝ օգտագործելով Հորների սխեման: Ուսանողները հետաքրքրված են նաև փոփոխականների փոխարինման տարբեր ստանդարտ տեսակներով, որոնք կարող են մեծապես պարզեցնել խնդիրը: Գրաֆիկական լուծման մեթոդները սովորաբար առանձնահատուկ հետաքրքրություն են ներկայացնում: Այս դեպքում դուք կարող եք լրացուցիչ ապամոնտաժել առաջադրանքները հավասարումների լուծման գրաֆիկական մեթոդի մեջ. քննարկել գրաֆիկի ընդհանուր տեսքը 3, 4, 5 աստիճանի բազմանդամի համար. վերլուծել, թե ինչպես է 3, 4, 5 աստիճանի հավասարումների արմատների թիվը կապված համապատասխան գրաֆիկի տեսակի հետ: Ստորև ներկայացված է գրքերի ցանկը, որտեղ կարող եք լրացուցիչ տեղեկություններ գտնել այս թեմայի վերաբերյալ:

Մատենագիտություն:

Vilenkin N. Ya.և այլք «Հանրահաշիվ. Դասագիրք 9-րդ դասարանի աշակերտների համար մաթեմատիկայի խորացված ուսումնասիրությամբ »- Մ., Կրթություն, 2007 - 367 էջ.
Vilenkin N.Ya., Shibasov L.P., Shibasova Z.F.«Մաթեմատիկայի դասագրքի էջերի հետևում. Թվաբանություն. Հանրահաշիվ. Դասարան 10-11 ”- Մ., Կրթություն, 2008 - 192 էջ.
Vygodsky M. Ya.«Մաթեմատիկայի ձեռնարկ» - Մ., ՀՍՏ, 2010 - 1055 էջ.
Գալիցկի Մ.Լ.«Խնդիրների ժողովածու հանրահաշիվում. Ուսուցողական 8-9-րդ դասարանների համար մաթեմատիկայի խորացված ուսումնասիրությամբ »- Մ., Կրթություն, 2008 - 301 էջ.
Զվավիչ Լ.Ի. et al. «Հանրահաշիվը և վերլուծության սկիզբը. 8-11 կլ. Ձեռնարկ մաթեմատիկայի խորը ուսումնասիրությամբ դպրոցների և դասարանների համար », - M., Bustard, 1999 - 352 p.
Զվավիչ Լ.Ի., Ավերյանով Դ.Ի., Պիգարև Բ.Պ., Տրուշանինա Տ.Ն.«Առաջադրանքներ մաթեմատիկայից 9-րդ դասարանի գրավոր քննությանը նախապատրաստվելու համար» - Մ., Կրթություն, 2007 - 112 էջ.
Իվանով Ա.Ա., Իվանով Ա.Պ.«Թեմատիկ թեստեր մաթեմատիկայում գիտելիքների համակարգման համար» մաս 1 - Մ., Ֆիզմատկնիգա, 2006 - 176 էջ.
Իվանով Ա.Ա., Իվանով Ա.Պ.«Թեմատիկ թեստեր մաթեմատիկայում գիտելիքների համակարգման համար» մաս 2 - Մ., Ֆիզմատկնիգա, 2006 - 176 էջ.
Իվանով Ա.Պ.«Թեստեր և թեստային փաստաթղթերՄաթեմատիկա. Ուսուցողական". - M., Fizmatkniga, 2008 - 304 p.
Լեյբսոն Կ.Լ.«Մաթեմատիկայում գործնական վարժությունների ժողովածու. Մաս 2-9 դասարան «- M., MCNMO, 2009 - 184 p.
Մակարիչև Յու.Ն., Մինդյուկ Ն.Գ.«Հանրահաշիվ. Լրացուցիչ գլուխներ դեպի դպրոցական դասագիրք 9-րդ դասարան. Դասագիրք դպրոցների և դասարանների աշակերտների համար՝ մաթեմատիկայի խորացված ուսումնասիրությամբ »: - Մ., Կրթություն, 2006 - 224 էջ.
Մորդկովիչ Ա.Գ.«Հանրահաշիվ. Ընդլայնված ուսումնասիրություն. 8-րդ դասարան. Դասագիրք «- M., Mnemosina, 2006 - 296 p.
A.P. Savin “Հանրագիտարանային բառարաներիտասարդ մաթեմատիկոս «- Մ., Մանկավարժություն, 1985 - 352 էջ.
Survillo G.S., Simonov A.S. “Դիդակտիկ նյութեր 9-րդ դասարանի հանրահաշիվում մաթեմատիկայի խորացված ուսումնասիրությամբ »- Մ., Կրթություն, 2006 - 95 էջ.
Չուլկով Պ.Վ.«Հավասարումներ և անհավասարություններ դպրոցական մաթեմատիկայի դասընթացում. Դասախոսություններ 1–4 ”- Մ., 1 սեպտեմբերի, 2006 - 88 p.
Չուլկով Պ.Վ.«Հավասարումներ և անհավասարություններ դպրոցական մաթեմատիկայի դասընթացում. Դասախոսություններ 5–8 ”- Մ., 1 սեպտեմբերի, 2009 - 84 p.

Հաշվի առեք հավասարումների լուծումներ, որոնց մեկ աստիճանով բարձր է երկրորդը:

P (x) = 0 հավասարման աստիճանը P (x) բազմանդամի աստիճանն է, այսինքն. նրա անդամների աստիճաններից ամենամեծը՝ զրոյի ոչ հավասար գործակցով։

Այսպիսով, օրինակ, (x 3 - 1) 2 + x 5 = x 6 - 2 հավասարումն ունի հինգերորդ աստիճան, քանի որ. Փակագծերը բացելու և նմանատիպերը բերելու գործողություններից հետո ստանում ենք հինգերորդ աստիճանի x 5 - 2x 3 + 3 = 0 հավասարումը։

Հիշենք այն կանոնները, որոնք անհրաժեշտ կլինեն երկուսից բարձր աստիճանի հավասարումներ լուծելու համար։

Բազմանդամի արմատների և նրա բաժանարարների մասին հայտարարություններ.

1. Բազմանդամ n-րդ աստիճանունի արմատների թիվը առավելագույնը n, իսկ m բազմապատկության արմատները տեղի են ունենում ուղիղ m անգամ:

2. Կենտ աստիճանի բազմանդամն ունի առնվազն մեկ իրական արմատ:

3. Եթե α-ն P (x)-ի արմատն է, ապա P n (x) = (x - α) Q n - 1 (x), որտեղ Q n - 1 (x) աստիճանի բազմանդամ է (n - 1):

5. Ամբողջ թվային գործակիցներով կրճատված բազմանդամը չի կարող կոտորակային ռացիոնալ արմատներ ունենալ։

6. 3 աստիճանի բազմանդամի համար

P 3 (x) = ax 3 + bx 2 + cx + d երկու բաներից մեկը հնարավոր է. կամ այն քայքայվում է երեք երկանդամների արտադրյալի

Р 3 (x) = а (х - α) (х - β) (х - γ), կամ քայքայվում է երկանդամի և քառակուսի եռանդամի արտադրյալի Р 3 (x) = а (х - α) (х 2): + բх + գ):

7. Չորրորդ աստիճանի ցանկացած բազմանդամ կարող է քայքայվել երկու քառակուսի եռանկյունների արտադրյալի։

8. F (x) բազմանդամը բաժանվում է g (x) բազմանդամի վրա առանց մնացորդի, եթե կա q (x) բազմանդամ, որ f (x) = g (x) q (x): Բազմանդամների բաժանման համար կիրառվում է «անկյունային բաժանման» կանոնը։

9. P (x) բազմանդամի (x) երկանդամի բաժանվելու համար անհրաժեշտ և բավարար է, որ c թիվը լինի P (x)-ի արմատը (Բեզութի թեորեմի հետևանքը)։

10. Վիետայի թեորեմ. Եթե x 1, x 2, ..., x n բազմանդամի իրական արմատներն են.

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, ապա գործում են հետևյալ հավասարումները.

x 1 + x 2 + ... + x n = -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n = a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n = -a 3 / a 0,

x 1 x 2 x 3 x n = (-1) n a n / a 0:

Լուծման օրինակներ

Օրինակ 1.

Գտե՛ք P (x) = x 3 + 2/3 x 2 - 1/9 (x - 1/3) բաժանելու մնացորդը։

Լուծում.

Բեզութի թեորեմի հետևանքով. «Բազմանդամը երկանդամի (x - c) բաժանելու մնացորդը հավասար է c-ի բազմանդամի արժեքին»: Գտնենք Р (1/3) = 0։ Հետևաբար, մնացորդը 0 է, իսկ 1/3 թիվը բազմանդամի արմատն է։

Պատասխան՝ R = 0:

Օրինակ 2.

2x 3 + 3x 2 - 2x + 3 անկյունով բաժանեք (x + 2): Գտե՛ք մնացորդը և թերի գործակիցը:

Լուծում:

2x 3 + 3x 2 - 2x + 3 | x + 2

2х 3 + 4 x 2 2x 2 - x

X 2 - 2 x

Պատասխան՝ R = 3; մասնավոր՝ 2x 2 - x.

Բարձրագույն աստիճանի հավասարումների լուծման հիմնական մեթոդները

1. Նոր փոփոխականի ներկայացում

Նոր փոփոխականի ներդրման մեթոդն արդեն ծանոթ է օրինակով։ երկքառակուսի հավասարումներ... Այն բաղկացած է նրանից, որ f (x) = 0 հավասարումը լուծելու համար ներմուծվում է նոր փոփոխական (փոխարինում) t = xn կամ t = g (x) և f (x) արտահայտվում է t-ով, ստանալով նոր. r (t) հավասարումը. Այնուհետև, լուծելով r (t) հավասարումը, հայտնաբերվում են արմատները.

(t 1, t 2, ..., t n): Դրանից հետո ստացվում է n հավասարումների բազմություն q (x) = t 1, q (x) = t 2, ..., q (x) = t n, որից հայտնաբերվում են սկզբնական հավասարման արմատները։

Օրինակ 1.

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0:

Լուծում:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0:

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0:

Փոխարինում (x 2 + x + 1) = t.

t 2 - 3t + 2 = 0:

t 1 = 2, t 2 = 1. Հակադարձ փոխարինում.

x 2 + x + 1 = 2 կամ x 2 + x + 1 = 1;

x 2 + x - 1 = 0 կամ x 2 + x = 0;

Պատասխան՝ Առաջին հավասարումից՝ x 1, 2 = (-1 ± √5) / 2, երկրորդից՝ 0 և -1:

2. Ֆակտորիզացիա՝ խմբավորման և կրճատված բազմապատկման բանաձևերի միջոցով

Այս մեթոդի հիմքը նույնպես նոր չէ և բաղկացած է տերմինների խմբավորումից այնպես, որ յուրաքանչյուր խումբ պարունակի ընդհանուր գործոն: Դա անելու համար երբեմն պետք է ինչ-որ արհեստական մեթոդներ կիրառել։

Օրինակ 1.

x 4 - 3x 2 + 4x - 3 = 0:

Լուծում.

Պատկերացրեք - 3x 2 = -2x 2 - x 2 և խումբ.

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0:

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0:

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0:

(x 2 - 1) 2 - (x - 2) 2 = 0:

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0:

(x 2 - x + 1) (x 2 + x - 3) = 0:

x 2 - x + 1 = 0 կամ x 2 + x - 3 = 0:

Պատասխան՝ Առաջին հավասարման մեջ արմատներ չկան, երկրորդից՝ x 1, 2 = (-1 ± √13) / 2:

3. Ֆակտորինգ չսահմանված գործակիցների մեթոդով

Մեթոդի էությունն այն է, որ սկզբնական բազմանդամը տարրալուծվում է անհայտ գործակիցներով գործոնների։ Օգտագործելով այն հատկությունը, որ բազմանդամները հավասար են, եթե նրանց գործակիցները հավասար են միևնույն աստիճաններում, գտնում ենք ընդլայնման անհայտ գործակիցները:

Օրինակ 1.

x 3 + 4x 2 + 5x + 2 = 0:

Լուծում.

3-րդ աստիճանի բազմանդամը կարող է ընդլայնվել գծային և քառակուսի գործոնի արտադրյալի:

x 3 + 4x 2 + 5x + 2 = (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b - a) x 2 + (cx - ab) x - ac.

Համակարգը լուծելով.

(b - a = 4,
(c - ab = 5,
(-ac = 2,

(a = -1,
(b = 3,
(c = 2, այսինքն.

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2):

(x + 1) (x 2 + 3x + 2) = 0 հավասարման արմատները հեշտ է գտնել:

Պատասխան՝ -1; -2.

4. Արմատի ընտրության մեթոդ ամենաբարձր և ազատ գործակցով

Մեթոդը հիմնված է թեորեմների կիրառման վրա.

1) Ամբողջ թվային գործակիցներով բազմանդամի ցանկացած ամբողջ արմատը հատման բաժանարար է։

2) Որպեսզի p / q անկրճատելի կոտորակը (p-ն ամբողջ թիվ է, q-ը բնական) լինի ամբողջ թվով գործակիցներով հավասարման արմատ, անհրաժեշտ է, որ p թիվը լինի a 0-ի ազատ անդամի ամբողջական բաժանարարը, և q - առաջատար գործակիցի բնական բաժանարար:

Օրինակ 1.

6x 3 + 7x 2 - 9x + 2 = 0:

Լուծում:

6: q = 1, 2, 3, 6:

Հետեւաբար, p / q = ± 1, ± 2, ± 1/2, ± 1/3, ± 2/3, ± 1/6:

Գտնելով մեկ արմատ, օրինակ՝ 2, մենք գտնում ենք մյուս արմատները՝ օգտագործելով անկյունով բաժանումը, չսահմանված գործակիցների մեթոդը կամ Հորների սխեման։

Պատասխան՝ -2; 1/2; 1/3.

Դեռ ունե՞ք հարցեր: Չգիտե՞ք ինչպես լուծել հավասարումները:
Կրկնուսույցից օգնություն ստանալու համար գրանցվեք:
Առաջին դասն անվճար է։

կայքը, նյութի ամբողջական կամ մասնակի պատճենմամբ, աղբյուրի հղումը պարտադիր է:

Ընդամենը:0
հետ շփման մեջ 0
Google+ 0
լավ 0
Ֆեյսբուք 0