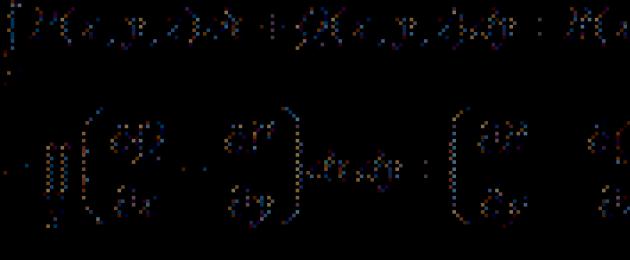Queste formule collegano l'integrale su una figura con un integrale sul confine di una data figura.

Sia le funzioni continue nel dominio DÌ Ossi e al suo confine G; regione D– connesso; G– curva liscia a tratti. Allora vero La formula di Verde:

qui a sinistra c'è un integrale curvilineo della prima specie, a destra c'è un integrale doppio; circuito G va in senso antiorario.

Permettere T– superficie su due lati liscia a tratti con confine liscio a tratti G. Se le funzioni P(X,sì,z), Q(X,sì,z), R(X,sì,z) e le loro derivate parziali del primo ordine sono continue nei punti della superficie T e confini G, allora si verifica Formula di Stokes:

(2.23)

a sinistra c'è un integrale curvilineo del secondo tipo; a destra – integrale di superficie di seconda specie, preso lungo quel lato della superficie T, che rimane a sinistra durante l'attraversamento della curva G.

Se una regione connessa WÌ Oxyz delimitato da una superficie liscia e chiusa a tratti T e le funzioni P(X,sì,z), Q(X,sì,z), R(X,sì,z) e le loro derivate parziali del primo ordine sono continue nei punti da W E T, allora si verifica Formula di Ostrogradskij-Gauss:

(2.24)

a sinistra – integrale di superficie del secondo tipo sul lato esterno della superficie T; a destra – integrale triplo sull’area W.

Esempio 1. Calcolare il lavoro compiuto dalla forza quando si attraversa il punto della sua applicazione del cerchio G: , partendo dall'asse Bue, in senso orario (Fig. 2.18).

Soluzione. Il lavoro è uguale a . Applichiamo la formula di Green (2.22), ponendo il segno “-” a destra prima dell'integrale (poiché il circuito si percorre in senso orario) e tenendo conto che P(X,sì)=X-sì, Q(X,sì)=X+sì. Abbiamo:
,
Dove SD– area di un cerchio D: , uguale a . Di conseguenza: – il lavoro di forza richiesto.

Esempio 2. Calcola l'integrale , Se G c'è un cerchio nell'aereo z=2, girando in senso antiorario.

Soluzione. Usando la formula di Stokes (2.23), riduciamo l'integrale originale all'integrale di superficie su un cerchio T:
T:

Quindi, premesso ciò, abbiamo:

L'ultimo integrale è un integrale doppio su una circonferenza DÌ Ossi, su cui è stato proiettato il cerchio T; D: . Passiamo alle coordinate polari: X=R cosj, sì=R sinj, jÎ, R O. Di conseguenza:
.

Esempio 3. Trova flusso P T piramidi W: (Fig. 2.19) nella direzione della normale esterna alla superficie.

Soluzione. Il flusso è . Applicando la formula di Ostrogradsky-Gauss (2.24), riduciamo il problema al calcolo dell'integrale triplo sulla figura W-piramide:

Esempio 4. Trova flusso P campo vettoriale attraverso tutta la superficie T piramidi W: ; (Fig. 2.20), nella direzione della normale esterna alla superficie.

Soluzione. Applichiamo la formula di Ostrogradsky-Gauss (2.24), dove V– volume della piramide. Confrontiamo con la soluzione del calcolo diretto della portata ( – facce della piramide).

,
dalla proiezione delle facce sul piano Ossi ha area zero (Fig. 2.21),

Formula Ostrogradsky-Verde

Questa formula stabilisce una connessione tra l'integrale curvilineo su un contorno chiuso C e l'integrale doppio sulla regione limitata da questo contorno.

Definizione 1. Una regione D si dice regione semplice se può essere suddivisa in un numero finito di regioni del primo tipo e, indipendentemente da questo, in un numero finito di regioni del secondo tipo.

Teorema 1. Siano le funzioni P(x,y) e Q(x,y) definite in un dominio semplice e continue insieme alle loro derivate parziali e

Allora la formula vale

dove C è il contorno chiuso dell'area D.

Questa è la formula Ostrogradsky-Green.

Condizioni per l'indipendenza di un integrale curvilineo dal percorso di integrazione

Definizione 1. Una regione squadrabile chiusa D si dice semplicemente connessa se qualsiasi curva chiusa l D può essere deformata con continuità in un punto in modo che tutti i punti di questa curva appartengano alla regione D (regione senza “buchi” - D 1) , se tale deformazione è impossibile, la regione viene chiamata molte volte connessa (con "buchi" - D 2).

Definizione 2. Se il valore dell'integrale di curva lungo la curva AB non dipende dal tipo di curva che collega i punti A e B, allora questo integrale di curva si dice indipendente dal percorso di integrazione:

Teorema 1. Siano definite le funzioni continue P(x,y) e Q(x,y) in un dominio chiuso semplicemente connesso D, insieme alle loro derivate parziali. Allora le seguenti 4 condizioni sono equivalenti:

1) integrale curvilineo su un anello chiuso

dove C è un qualsiasi anello chiuso in D;

2) l'integrale curvilineo su un anello chiuso non dipende dal percorso di integrazione nella regione D, cioè

3) la forma differenziale P(x,y)dx + Q(x,y)dy è differenziale completo una qualche funzione F nel dominio D, cioè che esiste una funzione F tale che (x,y) D vale l'uguaglianza

dF(x,y) = P(x,y)dx + Q(x,y)dy; (3)

4) per tutti i punti (x,y) D sarà soddisfatta la seguente condizione:

Dimostriamolo utilizzando il diagramma.

Dimostriamolo da.

Sia dato 1), cioè = 0 per la proprietà 2 §1, che = 0 (per la proprietà 1 §1) .

Dimostriamolo da.

È dato che cr.int. non dipende dal percorso di integrazione, ma solo dalla scelta dell'inizio e della fine del percorso

Considera la funzione

Mostriamo che la forma differenziale P(x,y)dx + Q(x,y)dy è il differenziale completo della funzione F(x,y), cioè , Che cosa

Impostiamo la crescita privata

x F (x,y)= F(x + x, y) -F (x,y)= = == =

(per la proprietà 3 del § 1, BB* Oy) = = P (c,y)x (per il teorema del valore medio, c -const), dove x

(a causa della continuità della funzione P). Abbiamo ottenuto la formula (5). La formula (6) si ottiene in modo simile.

Dimostriamolo da.

La formula è data

dF(x,y) = P(x,y)dx + Q(x,y)dy.

Ovviamente = P(x,y). Poi

Secondo le condizioni del teorema, i membri di destra delle uguaglianze (7) e (8) sono funzioni continue, quindi, per il teorema sull'uguaglianza delle derivate miste, anche i membri di sinistra saranno uguali, cioè, Quello

Dimostriamolo su 41.

Scegliamo un contorno chiuso qualsiasi della regione D che delimita la regione D 1 .

Le funzioni P e Q soddisfano le condizioni di Ostrogradsky-Green:

In virtù dell'uguaglianza (4), sul lato sinistro di (9) l'integrale è uguale a 0, il che significa che anche il lato destro dell'uguaglianza è uguale a

Osservazione 1. Il Teorema 1 può essere formulato sotto forma di tre teoremi indipendenti

Teorema 1*. Affinché un dominio squadrabile D semplicemente connesso abbia un int curvo. non dipendeva dal percorso di integrazione quindi la condizione (.1) è soddisfatta, cioè

Teorema 2*. Affinché un dominio squadrabile D semplicemente connesso abbia un int curvo. non dipendeva dal percorso di integrazione quindi la condizione (3) è soddisfatta:

la forma differenziale P(x,y)dx + Q(x,y)dy è il differenziale totale di una qualche funzione F nel dominio D.

Teorema 3*. Affinché un dominio squadrabile D semplicemente connesso abbia un int curvo. non dipendeva dal percorso di integrazione quindi la condizione (4) è soddisfatta:

Osservazione 2. Nel Teorema 2*, il dominio D può anche essere multiconnesso.

Relazione tra integrale doppio su un dominio D e un integrale curvilineo sul confine l Quest'area è stabilita dalla formula Ostrogradsky-Green, ampiamente utilizzata nell'analisi matematica.

Sali sull'aereo Ohoh zona specificata D, delimitato da una curva che interseca linee rette parallele agli assi delle coordinate in non più di due punti, cioè D regione

- corretto. Teorema 10.2. P(X; sì Se le funzioni Q(X; sì) E ) sono continue insieme alle loro derivate parziali E D nella zona

(10.8)

, allora la formula vale l Dove D– confine dell'area l e integrazione lungo la curva D viene prodotto nella direzione positiva (cioè quando ci si sposta lungo una curva, l'area

rimane a sinistra).

La formula (10.8) è chiamata formula di Ostrogradsky-Green. P
Ust - equazione dell'arco AnB
, UN - equazione dell'arco AmB
(vedi Fig. 8). Troviamolo prima

.Secondo la regola per il calcolo dell'integrale doppio, abbiamo:

Oppure secondo la formula (10.6), Fig.
(10.10)

Se sottraiamo l'uguaglianza (10.9) dall'uguaglianza (10.10), otteniamo la formula (10.8).

Commento. La formula (10.8) vale anche per una regione arbitraria, che può essere divisa in un numero finito di regioni regolari.

Esempio 10.3. Usando la formula Ostrogradsky-Green, calcola

Dove l– contorno di un rettangolo con vertici UN(3;2 ), IN(6;2 ), CON(6;4 ), D(3;4 ).

○ Soluzione: La Figura 9 mostra il ciclo di integrazione.

Da

secondo la formula (10.8) abbiamo:

La formula (10.8) è chiamata formula di Ostrogradsky-Green.
P 10.4. Condizioni per l'indipendenza di un integrale curvilineo di seconda specie dal cammino di integrazione(X 1 ; sì UN 1) e(X 2 ; sì B D 2) – due punti arbitrari di una regione semplicemente connessa Ohoh aereo D(aereo chiamato semplicemente connesso D, se ad ogni contorno chiuso che giace in quest'area appartiene interamente la parte del piano da esso delimitata UN(zona senza “buchi”)). Punti E IN l 1 , l possono essere collegati da linee diverse (in Fig. 10 questo è l 2 e
3).

Per ciascuna di queste curve l'integrale In generale, ha il suo significato. Se i suoi valori secondo tutte le curve possibili AB sono la stessa cosa, allora diciamo che l'integrale

IO AB non dipende dal tipo di percorso di integrazione. 10.4. Condizioni per l'indipendenza di un integrale curvilineo di seconda specie dal cammino di integrazione(X 1 ; sì 1 Riso. 10. In questo caso, per l'integrale 1) e(X 2 ; sì 2 ) è sufficiente segnarne solo il punto di partenza

(10.11)

) e il suo punto finale

modi. Scrivi: Quali sono le condizioni in cui un integrale curvilineo del secondo tipo non dipende dal tipo di percorso di integrazione?
Teorema 10.3. D In ordine per l'integrale curvilineo P(X; sì), Q(X; sì non dipendeva dal percorso di integrazione in un dominio semplicemente connesso =(10.12)

, in cui le funzioni ) sono continue insieme alle loro derivate parziali, è necessario e sufficiente che la condizione sia soddisfatta in ogni punto di questa regione Dimostriamo la sufficienza della condizione (10.12). Consideriamo un cerchio chiuso arbitrario l AmBnA D(O
) nella zona
(vedi Fig. 11). Per esso vale la formula di Ostrogradsky–Green (10.8). In virtù della condizione (10.12), abbiamo:

, O

.

Tenendo conto delle proprietà dell'integrale curvilineo, abbiamo: =, cioè.

L'uguaglianza risultante significa che l'integrale curvilineo non dipende dal percorso di integrazione.

Figura 11. Durante la dimostrazione del teorema si è ottenuto che se la condizione è soddisfatta , allora l'integrale su un cerchio chiuso è uguale a zero: = , allora l'integrale su un cerchio chiuso è uguale a zero:(X; sìÈ vero anche il contrario.

Corollario 10.1.

Se la condizione (10.12) è soddisfatta, allora l'integrando è il differenziale completo di qualche funzione

tu), cioè. Allora (vedi (10.11)) + La formula (10.14) è detta formula generalizzata di Newton–Leibniz per l'integrale curvilineo del differenziale totale. Corollario 10.2. l Se l'integrando
.

Pdx

Qdy X 0 ; sì 0) solitamente prende il punto (0;0) - l'origine delle coordinate (vedi esempio 10.5).

= ,=,=;

Esempio 10.4. Trovare

Soluzione: Qui P = sì, Q = X, == 1. Secondo il teorema precedente, l'integrale non dipende dal percorso di integrazione. sì = X Come percorso di integrazione, possiamo prendere un segmento di linea retta sì = X, arco di parabola 2, ecc. o utilizzare la formula (10.14). Perché ydx + xdy = d(xy)

, Quello Esempio 10.5. Assicurarsi che l'espressione sia il differenziale completo della funzione (X; sì U

Soluzione:) e trovarla.

Affinché l’espressione indicata sia un differenziale completo, devono essere soddisfatte le condizioni (10.12):

,

Le condizioni sono soddisfatte, quindi, e poiché il differenziale totale ha la forma

(10.16)

allora le relazioni sono corrette Integriamo tramite X la prima delle equazioni, considerando A
costante, e invece di integrazione costante si dovrebbe mettere la prima delle equazioni, considerando:

- una funzione sconosciuta che dipende solo da
:

Sostituendo l'espressione risultante nella seconda equazione (10.16), troviamo

Così, Assicurarsi che l'espressione sia il differenziale completo della funzione Si noti che la funzione

è più facile da trovare utilizzando la formula (10.15).

(Ostrogradsky Mikhail Vasilievich (1861-1862) - matematico russo,

Accademico Pietroburgo UN.)

(George Green (1793 – 1841) – matematico inglese)

A volte questa formula è chiamata formula di Green, tuttavia, J. Green propose nel 1828 solo un caso speciale della formula.

La formula di Ostrogradsky-Green stabilisce una connessione tra l'integrale curvilineo e l'integrale doppio, cioè dà un'espressione per l'integrale su un contorno chiuso attraverso l'integrale doppio sull'area limitata da questo contorno.

Se il contorno chiuso ha la forma mostrata in figura, allora la curva integrale lungo il contorno L si può scrivere come:

Se le sezioni AB e CD del contorno vengono prese come curve arbitrarie, dopo aver effettuato trasformazioni simili, otteniamo una formula per un contorno di forma arbitraria: Questa formula si chiama.

Formula di Ostrogradskij-Verde

La formula Ostrogradsky-Green è valida anche nel caso di una regione molte volte connessa, cioè una regione all'interno della quale ci sono aree escluse. In questo caso, il lato destro della formula sarà la somma degli integrali lungo il contorno esterno della regione e degli integrali lungo i contorni di tutte le sezioni escluse, e ciascuno di questi contorni è integrato in una direzione tale che la regione D rimane sempre sul lato sinistro della linea di bypass. Esempio.

Risolviamo l'esempio discusso sopra utilizzando la formula di Ostrogradsky-Green.

L'integrale di linea non dipende dalla forma del percorso se ha lo stesso valore lungo tutti i percorsi che collegano i punti iniziale e finale.

La condizione per l'indipendenza di un integrale curvilineo dalla forma del percorso equivale all'uguaglianza a zero di questo integrale lungo qualsiasi contorno chiuso contenente i punti iniziale e finale.

Sia π il piano in , sia il vettore unitario normale a π, D- dominio semplicemente connesso su π (cioè una curva chiusa liscia a tratti senza autointersezioni situate in D, delimita una regione di cui anche tutti i punti D). Permettere D soddisfa le condizioni:

1) confine CON regione Dè una curva liscia chiusa a tratti senza punti singolari;

2) su π si può scegliere un sistema di coordinate cartesiane rettangolari tale che tutte le rette parallele agli assi delle coordinate si intersecano D non più di 2 punti.

Permettere T- CON, coerente con, cioè, la direzione positiva di attraversamento della curva CON T con direzione T CON

T1 (formula di Green). PermettereUN - 1), 2), la direzione è continua . Allora la formula è valida

Giusto - circolazione del campo vettoriale lungo la curva CON, a sinistra - scorre il campo vettoriale D.

Dott. Tutte le funzioni incluse in (1) sono continue => entrambi integrali. Gli integrali sinistro e destro in (1) sono invarianti rispetto alla scelta di un sistema di coordinate rettangolari, poiché e invariante, gli elementi di area e lunghezza d'arco non dipendono dalla scelta del sistema di coordinate cartesiane => è sufficiente dimostrare (1) in un sistema appositamente scelto.

Scegliamo cartesiano sistema rettangolare coordinate Ohhz quindi la condizione 2) è soddisfatta, e Oz andiamo avanti. Poiché il campo vettoriale è piatto, allora =>

Per una regione pianeggiante e , dove l- lunghezza dell'arco CON, selezionato come parametro il cui incremento è coerente con la direzione di traslazione CON =>

Per dimostrare la formula di Green è sufficiente dimostrare 2 uguaglianze:

Sia una linea retta parallela all'asse OH, croci CON in punti . Permettere - ascissa più piccola e più grande dei punti di un'area, curva CON 1 si collega con , e la curva CON 2 - ñ e , sono orientati in accordo con C => secondo la formula per ridurre un integrale doppio ad uno ripetuto:

L'integrale si calcola in modo simile J.

Z1. Dal documento => la formula (1) può essere scritta nella forma (1"):

Oh "sì"; UN ha delle coordinate R" E Q", Quello

Trasformazione Jacobiana quando si passa ad un nuovo sistema di coordinate modulo = 1, la parametrizzazione utilizzando la lunghezza dell'arco non è correlata al sistema di coordinate =>

Permettere D- dominio semplicemente connesso in (cioè per una curva chiusa liscia a tratti C, situato in D,è possibile specificare una superficie liscia orientabile a tratti G, situato in D, avere un confine CON), superficie S- il suo confine che soddisfa le condizioni:

1) S- a tratti liscio su due lati completo delimitato chiuso e senza punti singolari;

2) si può scegliere un sistema di coordinate cartesiane rettangolari in modo che per ciascuno degli assi coordinati si intersechi una retta parallela a tale asse S non più di 2 punti.

Permettere N- vettore unitario della normale esterna a S.

T2 ( Formula di Ostrogradskij-Gauss ). PermettereUNè un campo vettoriale, diff in D, che soddisfa le condizioni 1), 2), e tale che la derivata rispetto a la direzione è continua . Poi

Giusto - flusso del campo vettoriale attraverso la superficie S, a sinistra c'è l'integrale di volume della divergenza del vettore sull'area D => L'integrale di volume della divergenza di un vettore sulla regione D è uguale al flusso del campo vettoriale attraverso la superficie S - il confine di questa regione.

Documento Tutte le funzioni incluse in (2) sono continue => entrambi integrali. La formula (2) è invariante rispetto alla scelta di un sistema di coordinate rettangolari, poiché tutte le quantità in esso contenute sono invarianti => basta dimostrare (2) con qualche 1 scelta del sistema cartesiano. Scegliamo un sistema di coordinate cartesiane rettangolari Ohhz per cui la condizione 2) è soddisfatta; lascia => dato:

Documento necessario:

Dimostriamolo L, altri no. Permettere D"- proiezione D all'aereo Ooh. Attraverso punti di confine D" disegniamo linee parallele Oz. Ognuno di essi si interseca con S solo a 1 punto. L'insieme di questi punti si separa S in 2 parti: . Se disegni una linea retta da un punto interno D" parallelo Oz, poi attraverserà S in 2 punti: E . e funzioni a tratti e continuamente diverse in D". Utilizzando la formula per ridurre un integrale triplo a un integrale iterato:

Abbiamo usato il fatto che , e la relazione

giusto, perché la normale esterna a forma un angolo ottuso con Oz(=> ).

Z2. Dal documento => formula (2) si può scrivere:

Documento Z1.

Formula di Stokes.

Permettere S semplicemente connessa (cioè una curva chiusa liscia a tratti senza autointersezioni situate su S, limita un insieme, tutti i cui punti S) superficie dentro , soddisfacendo le condizioni:

1) S- superficie delimitata completa su due lati liscia a tratti senza punti speciali; il suo confine è un contorno liscio chiuso a tratti CON;

2) il sistema di coordinate cartesiane può essere scelto in modo che Sè stato proiettato in modo univoco su 3 piani coordinati.

Permettere N- vettore normale unitario a S, T- vettore unitario tangente a C, d'accordo con N, cioè la direzione positiva dell'attraversamento della curva CON coincide nel punto di applicazione del vettore T con direzione T e se guardi dalla fine, allora il contorno CON orientato positivamente (gira in senso antiorario).

T (formula di Stokes). PermettereUN - campo vettoriale, differisce continuamente in qualche intorno della superficie S(cioè su qualche set aperto , contenente S). Poi

O: Vettore di flusso attraverso la superficie S è uguale alla circolazione del vettoreUN lungo un circuito chiuso C.

Documento. A causa delle condizioni del teorema, esistono gli integrali in (1). La formula (1) è invariante rispetto alla scelta della base => basta dimostrarlo per qualsiasi scelta della base. Scegliamo un sistema di coordinate cartesiane rettangolari Ohhz affinché Sè stato sicuramente progettato per tutti e tre piani coordinati. Permettere

Coordiniamo la scelta del sistema di coordinate in modo che il vettore normale formi angoli acuti con gli assi delle coordinate. Data un'espressione per nel sistema di coordinate cartesiane

E' sufficiente dimostrare:

S- a tratti liscio e proiettato in modo univoco Ooh. Permettere D- la sua proiezione, G - proiezione CON all'aereo Oh => diff-may f-i, che specifica l'equazione della superficie S. Allo stesso tempo

e superficie integrale sopra S = doppio integrale Di D. Secondo la formula di Green*:

Z1. δ > 0 tale che per parti F Taglia S< δ (può trovarsi in una sfera di raggio δ/2) possiamo scegliere un sistema di coordinate cartesiane tale F viene proiettato in modo univoco su tutti i piani coordinati. Permettere - punto fisso S. Disegniamo un piano tangente attraverso , sia il vettore normale unitario della superficie in . Scegliamo un sistema di coordinate rettangolare in modo che formi angoli acuti con gli assi. Perché il campo delle normali è continuo, allora l'intorno è tale che tutte le normali nei punti di questo intorno formano angoli acuti con gli assi => un intorno di raggio δ/2 del punto , che proietta in modo univoco su tutti i piani coordinati.

Si può scegliere un numero universale che non dipenda dal numero δ > 0. Sia tale δ => per ognuno si può specificare una parte della superficie S, le cui dimensioni< и которая не проектируется однозначно на все координатные плоскости декартовой системы коор­динат.

Scegliamo in ogni punto , dalla conseguenza ottenuta scegliamo una sequenza convergente ad alcune M S. U M un intorno proiettato univocamente sui piani coordinati di un certo sistema rettangolare. Questo quartiere è per un certo numero N contiene una parte che si proietterà in modo univoco su tutti e tre i piani coordinati => una contraddizione con la scelta.

Analizziamolo S in un numero finito di parti lisce, la cui dimensione è ciascuna< δ, указанного выше. однозначно проектируется на все координатные плос­кости некоторой декартовой системы координат =>La formula di Stokes è vera per ciascuno. Riassumiamo i lati sinistro e destro di queste formule. Gli integrali sulle sezioni comuni del confine sono presi in direzioni opposte e quindi si annullano => a sinistra otteniamo l'integrale sulla superficie di e a destra l'integrale sul confine CON da , cioè la formula di Stokes per il caso generale => la formula di Stokes è valida per superfici che soddisfano la condizione 1) e non soddisfano, in generale, la condizione 2).

Z2. La formula di Stokes è vera per le superfici S, consentendo il partizionamento utilizzando curve lisce a tratti in un numero finito di superfici semplicemente connesse aventi superfici di proprietà 1). Doc: somma gli integrali a sinistra e a destra nelle formule di Stokes per superfici semplicemente connesse e tieni conto che gli integrali lungo le curve comprese nella partizione vengono presi in direzioni diverse e quindi si annullano.

Z3. Dal documento => la formula (1) può essere scritta nella forma (1"):

Gli integrali a sinistra e a destra in (1") sono invarianti, poiché i valori degli integrandi sono rispettivamente uguali e - quantità invarianti. Anche la forma degli integrandi nella formula (1") non cambia quando ci si sposta A nuovo sistema Oh"y"z"; se nella nuova base il campo vettoriale UN ha delle coordinate R", Q" E R", Quello

Lo Jacobiano della trasformazione quando si passa ad un nuovo sistema di coordinate modulo = 1, la parametrizzazione utilizzando la lunghezza dell'arco non è correlata al sistema di coordinate => gli integrali a sinistra e a destra in (1") non cambiano il loro valore e la loro forma.

*: π - piano in , - vettore unitario normale a π, D- regione semplicemente connessa su π . Permettere D soddisfa le condizioni: 1) confine CON regione Dè una curva liscia chiusa a tratti senza punti singolari; 2) su π si può scegliere un sistema di coordinate cartesiane rettangolari tale che tutte le rette parallele agli assi delle coordinate si intersecano D non più di 2 punti.

Permettere T- vettore unitario della tangente alla curva CON, d'accordo con.

T1 (formula di Green). PermettereUN - differenza di campo vettoriale in D che soddisfa le condizioni 1), 2), e tale che sia derivata rispetto a la direzione è continua . Allora la formula è valida