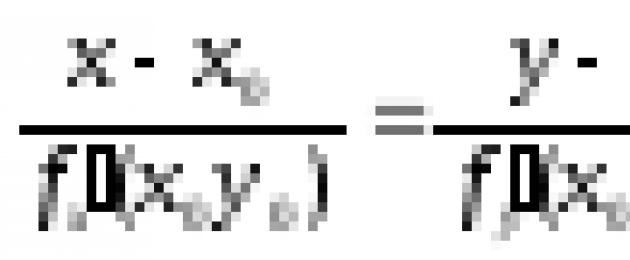Differenziale completo. Significato geometrico del differenziale totale

Piano tangente e normale alla superficie.

piano tangente

Siano N e N 0 punti della superficie data. Tracciamo una linea retta NN 0. Il piano che passa per il punto N 0 si chiama piano tangente alla superficie, se l'angolo tra la secante NN 0 e questo piano tende a zero, quando la distanza NN 0 tende a zero.

Definizione. Normale alla superficie nel punto N 0 è una retta passante per il punto N 0 perpendicolare al piano tangente a questa superficie.

In qualsiasi punto, la superficie ha un solo piano tangente o non lo ha affatto.

Se la superficie è data dall'equazione z = f (x, y), dove f (x, y) è una funzione derivabile nel punto М 0 (x 0, y 0), il piano tangente nel punto N 0 ( x 0, y 0, ( x 0, y 0)) esiste e ha l'equazione:

L'equazione della normale alla superficie in questo punto è:

significato geometrico differenziale completo funzione di due variabili f (x, y) nel punto (x 0, y 0) è l'incremento dell'applicata (coordinata z) del piano tangente alla superficie quando si passa dal punto (x 0, y 0) a il punto (x 0 + x, y 0 + y).

Come puoi vedere, il significato geometrico del differenziale totale di una funzione di due variabili è un analogo spaziale del significato geometrico del differenziale di una funzione di una variabile.

Esempio. Trova le equazioni del piano tangente e della normale alla superficie

al punto M (1, 1, 1).

Equazione del piano tangente:

Equazione normale:

20.4. Calcoli approssimativi utilizzando il differenziale totale.

Sia la funzione f (x, y) derivabile nel punto (x, y). Troviamo l'incremento totale di questa funzione:

Se sostituisci l'espressione

quindi otteniamo una formula approssimativa:

Esempio. Calcola il valore approssimativo in base al valore della funzione in x = 1, y = 2, z = 1.

Dall'espressione data, determiniamo x = 1,04 - 1 = 0,04, y = 1,99 - 2 = -0,01,

z = 1,02 - 1 = 0,02.

Trova il valore della funzione u (x, y, z) =

Trova le derivate parziali:

Il differenziale totale della funzione u è uguale a:

Il valore esatto di questa espressione è 1.049275225687319176.

20.5. Derivati ​​parziali di ordini superiori.

Se la funzione f (x, y) è definita in qualche dominio D, allora le sue derivate parziali saranno determinate nello stesso dominio o parte di esso.

Chiameremo questi derivati derivate parziali del primo ordine.

Le derivate di queste funzioni saranno derivate parziali del secondo ordine.

Continuando a differenziare le uguaglianze ottenute, si ottengono derivate parziali di ordine superiore.

Definizione. Derivate parziali della forma eccetera. sono chiamati derivati ​​misti.

Teorema. Se la funzione f (x, y) e le sue derivate parziali sono definite e continue nel punto M (x, y) e nei suoi dintorni, allora vale la seguente relazione:

Quelli. le derivate parziali di ordini superiori non dipendono dall'ordine di differenziazione.

I differenziali di ordini superiori sono definiti in modo simile.

…………………

Qui n è il grado simbolico della derivata, con il quale viene sostituito il grado reale dopo aver elevato l'espressione tra parentesi.

Il significato geometrico del differenziale totale di una funzione di due variabili f (x, y) nel punto (x 0, y 0) è l'incremento dell'applicata (coordinata z) del piano tangente alla superficie quando passa dalla punto (x 0, y 0) al punto (x 0 + Dx, y 0 + Dy).

Derivati ​​parziali di ordini superiori. : Se la funzione f (x, y) è definita in qualche dominio D, allora anche le sue derivate parziali saranno definite nello stesso dominio o parte di esso. Chiameremo queste derivate derivate parziali del primo ordine.

Le derivate di queste funzioni saranno derivate parziali del secondo ordine.

Continuando a differenziare le uguaglianze ottenute, si ottengono derivate parziali di ordine superiore. Definizione. Derivate parziali della forma eccetera. sono detti derivati ​​misti. Teorema di Schwarz:

Se le derivate parziali di ordine superiore delle f.m.s. sono derivate continue, quindi miste dello stesso ordine, che differiscono solo nell'ordine di differenziazione = tra loro.

Qui n è il grado simbolico della derivata, con il quale viene sostituito il grado reale dopo aver elevato l'espressione tra parentesi.

14. Equazione del piano tangente e della normale alla superficie!

Siano N e N 0 punti della superficie data. Tracciamo una linea retta NN 0. Il piano che passa per il punto N 0 si chiama piano tangente alla superficie, se l'angolo tra la secante NN 0 e questo piano tende a zero, quando la distanza NN 0 tende a zero.

Definizione. Normale alla superficie nel punto N 0 è una retta passante per il punto N 0 perpendicolare al piano tangente a questa superficie.

In qualsiasi punto, la superficie ha un solo piano tangente o non lo ha affatto.

Se la superficie è data dall'equazione z = f (x, y), dove f (x, y) è una funzione derivabile nel punto M 0 (x 0, y 0), piano tangente nel punto N 0 (x 0, y 0, (x 0, y 0)) esiste e ha l'equazione:

L'equazione della normale alla superficie in questo punto:

significato geometrico il differenziale totale della funzione di due variabili f (x, y) nel punto (x 0, y 0) è l'incremento dell'applicata (coordinata z) del piano tangente alla superficie nel passaggio dal punto (x 0 , y 0) fino al punto (x 0 + Dx, y 0 + Dy).

Come puoi vedere, il significato geometrico del differenziale totale di una funzione di due variabili è un analogo spaziale del significato geometrico del differenziale di una funzione di una variabile.

16. Campo scalare e sue caratteristiche.Linee Ur-ny, derivate in direzione, gradiente di campo scalare.

Se a ogni punto dello spazio viene assegnata una quantità scalare, appare un campo scalare (ad esempio, un campo di temperatura, un campo di potenziale elettrico). Se vengono immesse coordinate cartesiane, indicano anche o Il campo può essere piatto se al centro (sferico) se cilindrico se

Superfici e linee di livello: le proprietà dei campi scalari possono essere visualizzate utilizzando le superfici di livello. Sono superfici nello spazio su cui assume un valore costante. La loro equazione è: ... In un campo scalare piatto, le linee di livello sono curve sulle quali il campo assume un valore costante: In alcuni casi, le linee di livello possono degenerare in punti e le superfici di livello in punti e curve.

Derivata direzionale e gradiente di campo scalare:

Sia il vettore unitario con coordinate un campo scalare. La derivata direzionale caratterizza il cambiamento nel campo in una data direzione ed è calcolata dalla formula La derivata direzionale è il prodotto scalare di un vettore e un vettore con coordinate , che è chiamato gradiente della funzione ed è indicato , dove l'angolo è compreso tra e, quindi il vettore indica la direzione dell'aumento più rapido nel campo e il suo modulo è uguale alla derivata in questa direzione. Poiché le componenti del gradiente sono derivate parziali, non è difficile ottenere le seguenti proprietà del gradiente:

17. Estremi di un FMT Estremi locali di un FMT, condizioni necessarie e sufficienti per la sua esistenza. Il più grande e il più piccolo f.m.p. in sfaccettato zona chiusa.

Sia definita la funzione z = ƒ (x; y) in qualche dominio D, il punto N (x0; y0)

Un punto (x0; y0) si dice punto di massimo della funzione z = ƒ (x; y) se esiste un d-vicinato del punto (x0; y0) tale che per ogni punto (x; y) diverso da (xo; yo), da questo intorno la disuguaglianza ƒ (x; y)<ƒ(хо;уо). Аналогично определяется точка минимума функции: для всех точек (х; у), отличных от (х0;у0), из d-окрестности точки (хо;уо) выполняется неравенство: ƒ(х;у)>(x0; y0). Il valore di una funzione nel punto di massimo (minimo) è chiamato massimo (minimo) della funzione. Il massimo e il minimo di una funzione sono detti estremi. Si noti che, per definizione, il punto estremo della funzione si trova all'interno del dominio della funzione; il massimo e il minimo hanno un carattere locale (locale): il valore della funzione nel punto (x0; y0) viene confrontato con i suoi valori nei punti sufficientemente vicini a (x0; y0). Nell'area D, la funzione può avere più estremi o nessuno.

Condizioni necessarie (1) e sufficienti (2) per l'esistenza:

(1) Se nel punto N (x0; y0) la funzione derivabile z = ƒ (x; y) ha un estremo, allora le sue derivate parziali in questo punto sono uguali a zero: ƒ "x (x0; y0) = 0, ƒ" y (x0; y0 ) = 0. Commento. La funzione può avere un estremo nei punti in cui non esiste almeno una delle derivate parziali. Il punto in cui le derivate parziali del primo ordine della funzione z ≈ ƒ (x; y) sono uguali a zero, cioè f "x = 0, f" y = 0, è chiamato punto stazionario della funzione z.

I punti stazionari e i punti in cui non esiste almeno una derivata parziale sono detti punti critici.

(2) Supponiamo che in un punto stazionario (xo; yo) e in qualche suo intorno la funzione (x; y) abbia derivate parziali continue fino al secondo ordine compreso. Calcoliamo al punto (x0; y0) i valori A = f "" xx (x0; y0), B = ƒ "" xy (x0; y0), C = ƒ "" yy (x0; y0). indichiamo Poi:

1.se Δ> 0, allora la funzione ƒ (x; y) nel punto (x0; y0) ha un estremo: massimo se A< 0; минимум, если А > 0;

2.se< 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.

3. Nel caso Δ = 0, l'estremo nel punto (x0; y0) può esistere o meno. Sono necessarie ulteriori ricerche.

$ E \ sottoinsieme \ mathbb (R) ^ (n) $. Si dice che $ F $ abbia massimo locale al punto $ x_ (0) \ in E $, se esiste un intorno $ U $ del punto $ x_ (0) $ tale che per ogni $ x \ in U $ la disuguaglianza $ f \ left (x \ right ) \ leqslant f \ sinistra (x_ (0) \ destra) $.

Il massimo locale si chiama severa se il quartiere $ U $ può essere scelto in modo che per tutti $ x \ in U $ diversi da $ x_ (0) $, ci sia $ f \ left (x \ right)< f\left(x_{0}\right)$.

Definizione
Sia $ f $ una funzione reale sull'insieme aperto $ E \ subset \ mathbb (R) ^ (n) $. Si dice che $ F $ abbia minimo locale al punto $ x_ (0) \ in E $, se esiste un intorno $ U $ del punto $ x_ (0) $ tale che per ogni $ x \ in U $ la disuguaglianza $ f \ left (x \ right ) \ geqslant f \ sinistra (x_ (0) \ destra) $.

Un minimo locale è detto rigoroso se l'intorno $ U $ può essere scelto in modo tale che per tutti $ x \ in U $ diversi da $ x_ (0) $, $ f \ left (x \ right)> f \ left (x_ ( 0) \ destra) $.

L'estremo locale combina i concetti di minimo locale e massimo locale.

Teorema ( condizione necessaria estremo della funzione differenziabile)
Sia $ f $ una funzione reale sull'insieme aperto $ E \ subset \ mathbb (R) ^ (n) $. Se al punto $ x_ (0) \ in E $ la funzione $ f $ ha un estremo locale a questo punto, allora $$ \ text (d) f \ left (x_ (0) \ right) = 0. $$ L'uguaglianza a zero differenziale è equivalente al fatto che tutti sono uguali a zero, cioè $$ \ displaystyle \ frac (\ partial f) (\ partial x_ (i)) \ left (x_ (0) \ right) = 0. $$

Nel caso unidimensionale, lo è. Indichiamo $ \ phi \ left (t \ right) = f \ left (x_ (0) + th \ right) $, dove $ h $ è un vettore arbitrario. La funzione $ \ phi $ è definita per valori sufficientemente piccoli di $ t $ in valore assoluto. Inoltre, da, è differenziabile e $ (\ phi) '\ left (t \ right) = \ text (d) f \ left (x_ (0) + th \ right) h $.
Sia $ f $ un massimo locale nel punto x $ 0 $. Quindi, la funzione $ \ phi $ per $ t = 0 $ ha un massimo locale e, per il teorema di Fermat, $ (\ phi) '\ left (0 \ right) = 0 $.
Quindi, abbiamo ottenuto $ df \ left (x_ (0) \ right) = 0 $, ad es. della funzione $ f $ nel punto $ x_ (0) $ è uguale a zero su qualsiasi vettore $ h $.

Definizione
Punti in cui il differenziale è zero, ad es. quelle in cui tutte le derivate parziali sono uguali a zero si dicono stazionarie. Punti critici la funzione $ f $ è chiamata tali punti in cui $ f $ non è derivabile o è uguale a zero. Se il punto è stazionario, ciò non significa ancora che la funzione abbia un estremo in questo punto.

Esempio 1.
Sia $ f \ sinistra (x, y \ destra) = x ^ (3) + y ^ (3) $. Allora $ \ displaystyle \ frac (\ partial f) (\ partial x) = 3 \ cdot x ^ (2) $, $ \ displaystyle \ frac (\ partial f) (\ partial y) = 3 \ cdot y ^ (2 ) $, quindi $ \ left (0,0 \ right) $ è un punto stazionario, ma a questo punto la funzione non ha estremi. Infatti, $ f \ left (0,0 \ right) = 0 $, ma è facile vedere che in qualsiasi intorno del punto $ \ left (0,0 \ right) $ la funzione assume valori sia positivi che negativi.

Esempio 2.
La funzione $ f \ left (x, y \ right) = x ^ (2) - y ^ (2) $ ha origine come punto stazionario, ma è chiaro che non c'è estremo a questo punto.

Teorema (condizione sufficiente per un estremo).
Sia la funzione $ f $ derivabile due volte in modo continuo sull'insieme aperto $ E \ subset \ mathbb (R) ^ (n) $. Sia $ x_ (0) \ in E $ un punto stazionario e $$ \ displaystyle Q_ (x_ (0)) \ left (h \ right) \ equiv \ sum_ (i = 1) ^ n \ sum_ (j = 1 ) ^ n \ frac (\ parziale ^ (2) f) (\ parziale x_ (i) \ parziale x_ (j)) \ sinistra (x_ (0) \ destra) h ^ (i) h ^ (j). $ $ Allora

1. se $ Q_ (x_ (0)) $ -, allora la funzione $ f $ nel punto $ x_ (0) $ ha un estremo locale, cioè un minimo se la forma è definita positiva e un massimo se la forma è definito negativo;
2. se la forma quadratica $ Q_ (x_ (0)) $ non è definita, la funzione $ f $ nel punto $ x_ (0) $ non ha estremo.

Usiamo lo sviluppo secondo la formula di Taylor (12.7 p. 292). Tenendo conto che le derivate parziali del primo ordine nel punto $ x_ (0) $ sono uguali a zero, si ottiene $$ \ displaystyle f \ left (x_ (0) + h \ right) −f \ left (x_ (0) \ destra) = \ frac (1) (2) \ somma_ (i = 1) ^ n \ somma_ (j = 1) ^ n \ frac (\ parziale ^ (2) f) (\ parziale x_ (i ) \ partial x_ (j)) \ left (x_ (0) + \ theta h \ right) h ^ (i) h ^ (j), $$ dove $ 0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0 $ e $ \ epsilon \ left (h \ right) \ rightarrow 0 $ per $ h \ rightarrow 0 $, allora il membro di destra sarà positivo per qualsiasi vettore $ h $ di lunghezza sufficientemente piccola.
Quindi, siamo giunti alla conclusione che in qualche intorno del punto $ x_ (0) $ vale la disuguaglianza $ f \ left (x \ right)> f \ left (x_ (0) \ right) $, se solo $ x \ neq x_ (0) $ (mettiamo $ x = x_ (0) + h $ \ right). Questo significa che al punto $ x_ (0) $ la funzione ha un minimo locale stretto, e quindi la prima parte del nostro teorema è dimostrata.
Supponiamo ora che $ Q_ (x_ (0)) $ sia una forma indefinita. Allora ci sono vettori $ h_ (1) $, $ h_ (2) $ tali che $ Q_ (x_ (0)) \ left (h_ (1) \ right) = \ lambda_ (1)> 0 $, $ Q_ ( x_ (0)) \ sinistra (h_ (2) \ destra) = \ lambda_ (2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 $. Quindi otteniamo $$ f \ left (x_ (0) + th_ (1) \ right) −f \ left (x_ (0) \ right) = \ frac (1) (2) \ left [t ^ (2) \ lambda_ (1) + t ^ (2) | h_ (1) | ^ (2) \ epsilon \ left (th_ (1) \ right) \ right] = \ frac (1) (2) t ^ (2) \ left [\ lambda_ (1) + | h_ (1) | ^ (2) \ epsilon \ left (th_ (1) \ right) \ right]. $$ Per $ t> 0 $ sufficientemente piccoli il lato destro è positivo. Ciò significa che in qualsiasi intorno del punto $ x_ (0) $ la funzione $ f $ assume valori $ f \ left (x \ right) $ che sono maggiori di $ f \ left (x_ (0) \ right) $.
Analogamente, si ottiene che in qualsiasi intorno del punto $ x_ (0) $ la funzione $ f $ assume valori inferiori a $ f \ left (x_ (0) \ right) $. Questo, insieme al precedente, significa che al punto $ x_ (0) $ la funzione $ f $ non ha estremi.

Tenere conto caso speciale di questo teorema per la funzione $ f \ left (x, y \ right) $ di due variabili, definita in qualche intorno del punto $ \ left (x_ (0), y_ (0) \ right) $ e avente parziale continuo derivate del primo e del secondo ordine. Supponiamo che $ \ left (x_ (0), y_ (0) \ right) $ sia un punto stazionario e indichi $$ \ displaystyle a_ (11) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ sinistra (x_ (0), y_ (0) \ destra), a_ (12) = \ frac (\ parziale ^ (2) f) (\ parziale x \ parziale y) \ sinistra (x_ ( 0 ), y_ (0) \ destra), a_ (22) = \ frac (\ parziale ^ (2) f) (\ parziale y ^ (2)) \ sinistra (x_ (0), y_ (0) \ destra ) $$ Allora il teorema precedente assume la forma seguente.

Teorema
Sia $ \ Delta = a_ (11) \ cdot a_ (22) - a_ (12) ^ 2 $. Poi:

1. se $ \ Delta> 0 $, allora la funzione $ f $ ha un estremo locale nel punto $ \ left (x_ (0), y_ (0) \ right) $, cioè un minimo se $ a_ (11)> 0 $ e massimo se $ a_ (11)<0$;
2. se $ \ Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.

Esempi di problem solving

Algoritmo per trovare l'estremo di una funzione di più variabili:

1. Trova punti stazionari;
2. Trova il differenziale del 2° ordine in tutti i punti stazionari
3. Usando la condizione sufficiente per l'estremo di una funzione di più variabili, consideriamo il differenziale del secondo ordine in ogni punto stazionario

1. Esaminare la funzione per l'estremo $ f \ left (x, y \ right) = x ^ (3) + 8 \ cdot y ^ (3) + 18 \ cdot x - 30 \ cdot y $.
   Soluzione

   Trova le derivate parziali del 1° ordine: $$ \ displaystyle \ frac (\ partial f) (\ partial x) = 3 \ cdot x ^ (2) - 6 \ cdot y; $$ $$ \ displaystyle \ frac (\ partial f ) (\ partial y) = 24 \ cdot y ^ (2) - 6 \ cdot x. $$ Componiamo e risolviamo il sistema: $$ \ displaystyle \ begin (cases) \ frac (\ partial f) (\ partial x) ) = 0 \\\ frac (\ parziale f) (\ parziale y) = 0 \ fine (casi) \ Freccia destra \ inizio (casi) 3 \ cdot x ^ (2) - 6 \ cdot y = 0 \\ 24 \ cdot y ^ (2) - 6 \ cdot x = 0 \ fine (casi) \ Freccia destra \ inizio (casi) x ^ (2) - 2 \ cdot y = 0 \\ 4 \ cdot y ^ (2) - x = 0 \ end (casi) $$ Dalla 2a equazione, esprimi $ x = 4 \ cdot y ^ (2) $ - sostituisci nella 1a equazione: $$ \ displaystyle \ left (4 \ cdot y ^ (2) \ right ) ^ (2) -2 \ cdot y = 0 $$ $$ 16 \ cdot y ^ (4) - 2 \ cdot y = 0 $$ $$ 8 \ cdot y ^ (4) - y = 0 $$ $ $ y \ left (8 \ cdot y ^ (3) -1 \ right) = 0 $$ Di conseguenza, si ottengono 2 punti stazionari:
   1) $ y = 0 \ Freccia destra x = 0, M_ (1) = \ sinistra (0, 0 \ destra) $;
   2) $ \ displaystyle 8 \ cdot y ^ (3) -1 = 0 \ Rightarrow y ^ (3) = \ frac (1) (8) \ Rightarrow y = \ frac (1) (2) \ Rightarrow x = 1 , M_ (2) = \ sinistra (\ frac (1) (2), 1 \ destra) $
   Verifichiamo il soddisfacimento della condizione sufficiente per un estremo:
   $$ \ displaystyle \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) = 6 \ cdot x; \ frac (\ parziale ^ (2) f) (\ parziale x \ parziale y) = - 6; \ frac (\ parziale ^ (2) f) (\ parziale y ^ (2)) = 48 \ cdot y $$
   1) Per il punto $ M_ (1) = \ sinistra (0,0 \ destra) $:
   $$ \ displaystyle A_ (1) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (0,0 \ right) = 0; B_ (1) = \ frac (\ parziale ^ (2) f) (\ parziale x \ parziale y) \ sinistra (0,0 \ destra) = - 6; C_ (1) = \ frac (\ parziale ^ (2) f) (\ parziale y ^ (2)) \ sinistra (0,0 \ destra) = 0; $$
   $ A_ (1) \ cdot B_ (1) - C_ (1) ^ (2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
   2) Per il punto $ M_ (2) $:
   $$ \ displaystyle A_ (2) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (1, \ frac (1) (2) \ right) = 6; B_ (2) = \ frac (\ parziale ^ (2) f) (\ parziale x \ parziale y) \ sinistra (1, \ frac (1) (2) \ destra) = - 6; C_ (2) = \ frac (\ parziale ^ (2) f) (\ parziale y ^ (2)) \ sinistra (1, \ frac (1) (2) \ destra) = 24; $$
   $ A_ (2) \ cdot B_ (2) - C_ (2) ^ (2) = 108> 0 $, quindi c'è un estremo nel punto $ M_ (2) $, e poiché $ A_ (2)> 0 $, allora questo è il minimo.
   Risposta: Il punto $ \ displaystyle M_ (2) \ left (1, \ frac (1) (2) \ right) $ è il punto minimo della funzione $ f $.
   

2. Esaminare la funzione per l'estremo $ f = y ^ (2) + 2 \ cdot x \ cdot y - 4 \ cdot x - 2 \ cdot y - 3 $.
   Soluzione

   Trova punti stazionari: $$ \ displaystyle \ frac (\ partial f) (\ partial x) = 2 \ cdot y - 4; $$ $$ \ displaystyle \ frac (\ partial f) (\ partial y) = 2 \ cdot y + 2 \ cdot x - 2. $$
   Componiamo e risolviamo il sistema: $$ \ displaystyle \ inizio (casi) \ frac (\ parziale f) (\ parziale x) = 0 \\\ frac (\ parziale f) (\ parziale y) = 0 \ fine (casi ) \ Freccia destra \ inizio (casi) 2 \ cdot y - 4 = 0 \\ 2 \ cdot y + 2 \ cdot x - 2 = 0 \ fine (casi) \ Freccia destra \ inizio (casi) y = 2 \\ y + x = 1 \ fine (casi) \ Freccia destra x = -1 $$
   $ M_ (0) \ left (-1, 2 \ right) $ è un punto stazionario.
   Verifichiamo che sia soddisfatta la condizione di estremo sufficiente: $$ \ displaystyle A = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (-1,2 \ right) = 0; B = \ frac (\ parziale ^ (2) f) (\ parziale x \ parziale y) \ sinistra (-1,2 \ destra) = 2; C = \ frac (\ parziale ^ (2) f) (\ parziale y ^ (2)) \ sinistra (-1,2 \ destra) = 2; $$
   $ A \ cdot B - C ^ (2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
   Risposta: non ci sono estremi.
   

Limite di tempo: 0

Navigazione (solo numeri di lavoro)

0 di 4 domande completate

Informazione

Rispondi a questo quiz per verificare la tua conoscenza dell'argomento che hai appena letto, "Estremi locali di funzioni di molte variabili".

Hai già fatto il test prima. Non puoi riavviarlo.

Il test si sta caricando...

Devi effettuare il login o registrarti per iniziare il test.

È necessario completare i seguenti test per iniziare questo:

risultati

Risposte corrette: 0 su 4

Il tuo tempo:

Il tempo è finito

Hai totalizzato 0 punti su 0 (0)

Il tuo risultato è stato registrato nella classifica

1. Con la risposta
2. Contrassegnato come visualizzato

Compito 1 di 4

1 .

Punti: 1

Esaminare la funzione $ f $ per extrema: $ f = e ^ (x + y) (x ^ (2) -2 \ cdot y ^ (2)) $

Destra


Non proprio


1. Domanda 2 di 4

   2 .

   Punti: 1

   La funzione $ f = 4 + \ sqrt ((x ^ (2) + y ^ (2)) ^ (2)) $

   Destra

Per una funzione di una variabile sì = F(X) al punto X 0 per significato geometrico del differenziale si intende l'incremento dell'ordinata della tangente tracciata al grafico della funzione nel punto con l'ascissa X 0 quando vado a puntare X 0 +  X... E il differenziale di una funzione di due variabili in questo senso è l'incremento applicativi tangente aereo disegnato sulla superficie data dall'equazione z = F(X, sì) , al punto m 0 (X 0 , sì 0 ) quando vado a puntare m(X 0 +  X, sì 0 +  sì). Diamo la definizione del piano tangente ad una superficie:

Df . Piano passante per un punto R 0 superficie Sè chiamato piano tangente in un dato punto, se l'angolo tra questo piano e la secante passante per due punti R 0 e R(qualsiasi punto sulla superficie S) , tende a zero quando il punto R tende lungo questa superficie fino al punto R 0 .

Lascia che la superficie S data dall'equazione z = F(X, sì). Allora si può dimostrare che questa superficie ha nel punto P 0 (X 0 , sì 0 , z 0 ) il piano tangente se e solo se la funzione z = F(X, sì) differenziabile a questo punto. In questo caso, il piano tangente è dato dall'equazione:

z – z 0 = +
(6).

§5. Derivata direzionale, gradiente della funzione.

Derivate parziali di una funzione sì= F(X 1 , X 2 .. X n ) per variabili X 1 , X 2 . . . X n esprimere la velocità di variazione della funzione nella direzione degli assi delle coordinate. Ad esempio, è il tasso di variazione della funzione per X 1 - cioè si assume che il punto appartenente al dominio della definizione della funzione si muova solo parallelamente all'asse OH 1 , e tutte le altre coordinate rimangono invariate. Tuttavia, si può presumere che la funzione possa anche cambiare in qualche altra direzione, che non coincide con la direzione di nessuno degli assi.

Consideriamo una funzione di tre variabili: tu= F(X, sì, z).

Fissa il punto m 0 (X 0 , sì 0 , z 0 ) e qualche linea retta direzionale (asse) io passando per questo punto. Permettere M (X, sì, z) è un punto arbitrario di questa retta e m 0 m- distanza da m 0 prima di M.

tu = F (X, sì, z) – F(X 0 , sì 0 , z 0 ) - l'incremento della funzione nel punto m 0 .

Trova il rapporto tra l'incremento della funzione e la lunghezza del vettore
:

Df . Funzione derivata tu = F (X, sì, z) verso qualcosa io al punto m 0 è il limite del rapporto tra l'incremento della funzione e la lunghezza del vettore m 0 m quando quest'ultimo tende a 0 (o, che è la stessa cosa, quando il m a m 0 ):

(1)

Questa derivata caratterizza la velocità di variazione della funzione nel punto m 0 nella direzione io.

Lascia che l'asse io (vettore m 0 m) forme con assi BUE, OY, OZ angoli
rispettivamente.

Indica x-x 0 =
;

y - y 0 =
;

z - z 0 =
.

Allora il vettore m 0 M = (X - X 0 , sì - sì 0 , z - z 0 )=
e i suoi coseni di direzione:

;

;

.

(4).

(4) è la formula per calcolare la derivata direzionale.

Consideriamo un vettore le cui coordinate sono le derivate parziali della funzione tu= F(X, sì, z) al punto m 0 :

laurea tu - funzione gradiente tu= F(X, sì, z) al punto M (X, sì, z)

Proprietà del gradiente:

Conclusione: lunghezza del gradiente della funzione tu= F(X, sì, z) - c'è il maggior valore possibile a questo punto M (X, sì, z) , e la direzione del vettore laurea tu coincide con la direzione del vettore uscente dal punto m lungo il quale la funzione cambia più velocemente. Cioè, la direzione del gradiente della funzione laurea tu - c'è la direzione dell'aumento più ripido della funzione.

CALCOLO DIFFERENZIALE DI FUNZIONI DI PIU' VARIABILI.

Concetti di base e definizioni.

Quando si considerano funzioni di più variabili, ci si limita a una descrizione dettagliata delle funzioni di due variabili, poiché tutti i risultati ottenuti saranno validi per funzioni di un numero arbitrario di variabili.

Se, secondo una regola, uno o più valori della variabile z sono assegnati a ciascuna coppia di numeri indipendenti (x, y) da un certo insieme, allora viene chiamata la variabile z funzione di due variabili.

Se una coppia di numeri (x, y) corrisponde a un valore z, allora la funzione viene chiamata inequivocabile, e se più di uno, allora - ambiguo.

Lo scopo di la funzione z è chiamata l'insieme di coppie (x, y) per cui esiste la funzione z.

La vicinanza del punto 0 (x 0, y 0) di raggio r è detto insieme di tutti i punti (x, y) che soddisfano la condizione.

Il numero A si chiama limite funzione f (x, y) in quanto il punto M (x, y) tende al punto M 0 (x 0, y 0), se per ogni numero e> 0 esiste un numero r> 0 tale che per ogni punto M (x, y) per cui la condizione

la condizione .

Scrivono:

Sia il punto М 0 (x 0, y 0) appartenga al dominio di definizione della funzione f (x, y). Allora si chiama la funzione z = f (x, y) continuo al punto М 0 (x 0, y 0), se

(1)

inoltre, il punto M (x, y) tende al punto M 0 (x 0, y 0) in modo arbitrario.

Se in qualsiasi punto la condizione (1) non è soddisfatta, allora questo punto è chiamato punto di rottura funzione f (x, y). Questo può essere nei seguenti casi:

1) La funzione z = f (x, y) non è definita nel punto M 0 (x 0, y 0).

2) Non c'è limite.

3) Questo limite esiste, ma non è uguale a f (x 0, y 0).

Proprietà delle funzioni di più variabili relative alla loro continuità.

Proprietà. Se la funzione f (x, y, ...) è definita e continua in un dominio D chiuso e limitato, allora in questo dominio esiste almeno un punto

N (x 0, y 0, ...), tale che i punti rimanenti soddisfino la disuguaglianza

f (x 0, y 0, ...) ³ f (x, y, ...)

e anche il punto N 1 (x 01, y 01, ...), tale che per tutti gli altri punti la disuguaglianza

f (x 01, y 01, ...) £ f (x, y, ...)

allora f (x 0, y 0, ...) = M - maggior valore funzioni, e f (x 01, y 01, ...) = m - valore più piccolo funzione f (x, y, ...) nel dominio D.

Una funzione continua in un dominio chiuso e limitato D raggiunge almeno una volta il valore più grande e una volta il più piccolo.

Proprietà. Se la funzione f (x, y, ...) è definita e continua in un dominio chiuso D, e M e m sono rispettivamente i valori più grande e più piccolo della funzione in questo dominio, quindi per qualsiasi punto m c'è un punto

N 0 (x 0, y 0,…) tale che f (x 0, y 0,…) = m.

In poche parole, una funzione continua accetta nel dominio D tutti i valori intermedi tra M e m. Una conseguenza di questa proprietà può essere la conclusione che se i numeri M e m sono di segno opposto, allora nel dominio D la funzione si annulla almeno una volta.

Proprietà. La funzione f (x, y, ...), continua in un dominio chiuso D, limitato in questa regione, se esiste un numero K tale che per tutti i punti della regione la disuguaglianza .

Proprietà. Se la funzione f (x, y, ...) è definita e continua in un dominio chiuso D, allora uniformemente continuo in questa zona, cioè per ogni numero positivo e esiste un numero D > 0 tale che per due punti qualsiasi (x 1, y 1) e (x 2, y 2) della regione situata a distanza minore di D, la disuguaglianza

2. Derivate parziali. Derivati ​​parziali di ordini superiori.

Sia data la funzione z = f (x, y) in qualche dominio. Prendi un punto arbitrario M (x, y) e imposta l'incremento Dx alla variabile x. Quindi viene chiamata la quantità D x z = f (x + Dx, y) - f (x, y) dall'incremento parziale della funzione rispetto a x.

Tu puoi scrivere

.

poi chiamato derivata parziale funzioni z = f (x, y) in x.

Designazione:

Analogamente si definisce la derivata parziale della funzione rispetto a y.

significato geometrico la derivata parziale (ad esempio) è la tangente dell'angolo di inclinazione della tangente tracciata nel punto N 0 (x 0, y 0, z 0) alla sezione della superficie per il piano y = y 0.

Se la funzione f (x, y) è definita in qualche dominio D, allora anche le sue derivate parziali saranno definite nello stesso dominio o parte di esso.

Chiameremo questi derivati derivate parziali del primo ordine.

Le derivate di queste funzioni saranno derivate parziali del secondo ordine.

Continuando a differenziare le uguaglianze ottenute, si ottengono derivate parziali di ordine superiore.

Derivate parziali della forma eccetera. sono chiamati derivati ​​misti.

Teorema. Se la funzione f (x, y) e le sue derivate parziali sono definite e continue nel punto M (x, y) e nei suoi dintorni, allora vale la seguente relazione:

Quelli. le derivate parziali di ordini superiori non dipendono dall'ordine di differenziazione.

I differenziali di ordini superiori sono definiti in modo simile.

…………………

Qui n è il grado simbolico della derivata, con il quale viene sostituito il grado reale dopo aver elevato l'espressione tra parentesi.

Differenziale completo. significato geometrico differenziale completo. Piano tangente e normale alla superficie.

L'espressione si chiama incremento completo funzioni f (x, y) ad un certo punto (x, y), dove a 1 e a 2 sono funzioni infinitesime come Dх ® 0 e Dу ® 0, rispettivamente.

Differenziale completo la funzione z = f (x, y) è detta parte lineare principale rispetto a Dx e Dy dell'incremento della funzione Dz nel punto (x, y).

Per una funzione di un numero arbitrario di variabili:

Esempio 3.1. Trova il differenziale totale della funzione.