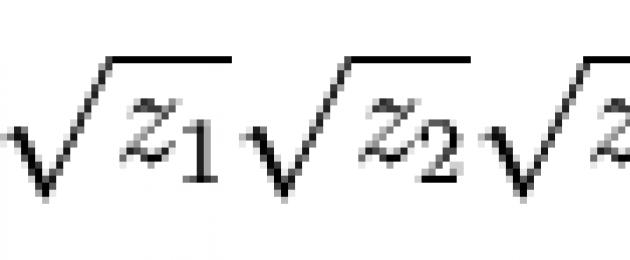Vai sul canale youtube del nostro sito per rimanere sempre aggiornato su tutte le nuove video lezioni.
Per prima cosa ricordiamo le formule base dei poteri e le loro proprietà.
Prodotto di un numero UN ricorre su se stesso n volte, possiamo scrivere questa espressione come a a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. un n / un m = un n - m
Potenza o equazioni esponenziali – si tratta di equazioni in cui le variabili sono espresse in potenze (o esponenti) e la base è un numero.
Esempi di equazioni esponenziali:
In questo esempio, il numero 6 è la base; è sempre in basso e la variabile X grado o indicatore.
Diamo altri esempi di equazioni esponenziali.
2x*5=10
16 x - 4 x - 6=0
Ora diamo un'occhiata a come vengono risolte le equazioni esponenziali?
Prendiamo una semplice equazione:
2 x = 2 3
Questo esempio può essere risolto anche nella tua testa. Si può vedere che x=3. Dopotutto, in modo che la sinistra e parte destra fossero uguali, è necessario sostituire x con il numero 3.
Vediamo ora come formalizzare questa decisione:
2 x = 2 3
x = 3
Per risolvere tale equazione, abbiamo rimosso motivi identici(cioè due) e ho scritto ciò che restava, questi sono i gradi. Abbiamo ottenuto la risposta che cercavamo.
Ora riassumiamo la nostra decisione.
Algoritmo per risolvere l'equazione esponenziale:
1. È necessario controllare lo stesso se l'equazione ha basi a destra e a sinistra. Se i motivi non sono gli stessi, stiamo cercando opzioni per risolvere questo esempio.
2. Dopo che le basi diventano le stesse, equiparare gradi e risolvere la nuova equazione risultante.
Ora diamo un'occhiata ad alcuni esempi:
Cominciamo con qualcosa di semplice.
Le basi sui lati sinistro e destro sono uguali al numero 2, il che significa che possiamo scartare la base e uguagliare i loro gradi.
x+2=4 Si ottiene l'equazione più semplice.
x=4 – 2
x=2
Risposta: x=2
Nell'esempio seguente puoi vedere che le basi sono diverse: 3 e 9.
3 3x - 9x+8 = 0
Per prima cosa, spostiamo i nove sul lato destro, otteniamo:
Ora devi creare le stesse basi. Sappiamo che 9=3 2. Usiamo la formula della potenza (a n) m = a nm.
3 3x = (3 2)x+8
Otteniamo 9 x+8 =(3 2) x+8 =3 2x+16
3 3x = 3 2x+16 Ora è chiaro che sui lati sinistro e destro le basi sono uguali e uguali a tre, il che significa che possiamo scartarle e uguagliare i gradi.
3x=2x+16 otteniamo l'equazione più semplice
3x - 2x=16
x=16
Risposta: x=16.
Diamo un'occhiata al seguente esempio:
2 2x+4 - 10 4 x = 2 4
Prima di tutto, guardiamo le basi, basi due e quattro. E abbiamo bisogno che siano uguali. Trasformiamo i quattro usando la formula (a n) m = a nm.
4 x = (2 2) x = 2 2x
E usiamo anche una formula a n a m = a n + m:
2 2x+4 = 2 2x 2 4
Aggiungi all'equazione:
2 2x 2 4 - 10 2 2x = 24
Abbiamo fatto un esempio per gli stessi motivi. Ma gli altri numeri 10 e 24 ci danno fastidio. Cosa farne? Se guardi da vicino puoi vedere che sul lato sinistro abbiamo 2 2x ripetuti, ecco la risposta: possiamo mettere 2 2x tra parentesi:
2 2x (2 4 - 10) = 24
Calcoliamo l'espressione tra parentesi:
2 4 — 10 = 16 — 10 = 6
Dividiamo l'intera equazione per 6:
Immaginiamo 4=2 2:
2 2x = 2 2 basi sono uguali, le scartiamo e uguagliamo i gradi.
2x = 2 è l'equazione più semplice. Dividilo per 2 e otteniamo
x = 1
Risposta: x = 1.
Risolviamo l'equazione:
9 x – 12*3 x +27= 0
Trasformiamo:
9 x = (3 2) x = 3 2x
Otteniamo l'equazione:
3 2x - 12 3 x +27 = 0
Le nostre basi sono uguali, pari a tre. In questo esempio puoi vedere che le prime tre hanno un grado doppio (2x) della seconda (solo x). In questo caso puoi risolvere metodo di sostituzione. Sostituiamo il numero con il grado più piccolo:
Allora 3 2x = (3 x) 2 = t 2
Sostituiamo tutte le potenze x nell'equazione con t:
t2 - 12t+27 = 0
Noi abbiamo equazione quadrata. Risolvendo attraverso il discriminante otteniamo:
D=144-108=36
t1 = 9
t2 = 3
Ritornando alla variabile X.
Prendi t1:
t1 = 9 = 3x
Questo è,
3 x = 9
3 x = 3 2
x1 = 2
È stata trovata una radice. Cerchiamo il secondo da t 2:
t2 = 3 = 3x
3 x = 3 1
x2 = 1
Risposta: x1 = 2; x2 = 1.
Sul sito puoi porre domande di tuo interesse nella sezione AIUTA A DECIDERE, ti risponderemo sicuramente.
Unisciti al gruppo
Soluzione di Cartesio-Eulero
Effettuata la sostituzione, otteniamo un'equazione nella seguente forma (è detta “incompleta”):
sì 4 + Psì 2 + Qsì + R = 0 .Radici sì 1 , sì 2 , sì 3 , sì 4 di tale equazione equivalgono ad una delle seguenti espressioni:
in cui le combinazioni di caratteri sono selezionate in modo tale da soddisfare la seguente relazione:
,
E z 1 , z 2 e z 3 sono le radici dell'equazione cubica
La soluzione Ferrari
articolo principale: Metodo Ferrari
Rappresentiamo l'equazione di quarto grado nella forma:
UNX 4 + BX 3 + CX 2 + DX + E = 0,La sua soluzione può essere trovata dalle seguenti espressioni:
se β = 0, soluzione tu 4+α tu 2 + γ = 0 e, effettuando la sostituzione 
, troviamo le radici: . 
, (qualsiasi segno radice quadrata andrà bene), (tre radici complesse, una delle quali andrà bene) 
Due ± s devono avere lo stesso segno, ± t - sono indipendenti. Per trovare tutte le radici, devi trovare x per le combinazioni con segno ± s ,± t = +,+ per +,− per −,+ per −,−. Le radici doppie appariranno due volte, le radici triple tre volte e le radici quaternarie quattro volte. L'ordine delle radici dipende da quale radice cubica U selezionato. Guarda anche
- Tipi di equazioni di 4° grado facilmente risolvibili: Equazione biquadratica, equazione reciproca di quarto grado
Letteratura
- Korn G., Korn T. (1974) Manuale di matematica.
Collegamenti
- La decisione di Ferrari
Fondazione Wikimedia. 2010.
Scopri cos'è un'"equazione di quarto grado" in altri dizionari:
Equazione di quarto grado- - [L.G. Dizionario inglese-russo sull'informatica. M.: Impresa statale TsNIIS, 2003.] Argomenti tecnologie dell'informazione in generale EN equazione quartica … Guida del traduttore tecnico
Grafico di un polinomio di 4° grado con quattro radici e tre punti critici. Un'equazione di quarto grado in matematica è un'equazione algebrica della forma: Quarto grado per equazioni algebricheè il più alto a cui... ... Wikipedia
Un'equazione della forma: anxn + an − 1xn − 1 + ... + a1x + a0 = 0 si dice reciproca se i suoi coefficienti in posizioni simmetriche sono uguali, cioè se an − k = ak, per k = 0, 1, ..., n. Indice 1 Equazione del quarto grado ... Wikipedia
In cui il termine sconosciuto è alla quarta potenza. Dizionario completo parole straniere, che sono entrati in uso nella lingua russa. Popov M., 1907. EQUAZIONE DEL BIQUADRO dal lat. bis, due volte, e quadratum, quadrato. Un'equazione in cui il massimo grado... ... Dizionario delle parole straniere della lingua russa
Insieme all'aritmetica c'è la scienza dei numeri e, attraverso i numeri, delle quantità in generale. Entrambe queste scienze, senza studiare le proprietà di quantità definite e concrete, indagano le proprietà delle quantità astratte in quanto tali, indipendentemente da... ... Dizionario enciclopedico F. Brockhaus e I.A. Efron
Un insieme di conoscenze applicate che consente agli ingegneri aeronautici di studiare nel campo dell'aerodinamica, problemi di resistenza, costruzione di motori e dinamica di volo degli aerei (cioè teoria) per creare un nuovo aereo o migliorare... ... Enciclopedia di Collier
La più antica attività matematica era contare. Era necessario un conto per tenere traccia del bestiame e condurre il commercio. Alcune tribù primitive contavano il numero degli oggetti abbinandoli alle varie parti del corpo, principalmente... ... Enciclopedia di Collier
Storia della tecnologia per periodo e regione: rivoluzione neolitica Tecnologie dell'antico Egitto Scienza e tecnologia antica India Scienze e tecnologia antica Cina Tecnologie Grecia antica Tecnologie Antica Roma Tecnologie del mondo islamico... ... Wikipedia
Un'equazione è una relazione matematica che esprime l'uguaglianza di due espressioni algebriche. Se l'uguaglianza è vera per qualcuno valori accettabili incognite incluse in esso, allora si chiama identità; ad esempio, un rapporto della forma... ... Enciclopedia di Collier
Il teorema di Abel Ruffini afferma che l'equazione generale del potere è irrisolvibile nei radicali. Indice 1 Dettagli... Wikipedia
Nel caso generale, la soluzione di un'equazione di quarto grado viene effettuata utilizzando metodi per risolvere equazioni per gradi più alti, ad esempio, con il metodo Ferrari o utilizzando lo schema di Horner. Ma alcune equazioni di 4° grado hanno una soluzione più semplice.
Esistono diversi tipi speciali di equazioni di quarto grado, i metodi per risolverli che imparerai di seguito:
- Equazione biquadratica $ax^4+bx^2+c=0$;
- Equazioni reciproche della forma $ax^4+bx^3+cx^2 +bx+ a=0$;
- Equazioni della forma $ax^4+b=0$.
Risoluzione di equazioni biquadratiche di quarto grado
Le equazioni biquadratiche $ax^4+bx^2+c=0$ vengono ridotte a equazioni quadratiche sostituendo la variabile $x^2$ con una nuova, ad esempio $y$. Dopo la sostituzione, la nuova equazione risultante viene risolta, quindi il valore della variabile trovata viene sostituito nell'equazione $x^2=y$. Il risultato della soluzione saranno le radici dell'equazione $x^2=y$.
Esempio 1
Risolvi l'equazione $x(x-1)(x-2)(x-3)=24$:
Espandiamo le parentesi nel polinomio:
$(x^2-3x)(x^2-3x+2)=24$
In questa forma diventa ovvio che possiamo scegliere l’espressione $y=x^2-3x$ come nuova variabile: sostituiamola:
$y\cpunto (y+2)=24$
Ora risolviamo due equazioni quadratiche $x^2-3x=-4$ e $x^2-3x=-6$.
Le radici della prima equazione sono $x_1(1,2)=4;-1$, la seconda non ha soluzioni.
Risoluzione di equazioni reciproche di grado 4
Queste equazioni della forma $ax^4+bx^3+cx^2 +bx+ a=0$ ripetono con i loro coefficienti per i termini di ordine inferiore i coefficienti per i polinomi di grado superiore. Per risolvere tale equazione, dividila prima per $x^2$:
$ax^4+bx^3+cx^2 +bx+ a=0|:x^2$
$ax^2+bx+c+\frac(b)(x) + \frac(a)(x^2)=0$
$a(x^2+\frac(1)(x^2))+b(x+\frac(1)(x)) + c=0$
Quindi sostituisci $(x+\frac(1)(x))$ con una nuova variabile, quindi $(x^2+\frac(1)(x^2))=y^2-2$, dopo la sostituzione otteniamo il seguente quadrato l'equazione:
$a(y^2-2)+per+c=0$
Successivamente, cerchiamo le radici delle equazioni $x+\frac(1)(x)=y_1$ e $x+\frac(1)(x)=y_2$.
Un metodo simile viene utilizzato per risolvere equazioni reciproche della forma $ax^4+bx^3+cx^2 +kbx+ k^2a=0$.
Esempio 2
Risolvi l'equazione:
$3x^4-2x^3-9x^2-4x+12=0$
Questa equazione è un'equazione reciproca della forma $ax^4+bx^3+cx^2 +kbx+ k^2a=0$. Pertanto, dividiamo l'intera equazione per $x^2$:
$3x^2-2x-9 \cdot \frac(2 \cdot 2)(x)+3 \cdot (\frac(2)(x))^2=0$
$3(x^2+\frac(4)(x^2))-2(x+\frac(2)(x)-9=0$
Sostituiamo l'espressione $x+\frac(2)(x)$: $3(y^2-4)-2y-9=0$
Calcoliamo le radici di questa equazione, sono uguali a $y_1=3$ e $y_2=-\frac(7)(3)$.
Di conseguenza, ora è necessario risolvere due equazioni $x+\frac(2)(x)=3$ e $x+\frac(2)(x)=-\frac(7)(3)$. La soluzione della prima equazione è $x_1=1, x_2=2$, la seconda equazione non ha radici.
Pertanto, le radici dell'equazione originale sono $x_1=1, x_2=2$.
Equazioni della forma $ax^4+b=0$
Le radici di questo tipo di equazione si trovano utilizzando formule di moltiplicazione abbreviate.
Subito dopo che Cardano pubblicò un metodo per risolvere le equazioni cubiche, i suoi studenti e seguaci trovarono il modo di ridurre l'equazione generale del quarto grado a un'equazione cubica. Presentiamo il metodo più semplice, che appartiene a L. Ferrari.
Quando presenterai il metodo, dovrai utilizzare il seguente lemma elementare.
Lemma. In modo da trinomio quadratico fosse il quadrato di un binomio lineare, è necessario e sufficiente che il suo discriminante sia uguale a zero.
Prova. Necessità. Permettere . Quindi Sufficienza. Allora
L'idea del metodo presentato è di presentare il lato sinistro dell'equazione come la differenza di due quadrati. Quindi può essere scomposto in due fattori di secondo grado e la soluzione dell'equazione porterà alla soluzione di due equazioni quadratiche. Per raggiungere l'obiettivo, rappresentiamo il lato sinistro nella forma:
Qui y è un'incognita ausiliaria, che deve essere selezionata in modo che l'espressione tra parentesi quadre risulti essere il quadrato di un binomio lineare. In virtù del lemma, per questo è necessario e sufficiente soddisfare la condizione
Questa condizione è un'equazione di terzo grado rispetto a y. Dopo aver aperto le parentesi, viene convertito nel modulo
Sia una delle radici di questa equazione. Allora la condizione sarà soddisfatta, quindi vale
per alcuni k e I. L'equazione originale assume la forma
Uguagliando ciascuno dei fattori a zero, troveremo le quattro radici dell'equazione originale.
Facciamo ancora un'osservazione. Sia le radici del primo fattore e siano le radici del secondo. Quindi, sommando queste uguaglianze, otteniamo questo
Pertanto, abbiamo ottenuto un'espressione per la radice dell'equazione cubica ausiliaria in termini di radici dell'equazione originale di quarto grado.
Esempio. Risolvi l'equazione. Secondo il metodo sopra descritto, trasformiamo il lato sinistro:
Ora mettiamo . Dopo le formazioni otteniamo l'equazione
È facile vedere che una delle radici di questa equazione è il numero . Sostituendolo nel lato sinistro trasformato dell'equazione originale, otteniamo:
Uguagliando i fattori a zero, otteniamo
Per quanto riguarda le equazioni superiori al quarto grado, erano note alcune classi di equazioni di forma relativamente particolare, che ammettevano soluzioni algebriche in radicali, cioè sotto forma di risultati operazioni aritmetiche e azioni di estrazione delle radici. Tuttavia, i tentativi di fornire soluzioni alle equazioni generali del quinto grado e superiori non hanno avuto successo fino all'inizio del XIX secolo. Ruffini e Abel non hanno dimostrato che una soluzione di questo tipo per equazioni generali superiori al quarto grado sia impossibile. Alla fine, nel 1830, il brillante matematico francese E. Galois riuscì a trovare il necessario e condizioni sufficienti(che sono abbastanza difficili da verificare) per la risolubilità di una specifica equazione in radicali. Allo stesso tempo, Galois creò e utilizzò la teoria dei gruppi di permutazione, nuova per il suo tempo.
2x 4 + 5x 3 - 11x 2 - 20x + 12 = 0
Per prima cosa devi trovare una radice usando il metodo di selezione. Di solito è un divisore del termine libero. In questo caso, i divisori del numero 12 Sono ±1, ±2, ±3, ±4, ±6, ±12. Iniziamo a sostituirli uno per uno:
1: 2 + 5 - 11 - 20 + 12 = -12 ⇒ numero 1
-1: 2 - 5 - 11 + 20 + 12 = 18 ⇒ numero -1 non è una radice di un polinomio
2: 2 ∙ 16 + 5 ∙ 8 - 11 ∙ 4 - 20 ∙ 2 + 12 = 0 ⇒ numero 2 è la radice del polinomio
Abbiamo trovato 1 delle radici del polinomio. La radice del polinomio è 2, il che significa che il polinomio originale deve essere divisibile per x-2. Per eseguire la divisione dei polinomi utilizziamo lo schema di Horner:
| 2 | 5 | -11 | -20 | 12 | |
| 2 |
I coefficienti del polinomio originale vengono visualizzati nella riga superiore. La radice che abbiamo trovato è posizionata nella prima cella della seconda riga 2. La seconda riga contiene i coefficienti del polinomio risultante dalla divisione. Si contano così:
| Nella seconda cella della seconda riga scriviamo il numero 2, semplicemente spostandolo dalla cella corrispondente della prima riga. | ||||||||||||
| 2 ∙ 2 + 5 = 9 | ||||||||||||
| 2 ∙ 9 - 11 = 7 | ||||||||||||
| 2 ∙ 7 - 20 = -6 | ||||||||||||
| 2 ∙ (-6) + 12 = 0 |
L'ultimo numero è il resto della divisione. Se è uguale a 0, allora abbiamo calcolato tutto correttamente.
2x 4 + 5x 3 - 11x 2 - 20x + 12 = (x - 2)(2x 3 + 9x 2 + 7x - 6)
Ma questa non è la fine. Puoi provare ad espandere il polinomio allo stesso modo 2x 3 + 9x 2 + 7x - 6.
Anche in questo caso cerchiamo una radice tra i divisori del termine libero. Divisori di numeri -6 Sono ±1, ±2, ±3, ±6.
1: 2 + 9 + 7 - 6 = 12 ⇒ numero 1 non è una radice di un polinomio
-1: -2 + 9 - 7 - 6 = -6 ⇒ numero -1 non è una radice di un polinomio
2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 - 6 = 60 ⇒ numero 2 non è una radice di un polinomio
-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) - 6 = 0 ⇒ numero -2 è la radice del polinomio
Scriviamo la radice trovata nel nostro schema Horner e iniziamo a riempire le celle vuote:
| Nella seconda cella della terza riga scriviamo il numero 2, semplicemente spostandolo dalla cella corrispondente della seconda riga. | ||||||||||||||||||
| -2 ∙ 2 + 9 = 5 | ||||||||||||||||||
| -2 ∙ 5 + 7 = -3 | ||||||||||||||||||
| -2 ∙ (-3) - 6 = 0 |
Pertanto, abbiamo fattorizzato il polinomio originale:
2x 4 + 5x 3 - 11x 2 - 20x + 12 = (x - 2)(x + 2)(2x 2 + 5x - 3)
Polinomio 2x2 + 5x - 3 può anche essere fattorizzato. Per fare questo, puoi risolvere l'equazione quadratica attraverso il discriminante, oppure puoi cercare la radice tra i divisori del numero -3. In un modo o nell'altro arriveremo alla conclusione che la radice di questo polinomio è il numero -3
| Nella seconda cella della quarta riga scriviamo il numero 2, semplicemente spostandolo dalla cella corrispondente della terza riga. | ||||||||||||||||||||||||
| -3 ∙ 2 + 5 = -1 | ||||||||||||||||||||||||
| -3 ∙ (-1) - 3 = 0 |
Pertanto, abbiamo scomposto il polinomio originale in fattori lineari.
- In contatto con 0
- Google+ 0
- OK 0
- Facebook 0
